오늘 리뷰할 논문은 BigGAN 논문이다. GAN의 크기, batch size도 키우고 데이터셋인 ImageNet도 커서 BigGAN이라고 이름붙인 것 같다.
너무 다양한 기법을 사용해서 이해도가 낮다.
아래 포스트를 먼저 보면 도움이 될 것이다.
- [논문] GAN ; BigGAN (Large Scale GAN Training for High Fidelity Natural Image Synthesis)
- [ICLR2019]BIGGAN-Large Scale GAN Training for High Fidelity Natural Image Synthesis
- PR-108 "Large Scale GAN Training for High Fidelity Natural Image Synthesis" BigGAN Review (2019 ICLR)(GAN)
Summary
GAN은 다양하고 퀄리티 좋은 이미지를 생성하게 발전했지만 여전히 ImageNet 같은 크고 복잡한 데이터셋은 잘 학습하지 못한다. 논문은 여태까지 시도된 것 중 largest scale에서 GAN을 학습하고 이 scale에서 불안정성을 연구한다. 또 논문은 generator에 orthogonal regularization를 적용하는 것이 간단한 "truncation trick"를 잘 받아들이도록 해서 generator input의 variance를 감소시킴으로써 sample fidelity와 variety 사이 trade-off를 미세조정 가능하게 함을 찾았다. 이는 class-conditional image synthesis에서 SOTA 결과를 얻었다.
논문은 ImageNet 학습을 통해 real-word image와 GAN이 생성한 image 사이 fidelity/variety의 차이를 줄이는 것을 목표로 한다.
논문의 기여는 다음과 같다.
- GAN이 scaling으로 크게 이득을 본다는 것을 입증한다. 기존의 art(SOTA 모델을 의미하는 듯)에 비해 2~4배 많은 parameter와 8배 큰 batch size로 학습한다. scalability를 향상시키는 두 간단한, 일반적인 architectural changes를 소개하고 conditioning을 향상시키기 위해 regularization scheme을 수정해서 성능을 높인다.
- 위의 수정으로 인해 모델이 "truncation trick"에 적합해지는데(amenable), 이는 sample variety와 fidelity 사이 tradeoff를 명시적으로 미세조정할 수 있게 하는 simple sampling technique이다.
- large scale GANs에 특수한 불안정성을 발견하고 경험적으로 characterize한다. 새로운 기술과 기존의 기술을 조합해서 이 불안정성을 감소할 수 있음을 보이고, 그러나 complete training stability는 성능의 큰 손해가 있어야만 가능함도 보인다.
이제 GAN에 scaling up을 하는 방법을 알아보자. baseline으로는 hinge loss를 사용하는 SAGAN을 사용했다. class information은 G에 class-conditional BatchNorm로 전달하고 D에 projection으로 전달한다. optimization settings은 Zhang et al.을 따르되 learning rate를 절반으로 하고 G step당 D step 2번을 한다. 평가를 위해 Karras et al.을 따라 moving averages of G’s weights를 사용한다. Orthogonal Initialization을 사용한다. (detail 이하 생략)
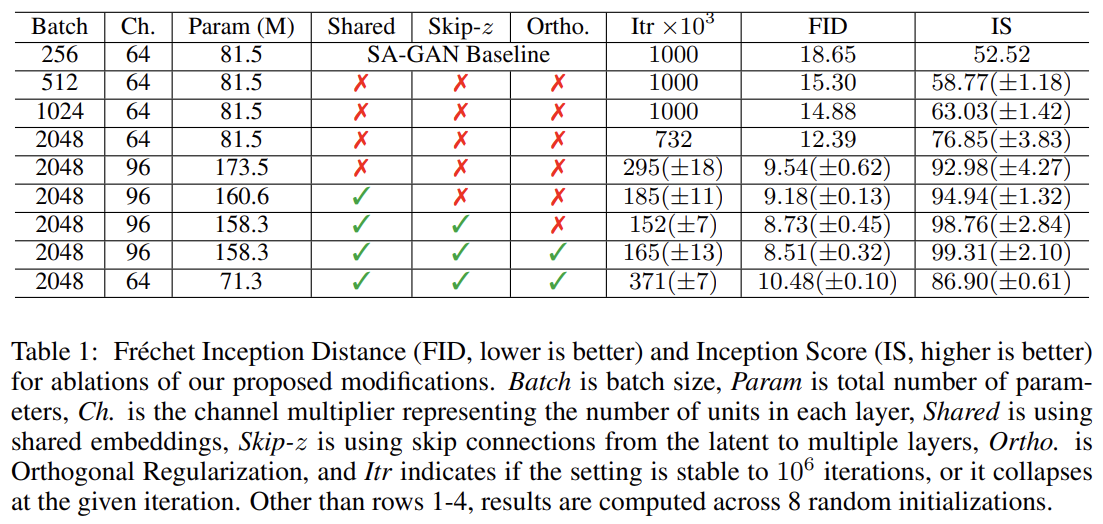
우선 baseline 모델의 batch size를 키우는 것부터 시작하며 여기서 큰 이점을 찾았다. Tab 1은 단순히 batch size를 8배로 키우는 것이 SOTA IS(inception score)를 46% 향상시킴을 보여준다. 이는 각 batch가 더 많은 mode를 cover함으로써 G와 D 모두에 더 좋은 gradient를 제공하기 때문으로 추측된다. 모델은 더 적은 iteration으로 final performance에 도달할 수 있지만 더 unstable하며 complete training collapse를 겪는다.
다음으로 각 layer에서 width (=number of channels)를 50% 늘려 두 model에서 parameter 수를 2배로 늘린다. 이는 IS를 21% 늘리며 dataset 복잡도에 비해 model capacity가 늘었기 때문으로 추측된다.
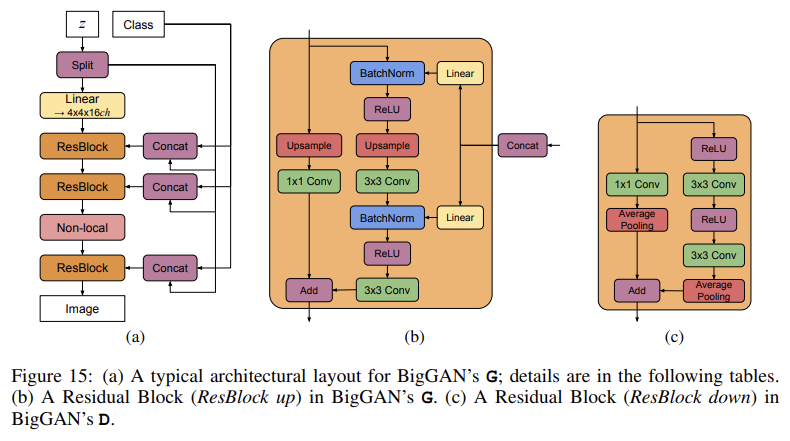
G에서 conditional BatchNorm layers에 사용되는 class embeddings c는 weights 수가 크다. 각 embedding에 서로 다른 layer를 사용하는 대신 논문은 각 layer의 gains와 biases에 linearly project되는 shared embedding를 사용한다. 이는 memory와 computation 비용을 줄여주고 학습 속도를 37% 향상시킨다. 다음으로 noise vector z를 (initial layer에만 넣는 게 아니라) G의 multiple layers로 잇는 direct skip connections (skip-z)을 추가한다. 이는 G가 다양한 resolution과 level of hierarchy에서 latent space를 사용해 직접 feature을 영향줄 수 있게 한다. BigGAN에서 이는 z를 resolution 당 one chunk로 split하고 각 chunk를 (BatchNorm gains와 biases로 project될) conditional vector c에 concatenate하는 식으로 구현된다. BigGAN-deep에선 더 간단한 디자인을 사용했는데, chunk로 split하지 않고 z 전체를 c에 concatenate한다. skip-z는 성능을 약 4% 향상시키고 training speed를 18% 향상시킨다.

이제 variety와 fidelity를 trade-off하는 truncation trick에 대해 알아보자. 기존의 GAN은 prior p(z)로 N(0, 1)이나 U[−1, 1]를 사용한다. 그러나 논문은 이 선택의 optimality에 의문을 가졌다(N(0, 1)의 경우 분포 그래프에서 알 수 있듯이 가장자리로 갈수록 likelihood가 낮아져 나올 가능성이 낮아진다). 놀랍게도 최고의 result는 sampling에 training에서와 다른 latent distribution를 사용할 때 얻을 수 있었다. z ~ N(0, 1)로 학습하고 truncated normal(range 바깥의 value는 range 안에 떨어지도록 resample함)에서 z를 sampling한 모델이 IS와 FID의 성능 향상이 있었다. 이를 truncation trick이라 부르는데, threshold보다 큰 magnitude를 가지는 values를 resampling함으로써 z vector을 truncating하는 것이다. 이는 전체적인 sample variety 감소를 대가로 sample quality를 늘리는 효과가 있다. threshold가 감소될수록 z의 원소가 0으로 truncate되고 individual samples이 mode of G’s output distribution로 근접한다.
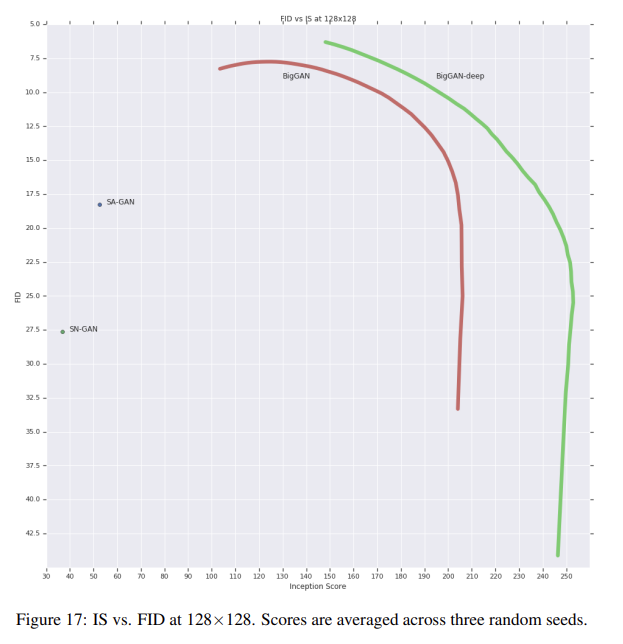
이 기술은 sample quality와 variety 사이 trade-off의 fine-grained, post-hoc selection를 가능하게 한다. Fig 17은 threshold 변화에 따라 FID와 IS의 변화를 그린 variety-fidelity curve다. IS가 variety의 부족을 penalize하지 않기 때문에 threshold를 낮추면 (variety는 감소하고 quality가 증가해서) IS가 증가한다. FID는 variety 부족을 penalize하고 precision을 reward해서 초기엔 FID가 증가하지만 truncation이 0에 근접할수록 variety가 줄어서 FID가 가파르게 감소한다.
그러나 training과 다른 latent에서 sampling하는 것으로 인해 발생한 distribution shift는 많은 모델에서 문제가 된다. 몇몇 모델은 truncated noise를 주면 Fig 2b처럼 saturation artifact를 발생시킨다. 이 문제를 해결하고자 G가 smooth하도록 conditioning하여 full space of z가 좋은 output samples로 map되게 할 것이다. 이는 orthogonality condition을 강제하는 Orthogonal Regularization를 이용한다.

W는 weight matrix이고 β는 hyperparameter이다. 이 regularization은 종종 너무 제한적이라고 알려졌기 때문에 constraint를 완화하기 위해 디자인된 여러 변형을 탐구했다. 그중 가장 잘 작동하는 버전은 diagonal terms을 제거하고 filters 사이 pairwise cosine similarity를 최소화하되 그들의 norm을 제한하지 않는 버전이었다.
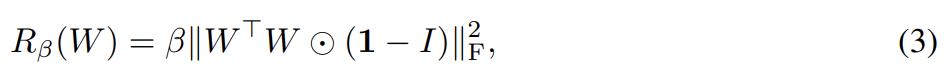
1은 모든 원소가 1인 matrix다. β는 를 선택했다. Tab 1을 보면 Orthogonal Regularization 없이는 모델 중 오직 16%만 truncation이 적합했는데 Orthogonal Regularization을 하면 60%가 적합함을 볼 수 있다.
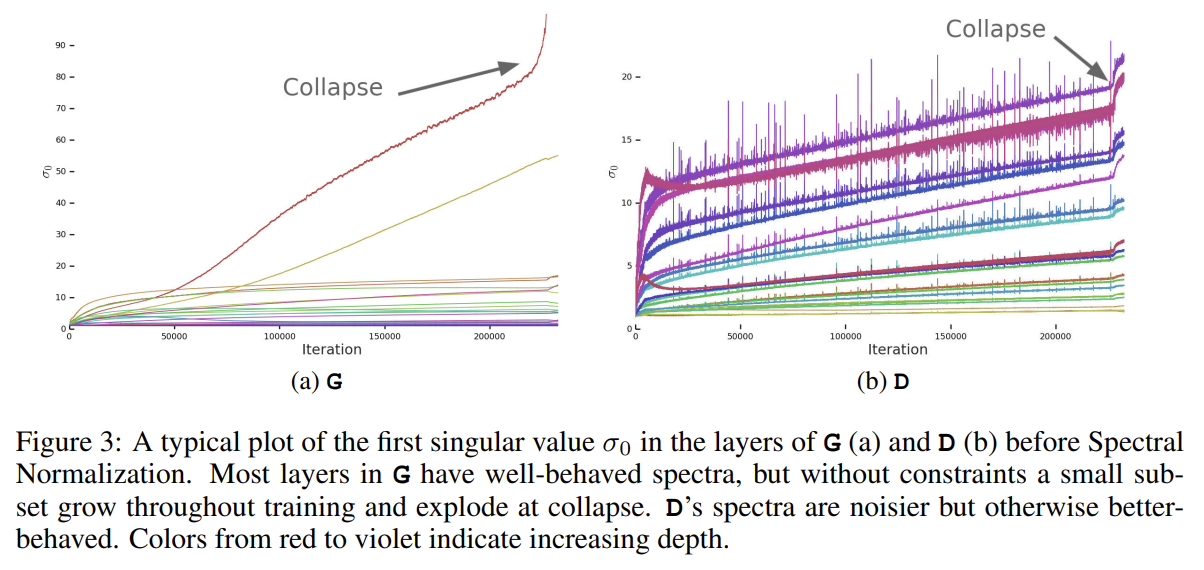
그럼에도 BigGAN은 training collapse를 겪는데, 이제 기존에는 잘 작동했던 setting이 왜 큰 크기에서 unstable한지 알아보자.
논문은 training 중 weight, gradient, loss statistics를 추적해 training collapse의 전조가 되는 metric을 찾고자 했다. 논문은 각 weight matrix의 top three singular values σ0, σ1, σ2가 가장 유용하다고 밝혔다. 이들은 Alrnoldi iteration method를 통해 효율적으로 계산 가능하다. Fig 3a에서 볼 수 있듯 뚜렷한 패턴이 나타난다. G의 대부분 layer은 잘 작동하는 spectral norm을 가졌으나 몇 layer은 (일반적으로 over-complete하고 not convolutional한, G의 첫 layer) 잘 작동하지 않았고 spectral norm이 training 중에 계속 증가하다가 collapse에서 폭발한다. 또 이게 collapse의 원인인지 단순히 현상인지도 탐구하는데 이에 관해서는 생략하겠다.
G처럼 D도 spectra of D’s weights를 분석하고 추가 constraint를 부과해서 training을 안정화하고자 한다. Fig 3b는 D의 σ0를 그린 것이다. G와 달리 spectra가 noisy하고 σ0/σ1가 잘 동작하며 singular values는 training 도중 증가하지만 collapse에서 explode하는 대신 jump한다.
spikes in D’s spectra는 D가 주기적으로 아주 큰 gradient를 받음을 추측하나 관찰 결과 Frobenius norms는 smooth했다. 이는 이 효과가 주로 top few singular directions에 집중됨을 시사한다. 논문은 노이즈가 (G가 주기적으로 D를 강력히 동요시키는 batches를 생성하는) adversarial training process를 통한 optimization의 결과라고 상정했다. spectral noise가 인과적으로 불안정성과 관련된다면 natural counter는 명시적으로 D’s Jacobian의 변화를 regularize하는 gradient penalty를 사용하는 것이다. 논문은 R1 zero-centered gradient penalty를 사용했다.
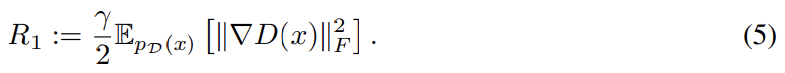
γ strength는 default를 10으로 두었다. training은 stable해지고 G와 D 모두 spectra의 smootheness와 boundedness가 향상되었으나 성능은 꽤 감소했다(IS 45% 감소).
또 D의 loss가 training 중 0으로 접근하다가 collapse에서 sharp upward jump를 겪음을 발견했다. 가능한 한 설명은 D가 training set에 overfitting되어 training exmample을 memorize한다는 것이다. Gulrajani et al.에 관련된 간단한 테스트를 해 본 결과 실제로 D가 overfit되어있ㅇ므을 확인했다.
요약하자면 논문은 stability가 G나 D에서 단독으로 얻어지는 게 아니라 adversarial training process를 통한 상호작용에서 옴을 찾았다. poor conditioning으로 인한 증상은 불안정성을 추적하는 데 사용할 수 있지만, reasonable conditioning을 보장하는 것은 training에 필요하지만 training collapse를 방지하는 데는 불충분함이 증명되었다. D를 강력하게 제약함으로써 stability를 강제할 수는 있지만 대신 성능이 급격히 하락했다.

실험은 ImageNet ILSVRC 2012에 128×128, 256×256, 512×512 resolutions으로 Tab 1 8행의 세팅으로 평가했다. IS와 FID는 Tab 2에 있다. (이하 생략)
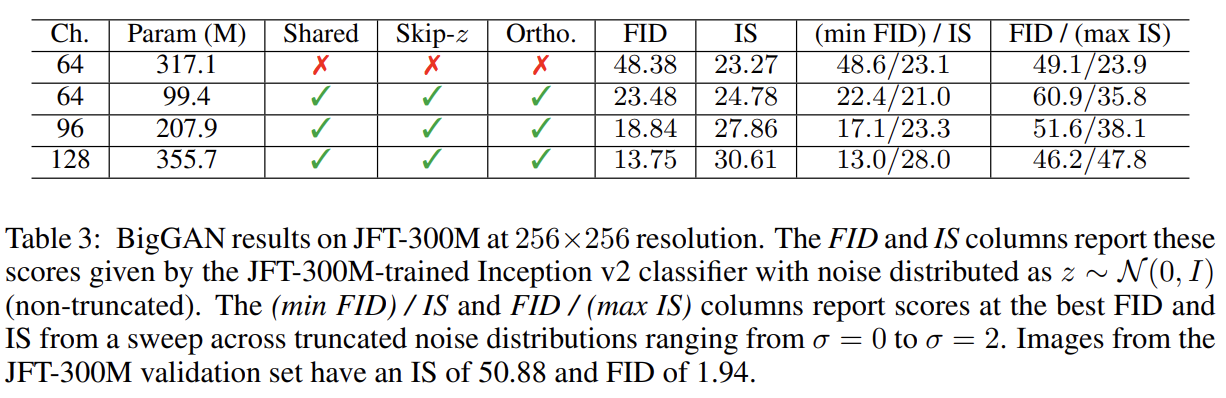
residual block의 configuration을 바꿔 BigGAN보다 4배 깊은 BigGAN-deeper 모델로도 실험했으며 모든 해상도와 metric에서 BigGAN보다 성능이 좋았다.


D가 overfit되어있다는 관찰은 G가 training point를 memorize하고 있는 게 아닌가하는 의문을 일으킨다. 이를 확인하기 위해 pre-trained classifier networks의 pixel space와 featue space에서 class-wise nearest neighbors analysis를 수행한다. 또 Fig 8, 9에서 samples 간 interpolation과 class-wise interpolation도 확인한다. BigGAN은 서로 전혀 다른 samples간 interpolate을 잘 했고 samples의 nearest neighbor도 서로 달랐다. 이는 G가 training data를 memorize하지 않음을 의미한다.
또 기존 GAN의 failure mode는 local artifacts, object 대신 texture blobs를 포함하는 images, canonical mode collapse인데 BigGAN은 Fig 4d처럼 사진이 다른 클래스의 특징도 가지는 class leakage를 관측했다. 또 ImageNet의 일부 클래스는 다른 클래스보다 학습하기 어려웠다.
BigGAN이 더 크고 복잡한 dataset에도 효과적임을 보이고자 JFT-300M dataset에도 실험한다. 설명은 생략하겠다.
Strengths
- 큰 데이터셋, 큰 모델, 큰 batch size에서 학습을 성공했다.
Weaknesses
- 논문에서 특징으로 내세우는 "quality와 variety의 trade-off"는 장점이라기보다는 quality와 variety 둘을 모두 잡지 못한 한계점 같다.
- 학습 안정을 위해 여러 기법을 사용했지만 여전히 학습이 불안정하다.
사실 참신하기보다는 여러 기술을 잡탕으로 사용한 느낌이라 논문 이해도 어려웠고 결과도 그닥 흥미롭지 않았다.