오늘 리뷰할 논문은 Wasserstein GAN, WGAN 논문이다. 기존 GAN은 두 확률 분포 비교를 위해 KL Divergence를 사용했는데 WGAN은 Wassestein Distance(EM distance)를 도입했다.
사실 논문에 수학적인 내용이 많아 리뷰 이해도가 낮다. 수학싫어
아래 포스트를 먼저 읽으면 도움이 될 것이다.
Summary
unsupervised learning은 probability distribution, 즉 probability density를 학습하는 것이다. 이는 parametric family of densities ()를 정의하여 data examples x에 대한 아래 likelihood 식을 maximize하는 것이다.
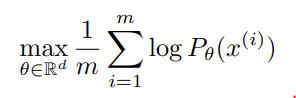
real data distribution 이 density고 가 parametrized density 의 distribution일 때 점근적으로 위 식은 두 분포의 Kullback-Leibler divergence 를 최소화하는 것과 같다.
존재하는지도 모르는 의 density를 추측하기보다 fixed distribution p(z)를 따르는 random variable Z를 정의해서 (일반적으로 neural network인) parametric function 에 넣어 를 따르는 sample을 직접 생성할 수 있다. θ를 바꾸는 것으로(즉 network의 parameter을 최적화하는 것으로) distribution 를 real data distribution 에 가깝게 바꿀 수 있다. VAE와 GANs가 이러한 방식의 예시다.
논문에선 여러 distance/divergence 을 정의해 model distribution과 real distribution가 얼마나 가까운지 측정하는 방법들에 집중한다.
논문의 기여는 다음과 같다.
- Earth Mover (EM) distance가 다른 유명한 distance/divergence에 비해 (distribution을 학습한다는 관점에서) 어떻게 다른지 포괄적인 이론적 해석을 제공한다.
- EM distance를 최소화하는 Wasserstein-GAN을 정의해 상응하는 optimization problem이 타당(sound)하다는 것을 이론적으로 보인다.
- WGANs이 GANs의 주요 training problems을 해결함을 경험적으로 보인다. 즉, WGANs의 학습은 generator과 discriminator 사이 조심스러운 balance나 조심스러운 network architecture 디자인이 필요하지 않다. GANs의 mode dropping phenomenon도 극적으로 감소했다. WGANs의 가장 강력한 장점 중 하나는 discriminator을 optimality까지 학습하며 EM distance를 연속적으로(continuously) 추정가능하다는 것이다. learning curves을 plotting하는 것은 debugging과 hyperparameter searches에 유용할 뿐 아니라 observed sample quality(즉 생성한 이미지의 품질)과도 현저한 상관관계가 있다.
다음으로 논문은 여러 distance를 소개한다. notation에 대한 설명은 아래와 같으며 이 포스트에서 무단으로(...) 가져왔다.

4종류의 distance는 다음과 같다.
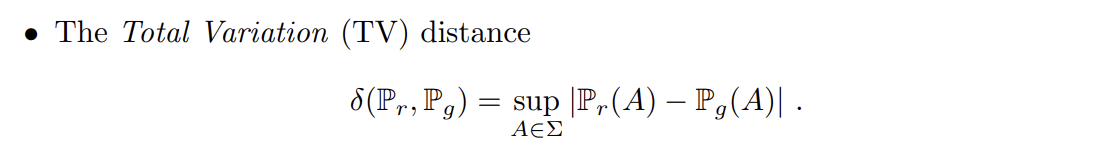
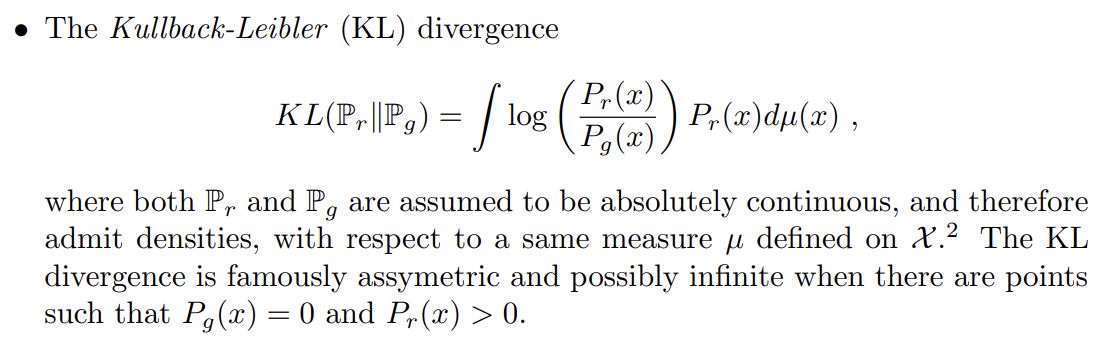


논문은 Example 1을 통해 EM distance에서는 probability
distributions이 수렴(converge)하지만 다른 distance/divergence는 수렴하지 못함을 보여준다. 다른 distance/divergence는 loss function이 연속조차 아니라서 probability distribution이 수렴할 수 없다.

Wasserstein distance이 JS distance보다 약하므로 이 가벼운 가정 아래 θ에 대한 continuous loss function이 되는지 의문일 수 있다. 이는 참이며, Theorem 1을 통해 증명된다.

Corollary 1은 EM distance를 최소화하는 식으로 학습하는 것이 neural network에서 타당하게 작동함을 보여준다.
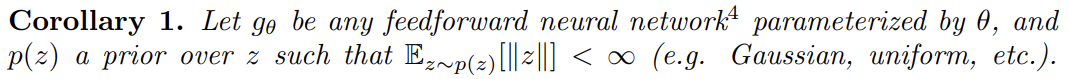
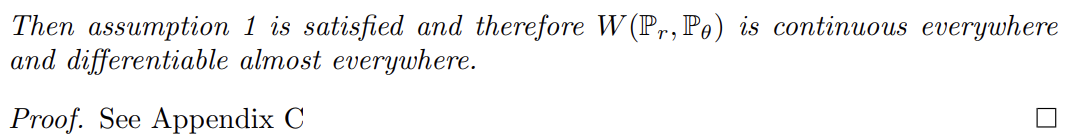
이 모든 것이 EM이 적어도 Jensen-Shannon divergence보다는 실용적인 cost function임을 보여준다. Theorem 2는 여러 distances/divergences에 의해 유발된 topologies의 상대적 세기를 묘사하며 그 결과 KL이 가장 강하고, JS, TV, EM 순으로 강하다.

이는 EM distance와 달리 KL, JS, TV distances가 low dimensional manifolds에 의해 지지되는(support) distribution을 학습하는 데 실용적인 cost function이 아님을 나타낸다.
하지만 식 (1)의 하한(infimum)은 몹시 다루기 힘들다. Kantorovich-Rubinstein duality에 따르면 상한(supremum)이 모든 1-Lipschitz functions f를 넘을 때 식 (2)가 성립한다.
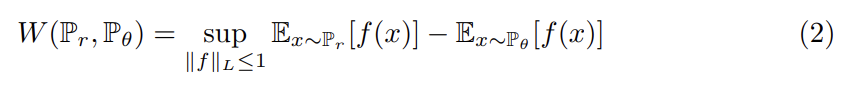
이때 어떤 상수 K에 대해 을 로 대체하면 식 (2)는 가 된다. 그러므로 어떤 K에 대해 모두가 K-Lipschitz인 parameterized family of functions 가 있다면 문제를 푸는 것을 식 (3)으로 간주할 수 있다.
만약 식 (2)의 상한(supremum)이 어떤 w ∈ W에 대해 달성된다면 이 과정은 의 연산을 multiplicative constant로 산출한다. 또 의 미분을, 를 추청하는 것을 통한 식 (2)의 back-proping으로 간주할 수 있다. 이 intuition을 (optimality assumption 하에) Theorem 3에서 증명한다.

이제 식 (2)의 최대화 문제를 푸는 f를 찾는 게 문제다. 이를 대략적으로 근사하기 위해서 일반적인 GAN처럼 compact space W 내의 weiths w를 parameter로 가지는 neural network를 로 backprop하여 학습할 수 있다. WGAN 알고리즘은 다음과 같다.

(중간 생략)
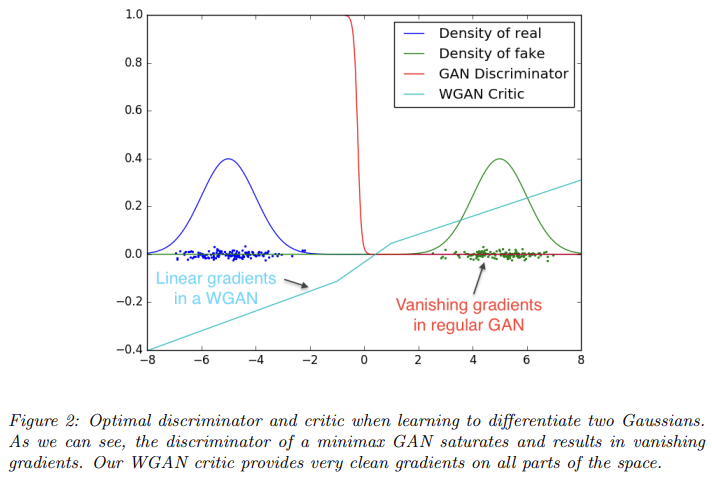
Fig 2는 GAN discriminator와 WGAN critic(=WGAN의 discriminator 역할 함수 )을 optimality까지 학습한 결과다. GAN의 discriminator은 fake/real 구분을 아주 빠르게 학습하고 reliable gradient information을 제공하지 못한다. 반면 critic은 saturate하지 못하고 linear function으로 수렴하여 모든 곳에서 clean gradients을 제공한다.
WGAN의 image generation 실험 결과 다음과 같은 두 장점이 있었다.
- generator의 convergence와 sample quality와 상관관계가 있는 의미있는 loss metric
- optimization process의 향상된 stability
실험은 LSUN-Bedrooms dataset [24]을 학습하게 했고 DCGAN을 baseline으로 삼았다.
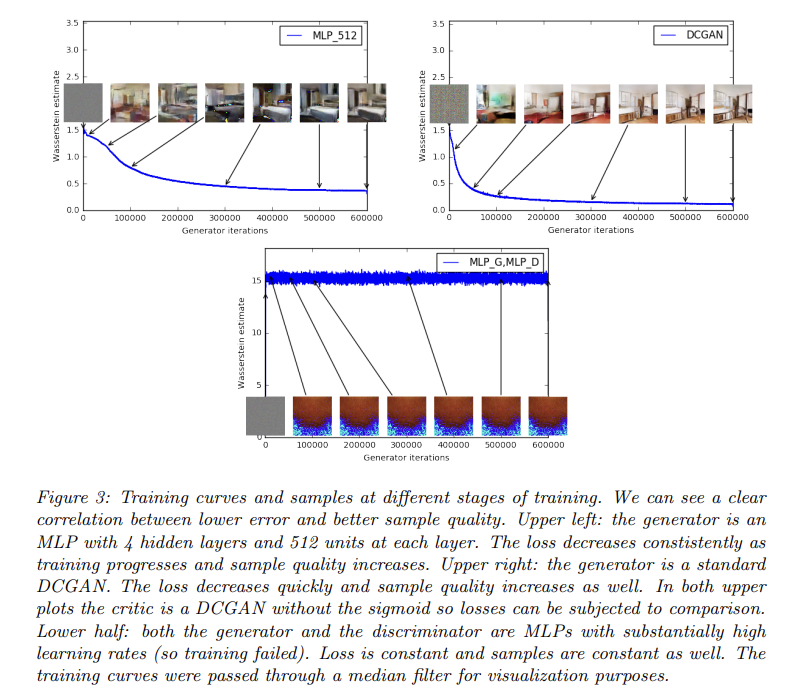
Fig 3은 DCGAN과 MLP에 EM distance의 추정을 loss function으로 삼아 학습한 것이다. plot된 곡선은 Wasserstein estimate가 생성된 sample의 visual quality와 상관관계가 있음을 보여준다. 또 이는 지금까지의 GAN literature(문헌) 중에서 GAN의 loss가 수렴하는 특징을 최초로 보여준다. 이 특징은 (failure modes을 이해하거나 다른 모델과 성능을 비교하기 위해) 생성된 samples을 볼 필요가 없기 때문에 adversarial network를 연구할 때 몹시 유용하다.
하지만 논문은 이를 generative models의 양적 평가를 위한 새로운 방법이라고 주장하지는 않는다. critic의 architecture에 의존하는 constant scaling factor은 다른 critic을 가지는 models와의 비교를 힘들게 하기 때문이다. 또 critic이 infinite capacity이 없다는 사실은 추정값(estimate)이 실제로 EM distance와 얼마나 가까운지 알 수 없게 한다.
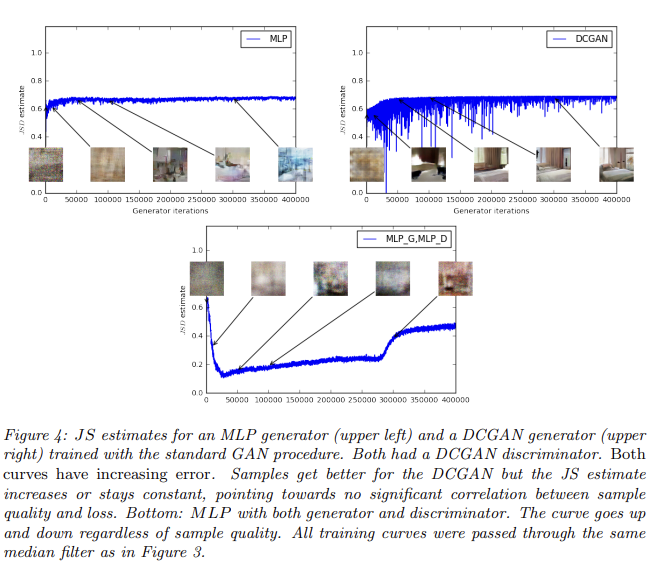
반면 Fig 4는 JS distance에 실험한 결과이며, 곡선이 sample quality와 상관관계가 적음을 보여준다. 또 JS estimate은 상수값을 유지하거나 심지어 증가하기까지 한다. 이는 JS distance가 saturate하고 discriminator이 zero loss를 가지며 생성된 samples이 일부는 의미있지만 나머지는 single nonsensical image로 붕괴함을 나타낸다.
또 WGAN이 Adam 같은 momentum에 기반한 optimizer을 사용하면 training이 unstable해진다. 그래서 논문은 대신 nonstationary problems에도 잘 작동하는 RMSProp을 사용했다.

WGAN의 장점 중 하나는 critic을 optimality까지 학습할 수 있다는 것이다. critic의 학습이 완성되면 critic은 단순히 generator에게 (다른 neural network를 학습하는 것과 같은) loss를 제공한다. 이는 generator과 discriminator의 capacity를 balance할 필요가 없음을 의미한다. critic이 좋을수록 generator을 학습하는 데 더 quality 높은 gradient를 얻을 수 있다.
Strengths
- EM distance의 추정값을 통해 GAN의 학습 과정을 효과적으로 plot할 수 있는 방법을 제시했다.
- learning stability가 향상했고 mode collapse 같은 문제가 제거되었다.