오늘 리뷰할 논문은 InfoGAN 논문이다.
아래 포스트를 먼저 보면 도움이 될 것이다.
- InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets
- InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets
- Disentanglement
InfoGAN은 비지도학습으로 disentangled representations을 학습하고 latent variables와 observation(=생성한 이미지) 사이의 mutual information을 최대화한다. 논문은 효율적으로 최적화될 수 있는 mutual information objective의 lower bound를 구한다. 특히 논문은 MNIST 데이터셋에서 writing styles과 digit shapes를 disentangle하며, SVHN 데이터셋에서 pose와 lighting of 3D rendered images을, background digits와 central digit을 disentangle한다. CelebA face 데이터셋에서 hair styles, 안경의 유무, emotions 등의 visual concepts를 발견한다.
논문은 GAN의 objective가 fixed small subset of the GAN’s noise variables와 observations 사이 mutual information을 극대화하도록 변형해 여러 이미지 데이터셋에서 highly semantic, meaningful hidden representation을 발견했다. 이는 mutual information cost로 augment된 generative modelling이 disentangled representations를 배울 수 있음을 시사한다.
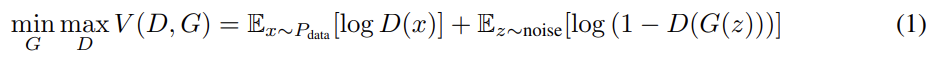
GAN은 simple factored continuous input noise vector z를 사용하는데, generator가 어떻게 z를 사용할지 제한을 두지 않는다. 그 결과 noise는 몹시 entangle된 상태로 사용되며, 즉 z의 각 dimension이 데이터의 semantic feature에 각각 대응하지 않는다는 뜻이다.
그래서 논문은 단일한 unstructured noise vector를 사용하는 대신 input noise vector를 다음과 같이 두 부분으로 분해하고자 한다.
- z : 압축할 수 없는 noise의 source
- c : latent code라고 이름붙인, data distribution의 salient structured semantic features를 traget하는 부분
Generator은 incompressible noise z와 latent code c를 함께 받아 G(z, c)의 형태가 된다. 그런데 generator은 라는 해를 찾는 방식으로 c를 무시해버릴 수도 있다. 이 문제를 다루기 위해 논문은 information-theoretic regularization를 제안한다. latent codes c와 generator distribution G(z, c) 사이 mutual information, 즉 I(c; G(z, c))가 높아야 한다는 것이다.
정보 이론에서 X와 Y 사이 mutual information I(X; Y)는 random variable Y에서 다른 random variable X에 대해(?) 얻을 수 있는 정보의 양을 나타낸다. 그리고 다음과 같이 두 엔트로피의 차로 표현한다.
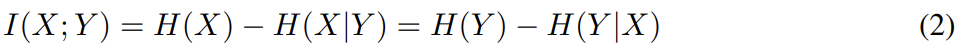
I(X; Y)의 정의는 직관적으로 이해하면 Y가 관측되었을 때 X에서 uncertainty의 감소로 볼 수 있다. X, Y가 독립이면 하나를 관찰해도 다른 하나의 정보를 얻을 수 없으므로 I=0이 된다. 반대로 X, Y가 deterministic, invertible function로 연관되어 있다면 maximal mutual information이 얻어진다.
우리는 x ~ 가 주여졌을 때 가 작은 entropy를 가지길 원한다. 다시 말해 latent code c의 정보가 generation process 중 소실되길 원하지 않는다. 따라서 논문은 다음과 같은 information-regularized minimax game을 제안한다.
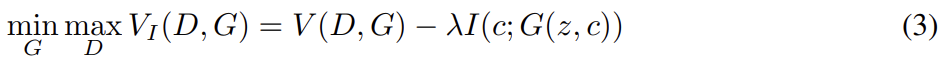
하지만 실제로는 mutual information term I(c; G(z, c))는 posterior P(c|x)가 필요하기 때문에 직접 최대화하기 어렵다. 그래서 대신 P(c|x)를 근사하는 auxiliary distribution Q(c|x)를 정의하여 lower bound를 얻을 수 있다.
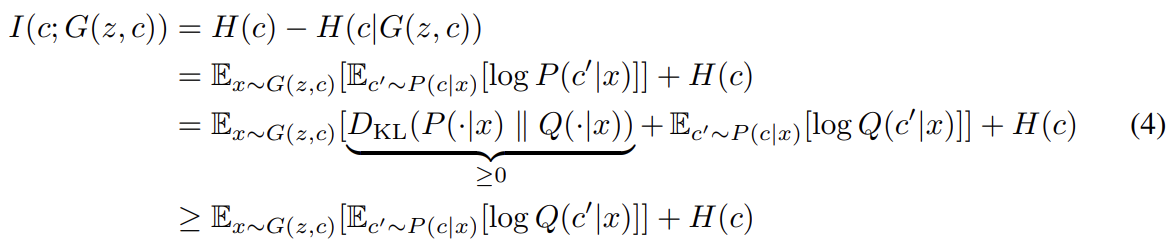
이 lower bound 방법은 Variational Information Maximization [29]이라고 불린다. (P(c|x)를 안 사용하게 우회하려 하는데) 하지만 여전히 기댓값 항 내부에서 posterior P(c|x)로부터 sample을 해야하니 다음의 lemma를 사용해 variational lower bound 를 정의한다.
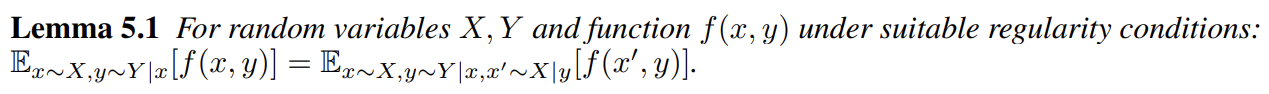
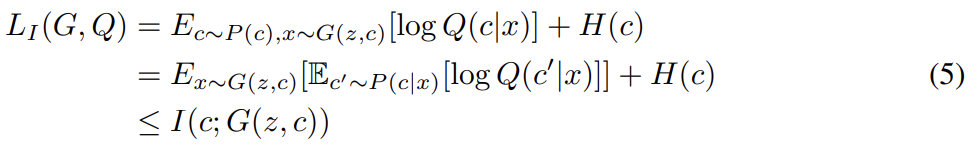
는 Monte Carlo simulation으로 쉽게 시뮬레이션 가능하다. 특히 은 Q에 관해서는 직접 최대화될 수 있고 G에 관해서는 reparametrization trick을 통해 최대화될 수 있다. 따라서 은 GAN의 training procedure에 변화 없이 GAN의 objective에 추가될 수 있다.
식 (4)는 auxiliary distribution Q가 true posterior distribution에 근접할수록 lower bound가 tight해짐을 보여준다. 그리고 discrete latent codes에 대해 이면 variational lower bound가 maximum이 되어 maximal mutual information이 얻어진다.
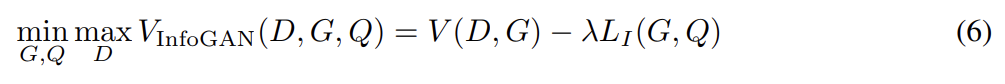
따라서 InfoGAN은 식 (6)과 같이 variational regularization of
mutual information과 hyperparameter λ를 가진 minimax game로 정의된다.
실제로는 auxiliary distribution Q를 neural network로 parametrize한다. 대부분 실험에서 Q와 D는 모든 convolutional layers를 공유하며, conditional distribution Q(c|x)를 위한 parameter를 output하는 하나의 final fully connected layer가 추가되어 GAN에 무시할 수 있는 연산량만 더한다.
categorical latent code 에 대해 를 표현하기 위해 softmax nonlinearity를 사용한다. continuous latent code 에 대해선 true posterior 가 무엇이냐에 따라 더 많은 선택지가 있는데 실험을 통해 단순히 를 factored Gaussian로 취급하는 게 효과적임을 찾았다.
extra hyperparameter λ는 tune하기 쉽고 discrete latent codes에 대해선 1로 둬도 충분하다. latent code가 continuous variables를 포함하면 differential entropy를 포함하는 가 GAN objectives와 같은 scale에 있음을 보장하기 위해 더 작은 λ를 사용한다.
GAN은 학습이 (불안정해서) 어렵다고 알려져있기 때문에 DC-GAN이 사용한 방식으로 학습을 시켰다.
실험은 두 종류로 진행했다. 첫번째 목표는 mutual information이 효과적으로 maximize되는지 조사하는 것이고 두번째 목표는 InfoGAN이 disentangled, interpretable representations을 학습하는지 확인하는 것이다. 이는 generator를 사용해 한 번에 하나의 latent factor만을 바꿔 생성된 이미지에서 semantic variation이 한 종류만 변하는지 확인하는 식으로 이루어진다.
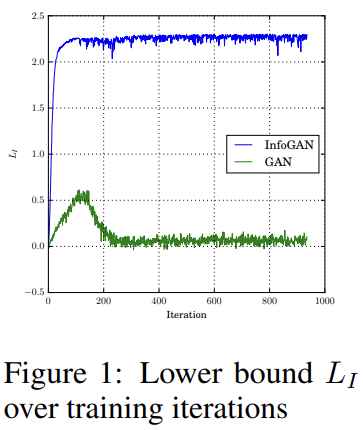
mutual information이 효과적으로 최대화되는지 확인하고자 InfoGAN을 uniform categorical distribution on latent codes c ∼ Cat(K = 10, p = 0.1)를 가진 MNIST 데이터셋으로 학습한다. Fig 1은 baseline인 GAN과 비교했을 때 InfoGAN이 bound가 tight하고 maximal mutual information를 얻었음을 보여준다.

MNIST의 digit shape와 styles을 분리하기 위해 discontinuous variation을 model하는 하나의 categorical code c1 ∼ Cat(K = 10, p = 0.1)와 continuous variations을 capture하는 두 continuous codes c2, c3 ∼ Unif(−1, 1)를 가지고 latent codes를 model했다.
Fig 2는 discrete code c1이 모양의 극단적인 변화를 포착함을 보여준다. categorical code c1를 변경하면 digit이 변하는 것이다. 이는 label 없이 비지도학습으로도 InfoGAN이 MNIST를 5% error rate로 classify할 수 있음을 보여준다.
Continuous codes c2, c3는 style의 continuous variations을 포착한다. c2는 rotation을, c3은 width를 조절한다. 흥미로운점은 generator가 단순히 rotation, width를 조절하는 게 아니라 thickness나 stroke style 등의 다른 detail도 조절해서 결과 이미지가 자연스러워 보이게 만든다는 것이다. InfoGAN이 학습한 latent representation이 일반화 가능한지 확인하고자 latent codes 범위를 [-1, 1]에서 (network가 학습한 적 없는) [-2, 2]로 바꿔도 여전히 일관된 결과를 얻었다.


다음으로 (비교대상인 DC-IGN이 highly interpretable graphics codes를 배운) 두 3D image 데이터셋, 얼굴과 의자에 InfoGAN을 평가했다.
face 데이터셋에서 DC-IGN은 supervision을 통해 azimuth (pose), elevation, lighting을 continuous latent variables로 표현하도록 학습했는데, InfoGAN도 마찬가지로 동일한 latent factor를 학습했다. DC-IGN은 supervision을 요구하기 때문에 label되지 않은 variation에 대한 latent code는 학습할 수 없었는데 InfoGAN은 그런 variation을 스스로 깨우친다. 예를 들어 Fig 3d에서 InfoGAN은 (DC-IGN이 배우지 못한) wide, narrow를 조절하는 latent code를 보여준다.
chair 데이터셋에서 DC-IGN은 rotation을 표현하는 continuous code를 학습한다. InfoGAN은 rotation을 continuous code로 표현할 수 있을 뿐 아니라 하나의 continuous code를 사용해 다른 width를 가진 비슷한 의자 종류 사이를 연속적으로 interpolate할 수도 있다.


또 Street View House Number (SVHN)와 CelebA 데이터셋에도 InfoGAN을 평가했으며 결과능 위와 같다.
Strengths
- GAN의 objective에 mutual information 항을 추가하는 간단한 방법으로 인상적인 성과를 이루었다.
- z, c를 구분하여 z로 인한 생성하는 이미지의 무작위성은 유지하면서도 c로 다양한 variation을 줄 수 있는 설계가 좋았다. 실제로 c를 조작하여 생성된 이미지의 변화를 확인하니 신기했다.
Weaknesses
- MNIST 평가한 부분에서 논문은 rotation/width를 조절하면 generator가 thickness나 stroke style 등의 다른 detail도 조절해서 결과 이미지가 자연스러워 보이게 만든다며 흥미롭다(remarkable)고 했는데, 이는 논문의 의도인 disentanglement와 정면으로 어긋나는 결과 같다. disentanglement가 정밀하다면 다른 detail 변화가 없거나 최소화되어야하는 것 아닌가? InfoGAN이 완벽하지 않음을 보여주는 예시 같다.