최단 경로_플로이드 워셜

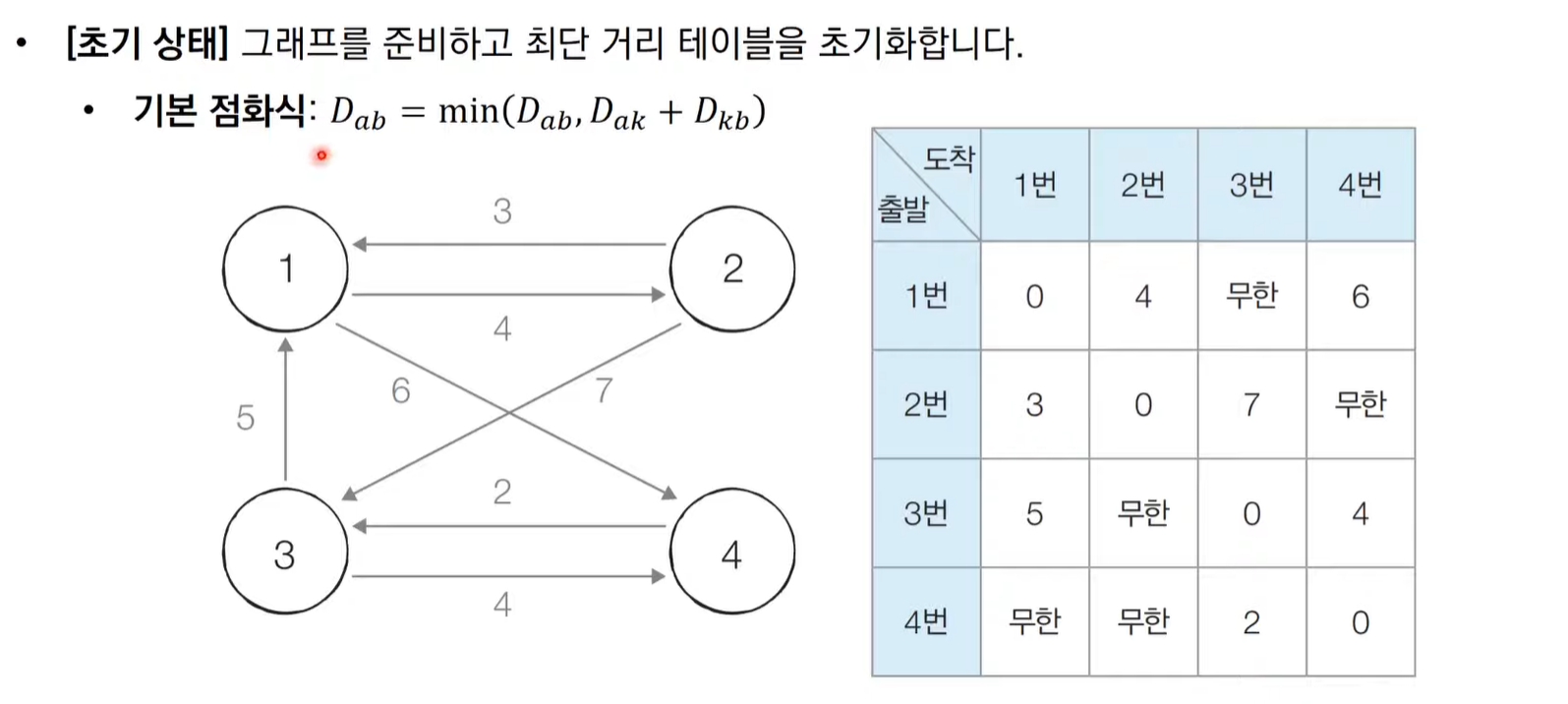
플로이드 워셜 알고리즘

• 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산
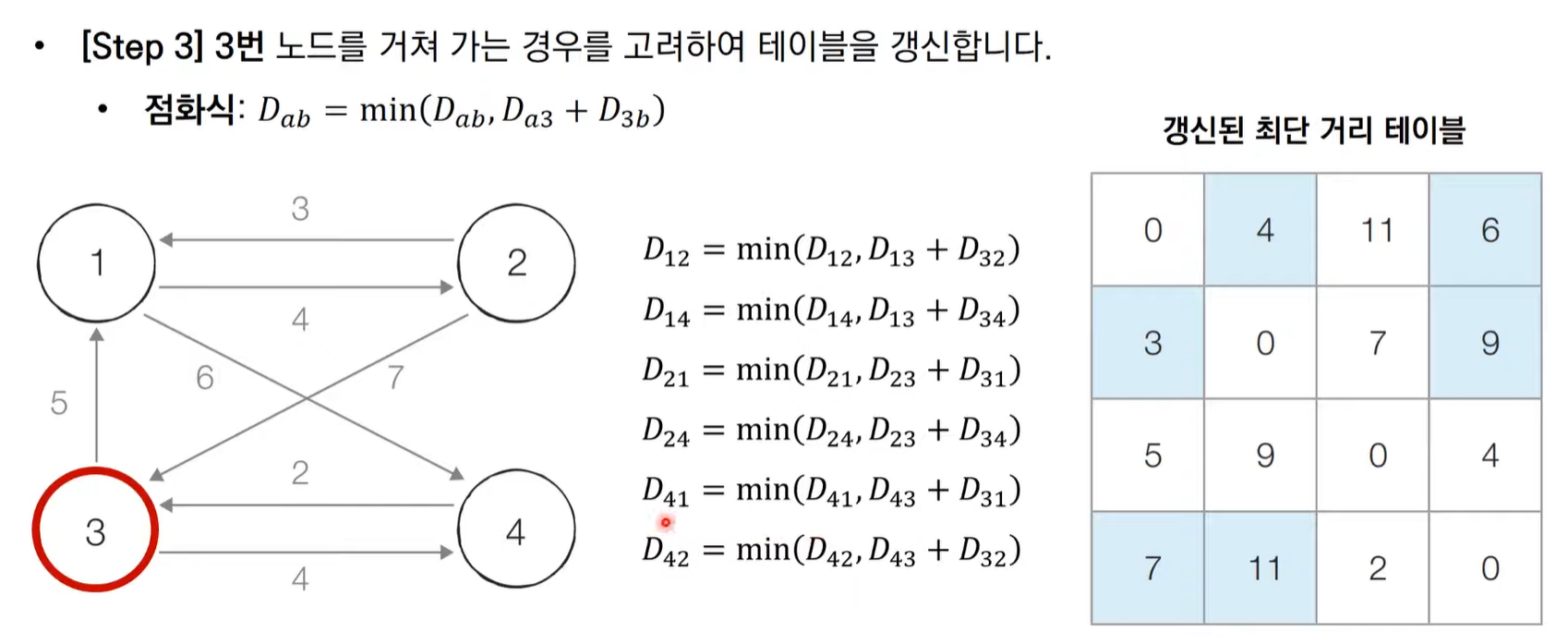
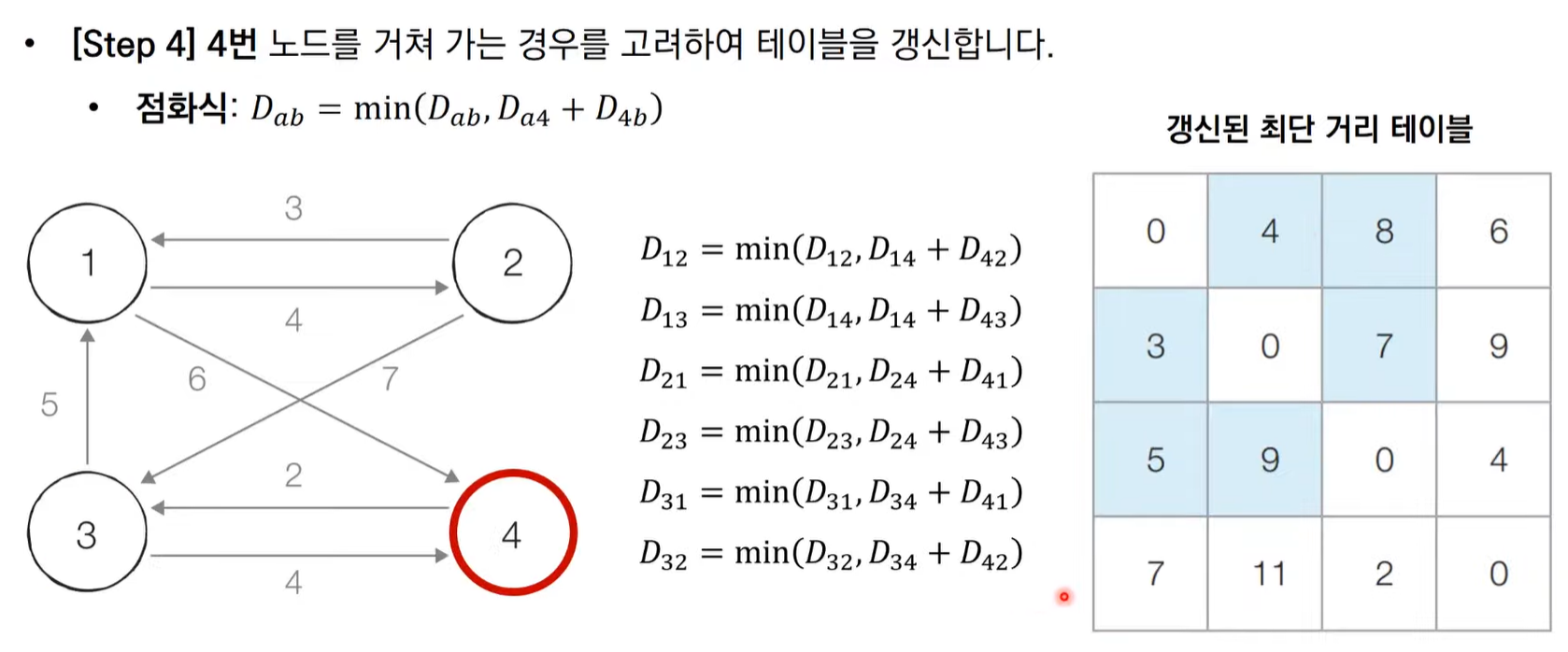
• 단계별로 거쳐가는 노드를 기준으로 알고리즘 수행
  • 다만 매 단계마다 방문하지 않은 노드 중에 최단 거리를 갖는 노드를 찾는 과정 필요 X
• 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장
• 플로이드 워셜 알고리즘은 다이나믹 프로그래밍 유형에 속함

플로이드 워셜 알고리즘 동작 과정 살펴보기

INF = int(1e9)

n = int(input())
m = int(input())
graph = [[INF] * (n+1) for _ in range(n+1)]

for a in range(1,n+1):
    for b in range(1,n+1):
        if a == b:
            graph[a][b] = 0

for _ in range(m):
    a,b,c = map(int,input().split())
    graph[a][b] = c

for k in range(1,n+1):
    for a in range(1,n+1):
        for b in range(1,n+1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

for a in range(1,n+1):
    for b in range(1,n+1):
        if graph[a][b] == INF:
            print("INFINITY", end = " ")
        else:
            print(graph[a][b], end = " ")
    print()

플로이드 워셜 알고리즘 성능 분석

문제 1: 미래 도시

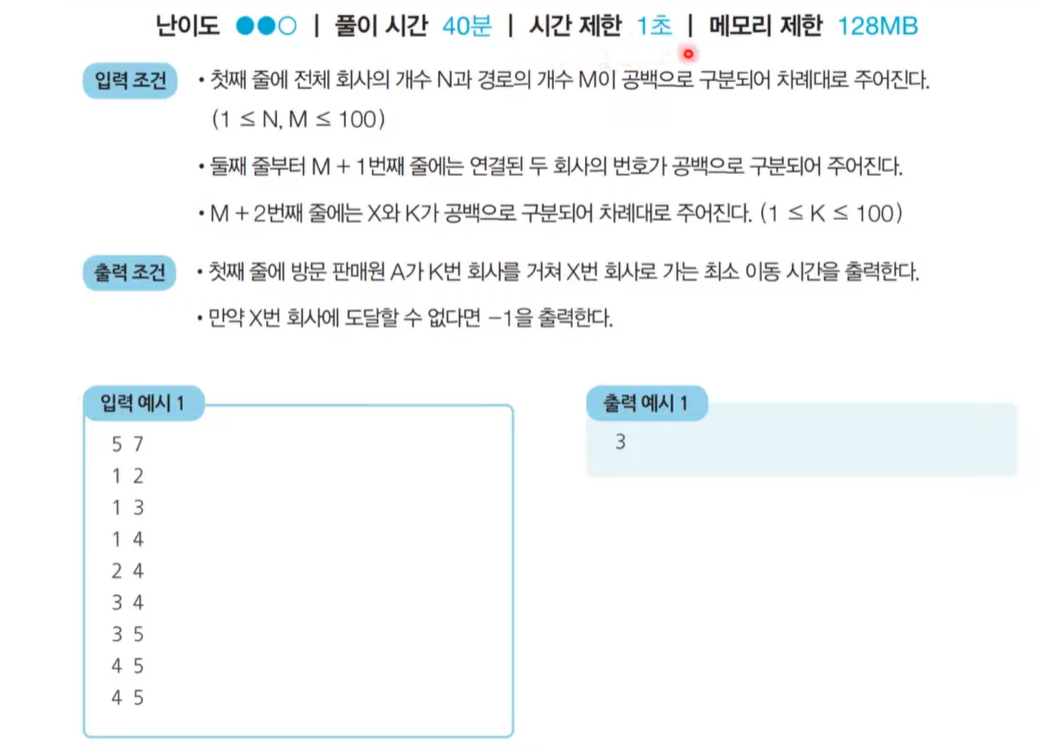
문제 풀이

INF = int(1e9)

n,m = map(int,input().split())
graph = [[INF] * (n+1) for _ in range(n+1)]

for a in range(1,n+1):
    for b in range(1,n+1):
        if a == b:
            graph[a][b] = 0

for _ in range(m):
    a,b = map(int,input().split())
    # A와 B가 서로에게 가는 비용은 1이라고 설정
    graph[a][b] = 1
    graph[b][a] = 1

x,k = map(int,input().split())

# 플로이드 워셜 알고리즘
for k in range(1,n+1):
    for a in range(1,n+1):
        for b in range(1,n+1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

distance = graph[1][k] + graph[k][x]

if distance >= INF:
    print(-1)
else:
    print(distance)