플로이드 알고리즘이란?
플로이드 알고리즘이란 그래프에서 각 정점과 가중치가 주어져 있을 때, 특정 시작 정점에서 도착 정점까지 가는 최단 비용을 의미한다.
쉽게 정리하자면 모든 정점 쌍 사이의 최단 거리를 구하는 알고리즘이다.
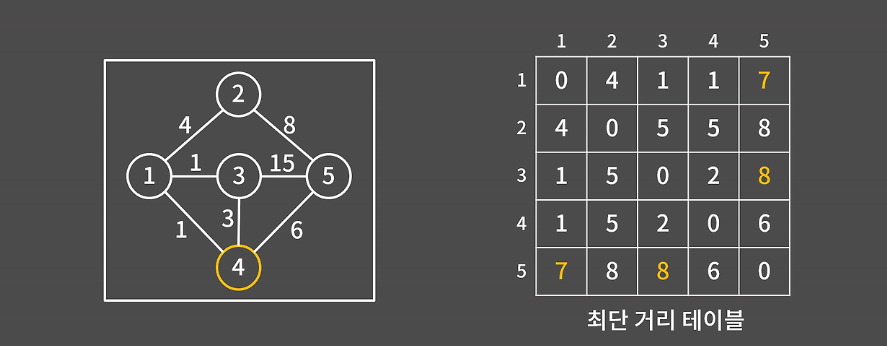
예를 들자면, 아래의 그림에서 정점3에서 정점5까지 이동한다고 할 때의 최단 비용인 8을 반환하는 것과 동일하다.
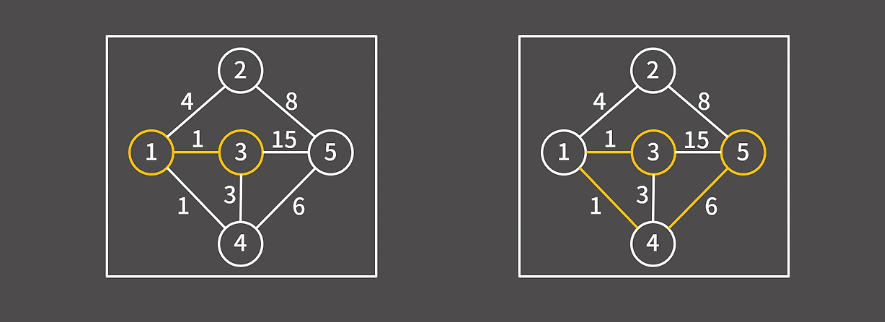
플로이드 알고리즘은 인접 행렬을 사용해 모든 정점 간 최단 거리 테이블을 구성한다.
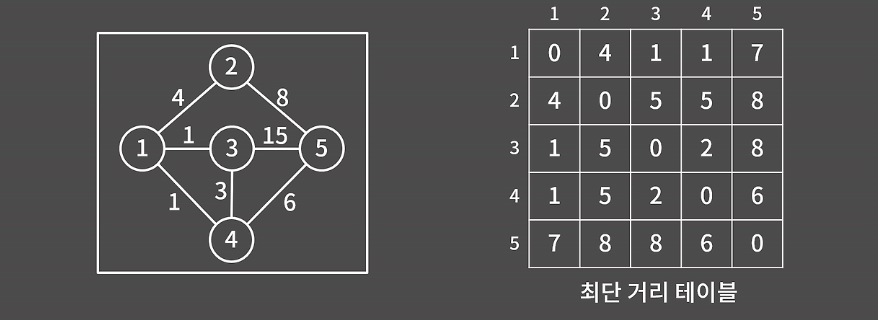
이렇게 모든 정점 간 최단 거리 테이블을 작성하기 때문에 그래프가 방향, 무방향이든 상관이 없다. 음수도 잘 적용하나 음수인 사이클이 있으면 제대로 동작하진 못한다.
최단 거리 테이블 동작 순서
위 그림의 최단 거리 테이블은 다음과 같은 순서로 동작한다.
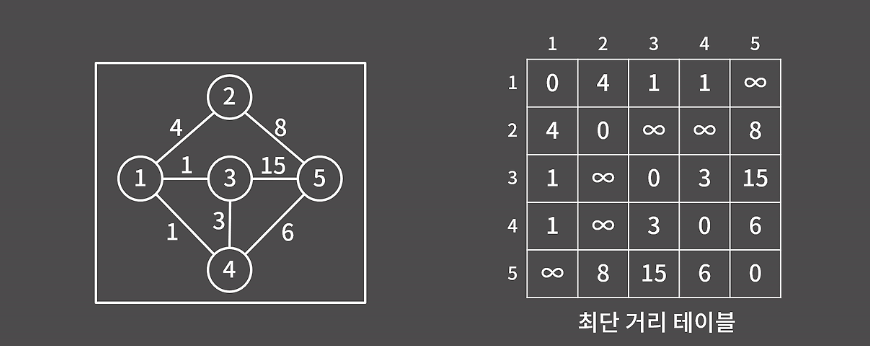
- 자기 자신으로의 거리는 0, 간선이 존재하는 정점은 해당 가중치를, 없는 경우는 무한(∞)으로 초기화한다.
- 정점 개수를 V라 할 때, 모든 시작 정점 st, 도착 정점 en, 그리고 중간 경유 정점 x에 대해 d[st][en] > d[st][x] + d[x][en]인 경우 값을 갱신한다.
설명이 조금 복잡하지만 내용 자체는 간단하기에 그림을 통해 동작 원리를 더욱 잘 파악할 수 있다.
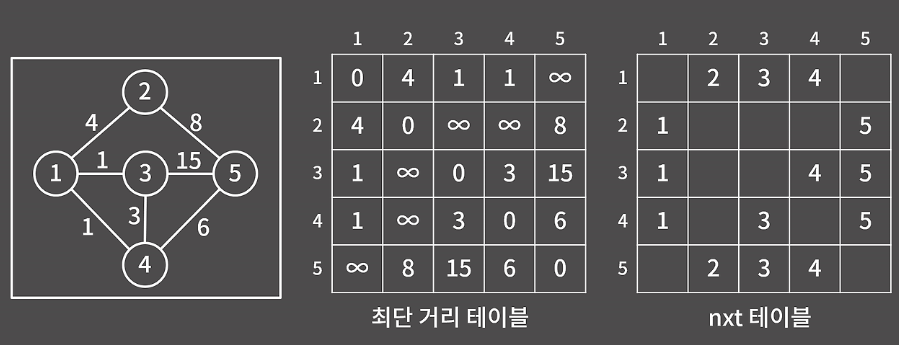
초기 테이블 값 설정
정점끼리 연결된 간선의 값을 대입하고 자기 자신은 0, 연결된 간선이 없는 경우 값을 최대로 설정한다.
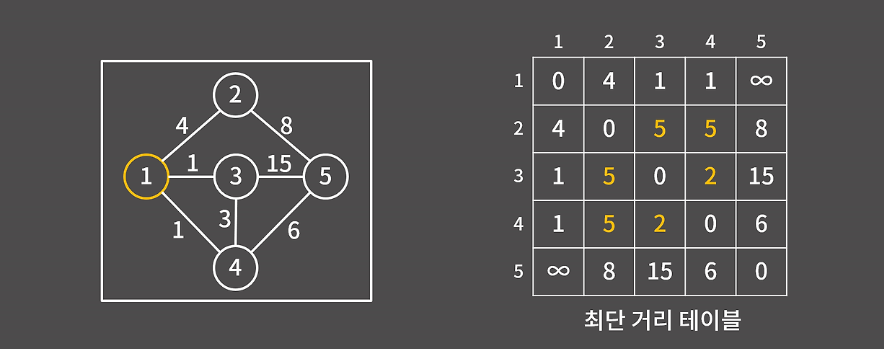
1번 정점을 경유하는 경우
그림에서 1번 정점을 경유할 때 비용이 더 작아지는 경로가 존재한다.
바로 d[2][3], d[2][4], d[3][4] 등 이렇게 연결되지 않은 정점 혹은 최단 비용으로 값이 갱신된다.
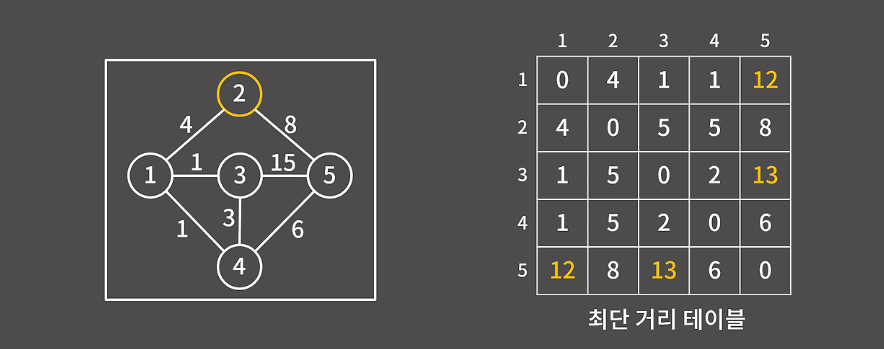
2번 정점을 경유하는 경우
2번 정점도 마찬가지로 2번 정점을 경유해서 가는 경우가 더 최단 경로일 때로 값이 갱신된다.
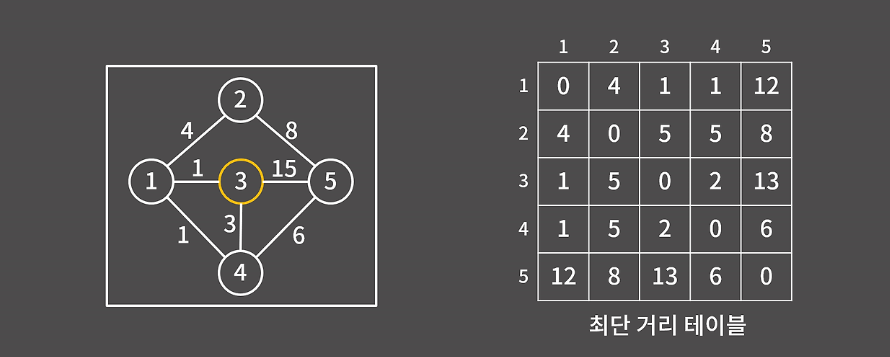
3번 정점을 경유하는 경우
3번 정점의 경유 현재 경유해서 최단으로 갱신되는 경우가 없으므로 그대로이다.
4번 정점을 경유하는 경우
4번 정점을 경유하는 경우 다음과 같이 값이 갱신된다. d[1][5]의 경우 원래 d[1][2] + d[2][5]로 값이 적용되어 있었는데 4번 정점을 경유하여 가는 게 비용이 덜 들므로 값이 갱신되었다.
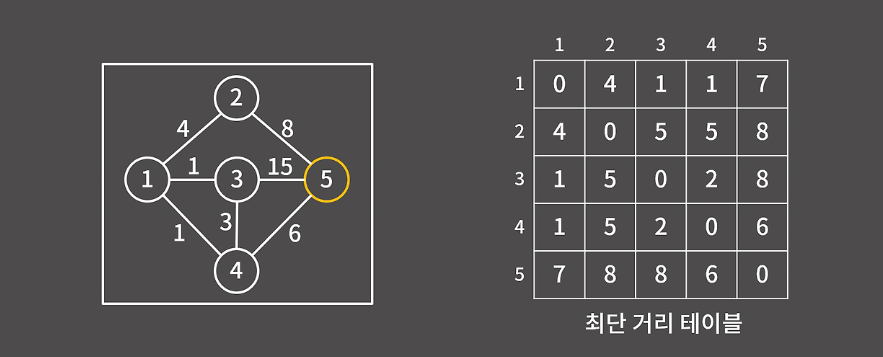
5번 정점(V)을 경유하는 경우
이미 모든 값이 갱신되어 있거나, 5번을 경유하는 게 최단 비용이 아니므로 테이블에 변화가 없다.
내용 정리
위 동작 방식과 알고리즘을 통해 코드로 구현하기 위한 알고리즘을 정리하려고 한다. 우선 위 내용의 시간 복잡도를 계산해 보면 다음과 같다.
임의의 정점을 선택한다O(V), 각 시작 정점O(V)과 도착 정점O(V)이 임의의 정점을 경유하는 것이 더 최단 비용인지를 판단하므로 총 3개의 정점을 선택하여 비교하기 때문에 시간 복잡도는 O(V^3)이 된다.
알고리즘
- 인접 행렬 초기화: 자기 자신은 0, 연결된 정점은 가중치, 나머지는 무한.
2.3중 for문으로 모든 경유 정점, 시작 정점, 도착 정점에 대해 최단 거리 비교 및 갱신.- 경유하는 것이 더 짧으면 테이블을 갱신.
경로 복원
플로이드 알고리즘은 단순히 각 정점 간 최단 비용을 찾는 알고리즘뿐만 아니라 경로도 복원할 수 있다. 방법은 경로 테이블을 설정하는 것이다.
?
최단 거리 테이블을 초기화할 때는, 시작 정점에서 도착 정점으로 바로 이동하는 경우이다.
따라서 이때의 경로는 곧 도착 정점에 직접 연결된 시작 정점이 되며, 경로 테이블은 다음과 같이 설정된다.
- nxt[st][en] = en;
플로이드의 핵심은 중간에 어떤 정점 x를 경유하는 것이 더 짧은 경로인지를 파악하는 것이다.
즉, d[st][en] > d[st][x] + d[x][en]인 경우에 st에서 en으로 바로 가는 것보다 중간 정점 x를 거쳐 이동하는 경로가 더 짧다는 의미이다.
따라서 st -> x -> en의 경로 형태가 보이는데 여기서 중요한 점은 nxt[st][en]을 단순히 x로 설정하면 안 된다는 것이다.
왜냐하면 st에서 x로 가는 경로 역시 여러 정점을 거칠 수 있기 때문이다.
즉, st → x 경로의 실제 첫 번째 이동 정점을 알아야 하므로 nxt[st][en] = nxt[st][x]로 경로 테이블을 갱신해야 한다.
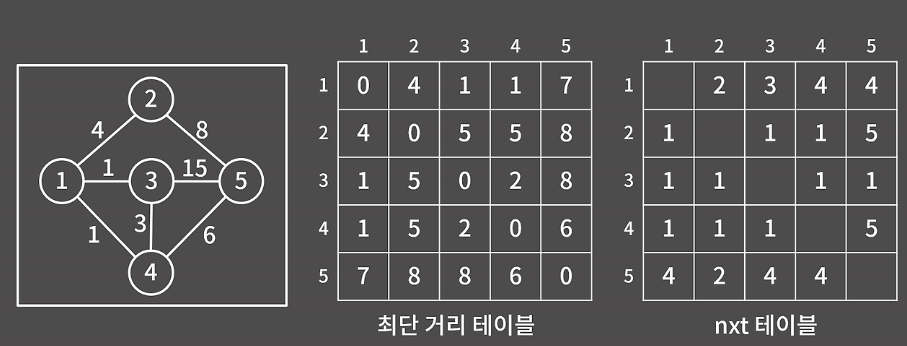
마지막으로 이 테이블을 구현하였으니 해당 테이블을 이용하여 경로를 복원하는 방법을 알아야 한다.
위 그림에서 정점 3에서 정점 5로가는 경로를 생각해 보자.
1. nxt[3][5]는 1를 반환하므로 해당 정점은 1번 정점을 경유하는 d[3][1] + d[1][5]임을 알 수 있다. 따라서 경로는 3-> 1와 nxt[1][5]을 보면 된다.
2. nxt[1][5]는 4를 반환하므로 d[1][5] = d[1][4] + d[4][5]이다.
따라서 경로는 3->1->4와 nxt[4][5]를 보면 된다.
3. nxt[4][5]를 보면 5로 nxt 테이블에서 4번 정점이 다른 정점을 경유하지 않음을 알 수 있으니 결국 경로는 3->1->4->5 임을 알 수 있다.
이를 코드로 구현하기 위한 알고리즘을 정리하면 다음과 같다.
경로 복원 알고리즘
- 시작 정점을 변수 x에 저장하고, 경로를 저장할 리스트 vec에 x를 추가한다.
- x가 도착 정점 j와 같아질 때까지 다음을 반복한다
- x = nxt[x][j]로 갱신
- vec에 x를 추가
- 반복이 끝나면 vec에는 전체 경로가 저장됨
코드
#include <bits/stdc++.h>
using namespace std;
int d[10][10];
int path[10][10];
int v, e, inf = 0x3fffffff;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> v >> e;
fill(d[0], d[v]+v+1, inf); // d[0][0] ~ d[n][n]
for(int i=0; i<e; i++)
{
int a, b, c;
cin >> a >> b >> c;
d[a][b] = c;
d[b][a] = c;
path[a][b] = b;
path[b][a] = a;
}
for(int i=1; i<=v; i++) d[i][i] = 0;
for(int k=1; k<=v; k++)
{
for(int i=1; i<=v; i++)
{
for(int j=1; j<=v; j++)
{
if(d[i][j] > d[i][k] + d[k][j])
{
d[i][j] = d[i][k] + d[k][j];
path[i][j] = path[i][k];
}
}
}
}
cout << "각 정점 간 최단 비용\n";
for(int i=1; i<=v; i++){
for(int j=1; j<=v; j++){
if(d[i][j] == inf) cout << "-1 ";
else cout << d[i][j] << ' ';
} cout << "\n";
}
cout << "경로 테이블블\n";
for(int i=1; i<=v; i++){
for(int j=1; j<=v; j++){
if(path[i][j] == 0) cout << "-1 ";
else cout << path[i][j] << ' ';
} cout << "\n";
}
cout << "경로 복원" << '\n';
for(int i=1; i<=v; i++){
for(int j=1; j<=v; j++){
if(d[i][j] == 0 || d[i][j] == inf)
{
cout << "0\n";
continue;
}
int x = i;
vector<int> vec(1,x);
while(x != j)
{
x = path[x][j];
vec.push_back(x);
}
for(auto c : vec)
cout << c << ' ';
cout << '\n';
}
}
return 0;
}
// Input
5 7
1 2 4
1 3 1
1 4 1
3 4 3
2 5 8
3 5 15
4 5 6
// Output
각 정점 간 최단 비용
0 4 1 1 7
4 0 5 5 8
1 5 0 2 8
1 5 2 0 6
7 8 8 6 0
경로 테이블블
-1 2 3 4 4
1 -1 1 1 5
1 1 -1 1 1
1 1 1 -1 5
4 2 4 4 -1
경로 복원
0
1 2
1 3
1 4
1 4 5
2 1
0
2 1 3
2 1 4
2 5
3 1
3 1 2
0
3 1 4
3 1 4 5
4 1
4 1 2
4 1 3
0
4 5
5 4 1
5 2
5 4 1 3
5 4
0마무리
플로이드 알고리즘은 구조 자체는 간단하지만 경유 정점을 활용한 테이블 갱신 방식과 경로 복원 과정은 처음에는 다소 헷갈릴 수 있다.
직접 손으로 테이블을 그려보고, 다양한 그래프에 적용해 보는 연습을 통해 알고리즘에 자연스럽게 익숙해질 것 같다.
따라서 관련 문제를 많이 풀어보며 체득해 보려 한다.
Reference
[실전 알고리즘] 0x1C강 플로이드 알고리즘 - BaaaaaaaarkingDog