위상 정렬

위상 정렬이란?

방향 그래프에서 간선이 주어진 정점 간 선후관계를 위배하지 않게끔 나열하는 정렬을 의미한다. 한마디로 간선에 방향이 있는 연결 그래프를 정렬한다는 의미이다.

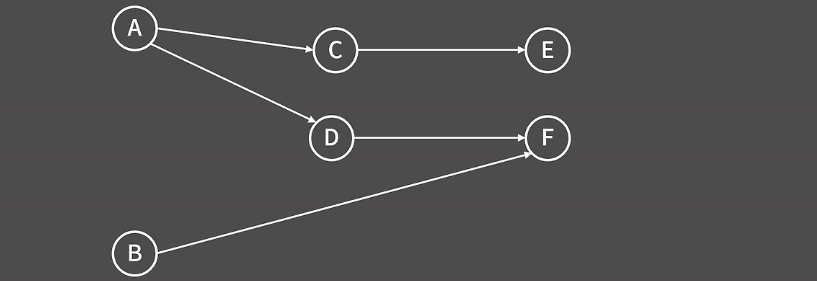
해당 그림에서 E는 C가 부모, F는 B,D가 부모, C,D는 A가 부모인 관계를 가 때 위상정렬을 표현하자면 ABCDEF, ACEDBF, BADCEF, BADFCE 등 다양한 위상 정렬을 표현할 수 있다.
다만 ACEDFB라고하면 B는 F의 부모이므로 무조건 F보다는 먼저 나열되어야 하기 때문에 이는 잘못된 위상 정렬이다.

또한 위상 정렬은 사이클이 존재하지 않는다.
사이클이 존재하면 선후 관계가 모순되어 위상 정렬이 불가능하기 때문이다.

위상 정렬 알고리즘

그렇다면 위상 정렬은 의존 관계에 따라 정점을 배열하는 작업을 이해했으나 이를 코드로 구현하려면 어떻게 해야 할지 조금 막막하다.
우선 생각만큼 어렵지가 않다. 만약 다음과 같은 그림에서 위상 정렬을 우선 구해보도록 하자.

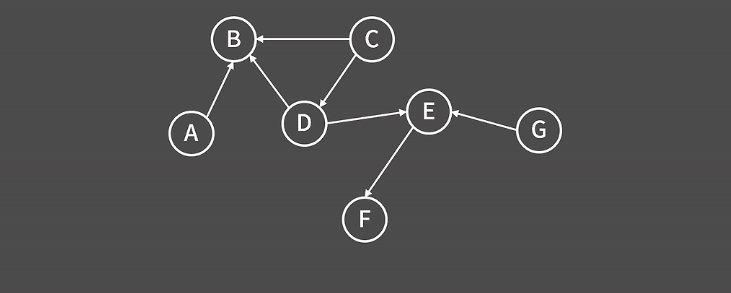
해당 그림에서 위상 정렬이 여러 개 나오겠지만 나는 ACGDEBF가 나왔다.
이를 구하는 방법을 그림으로 표현하면 다음과 같다.

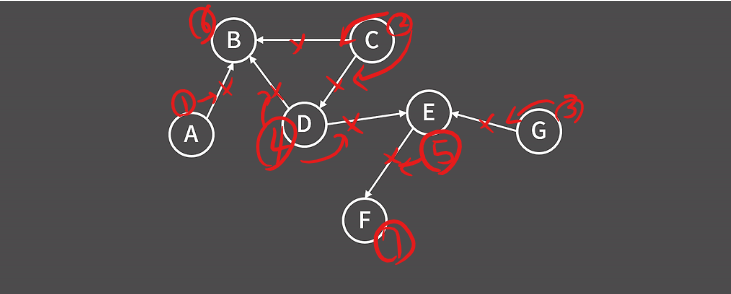
글씨가 조금 아쉽지만 문제를푸는 게 더 중요하므로 문제 풀이에 대해 더 집중하겠다.
먼저 숫자는 보다시피 위상 정렬을 하기 위한 정점의 순서를 나타냈다.
그리고 중간에 간선마다 x표시가 되어있는데 이는 선택된 정점의 OutDegeree를 제거한 것이다.
지금은 결과에 대한 설명이고 이제 과정에 대해 설명하겠다.

맨 처음 위상 정렬에 들어올 수 있는 정점들을 생각해 보자
아마도 대부분 A,C,G를 생각했을 것이다. 왜냐하면 InDegeree가 0 즉, 들어오는 간선이 없기 때문에 가장 먼저 정렬할 수 있다 생각했을 것이다.
따라서 해당 정점이 선택되면 사실상 남은 정점들만 비교하면 되기 때문에 정점을 선택하고 나면 연결된 정점의 InDegree를 1씩 감소시켜 주면 된다.

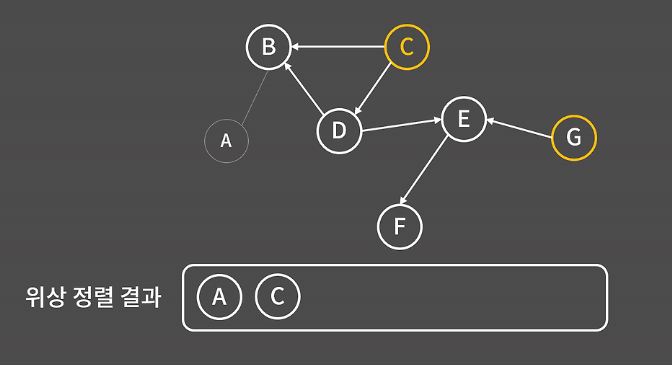
아마 진행 과정을 그림에 표현하자면 이런 느낌일 것이다. 그림처럼 A는 이미 위상정렬을 마쳤기 때문에 사라졌고 현재는 그다음 C 정점의 위상 정렬을 진행 중인 과정이다.
이렇게 정점을 진행하다 보면

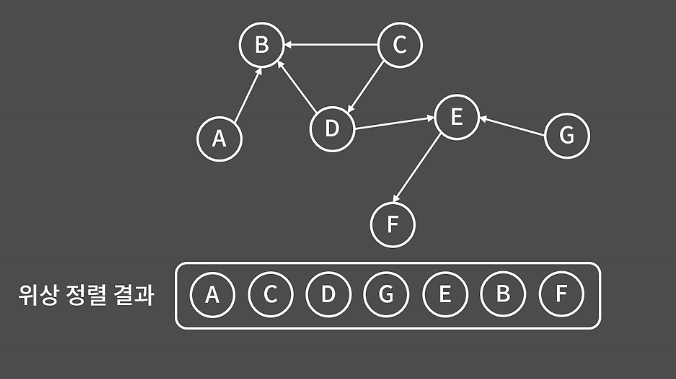
마지막에 정렬이 다 될 때 결과를 받을 수 있다.
이 흐름이 이해됐다면 아마 알고리즘은 자체는 이해를 했을 것이다. 이제 그러면 코드로 구현하기 위해 알고리즘을 정리하고 구현해보려 한다.

알고리즘 정리

1. 각 정점에 대해 연결된 정점(자식 노드)을 저장한다.
2. 각 정점의 진입 차수(In-degree)를 계산한다.
3. 진입 차수가 0인 정점을 큐에 넣는다.
4. 큐에서 정점을 꺼내고, 해당 정점과 연결된 정점들의 진입 차수를 1씩 줄인다.
5. 진입 차수가 0이 된 정점은 다시 큐에 넣는다.
6. 모든 정점이 정렬될 때까지 위 과정을 반복한다.

코드

#include <bits/stdc++.h>
using namespace std;

vector<char> adj[10];
vector<char> vec; 
queue<int> q;
int indegree[10];
int v, e;

void test()
{
	v = 7, e= 7;
	
	adj['A'-'A'].push_back('B');
	indegree['B' - 'A']++;
	adj['C'-'A'].push_back('B');
	indegree['B' - 'A']++;
	adj['C'-'A'].push_back('D');
	indegree['D' - 'A']++;
	adj['D'-'A'].push_back('B');
	indegree['B' - 'A']++;
	adj['D'-'A'].push_back('E');
	indegree['E' - 'A']++;
	adj['E'-'A'].push_back('F');
	indegree['F' - 'A']++;
	adj['G'-'A'].push_back('E');
	indegree['E' - 'A']++;
}

int main() {
	
	test();

	for(int i=0; i<v; i++)
		if(indegree[i] == 0) q.push(i);
	
	while(!q.empty())
	{
		int cur = q.front(); q.pop();
		vec.push_back('A'+cur);
		for(auto a : adj[cur])
		{
			indegree[a - 'A']--;
			if(indegree[a-'A'] == 0) q.push(a-'A');
		}
	}
	
	for(int i=0; i<v; i++)
		cout << vec[i];
	
	return 0;
}
// Output
// ACGDBEF

마무리

위상 정렬은 이번에 처음 접해본 정렬 방식이었다.
처음엔 생소했지만 그래프의 선후 관계를 정렬한다는 개념과 알고리즘 과정을 이해하니 꽤 흥미로운 주제였다.
앞으로 실제 문제를 더 많이 풀어보며 개념을 더 확실히 익히고 다양한 응용 예제를 접해보며 익숙해질 계획이다.

Reference
[실전 알고리즘] 0x1A강 위상 정렬 - BaaaaaaaarkingDog