최소 신장 트리

최소 신장 트리란?

최소 신장 트리(Minimum Spanning Tree, MST)란 그래프에서 모든 정점을 연결하면서 간선의 총 가중치가 최소가 되도록 구성된 트리를 의미합니다.
조금 더 쉽게 말하면 모든 정점을 연결하면서 가장 적은 비용으로 구성된 연결 그래프입니다.

크루스칼

크루스칼(Kruskal) 알고리즘은 간선에 가중치가 주어진 그래프에서 가장 가중치가 낮은 간선부터 선택하여 싸이클이 생기지 않도록 최소 신장 트리를 만들어가는 방법입니다.

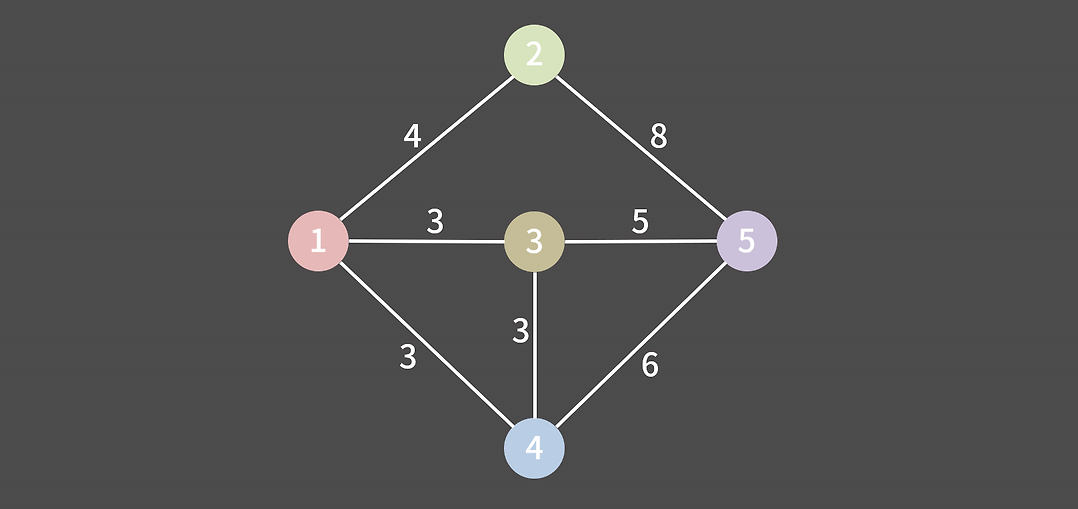
다음 그림에서 크루스칼 알고리즘을 적용하여 최소 신장 트리를 구현해 보려고 한다.
먼저 가장 가중치가 가작 작은 1-3, 1-4, 3-4 중 1-3을 먼저 선택하여 최소 신장 트리에 추가한다.
그 다음 마찬기로 1-4간선을 선택하고 최소 신장 트리에 추가한다. 그러면 이제 3-4가 남는데
이걸 추가하면 사이클이 생기므로 해당 간선은 제외한다.
그 다음 작은 가중치를 골라 1-2, 3-5를 골라 최소 신장 트리를 완성하게 된다

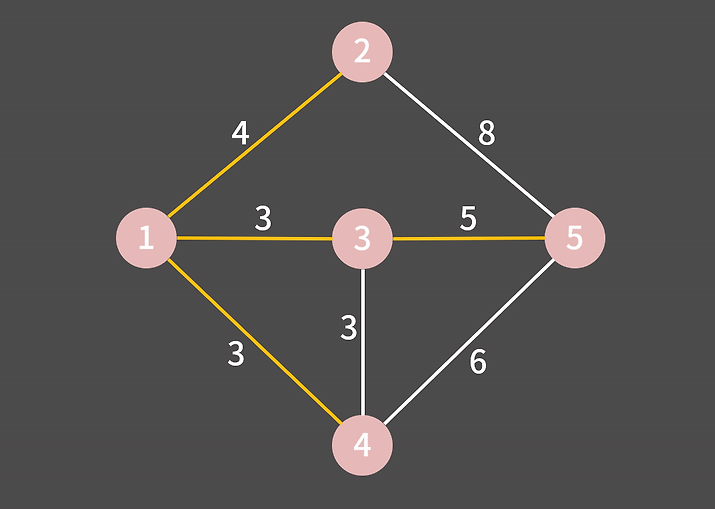
이를 코드로 구현하려면 먼저 Union Find 알고리즘을 알고 있어야 한다. 그래서 현재는 간단하게 구현된 코드에 대해서만 적고 Union Find를 공부한 뒤에 정리해 보려 한다.

알고리즘

1. 모든 간선을 가중치 기준 오름차순 정렬
2. 가장 작은 간선을 선택하여 해당 간선이 싸이클을 만들지 않으면 트리에 포함
3. 최소 신장 트리에 v-1개의 간선을 추가했다면 과정을 종료, 그렇지 않다면 2번 과정을 반복

크루스칼 코드

#include <bits/stdc++.h>
using namespace std;

vector<int> p(10005, -1);

int find(int x)
{
	if(p[x] < 0) return x;
	return p[x] = find(p[x]);
}

bool is_diff(int u, int v)
{
	u = find(u); v= find(v);
	if(u==v) return 0;
	if(p[u] == p[v]) p[u]--;
	if(p[u] < p[v]) p[v] = u;
	else p[u] = v;
	return 1;
}

int v, e;
tuple<int, int, int> edge[100005];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> v >> e;
	for(int i=0; i<e; i++)
	{
		int a, b, cost;
		cin >> a >> b >> cost;
		edge[i] = {cost,a,b};
	}
	sort(edge, edge+e);
	
	int cnt = 0;
	int ans = 0;
	
	for(int i = 0; i<e; i++)
	{
		int a, b, cost;
		tie(cost,a,b) = edge[i];
		if(!is_diff(a,b)) continue;
		ans += cost;
		cnt++;
		if(cnt==v-1) break;
	}
	
	cout << ans;
	
	return 0;
}

// Input
5 7
1 3 3
1 4 3
3 4 3
1 2 4
3 5 5
4 5 6
2 5 8

// Output
15

이 부분은 Union Find의 개념을 알아야하니 간단하게 구현은 이런식이라고만 생각하자.

프림

프림 또한 크루스칼과 동일하게 최소 신장 트리를 구하는 알고리즘이다. 다만 다른 점이 있는데 프림의 경우 임의의 점에서부터 시작하여 최소 신장 트리를 구하는 알고리즘이다.

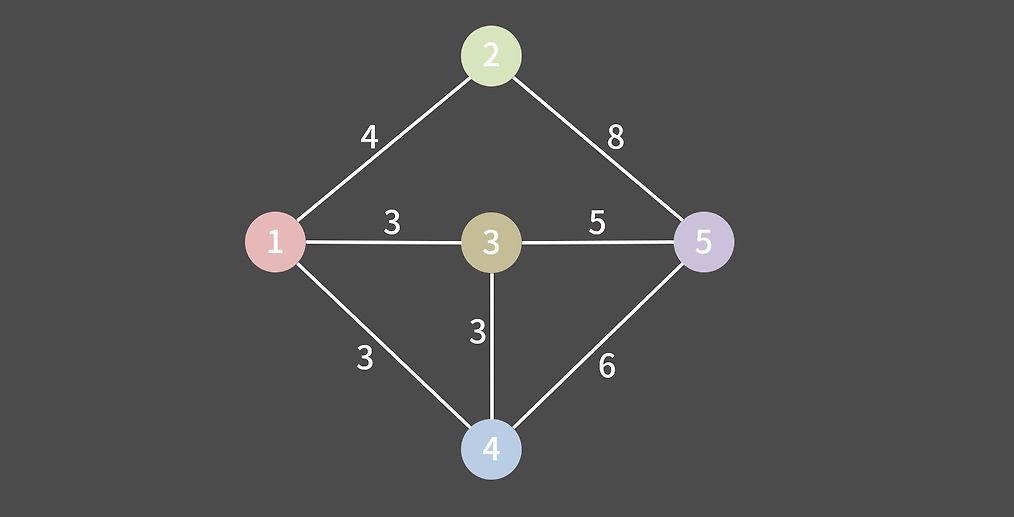
해당 그림에서 프림 알고리즘을 적용하면 다음과 같다.
임의의 정점을 1번이라고 가정할 때 1번을 최소 신장 트리에 들어간 정점으로 설정한다.
연결된 정점을 크기 순으로 1-3,1-4,1-2 간선을 추가하고 가중치가 가장 낮은 1-3을 선택하여 최소 신장 트리에 추가한다.
3번 정점도 방문한 정점이 되기 때문에 3번과 연결된 3-4, 3-5의 간선도 추가한다.
단, 간선은 가중치 순으로 정렬된다. 그렇게 임의로 1-4, 3-4중 3-4 간선을 최소 신장 트리에 추가한다. 이렇게 되면 1,3,4가 전부 최소 신장 트리에 들어간 정점으로 자연스럽게 1-4는 추가할 수 없다. 이런 흐름으로 최소 신장 트리를 추가하면

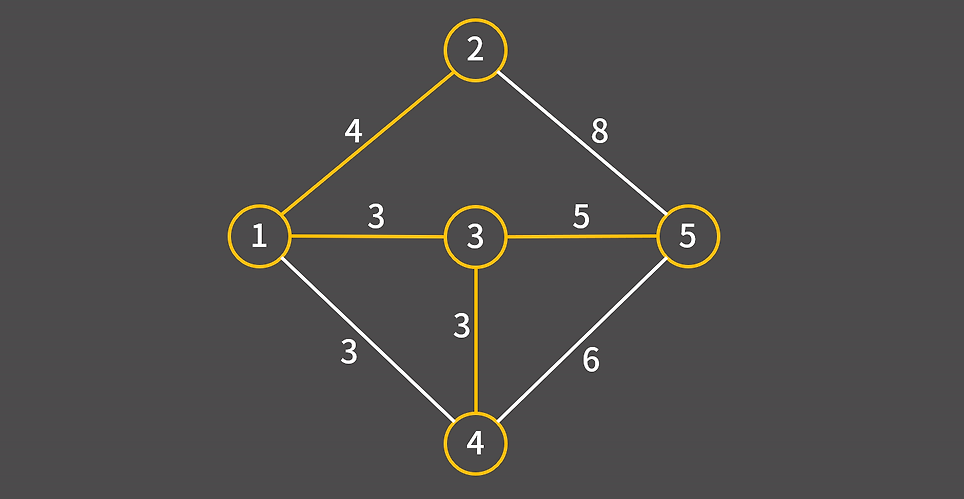
이렇게 최소 신장 트리가 완성된다.

알고리즘

1. 임의의 정점을 선택해 최소 신장 트리에 추가하고 연결된 간선을 우선순위 큐에 저장
2. 우선 순위 큐에서 비용이 가장 작은 간선을 선택
3. 간선이 최소 신장 트리에 포함된 두 정점이라면 넘어가고 아니면 간선을 최소 신장 트리에 포함한다.
4. 최소 신장 트리의 간선이 V-1개가 될 때 까지 2,3반복

#include <bits/stdc++.h>
using namespace std;

#define tp tuple<int,int,int>
#define X first
#define Y second

priority_queue<tp, vector<tp>, greater<tp>> pq; // cost, a, b
vector<pair<int,int>> vec[10002]; // cost, nearVertex
bool check[10002];
int v, e;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> v >> e;
	
	for(int i=0; i<e; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		vec[a].push_back({c,b});
		vec[b].push_back({c,a});
	}
	
	check[1] = 1;
	for(auto c : vec[1])
		pq.push({c.X, 1, c.Y});
	
	int cnt = 0;
	int ans = 0;
	while(cnt < v-1)
	{
		int cost, a, b;
		tie(cost, a, b) = pq.top(); pq.pop();
		if(check[b]) continue;
		check[b] = 1;
		ans += cost;
		for(auto cur : vec[b])
			if(!check[cur.Y]) pq.push({cur.X, b, cur.Y});
		cnt++;
	}
	
	cout << ans;
	
	return 0;
}
// Input
5 7
1 3 3
1 4 3
3 4 3
1 2 4
3 5 5
4 5 6
2 5 8

// Output
15

마무리

크루스칼 알고리즘은 Union Find를 공부하고 다시 정리해 보려고 한다.
프림 알고리즘은 크루스칼보다 더 복잡했지만 임의의 정점을 선정하는 것과 우선순위 큐를 통해 간선을 선택하는 핵심을 안다면 MST 관련 문제는 잘 해결할 수 있을듯하다.
앞으로 문제를 많이 풀어보며 익히는 것이 관건인듯하다.

Reference
[실전 알고리즘] 0x1B강 최소 신장 트리 - BaaaaaaaarkingDog