1. 개괄

이번 글에서는 MNIST 손글씨 데이터를 선형 모델로 분류하면서, 학습 방식에 따라 성능이 어떻게 달라지는지를 실험합니다. 구체적으로는 Batch Gradient Descent, Stochastic Gradient Descent(SGD), Mini-Batch Gradient Descent 세 가지 최적화 방식을 비교해볼 예정입니다.

다만, MNIST의 훈련 데이터는 총 60,000개로, Batch Gradient Descent를 엄밀하게 구현하려면 동일한 크기의 배치를 사용해야 합니다. 그러나 이 경우 메모리 과부하가 발생할 수 있어, 실험을 간소화하여 각각 배치 크기를 1024, 32, 1로 설정한 세 가지 케이스로 대체하여 실험을 진행할 예정입니다. 분류 문제이므로 손실 함수는 CrossEntropy Loss를 사용하고, 동일한 모델 구조와 하이퍼파라미터 조건 하에서 학습 방식만 달리하여 그 차이를 분석할 계획입니다.

2. GD vs Mini-Batch GD vs SGD

2.1 정의

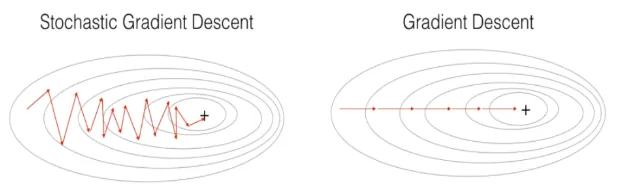
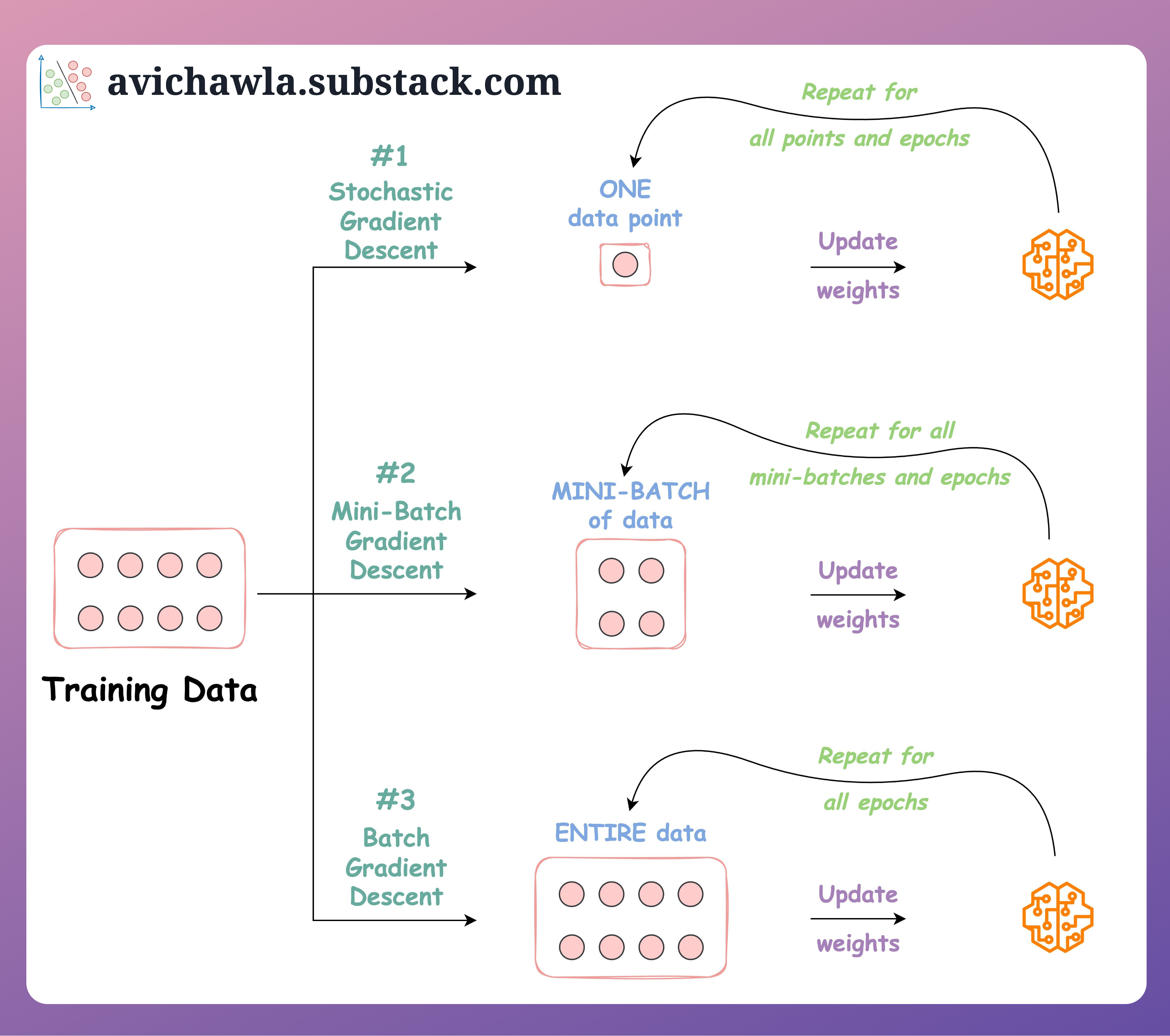
Batch Gradient Descent는 모든 학습 데이터를 한 번에 사용하여 손실 함수의 기울기를 계산하고 파라미터를 업데이트하는 방식입니다. 모든 샘플을 기반으로 예측값과 실제값 사이의 오차를 계산하므로 가장 정확한 방향으로의 경사 하강이 가능하지만, 연산량이 많고 메모리 사용이 커서 대규모 데이터셋에는 적합하지 않습니다. 이 방식은 이론적으로는 딥러닝 최적화의 기본 개념으로 사용되지만, 실전에서는 잘 활용되지 않습니다.

Mini-Batch Gradient Descent는 전체 데이터셋을 일정한 크기의 미니배치로 나누어 학습하는 방식으로, 실전에서 가장 널리 사용되는 최적화 방법입니다. 각 미니배치에 대해 손실과 기울기를 계산하여 파라미터를 조금씩 업데이트하므로, 연산 효율성과 안정적인 수렴을 동시에 얻을 수 있습니다. 이 방식은 하드웨어 병렬 처리를 활용할 수 있고, Batch Gradient Descent보다 빠르면서도 Stochastic Gradient Descent보다 안정적인 특징을 가지고 있어 실무에서 가장 실용적인 선택입니다.

Stochastic Gradient Descent는 학습 데이터에서 무작위로 선택한 단일 샘플에 대해 매번 손실과 기울기를 계산하고 파라미터를 업데이트하는 방식입니다. 이 방식은 업데이트가 자주 일어나기 때문에 빠르게 수렴할 수 있지만, 매우 불안정하게 진동하며 최적점 근처에서 정확하게 수렴하지 못하는 경우도 있습니다. 다만 이러한 노이즈 성질이 오히려 지역 최적점에서 벗어나 전역 최적점을 찾는 데 도움을 줄 수 있어 이론적으로는 중요한 기법입니다.

2.2 수식화

• 전체 샘플 수: $N$

• 모든 샘플에 대해 예측 수행:

  $\hat{y} = f(n), \quad n = 1, \dots, N$

• 전체 손실의 평균 계산:

  $\text{Loss} = \frac{1}{N} \sum_{i=1}^{N} \mathcal{L}(\hat{y}_i, y_i)$

• Loss는 스칼라 값, 이후 역전파 수행:

BGD는 전체 데이터를 모두 사용해 한 번의 평균 손실을 계산하고 파라미터를 한 번만 업데이트하기 때문에, 한 에폭(epoch)당 업데이트가 1번만 일어납니다. 반면, SGD는 개별 샘플 단위로 손실을 계산하고 그때마다 파라미터를 업데이트하므로, 한 에폭 동안 샘플 수만큼 업데이트가 발생합니다. 따라서 같은 에폭 기준으로 보면, SGD는 BGD보다 훨씬 더 많은 반복(iteration)과 업데이트가 일어나며, 그만큼 더 빠르게 파라미터가 변할 수 있는 장점이 있지만, 동시에 노이즈도 많아집니다.

3. 실험

3.1 코드

from torch import nn

experimental_config = {
    "case1" : {
        "batch_size" : 1024,
        "epochs" : 30,
    },
    "case2" : {
        "batch_size" : 32,
        "epochs" : 30
    },
    "case3" : {
        "batch_size" : 1,
        "epochs" : 30
    }
}

class Model(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.hidden_layers = nn.ModuleDict() 
        for i, (name, (input_dim, output_dim)) in enumerate(config.items()):
            if i + 1 != len(config):
                self.hidden_layers[f"{name}_layer"] = nn.Linear(input_dim, output_dim)
                self.hidden_layers[f"{name}_activation"] = nn.ReLU()

        self.final_layer = nn.ModuleDict() 
        self.final_layer[f"{list(config.keys())[-1]}_layer"] = nn.Linear(list(config.values())[-1][0], list(config.values())[-1][-1])

    def forward(self, x):
        x = x.flatten(start_dim=1)
        for layer in self.hidden_layers.values():
            x = layer(x)
        for layer in self.final_layer.values():
            x = layer(x)
        return x

# Define the model for each case
for case_name, config in experimental_config.items():
    data = iter(config['dataset']['train'])
    input_dim = (
        next(data)[0][0].shape[0] 
        * next(data)[0][0].shape[1] 
        * next(data)[0][0].shape[2]
    )
    model_config = {
        "layer1":(input_dim, n_dim),
        "layer2":(n_dim, n_dim),
        "final":(n_dim, 10)
    }
    model = Model(model_config)
    model = model.to(device)
    config['model'] = model
    print(case_name, end="\n\n")
    print(model)
    print("#####")

case1

Model(
  (hidden_layers): ModuleDict(
    (layer1_layer): Linear(in_features=784, out_features=1024, bias=True)
    (layer1_activation): ReLU()
    (layer2_layer): Linear(in_features=1024, out_features=1024, bias=True)
    (layer2_activation): ReLU()
  )
  (final_layer): ModuleDict(
    (final_layer): Linear(in_features=1024, out_features=10, bias=True)
  )
)
#####
case2

Model(
  (hidden_layers): ModuleDict(
    (layer1_layer): Linear(in_features=784, out_features=1024, bias=True)
    (layer1_activation): ReLU()
    (layer2_layer): Linear(in_features=1024, out_features=1024, bias=True)
    (layer2_activation): ReLU()
  )
  (final_layer): ModuleDict(
    (final_layer): Linear(in_features=1024, out_features=10, bias=True)
  )
)
#####
case3

Model(
  (hidden_layers): ModuleDict(
    (layer1_layer): Linear(in_features=784, out_features=1024, bias=True)
    (layer1_activation): ReLU()
    (layer2_layer): Linear(in_features=1024, out_features=1024, bias=True)
    (layer2_activation): ReLU()
  )
  (final_layer): ModuleDict(
    (final_layer): Linear(in_features=1024, out_features=10, bias=True)
  )
)
#####

3.2 모델 분석

이 모델은 MNIST 손글씨 숫자 이미지(28×28)를 처리하기 위한 다층 퍼셉트론(Multi-Layer Perceptron, MLP) 구조로 구성되어 있습니다. 입력 이미지는 784(=28×28) 차원의 벡터로 평탄화되어 모델에 전달되며, 두 개의 은닉층(hidden layer)을 거쳐 최종적으로 10개의 클래스로 분류됩니다.

각 은닉층은 1024개의 노드를 가지며, 활성화 함수로는 ReLU(Rectified Linear Unit)가 사용되어 비선형성을 부여하고, 학습 과정에서의 표현력을 향상시킵니다. 최종 출력층은 10개의 노드를 가지는 선형 계층으로, 각 노드는 0부터 9까지 숫자 클래스에 해당하는 확률값을 출력하도록 설계되어 있습니다. 이 모델 구조는 이미지의 공간적 구조를 직접적으로 고려하지는 않지만, 다층 비선형 변환을 통해 충분한 표현 능력을 확보하고 있어 단순한 분류 문제에는 효과적으로 작동할 수 있습니다.

4. 결과 분석

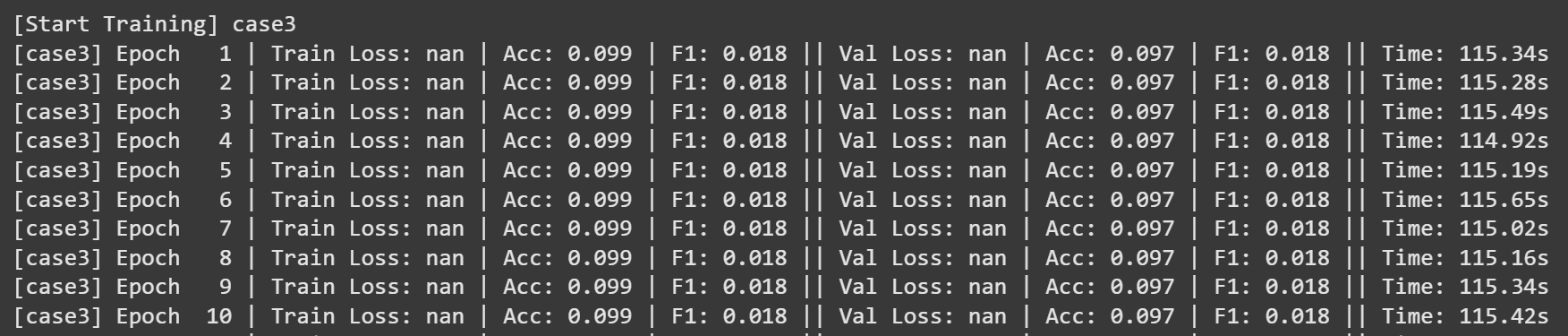
4.1 훈련 log

4.2 훈련 metric

4.2.1 test metric

[Test Evaluation] case1
Test | Loss: 0.254 | Accuracy: 0.951 | F1_Score: 0.950

[Test Evaluation] case2
Test | Loss: 0.150 | Accuracy: 0.967 | F1_Score: 0.967

[Test Evaluation] case3
Test | Loss: nan | Accuracy: 0.102 | F1_Score: 0.018

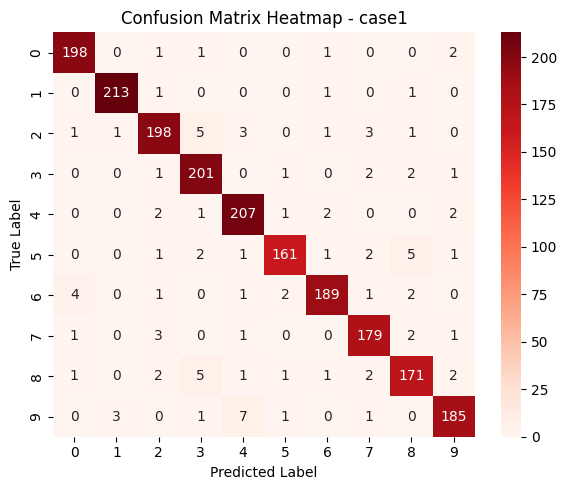
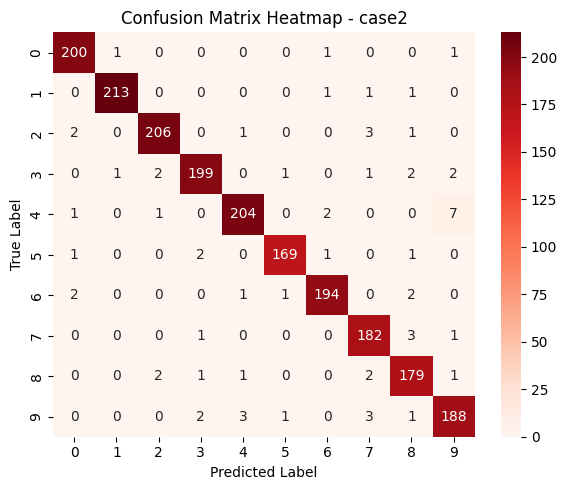
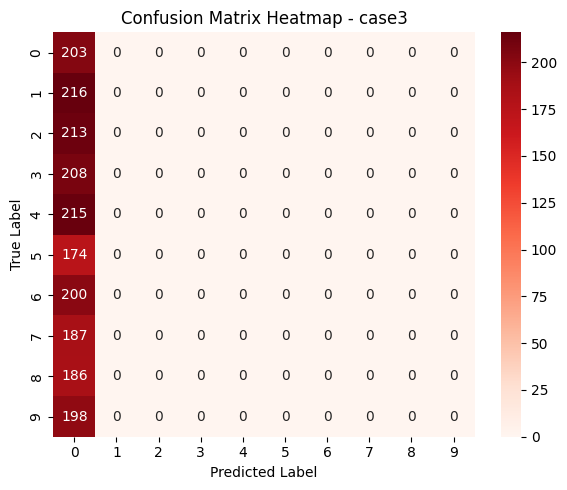
4.2.2 heat map

4.3 훈련 결과 분석

4.3.1 Case1

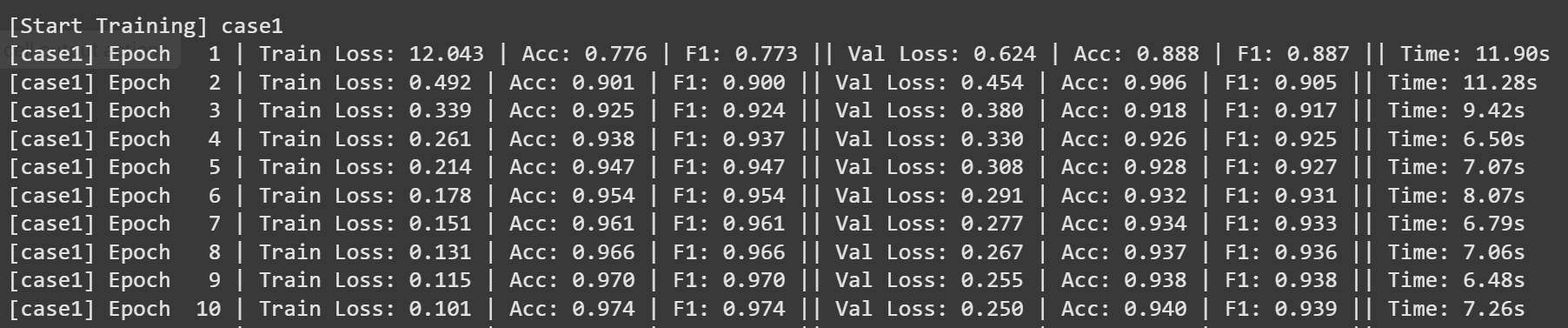
Case 1은 비교적 큰 배치 사이즈인 1024를 사용하여 학습을 진행한 실험으로, 한 번에 많은 데이터를 처리할 수 있어 연산 효율이 높고 에폭당 소요 시간이 짧다는 장점이 있습니다. 따라서 1에폭당 훈련 시간이 상대적으로 짧게 나왔습니다.

그러나 파라미터 업데이트 횟수가 적기 때문에 같은 에폭 수 기준으로는 학습 속도가 느리며, 성능 개선이 점진적으로 일어나는 특징을 보였습니다. 실제 실험에서도 정확도와 F1 점수가 안정적으로 상승하긴 했지만, 빠른 수렴을 보이진 않았고 성능 향상이 느리게 진행되는 경향이 관찰되었습니다.

4.3.2 Case2

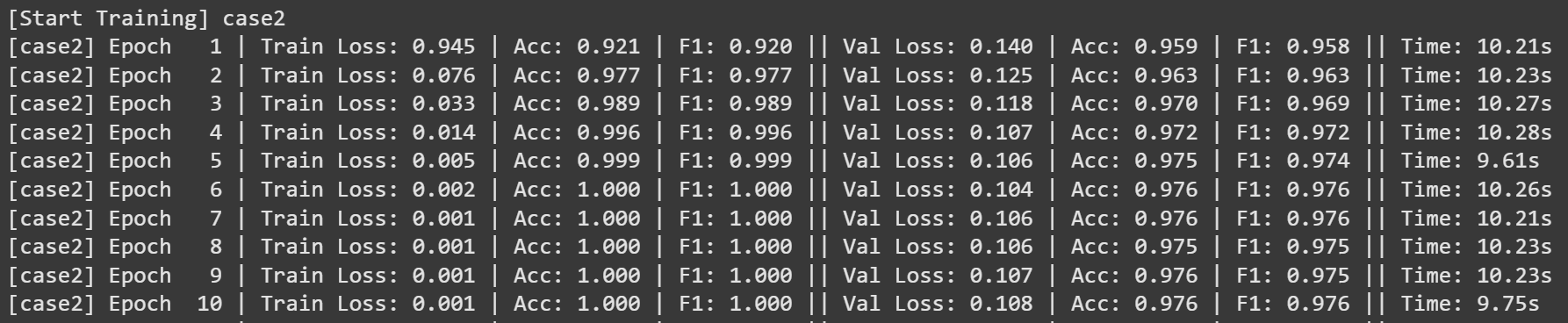
Case 2는 배치 사이즈를 32로 설정한 실험으로, 실무에서 가장 자주 사용되는 미니배치 크기입니다. 이 경우 적절한 빈도로 파라미터 업데이트가 이루어지기 때문에 학습 속도와 안정성 사이의 균형이 잘 맞고, 연산 효율도 무난한 수준을 유지합니다.
실험 결과, 매우 빠른 속도로 정확도와 F1 점수가 향상되었으며, 일정 수준 이상의 성능에 도달한 이후에도 과적합 없이 안정적인 학습을 이어갔습니다. 전체적으로 세 케이스 중 가장 빠르고 안정적인 수렴을 보여준 사례입니다.

4.3.3 Case3

Case 3은 Stochastic Gradient Descent 방식으로, 배치 사이즈를 1로 설정하여 매 샘플마다 파라미터를 업데이트하는 실험입니다. 이론적으로는 빠르게 반응하고 다양한 gradient 방향을 탐색할 수 있지만, 그만큼 진동이 크고 학습 안정성이 떨어지는 단점이 있습니다.

실제 실험에서는 학습 초반부터 손실값이 NaN으로 출력되었고, 정확도와 F1 점수 모두 약 10%와 0.018 수준에서 더 이상 향상되지 않는 현상이 나타났습니다. 또한 에폭당 115초 이상이 소요되어 시간 면에서도 가장 비효율적인 결과를 보였으며, 학습률이 크거나 gradient가 불안정할 경우 발생할 수 있는 발산 문제가 원인일 가능성이 높습니다.

4.4 소결: SGD와 학습 불안정성

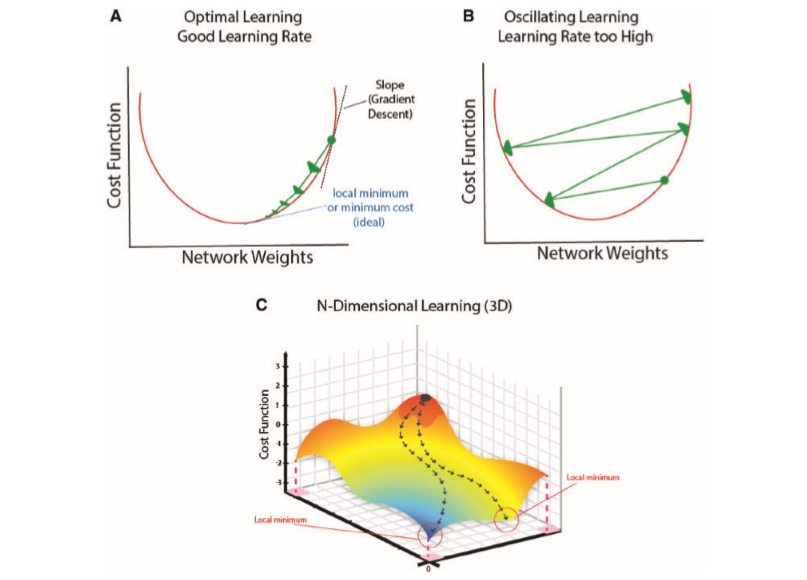
SGD는 말 그대로 단 하나의 샘플만을 가지고 모델의 가중치를 업데이트하는 방식입니다. 이를 비유하자면, 마치 책 한 권만 읽고 세상에 대한 가치관을 바꾸는 것과 같습니다. 이때 책 한 권을 통해 아주 조금씩 사고를 확장해 나간다면, 점진적인 성장이 가능하겠지만, 단 한 권의 내용만으로 사고방식을 극단적으로 바꿔버린다면 현실과 괴리된 편향된 시각을 가질 수 있습니다. 마찬가지로, 하나의 샘플로 과도하게 파라미터를 업데이트한다면 모델이 불안정해지고, 오히려 최적의 해로부터 멀어질 수 있습니다.

SGD는 특성상 각 iteration마다 샘플이 달라지기 때문에 loss의 변화가 일관되지 않고 진동이 심한 경향이 있습니다. 이러한 불안정성 속에서 학습률이 지나치게 크면, 이전 손실값에 과도하게 반응하여 파라미터를 잘못된 방향으로 갱신하게 되고, 결국 loss가 발산하는 현상이 발생할 수 있습니다.

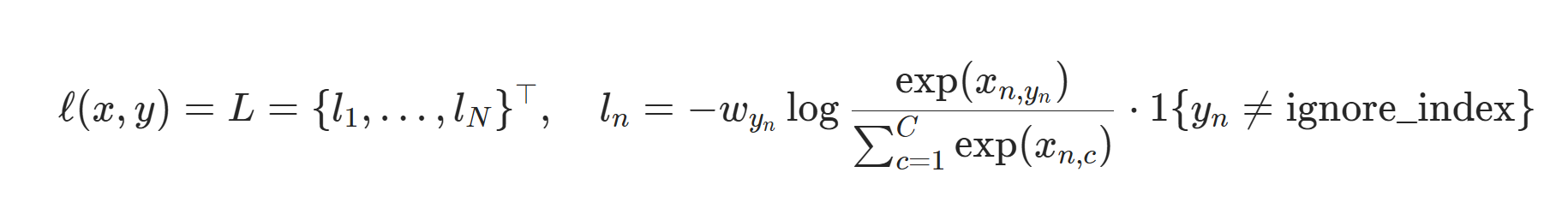
또한, CrossEntropyLoss는 softmax를 거친 결과에 로그를 취하는 방식인데, 이때 softmax 출력값이 0에 가까워지면 log(0) 특성상 -무한대로 발산하게 됩니다. 모델이 정답 클래스에 대해 0에 가까운 확률을 예측하게 되는 상황, 그리고 그 상황이 반복될수록 loss는 계속해서 커지고 학습은 악순환에 빠지게 됩니다. 결국 이는 최적해로 수렴하는 것이 아니라 오히려 멀어지는 방향으로 학습이 이루어지는 구조로 이어집니다.

5. 결론

5.1 배치 사이즈가 작아질수록 learning rate를 더 세밀하게 해야한다.

배치 사이즈가 작아질수록 각 미니배치에 포함되는 샘플 수가 적어지기 때문에, 그로부터 계산되는 gradient는 전체 데이터의 방향을 잘 대표하지 못하고 노이즈가 커지게 됩니다. 이러한 상황에서 학습률(learning rate)이 너무 크면, 파라미터가 급격히 변하면서 모델이 불안정해지고, 손실(loss)이 발산하거나 최적점에서 멀어지는 현상이 발생할 수 있습니다. 따라서 작은 배치 사이즈를 사용할수록 gradient의 불안정성을 보완하기 위해 학습률을 더 세밀하게 조정해야 하며, 일반적으로는 더 작은 값을 사용하는 것이 안정적인 학습에 도움이 됩니다.

5.2 배치 사이즈가 클수록 1에폭의 학습 시간이 학습 포화가 되기 위하여 많은 에폭이 필요하다

배치 사이즈가 클수록 1에폭 당 걸리는 시간을 줄어듭니다. 왜냐하면 훈련 시간의 상당 크기를 잡아먹는 것은 가중치 갱신인데, 배치 사이즈가 클수록 1에폭 당 갱신 횟수가 줄어들기 때문입니다.

그러나 갱신 횟수가 줄어들기 때문에 모델이 충분히 수렴하거나 학습 포화 상태에 도달하기 위해서는 더 많은 에폭 수가 필요하게 됩니다. 큰 배치 사이즈는 안정적인 방향으로 수렴하는 장점이 있고 1에폭당 학습 시간이 짧지만, 전체적으로 보았을 때 학습이 느리고 자주 업데이트되지 않기 때문에 빠른 성능 향상을 기대하기는 어렵습니다.

6. 의문

Case3에서 학습이 불안정했던 이유는 충분히 이해되지만, 모든 샘플을 동일하게 0번 클래스로 예측하고 있다는 점은 의문으로 남습니다. 모델의 gradient가 exploding 되어 학습이 발산한 상황이라면, 일반적으로는 출력이 무작위에 가까워지고 클래스 예측도 랜덤하게 분포될 것으로 예상됩니다. 그러나 현재는 모든 샘플에 대해 동일하게 0번 클래스로 예측이 고정되어 있어, 단순히 발산을 넘어서 출력값이 한 방향으로 치우치는 현상이 발생한 것으로 보입니다.