리뷰 작성자 서론
- Survey 논문은 처음 보지만 시계열 연구 분야에 대해 잘 정리되어 있다고 판단하여 작성한다.
- Timesnet이라고 하는 시계열 예측 알고리즘을 활용할 때 참고하였던 라이브러리를 소개하고 있다.
Abstract
불연속적인 시계열 패턴은 실생활에서 흔히 볼 수 있는 데이터이다. 다른 유형의 데이터 모델들과 다르게 시계열 모델은 복잡하고 역동적인 특성으로 인해 다음과 같은 고유한 과제를 있는데 비선형 패턴과 시간 변화에 따른 추세가 서로 얽혀 있다는 것이다.
시계열 데이터를 분석하는 것은 실생활에서 매우 중요하며 수세기에 걸쳐 널리 연구 되어 왔다. 최근 몇년동안에는 시계열 분석 분야에서 놀라운 발전이 있었다. 전통적인 통계 방법에서 고급 딥러닝 알고리즘을 활용한 모델로 전환되고 있다.
이 논문에서는 다양한 분석 방법들 중에서 심층 시계열 모델의 벤치마크로 24개의 주요 모델을 구현하였고, 다양한 도메인의 데이터세트 30개를 다루며, 5개의 보편적인 분석작업을 지원할 수 있는 시계열 라이브러리를 개발하고 공개하였다.
저자는 앞서 소개한 라이브러리를 기반으로 다양한 작업에 대한 12개의 고급 딥러닝 모델을 철저하게 비교하였다. 경험적인 결과에 따르면 특정 구조를 가진 모델은 고유한 분석 작업에 적합하였으며, 이는 시계열 모델의 연구 및 선택을 위한 인사이트를 제공한다.
1. Introduction
시계열 데이터는 금융 위험 평가, 지속 가능한 에너지, 일기 예보 등 실제 어플리케이션에 널리 사용된다. 다양한 영역에 걸쳐 방대한 양의 시계열 데이터들이 필요성이 증가함에 따라 시계열 분석 분야 또한 엄청난 발전을 거듭하고 있다. 객관적으로 규정된 구문이나 직관적인 패턴이 있는 이미지나 텍스트 데이터에 비해 시계열 데이터는 시간적 변화에 따라 달라져 순차 의존성, 계절적 패턴, 복잡한 관계 등을 파악하는데 상당히 큰 어려움이 있다. 그래서 시계열 데이터를 분석하기 위해서는 복잡한 시간적 표현을 포착하고 활용할 수 있는 정교한 방법이 필요하다.
전통적인 시계열 분석 방법에는 ARIMA, 지수평활화, 스펙트림 분석 등이 있었지만 실제 시계열 데이터에는 존재하는 복잡한 비선형적인 관계와 시간 종속성 등을 발견하기에는 선형성과 같은 여러 통계적 가정들로 인해 제한적인 한계가 있었다.
최근에는 이러한 한계점들을 극복하기 위해 딥러닝 모델을 활용하였고 시계열 데이터 내의 복잡한 종속성을 포착할 수 있는 능력을 입증하였다.
관련하여 최근 몇 년간 다양한 Survey가 있었지만 비교적 종합적으로 시계열 모델에 관해 정리한 내용이 부족하였다. 이 Survey 논문에서는 종합적인 시계열 모델에 대한 인사이트를 제공하기 위해 기본 모듈부터 최신 아키텍처까지 포괄적으로 비교하고 배경을 설명하며 연구자들과 실무자들을 위해 라이브러리형태로 제공한다.
2. PRELIMINARIES
2.1 Time Series
Time Series 데이터는 센서나 시스템으로부터 얻은 물리적 측정값인 경우가 많아 종종 여러 변수가 함께 기록된다. 따라서 실제 환경의 Time Series는 대개 다변량 형태로 기록된다. 이론 연구들에 따르면 두 개 이상의 비정상 시계열(non-stationary series)이 있을 경우 이들의 선형 결합은 정상 시계열(stationary series)이 될 수 있다고 한다. 이러한 공적분(co-integration) 특성은 비정상 시계열 간의 장기적인 관계를 발견하고 모형화하는 데 도움이 된다. 따라서 Time Series 분석의 핵심은 관측치에 내재된 Temporal Dependency와 변수 간 상관관계를 포착하여 활용하는 것이다.
Temporal Dependency. 관측치에 내재된 순차적 특성을 고려할 때, 대표적인 기술적 접근법 중 하나는 과거 데이터 집합의 Temporal Dependency를 포착하는 것이다. Temporal Dependency 개념의 기본은 시간 축상의 각 시점이나 부분 시계열(sub-series) 사이의 복잡한 상관관계를 의미한다. 전통적인 통계 모델들은 Temporal Dependency를 모형화하기 위한 기초를 다져왔다. 대표적인 모델로는 ARIMA (Autoregressive Integrated Moving Average) 등이 있으며, 이는 Time Series 모달리티에서 복잡한 시간 패턴을 포착하기 위해 폭넓게 연구되어 왔다. 이러한 통계 기법들은 단순성과 해석 용이성 덕분에, 데이터의 시간적 역동성(temporal dynamics)이 높지 않은 작업에서는 여전히 널리 사용된다. 현실 세계의 Time Series가 갖는 고차원성과 비정상성을 고려하면, 연구의 초점이 Time Series 분석을 위한 딥러닝으로 이동하게 되었다. 이러한 고도화된 방법들은 더욱 복잡한 시간적 역동성을 다룰 수 있도록 설계되었으며, Time Series 데이터의 Temporal Dependency를 포착하는 데 더 큰 유연성을 제공한다.
Variate Correlation. Temporal Dependency를 포착하는 것 외에도, 고차원 데이터 내 Variate Correlation을 파악하는 것은 multivariate Time Series를 분석하는 데 핵심적인 역할을 한다. 이는 시간의 흐름에 따라 변화하는 서로 다른 변수들 사이의 복잡한 상호 작용과 연관성을 의미한다. 이러한 상관관계는 측정치들 사이에 존재하는 내재된 역동성과 의존성에 대한 귀중한 통찰을 제공하여 잠재 프로세스를 보다 포괄적으로 이해할 수 있게 한다. Vector Autoregressive (VAR) 모델 등의 전통적인 접근법은 자기회귀(autoregression) 개념을 다변수로 확장하여 시간 경과에 따라 변화하는 여러 변수 사이의 관계를 포착할 수 있다. 그러나 VAR에서는 각 변수를 자기 자신의 시차(lagged) 값들과 모델 내 다른 모든 변수들의 시차 값들의 선형 결합으로 표현하기 때문에, 복잡하고 비선형적인 관계는 포착할 수 없다. 최근에는 Graph Neural Network나 Transformer 등의 고급 딥러닝 모델들도 Variate Correlation 모형화에 도입되고 있다.
2.2 Time Series Analysis Tasks
Time Series 분석은 데이터 내 근본적인 패턴과 추세에 대한 이해를 바탕으로, 예측 , 결측치 대체, 분류, 이상 탐지 등 다양한 후속 응용 작업을 포괄하며, 각각의 작업은 다양한 도메인에서 고유한 목적을 수행한다. 그림 1에는 대표적인 Time Series 분석 작업들이 도식적으로 나타나 있다.

예측은 Time Series 분석의 기본적인 작업 중 하나로, 모델이 데이터에 내재된 Temporal Dependency와 동적 패턴을 파악해야 하는 작업이다. 과거와 미래 데이터 사이의 관계를 포착함으로써 예측 모델은 주어진 Time Series의 미래 값이나 추세를 예측하는 것을 목표로 한다.
센서 고장, 데이터 손상 또는 측정치 누락으로 인해 발생하는 결측 데이터(missing data)는 실제 응용에서 흔하며, 이로 인해 더 높은 품질의 데이터를 얻기 위한 Time Series imputation에 대한 수요가 증가하고 있다. 예측 작업이 과거 관측치를 바탕으로 미래 값을 예측하는 데 중점을 둔다면, imputation은 사용 가능한 맥락 정보를 활용하여 누락된 값을 복원하는 데 초점을 맞춘다.
이상 탐지는 Time Series 내에서 특이하거나 비정상적인 패턴을 식별하는 작업이다. 이러한 패턴은 중대한 사건이나 시스템 결함, 혹은 추가 조사가 필요한 이상치(outlier)를 나타낼 수 있다. 마지막으로, 분류는 주어진 Time Series의 특성에 따라 해당 Time Series에 레이블이나 범주를 지정하는 작업이며, 의료 진단 등의 분야에서 널리 활용된다.
3. BASIC MODULES
3.1 Stationarization
Time Series 분석의 기본적인 개념 중 하나인 stationarity(정상성)는 시계열의 통계적 특성이 시간에 따라 일정하게 유지되는 성질을 의미한다. 정상 시계열(stationary time series)은 평균과 분산이 시간에 따라 변하지 않아 통계 분석을 단순화하고, 시계열에 내재된 패턴과 특성을 포착하기 쉽게 만든다. 많은 전통적 통계 기법들이 정상성을 기본 가정으로 하기 때문에, 비정상 시계열 데이터를 정상화(stationarize)하는 작업이 필수적이다. 전통적인 모델에서는 차분(differencing) 또는 로그 변환(log-transformation)을 사용하여 데이터를 정상화하지만, 최근 딥러닝 기법에서는 data normalization이 효과적인 방식으로 이를 수행한다. 예를 들어, DAIN, RevIN, Non-Stationary Transformer 등에서는 데이터를 정규화한 후 딥러닝 모델에 입력하며, 이후 다시 역정규화(de-normalization)를 통해 원래 데이터의 분포를 복원한다. 최근 연구인 SAN에서는 비정상 데이터를 균등한 구간으로 나누어 각 구간별로 정규화하는 방식을 시도했다.
3.2 Decomposition
Decomposition은 복잡한 시계열 데이터를 명확한 패턴을 가진 여러 개의 구성요소로 나누어 분석을 용이하게 하는 기법이다.
3.2.1 Seasonal-Trend Decomposition
가장 흔히 사용되는 기법 중 하나로, 데이터에서 추세(trend), 계절성(seasonal), 주기적(cyclical), 그리고 불규칙성(irregular) 성분을 분리한다. 수학적으로는 다음과 같다:
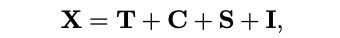
전통적 통계 분석에서는 주로 전처리 단계에서 이런 분해를 수행했으나, 최근 딥러닝 기법인 Autoformer에서는 데이터 특징을 seasonal과 trend-cyclical로 자동 분리하는 모듈을 설계하여 후속 연구들에서도 활발히 사용되고 있다.
3.2.2 Basis Expansion
Basis Expansion은 주어진 데이터를 미리 정의된 여러 기본 함수(basis function)의 조합으로 표현하는 수학적 방법이다. 대표적으로 N-BEATS 모델이 있으며, 이 모델은 데이터를 계층적으로 분해하여 해석 가능성을 높인다. 후속 연구인 N-HiTs, DEPTS, DEWP 등은 이를 발전시켜 다변량 시계열 데이터를 위한 정교한 계층적 분해 구조를 제안했다.
3.2.3 Matrix Factorization
Matrix Factorization은 고차원 다변량 시계열 데이터를 낮은 차원의 잠재 공간(latent space)에 표현하기 위한 행렬 분해 기법이다. 이는 데이터의 높은 변수 간 상관성을 고려하여 데이터를 압축하는 방식이다. 대표적인 방법으로는 TRMF, NoTMF, DeepGLO 등이 있으며, 최근 딥러닝 모델에서는 LSTM 기반의 시간적 규제(temporal regularization)나 Graph Laplacian 기반의 공간적 규제(spatial regularization)를 활용하는 경우도 많다.
3.3 Fourier Analysis
Fourier Analysis는 물리적 신호를 주파수 도메인으로 변환하여 원본 데이터의 주파수 특성을 분석하는 방법이다. 이 방법은 신호의 주기적 특성을 밝히고 시계열 데이터를 분석하는 데 매우 효과적이다. 특히 최근의 TimesNet 과 같은 모델에서는 FFT(Fast Fourier Transform)를 이용하여 데이터를 2차원으로 변환한 후, CNN 기반의 inception 모듈로 시계열을 모델링한다. 이외에도 Autoformer는 Wiener-Khinchin theorem을 기반으로 Auto-Correlation을 계산하여 효율적인 연산을 수행한다. 또 FEDformer 같은 연구는 무작위로 선택한 다양한 주파수 성분을 이용하여 시계열의 다양한 특성을 포착하고 있다. 최근의 연구는 시계열 데이터를 시간 도메인뿐만 아니라 주파수 도메인에서 동시에 분석하는 방향으로 발전하고 있다.
4. MODEL ARCHITECTURES
이 섹션에서는 기존의 Deep Time Series Model을 모델의 구조적 특징(backbone architecture)에 따라 크게 5가지 유형으로 나누어 살펴본다: MLP-based, RNN-based, CNN-based, GNN-based, Transformer-based.
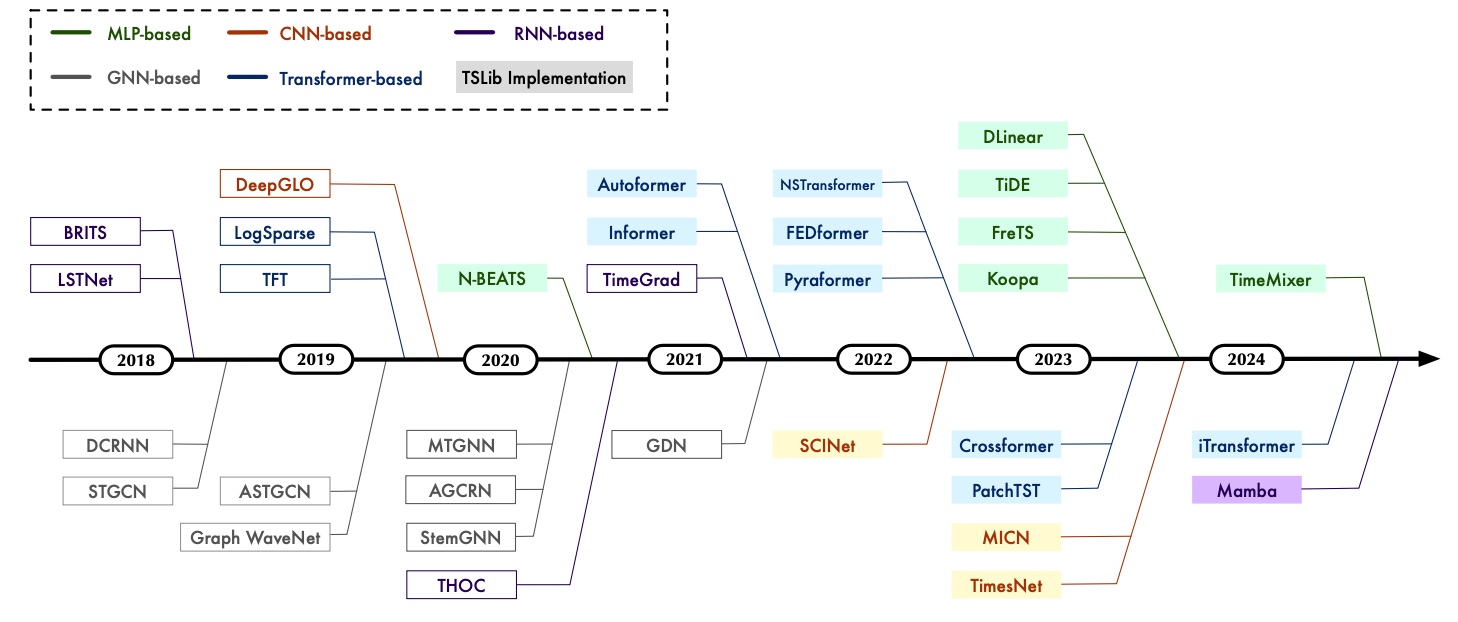
4.1 Multi-Layer Perceptrons (MLP)
MLP 모델은 전통적인 자기회귀(AR) 모델에서 영감을 얻은 단순하고 효율적인 신경망 구조로, 시계열의 시간적 패턴을 포착한다. 대표적인 예로, N-BEATS는 별도의 도메인 지식 없이 완전연결층(fully-connected layer)만으로 구성된 모델이다. DLinear는 복잡한 구조 없이 간단한 선형 회귀로만 시계열의 특징을 학습하여 우수한 성능을 나타낸다. 최근에는 MLP-Mixer와 같은 아이디어를 도입하여 시계열 데이터의 시간적, 변수 간의 상관관계를 동시에 포착하는 모델(TSMixer, FreTS, TimeMixer 등)이 제안되고 있다.
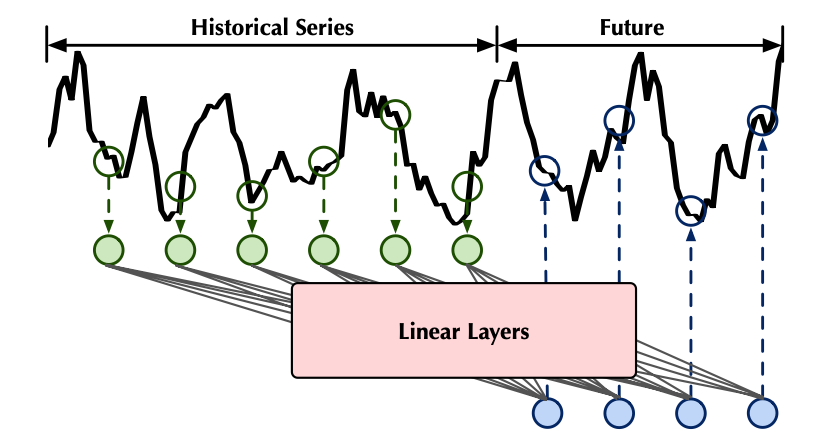
4.2 Recurrent Neural Networks (RNN)
RNN은 본래 순차적 데이터를 모델링하기 위해 설계된 구조로, 시간 흐름에 따라 정보를 전달하는 특성으로 인해 자연스럽게 시계열 분석에 사용된다. LSTNet은 순환 구조와 컨볼루션 층을 결합하여 단기 및 장기 패턴을 포착한다. DA-RNN은 dual-stage attention을 활용하여 각 시점마다 관련된 정보를 자동으로 선별한다. 또한 S4, Mamba 등 최근 연구에서는 State Space Model(SSM)의 수학적 기반을 RNN 구조와 결합하여 긴 맥락(long-term dependency)을 효과적으로 포착한다.
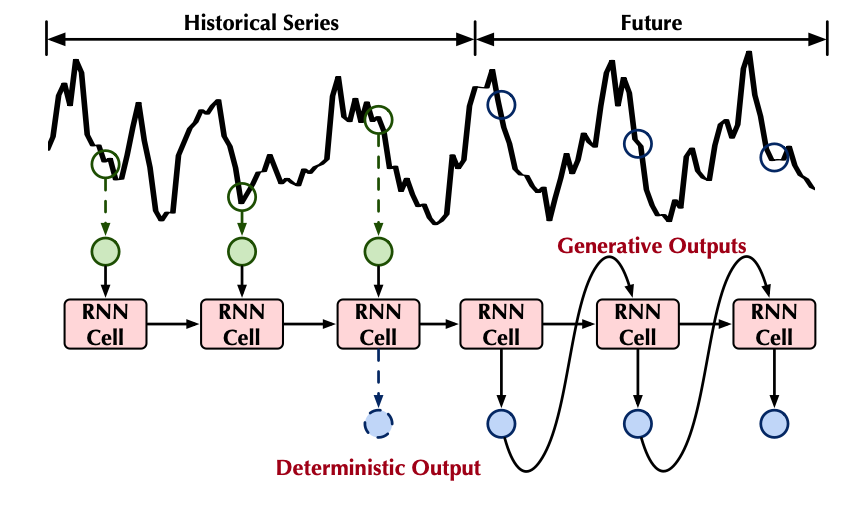
4.3 Convolutional Neural Networks (CNN)
CNN 기반 모델은 지역적 패턴(local pattern)을 효과적으로 학습하여 시계열 데이터의 짧은 구간 내 변화 특성을 잡아낸다. SCINet은 계층적 컨볼루션을 활용하여 시계열을 다중 해상도(multi-resolution)로 분석한다. WaveNet과 Temporal Convolutional Network (TCN)는 dilation convolution을 사용하여 큰 수용 영역(receptive field)을 확보한다. TimesNet은 FFT를 통해 데이터를 2D tensor로 변환하여 inception block을 이용해 다중 주기적 특성을 학습하는 등, 2차원 CNN을 활용한 시계열 분석 기법으로 확장하고 있다.

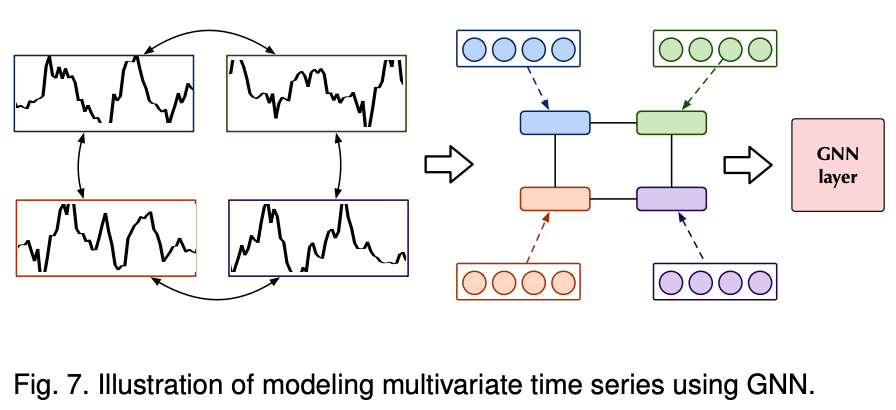
4.4 Graph Neural Networks (GNN)
다변량 시계열 데이터의 변수 간 복잡한 상호작용을 모델링하는 데 GNN이 활발히 사용된다. 각 변수를 그래프의 노드로 표현하여 시공간적(spatio-temporal) 특성을 포착할 수 있다. DCRNN 은 그래프상에서의 확산 프로세스를 통해 공간적 종속성을 학습하고, STGCN은 공간적 그래프 컨볼루션과 시간적 컨볼루션을 통합하여 트래픽 예측 등을 수행한다. 최근 연구들은 그래프 구조를 미리 정의하지 않고 데이터로부터 직접 학습하는 방법(AGCRN, MTGNN)을 통해 더욱 유연하게 공간적 관계를 포착하고 있다.
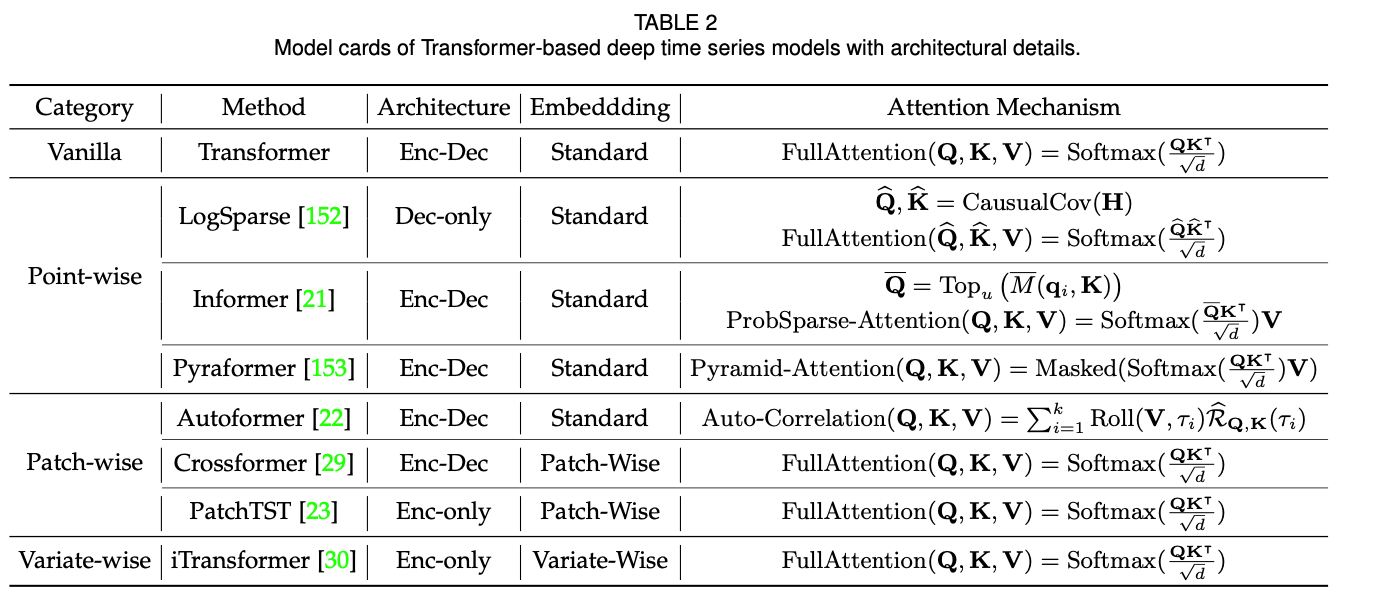
4.5 Transformers
Transformer 구조는 자기주목(self-attention) 메커니즘 덕분에 긴 시계열의 장기적 종속성(long-term dependency)과 복잡한 변수 간 상관관계를 효과적으로 학습한다. Transformer 기반의 시계열 모델은 주로 입력 데이터를 어떻게 토큰화(tokenization)하는지에 따라 point-wise, patch-wise, series-wise 등으로 나뉜다. Informer는 attention 연산의 복잡성을 낮추기 위해 ProbSparse attention을 도입하였고, Autoformer는 Auto-Correlation 메커니즘을 통해 주기적인 부분 시계열 간 유사성을 찾는다. 최근 PatchTST는 데이터의 패치(patch)를 이용하여 시간적 의존성을 포착하고, Crossformer는 시간 및 변수 차원을 교차로 학습하여 시공간적 특성을 동시에 포착하는 방식을 활용한다. iTransformer는 각 변수를 시리즈 단위의 토큰으로 보고 전체 변수를 한 번에 모델링하여 변수 간 종속성을 효율적으로 포착한다.