[DSP] Wavelet Transform (CWT, DWT)

whateverpartysover·2025년 3월 9일

DSP 이론

목록 보기

4/4

코드는 깃헙

웨이블릿 변환(Wavelet Transform, WT)은 신호를 분석하는 강력한 방법 중 하나로, 시간-주파수 분석을 수행할 수 있는 기법이다. 특히, STFT와 비교했을 때, 해상도를 동적으로 조절할 수 있다는 강점이 있다.

웨이블릿 변환의 개념

아묻따 수식먼저 박아보자

W_x(s, \tau) = \int_{-\infty}^{\infty} x(t) \psi^*_{s, \tau}(t) dt

어? 또 내적이야?

그렇습니다. 선형대수학을 필수 과목으로

그럼 원신호 $x(t)$ 를 뭐랑 내적을 치는거냐?

$\psi_{s, \tau}(t)$ 가 바로 웨이블릿이라는거다.

웨이블릿(Wavelet)의 정의

웨이블릿(Wavelet)은 국소적으로 정의된 작은 파형을 의미하며, 다음과 같은 특성을 가진다:

유한한 길이를 가짐: 웨이블릿은 특정 구간에서만 의미 있는 값을 가지고, 그 외 영역에서는 거의 0에 가까운 값을 가진다.
양쪽 끝이 0으로 수렴: 웨이블릿 함수는 주로 신호 분석을 위해 사용되며, 양끝이 0으로 수렴하는 형태를 가진다. 이는 웨이블릿이 신호의 특정 구간에서만 영향을 주도록 하기 위함이다.
유닛 에너지 조건 (Unit Energy Condition)
$\int_{-\infty}^{\infty} |\psi(t)|^2 dt = 1$
즉, 웨이블릿 함수는 신호의 전체 에너지를 1로 정규화해야 한다.
소멸 평균 조건 (Zero Mean Condition)
$\int_{-\infty}^{\infty} \psi(t) dt = 0$
즉, 웨이블릿의 전체 평균값은 0이어야 하며, DC 성분을 포함하지 않아야 한다.

그리고 실제 사용이 자주되는 wavelet 함수들의 예시이다.

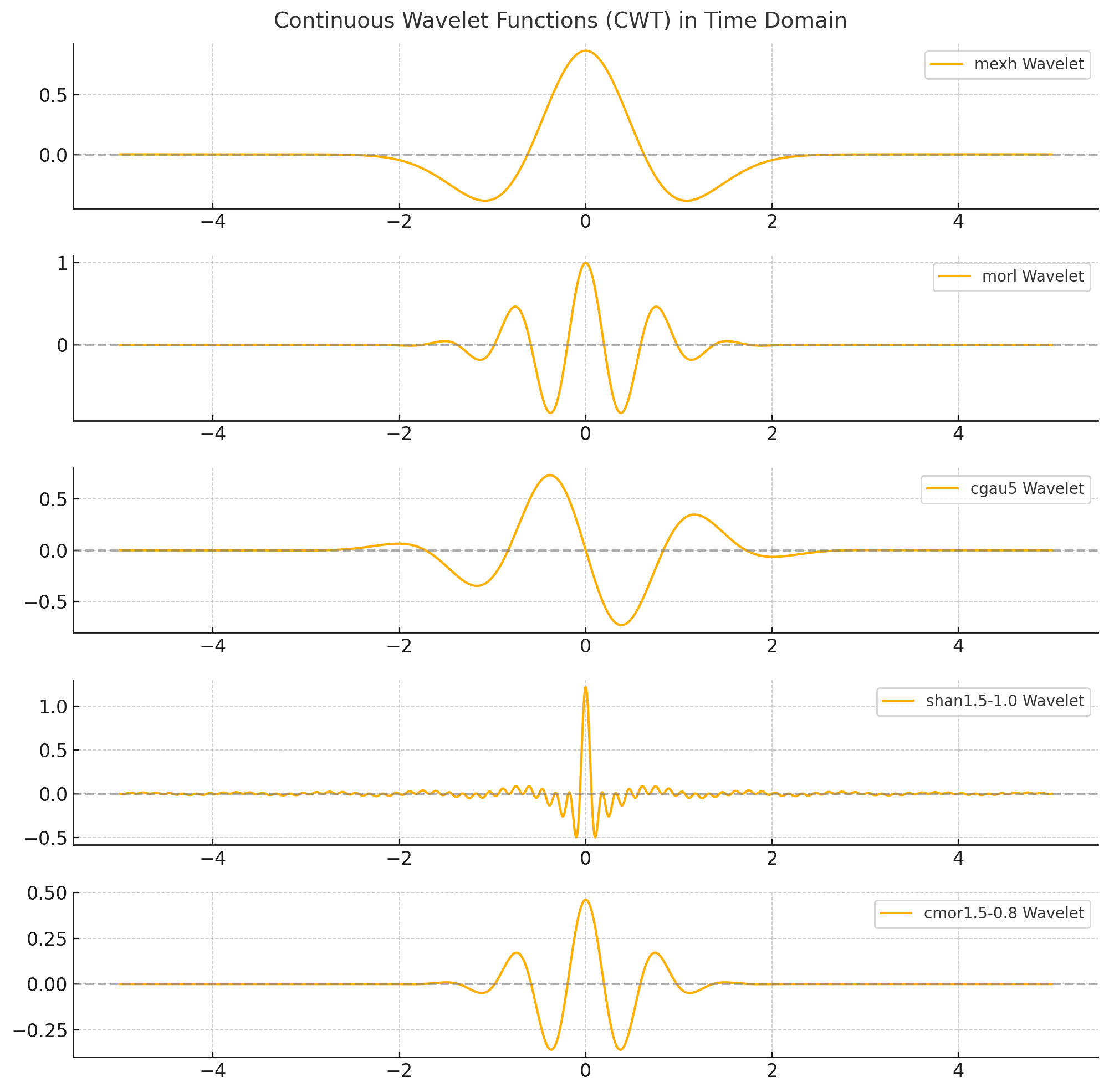
Q. 어 근데 shan wavelet 저거는 유한한 길이를 가지는게 아닌거 같은데요?

A. 예 맞아요 저건 sinc 함수인데 길이가 유한하지 않습니다.
대신 MFCC의 LPF에서 설명했던것 처럼 저게 푸리에치면 사각형 필터가 이쁘게 나와서 필터링 기능자체는 기깔나기 때문에 트레이드 오프를 감수하고 쓸수도 있다고 합니다.
또 이외에 morlet wavelet 같은 경우 소멸 평균 조건을 만족하지 않아서 DC 성분을 추가로 빼주는 식으로도 한다구 하네요

암튼 WT의 개념으로 다시 돌아가서, 결국 신호의 특성을 가장 잘 알려줄 수 있는 wavelet을 선택해서 내적을 때려주고 신호에 wavelet 성분이 얼마만큼 들어 있는지를 분석하는게 WT의 개념이다.

Q. $s$ 랑 $\tau$ 는 뭐에요?

A. (대충 수식 때려넣기)

\psi_{s, \tau}(t) = \frac{1}{\sqrt{s}} \psi\left( \frac{t - \tau}{s} \right)

아하! $s$ 를 통해서 wavelet의 진폭을 조절해주고 (앞의 루뜨 항은 정규화를 위한거고)
$\tau$ 를 통해서 wavelet을 shifting 해주고
이렇게 wavelet을 막 옮기고 지지고 볶아가면서 다 내적을 때려주는거구나!

그렇다면, $s$ 를 조절하면서, 짧은 웨이블릿으로 내적쳐서 고주파 성분 분석하고, 긴 웨이블릿으로 저주파 분석을 하면 되겠네!

그리고 원신호를 다 조져놓고 짜르고 할거 없이 그냥 $\tau$ 조절해서 시간별로 신호 특성을 파악하면 될거고

근데 그러면 $s$ 랑 $\tau$ 를 정하는 기준도 빡셀거고 연산량이 그냥 FFT보다도 뒤지게 빡세서 DWT가 정말 중요하겠군요!

DWT (Discrete Wavelet Transform)

아무튼 dicrete이니까 신호도 이산 신호를 쓰겠죠잉?
수식먼저 봅시다

W_x(j, k) = \sum_{n} x[n] \psi^*_{j,k}[n]

\psi_{j,k}[n] = \frac{1}{\sqrt{2^j}} \psi\left(\frac{n - k2^j}{2^j}\right)

scale 과 shift를 더 다른 방식으로 조정하는 방식도 있지만, 일단 가장 기본적인 식을 가져왔습니다. 2의 멱승단위로 조정하는 dyadic scale 방식

멀티해상도 분석 (Multi-Resolution Analysis, MRA)

DWT는 멀티해상도 분석이라는 형태로 여러 단계에 걸쳐 수식의 연산을 수행한다.

$j$ 는 이러한 단계의 차수이다. 수식을 자세히 들여다보면 $j$ 가 낮을때는 고주파 형태, $j$ 가 높을때는 저주파 형태의 wavelet을 가지는 것을 알 수 있다. 즉 초반에는 상대적으로 고주파를 러프하게 분석하고 차수가 늘어날 수록 점점 더 저주파 분석을 세밀하게 수행하는 형태로 분석을 한다.

$k$ 는 shifting index로 0, 1, 2, ... 로 변화시키면서 신호를 삭 훑어서 분석하게 하며, 차수가 높을 수록 점점 더 띄엄띄엄 분석한다.

차수가 점점 높아질수록 저주파 분석 위주로 갈거기 때문에 필요없고 데이터양만 차지하는 고주파는 버리면서 저주파에 다시 DWT를 적용하는 형태의 필터뱅크가 운용된다.

DWT의 필터 뱅크 구조

고주파 필터(High-Pass Filter, HPF)
→ 세부적인 변화(Detail, 고주파 성분) 추출
저주파 필터(Low-Pass Filter, LPF)
→ 부드러운 신호(Approximation, 저주파 성분) 추출

필터를 통과한 저주파 성분은 다시 DWT에 넣어서 더 세분화한다.
즉, 고주파는 한 번만 계산하고, 저주파를 계속 반복적으로 쪼개면서 분석

저주파 성분 구할때는 사실 언급한 wavelet function이 아니라 scale function이라는 함수가 따로 사용된다.

DWT에서 주로 사용되는 다우베쉬(Daubechies) 계열의 웨이블릿 기준으로 설명

스케일링 함수 $\phi(t)$ 는 다음의 다중 해상도 관계를 만족해야 한다:

\phi(t) = \sum_k h_k \phi(2t - k)

여기서 $h_k$ 는 스케일링 필터 계수 (Low-Pass Filter 계수)
즉 "스케일링 함수는 자기 자신을 2배 크기로 확대하여 선형 조합할 수 있다"는 의미이다.

이후 스케일링 함수 $\phi(t)$ 를 사용하여 웨이블릿 함수 $\psi(t)$ 를 정의한다:

\psi(t) = \sum_k g_k \phi(2t - k)

여기서 $g_k$ 는 웨이블릿 필터 계수 (High-Pass Filter 계수)이다.

하지만, Haar 웨이블릿과 같이 스케일링 함수와 웨이블릿 함수가 독립적으로 정의되는 경우도 있다.

다운 샘플링(Down Sampling)

각 필터를 통과하고 난 후에는 다운 샘플링 과정을 거쳐주어야 한다.

낮아진 주파수 대역에 맞게 해상도를 맞춰 불필요한 데이터를 덜어내고 연산 효율성을 높인다. HPF 필터 통과한건 이제 안쓸거라 상관없고, LPF 통과를 한건 $f_{max}$ 가 이미 반으로 줄었기 때문에 Nyquist Theorem도 만족한다.
이전 차수에서 활용한 basis와 중복되는 패턴이 남기 때문에 basis orthogonality를 유지하기 위해 이걸 털어내는 용도로도 다운 샘플링을 해주어야 한다.

수식으로 요약한 DWT 과정

신호 $x[n]$ 을 스케일링 함수 $\phi$ 와 웨이블릿 함수 $\psi$ 로 내적하여 Approximation $A_j$ 와 Detail $D_j$ 계수를 계산
$A_j[k] = \sum_n x[n] \phi_{j,k}[n]$ $D_j[k] = \sum_n x[n] \psi_{j,k}[n]$
필터뱅크를 사용하여 신호를 저주파/고주파로 분해 (LPF, HPF 적용 후 다운샘플링), 다음단계에서는 Approximation 만 사용함
$A_{j+1}[k] = \sum_n h[n - 2k] A_{j}[n]$ $D_{j+1}[k] = \sum_n g[n - 2k] A_{j}[n]$

즉, DWT는 신호를 저주파 성분(부드러운 구조)과 고주파 성분(세부 변화)으로 반복적으로 분해하는 과정이다.

실습

아우 귀찮아.. DWT는 자료도 없어서 실습 자료를 내가 거의 짜야 하다보니 뭔가 멋들어지게 못하겠다.
DWT 자체는 PyWavelets 패키지 받으면 쉽게 할 수 있다..

DWT 수행 및 계수 시각화

import librosa
import pywt
import matplotlib.pyplot as plt

# 트럼펫 샘플 불러오기
y, sr = librosa.load(librosa.ex('trumpet'))

# 다중 해상도 분석 (Multi-Resolution Analysis, MRA)
wavename = 'db4' # Daubechies 4 wavelet 사용
max_level = 4  # 4단계 DWT 수행
coeffs = pywt.wavedec(y, wavename, level=max_level)

# 원본 신호 시각화
plt.figure(figsize=(12, 10))
plt.subplot(max_level + 2, 1, 1)
plt.plot(y, color='black')
plt.title("Original Signal")
plt.xlim([0, len(y)])

# 각 단계별 Approximation 및 Detail 계수 시각화
for i in range(1, max_level + 1):
    plt.subplot(max_level + 2, 1, i + 1)
    plt.plot(coeffs[i], color='red')
    plt.title(f"Detail Coefficients at Level {i}")
    plt.xlim([0, len(coeffs[i])])

# 마지막 Approximation 계수 시각화
plt.subplot(max_level + 2, 1, max_level + 2)
plt.plot(coeffs[0], color='blue')
plt.title("Final Approximation Coefficients")
plt.xlim([0, len(coeffs[0])])

plt.tight_layout()
plt.show()

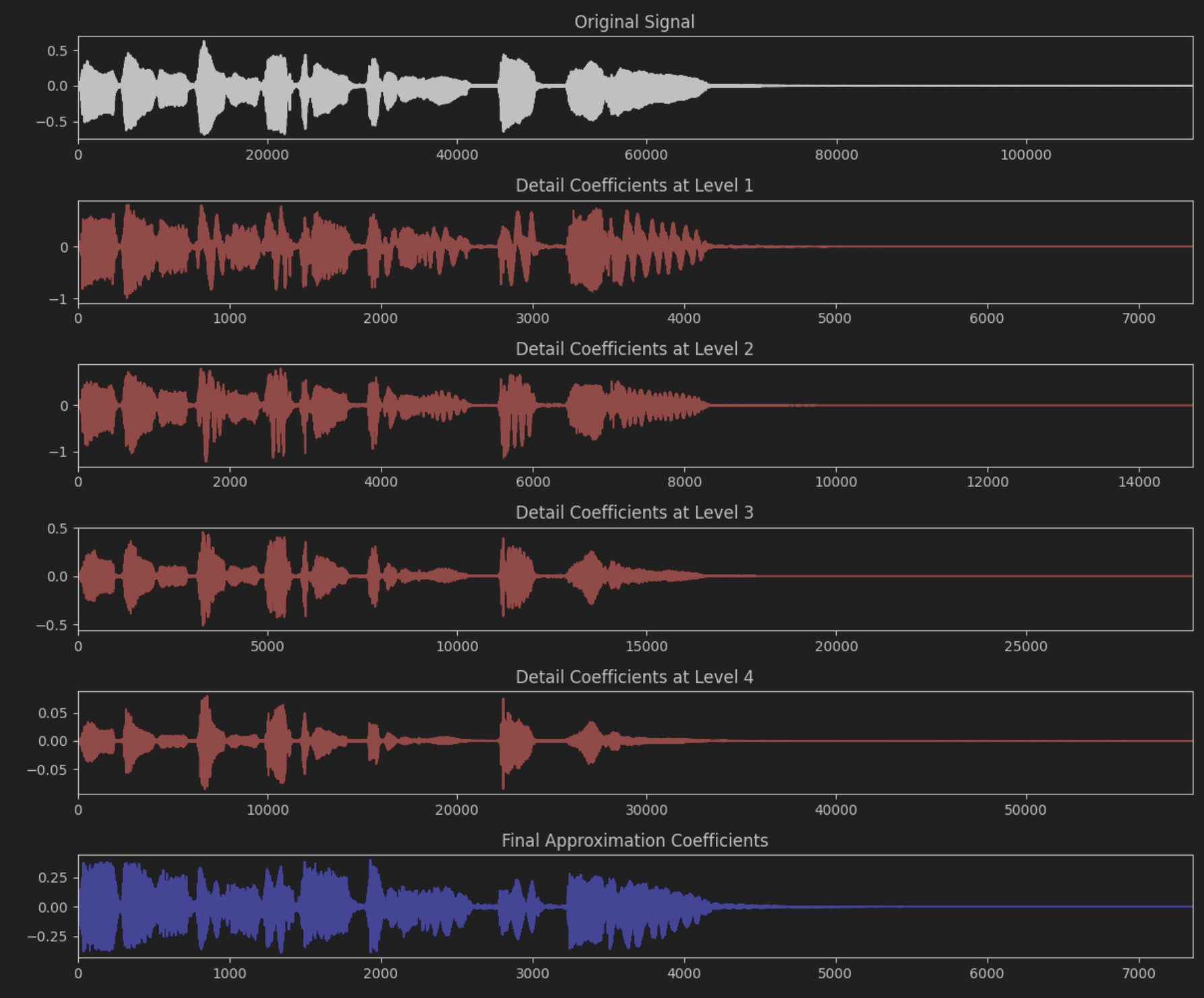
이르케 detail에 고주파 성분, approximation에 저주파 성분이 남는다.

그냥 그렇다는 사실만 확인하는 거 같아서 좀 더 와닿을수 있게

noise 제거 및 IDWT

합성 사인파에 고주파 노이즈를 추가해서 DWT로 details를 분리해내고 다시 IDWT 태워서 노이즈 제거가 되는지를 확인해보았다.

import numpy as np
import pywt
import matplotlib.pyplot as plt

# 샘플링 주파수 및 시간 설정
fs = 1000  # 샘플링 주파수 (Hz)
t = np.linspace(0, 0.3, fs, endpoint=False)  # 1초 동안의 샘플

# 사인파 합성 (기본 신호)
freqs = [5, 50, 100]  # 주파수 성분 (Hz)
signal = sum(np.sin(2 * np.pi * f * t) for f in freqs)  # 여러 주파수를 합성

# 고주파 노이즈 추가
np.random.seed(42)
noise = 0.5 * np.random.randn(len(t))  # 고주파 노이즈 생성
noisy_signal = signal + noise  # 원래 신호에 노이즈 추가

# DWT 수행 (다중 레벨)
wavelet = 'db4'
coeffs = pywt.wavedec(noisy_signal, wavelet, level=3)

# 고주파 성분 제거 (D1, D2를 0으로 설정)
coeffs_filtered = [coeffs[0], coeffs[1], coeffs[2], np.zeros_like(coeffs[3])]

# IDWT 수행 (노이즈 제거된 신호 복원)
denoised_signal = pywt.waverec(coeffs_filtered, wavelet)

# 시각화
plt.figure(figsize=(12, 8))

plt.subplot(3, 1, 1)
plt.plot(t, noisy_signal, label="Noisy Signal")
plt.title("Noisy Signal (Original + High-Frequency Noise)")
plt.legend()

plt.subplot(3, 1, 2)
plt.plot(t, signal, label="Original Clean Signal")
plt.title("Original Signal (Without Noise)")
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(denoised_signal[:len(t)], label="Denoised Signal (DWT-based)")
plt.title("Denoised Signal (High-Frequency Noise Removed)")
plt.legend()

plt.tight_layout()
plt.show()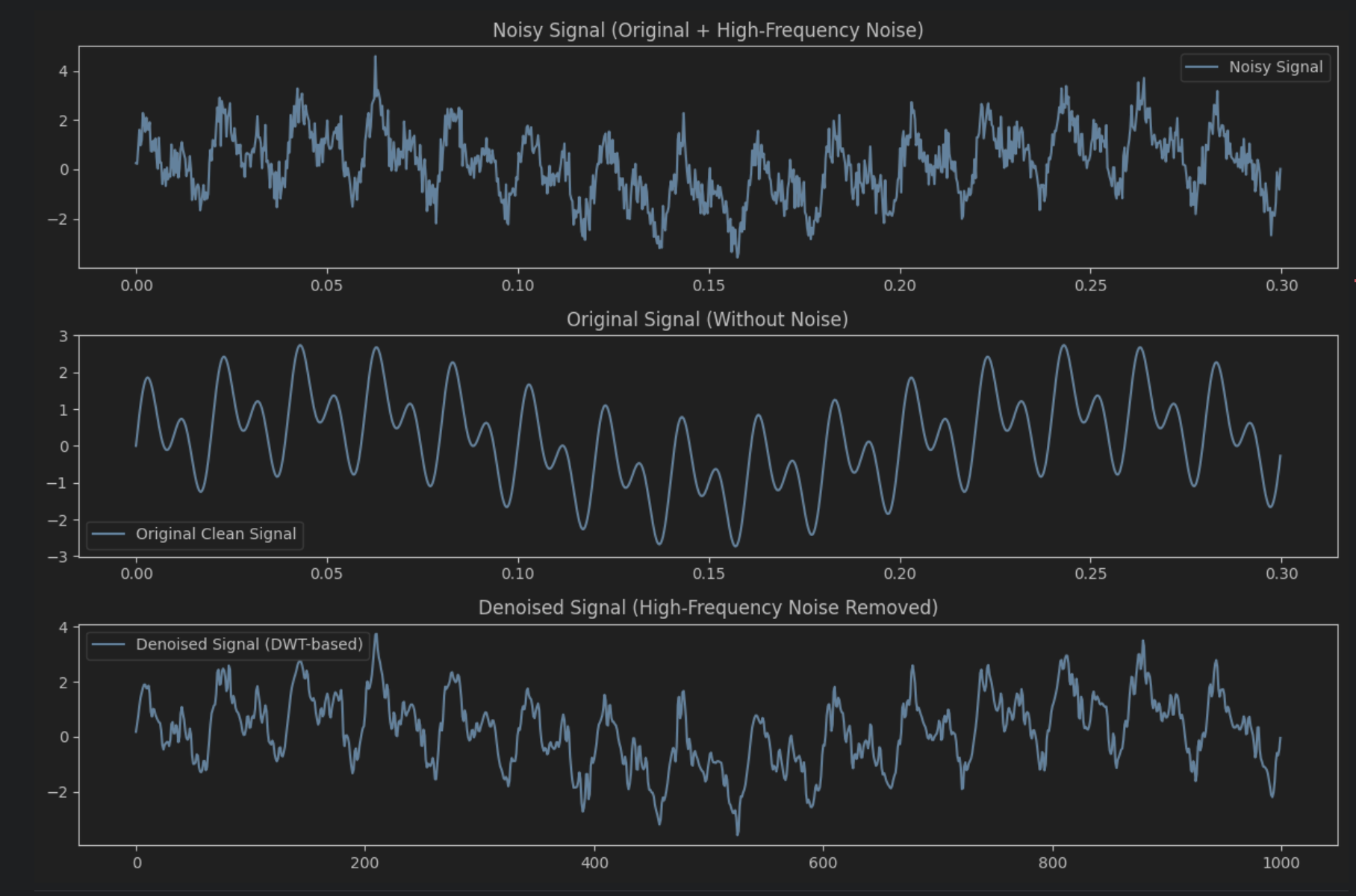

어느정도 노이즈 스무딩이 된것을 확인할수 있었따 쩜쩜

whateverpartysover

인공지능 못해요

이전 포스트