[DSP] MFCC (STFT, Mel Spectogram, DCT)

whateverpartysover·2025년 3월 8일
DSP

DSP 이론

목록 보기
3/4
post-thumbnail

코드는 깃헙

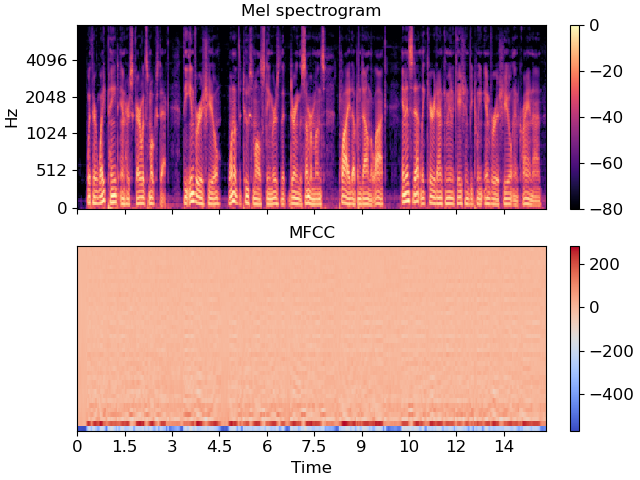
MFCC는 Mel-Frequency Cepstral Coefficient의 약자로, 음성 신호에서 피쳐를 추출할 때 가장 많이 쓰이는 방법이다. 특히 음성 인식이나 스피커 식별, 감정 분석 등 음성 데이터 관련 작업에서 거의 표준처럼 사용되고 있다.

왜 MFCC를 쓸까?

음향 배우는 사람들은 등청감 곡선이라는것을 배운다.

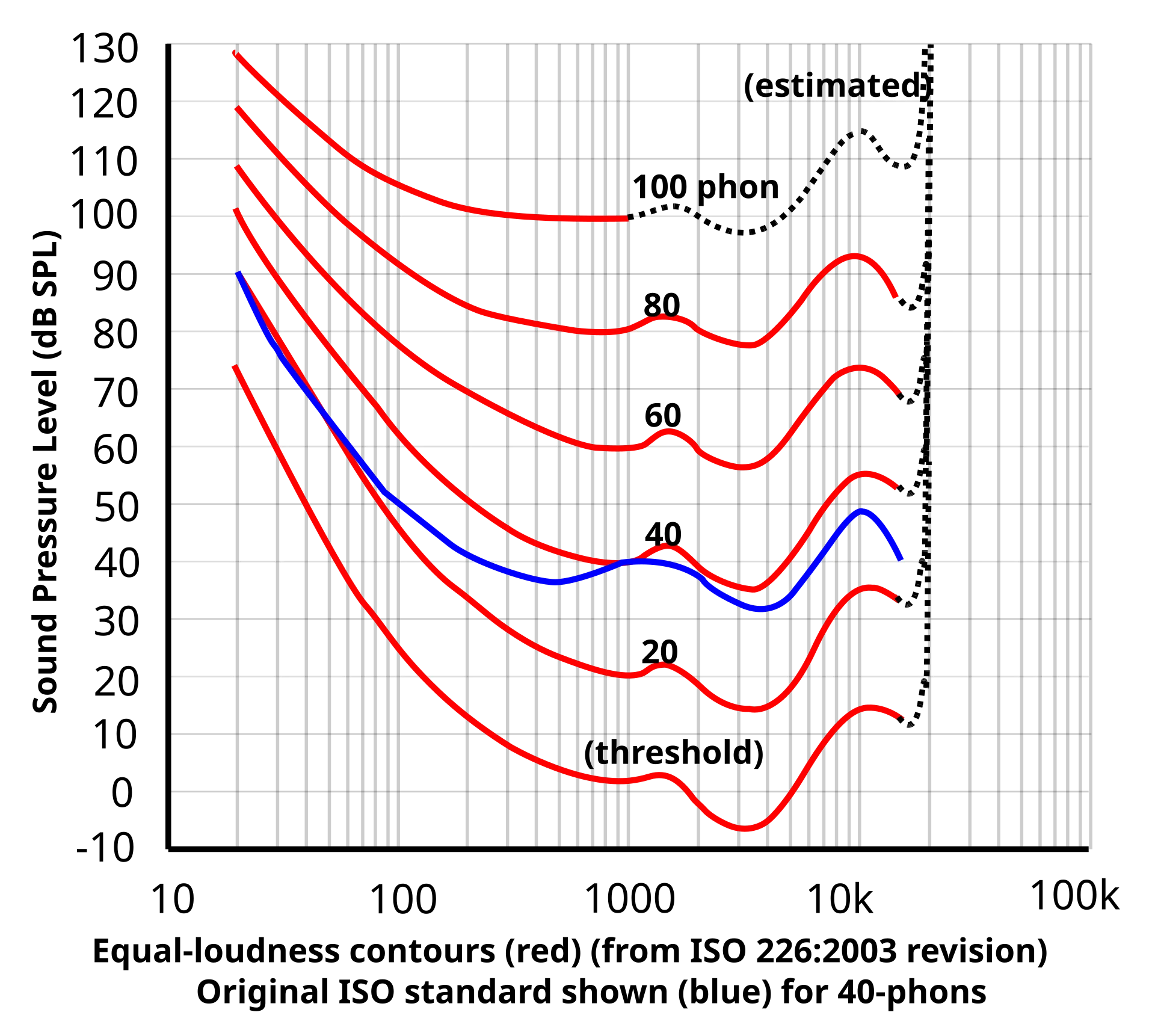
주파수에 따라 사람이 느끼는 음압이 다르다는거다. 위 그래프를 대충 해석하자면 한 곡선위의 점들은 사람이 같은 음압으로 인식한다는 것이다. 저음에서는 실제 음압을 와방 올려줘야 좀 같게 느끼고 (베이스 연주자의 비애), 사람의 목소리가 포함되는 중음역대는 민감하게 반응해서 또 더 잘듣는다. 사람의 소리 인식은 선형적이지 않다.

Mel Scale

인간의 귀는 주파수 자체 또한 선형으로 느끼지 않고, 멜 스케일(Mel Scale)이라는 비선형 척도로 느낀다.

가로축이 주파수 선형으로 나타낸거고, 세로축이 사람이 실제 느끼는 피치감이다. 로그함수 그래프와 비스무리한 형태의 비선형성을 보인다.

MFCC는 바로 이 멜 스케일을 반영한 음성 특성 추출 방법이다. 단순히 푸리에 변환만 하는 것보다, 사람이 실제로 듣는 방식과 더 유사한 특징을 추출할 수 있다.

MFCC 추출 과정

전체 과정 일단 간단 설명하고 중요한 각 과정에 대해 보충 설명 및 실습 드러가보겠습니다잉

푸리에 변환 (Fourier Transform)

이전 FFT 에서 설명했던 프레이밍, 윈도잉 당연히 적용

각 프레임의 신호를 주파수 영역으로 변환하여 이 과정에서 스펙트럼을 얻는다.

요게 사실상 STFT인거다.

멜 필터 뱅크 (Mel Filter Bank) 적용

스펙트럼 성분들을 다 써먹을 수는 없다. 어떤걸 버리고 어떤걸 쓸까?

인간이 실제로 느끼는게 중요하고 그 성분을 피쳐로 뽑아먹는게 중요하다. 그렇기 때문에 필터를 통과 시켜서 피쳐를 구성하기 좋은 데이터만 남겨 강조시키고, 쓰잘데 없는 노이즈 성분은 버리게 한다.

사람은 저주파 대역에 민감하고, 고주파 대역에 둔감하게 반응한다. 그래서 저주파의 필터는 촘촘하게, 고주파 필터는 널찍하게 분포한다.

암튼 요 멜필터 적용된 스펙트럼이 바로 Mel Spectrum이다.

로그 스펙트럼 (Log Spectrum)

필터 뱅크 출력 (에너지)를 로그 스케일로 변환한다.

등청감곡선에서 언급했듯이 사람은 피치 뿐만 아니라 음량 변화 또한 로그 스케일로 느끼기 때문에 이걸 반영해주기 위함이다.

이거도 결국 사람 인지 특성 반영을 위해선 중요한 요소인데 왜 mel 만 붙은겨

암튼 아마 에너지에 로그 붙이는건 원래 해왔고 아마 mel scale 도입에 대한 최초 기여였을거라 그랬을것 같다

DCT (Discrete Cosine Transform)

여태진행한거: FFT, mel scale, log 에너지 반영하여 스펙트럼에 장난질 쳐준거정도 밖에는 없다. MFCC는 결국 특징을 추출하는 작업이고 특징 추출에 가장 중요한게 DCT이다.

여기까지 진행되어 얻은 로그 에너지 값에 코사인 성분의 벡터들을 내적하여 나온 값이 MFCC 계수이다. 이전 상태의 값들은 필터들이 겹쳐있고 하다보니 서로 상관관계가 높다. DCT를 통해 서로 상관관계가 적은 독립적인 특징들로 변환해줄 수 있다.

STFT (Short-Time Fourier Transform)

원리

긴 신호 (대략 몇초~몇십초 가량)를 한꺼번에 푸리에 태워서 주파수 분석을 하고 싶겠지만. 사실 큰 의미가 없다. 그쯤되면 워낙 많은 주파수 대역이 섞여버리니까 주파수 도메인 출력물이 거냥 노이즈 낀거마냥 될 것이다.

이전에도 설명했듯 이런건 그냥 여러 구간 짤라서 스펙트럼을 만드는게 낫다.

스펙트럼 만드는건 대충 해봤으니 실제 많이 사용되는 stft와 활용 변수들에 대한 소개

X(l,k)=∑n=0N−1w(n)⋅x(n+lH)⋅e−j2πknNX(l,k)=\sum_{n=0}^{N-1}w(n)\cdot x(n+lH) \cdot e^{\frac{-j2\pi kn}{N}}
기호의미설명
X(l,k)STFT 결과값시간 구간 index l에서 주파수 bin k의 푸리에 계수 (스펙트럼 값)
x(n)원래 신호시간 도메인 신호
w(n)윈도우 함수Hanning, Hamming 같은 창 함수 (길이 N짜리)
N창 길이한 번에 FFT하는 구간 길이 (윈도우 길이)
HHop size윈도우가 겹치는 사이즈
l창 인덱스몇 번째 창인지 (시간축 인덱스)
k주파수 인덱스FFT 결과에서 몇 번째 주파수 bin인지
  • 창 길이 N은 크면 주파수 해상도가 올라간다. 이전에 설명했던것 처럼 연산에 들어가는 샘플 수 자체가 늘어남에 따라 주파수 인덱스 자체가 많아지기 때문이다. 다만 주파수 해상도를 포기하여 N을 작게한다면 어느 시간대에서 어떤일이 발생하는지를 스펙토그램을 보고 파악하기 쉬워진다.
  • 기존에 알고 있던 stft에 Hop size라는게 추가되었다. stft를 진행할 때 윈도우를 뚝뚝 끊어서 계산하는게 아니라 어느정도 겹쳐가면서 스펙트로그램이 시간에 따라 부드럽게 연결될 수 있도록한다. 보통 창 길이의 50~75%를 hop size로 활용한다고 한다.

실습

이전까지 numpy 혹은 직접 구현으로 보여줬는데, 파이썬은 librosa라는 wav를 다룰 좋은 패키지가 있다. 앞으로의 실습들도 요걸 활용할 예정

우선 실습에 사용할 샘플 웨이브도 요렇게 받아올 수 있다.

import librosa
import matplotlib.pyplot as plt

# 트럼펫 샘플 불러오기
y, sr = librosa.load(librosa.ex('trumpet'))

# 기본 정보 확인
print(f'Sample rate: {sr}')
print(f'Signal shape: {y.shape}')

fig = plt.figure(figsize = (14,5))
librosa.display.waveshow(y, sr=sr, color="blue")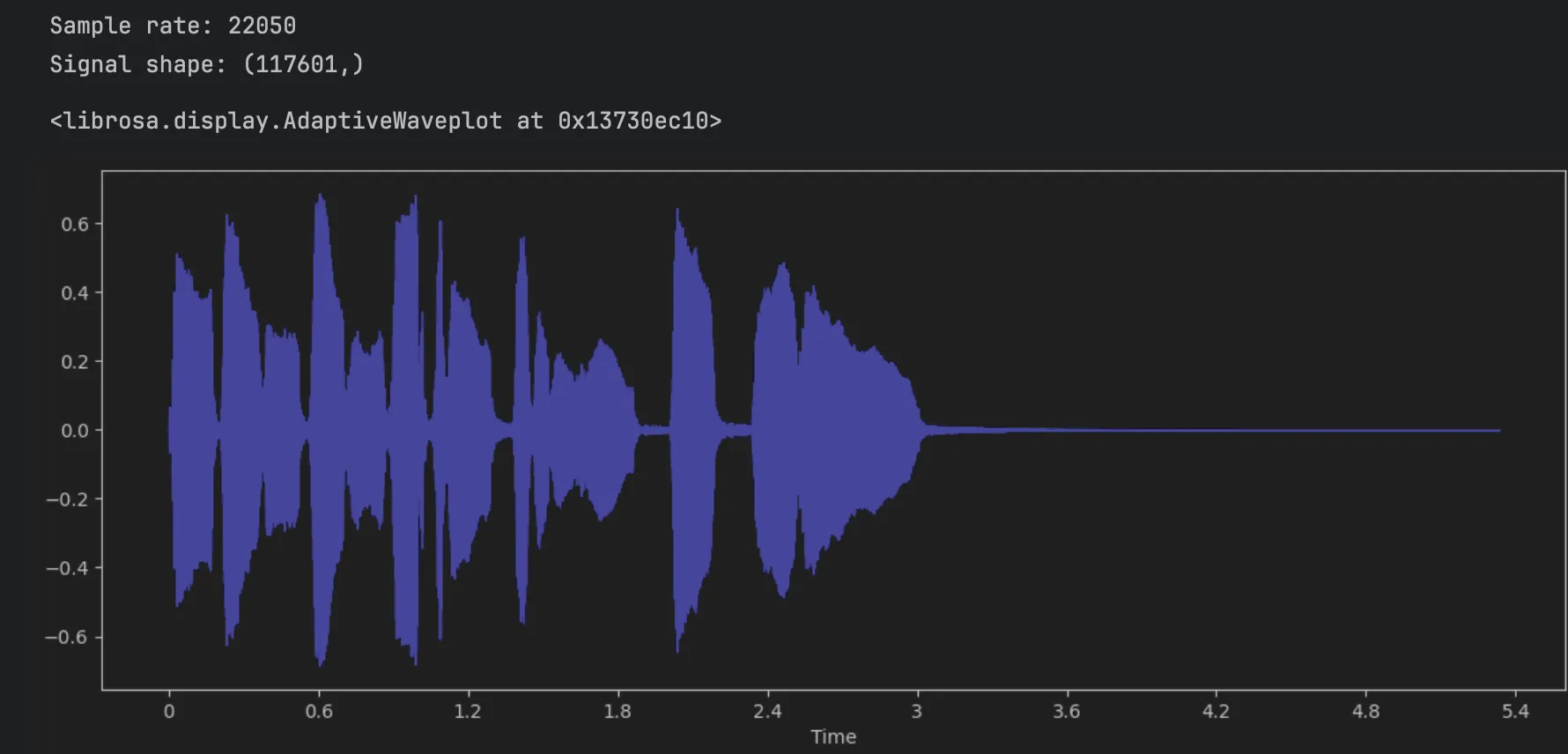

당연하게도, 이 파형으로 에너지 레벨정도는 유추해볼 수 있겠지만 어떤 음역대의 음색을 사용했고, 음정이 어떻게 변화해갔는지 알 수는 없다.

import numpy as np

# STFT 수행
D = librosa.stft(y, n_fft=1024, hop_length=512, window='hann')

# 복소수 출력됨 (실수부+허수부)
print(f'STFT Shape: {D.shape}')  # (frequency_bins, time_frames)

# 진폭 스펙트럼을 dB로 변환 (시각화 편의)
D_db = librosa.amplitude_to_db(np.abs(D), ref=np.max)

# 시각화
plt.figure(figsize=(5, 3))
librosa.display.specshow(D_db, sr=sr, hop_length=512, x_axis='time', y_axis='log')
plt.colorbar(format="%+2.0f dB")
plt.title('Spectrogram (dB)')
plt.show()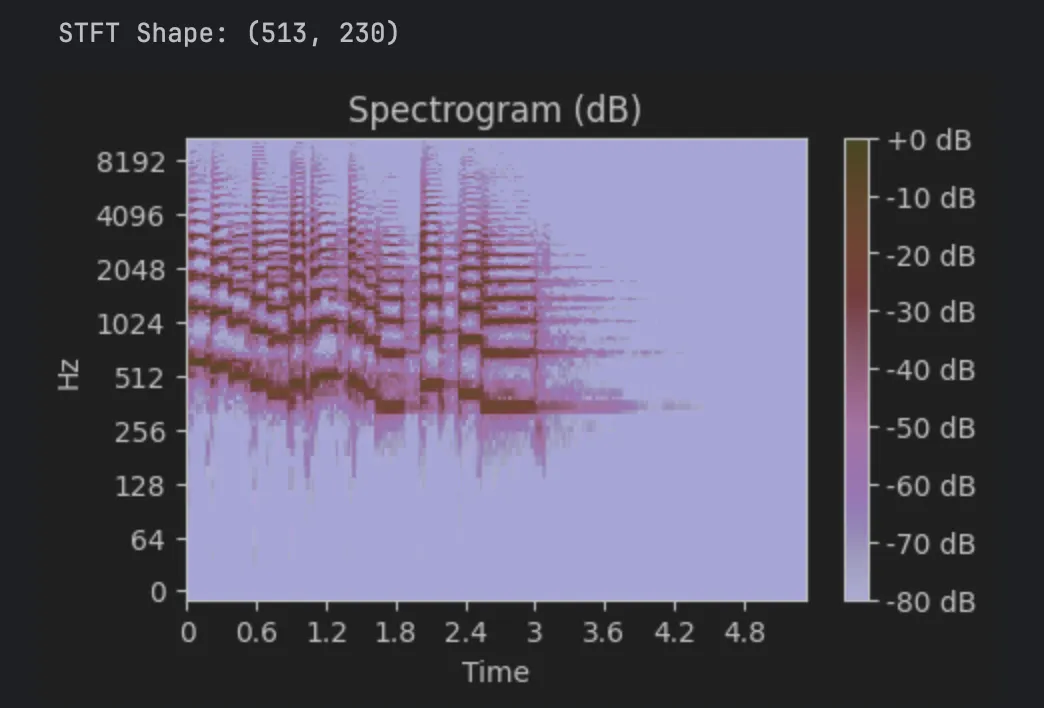

창 사이즈 1024로 stft를 조져주었다. hop_length 512로 하였으니 50% 겹치도록 홉을 해준거다. window 함수로는 hanning window를 활용했다.

stft 를 통해서 주파수 대역의 스펙트럼을 얻을 수 있다. 음정이 내려갔다 살짝올라갔다 내려갔다 살짝올라갔다 다시 내려가는 형태를 볼 수 있다. 들어보면 정확하다.

층이 쌓인거같이 보이는건 배음이다. 억지로 신스에서 단순파 만든게 아닌 이상 자연계의 모든 소리들은 배음을 포함한다.

Mel Filter와 Mel Spectrum

원리

필터 뱅크 구성을 좀 더 자세하게 설명하면 다음과 같다.

  1. 주파수 범위 정의
  • 샘플링 주파수에 따라 분석 가능한 대역은 0Hz ~ Nyquist 주파수 (샘플링 주파수의 절반)
  • 음성처리 기준에서 대역들은 다음과 같이 주로 쓰인다.
    • Narrowband (NB): 300Hz ~ 3400Hz (아날로그 전화 기준, 오래된 방식)
    • Wideband (WB): 0Hz ~ 8kHz (보통 VoIP, 스마트폰, 화상회의 등에서 사용)
    • Super Wideband (SWB): 0Hz ~ 16kHz (고품질 음성인식, 스튜디오 녹음 등에서 사용)
  1. 멜 스케일 기준 필터 배치

Hz → Mel 변환:

mel=2595⋅log⁡10(1+f700)mel = 2595 \cdot \log_{10}(1+\frac{f}{700})

Mel → Hz 변환:

f=700⋅(10mel2595−1)f = 700 \cdot (10^{\frac{mel}{2595}} - 1)

위 공식대로 대역의 최저 및 최고 주파수를 mel scale로 변환해준다.

이걸 가지고 mel scale 상에서 등간격으로 필터 배치의 중심점을 잡아준다. 필터 개수는 NB 기준으로 MFCC 13차원, 필터 개수 26개를 많이 쓴다고 한다. 요즘은 밴드가 넓어지다보니 더 많이 쓰는 경우가 많다.

다시 mel scale 축을 frequency 대역으로 바꾸어줘서 필터 배치 점들을 삼각형 형태로 연결되게 필터들을 구성한다.

이 필터를 통과시킨 스펙트럼이 mel spectrum이다.

실습

  • mel filter bank 구현

코드로 구현한 mel_filter_bank는 아래와 같다.

import numpy as np

def hz_to_mel(hz):
    return 2595 * np.log10(1 + hz / 700)

def mel_to_hz(mel):
    return 700 * (10**(mel / 2595) - 1)

def mel_filter_bank(num_filters, fft_size, sample_rate, f_min=300, f_max=8000):
    # Step 1: 주파수 범위 설정
    nyquist = sample_rate / 2
    f_max = min(f_max, nyquist)

    # Step 2: Hz -> Mel 변환
    mel_min = hz_to_mel(f_min)
    mel_max = hz_to_mel(f_max)

    # Step 3: 멜 스케일에 등간격으로 필터 중심 배치
    mel_points = np.linspace(mel_min, mel_max, num_filters + 2)
    hz_points = mel_to_hz(mel_points)

    # Step 4: Hz를 FFT bin index로 변환
    bin_points = np.floor((fft_size + 1) * hz_points / sample_rate).astype(int)

    # Step 5: 각 필터를 삼각형으로 구성
    filters = np.zeros((num_filters, fft_size // 2 + 1))

    for m in range(1, num_filters + 1):
        left = bin_points[m - 1]
        center = bin_points[m]
        right = bin_points[m + 1]

        for k in range(left, center):
            filters[m-1, k] = (k - left) / (center - left)
        for k in range(center, right):
            filters[m-1, k] = (right - k) / (right - center)
    return filters
import matplotlib.pyplot as plt

sample_rate = 16000
fft_size = 512
num_filters = 26

filters = mel_filter_bank(num_filters, fft_size, sample_rate)

plt.figure(figsize=(8, 4))
for i in range(num_filters):
    plt.plot(filters[i])
plt.title('Mel Filterbank (26 filters)')
plt.xlabel('FFT Bin')
plt.ylabel('Amplitude')
plt.grid()
plt.show()

시각화 해보면 다음과 같이 생긴 filter bank를 확인할 수 있다.

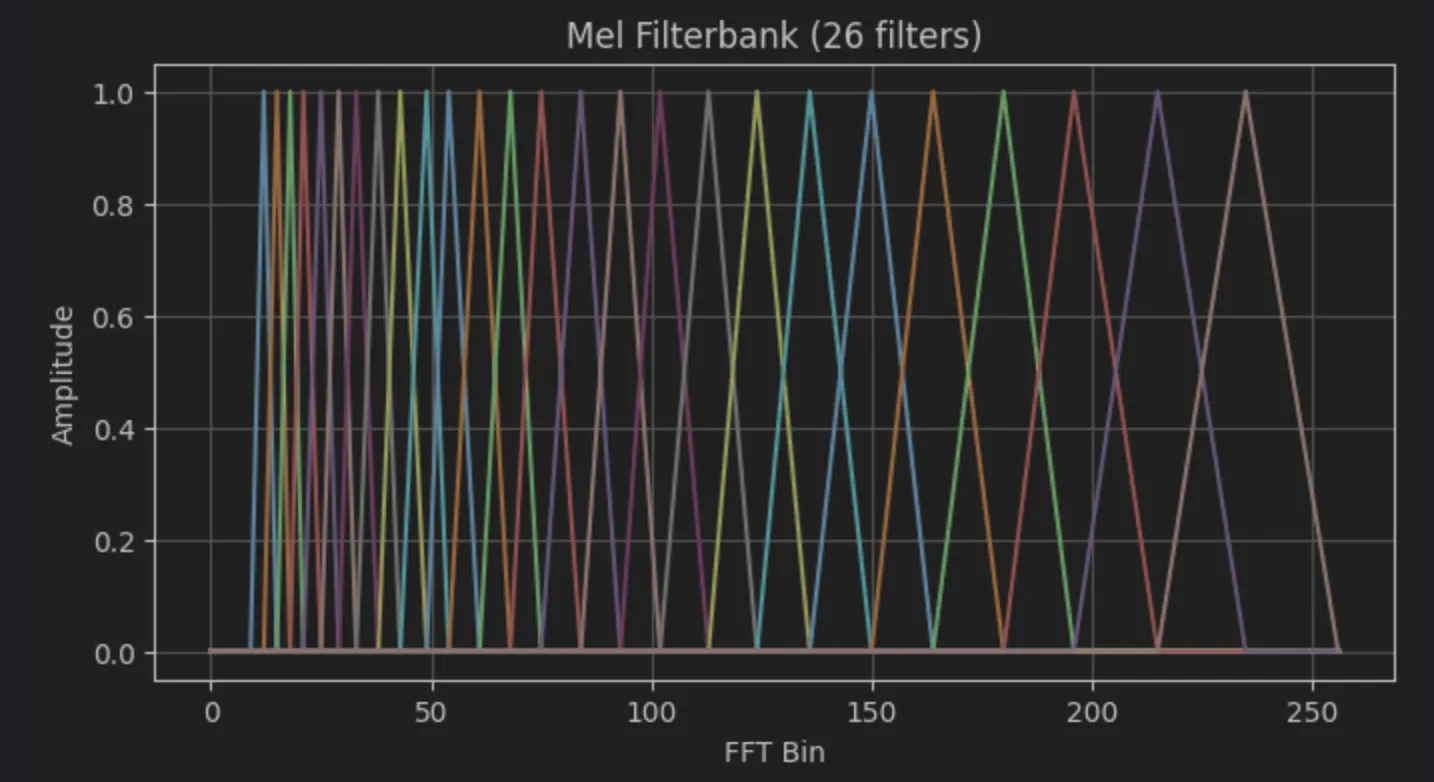
샘플의 스펙토그램에 이 필터를 통과시켜 mel spectogram으로 만들어보자.

import numpy as np
import librosa
import matplotlib.pyplot as plt

# 트럼펫 샘플 불러오기
y, sr = librosa.load(librosa.ex('trumpet'))
# STFT 수행
D = librosa.stft(y, n_fft=1024, hop_length=512, window='hann')

power_spectrum = np.abs(D)**2  # 크기의 제곱으로 파워 스펙트럼 구함

num_filters = 26
filters = mel_filter_bank(num_filters, 1024, sr)
mel_spectrum = np.dot(filters, power_spectrum)  # (26, 프레임 수)

plt.figure(figsize=(12,6))
plt.imshow(10 * np.log10(mel_spectrum + 1e-10), aspect='auto', origin='lower')
plt.colorbar(label='Log Power (dB)')
plt.title('Mel Spectrogram')
plt.xlabel('Frame Index')
plt.ylabel('Mel Filter Index')
plt.show()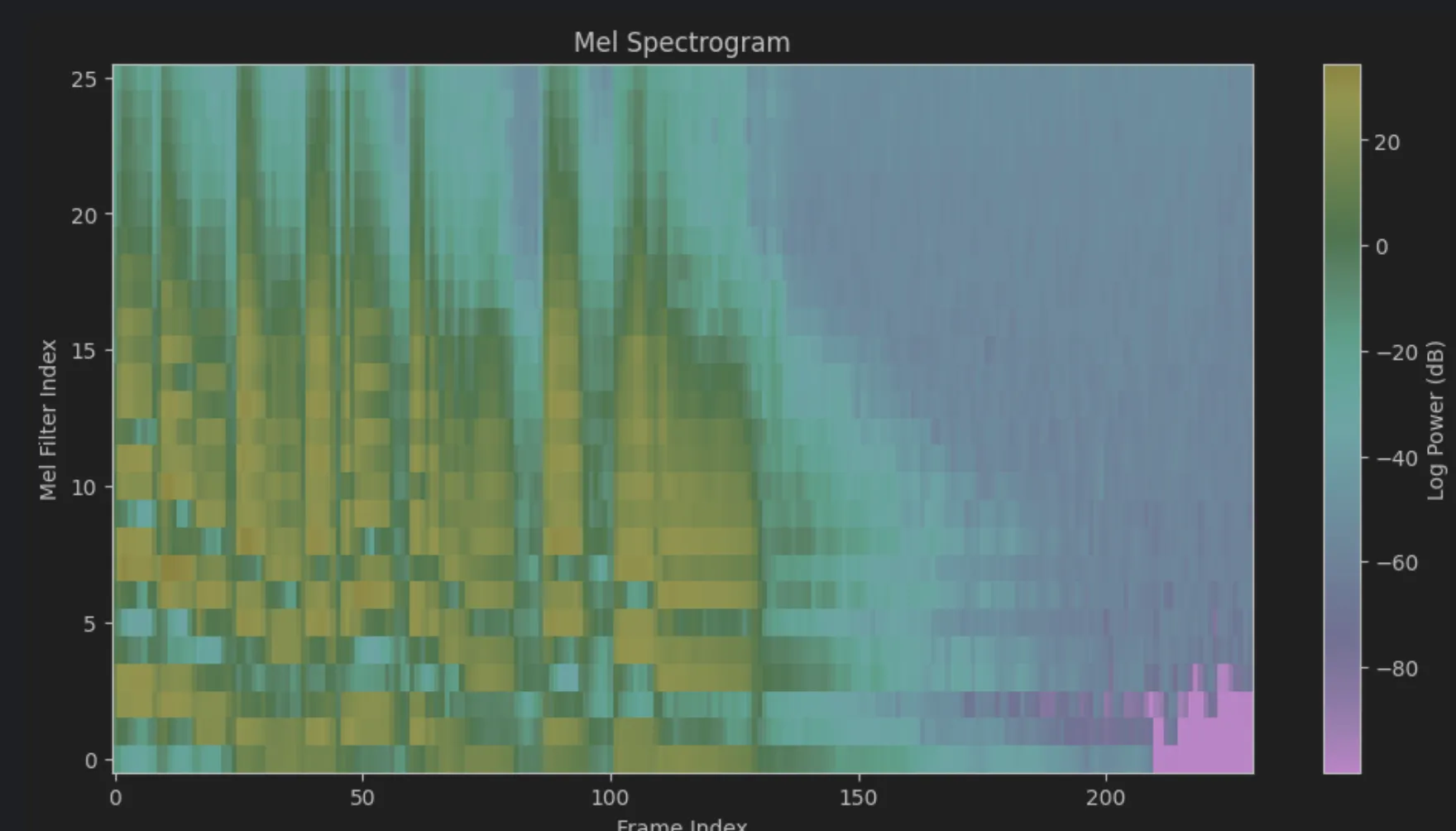

  • librosa를 통한 mel spectogram

사실 librosa의 feature.melspectrogram 함수를 통해 한줄로 할수 있다.

import librosa
import librosa.display
import matplotlib.pyplot as plt
import numpy as np

# 트럼펫 샘플 불러오기
y, sr = librosa.load(librosa.ex('trumpet'))

# 멜 스펙트로그램 계산
mel_spec = librosa.feature.melspectrogram(
    y=y, sr=sr, n_fft=1024, hop_length=512, n_mels=26, fmin=300, fmax=8000
)

# 로그 스케일 (dB로 변환)
log_mel_spec = librosa.power_to_db(mel_spec, ref=np.max)

# 시각화
plt.figure(figsize=(12,6))
librosa.display.specshow(log_mel_spec, sr=sr, hop_length=512, x_axis='time', y_axis='mel', fmin=300, fmax=8000)
plt.colorbar(label='Log Power (dB)')
plt.title('Mel Spectrogram (librosa)')
plt.show()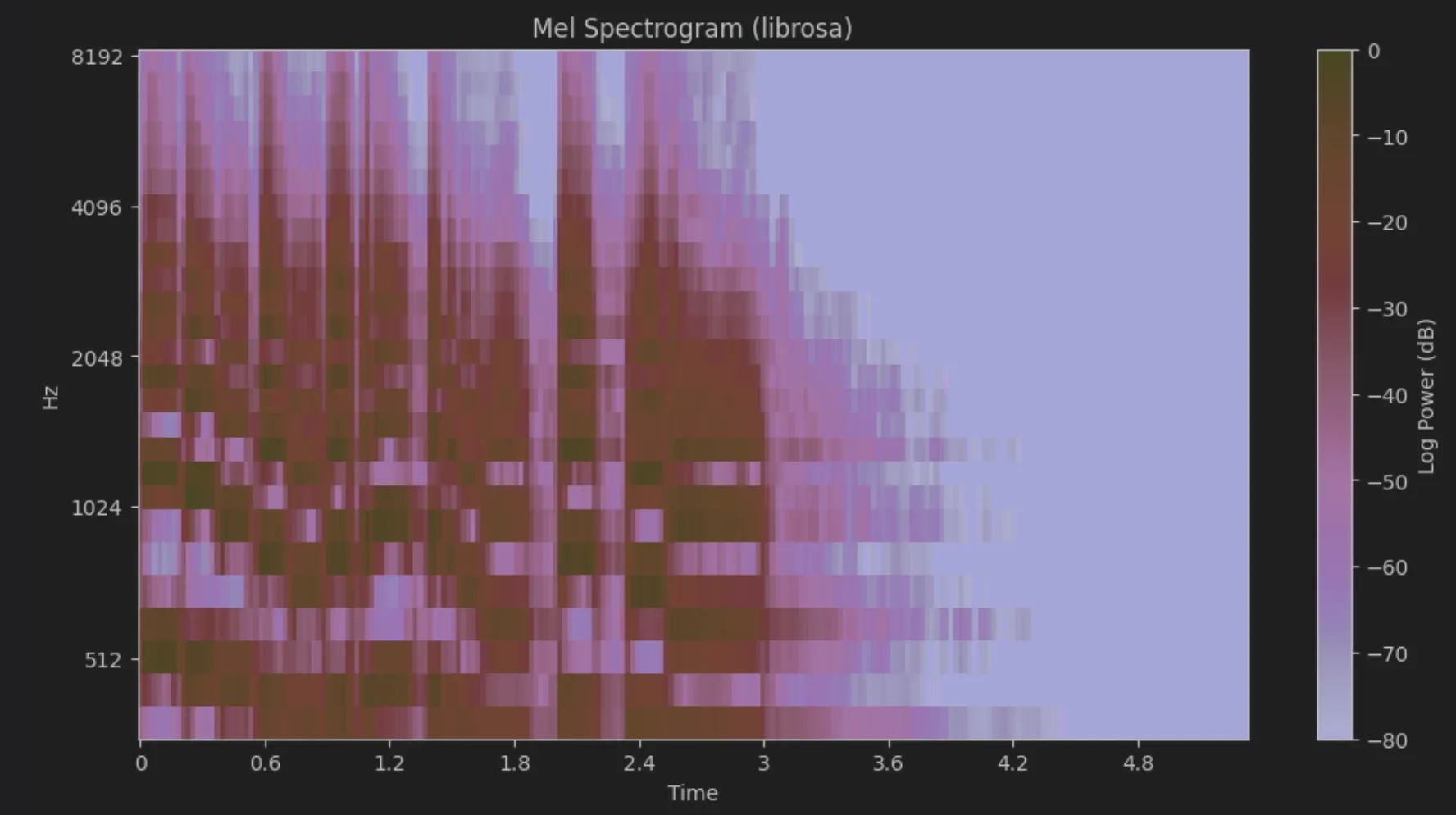

형태가 비슷한걸 볼수 있다.

log power 값이 조금 다른데, dB는 애초에 상대값인거라 0dB의 기준과 정규화 방식에 따라 값자체는 다를 수 있다. 형태 맞으니까 대충 맞은거란 소리

DCT 원리 설명

원리

MFCC에서 가장 많이 쓰는 Type-II DCT 기준으로 설명

멜 필터링 + 로그 씌우기까지 진행된 다음에는 각 필터 출력 에너지가 나열되어있다.

x=[x0,x1,x2,...,xK−1]x=[x_0,x_1,x_2,...,x_{K−1}]

각 주파수 인덱스 kk마다 다음 코사인 함수를 정의할수 있고, 이는 각 주파수 성분에 대해 일정한 주기적 패턴을 가지는 기저함수로 간주할 수 있다.

cos⁡(πK(k+12)n)\cos(\frac{π}{K}(k+\frac{1}{2})n)

결국 이 에너지 벡터와 기저함수를 내적하여 피쳐값을 얻어내는것이 DCT의 과정이다.

cn=∑k=0K−1xkcos⁡(πK(k+12)n)c_n=∑_{k=0}^{K−1}x_k \cos(\frac{π}{K}(k+\frac{1}{2})n)

여기서 nn은 최종적으로 구하게 되는 MFCC 계수의 인덱스이자, DCT 기저함수의 모드 번호를 의미한다. n=0n=0은 DC 성분 (가장 낮은 주파수 성분)에 해당한다. 이때의 코사인 기저 함수는 거의 상수에 가까운 형태로, 전체적인 에너지의 평균적인 크기를 반영하는 역할을 한다. nn이 커질수록, 기저 함수는 점점 더 빠르게 진동하는 형태가 된다.이는 멜 필터 출력 에너지의 세밀한 변화를 포착하는 역할을 하며, 고차 MFCC일수록 더 높은 주파수의 변화를 담는다고 볼 수 있다.

  • DCT에서 코사인을 쓰는 이유?
  1. 주파수 도메인에서 코사인 함수는 실수부를 의미한다. (오일러 공식을 생각) 음성 신호는 기본적으로 실수 데이터라서 코사인만 써도 특징 표현이 다 잘 된다.
  2. n=0 인 성분을 DC 성분이라고 하고, 이 DC 성분이 제일 크고 중요한데, sin 함수는 값이 0이라 요 경계 처리가 좀… 그릏다
    (수정) 라고 공부하고 적어뒀었는데 다시 복기하면서 보니까 DC 성분이 0인 이유가 애초에 sin이 허수부를 나타내기 때문이겠네요... 결론적으로 이유 자체는 그냥 1번 하나로 보면 될거같음

실습

scipy의 fftpack.dct 는 discrete cosine transform을 수행해준다. 실제 수학 계산을 해주는거다.

import scipy
mfcc_scipy = scipy.fftpack.dct(log_mel_spec, type=2, axis=0, norm='ortho')
mfcc_scipy.shape
>> (26, 230)

근데, mfcc를 뽑기 위해서 dct 계산을 하고 나서는 보통 필터개수 절반만큼의 차원만을 사용을 하는데, scipy는 단순 계산만을 제공하기 때문에 실제 스펙토그램의 차원을 다 제공하기 때문에 직접 잘라서 사용해야한다.

물론 librosa에서도 직접 제공을한다.

mfcc_librosa = librosa.feature.mfcc(
    y=y,
    sr=sr,
    n_fft=1024,
    hop_length=512,
    n_mfcc=13,
    n_mels=26,
    fmin=300,
    fmax=8000,
)
mfcc_librosa.shape
>> (13, 230)

얘는 애초에 wav 처리이기 때문에 n_mfcc를 입력가능하게 해주었다.

실제로 값이 같은지 확인을 해보면, DC 성분에서 차이가 꽤 크게 나와 값이 비슷하지는 않다. DC 성분은 전체 평균 에너지값을 대표하다보니 로그 변환방식, 정규화 차이등으로 인해 차이가 생길수도 있고, librosa는 목적이 확실하다 보니 실제 계산 이후에 normalization이나 필터 보정이 추가되었기 때문으로 보인다.

실제로 음성인식에서도 DC 성분은 녹음 환경, 음질등으로 인한 차이를 주로 담는 경우가 많아 실제 스펙트럼 형태인 n≥1 의 성분을 사용하는 경우도 많고, 이에 따라 n≥1 이상의 값만 비교해도 같다면 충분히 같은 값으로 볼 수 있다.

그래서 DC 성분을 제외하고 비교를 해보았을때 거의 비슷한것 확인

profile
whateverpartysover
인공지능 못해요
이전 포스트

[DSP] Sampling (Nyquist Sampling Theorem, LPF)

다음 포스트

[DSP] Wavelet Transform (CWT, DWT)

0개의 댓글