[DSP] Fourier Transform (Frequency Domain, DFT, FFT, Spectogram)

whateverpartysover·2025년 3월 8일
DSP

DSP 이론

목록 보기
1/4
post-thumbnail

음 공부한거 노션에 끄적여보다가 일단 블로그 만들어서 올려봄
작심삼일일수도 있음 감사합니다

암튼 음악 인공지능 회사에서 미디만 만지작거리다 이직 커피챗 하니까 나를 wav 다룰 줄 알거라는 기대섞인 초롱초롱한 눈빛으로 보길래 DSP 공부를 해야겠다고 마음을 먹었다...
논문 읽기전에 기초 DSP 공부 다시...

참고로 코드는
깃헙에 정리하였습니다.

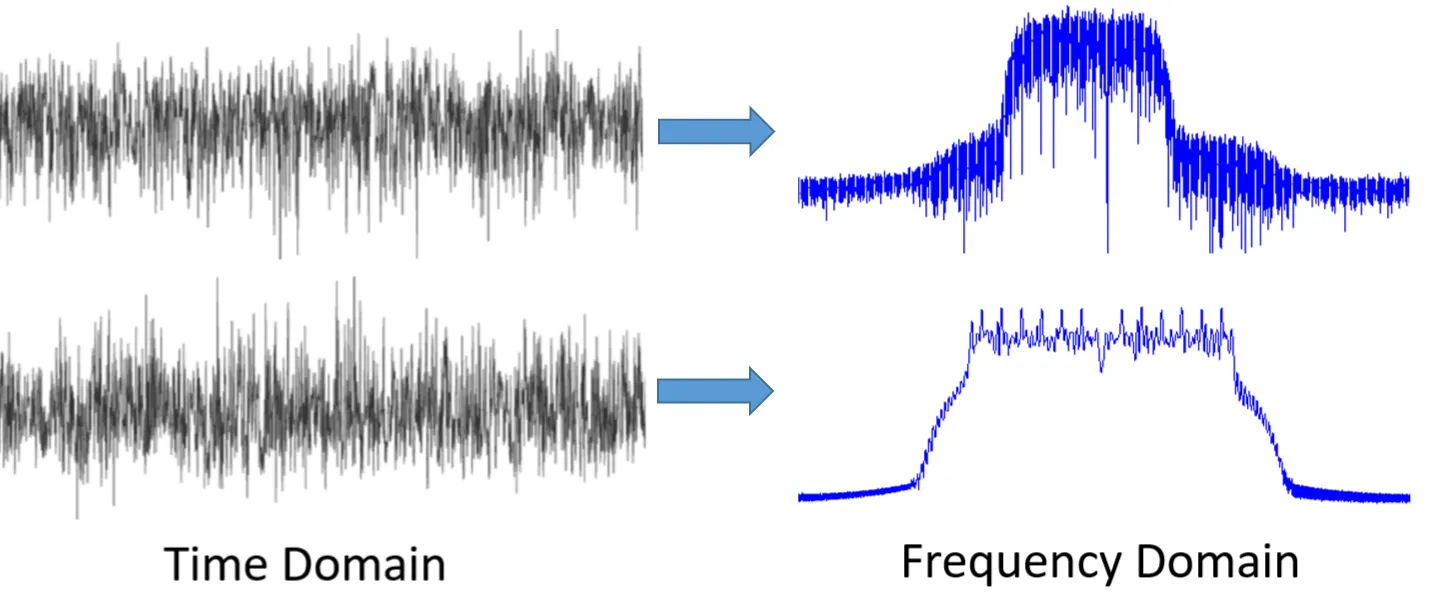
우리는 신호를 볼 때 Time Domain 보다 Frequency Domain으로 보는것을 선호한다. 왜 그럴까?

Time Domain에서 신호 자체의 주요 특징은 찾아내기 힘들기 때문이다. 뭐 예를들어 기껏해야 전체 신호의 크기 정도. Frequency Domain 에 익숙해있다면 수학적인 의미를 파악하지 못하더라도 신호의 특성을 어느정도 알아차릴 수 있다.

Fourier Transform

Fourier Series

Frequency Domain의 이해는 푸리에 급수로부터 시작한다. 수식 등은 그냥 제끼고.. 핵심은 결국 모든 신호는 sinusoidal한 신호들의 합으로 표현될 수 있다는 것이다.

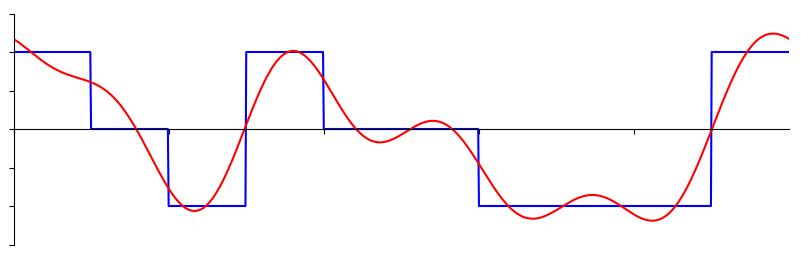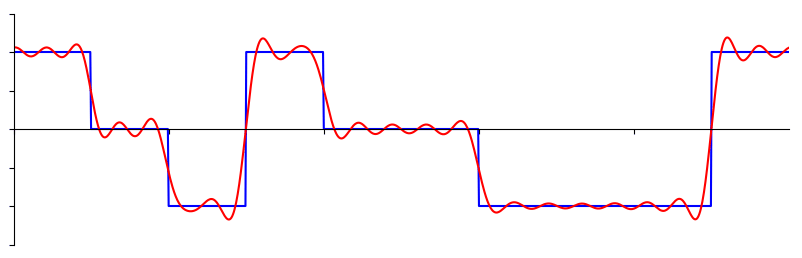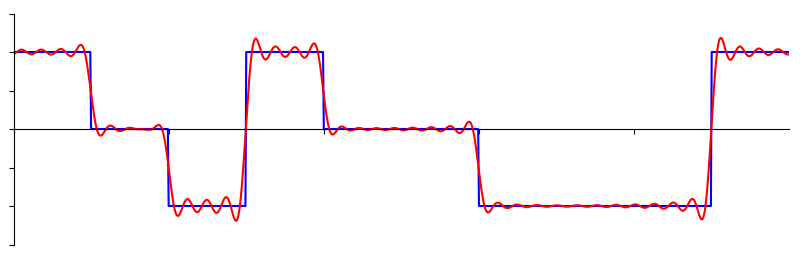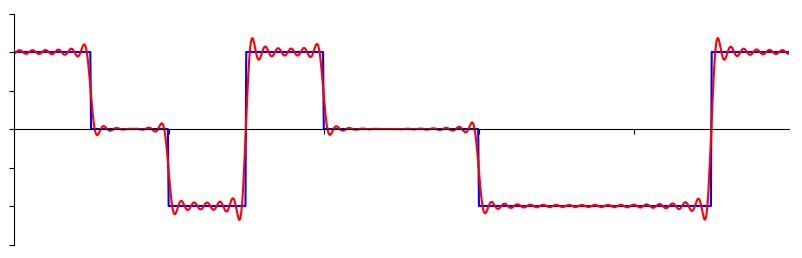
Fourier Transform

나는 공학수학에서 배웠으니까 디지게 불친절한 핵심

주어진 신호 x(t)x(t)를 주파수 ff에 대응하는 정현파 함수 ej2πfte^{j2\pi ft}와 내적함을 통해서 신호가 주파수 성분을 얼마나 가지고 있는지를 계산한 것이 푸리에 변환이다.

여기서

ej2πft=cos⁡(2πft)+jsin⁡(2πft)e^{j2\pi ft} = \cos(2\pi ft) + j\sin(2\pi ft)

(오일러 공식)

내적이 취해지는 벡터 공간은 sin과 cos이 orthonormal 한 함수 공간

그리고 함수 공간에서 내적의 공식 자체는

⟨f(t),g(t)⟩=∫−∞∞f(t)⋅g∗(t)dt⟨f(t),g(t)⟩=∫_{−∞}^{∞}f(t)⋅g^∗(t)dt

이라서

푸리에 변환 자체는 결국

X(f)=⟨x(t),ej2πft⟩=∫−∞∞x(t)⋅e−j2πftdtX(f)=⟨x(t),e^{j2πft}⟩=∫_{−∞}^∞ x(t)⋅e^{−j2πft}dt

의 식을 가지게 된다.

근데 연속적인거는 사실 DSP에서 다루지는 못하니께… 결국 DSP에서 주로 다루게 되는 푸리에 변환 식 자체는

Xk=∑n=0N−1xne−j2πNknX_k=\sum_{n=0}^{N-1}x_ne^{-\frac{j2\pi}{N}kn}

Time-Frequency Properties

  • Linearity Property
ax(t)+by(t)↔aX(f)+bY(f)ax(t)+by(t)↔aX(f)+bY(f)
  • Frequency Shift Property
ej2πf0tx(t)↔X(f−f0)e^{j2πf_0t}x(t)↔X(f−f_0)
  • Scaling in Time Property

(여기서 scale 계수 빠진건 그냥 단순화하고 싶다고 걍 뺐다함)

x(at)↔X(fa)x(at)↔X(\frac{f}{a})

위 세개는 그냥 식 넣어서 쉽게 증명해볼 수 있거나 유추해볼 수 있는 성질

  • Convolution in Time Property
x(t)∗y(t)↔X(f)Y(f)x(t)*y(t)↔X(f)Y(f)
  • Convolution in Frequency Property
x(t)y(t)↔X(g)∗Y(g)x(t)y(t)↔X(g)*Y(g)

여기서 *는 합성곱 (convolution) 연산

x(t)∗y(t)=∫x(τ)y(t−τ)dτx(t)*y(t) = ∫x(τ)y(t−τ)dτ

요 컨볼루션 성질이 푸리에 변환에서 상당히 중요하다.

중요한 이유에 대한 간단 예시:

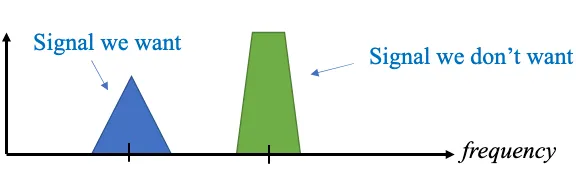
신호에 필터링 걸려면 아래 신호를 곱해버리면 딱 좋을텐데

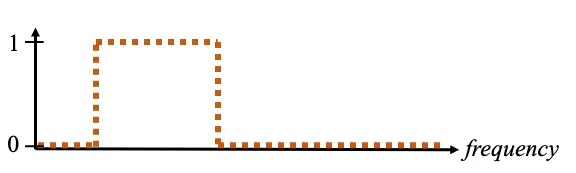
⇒ time 도메인에서 대응되는 신호 컨볼루션 걸어버린다면 쉽게 필터링 할 수 있음

Fast Fourier Transform

연속적인거는 당연히 힘들고, 근데 이산 푸리에 변환 자체도 그냥 하기엔 빡세다. FFT는 이산 푸리에 변환을 빠르고 효율적으로 계산하는 알고리즘이다.

결국 FFT의 원리 자체는 time domain의 전체 신호를 잘게 샘플링해다가 샘플단위의 푸리에 변환 결과를 분할정복 방식으로 합쳐가며 frequency domain의 결과물을 얻는 것이다.

또한 그림을 통해서 알수 있는 거중 하나는 결국 Δt\Delta t를 작게 해서, 즉 샘플링 속도를 높여 잘게 신호를 쪼개주고 FFT를 태워야 결과물이 더 해상도 높은 frequency index를 갖게 될거라는 것이다.

또 알아야 될거 하나는 FFT의 출력은 샘플링 속도 fsf_s에 대하여 −fs/2∼fs/2-f_s/2 \sim f_s/2의 범위만을 보여준다는 것이다. 왜 절반이냐? 다음 시간에 계속.. (Nyquist sampling theorem)

음의 주파수가 머냐 할수 있는데 음의 주파수는 신호의 위상을 표현하는데 필요하다. 사실 음성같은 실수 신호의 경우 음의 주파수 성분이 양의 주파수 성분과 대칭적으로 나타난다. 그래두 없애면 안됨

또한 타임 도메인에서의 순서를 바꿔도 주파수 도메인의 결과는 변하지 않는다. 이건뭐 당연한거라 (위상은 변화가 있겠지만)

FFT의 실제 알고리즘

가장 유명한 FFT 알고리즘은 Cooley-Tukey 알고리즘이다.

기원은 무려 1805년 가우스가 처음 발명한 건데, 이후 1965년 Cooley와 Tukey가 재발견하고 대중화하였다.

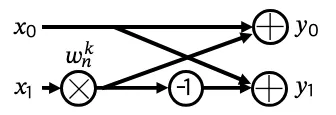
알고리즘의 핵심 빌딩 블록은 버터플라이(butterfly) 구조인데,

버터플라이는 FFT size가 2인 작은 단위이다.

y0=x0+x1⋅wNky1=x0−x1⋅wNky_0=x_0+x_1⋅w_N^k\\y_1=x_0−x_1⋅w_N^k

여기서 wNk=ej2πk/Nw_N^k=e^{j2πk/N} 는 twiddle factor라고 불린다.

요 구조를 재귀적으로 반씩 나누어가면서 주욱 수행해서 버터플라이 배열만 남겨서 concat 하는 방식이다. 대학생때 이거 매트랩으로 짜는 과제가 생각나서 약간 PTSD가 온다.

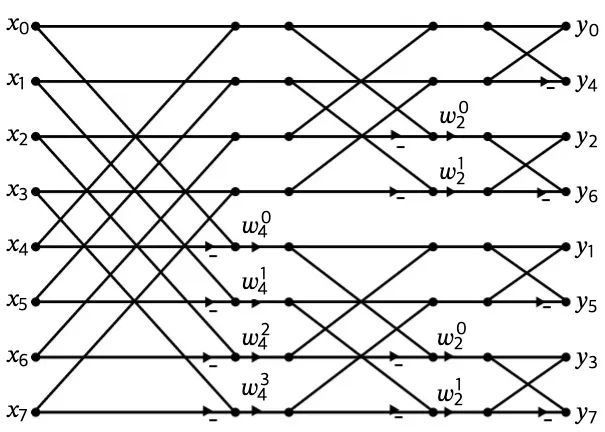
각 operation들은 병렬수행 가능하게 되어서 O(nlog⁡n)O(n\log n) 의 시간 복잡도를 달성할 수 있다.

  • 구현
import numpy as np
import matplotlib.pyplot as plt

def fft(x):
    N = len(x)
    if N == 1:
        return x
    twiddle_factors = np.exp(-2j * np.pi * np.arange(N//2) / N)
    x_even = fft(x[::2]) # yay recursion!
    x_odd = fft(x[1::2])
    return np.concatenate([x_even + twiddle_factors * x_odd,
                           x_even - twiddle_factors * x_odd])

# Simulate a tone + noise
sample_rate = 1e6
f_offset = 0.2e6 # 200 kHz offset from carrier
N = 1024
t = np.arange(N)/sample_rate
s = np.exp(2j*np.pi*f_offset*t)
n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # unity complex noise
r = s + n # 0 dB SNR

# Perform fft, fftshift, convert to dB
X = fft(r)
X_shifted = np.roll(X, N//2) # equivalent to np.fft.fftshift
X_mag = 10*np.log10(np.abs(X_shifted)**2)

# Plot results
f = np.linspace(sample_rate/-2, sample_rate/2, N)/1e6 # plt in MHz
plt.plot(f, X_mag)
plt.plot(f[np.argmax(X_mag)], np.max(X_mag), 'rx') # show max
plt.grid()
plt.xlabel('Frequency [MHz]')
plt.ylabel('Magnitude [dB]')
plt.show()

그리고 결과

FFT with Python

import numpy as np
import matplotlib.pyplot as plt

t = np.arange(100)
s = np.sin(0.15*2*np.pi*t)
plt.figure(figsize=(10, 5))
plt.plot(t, s, label='sin wave (freq=0.15 Hz)')
plt.xlabel('Time (t)')
plt.ylabel('Amplitude')
plt.grid(True)

plt.show()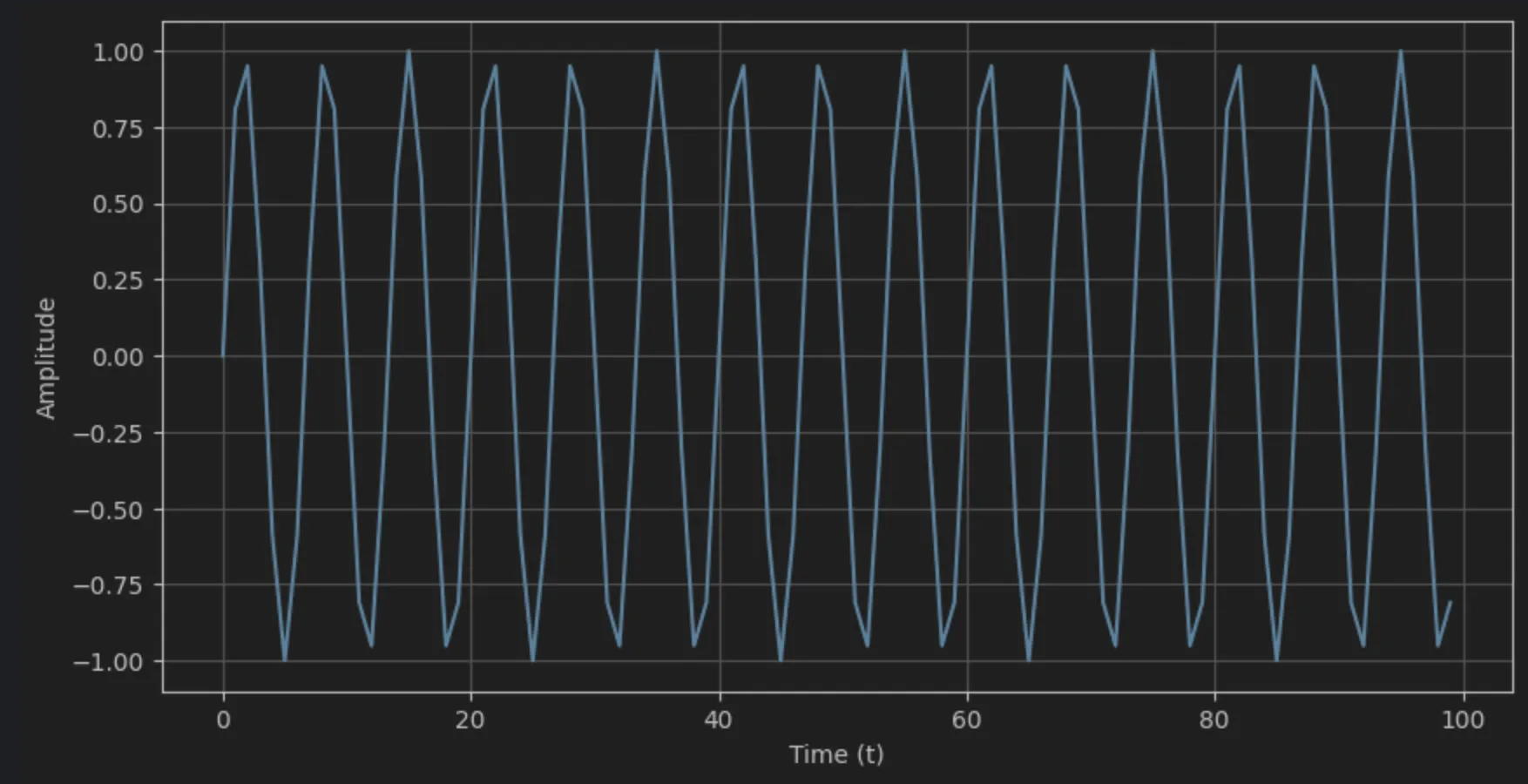

sin 파가 이렇게 주어졌을때

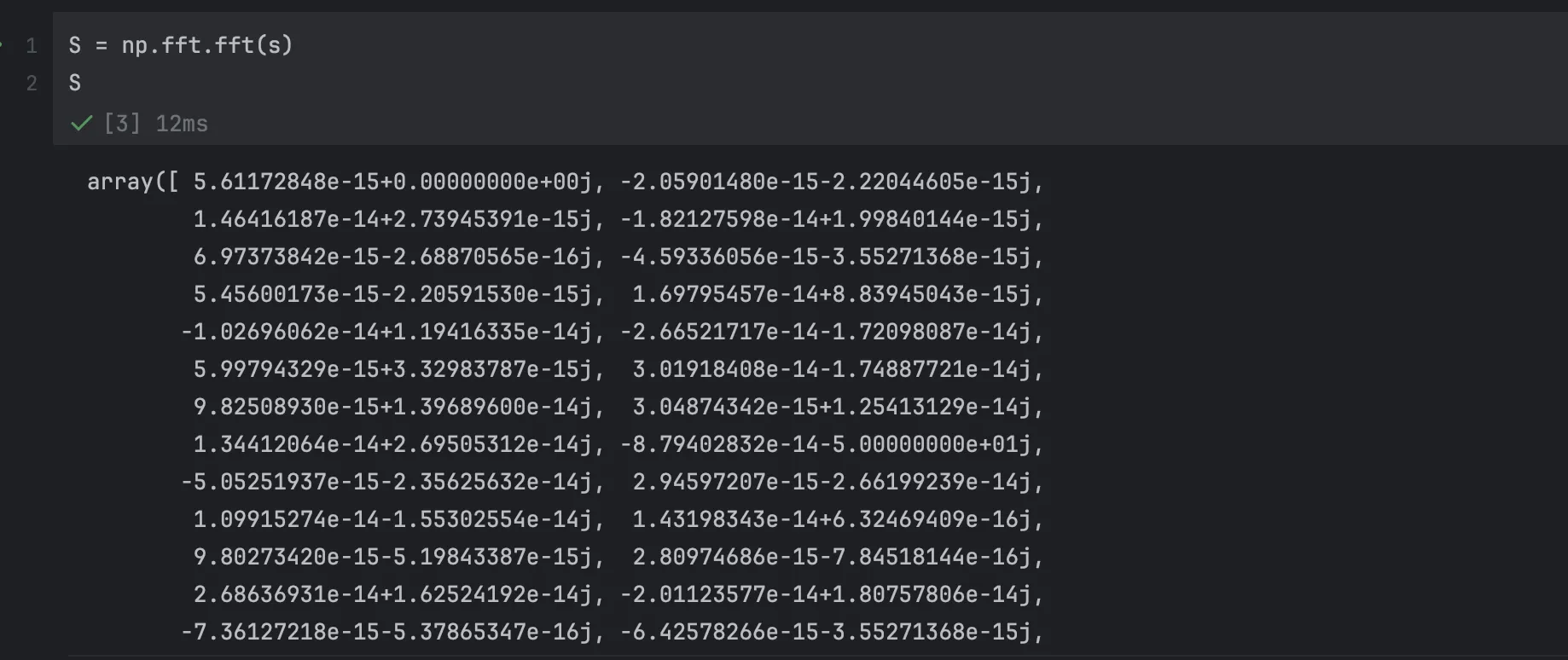
fft를 돌리면 이렇게 복소수 배열이 나오는 것을 알수 있다.

S_mag = np.abs(S)
S_phase = np.angle(S)
plt.subplot(2, 1, 1)
plt.plot(t,S_mag,'.-')
plt.ylabel('Magnitude')
plt.subplot(2, 1, 2)
plt.plot(t,S_phase,'.-')
plt.xlabel('FFT Index')
plt.ylabel('Phase (radians)')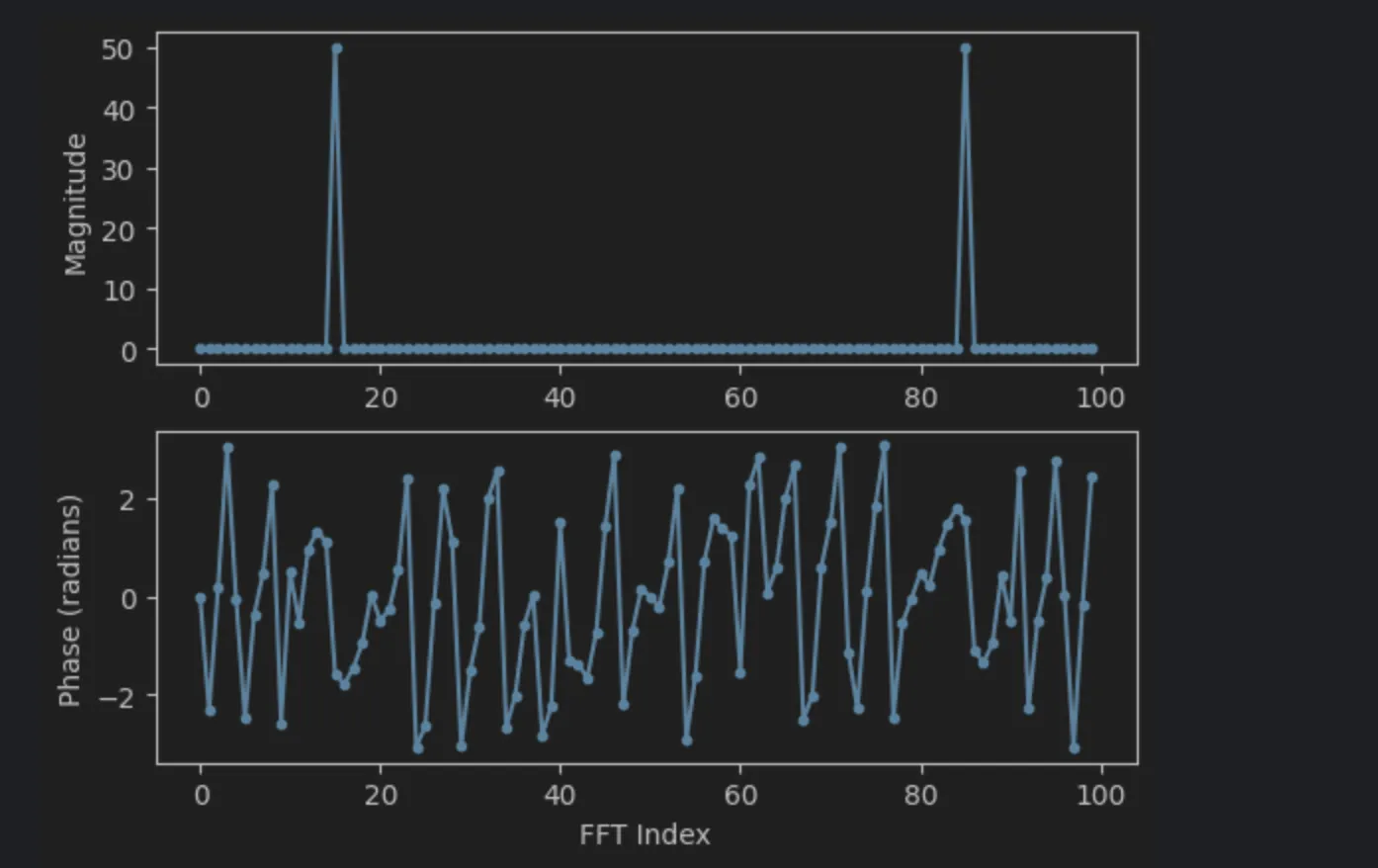

magnitude는 절대값만 확인하면되고, phase 변화는 np.angle 을 통해 라디안 단위로 볼 수 있다.

하지만 여기서 가로축을 보면 언급된 형태의 −fs/2∼fs/2-f_s/2 \sim f_s/2 형태가 아니어보인다.

현재 FFT 결과물은 아래 그림과 같은 상태이다.

그렇기 때문에 아래와 같은 FFT Shift 라는 과정을 거쳐주어야 최종 FFT 결과를 얻을 수 있다.

import numpy as np
import matplotlib.pyplot as plt

# do fft with fft shift

Fs = 1 # Hz
N = 100 # number of points to simulate, and our FFT size
t = np.arange(N) # because our sample rate is 1 Hz
s = np.sin(0.15*2*np.pi*t)
S = np.fft.fftshift(np.fft.fft(s))
S_mag, S_phase = np.abs(S), np.angle(S)
f = np.arange(Fs/-2, Fs/2, Fs/N)
plt.subplot(2, 1, 1)
plt.plot(f, S_mag,'.-')
plt.ylabel('Magnitude')
plt.subplot(2, 1, 2)
plt.plot(f, S_phase,'.-')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.show()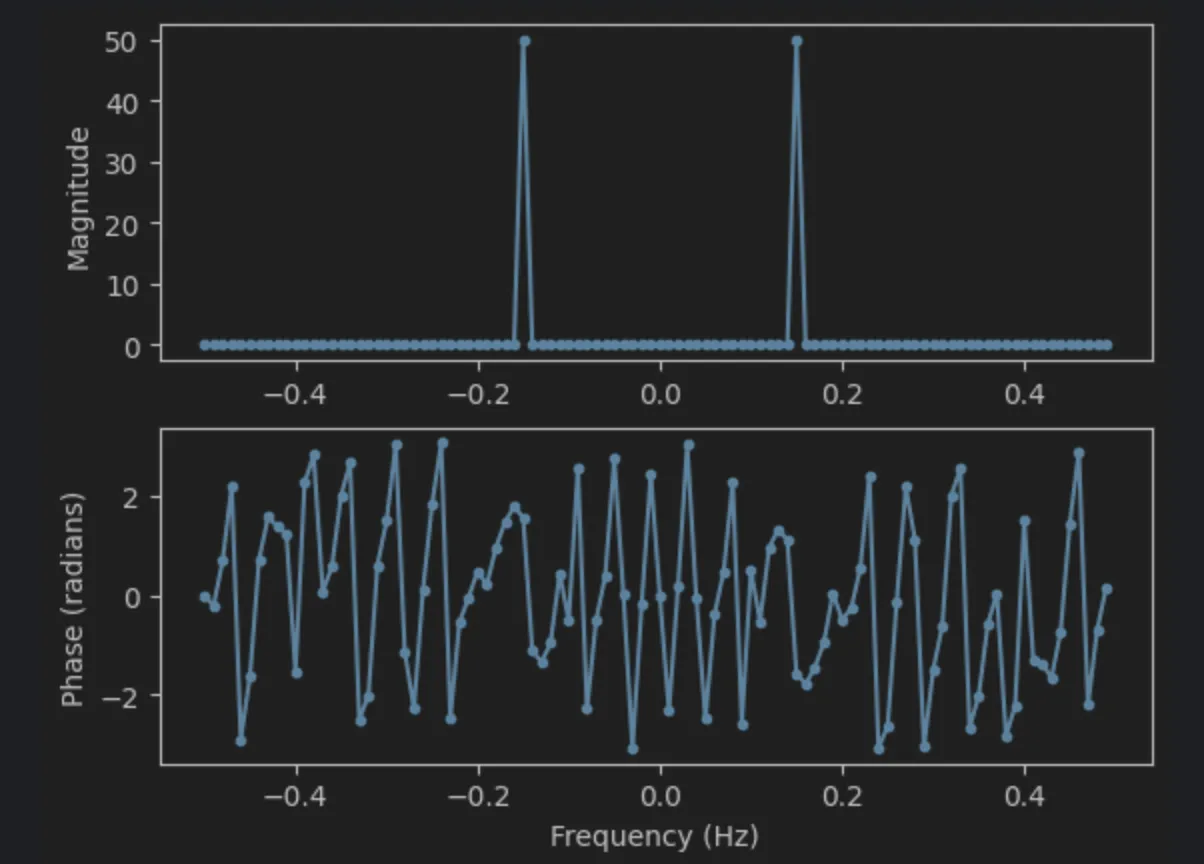

np.fft.fftshift로 이를 수행해 줄 수 있다.

Windowing

FFT를 할 때 기본 가정은 결국 FFT에 input되는 신호가 주기적인 신호의 일부라고 가정하는 것이다. 빠르게 하겠다고 일부만 샘플링해서 넣었는데 주기성이 없으면 해석한 frequency가 실제와 달라 무너지게 될테니..

하지만 결국 실제 시간 도메인의 신호는 변화가 생긴다. 이를 보정해주기 위해 windowing 이라는 기법을 활용한다. 이는 FFT를 수행하기 전 신호에 양 끝이 0 혹은 0에 근접하는 형태의 함수를 곱해 급격환 변화를 보정해주는 것이라 볼 수 있다.

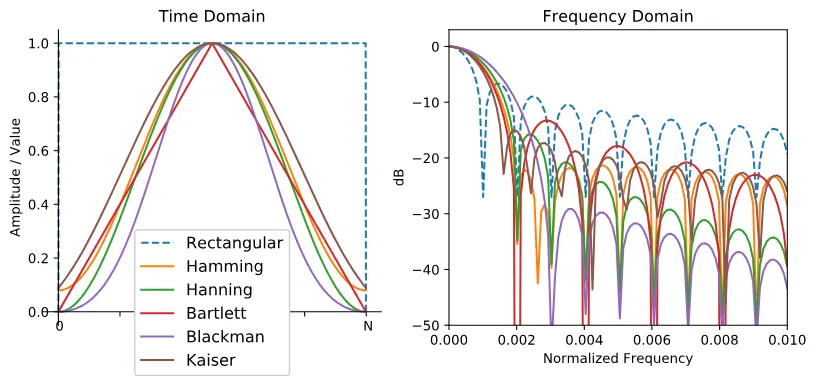
windowing을 사용하지 않는거는 rectangular 함수를 곱한것과 같아서 이를 rectangular windowing이라 하며, 아래 그림과 같은 형태의 다양한 windowing 함수들이 있다.

Hamming window만 librosa 쓰면서 본적이 있는거 같은데 함수 이름인줄 몰랐다… 아무튼 가장 간단하게 쓰기 좋은게 Hamming window라 한다.

import numpy as np
import matplotlib.pyplot as plt

Fs = 1 # Hz
N = 100 # number of points to simulate, and our FFT size
t = np.arange(N) # because our sample rate is 1 Hz
s = np.sin(0.15*2*np.pi*t)
s *= np.hamming(N)
S = np.fft.fftshift(np.fft.fft(s))
S_mag, S_phase = np.abs(S), np.angle(S)
f = np.arange(Fs/-2, Fs/2, Fs/N)
plt.subplot(2, 1, 1)
plt.plot(f, S_mag,'.-')
plt.ylabel('Magnitude')
plt.subplot(2, 1, 2)
plt.plot(f, S_phase,'.-')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.show()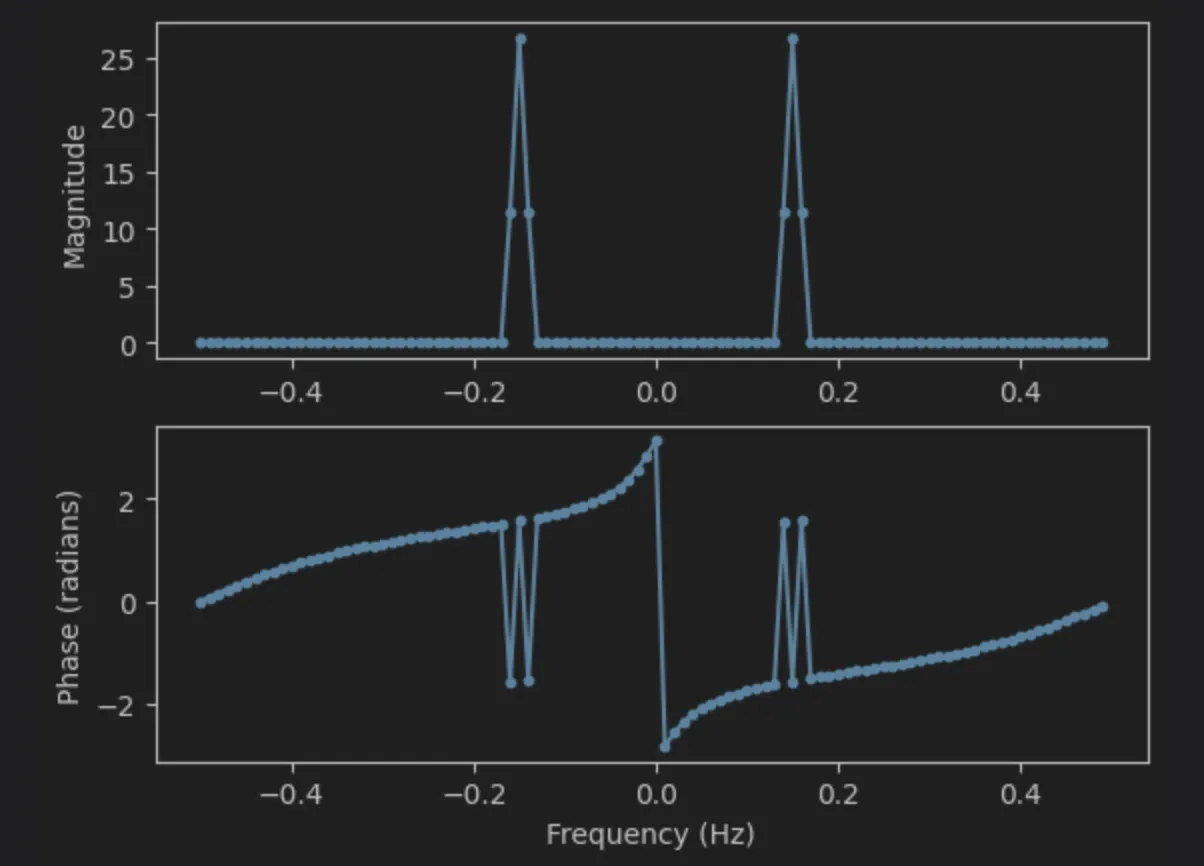

s *= np.hamming(N) 처럼 windowing을 수행해 주면 된다.

phase의 변화가 이전보다 훨씬 이해가능한 수준이 되었다.

FFT 실제 수행 팁

  • FFT size는 2의 배수로: 그래야 더 빠르다
  • 일반적으로 128~4096의 size를 쓴다.
  • 긴 신호는 한번에 변환하지 말고 쪼개서 주파수 도메인 자체의 변화를 시간에 따라 추적하는게 낫다 (음악 eq 그래프 보는 거처럼)
  • 모든 샘플을 FFT에 태울 필요는 없다. 신호 자체가 연속적으로 잘 이어져 있는 상태라면 중간중간 샘플링 뽑아서 태워도 충분히 의미있는 주파수 도메인 데이터를 얻을 수 있다.

Spectogram

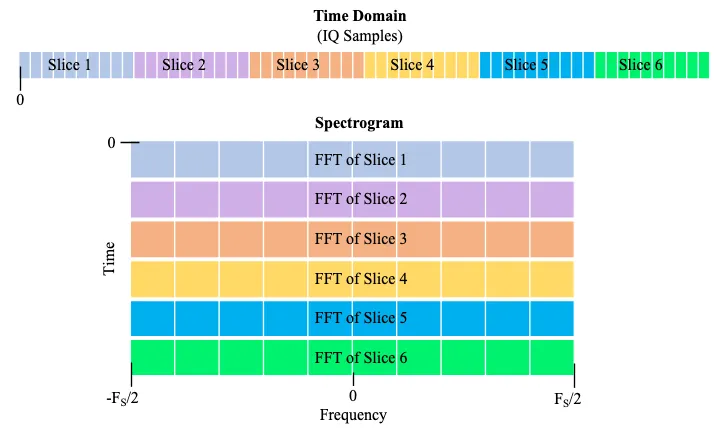
위의 팁에서 말한거처럼 긴 신호를 쪼개서 시간에 따른 주파수 대역의 변화를 보여주는것이 스펙토그램이다.

Time축을 더 만들었으니 3차원이 되어야하는데, 보통 magnitude는 색깔로 표현한다.

파이썬으로 스펙토그램을 한번 만들어봅시다.

import numpy as np
import matplotlib.pyplot as plt

sample_rate = 1e6
# Generate tone plus noise
t = np.arange(1024*1000)/sample_rate # time vector
f = 50e3 # freq of tone
tone = np.sin(2*np.pi*f*t)
noise = 0.2*np.random.randn(len(t))
x = tone + noise
plt.figure(figsize=(10, 5))
plt.plot(t[:200], x[:200], linestyle='-')
plt.xlabel('Time (t)')
plt.ylabel('Amplitude')

요렇게 정현파로 tone을 만들고 랜덤 노이즈를 붙여 신호를 만들고 신호 샘플 200개를 표시했다.

fft_size = 1024
num_rows = len(x) // fft_size # // is an integer division which rounds down
spectrogram = np.zeros((num_rows, fft_size))
for i in range(num_rows):
    spectrogram[i,:] = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(x[i*fft_size:(i+1)*fft_size])))**2)

plt.imshow(spectrogram, aspect='auto', extent = [sample_rate/-2/1e6, sample_rate/2/1e6, len(x)/sample_rate, 0], origin="lower")
plt.xlabel("Frequency [MHz]")
plt.ylabel("Time [s]")
plt.show()

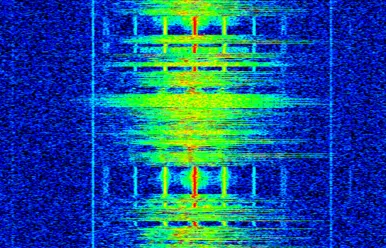
이를 spectogram으로 표현했을때 위와 같이 나온다.

참조

내용 구성, 대부분의 사진, 일부 코드
PySDR
을 참고하였습니다. 사실 초반엔 거의 배꼈습니다.

profile
whateverpartysover
인공지능 못해요
다음 포스트

[DSP] Sampling (Nyquist Sampling Theorem, LPF)

0개의 댓글