샘플링이란?
아날로그 신호를 일정한 간격으로 찍어서 디지털 신호로 변환하는 과정
→ 즉, 연속적인 신호를 이산적인 샘플들로 표현하는 과정
어떻게?
신호 f(t)에 Dirac Comb (a.k.a Train Impulse, sha function)를 곱해주면된다. 참고로 빗모양의 문자가 키릴문자 Sha 이다.

내가 그리기 귀찮은 그래프 챗지피티가 잘그려준다… 인간시대의 종말 도래
샘플 함수 (Sampled Function)의 수식표현
샘플 함수의 푸리에 변환
푸리에 변환의 기본 성질을 사용하여 의 푸리에 변환을 구한다.
푸리에 변환의 성질 중, 곱셈이 컨볼루션으로 변하는 성질을 이용하면:
Dirac Comb 의 푸리에 변환은 또 다른 Dirac Comb 형태로 나타난다:
즉, 주파수 영역에서 샘플링 주파수 간격으로 반복되는 델타 함수 배열이 된다.
컨볼루션 연산을 수행하면:
즉, 원래 신호의 푸리에 변환 가 주파수 간격으로 무한 반복되는 형태가 됨:
다양한 샘플률을 가지고 샘플 함수들의 푸리에 변환을 함 봐보자.
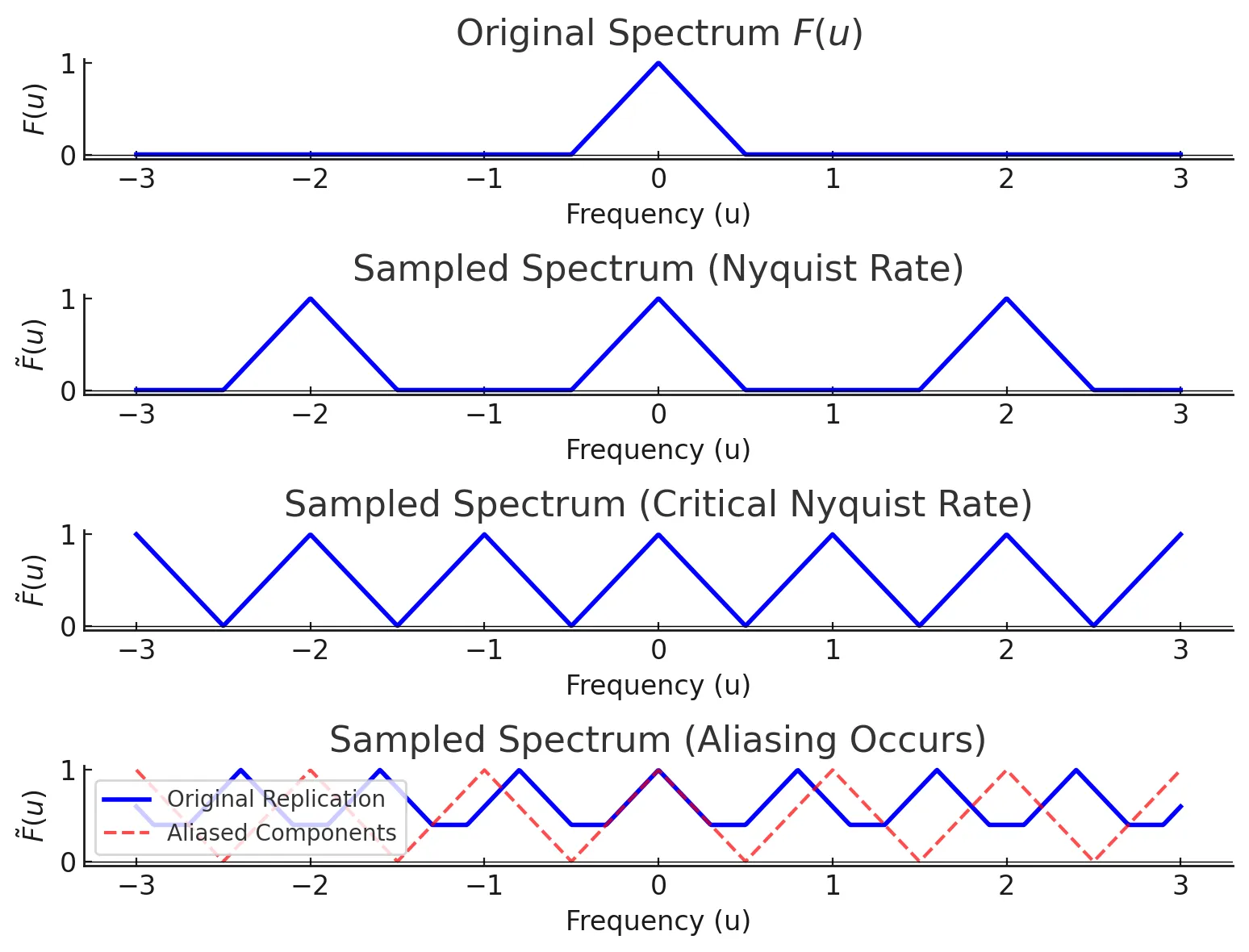
샘플링 레이트 가 충분히 크다면 문제가 없는데, 샘플링 레이트가 작아버리면 맨 아래처럼 주파수 도메인에서의 신호가 겹쳐버리고, 원래 신호를 복원해내기 어려워진다. 이렇게 겹치는 현상을 aliasing이라고 한다.
Nyquist Sampling Theorem
연속 신호를 디지털 신호로 변환할 때, 원래 신호를 정확히 복원하려면 샘플링 주파수 , 원 신호 주파수 에 대해 다음 조건을 만족해야한다.
그냥 위의 그림을 보면서 생각해보면 당연하다.
암튼 위 식을 만족하는 는 신호 복원이 가능한 샘플률이므로 이를 Nyquist Rate이라한다. 두배일때가 딱 맞닿은 형태의 샘플률이고 이는 Critical Nyquist Rate이라고 한다.
보통 샘플링 과정에서는 Critical Nyquist Rate 보다 높은 값으로 처리하는데, 뭐 완벽한 LPF(이후 설명)를 만들수도 없어서도 있고, 시스템 클럭오차 등의 이유도 있지만, 주기성이 완벽하게 겹쳐버리면 복원이 안되는 이유 때문인것도 있다.
요즘은 LPF 만드는거 어려우니까 쉽게 만드려고 오버샘플링을 빡 때린다고 한다.
Low Pass Filter
Low Pass Filter는 샘플링에서 굉장히 중요하며, 샘플링 과정에서 두가지 역할로 두번 쓰인다.
- 샘플링 전 LPF 적용 → Aliasing 방지
샘플링 전에 불필요한 고주파 성분을 제거한다. 이러면 값이 작아지니까 나이퀴스트 부등식 을 만족하기 쉽게 만들어준다. 즉 샘플링 후 주파수 스펙트럼이 깔끔하게 반복되도록 정리하는 역할이다.
- 샘플링 후 LPF 적용 → 신호 복원
샘플링 후에는 주파수 영역에서 간격으로 반복된 스펙트럼 중 하나만 남기도록 한다. 이전에 설명되었던거처럼 그 대표 하나 역변환이 원본신호이니까.
LPF는 시간 도메인에서 sinc 함수로 표현된다.
요걸 푸리에 때려주면 주파수 도메인에서 직사각형 형태의 필터가 된다:
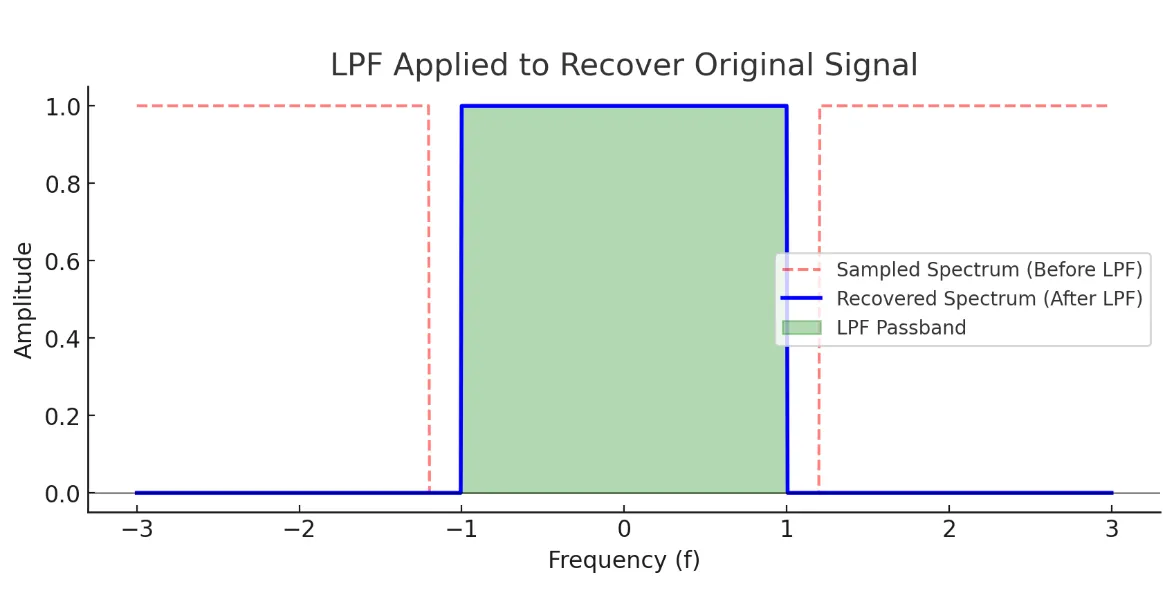
이를 역푸리에 변환(IFT) 하면 원래 신호를 매끄럽게 복원할 수 있다.
