Correlation Coefficient

여기서 말하는 Correlation Coefficient는 Pearson 상관계수를 말한다. 평균과 분산은 단일변수의 특징을 잡아내기 위한 통계이고 상관 계수는 두 변수의 상관관계를 의미한다. 여기서 상관관계란 변수 X가 상승할 때, 변수 Y가 상승하는가, 관련 없는가 혹은 반비례하는가를 X와 Y의 척도에 구애되지 않고 수치화 하는 것을 의미한다.

상관계수 공식

$r = \frac{\sum_{i=1}^n(x_i - \bar{x})(y_i - \bar{y})}{(n-1)s_xs_y}$

공식을 보면 x의 편차와 y의 편차를 관찰값의 개수로 나누고, 변수 X와 Y의 표준편차로 각각 나누어 준것을 볼 수가 있다. Scaling을 통해 척도를 제거하게 되어, 두 변수를 동일 선상에서 비교 할 수 있도록 한다.

상관계수는 -1 <= r <= 1 값으로 0에 가까우면 두 변수간에 비례하거나 반비례하는 정도가 거의 없는 것이고, 1이면 완전 비례, -1이면 완전 반비례하는 것으로 볼 수 있다.

R 에서는 상관계수를 다변수에서 적용해 아래와 같은 상관계수 행렬을 그래프로 표현 할 수 있다.(Dataset은 iris 를 사용하였다.)

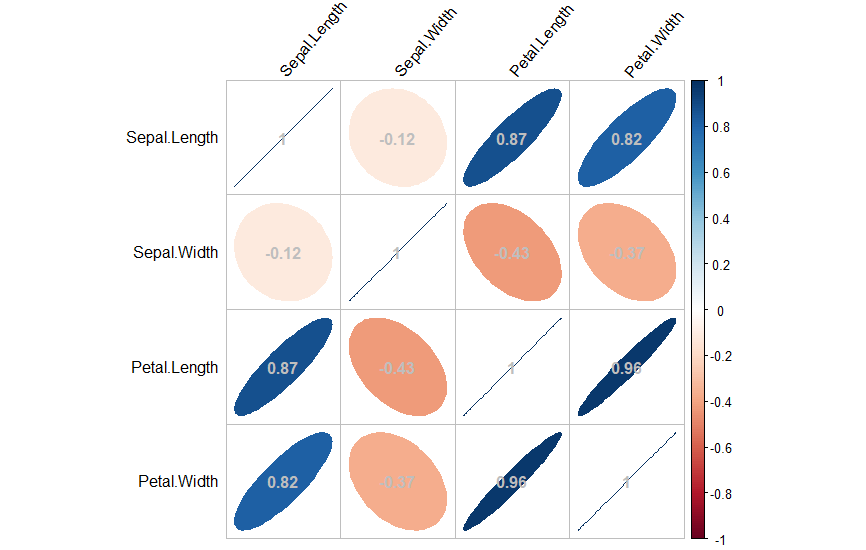
데이터를 통해 Petal.Width와 Petal.Length 의 상관 정도가 굉장히 강한 것으로 볼 수 있다. 반면에 Petal.Length와 Sepal.Width는 상관계수가 음수로 반비례하는 것으로 볼 수 있다.

Graphs

두 연속형 변수를 그래프로 표현 할 때 보통 scatter plot을 사용한다.

위의 데이터는 데이터의 수가 150개 밖에 없기 때문에 괜찮지만, 데이터의 수가 많을 경우 문제가 된다. 왜냐하면 데이터의 밀도가 얼마나 높은지를 시각적으로 판가름 하기에 scatter plot은 그다지 큰 도움이 되지 않기 때문이다. 이 문제를 해결하기 위해 몇가지 도움이 되는 그래프들을 소개하고자 한다. 그 외에도, 유용한 그래프를 소개한다.

육각형 구간(hexbin)

육각형 구간은 그래프를 육각형의 격자로 나누어 그 구간에 데이터의 밀도를 색으로 표기할 수 있는 유용한 방법중 하나이다.

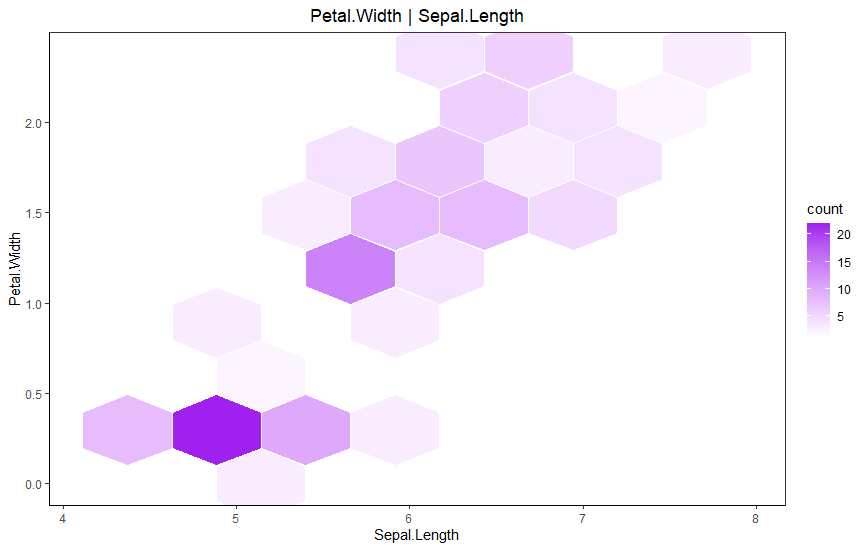
등고 도표(coutour plot)

등고 도표는 두 변수의 밀도를 등고선으로 표기한다. 사용 목적은 육각형 구간과 동일하다.

바이올린 도표(violine plot)

위의 육각형구간, 등고도표와 이 그래프는 성격이 다르다. 위의 두 그래프의 대상 데이터는 연속형 데이터의 분포이지만 바이올린 도표는 연속형 데이터와 명목형 데이터가 대상이기 때문이다. 아래는 mpg dataset의 drv와 displ 컬럼의 바이올린 도표이다.

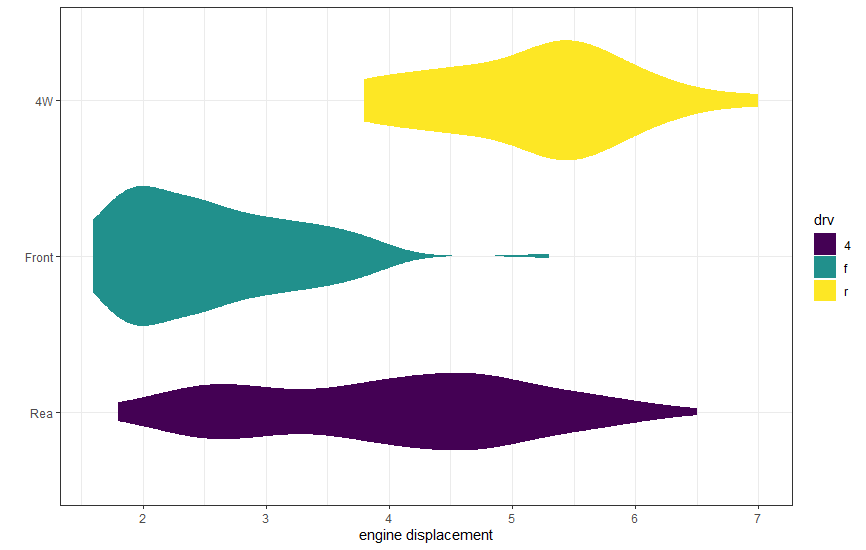
자주 쓰는 상자 도표와 비슷하다고 할 수있지만, 상자도표는 중앙값, 백분위 25% 와 75%가 어디에 위치하는지, 마지막으로 IQR * 1.5에 해당하는 tail을 표기할 뿐이다. 즉, 데이터의 밀도를 표기하지 않는다. 바이올린은 밀도까지 표기 할 수 있으며, 위에서 제시한 도표 이외에, 기존 상자도표에서 제공하던 데이터도 포함하는 그래프를 찾을 수 있다.

Conditioning

Conditioning은 3개 이상의 변수의 관계를 시각적으로 표현 할 수 있는 효과적인 방법이다. 아래는 R의 facet_wrap 함수를 이용하여 iris 데이터를 Species 컬럼별로 Conditioning을 사용한 것이다.

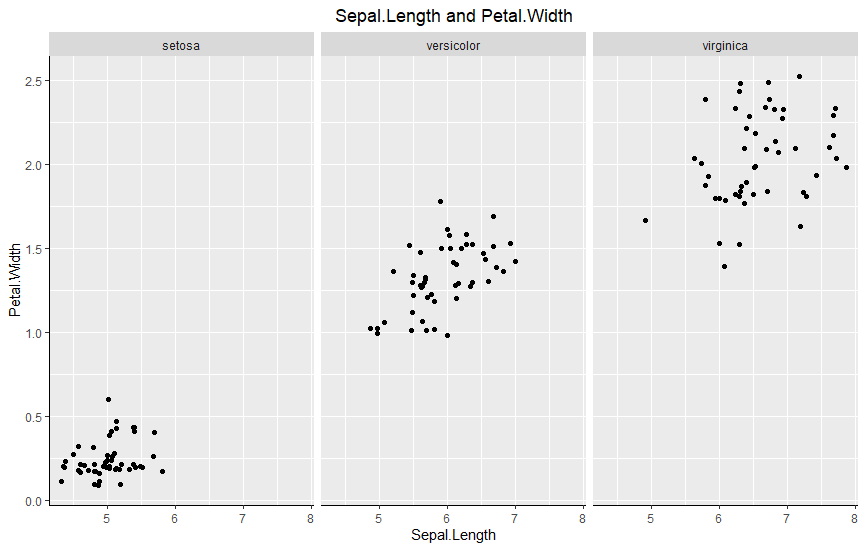
X축에 Sepal.Length, Y축에 Patal.Width, 그리고 그래프를 Species 로 나누어 보니 종별로 데이터의 분포의 위치가 확연히 다름을 알 수 있다.