이글은 John Elder 의 Target Shuffling 에 관한 글의 내용을 정리한 내용을 밝힙니다.

Vast Search Effect

방대한 검색 효과(Vast Search Effect)는 중복 데이터 모델링이나 너무 많은 예측변수를 고려하는 몯델링에서 비롯되는 편향 혹은 비재현성을 의미한다. 설명 들으면 어렵다. 간단하게 말하자면, 이 글을 읽는 여러분이 만든 모델의 성능이 우연히 좋게 나오는 경우를 말한다. 좋은 예로는 멜론가격과 주식의 가격을 들 수 있다. 멜론의 가격이 올랐는데, 주식의 가격도 올랐다. 그렇다면 멜론의 가격을 feature 로 주식의 가격이 오른다는 모델을 만들었다 치자. 성능은 잘 나올 것이다. 하지만 멜론과 주식은 아무 관련도 없다. 우연히 발생한 연관성을 근거로 casuality를 주장한 모델을 만든것이다. 이런 것을 Vast Search Effect라고 한다.

John Elder는 Vast Search Effect를 처음 주장한 사람이다. John Elder에게 한 클라이언트가 왔다. 이 클라이언트는 Hedge Fund를 들었고, 펀드는 성공적으로 수익을 오렸지만 수익의 얻는 과정이 불안전 해서 Elder 씨에게 이 펀드를 계속 들어도 될지, 즉 지금의 성공이 우연인지 아닌지를 궁금해 했다. 이에 Elder씨는 Hedge Fund를 산다와 사지 않는다를 1000번을 수행해서 클라이언트가 성공한 것이 우연일 확률이 1.5%라는 것을 증명해 보였다. 클라이언트는 더 많은 투자를 그 Hedge Fund에 하여 해피엔딩이 맞이하였다.

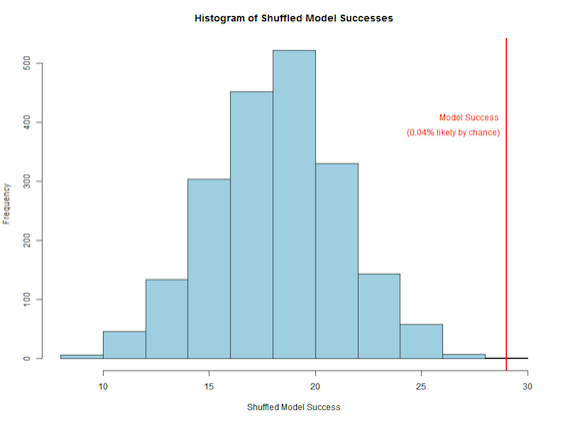
이와 같이 모델을 만들고 그 모델의 성능이, target을 섞어 모델을 수행했을 때의 성능의 분포에서 모델이 그 분포의 어디에 있느냐에 따라 그 모델의 성능이 우연이었는지 아니면 필연이었는지를 알 수 있다. 이를 Target Shuffling이라고 한다.

John Elder가 밝인 방법론은 아래 와 같다. 오역이 있을 수 있으니 프로세스의 원문과 역문을 같이 올린다.

Target Shuffling Process

1. Randomly shuffle the output (target variable) on the training data to “break the relationship” between it and the input variables.

   • input 변수들과 target의 연관성을 끊기 위해 target의 값을 랜덤하게 섞는다.

2. Search for combinations of variables having a high concentration of interesting outputs

   • 변수들 중에 좋은 결과를 내는 조합들을 찾는다.

3. Save the “most interesting” result and repeat the process many times.

   • 가장 흥미로운 결과를 저장하고, 이 작업을 다수 반복한다.

4. Look at a distribution of the collection of bogus “most interesting results” to see how much of apparent results can be extracted from random data.

   • 얼마나 명확한 결과를 random data로부터 얻을 수 있는지를 보기 위해, 가장 흥미로운 가짜 결과들의 분포를 확인해라.

5. Evaluate where on (or beyond) this distribution your actual results stand.

   • 원래 사용하던 모델의 결과가 성능의 분포에서 어디에 위치하는지 평가한다.

6. Use this as your “significance” measure.

   • 이 것을 significance로 삼는다.

예를 들어보자. 여러분이 SVM으로 n개의 feature에서 이진 분류를 수행했는데 성능이 좋았다. 그렇다면 정말 부분집합 S는 필연적으로 좋은 성능을 내는 것인가? 이를 확인하기 위해 먼저 관잘값들의 target 데이터를 무작위로 섞는다. 그런 다음 결과를 낸다. target을 섞고, 다시 결과를 내는 것을 반복하면 성능의 분포를 볼 수가 있다. 이 성능의 분포에서 target shuffling 전의 모델의 성능이 분포에 어디에 위치하는지 확인한다면, 자신의 모델의 결과가 필연인지를 알수 있다.