Statistics to Detect Fraud

1991년 터프츠 대학교의 한 연구원 테레자 이마니시-카리(Thereza Imanishi-Kari)는 연구 데이터를 조작한 것으로 기소되어 논란이 되었다고 한다. 이 논란중 한가지 요소는 실험실에서 관찰한 데이터의 숫자 분포에 관한 통계적 증거를 수사관이 제시한 점이다. 수사관은 실험실 데이터에서 균등확률분포(Uniform Random Distribution)을 따를 것으로 기대되는 중간 자리의 숫자(예를 들어 312에서 중간 값은 1이다.)가 실험데이터에서 특이적으로 나타났다는 것을 근거로, 데이터가 조작됨을 밝히려 했다. 아래는 그 당시 데이터이다.

	frequency
0	14
1	71
2	7
3	65
4	23
5	19
6	12
7	45
8	53
9	6

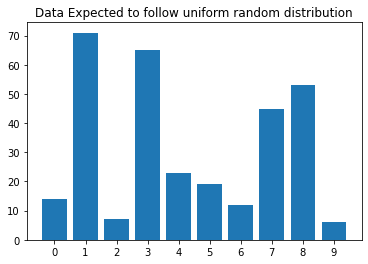
전체 데이터 개수는 315개였고, 균등분포를 따른다고 가정한다면 0 ~ 10 까지 까지 모두 $315 / 10 =31.5$가 될 터였다. 이를 카이제곱검정을 이용해 위의 데이터가 랜덤상에서 발생 할 가능성이 극히 낮은 데이터라는 것을 보일 수 있다.

아래는 카이제곱통계치를 구하는 함수이다. 카이제곱은 각 도수에 기대값을 뺀 뒤에 기대값에 루트를 씌운 값을 곱한 뒤에 그 값들을 제곱한 값들의 합으로 계산할 수 있다.

$\chi^2 = \sum_{i=1}^n\frac{(x - E(x))^2}{E(x)}$
$x=$ observation
$E(x)=$ x가 uniform random distribution을 따른다고 할 때의 기대값.

def chi2(observed, expected):
    pearson_residuals =[]
    for observe, expect in zip(observed, expected):
        pearson_residuals.append(((observe - expect) **2 ) / expect)
    return sum(pearson_residuals)

아래의 함수는 순열검정을 수행하는 함수이다. 균등 확률분포를 따르는 랜덤값으로 315개의 만들었을 때, 이 값의 카이제곱통계량은 얼마인가를 구할 수 있다.

def perm_fun(expected):
    samples = np.floor(np.random.rand(315) * 10).tolist()
    deg = countby(identity, samples)
    deg = dict(sorted(deg.items(), key=first))
    return chi2(deg.values(), expected)

이제 기존 데이터와, 1000번 수행하는 순열검정의 카이제곱통계량을 구한다.

chi2observed = chi2(data, expected)
perm_chi2 = np.array([perm_fun(expected) for _ in range(1000)])

카이제곱은 그 수식과이 의미하는 바가 기대하는 값과 실제값이 얼마나 차이가나는지를 나타낸다. 그러므로 순열 검정을 1000번 한것과 실제 데이터의 카이제곱통계량을 비교하는 것은 실제 데이터가 균등분포로 랜덤하게 생성된 데이터로 발생할 정도를 보여준다.

resampled_p_value = sum(perm_chi2 > chi2observed) / len(perm_chi2)
print(f'Observed chi2: {chi2observed}')
print(f'Resampled p-value : {resampled_p_value}')

출력 결과는

Observed chi2 : 174.365079
Resampled p-value : 0

p-value가 0이라는 것은 이 데이터가 균등분포를 따라 발생할 확률이 0%라는 것이다. 즉, 테레자 이마니시-카리의 데이터는 조작되었다는 결론에 이른다. 물론 테레자 이마니시-카리는 무죄로 풀려났지만 말이다.