벡터 함수와 공간곡선

이 내용은 James Stewart의 미적분 2 의 내용임을 밝힙니다.

벡터값 함수 또는 벡터 함수는 정의역이 실수인 집합이고 치역이 벡터의 집합인 함수이다.

$f(t), g(t), h(t)$ 가 벡터 $r(t)$의 성분일 때, $f, g, h$는 실수값 함수로 $r$의 성분함수라고 하며 다음과 같이 나타낼 수 있다.

$r(t) = <f(t), g(t), r(t)> = f(t)i + g(t)j + h(t)k$

※ i, j, k는 표준 벡터이다.

벡터 함수 $r$의 극한은 다음과 같이 이것의 성분함수들의 극한을 택해서 정의한다.

definition
$r(t) = <f(t), g(t), r(t)>$ 일 때, (아래 성분의 극한이 존재하면) 다음과 같이 정의한다.

$\lim_{t\to a}r(t) = <lim_{t\to a}f(t), lim_{t\to a}g(t), lim_{t\to a}r(t)>$

즉, 벡터 함수의 극한은 실수값 함수의 극한과 똑같은 규칙을 따른다.

보기 2

$r(t) = <(1 + t^3), te^{-t}, \frac{\sin t}{t}>$ 일 때, $\lim_{t\to 0}r(t)$를 찾아라.

따로 극한을 따져 보면

$\lim_{t\to 0}(1 + t^3) = 1$

$\lim_{t\to 0}te^{-t} = 0$

$\lim_{t\to 0}\frac{\sin t}{t}$은 로피탈 정리에 따라 $\frac{0}{0}$ 부정형 형태를 가짐으로 $\frac{(\sin t)'}{(t)'} = (\frac{\cos t}{1}) = 1$ 을 가진다.

즉, $r(t) = <(1 + t^3), te^{-t}, \frac{\sin t}{t}>$의 $t \to 0$ 극한은 $<1, 0, 0>$ 이다.

보기 6

기둥 $x^2 + y^2 = 1$ 과 평면 $y + z = 2$의 교선의 방정식을 표현하는 벡터함수를 찾아라.

solution

$x^2 + y^2 = 1$ 은 다시 표현하면 $\sin^2 x + \cos^2 x = 1$ 과 같음으로 $x = \sin x, y=\cos x$로 볼 수 있다. $z = 2 - \cos x$ 가 됨으로, 벡터 함수 $r(x)$ 는

$r(x) = <\sin x, \cos x, 2 - \sin x>$ 이다.

벡터함수의 도함수

$\frac{dr}{dt} = r'(t) = \lim_{h \to 0}\frac{r(t + h) - r(t)}{h}$

$r'(t)$ 가 존재하고 $r'(t) \ne 0$ 일 때, $r'(t)$를 벡터 함수의 치역인 곡선의 임의의 점 $P$ 에서 $r$로 정의된 곡선에 대한 접선 벡터라고 한다.

다음 정리는 벡터 함수 $r$의 도함수를 셈하는 간편한 방법을 제공한다. 곧, $r$의 각 성분을 미분하면 다음이 성립한다.

Thereom
$r(t) = <f(t), g(t), r(t)> = f(t)i + g(t)j + h(t)k$이고, $f, g, h$가 미분가능한 삼수일 때, 다음이 성립한다.

$r'(t) = <f(t)', g(t)', r(t)'> = f(t)'i + g(t)'j + h(t)'k$

보기 9

곡선 $r(t) = \sqrt{t}i + (2-t)j$에 대해 $r'(t)$를 찾고, 위치 벡터 $r(1)$과 접선 벡터 $r'(1)$ 을 그려라.

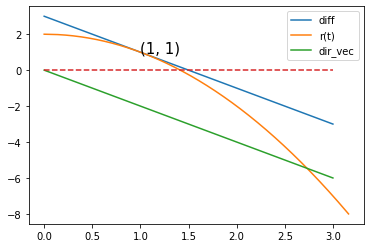
그래프와 같이 벡터함수의 미분값이 곡선의 기울기와 평행함을 알 수 있다.

미분 법칙

[5] Theorem

$u, v$는 미분 가능한 벡터 함수이고, $c$는 스칼라이며, $f$는 실수값 함수라고 하자. 그러면 다음이 성립한다.

1. $\frac{d}{dt}\{u(t) + v(t)\} = u'(t) + v'(t)$

2. $\frac{d}{dt}\{cu(t)\} = cu'(t)$

3. $\frac{d}{dt}\{f(t)u(t)\} = f'(t)u(t) + f(t)u'(t)$

4. $\frac{d}{dt}\{u(t)\cdot v(t)\} = u'(t) \cdot v(t) + u(t) \cdot v'(t)$

5. $\frac{d}{dt}\{u(t) \times v(t)\} = u'(t) \times v'(t) + u(t) \times v'(t)$ ※ $\times$는 outer product 이다

6. $\frac{d}{dt}\{u(f(t))\} = f'(t)u'(f(t))$

보기 11

$|r(t)| = c$이면, 모든 $t$에 대해 $r'(t)$는 $r(t)$ 에 수직임을 보여라.

$r(t) \cdot r(t) = c^2$ 이다. 이를 미분하면 [5] Theorem 4번에 따라,

$\{r(t) \cdot r(t)\}' = r'(t) \cdot r(t) + r(t) \cdot r'(t)$

$r'(t) \cdot r(t) + r(t) \cdot r'(t) = 2r(t)\cdot r'(t) = 0$

즉, $r(t) \cdot r'(t) = 0$ 임으로 $r'(t)$는 $r(t)$ 에 수직임을 알 수 있다.

적분

벡터 함수에 대한 정적분은 실수값 함수와 같은 방법으로 정의된다. 다만 적분 결과가 벡터이다.

$\int_a^br(t)dt = \left(\int_a^bf(t)dt\right)i + \left(\int_a^bg(t)dt\right)j + \left(\int_a^bg(t)dt\right)k$

즉, 미적분학의 기본정리를 적용할 수 있어 아래와 같이 풀어 낼 수 있다.

$\int_a^br(t)dt = \mathbf{R}(b) - \mathbf{R}(a)$
※ $\mathbf{R}$ 은 $r$의 역도함수이다.