✅ DP ✅ Bottom up

문제

링크

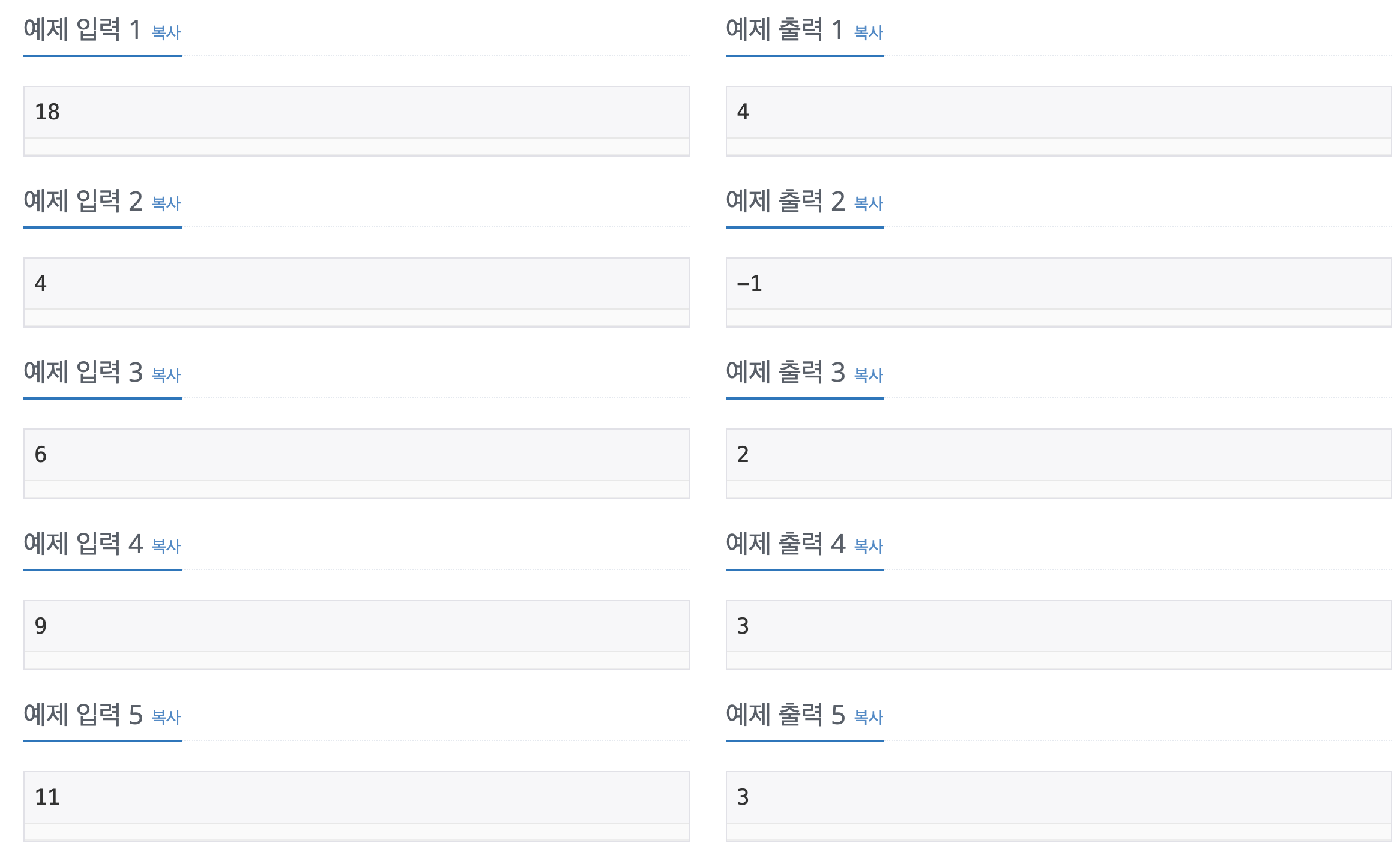
풀이

2839 설탕배달 (그리디) 이전에는 그리디로 풀어봤으니 이번에는 점화식을 이용하여 DP (Bottom up) 로 풀어보자.

1. 문제 접근 및 해결 로직

정확하게 N킬로그램을 만들 수 없다면 -1을 출력하므로
3킬로그램 봉지와 5킬로그램 봉지로 만들 수 없는 경우는 몇 봉지인지 세어줄 필요 없다.

18kg을 나눠담는다고 생각해보자.
일차원 배열에 1kg씩 넣어두고 각 index에서의 봉지수를 저장한다.
(index는 1부터 시작)

sugar[1] = -1
sugar[2] = -1
sugar[3] = 1
sugar[4] = -1
sugar[5] = 1
sugar[6] = 2
sugar[7] = -1
sugar[8] = -1
sugar[9] = 3
...

이런 형태이다.

sugar[9]의 값을 구한다는 것은 index = 9에서 3kg로 담을지, 5kg으로 담을지 결정을 한다는 뜻이다.

• 3kg
  이전 sugar[9-3] 에서 나눠담았어야(sugar[6] != -1)
  이번 index = 9 에서 3kg으로 담을 수 있다.

• 5kg
  동일하게 이전 sugar[9-5] 에서 나눠담았어야(sugar[4] != -1)
  이번 index = 9 에서 5kg으로 담을 수 있다.

1. sugar[9-3], sugar[9-5]에서 둘 모두 나눠담았었다면 둘 중에 작은 경우를 택한다.
2. sugar[9-3], sugar[9-5] 둘 중 하나에서만 나눠담았었다면 그 경우를 택한다.
3. 둘 다 나눠담지 못했었다면 이번 index가 3이나 5로 딱 나눠지지 않는다는 뜻이므로 sugar[index] = -1 이다.

• 정의
  $f(n)$ : $n$ kg의 최소 봉지 개수
• 구하는 답
  $f(n)$
• 초기값
  $f(1)=-1,f(2)=-1,f(3)=1,f(4)=-1,f(5)=1$
  0으로 시작하는 계단수는 없다고 했으므로 $f(1,0)=0$
• 점화식
  $f(n)=min(f(n-3),f(n-5)),(f(n-3)!=-1,f(n-5)!=-1)$
  $f(n)=f(n-3),(f(n-3)!=-1,f(n-5)==-1)$
  $f(n)=f(n-5),(f(n-3)==-1,f(n-5)!=-1)$
  $f(n)=-1,(f(n-3)==-1,f(n-5)==-1)$

의사코드

cin >> N

fill(sugar,-1)

sugar[3] = 1
sugar[5] = 1

for(i : 6 ~ 18){
	if(sugar[i-3]!=-1 && sugar[i-5]!=-1) sugar[i] = min(sugar[i-3], sugar[i-5])
    if(sugar[i-3]!=-1 && sugar[i-5]==-1) sugar[i] = sugar[i-3]
    if(sugar[i-3]==-1 && sugar[i-5]!=-1) sugar[i] = sugar[i-3]
    if(sugar[i-3]==-1 && sugar[i-5]==-1) sugar[i] = -1
}

cout << sugar[N]

2. 코드

3. 시간 복잡도 분석

경우의 수를 모두 구하므로
$O(N)$

4. 문제에서 중요한 부분

DP문제는 점화식을 도출하는 것이 중요하다.
Bottm Up(반복문)으로 풀지 Top Down(재귀)으로 풀지는 선택사항