✅ DP

문제

링크

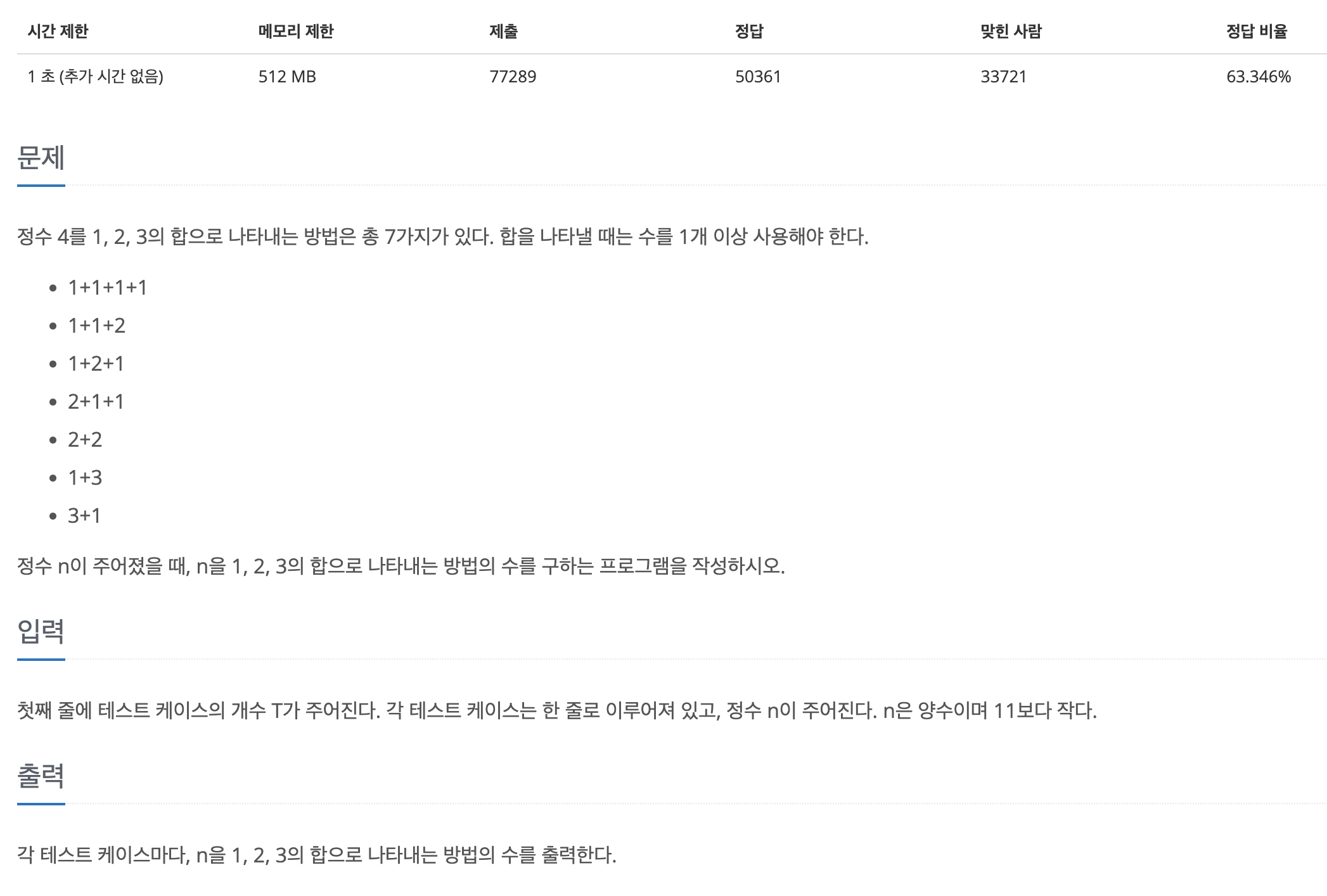
1. 문제 접근 및 해결 로직

구성 숫자가 같아도 순서가 다른 것은 다른 조합으로 친다.
따라서 $f(n)$을 정수 $n$ 을 1,2,3의 합으로 나타내는 방법의 수라고 하고
몇가지를 구해보면
$f(1)=1$

{1}

$f(2)=2$

{1,1}
{2}

$f(3)=4$

{1,1,1}
{1,2}
{2,1}
{3}

$f(4)=7$

{1,1,1,1}
{1,2,1}
{2,1,1}
{1,1,2}
{3,1}
{1,3}
{2,2}

여기서 다음과 같은 규칙을 발견할 수 있다.
$f(4)=f(3)+f(2)+f(1)=4+2+1=7$

따라서 점화식은
$f(n)=f(n-1)+f(n-2)+f(n-3)$ 이다.

의사코드

• 정의
  $f(n)$ : 정수 $n$ 을 1,2,3의 합으로 나타내는 방법의 수
• 구하는 답
  $f(n)$
• 초기값
  $f(1)=1$
  $f(2)=2$
  $f(3)=4$
• 점화식
  $f(n)=f(n-1)+f(n-2)+f(n-3),(n>3)$

2. 코드

3. 시간 복잡도 분석

경우의 수를 모두 구하므로
$O(N)$

4. 문제에서 중요한 부분

DP문제는 점화식을 도출하는 것이 중요하다.
Bottm Up(반복문)으로 풀지 Top Down(재귀)으로 풀지는 선택사항