✅ BFS ✅ 최단경로

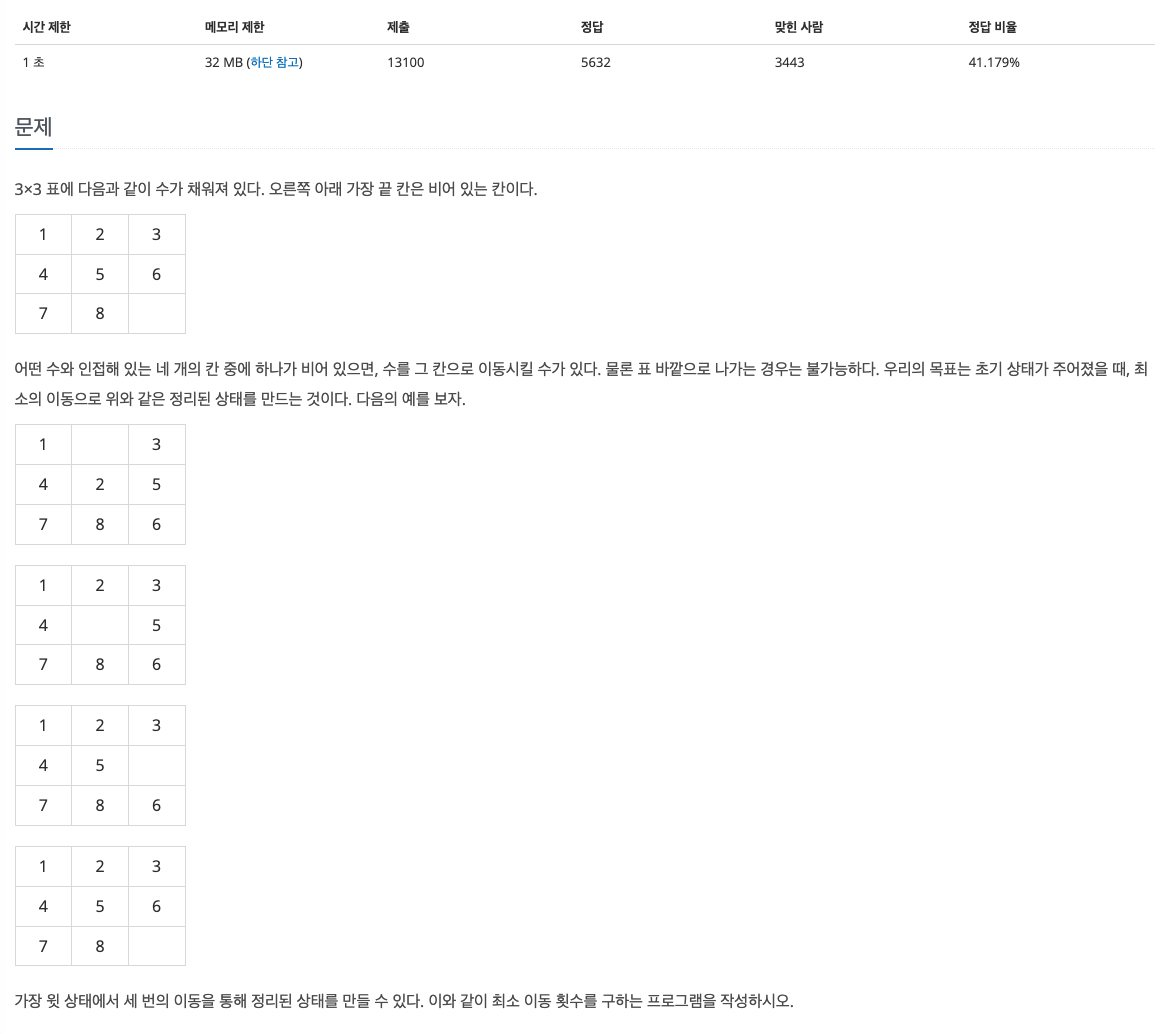
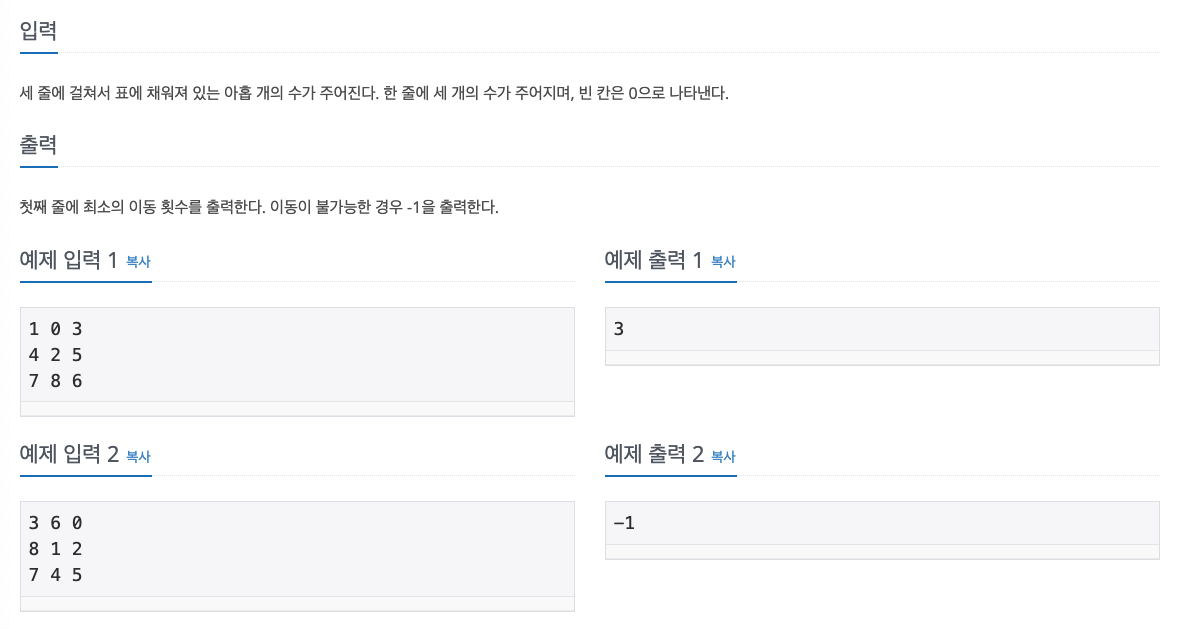
문제

링크

풀이

1. 문제 접근

• 인접해 있는 네 개의 칸 중에 하나가 비어 있으면, 수를 그 칸으로 이동
• 이동을 통해 정리된 상태를 만들어야 함
• 최소 이동 횟수를 구하라

2. 문제 해결 로직 (풀이법)

즉,

• 정해진 경로로만 이동할 수 있으며
• 최소 이동으로
• 특정 상태를 만족시키게 이동시켜야 하는 문제이므로

  정해진 경로로만 이동하여 도착지에 도달하는 최단경로를 구하는 문제라고 볼 수 있다.
  따라서 BFS 사용

주의해야 할 점은

보통의 최단경로 문제와 다르게 이동할 때마다 map이 바뀐다는거
따라서 이동할 때마다 map을 최신화 해줘야 함

의사코드

int ans[3][3] = {{1,2,3},{4,5,6},{7,8,0}} // 정리된 상태 (도착지)
int dist[3][3] // 이동거리
int map[3][3]
queue<pair<int, int>> que
bool success
bool

dx = {0, 1, 0, -1}
dy = {1, 0, -1, 0}

BFS(){
	while(!que.empty){
    	y = que.front.first
        x = que.front.second
        que.pop
        
        // 정리된 상태인지 확인
        success = true
        for(i : 0 ~ 3){
    		for(j : 0 ~ 3){
        		if(ans[i][j] != map[i][j]){
                	success = false
                }
            }
        }
        if(success == true){
        	cout << dist[y][x]
            return
        }
        
        // 이동할 수 없는 상태인지 확인
        status = false
        for(i : 0 ~ 3){
        	nx = x + dx[i]
            ny = y + dy[i]
        	if(map[ny][nx] == 0) status = true
        }
        if(status == false){ // 이동할 수 없는 상태
        	cout << "-1"
            return
        }
        
        // 이동
        for(i : 0 ~ 3){
        	nx = x + dx[i]
            ny = y + dy[i]
        	if(map[ny][nx] != 0) continue // 0이 아닌 곳으로는 이동 불가능
            if(nx < 0 || ny < 0 || nx >= 3 || ny >= 3) continue // map을 벗어날 경우
            if(dist[ny][nx] != 0) continue // 이전에 이동했던 위치로는 이동 불가능
            
            que.push({ny, nx})
            dist[ny][nx] = dist[y][x] + 1
            
            // map 최신화
            tmp = map[y][x]
            map[y][x] = map[ny][nx]
            map[ny][nx] = tmp
        }
        
        
    }
        
    }
}

main(){
	for(i : 0 ~ 3){
    	for(j : 0 ~ 3){
        	cin >> map[i][j]
            if(map[i][j] == 1){
            	que.push({i,j})
            }
        }
    }
    
    BFS()
}

3. 시간 복잡도 분석

O(N^2)

4. 문제에서 중요한 부분

최단경로를 구하는 문제라는 것을 알아채기 쉽지 않았던 문제였고
이동할 수 없는 상태인지 확인해줘야 한다는 것과 이동할 때마다 map이 바뀐다는걸 반영해줘야 했던 문제