✅ BFS ✅ 최단경로

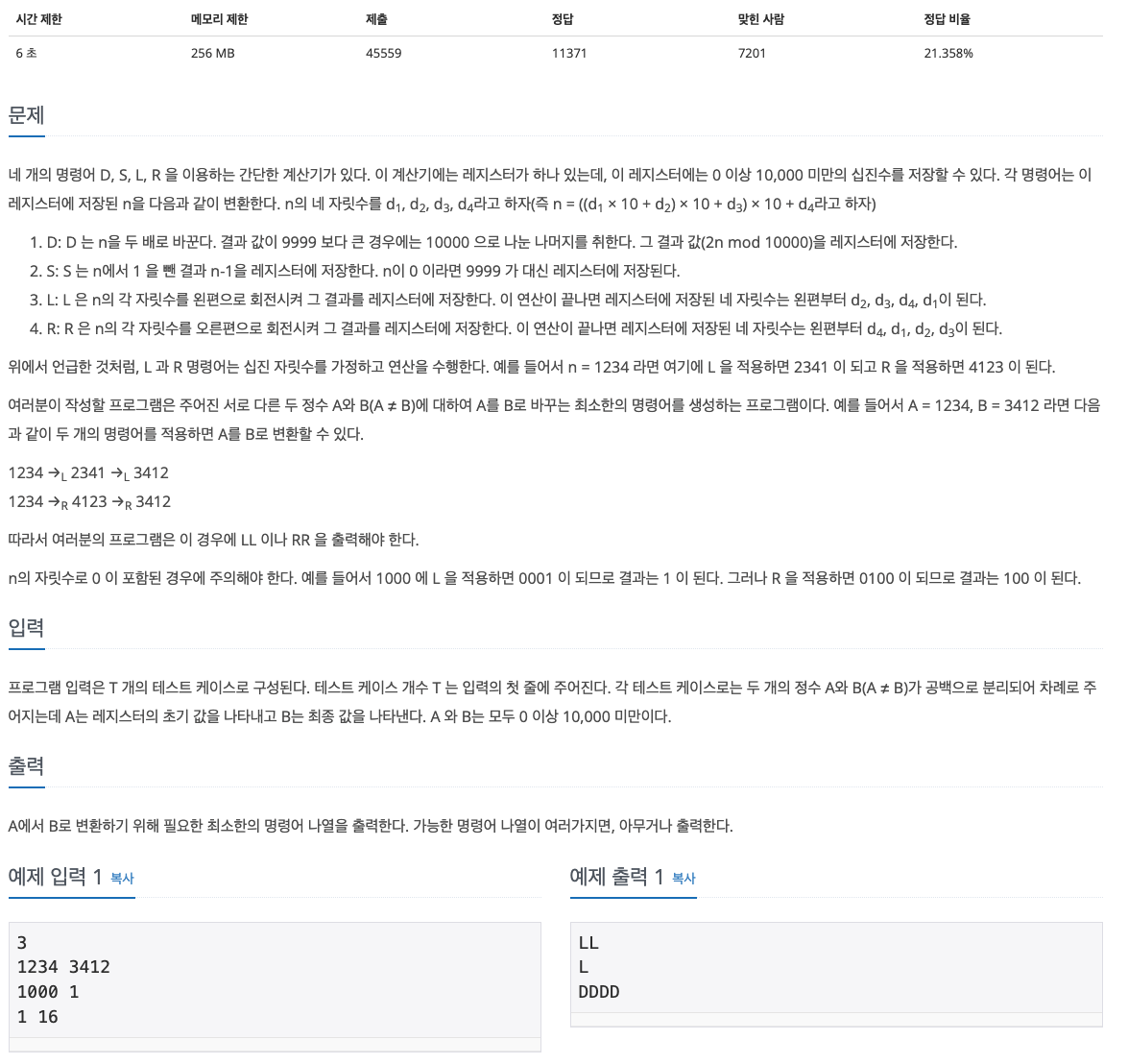
문제

링크

풀이

1. 문제 접근

숫자 A를 4가지 연산을 통해 B로 바꾸는 최소한의 명령어를 구하는 프로그램이므로 최단경로 문제라고 생각할 수 있다.
-> 이동 할 수 있는 경우는 각연산자가 수행하는 연산과 같다.

• n의 자릿수로 0 이 포함된 경우에 주의해야 한다.
  • 예를 들어서 1000 에 L 을 적용하면 0001 이 되므로 결과는 1
  • R 을 적용하면 0100 이 되므로 결과는 100

2. 문제 해결 로직 (풀이법)

• 최단경로 문제이므로 BFS 사용
• 숫자를 변화시키는 것이므로 1차원 array를 사용하여 방문 했는지 안했는지 체크한다.
• 보통의 문제에서 최소경로의 길이를 구할때 특정 지점까지 오는데 걸린 경로의 길이를 저장해가며 진행하는 것처럼
  이문제에서는 사용한 연산자들을 구해야 하므로 연산자들을 저장해가며 진행한다.

의사코드

string op[10000] // 방문 체크 겸, 특정 숫자까지 사용한 연산자들 저장
queue<int> que

BFS(){
	while(!que.empty){
    	int x = que.front
        que.pop
        
        if(x == B){
        	cout << op[x]
            return
        }
        
        // D
        nx = x * 2
        if(nx > 9999) nx % 10000
        if(nx >= 0 && nx < 10000 && !op[nx]){ // nx 범위 확인 && 방문 여부 확인 (nx까지 오는데 사용한 연산자가 없다는건 방문하지 않았다는 것)
            op[nx] = op[nx] + "D" // nx까지 오는데 사용한 연산자 추가
            que.push(nx)
        }
        
        // S
        if(x == 0) nx = 999
        else nx = x - 1
        if(nx >= 0 && nx < 10000 && !op[nx]){
        	op[nx] = op[nx] + "S"
            que.push(nx)
        }
        
        // L
        d1 = x / 1000
        d2 = (x % 1000) / 100
        d3 = (x % 100) / 10
        d4 = x % 10
        nx = ((d2 × 10 + d3) × 10 + d4) × 10 + d1
        if(nx >= 0 && nx < 10000 && !op[nx]){
        	op[nx] = op[nx] + "L"
            que.push(nx)
        }
        
        // R
        d1 = x / 1000
        d2 = (x % 1000) / 100
        d3 = (x % 100) / 10
        d4 = x % 10
        nx = ((d4 × 10 + d1) × 10 + d2) × 10 + d3
        if(nx >= 0 && nx < 10000 && !op[nx]){
        	op[nx] = op[nx] + "R"
            que.push(nx)
        }
    }
}

main(){
	cin >> T
	while(T--){ // 테스터케이스만큼 반복
    	cin >> A >> B
    	visted[A] == true
    	que.push(A)
    	BFS(A)
        
        // op 초기화 해줘야 함
    }
	
}

3. 시간 복잡도 분석

O(N^2)

4. 문제에서 중요한 부분

처음 의사코드를 작성할 때,
보통의 문제에서 최소경로의 길이를 구할때 특정 지점까지 오는데 걸린 경로의 길이를 저장해가며 진행하는 것처럼
이문제에서는 사용한 연산자들을 구해야 하므로 연산자들을 저장해가며 진행해야 한다는 것을 놓쳤었다