✅ BFS ✅ 최단경로

문제

링크

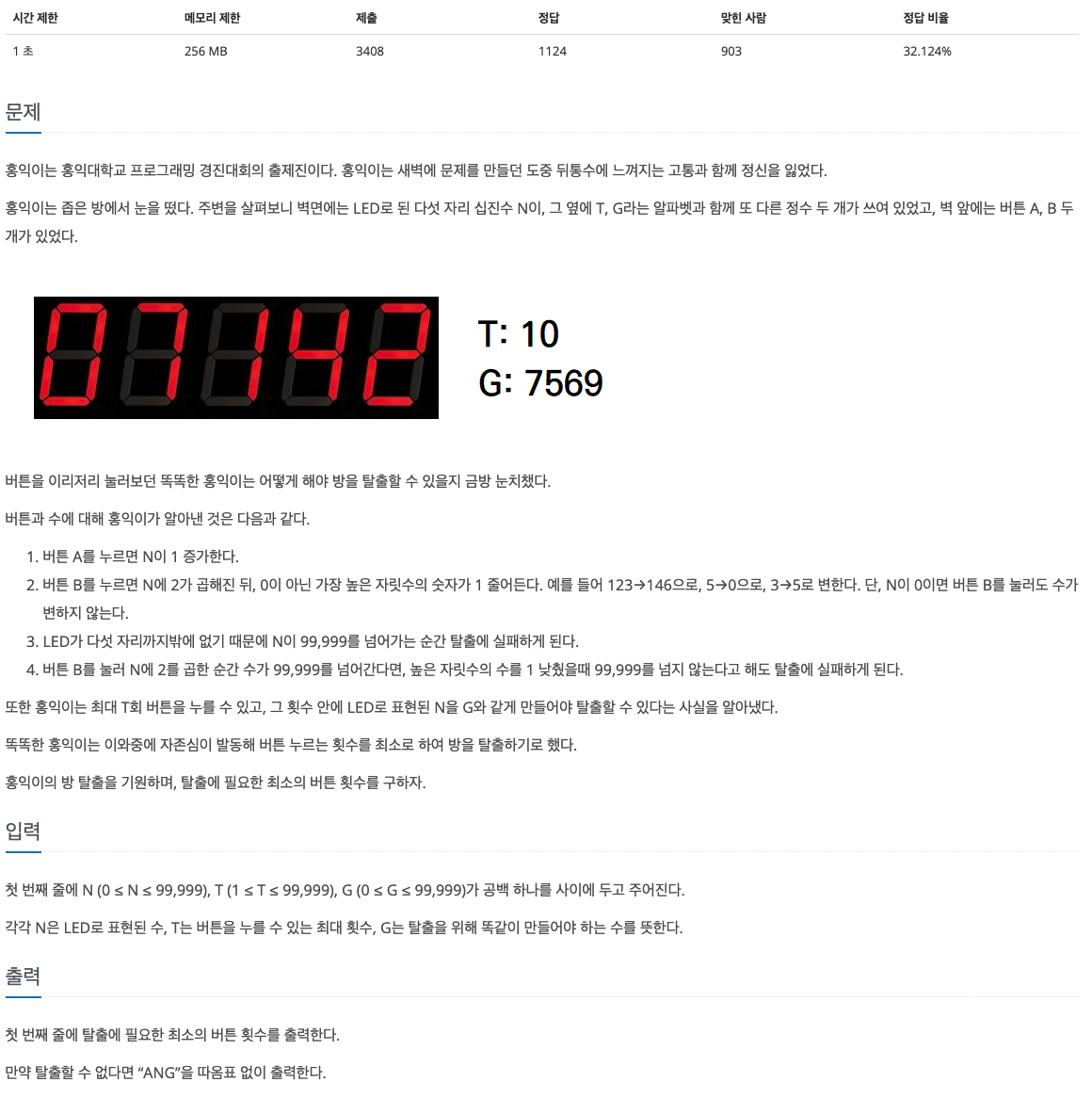
풀이

1. 문제 접근

시작 숫자 N이 목표 숫자 G까지 도달하는데 최소의 버튼 횟수를 구하는 문제이다.
즉, 최단경로 문제와 같다.

버튼의 종류
1. +1
2. *2 -> 가장 큰 자릿수 -1

2. 문제 해결 로직 (풀이법)

최단경로 문제이므로 BFS로 풀었고
버튼은 2종류로, 숫자는 커지거나 작아지거나 둘중 하나이므로 일차원 map이라고 생각하면 된다.

• 버튼을 누를 수 있는 횟수 ( = 최단경로 최대 크기)가 정해져 있으므로 이동할때 최단경로 최대 크기가 넘는지 안넘는지 확인해야 함
• 숫자 N이 두가지 버튼에 의해 크기가 커졌을 때 99,999을 넘는지 확인해야함

의사코드

int map[100000]
int dist[100000]
queue<int> que

BFS(){
	while(!que.empty){
    	x = que.front
        que.pop
        
        for(i : 1 ~ 2){
        	if(x+1 >= 100000 || x*2 >= 100000){
            	cout << "ANG"
                return
            }
            
        	if(i == 1) nx = x + 1 // 버튼 A를 누른 경우
            if(i == 2){ // 버튼 B를 누른 경우
                for(j = 10000;j>=10;j/=10){
                	if(2*x / j != 0){ // 몫이 있다는건 j자리에서 최댓자리수라는 것
                    	nx = ((2*x / j - 1) * j) + (2*x % j)
                        break
                    }
                }
            }
            
            if(map[nx] == 1) contine
            
            que.push(nx)
            map[nx] = 1
            dist[nx] = dist[x] + 1
            
            if(map[nx] == G){
            	cout << dist[nx]
                return
            }
            if(dist[nx] > T){
            	cout << "ANG"
                return
            }
        }
    }
}

main(){
	cin >> N >> T >> G
    que.push(1)
    dist[1] = 0
    map[1] = 1
    
    BFS
}

3. 시간 복잡도 분석

O(N^2)

4. 문제에서 중요한 부분

이동이 제한되는 조건 (N이 99,999을 넘는지, 버튼 횟수를 다 썼는지)을 잘 체크해야하는 문제였다.
잘 체크 했는지는 실제 코드를 구현해서 확인을 해봐야 알 것 같다.