이글은 위키독스 딥러닝을 이용한 자연어 처리입문을 참고하여 복습용으로 작성하였음
1. 다층 퍼셉트론(MultiLayer Perceptron)
MLP(다층 퍼셉트론)은 단층 퍼셉트론 형태에서 은닉층이 1개 이상 추가된 신경망이다.
MLP는 피드 포워드 신경망(Feed Forward Neural Network, FFNN)의 기본적인 형태이다. FFNN은 입력층부터 출력층까지 한 방향으로만 연산되는 신경망을 말한다. 과거에는 SLM이라는 확률기반 모델이 사용되었지만 현재는 인공신경망 모델로 대부분 대체 되었다.
2. 기존 N-gram 모델의 한계
1. Sparsity problem
주어진 문맥으로부터 다음 단어를 예측하는 것을 언어 모델링이라고 한다.
N-gram은 앞의 N개의 단어를 참고해서 예측을 한다. 하지만 n-gram 모델의 훈련 데이터에 예측하고자 하는 예제가 없으면 정확히 모델링을 하지 못하는 Sparsity problem이 발생한다.
ex) 훈련 코퍼스에 라는 데이터가 없으면 확률이 0이 된다. 하지만 이 문맥은 현실에서 충분히 나올 수 있는 문장이므로 잘못된 모델링이다.
2. 단어의 의미적 유사성 파악의 어려움
희소문제는 단어의 의미적 유사성을 파악하면 해결이 가능하다
n-gram의 경우에 발표자료를 살펴보다 라는 문장은 학습되어도 다시보다 라는 문장은 없었다고 가정해보자. 우리가 아래 문장들의 확률을 봤을 때 의 확률이 훨씬 높은 것을 알 수 있다. 하지만 n-gram은 다시보다 라는 말이 훈련데이터에 없었기 때문에 두 문장 모두 확률은 0이 나온다.
이처럼 단어의 의미적 유사성을 학습하는 것은 언어모델에 있어 굉장히 중요하다. 이를 반영한게 NNLM이고 단어 벡터 간의 유사도를 구할 수 있는 벡터를 얻어내는 word embedding의 아이디어이다.
3. 피드 포워드 신경망 언어 모델(NNLM)
다음은 NNLM이 언어모델링을 하는 과정이다.
예문 : "what will the fat cat sit on"
LM(언어모델)은 주어진 단어 시퀀스로부터 다음 단어를 예측한다. 훈련 과정에서 what will the fat cat이라는 훈련 코퍼스가 주어지면 sit을 예측하는 것이다. 첫번째는 기계에게 이를 인식시키기 위해서 훈련데이터는 예문이 전부라고 가정하고 원핫인코딩을 진행한다.
what = [1, 0, 0, 0, 0, 0, 0]
will = [0, 1, 0, 0, 0, 0, 0]
the = [0, 0, 1, 0, 0, 0, 0]
fat = [0, 0, 0, 1, 0, 0, 0]
cat = [0, 0, 0, 0, 1, 0, 0]
sit = [0, 0, 0, 0, 0, 1, 0]
on = [0, 0, 0, 0, 0, 0, 1]이는 단어 집합의 크기인 7차원의 벡터가 되었고 what, will, the, fat, cat의 원-핫 벡터를 입력받아 sit의 원-핫 벡터를 예측하는 문제가 되었다.
N-gram에서 N이 4라고 하자. n을 window라고 부르기도 한다.
즉, 'will the fat cat'까지만 참고하여 'sit'을 예측하는 것이다.
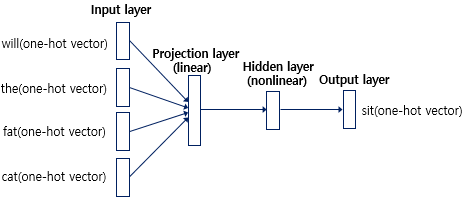
NNLM은 4개의 층으로 구성된 인공신경망이다.
input layer는 N이 4이므로 4개 단어의 one hot vector로 이루어져있다.
output layer는 예측을 하고자하는 sit이 ont hot vector로 이루어져 있고 이는 예측 값의 오차를 구하기 위한 레이블로 사용된다. 그리고 오차로부터 손실함수를 사용하여 인공신경망을 학습한다.
4개의 one hot vector를 입력받은 NNLM은 projection layer로 이동하게 된다. projection layter는 보통 hidden layer와 달리 가중치 행렬과의 곱셈을 이루어지지만 활성화 함수가 존재하지 않는다.
projection layer의 size를 M으로 설정하면, 각 입력 단어들은 이 layer에서 V*M의 weight metrics와 곱해진다. 이때 V는 단어집합의 크기이다. 해당 예에서 단어가 7개 있으므로 V는 7이다. M은 5라고 가정하자.
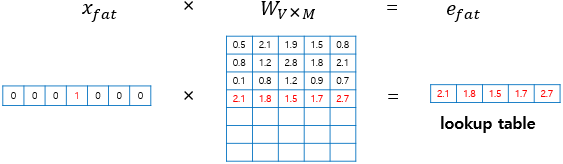
이때 input이 원핫벡터라는 특징으로 인해 W행렬의 i번째 행을 그대로 읽어오는 것(look up)과 같다. 따라서 이를 look up table 이라고 한다.
lookup table 이후 V차원의 원핫벡터는 M차원의 벡터로 mapping 된다.
위 그림에서 단어 fat을 의미하는 원-핫 벡터를 으로 표현했고, 테이블 룩업 과정을 거친 후의 단어 벡터는 으로 표현했습니다. 이 벡터는 초기에는 랜덤한 값을 갖지만 학습과정에서 값이 변경되는데 이 단어 벡터를 embedding vector라고 표현한다.
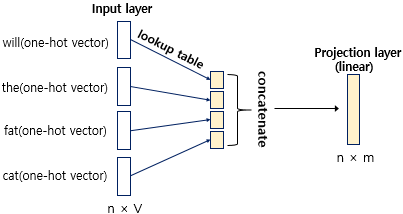
각 단어가 table lookup을 통해 임베딩 벡터로 전환되고 모든 임베딩 벡터는 concatenate를 통해 연결된다. 5차원 벡터 4개를 연결한다는 의미는 20차원 벡터를 얻는다는 의미이다. ( 가로로 연결이 된다고 생각하면 좋다)
이때 은닉층은 활성화 함수가 없기 때문에 linear layer이다(일반적으로 활성화 함수를 사용하는 층은 nonlinear layer이다)
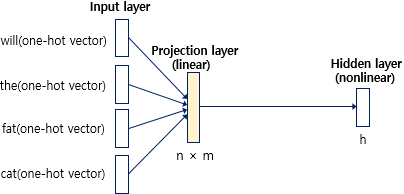
이 결과는 h의 크기를 갖는 hidden layer를 통과한다. 이때 가중치가 곱해지고 편향이 더해져서 활성화 함수의 입력이 된다. 만약 은닉층이 활성화함수로 tanh를 사용하면 식은 다음과 같다.
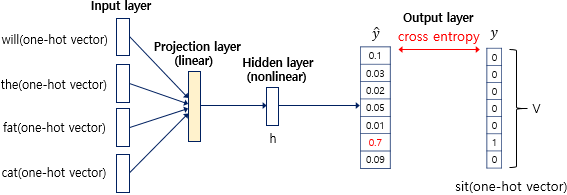
은닉층의 출력은 V의 크기를 갖는 출력층으로 전달된다. 이때 다시 가중치가 곱해지고 편향이 더해져서 입력이었던 원핫 벡터와 같은 V차원의 벡터가 된다. 이 때 활성화함수로 softmax를 사용한다. 측 V차원의 벡터는 총 합이 1인 예측값 을 얻게된다.
이때 두 벡터 와 가 가까워지게 하기위해 cross-entropy 함수를 사용하게된다. 즉, 해당 문제는 단어집합에 해당하는 V개의 선택지 중에서 정답인 sit을 예측하는 다중 클래스 분류 문제인 것이다. 그리고 역전파가 이루어지면 모든 가중치 행렬들이 학습되는데, 여기에는 투사층에서의 가중치 행렬도 포함되므로 임베딩 벡터값 또한 학습됩니다.
이 과정을 통해 수 많은 문장에서 유사한 목적으로 사용되는 단어들은 유사한 임베딩 벡터값을 얻게된다. 이를 통해 훈련 코퍼스에 없는 단어라도 다음 단어를 선택할 수 있게 된다.
NNLM은 단어표현을 임베딩벡터로 하므로 단어 유사도를 구할 수 있고 sparsity problem을 해결한다. 하지만 단어 예측을 위해 모든 단어를 참고하는 것이 아닌 N개의 단어만 참고한다는 한계가 있다. 이를 극복한 것이 RNN이다.
알게된 점
NNLM은 n-gram의 희소문제와 의미적 유사성을 고려 못한다는 문제를 해결하기 위해 만들어졌다. NNLM은 input layer, projection layer, hidden layer, output layer에 해당하는 4개의 층으로 구성된다. input layer는 고려할 n개의 원핫벡터를 입력받는다.
projection layer는 input이 V*M의 weight metrics를 통과하여 M차원의 임베딩 벡터를 만든다. 이는 input이 원핫벡터라는 특성으로 인해 lookup table이라고 부르며 결과를 concatenate한다. 또 projection layer는 가중치와 편향이 있어서 학습이 되지만 활성화함수가 존재하지않는 linear layer이다. 이는 hidden layer를 통과한다.
Hidden layer에서는 가중치와 편향이 존재하고 활성화함수를 통과하여 output layer로 전해진다
Output layer에서는 다시 가중치와 편향으로 입력의 차원과 동일한 V차원으로 바뀐다. 이곳에서 활성화함수로 softmax가 사용되어서 예측하는 확률로 바뀌게된다. 이를 통해 예측값 을 구한다. 이를 cross-entropy 함수를 이용해 실제값 와 예측값 을 통해 V차원의 선택지 중 정답 sit의 확률을 구하는 문제로 바뀌게된다. 이를 역전파 함으로써 projection layer에서 embedding vector가 학습된다
이 임베딩 벡터를 통해 의미적 유사성을 구할 수 있게 되었고 희소문제도 해결했다. 하지만 단어 예측에 있어 모든 단어를 고려하는게 아닌 N개의 단어만 고려한다는 한계는 여전히 존재한다.