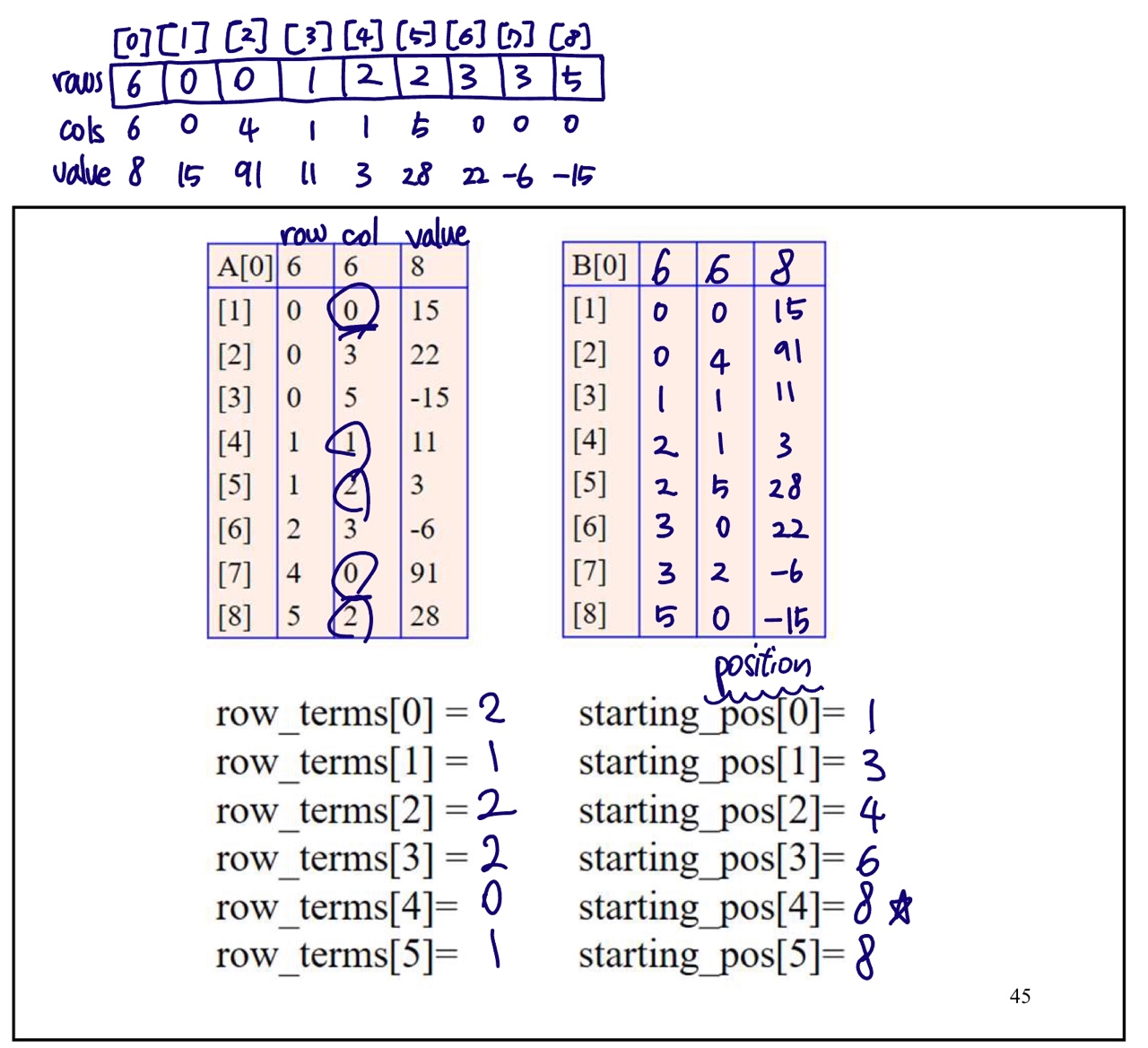
sparse한 2차원 매트릭스를 효율적으로 사용하려면 <row, column, value> 3 tuples(triples)의 array 이용해
non-zero element만 저장할 수 있음.
매트릭스의 트랜스포즈 -> n x m 을 m x n 으로
1 2 3 1 4
4 5 6 2 5 이렇게!
3 6
매트릭스 트랜스포징을 구현하려면 :
for (j = 0; j < n; j++)
for (i = 0l i < m; i++)
b[j][i] = a[i][j];
시간복잡도 -> O(m x n)
But 3 tuple 사용하면 시간복잡도 단축시킬 수 있음.
3 tuple을 이용해 매트릭스를 transpose 하려면 row와 col 값만 바꿔주면 됨.
바꿔준 후 non-zero elements를 저장한 순서를 row-major order로 정렬 해야함.
a의 col이 0인 경우 b의 0번 행이 됨.
일단 a의 col이 0인 elements 저장, 1인 elements 저장, ...
열번호는 odering 딱히 필요없음. row가 낮은 순서로 cols로 들어갈 것이므로.
r x c 크기의 matrix m 을 파일 m.txt 로 입력 받아, row-major order 방식의 sparse matrix 3-tuple
형식으로 저장하여 화면 출력한 뒤, 강의 교재에 제시된 fastTranspose 알고리즘을 수행한 결과를 파일
out.txt 에 출력하라. 입력 파일과 출력 파일은 강의에서 배운 3-tuple 형식 <row, col, val> 으로 구성된다.
*m.txt 의 형식:
첫줄에서 r (행의 개수), c(열의 개수)가 주어지고, 다음 줄부터 원소들이 row-major order 로 주어짐.
#include <iostream>
#include <fstream>
#define _CRT_SECURE_NO_WARNINGS
#define MAX_TERMS 101
using namespace std;
typedef struct {
int col;
int row;
int value;
} term;
term a[MAX_TERMS]; term b[MAX_TERMS];
void fastTranspose(term a[], term b[], int max_col) {
int* rowTerms;
int* startingPos;
rowTerms = (int*)malloc(sizeof(int*) * max_col);
startingPos = (int*)malloc(sizeof(int*) * max_col);
int i, j, numCols = a[0].col, numTerms = a[0].value;
//numCols: 행의 개수 numTerms: 항의 개수
b[0].row = numCols; b[0].col = a[0].row;
b[0].value = numTerms; //a = n x m 이면 b = m x n
if (numTerms > 0) { // 항이 0개가 아니면
for (i = 0; i < numCols; i++)
rowTerms[i] = 0; // rowTerms 0으로 초기화
for (i = 1; i <= numTerms; i++)//1부터 8까지 반복
rowTerms[a[i].col]++;
startingPos[0] = 1;
for (i = 1; i < numCols; i++)
startingPos[i] = startingPos[i - 1] + rowTerms[i - 1];
//startingPos 초기화
for (i = 1; i <= numTerms; i++) { //matrix transposing
j = startingPos[a[i].col]++;
b[j].row = a[i].col; b[j].col = a[i].row; b[j].value = a[i].value;
}
}
}
;
int main() {
fstream fp("m.txt");
int r, c, val = 0, count = 0, max = 0;; //count는 val의 개수
fp >> r; fp >> c;
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
fp >> val;
if (val != 0) { //읽은값을 파일에 저장
++count; //value의 개수
a[count].row = i; a[count].col = j; a[count].value = val;
} // i행 j열 value
}
}
/* r c v
a[0] 10 12 4
a[1] 0 0 5
a[2] 0 1 2
a[3] 1 0 7
a[4] 9 8 1 */
a[0].row = r; a[0].col = c; a[0].value = count; //구조체 0번 인덱스 할당함
//a.txt 값 읽기 끝
for (int i = 1; i <= count; i++) {
if (a[i].col > max) {
max = a[i].col;
}
}
fastTranspose(a, b, max);
ofstream HzWriteFile("out.txt");
for (int i = 0; i < count + 1; i++) {
printf("%d %d %d\n", a[i].row, a[i].col, a[i].value);
}
for (int i = 0; i < count + 1; i++) {
HzWriteFile << b[i].row << " " << b[i].col << " " << b[i].value << "\n";
}
}
a는 순차적으로 읽어 a elements가 해당하는 b의 starting_pos 인덱스에 할당
b의 starting_pos 인덱스에 a의 element를 넣으면 starting_pos++ 해서 인덱스 한칸 밀기
row_terms를 효율적으로 구하기 :
row_terms[0~5]는 다 0으로 초기화.
a에서 col이 0이면 row_terms[0]++
col이 3이면 row_terms[3]++ 이렇게 구현하면 한번만 돌게 할 수 있음.
m.txt 10 12 5 2 0 0 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 out.txt 12 10 8 0 0 5 0 1 7 1 0 2 3 8 3 4 5 2 5 3 8 6 3 9 8 9 1
###matrix에서 자주 사용되는 연산들###
- addition
matrix + matrix 하려면 matrix size가 동일해야함
예) a -> 2x3 (2 by 3 이라고 읽음) 매트릭스면 b가 2x3이어야지만 덧셈할수있음
a00 a01 a02 b00 b01 b02
a10 a11 a12 b10 b11 b12
두 매트릭스 덧셈, 뺄셈 :
a00 + b00 a01 + b01 a02 + b02
a10 + b10 a11 + b11 a12 + b12 이렇게 인덱스 같은애들끼리 더하면됨for(int i = 0; i < 2; i++) for (int j = 0; j <3; j++) c[i][j] = a[i][j] + b[i][j]
두 매트릭스 곱셈 :
조건 : a의 column 개수 = b의 row 개수
a = m x n이면 b = n x p (n에 주목)
a x b = c
c는 m x p 사이즈 가짐c[i][j] = 0 for(int i = 0; i < m; i++) for(int j = 0; j < p; j++) //c의 크기 mxp 일단 구현 for(k = 0; k < n; k++) c[i][j] = a[i][k] x b[k][j]
상식으로 알아두기!