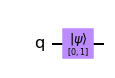양자 상태와 큐비트 - 양자 상태의 표현

Pt J·2020년 11월 8일

[斷] QISKit

목록 보기

6/11

이 포스트의 내용은 Qiskit Textbook | Quantum States and Qubits - Representing Qubit States을 통해 공부한 흔적임을 밝힙니다.

양자 컴퓨터에서 사용되는 큐비트는 고전적인 컴퓨터의 비트와 유사하다.
정보를 저장하는 최소 단위로, 0 또는 1을 출력값으로 갖는다.
하지만 큐비트는 양자역학으로 기술되는 방법들로 관리될 수 있다는 점에서
비트와는 차이가 있다.

고전 비트와 양자 비트 Classical vs Quantum Bits

상태벡터 Statevectors

양자 물리학에서 시스템의 상태는 상태벡터를 통해 기술된다.
상태벡터는 이름 그대로, 상태를 스칼라값이 아닌 벡터를 통해 나타낸다.

예를 들어, "4번째 공간에 위치하고 있다"는 것을 4가 아니라
0 0 0 0 1 0 0 0로 나타내는 것이다.
// 인덱스는 0부터 시작한다는 것을 잊지 말자.
물론 상태라는 것은 공간만을 의미하는 게 아니라 속도, 색상 등 다양한 속성이 될 수 있다.

고전적인 컴퓨터에서는 상태 벡터를 사용할 경우
하나의 값을 나타내기 위해 전체 벡터만큼의 공간을 유지해야 하는 낭비가 존재한다.
하지만 차차 이야기하겠지만 양자 컴퓨터에서는 상태벡터가 아주 효과적인 방법이다.

큐비트 표현 Qubit Notation

고전적인 비트는 항상 0 또는 1로 상태가 명확히 정의된다.
따라서 다른 부가적인 상세 정보 없이 이진수 값을 통해 나타낼 수 있다.
c = 0와 같은 형태로 충분하다는 것이다.

하지만 큐비트는 출력값을 측정할 때만 0 또는 1로 상태가 명확히 정의되면 된다.
그리고 나머지 순간들에는 둘 중 하나를 나타는 것보다 복잡한 상태를 유지한다.

큐비트의 상태를 어떻게 기술하는지에 대해 이야기하기에 앞서 가장 간단한 경우들을 살펴보자면,
지난 시간에 보았던, 항상 확실히 0이 되는 녀석과 항상 확실히 1이 되는 녀석이 있다.
그들은 직관적으로 각각 $0$ 과 $1$ 이라고 부르며 직교 벡터로 표현된다.

|0⟩ = \begin{bmatrix}1\\0\end{bmatrix}\quad|1⟩ = \begin{bmatrix}0\\1\end{bmatrix}

|와 ⟩는 이것이 벡터임을 명시해주기 위해 사용된다.
선형대수 이야기를 할 때 살짝 언급되긴 했지만, 이런 표현 방식을 bra-ket이라고 한다.

$|0⟩$ 와 $|1⟩$ 를 일반적으로 잘 정의된 상태well-defined state라고 부르며,
벡터를 통해 $|0⟩$ 나 $|1⟩$ 외에도 다음과 같이 더 복잡한 상태도 표현할 수 있다.

|q_0⟩ = \begin{bmatrix}1\over\sqrt2\\i\over\sqrt2\end{bmatrix}

이 상태벡터는 정규직교기저 $|0⟩$ 와 $|1⟩$ 의 선형결합을 이용하여 다시 쓸 수 있다.

|q_0⟩ = {1\over\sqrt2}|0⟩ + {i\over\sqrt2}|1⟩

$|q0⟩$ 는 큐비트의 상태벡터이며,
완전히 $|0⟩$ 라고도, 완전히 $|1⟩$ 라고도 할 수 없는 그들의 선형결합으로 이루어져 있다.
양자 컴퓨팅에서는 이런 선형결합에 중첩superposition이라는 표현을 사용한다.

Qiskit 사용하기

중첩에 대해 좀 더 알아보기 위해 Qiskit을 사용해보자.
실습을 위해서는 다음과 같은 패키지들이 필요하다.

from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi

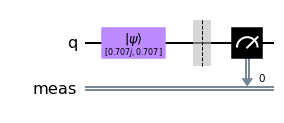
양자회로를 구성하기 위해 1큐비트짜리 QuantumCircuit 객체를 생성하자.
그리고 아무것도 하지 않은 상태에서의 큐비트는 기본적으로 $|0⟩$ 상태인데
상태벡터를 이용하여 $|1⟩$ 로 설정할 수 있다.
어떤 큐비트를 상태벡터를 통해 초기화할 땐 initialize 메서드를 사용한다.

qc = QuantumCircuit(1)
initial_state = [0, 1]
qc.initialize(initial_state, 0)
qc.draw()

get_backend 메서드를 통해 사용할 시뮬레이터를 설정할 수 있는데
여기선 statevector_simulator를 사용하도록 하자.
execute 메서드로 회로를 실행시키고 그 결과를 result 메서드로 받아와
get_statevector 메서드로 출력값의 상태벡터를 확인할 수 있다.

backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result()
out_state = result.get_statevector()
print(out_state)

[0.+0.j 1.+0.j]

python에서 상태벡터는 복소수 벡터로 표현되며 j는 복소수 $i$ 를 의미한다는 것을 알아두자.

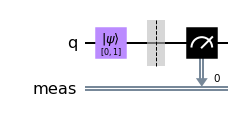
상태벡터가 아닌, 실제 측정 결과를 확인해보자.
큐비트의 출력값은 measure_all 메서드를 통해 측정할 수 있다.

qc.measure_all()
qc.draw()

회로를 실행하고 그 출력 결과를 히스토그램으로 확인해보면 다음과 같다.

result = execute(qc, backend).result()
counts = result.get_counts()
plot_histogram(counts)
상태벡터가 나타내는 값처럼 항상 $1$ 이 출력되는 것을 확인할 수 있다.

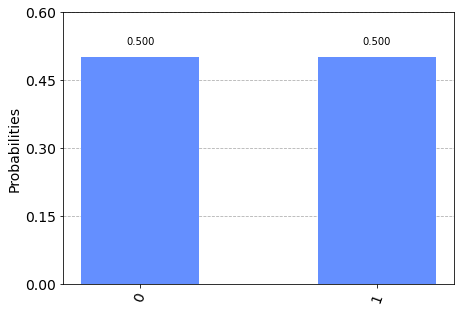
이번엔 중첩된 상태의 큐비트를 사용하여 같은 작업을 해보자.
다음과 같은 상태 벡터를 사용할 것이다.

|q_0⟩ = {1\over\sqrt2}|0⟩ + {i\over\sqrt2}|1⟩

qc = QuantumCircuit(1)
initial_state = [1/sqrt(2), 1j/sqrt(2)]
qc.initialize(initial_state, 0)
state = execute(qc, backend).result().get_statevector()
print(state)

[0.70710678+0.j 0. +0.70710678j]

results = execute(qc, backend).result().get_counts()
plot_histogram(results)

절반의 확률로 $0$ 이, 또 절반의 확률로 $1$ 이 측정됨을 학인할 수 있다.

측정 규칙

어떤 상태벡터 $|ψ⟩$ 가 $|x⟩$ 로 측정될 확률은 $p(|x⟩) = |⟨x|ψ⟩|^2$ 로 계산된다.
선형대수 이야기를 할 때 이야기했지만 $⟨|⟩$ 는 내적을 의미한다.

예를 들어, $|q_0⟩$ 가 $|0⟩$ 로 측정될 확률은 다음과 같이 계산할 수 있다.

|q_0⟩ = {1\over\sqrt2}|0⟩ + {i\over\sqrt2}|1⟩

⟨0|q_0⟩ = {1\over\sqrt2}⟨0|0⟩ + {i\over\sqrt2}⟨0|1⟩ = {1\over\sqrt2}·1 + {i\over\sqrt2}·0= {1\over\sqrt2}

|⟨0|q_0⟩|^2 = {1\over2}

이 측정 규칙은 양자 상태에서 정보를 얻는 방법을 제어한다.
규칙에 내재되어 있는 의미를 해석해보자.

정규화 Normalisation

이 규칙은 진폭과 확률의 연관성을 보여준다.

확률은 모두 더해서 1이 되어야 하므로 상태벡터는 정규화되어 있어야 한다.
정규화되어 있다는 건 벡터의 크기가 1이 되어야 한다는 건데,
다시 말해 $⟨ψ|ψ⟩=1$ 가 성립해야 한다는 것이다.

어떤 벡터 $|ψ⟩=α|0⟩+β|1⟩$ 에 대해서 그 크기가 1이 되기 위해서는 $\sqrt{|α|^2+|β|^2}=1$ 이 성립해야 한다.

만약 우리가 initialize 메서드를 통해
어떤 큐비트를 어떤 상태벡터의 값으로 초기화하고자 할 때
그 상태벡터가 $\sqrt{|α|^2+|β|^2}=1$ 를 만족하지 않는다면 오류가 발생할 것이다.

$1/3$ 확률로 $|0⟩$ , $2/3$ 확률로 $|1⟩$ 로 측정되는 상태를 원한다면...

일반적으로 $|0⟩$ 와 $|1⟩$ 의 확률을 측정하지만
서로 직교인 다른 조합의 상태벡터일 확률을 구해도 문제 없다는 것은 여담.
단지 고전적인 비트에 $0$ 또는 $1$ 로 기록하는 경우가 많을 뿐이다.

전역 위상 Global Phase

// 여기서 '전역'이라는 것은, 물리학 외적인, 가령 수학 같은 분야에 통용되는 것을 의미한다.

상태벡터 $|1⟩$ 는 오직 $1$ 로만 측정된다.
그러나 우리는 다음과 같이 복소수 $i$ 가 붙은 상태도 작성할 수 있다.

\begin{bmatrix}0\\i\end{bmatrix} = i|1⟩

측정 규칙을 적용해보면 $|⟨x|(i|1⟩)|^2=|i⟨x|1⟩|^2=|⟨x|1⟩|^2$ 으로 전혀 문제되지 않는다.
이는 크기를 제곱하는 과정에서 복소수 $i$ 의 부호가 사라지기 때문이다.
이것은 $|x⟩$ 의 측정에 영향을 주지 않아 $i|1⟩$ 의 확률은 $|1⟩$ 의 확률과 동일하다.
큐비트로부터 정보를 얻을 수 있는 유일한 방법이 측정이기 때문에
측정 상 차이가 없는 두 상태는 물리학적으로 동일하다고 할 수 있다.

비단 $i$ 뿐만 아니라 $|\gamma| = 1$ 을 만족하는 모든 $\gamma$ 를 전역 위상이라고 하며
전역 위상만 다르고 동일한 상태들은 물리적으로 구분되지 않는다.

관찰자 효과 The Observer Effect

진폭은 큐비트가 특정 상태로 발견될 확률 정보만을 가지고 있지만
그것을 측정하면 그 구체적인 값을 알 수 있다.

예를 들어, $|q⟩=α|0⟩+β|1⟩$ 가 있을 때 측정 시 100% $|0⟩$ 로 관측된다면
이는 $|q⟩$ 가 $|0⟩$ 임을 의미한다.

|q⟩ = \begin{bmatrix}α\\β\end{bmatrix}\overset{\text{Measure} |0⟩}\longrightarrow|q⟩ = |0⟩ = \begin{bmatrix}1\\0\end{bmatrix}

이와 같이 어떤 상태벡터가 측정을 통해 잘 정의된 상태로 변화하는 것을 붕괴collapse라고 한다.
붕괴의 효과는 강력하여 현명하게 사용해야 한다.
진정한 양자 계산을 하기 위해서는 계산 과정에서 잘 정의된 상태를 갖기 보다는
복합적인 상태를 유지하다가 출력값을 추출할 때 잘 정의된 상태로 붕괴되도록 하는 것이 좋다.
따라서 모든 측정은 양자회로의 마지막에 위치한다.

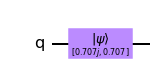
중첩으로 초기화된 큐비트를 Qiskit으로 측정해보자.

qc = QuantumCircuit(1)
initial_state = [0.+1.j/sqrt(2), 1/sqrt(2)+0.j]
qc.initialize(initial_state, 0)
qc.draw()

큐비트는 다음과 같이 초기화된다.

|q⟩ = {i\over\sqrt2}|0⟩ + {1\over\sqrt2}|1⟩

시뮬레이터를 통해 이것이 잘 반영되었음을 확인할 수 있다.

state = execute(qc, backend).result().get_statevector()
print("Qubit State: " + str(state))
Qubit State: [0. +0.70710678j 0.70710678+0.j ]

그리고 큐비트를 측정해보자.

qc.measure_all()
qc.draw()

출력값의 상태를 확인해보면 $|0⟩$ 또는 $|1⟩$ 로 진폭의 한 쪽은 항상 0임을 확인할 수 있다.

state = execute(qc, backend).result().get_statevector()
print("State of Measured Qubit = ", str(state))
State of Measured Qubit = [0.+1.j 0.+0.j]
// 또는
State of Measured Qubit = [0.+0.j 1.+0.j]

실행할 때 마다 위 두 가지 중 하나가 출력되며 그 외의 중첩값은 나타나지 않는다.

큐비트의 상태를 기록하기 위해서는 두 복소수 값을 추적해야 하지만
실제 양자 컴퓨터를 통해 측정하면 0 또는 1 밖에 나오지 않는다.
그 중간 상태를 확인할 수 없는 것이다.
따라서 Qiskit은 여러 가지 양자 시뮬레이터를 제공하는데
지난 번에 사용한 qasm_simulator의 경우
실제 양자 컴퓨터와 상호작용하듯 동작하여 상태벡터를 확인할 수 없지만
이번 시간에 사용한 statevector_simulator의 경우 그것이 가능하다.
따라서 상황과 목적에 맞는 양자 시뮬레이터를 사용해야 한다.

블로흐 구면 The Bloch Sphere

제한된 큐비트 상태의 기술

앞서 살펴본 방식의 큐비트 상태 규칙으로는
물리학적으로 구분되지 않는 상태까지 기술할 수 있는 문제가 있다.
그런 의미에서 좀 더 제한된 기술 방법을 알아보자.

어떤 복소수 $α$ 와 $β$ 에 대하여 큐비트의 상태 벡터 $|q⟩$ 는 $|q⟩ = α|0⟩ + β|1⟩$ 로 나타낼 수 있다.
측정 규칙에 대해 이야기할 때 살펴 봤듯이 전역 위상을 측정할 수 없기 때문에
오직 $|0⟩$ 와 $|1⟩$ 사이의 위상만 측정할 수 있다.

복소수 표현으로 인한 복잡성을 줄이기 위해
$α$ 와 $β$ 를 복소수 범위로 설정하는 대신 실수로 한정하고
그들 사이의 상대 위상을 나타내는 값을 추가하여 표현하는 방식이 있다.
실수 $ϕ$ 를 사용하여 $|q⟩ = α|0⟩ + e^{iϕβ}|1⟩$ 로 나타내는 것이다.

그리고 $\sqrt{α^2 + β^2} = 1$ 와 같이 정규화되어야 한다는 특성은
삼각함수 항등식 $\sqrt{sin^2x + cos^2x} = 1$ 을 이용하여
$α = cos{θ\over2}$ , $β = sin{θ\over2}$ 로 나타낼 수 있다.

즉, $|q⟩$ 는 실수 $θ$ 와 $ϕ$ 에 대하여 다음과 같이 나타낼 수 있다.

|q⟩ = cons{θ\over2}|0⟩ + e^{iϕ}sin{θ\over2}|1⟩

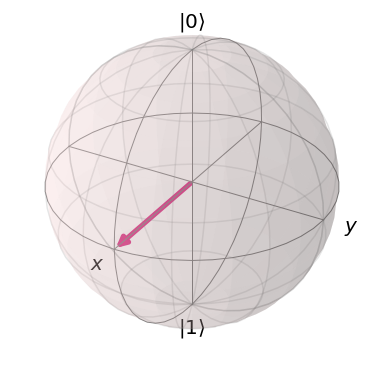
큐비트 상태의 시각적 표현

그렇다면 $|q⟩ = cons{θ\over2}|0⟩ + e^{iϕ}sin{θ\over2}|1⟩$ 로 표현되는 큐비트는 어떻게 시각화할 수 있을까?

큐비트 상태의 크기는 1인 것을 감안하여 $r = 1$ 인 구면좌표계를 생각할 수 있다.
이 구면좌표계를 통해 구의 중심에서 시작하여 표면으로 향하는 상태벡터를 표현할 수 있다.
이 구면을 블로흐 구면이라고 부른다.

Qiskit은 블로흐 구면을 그리는 함수 plot_bloch_vector를 제공한다.
이 함수는 세 개의 원소를 가진 리스트를 인자로 받는데
그것은 앞에서부터 $r$ , $θ$ , $ϕ$ 을 의미한다.

이를 코드로 작성하면,

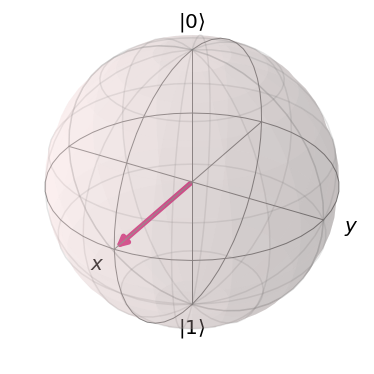
from math import pi
from qiskit.visualization import plot_bloch_vector
plot_bloch_vector([1,pi/2,0], coord_type='spherical')

// textbook이 작성된 시점에는 이 방식이 아니었기에 그것과 코드가 다르다

몇 가지 더 출력해보자면,

|0⟩

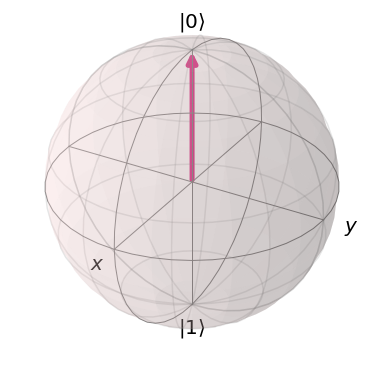
from math import pi
from qiskit.visualization import plot_bloch_vector
plot_bloch_vector([1,0,0], coord_type='spherical')

|1⟩

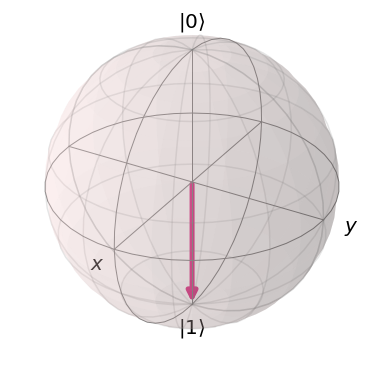
from math import pi
from qiskit.visualization import plot_bloch_vector
plot_bloch_vector([1,pi,0], coord_type='spherical')

${1\over\sqrt2}(|0⟩+|1⟩)$
from math import pi
from qiskit.visualization import plot_bloch_vector
plot_bloch_vector([1,pi/2,0], coord_type='spherical')