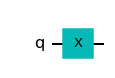이 포스트의 내용은 Qiskit Textbook | Quantum States and Qubits - Single Qubit Gates을 통해 공부한 흔적임을 밝힙니다.

큐비트의 상태는 다음과 같이 제한된 형태로 표현되는 2차원 벡터로 나타낼 수 있다.

여기서 $\theta$와 $\phi$는 실수다.

큐비트의 상태를 변화시키는 연산을 게이트gates라고 하는데,
이번 시간에는 하나의 큐비트에 적용할 수 있는 단일 큐비트 게이트에 대해 알아보도록 하겠다.
이러한 게이트는 가역행렬로 나타낼 수 있다는 건 여담.

먼저 실습을 위한 패키지를 준비하고 시작하자.

from qiskit import *
from math import pi
from qiskit.visualization import plot_bloch_multivector

파울리 게이트 The Pauli Gates

X 게이트 The X-Gates

X 게이트는 파울리 X 행렬로 표현된다.

게이트는 행렬곱을 통해 적용할 수 있다.

코드로는 다음과 같이 작성할 수 있다.

qc = QuantumCircuit(1)
qc.x(0)
qc.draw('mpl')

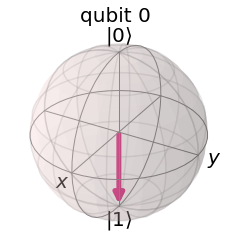
이 회로의 결과값 상태벡터를 블로흐 구면에 나타내보면,

backend = Aer.get_backend('statevector_simulator')
out = execute(qc, backend).result().get_statevector()
plot_bloch_multivector(out)

블로흐 구면의 $x$축을 기준으로 $\pi$ 라디안 회전한 것이라고 볼 수 있겠다.
X 게이트는 고전적인 NOT 게이트와 유사하게 취급되기도 한다.

Y 게이트와 Z 게이트 The Y & Z-Gates

X 게이트와 마찬가지로 Y 게이트와 Z 게이트도 각각 파울리 Y 행렬, 파울리 Z 행렬로 표현된다.

또한 이들은 각각 블로흐 구면의 $y$축, $z$축을 기준으로 $\pi$ 라디안 회전한 효과를 보인다.

textbook에서 제공하는 위젯을 통해 이를 확인해볼 수 있다.

from qiskit_textbook.widgets import gate_demo
gate_demo(gates='pauli')

그리고 코드 상에서는 다음과 같이 큐비트에 적용할 수 있다.

qc.y(0)
qc.z(0)
qc.draw('mpl')

여담

$|0\rangle$ 상태와 $|1\rangle$ 상태에서는 Z 게이트를 적용해도 그 어떤 변화도 확인할 수 없다.
이는 $|0\rangle$와 $|1\rangle$가 Z 게이트의 고유상태The eigenstates이기 때문이다.
이들은 종종 Z 기저라고 불린다.

Z 기저 외에도, X 게이트의 고유상태인 X 기저도 많이 쓰이는데 그것은 $|+\rangle$과 $|-\rangle$라고 불린다.

그리고 Y 게이트의 고유상태인 Y 기저는 다음과 같다.

하다마드 게이트 The Hadamard Gates

하다마드 게이트는 주로 H 게이트로 줄여 부르는, 기본적인 양자 게이트다.

이 게이트를 통해 $|0\rangle$과 $|1\rangle$의 중첩을 만들 수 있다.
즉, 다음과 같은 변환이 성립한다.

이 게이트는 블로흐 구면에서 $x$축과 $z$축의 중앙에 있는 축을 기준으로 뒤집는 효과가 있다.

여담

Z 기저는 본질적으로 특별한 녀석이 아니며 그 외에도 다양한 기저가 있음을 이야기하며
그 다양한 기저 중 대표적인 것 일부를 알아보았다.

그렇게 다양한 기저가 있듯이 측정할 때도 반드시 Z 기저를 측정해야 하는 것은 아니다.
예를 들어, X 기저인 $|+\rangle$과 $|-\rangle$을 측정할 수 있다.

Qiskit은 Z 기저만을 측정하기에 X 기저를 측정하기 위해서는 H 게이트를 사용해야 한다.

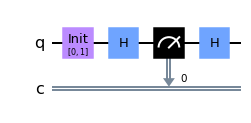
from qiskit.extensions import Initialize 

def x_measurement(qc,qubit,cbit):
    """Measure 'qubit' in the X-basis, and store the result in 'cbit'"""
    qc.h(qubit)
    qc.measure(qubit, cbit)
    qc.h(qubit)
    return qc

qc = QuantumCircuit(1,1)
initial_state = [0,1]
initializer = Initialize(initial_state)
initializer.label = "init"
qc.append(initializer, [0])
x_measurement(qc, 0, 0)
qc.draw()

위 예제는 Z 게이트와 H 게이트를 이용하여 X 게이트를 만드나.

이것이 성립하는 것은 다음과 같은 과정으로 확인할 수 있다.

그리고 같은 원리로 두 개의 H 게이트 사이에 Z 기저 측정을 넣어 X 기저를 측정할 수 있다.

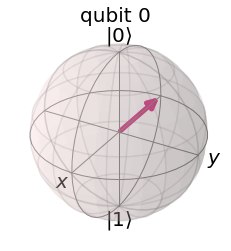
backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
out_state = execute(qc,backend).result().get_statevector() # Do the simulation, returning the state vector
plot_bloch_multivector(out_state) # Display the output state vector

$또는$

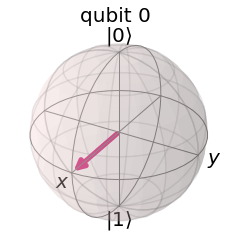
initial_state를 $|1\rangle$로 초기화하고 실행하였는데
$|+\rangle$ 또는 $|-\rangle$로 붕괴되는 것을 확인할 수 있다.

$R_\phi$ 게이트 The $R_\phi$-Gates

$R_\phi$ 게이트는 실수 매개변수 $\phi$를 필요로 하며, $z$축 방향으로 $\phi$만큼 회전한다.
$R_z$ 게이트라고도 불리며 다음과 같은 행렬로 나타낼 수 있다.

코드 상에서는 다음과 같이 작성할 수 있다.

qc = QuantumCircuit(1)
qc.rz(pi/4, 0)
qc.draw('mpl')

첫번째 인자가 $\phi$, 두번째 인자가 대상 큐비트다.

Z 게이트는 $R_\phi$ 게이트의 특수한 경우이며, Z 게이트 외에도 $R_\phi$ 게이트의 특수한 형태는 몇 가지 더 있다.

I 게이트 The I-Gates

I 게이트는 Identity 게이트다.
단위 행렬로 표현되며 이 게이트는 아무 일도 하지 않는다.

의미 없어보이지만 때로는 계산에 사용되므로 게이트가 존재한다.
그리고 때로는 아무 작업도 하지 않는 상황에서 이를 명시해줄 필요가 있는 경우도 있다.

S 게이트 The S-Gates

S 게이트는 Phase 게이트다.
$\sqrt Z$ 게이트라고 불리며 $\phi={\pi\over2}$인 특수한 경우의 $R_\phi$다.
이것은 큐비트를 블로흐 구면 상에서 90도 회전하게 한다.
여기서 다루는 다른 게이트들과 달리 S 게이트는 거듭행렬이 아니며, 따라서 종종 $S^\dagger$ 게이트를 만나게 된다.
$S^\dagger$ 게이트는 $\phi=-{\pi\over2}$인 특수한 경우의 $R_\phi$다.

$\sqrt Z$ 게이트라는 이름은 다음과 같은 특성에 의해 붙었다.

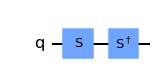
$S$ 게이트와 $S^\dagger$ 게이트는 코드 상에서 각각 다음과 같이 표현된다.

qc = QuantumCircuit(1)
qc.s(0)
qc.sdg(0)
qc.draw('mpl')

T 게이트 The T-Gates

T 게이트는 $\phi={\pi\over4}$인 특수한 경우의 $R_\phi$다.

T 게이트는 S 게이트와 같은 맥락에서 $\sqrt[4]Z$라고도 불리며,
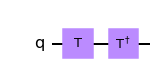
코드로는 다음과 같이 작성할 수 있다.

qc = QuantumCircuit(1)
qc.t(0)
qc.tdg(0)
qc.draw('mpl')

일반적인 $U_3$ 게이트 The General $U_3$-Gates

I, Z, S, T 게이트가 $R_\phi$의 특수한 형태인 것과 같이
모든 단일 큐비트 게이트는 그것의 일반적인 형태의 특수한 경우다.
모든 단일 큐비트 게이트의 일반적인 형태는 $U_3$ 게이트라고 불린다.

물론 이 표현은 복잡하기에 회로에서 직접 보기는 쉽지 않을 것이다.
$R_z$ 게이트 외에도 $R_x$ 게이트나 $R_y$ 게이트도 존재하지만 잘 쓰이지는 않는다.
그렇기에 S나 T 게이트와 달리 따로 이름 붙이지 않는다.