이 포스트의 내용은 Qiskit Textbook | Multiple Qubits and Entanglement - Multiple Qubits and Entangled States 을 통해 공부한 흔적임을 밝힙니다.
지난시간 까지 단일 큐비트와 단일 큐비트 연산에 대해 알아보았다.
다중 큐비트 상태 표현
하나의 비트는 두 가지 가능한 상태를 가지고 있고
그것은 다음과 같은 4차원 벡터에 표현할 수 있다.
∣ a ⟩ = a 00 ∣ 00 ⟩ + a 01 ∣ 01 ⟩ + a 10 ∣ 10 ⟩ + a 11 ∣ 11 ⟩ = [ a 00 a 01 a 10 a 11 ] |a\rangle = a_{00}|00\rangle + a_{01}|01\rangle + a_{10}|10\rangle + a_{11}|11\rangle = \begin{bmatrix}a_{00}\\a_{01}\\a_{10}\\a_{11}\end{bmatrix} ∣ a ⟩ = a 0 0 ∣ 0 0 ⟩ + a 0 1 ∣ 0 1 ⟩ + a 1 0 ∣ 1 0 ⟩ + a 1 1 ∣ 1 1 ⟩ = ⎣ ⎢ ⎢ ⎢ ⎡ a 0 0 a 0 1 a 1 0 a 1 1 ⎦ ⎥ ⎥ ⎥ ⎤ 확률을 구하는 방식도 단일 큐비트와 다르지 않다.
p ( ∣ 00 ⟩ ) = ∣ ⟨ 00 ∣ a ⟩ ∣ 2 = ∣ a 00 ∣ 2 p(|00\rangle) = | \langle00|a\rangle|^2 = |a_{00}|^2 p ( ∣ 0 0 ⟩ ) = ∣ ⟨ 0 0 ∣ a ⟩ ∣ 2 = ∣ a 0 0 ∣ 2 ∣ a 00 ∣ 2 + ∣ a 01 ∣ 2 + ∣ a 10 ∣ 2 + ∣ a 11 ∣ 2 = 1 |a_{00}|^2 + |a_{01}|^2 + |a_{10}|^2 + |a_{11}|^2 = 1 ∣ a 0 0 ∣ 2 + ∣ a 0 1 ∣ 2 + ∣ a 1 0 ∣ 2 + ∣ a 1 1 ∣ 2 = 1 다중 큐비트의 상태는 큐비트 간의 텐서곱을 통해 나타낼 수 있다.
예를 들어, ∣ a ⟩ = [ a 0 a 1 ] |a\rangle = \begin{bmatrix}a_0\\a_1\end{bmatrix} ∣ a ⟩ = [ a 0 a 1 ] ∣ b ⟩ = [ b 0 b 1 ] |b\rangle = \begin{bmatrix}b_0\\b_1\end{bmatrix} ∣ b ⟩ = [ b 0 b 1 ]
∣ b a ⟩ = ∣ b ⟩ ⊗ ∣ a ⟩ = [ b 0 × [ a 0 a 1 ] b 1 × [ a 0 a 1 ] ] = [ b 0 a 0 b 0 a 1 b 1 a 0 b 1 a 1 ] |ba\rangle = |b\rangle \otimes |a\rangle = \begin{bmatrix}b_0 \times \begin{bmatrix}a_0\\a_1\end{bmatrix}\\ b_1 \times \begin{bmatrix}a_0\\a_1\end{bmatrix}\end{bmatrix} = \begin{bmatrix}b_0a_0\\b_0a_1\\b_1a_0\\b_1a_1\end{bmatrix} ∣ b a ⟩ = ∣ b ⟩ ⊗ ∣ a ⟩ = ⎣ ⎢ ⎢ ⎢ ⎡ b 0 × [ a 0 a 1 ] b 1 × [ a 0 a 1 ] ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ b 0 a 0 b 0 a 1 b 1 a 0 b 1 a 1 ⎦ ⎥ ⎥ ⎥ ⎤ 그리고 마찬가지로 3개 혹은 그 이상의 큐비트에 대해서도 텐서곱으로 상태벡터를 구할 수 있다.
∣ c b a ⟩ = [ c 0 b 0 a 0 c 0 b 0 a 1 c 0 b 1 a 0 c 0 b 1 a 1 c 1 b 0 a 0 c 1 b 0 a 1 c 1 b 1 a 0 c 1 b 1 a 1 ] |cba\rangle = \begin{bmatrix}c_0b_0a_0\\c_0b_0a_1\\c_0b_1a_0\\c_0b_1a_1\\c_1b_0a_0\\c_1b_0a_1\\c_1b_1a_0\\c_1b_1a_1\end{bmatrix} ∣ c b a ⟩ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ c 0 b 0 a 0 c 0 b 0 a 1 c 0 b 1 a 0 c 0 b 1 a 1 c 1 b 0 a 0 c 1 b 0 a 1 c 1 b 1 a 0 c 1 b 1 a 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ n n n 2 n 2^n 2 n
이를 코드 상에서 작성해보자.
from qiskit import *
from math import pi
import numpy as np
from qiskit. visualization import plot_bloch_multivector, plot_histogram
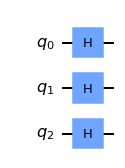
그리고 세 개의 큐비트를 준비하고 H 게이트를 각각 적용한다.
qc = QuantumCircuit( 3 )
for qubit in range ( 3 ) :
qc. h( qubit)
qc. draw( )
H 게이트로 인해 각각의 큐비트는 ∣ + ⟩ |+\rangle ∣ + ⟩
∣ + + + ⟩ = 1 8 [ 1 1 1 1 1 1 1 1 ] |+++\rangle = {1\over\sqrt8}\begin{bmatrix}1\\1\\1\\1\\1\\1\\1\\1\end{bmatrix} ∣ + + + ⟩ = 8 1 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 1 1 1 1 1 1 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ 실제로 실행해보면,
backend = Aer. get_backend( 'statevector_simulator' )
final_state = execute( qc, backend) . result( ) . get_statevector( )
from qiskit_textbook. tools import array_to_latex
array_to_latex( final_state, pretext= "\\text{Statevector} = " ) Statevector = [ 1 8 1 8 1 8 1 8 1 8 1 8 1 8 1 8 ] \text{Statevector} = \begin{bmatrix}{1\over\sqrt8}\\{1\over\sqrt8}\\{1\over\sqrt8}\\{1\over\sqrt8}\\{1\over\sqrt8}\\{1\over\sqrt8}\\{1\over\sqrt8}\\{1\over\sqrt8}\end{bmatrix} Statevector = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 8 1 8 1 8 1 8 1 8 1 8 1 8 1 8 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
다중 큐비트 상태 벡터에 단일 큐비트 게이트 적용
지금까지 다뤘던 게이트들은 단일 큐비트 게이트다.
X = [ 0 1 1 0 ] X = \begin{bmatrix}0&1\\1&0\end{bmatrix} X = [ 0 1 1 0 ] ∣ 0 ⟩ |0\rangle ∣ 0 ⟩
X ∣ 0 ⟩ = [ 0 1 1 0 ] [ 1 0 ] = [ 0 1 ] X|0\rangle = \begin{bmatrix}0&1\\1&0\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}0\\1\end{bmatrix} X ∣ 0 ⟩ = [ 0 1 1 0 ] [ 1 0 ] = [ 0 1 ] 그런데 다중 큐비트 벡터의 한 큐비트에 대해 X 게이트를 적용하려면 어떻게 해야 될까?
다중 큐비트 상태벡터를 구할 때 텐서곱을 사용했던 것처럼
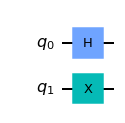
예를 들어, 다음과 같은 코드가 있다고 하자.
qc = QuantumCircuit( 2 )
qc. h( 0 )
qc. x( 1 )
qc. draw( )
상태벡터의 연산은 다음과 같이 이루어진다.
X ∣ q 1 ⟩ ⊗ H ∣ q 0 ⟩ = ( X ⊗ H ) ∣ q 1 q 0 ⟩ X|q_1\rangle\otimes H|q_0\rangle = (X\otimes H)|q_1q_0\rangle X ∣ q 1 ⟩ ⊗ H ∣ q 0 ⟩ = ( X ⊗ H ) ∣ q 1 q 0 ⟩ X ⊗ H = [ 0 1 1 0 ] ⊗ 1 2 [ 1 1 1 − 1 ] = 1 2 [ 0 × [ 1 1 1 − 1 ] 1 × [ 1 1 1 − 1 ] 1 × [ 1 1 1 − 1 ] 0 × [ 1 1 1 − 1 ] ] = 1 2 [ 0 0 1 1 0 0 1 − 1 1 1 0 0 1 − 1 0 0 ] = [ 0 H H 0 ] X\otimes H = \begin{bmatrix}0&1\\1&0\end{bmatrix}\otimes{1\over\sqrt2}\begin{bmatrix}1&1\\1&-1\end{bmatrix} = {1\over\sqrt2}\begin{bmatrix}0\times\begin{bmatrix}1&1\\1&-1\end{bmatrix}&1\times\begin{bmatrix}1&1\\1&-1\end{bmatrix}\\1\times\begin{bmatrix}1&1\\1&-1\end{bmatrix}&0\times\begin{bmatrix}1&1\\1&-1\end{bmatrix}\end{bmatrix}\\\ \\ = {1\over\sqrt2}\begin{bmatrix}0&0&1&1\\0&0&1&-1\\1&1&0&0\\1&-1&0&0\end{bmatrix} = \begin{bmatrix}0&H\\H&0\end{bmatrix} X ⊗ H = [ 0 1 1 0 ] ⊗ 2 1 [ 1 1 1 − 1 ] = 2 1 ⎣ ⎢ ⎢ ⎢ ⎡ 0 × [ 1 1 1 − 1 ] 1 × [ 1 1 1 − 1 ] 1 × [ 1 1 1 − 1 ] 0 × [ 1 1 1 − 1 ] ⎦ ⎥ ⎥ ⎥ ⎤ = 2 1 ⎣ ⎢ ⎢ ⎢ ⎡ 0 0 1 1 0 0 1 − 1 1 1 0 0 1 − 1 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ = [ 0 H H 0 ] 따라서 X ⊗ H = [ 0 H H 0 ] X \otimes H = \begin{bmatrix}0&H\\H&0\end{bmatrix} X ⊗ H = [ 0 H H 0 ] ∣ q 1 q 0 ⟩ |q_1q_0\rangle ∣ q 1 q 0 ⟩
이를 직접 계산하지 않아도 회로의 모든 연산을 합쳐 하나의 행렬로 만들어주는unitary_simulator를 사용하면 X ⊗ H X \otimes H X ⊗ H
backend = Aer. get_backend( 'unitary_simulator' )
unitary = execute( qc, backend) . result( ) . get_unitary( )
from qiskit_textbook. tools import array_to_latex
array_to_latex( unitary, pretext= "\\text{Circuit = }\n" ) Circuit = [ 0 0 1 2 1 2 0 0 1 2 − 1 2 1 2 1 2 0 0 1 2 − 1 2 0 0 ] \text{Circuit}=\begin{bmatrix}0&0&{1\over\sqrt2}&{1\over\sqrt2}\\0&0&{1\over\sqrt2}&-{1\over\sqrt2}\\{1\over\sqrt2}&{1\over\sqrt2}&0&0\\{1\over\sqrt2}&-{1\over\sqrt2}&0&0\end{bmatrix} Circuit = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 0 0 2 1 2 1 0 0 2 1 − 2 1 2 1 2 1 0 0 2 1 − 2 1 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
만약 한 번에 하나의 큐비트만 게이트를 적용하고자 한다면
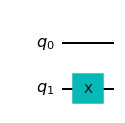
코드 상으로는 다음과 같이 작성되며
qc = QuantumCircuit( 2 )
qc. x( 1 )
qc. draw( )
실행해보면,
backend = Aer. get_backend( 'unitary_simulator' )
unitary = execute( qc, backend) . result( ) . get_unitary( )
array_to_latex( unitary, pretext= "\\text{Circuit = } " ) Circuit = [ 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 ] \text{Circuit}=\begin{bmatrix}0&0&1&0\\0&0&0&1\\1&0&0&0\\0&1&0&0\end{bmatrix} Circuit = ⎣ ⎢ ⎢ ⎢ ⎡ 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 ⎦ ⎥ ⎥ ⎥ ⎤
X ⊗ I = [ 0 I I 0 ] X\otimes I = \begin{bmatrix}0 & I \\ I & 0\end{bmatrix} X ⊗ I = [ 0 I I 0 ]
다중 큐비트 게이트
다중 큐비트 벡터에 단일 큐비트 게이트를 적용할 수도 있지만
중요하게 사용되는 대표적인 2-큐비트 게이트로는 CNOT 게이트가 있다.
CNOT 게이트
CNOT 게이트가 적용되는 두 개의 큐비트를 각각 컨트롤과 타겟이라고 하며,∣ 1 ⟩ |1\rangle ∣ 1 ⟩
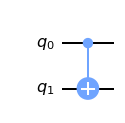
코드로 작성하면 담음과 같다.
qc = QuantumCircuit( 2 )
qc. cx( 0 , 1 )
qc. draw( )
cx 메서드에서 첫번째 인자가 컨트롤, 두번째 인자가 타겟이다.
큐비트들이 중첩 상태에 있지 않고 ∣ 0 ⟩ |0\rangle ∣ 0 ⟩ ∣ 1 ⟩ |1\rangle ∣ 1 ⟩
Input (t, c) Output (t, c) 00 00 01 11 10 10 11 01
이는 다음과 같은 두 개의 행렬 중 하나를 통해 이루어진다.
CNOT = [ 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ] CNOT = [ 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ] \text{CNOT} = \begin{bmatrix}1&0&0&0\\0&0&0&1\\0&0&1&0\\0&1&0&0\end{bmatrix} \quad \text{CNOT} = \begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix} CNOT = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ CNOT = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ⎦ ⎥ ⎥ ⎥ ⎤ 둘 중 무엇이 사용되는지는 컨트롤과 타겟의 순서에 달려 있다.
q 0 q_0 q 0 q 1 q_1 q 1
∣ a ⟩ = [ a 00 a 01 a 10 a 11 ] CNOT ∣ a ⟩ = [ a 00 a 11 a 10 a 01 ] ← ← |a\rangle = \begin{bmatrix}a_{00}\\a_{01}\\a_{10}\\a_{11}\end{bmatrix} \quad \text{CNOT}|a\rangle = \begin{bmatrix}a_{00}\\a_{11}\\a_{10}\\a_{01}\end{bmatrix}\begin{matrix}\\\leftarrow\\\\\leftarrow\end{matrix} ∣ a ⟩ = ⎣ ⎢ ⎢ ⎢ ⎡ a 0 0 a 0 1 a 1 0 a 1 1 ⎦ ⎥ ⎥ ⎥ ⎤ CNOT ∣ a ⟩ = ⎣ ⎢ ⎢ ⎢ ⎡ a 0 0 a 1 1 a 1 0 a 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ ← ← ∣ 01 ⟩ |01\rangle ∣ 0 1 ⟩ ∣ 11 ⟩ |11\rangle ∣ 1 1 ⟩
중첩된 큐비트의 CNOT
CNOT 게이트에서 컨트롤이 ∣ 0 ⟩ |0\rangle ∣ 0 ⟩ ∣ 1 ⟩ |1\rangle ∣ 1 ⟩
그런데 컨트롤이 중첩된 ∣ + ⟩ |+\rangle ∣ + ⟩
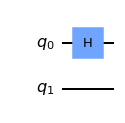
qc = QuantumCircuit( 2 )
qc. h( 0 )
qc. draw( )
초기 상태의 상태벡터를 확인해보면,
backend = Aer. get_backend( 'statevector_simulator' )
final_state = execute( qc, backend) . result( ) . get_statevector( )
array_to_latex( final_state, pretext= "\\text{Statevector = }" ) Statevector = [ 1 2 1 2 0 0 ] \text{Statevector}=\begin{bmatrix}{1\over\sqrt2}\\{1\over\sqrt2}\\0\\0\end{bmatrix} Statevector = ⎣ ⎢ ⎢ ⎢ ⎡ 2 1 2 1 0 0 ⎦ ⎥ ⎥ ⎥ ⎤
계산을 통해서도 같은 결과를 확인할 수 있다.
∣ 0 ⟩ ⊗ ∣ + ⟩ = ∣ 0 + ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 01 ⟩ ) |0\rangle\otimes|+\rangle=|0+\rangle={1\over\sqrt2}(|00\rangle+|01\rangle) ∣ 0 ⟩ ⊗ ∣ + ⟩ = ∣ 0 + ⟩ = 2 1 ( ∣ 0 0 ⟩ + ∣ 0 1 ⟩ ) 이제 CNOT 게이트를 적용해보자.
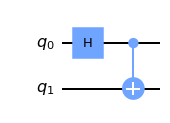
qc = QuantumCircuit( 2 )
qc. h( 0 )
qc. cx( 0 , 1 )
qc. draw( )
상태벡터를 확인해보면,
backend = Aer. get_backend( 'statevector_simulator' )
final_state = execute( qc, backend) . result( ) . get_statevector( )
array_to_latex( final_state, pretext= "\\text{Statevector = }" ) Statevector = [ 1 2 0 0 1 2 ] \text{Statevector}=\begin{bmatrix}{1\over\sqrt2}\\0\\0\\{1\over\sqrt2}\end{bmatrix} Statevector = ⎣ ⎢ ⎢ ⎢ ⎡ 2 1 0 0 2 1 ⎦ ⎥ ⎥ ⎥ ⎤
CNOT ∣ 0 ⟩ ⊗ ∣ + ⟩ = ∣ 0 + ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) \text{CNOT}|0\rangle\otimes|+\rangle=|0+\rangle={1\over\sqrt2}(|00\rangle+|11\rangle) CNOT ∣ 0 ⟩ ⊗ ∣ + ⟩ = ∣ 0 + ⟩ = 2 1 ( ∣ 0 0 ⟩ + ∣ 1 1 ⟩ )
얽힌 상태
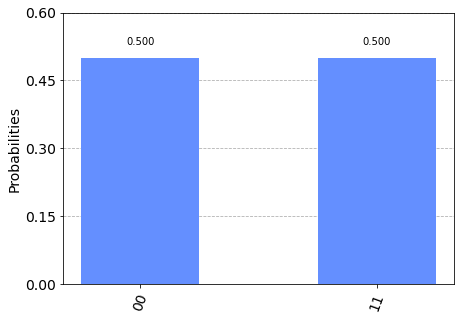
절반의 확률로 ∣ 00 ⟩ |00\rangle ∣ 0 0 ⟩ ∣ 11 ⟩ |11\rangle ∣ 1 1 ⟩ ∣ 01 ⟩ |01\rangle ∣ 0 1 ⟩ ∣ 10 ⟩ |10\rangle ∣ 1 0 ⟩ Bell
results = execute( qc, backend) . result( ) . get_counts( )
plot_histogram( results)
이렇게 결합된 상태는 두 개의 개별적인 큐비트 상태로 작성할 수 없으며 이는 흥미로운 의미를 갖는다.∣ 1 ⟩ |1\rangle ∣ 1 ⟩
1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) ⟶ measure ∣ 11 ⟩ {1\over\sqrt2}(|00\rangle+|11\rangle)\overset\text{measure}\longrightarrow|11\rangle 2 1 ( ∣ 0 0 ⟩ + ∣ 1 1 ⟩ ) ⟶ measure ∣ 1 1 ⟩ 심지어 광년 단위의 먼 거리에 분리하더라도 한 큐비트가 측정되면 다른 하나도 즉각적으로 붕괴되는 것으로 보인다.
다음과 같은 코드를 사용하면 1 2 ( ∣ 01 ⟩ + ∣ 10 ⟩ ) {1\over\sqrt2}(|01\rangle+|10\rangle) 2 1 ( ∣ 0 1 ⟩ + ∣ 1 0 ⟩ )
qc = QuantumCircuit( 2 )
qc. x( 1 )
qc. h( 0 )
qc. cx( 0 , 1 )
backend = Aer. get_backend( 'statevector_simulator' )
final_state = execute( qc, backend) . result( ) . get_statevector( )
array_to_latex( final_state, pretext= "\\text{Statevector = }" ) Statevector = [ 0 1 2 1 2 0 ] \text{Statevector}=\begin{bmatrix}0\\{1\over\sqrt2}\\{1\over\sqrt2}\\0\end{bmatrix} Statevector = ⎣ ⎢ ⎢ ⎢ ⎡ 0 2 1 2 1 0 ⎦ ⎥ ⎥ ⎥ ⎤