이 포스트의 내용은 Qiskit Textbook | Multiple Qubits and Entanglement - Phase Kickback을 통해 공부한 흔적임을 밝힙니다.

지난 시간에는 CNOT 게이트의 매우 기본적인 결과값을 보았으며
컨트롤 큐비트가 $|+\rangle$일 때 다음과 같이 얽힘이 발생되는 것을 확인했다.

그런데 만약 $q_0$뿐만 아니라 $q_1$도 중첩 상태라면 어떨까?

$\text{CNOT}|++\rangle$

이를 확인해보기 위해 먼저 필요한 패키지들을 준비한다.

from qiskit import QuantumCircuit, Aer, execute
from math import pi
import numpy as np
from qiskit.visualization import plot_bloch_multivector, plot_histogram
from qiskit_textbook.tools import array_to_latex

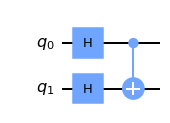
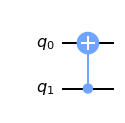
그리고 $q_0$와 $q_1$에 H 게이트를 설정한 후에 CNOT 게이트를 설정하는 코드를 작성한다.

qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
qc.draw()

위 회로에서 상태벡터는 다음과 같이 나타날 것이다.

CNOT 게이트를 적용하면 $|01\rangle$과 $|11\rangle$가 뒤바뀌지만 티가 나지 않는다.

실제로 실행해보면,

statevector_backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc,statevector_backend).result().get_statevector()
array_to_latex(final_state, pretext="\\text{Statevector} = ", precision=1)
plot_bloch_multivector(final_state)

$\text{Statevector}=\begin{bmatrix}{1\over2}\\{1\over2}\\{1\over2}\\{1\over2}\end{bmatrix}$

$\text{CNOT}|-+\rangle$

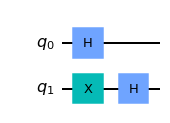
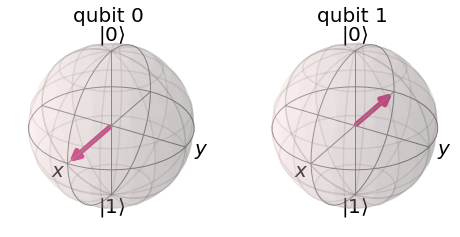
이번에는 타겟이 $|-\rangle$인 경우를 생각해보자.

qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.h(1)
qc.draw()

위 회로에서 상태벡터는 다음과 같이 나타날 것이다.

final_state = execute(qc,statevector_backend).result().get_statevector()
array_to_latex(final_state, pretext="\\text{Statevector} = ", precision=1)
plot_bloch_multivector(final_state)

$\text{Statevector}=\begin{bmatrix}{1\over2}\\{1\over2}\\-{1\over2}\\-{1\over2}\end{bmatrix}$

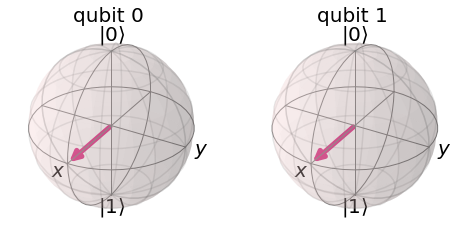
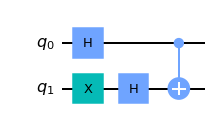
그리고 여기에 CNOT 게이트를 설정하면 다음과 같이 $|01\rangle$과 $|11\rangle$가 뒤바뀐다.

이것은 타겟 큐비트의 상태를 $|-\rangle$로 유지한 채 컨트롤 큐비트를 $|+\rangle$에서 $|-\rangle$로 바꾼다.
실제로 코드를 작성해보면,

qc.cx(0,1)
display(qc.draw())

final_state = execute(qc,statevector_backend).result().get_statevector()
array_to_latex(final_state, pretext="\\text{Statevector} = ", precision=1)
plot_bloch_multivector(final_state)

$\text{Statevector}=\begin{bmatrix}{1\over2}\\-{1\over2}\\-{1\over2}\\{1\over2}\end{bmatrix}$

역방향 CNOT 게이트

H 게이트는 $|+\rangle$을 $|0\rangle$로, $|-\rangle$을 $|1\rangle$로 변화시킨다.
이러한 H 게이트의 항등식으로 인해
H 게이트들로 둘러쌓인 CNOT 게이트는 역방향 CNOT 게이트와 동일하다.

// 이에 대해서는 다음 시간에 더 자세히 알아보도록 하겠다.

실제로 코드를 통해 행렬을 출력해봄으로써 이를 확인해보자.
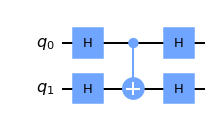
먼저 H 게이트들로 둘러쌓인 CNOT 게이트의 행렬을 출력해보면,

qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
qc.h(0)
qc.h(1)
display(qc.draw()) 

unitary_backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,unitary_backend).result().get_unitary()
array_to_latex(unitary, pretext="\\text{Circuit = }\n")

$\text{Circuit}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}$

그리고 역방향 CNOT 게이트의 행렬을 출력해보면,

qc = QuantumCircuit(2)
qc.cx(1,0)
display(qc.draw())

unitary_backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,unitary_backend).result().get_unitary()
array_to_latex(unitary, pretext="\\text{Circuit = }\n")

$\text{Circuit}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}$

위상 반동 Phase Kickback

CNOT 게이트에서의 반동

우리는 방금 다음이 성립하는 것을 확인했다.

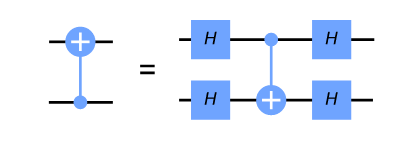
이것은 위상 반동의 한 예시다.
위상 반동은 매우 중요하며 양자 알고리즘에서 많이 사용되는 것으로,
게이트에 의해 큐비트에 추가된 고유값이 제어된 연산을 통해 다른 큐비트에 반동을 일으키는 것을 의미한다.

예를 들어, $|-\rangle$에 X 게이트를 적용하면 그 위상이 $-1$이 된다.

$|-\rangle$을 타겟으로 하는 CNOT 게이트에서
컨트롤 큐비트가 $|0\rangle$ 또는 $|1\rangle$일 때 이 위상은 전체 상태에 영향을 주지만
이것은 전역 위상이기 때문에 관찰 가능한 효과는 없다.
// 양자 상태의 표현에 대해 이야기할 때 언급했듯이,
// 전역 위상만 다르고 나머지는 동일한 상태들은 물리적으로 구분되지 않는다.

흥미로운 점은, 컨트롤 큐비트가 중첩 상태에 있다면
컨트롤 큐비트의 $|1\rangle$ 방향 구성요소가 타겟 큐비트의 위상 계수에 영향을 주고
이것은 다시 컨트롤 큐비트의 상대 위상에 반동을 형성한다는 것이다.

CNOT 게이트를 H 게이트로 감싸는 것은 큐비트의 기저를 ($|0\rangle$, $|1\rangle$)에서 ($|+\rangle$, $|-\rangle$)으로 변환한다.
어떤 하드웨어는 한 방향으로의 CNOT만 허용하는데
이 변환 특성을 통해 CNOT을 양 방향 모두 가능하게 할 수 있어 유용하다.

T 게이트에서의 반동

지금까지는 X 게이트에 컨트롤을 추가한 제어된 X 게이트 즉, CNOT 게이트만을 봐왔지만
T 게이트에도 컨트롤을 추가하여 제어된 T 게이트를 만들 수 있다.
이것은 따로 제공되지는 않고 다음과 같이 만들어 사용한다.

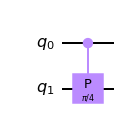
qc = QuantumCircuit(2)
qc.cp(pi/4, 0, 1)
qc.draw()

T 게이트의 행렬은 다음과 같다.

그리고 제어된 T 게이트의 행렬은 다음과 같다.

이것은 코드를 통해서도 확인할 수 있다.

unitary_backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,unitary_backend).result().get_unitary()
array_to_latex(unitary, pretext="\\text{Controlled-T} = \n")

$\text{Controlled-T} = \begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&{1\over\sqrt2}(1+i)\end{bmatrix}$

이걸 일반화하면 $\text{U}=\begin{bmatrix}u_{00}&u_{01}\\u_{10}&u_{11}\end{bmatrix}$에 대하여 제어된 U 연산을 다음과 같이 나타낼 수 있다.

혹은, 큐비트의 순서에 따라 다음과 같이 나타낼 수도 있다.

상태벡터 $|1\rangle$에 T 게이트를 적용하면 이 큐비트에 $e^{i\pi/4}$만큼의 위상이 더해진다.
이것은 전역 위상이기에 관측할 수 없지만
$|+\rangle$에 있는 다른 큐비트를 이용해 제어함으로써 제어 큐비트의 상대 위상을 변경한다.

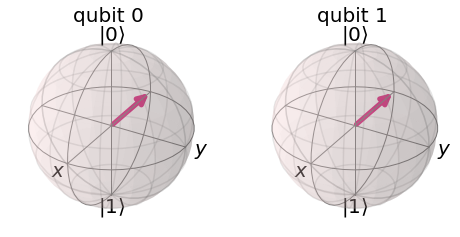
예를 들어,

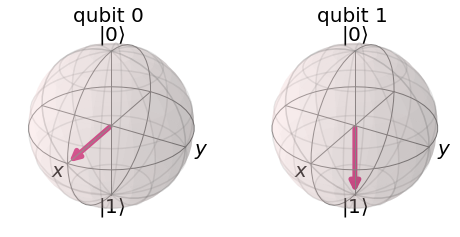
$|1+\rangle = |1\rangle\otimes{1\over\sqrt2}(|0\rangle+|1\rangle)={1\over\sqrt2}(|10\rangle+|11\rangle)$ 는 코드로 다음과 같이 나타낼 수 있는데

qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
display(qc.draw())

final_state = execute(qc,statevector_backend).result().get_statevector()
plot_bloch_multivector(final_state)

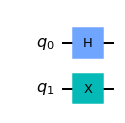
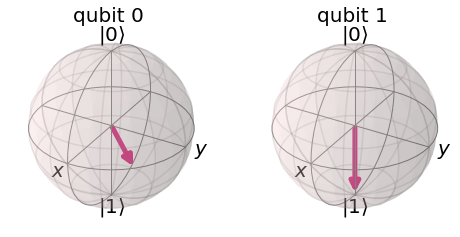
여기에 제어된 T를 적용하면

qc.cp(pi/4, 0, 1)
display(qc.draw())

final_state = execute(qc,statevector_backend).result().get_statevector()
plot_bloch_multivector(final_state)

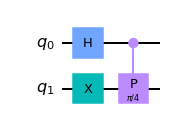
컨트롤로 사용된 $q_0$가 $z$축을 기준으로 $\pi/4$만큼 회전한 것을 확인할 수 있다.
정확히는 제어된 T 게이트로 연결된 두 큐비트 모두 회전한 건데
이는 제어된 $R_\phi$ 게이트는 컨트롤과 타겟을 하나씩 갖는 대신
두 개의 컨트롤 큐비트를 갖는다는 것을 보여준다.
// 만약 $q_1$가 $|1\rangle$이 아니라 $|0\rangle$이라면 컨트롤이 0이므로 회전하지 않을 것이다.

이것이 Qiskit에서 제어된 Z 게이트를 다음과 같이 방향성 없이 그리느 이유이기도 하다.