노션 기록

행렬분해(matrix decomposition)의 의미

주어진 행렬을 행렬분해된 상태로 가지고 있으면 여러모로 계산이 편한 경우가 많습니다

다음은 대표적인 행렬분해입니다

• $LU$ 분해 ($LU$ decomposition)
• $QR$ 분해 ($QR$ decomposition)
• 특이값 분해(SVD, Sigular Value Decomposition)

$LU$ 분해와 $QR$ 분해는 $n \times n$ 정방행렬(square matrix)에 대한 행렬분해인 반면,
특이값 분해는 일반적인 $m \times n$ 행렬에 관한 행렬 분해입니다.

특이값 분해는 직교분할, 확대축소, 차원변환 등과 관련이 있습니다

특이값 분해(Singular Value Decomposition, SVD)

특이값 분해는 주어진 행렬을 아래의 형태를 가지는 세 행렬의 곱으로 나누는 행렬분해입니다

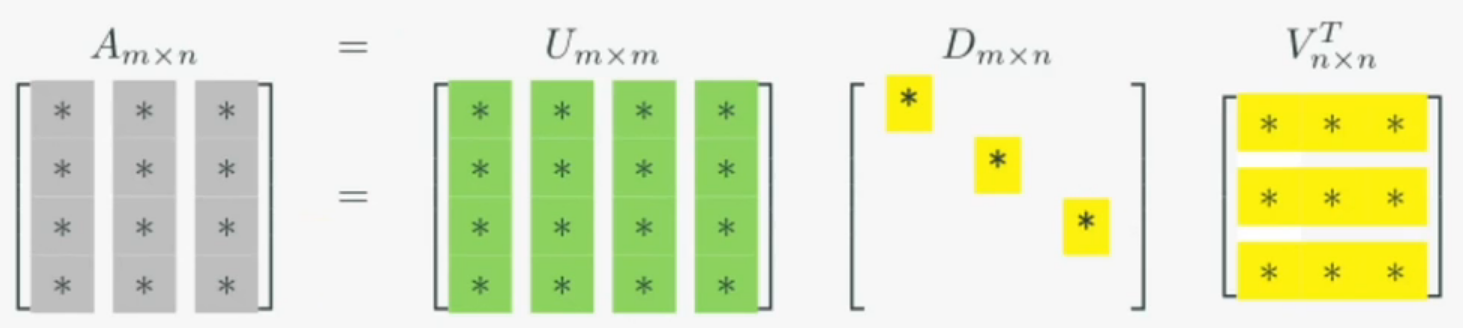
행렬 $U, D, V$는 그 특성에 따라 다음과 같은 의미가 있습니다

• $U$ : $m$차원 회전행렬 (정규직교행렬)
• $D$ : $n$차원 확대축소 (확대축소 크기에 따른 정렬 형태)
• $V$ : $n$차원 회전행렬(정규직교행렬)
  
  

즉, 특이값 분해는 어떤 행렬 $A$를 3단계로 나눈다고 생각하면 됨

1. $n$차원에 대해서 회전
2. $n$차원에 대해서 확대,축소를 수행 후 차원 변환
3. $m$차원에 대해 회전

특이값 분해의 의미

특이값 분해는 행렬을 회전과 확대축소로 분해하는 방법입니다.

간단히 말하자면,

• $U$ : 입력 차원인 $\mathbb{R}^m$ 공간에서의 회전
• $D$ : 입력 차원인 $\mathbb{R}^m$ 공간에 대해 축방향으로의 확대축소한 후, $\mathbb{R}^n \rightarrow \mathbb{R}^m$ 으로 차원 변환
• $V$ : 입력 차원인 $\mathbb{R}^n$공간에서의 회전

특이값 분해의 활용

$A$의 특이값 분해 $U, D, V$는 각각 열벡터의 순서대로 행렬 $A$의 열벡터가 어떤 방향으로 강한 응집성을 보이고 있는지를 분석한 것입니다.

$U, D, V$의 열벡터를 순서대로 $p$개 취한다면, 강한 응집성을 가지는 $p$개의 방향으로 수선의 발을 내린 $A$의 근사치 ${A^\prime}$를 재구성할 수 있습니다.

$D$는 응집성에 따라 정렬되어 구성되므로 0에 가까운 애들은 버려서 근사치 만들 수 있다!

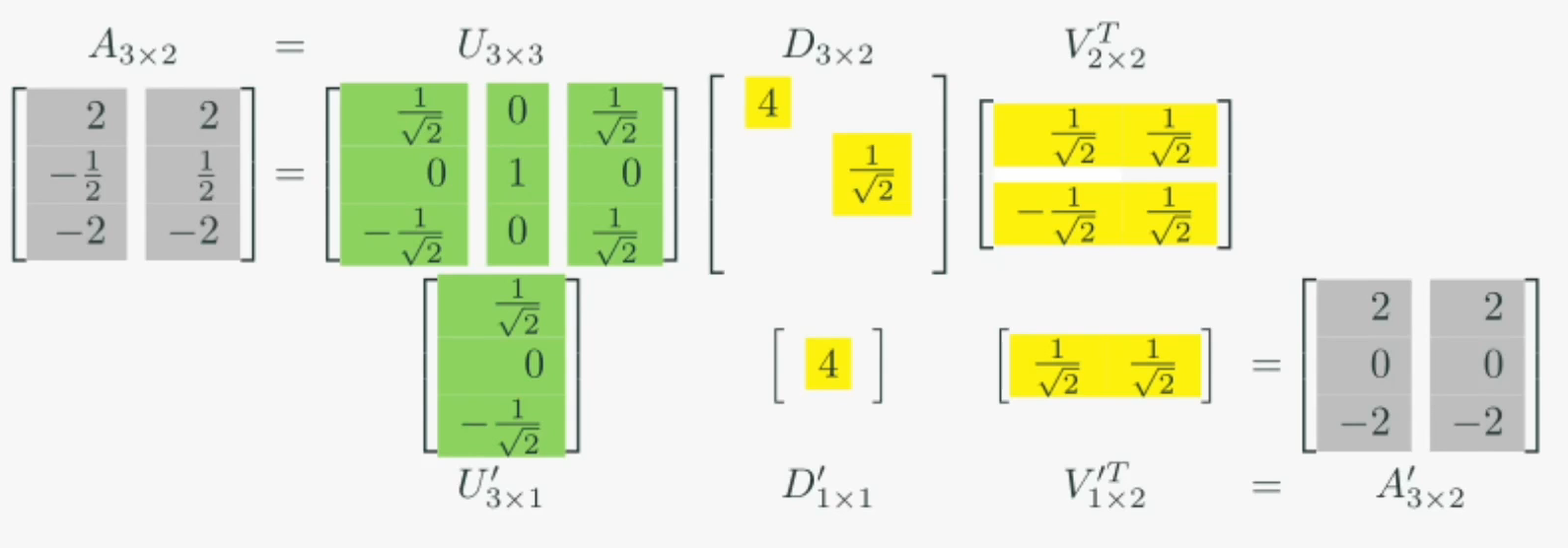
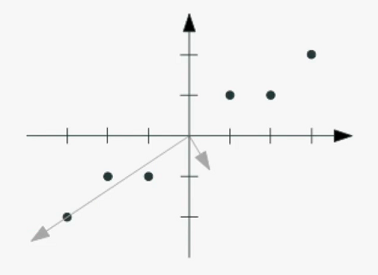
SVD를 활용해 $A$의 근사치 $A^\prime$를 다음과 같이 구했을 때 기하적인 해석은 그림과 같습니다

주성분분석(Principal Component Analysis, PCA)

주성분분석이란?

주성분분석(PCA)은 다수의 $n$차원 데이터에 대해, 데이터의 중심으로부터 데이터의 응집력이 좋은 $n$개의 직교 방향을 분석하는 방법입니다.

주성분분석(PCA)은 데이터의 공분산행렬(covariance matrix)에 대한 고유값분해에 기반을 둔 직교분해입니다

** 여기서는 고유값(eigenvalue)에 대해 자세히 설명하지 않겠습니다

• 참고사항

  고윳값과 고유벡터

  주성분 분석(PCA)

$K$개의 $n$차원 데이터 $\{{\bf x}_i \}^K_{i=1}$가 있을 때, 데이터의 중심 $\bf m$과 공분산행렬 $C$는 다음과 같이 구합니다

공분산행렬에 대해 주성분분석(PCA)은 아래와 같습니다

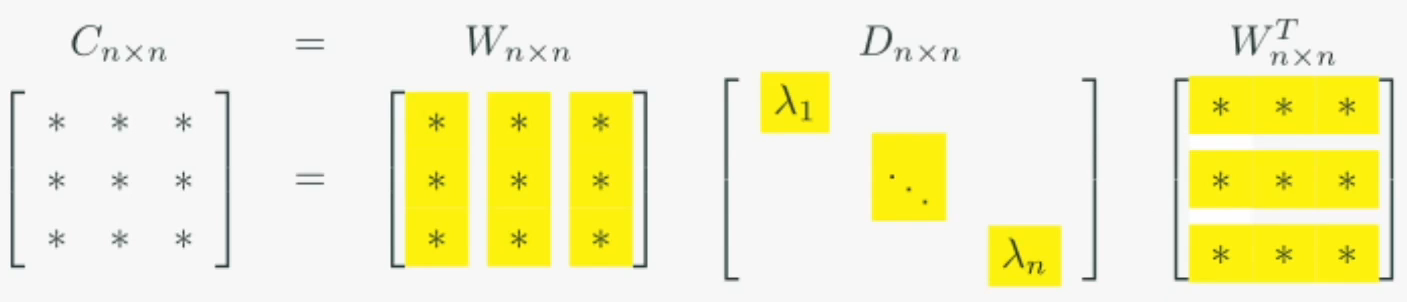
주성분분석을 통해 얻은 행렬 $W, D$는 다음과 같은 의미가 있습니다

• $W$ : $n$차원 회전행렬 (정규직교행렬)
• $D$ : $n$차원 확대축소 (확대축소 크기에 따른 정렬 형태)

주성분분석(PCA)의 활용

그림과 같이 데이터가 있을 때, 공분산행렬과 이에 대한 주성분분석(PCA)은 다음과 같습니다