차원축소를 공부해본 사람이라면 t-SNE(t-distributed Stochastic Neighbor Embedding)라는 용어가 PCA와 함께 언급되는 걸 종종 보았을 것이다. t-SNE와 PCA는 둘 다 차원축소 기법이지만, t-SNE는 거리를 확률로 바꾸어 생각한다는 점에서 PCA와 차이점을 보인다. 이번 글을 통해 t-SNE가 정확히 어떻게 작동하는지 알아보자. (t-SNE를 소개한 논문 Visualizing Data using t-SNE는 이 링크에서 확인할 수 있다. 아울러 차원축소와 PCA에 대한 설명은 이 글을 참고하자.)

SNE의 원리

기본 아이디어

t-SNE는 SNE 즉 Stochastic Neighbor Embedding을 약간 변형한 기법이다. 즉 t-SNE를 이해하기 위해서는 SNE를 먼저 이해해야 한다.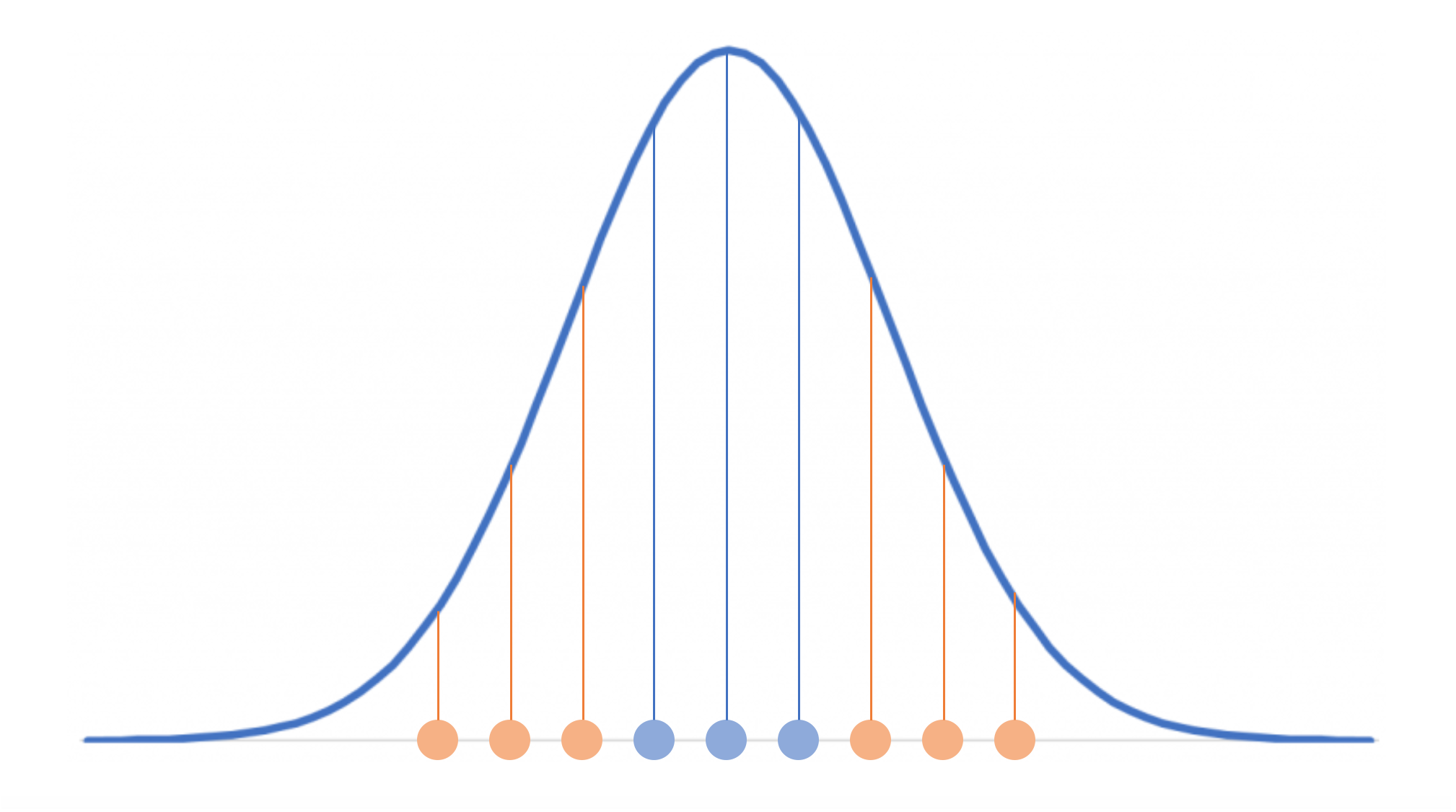글의 서두에서 t-SNE는 거리를 확률로 바꾸어 접근하는 방식이라고 언급하였다. 이 말의 의미는 무엇일까? 위와 같은 1차원 데이터를 생각해보자. 가운데 파란색 점을 기준으로 할 때, 양옆의 파란색 점은 기준점과 가까이 위치해 있다. 이렇게 가까운 파란 점에게는 높은 점수를 부여한다고 해보자. 반면 기준점과 멀리 떨어져 있는 주황색 점들에게는 낮은 점수를 부여한다. 이렇게 놓고 보면, 기준점을 평균으로 갖는 정규분포를 생각할 수 있다. 기준점과 가까운 점들에 대해서는 높은 값이 부여되고, 멀리 떨어져 있는 점들에 대해서는 낮은 값이 부여되는 것이다.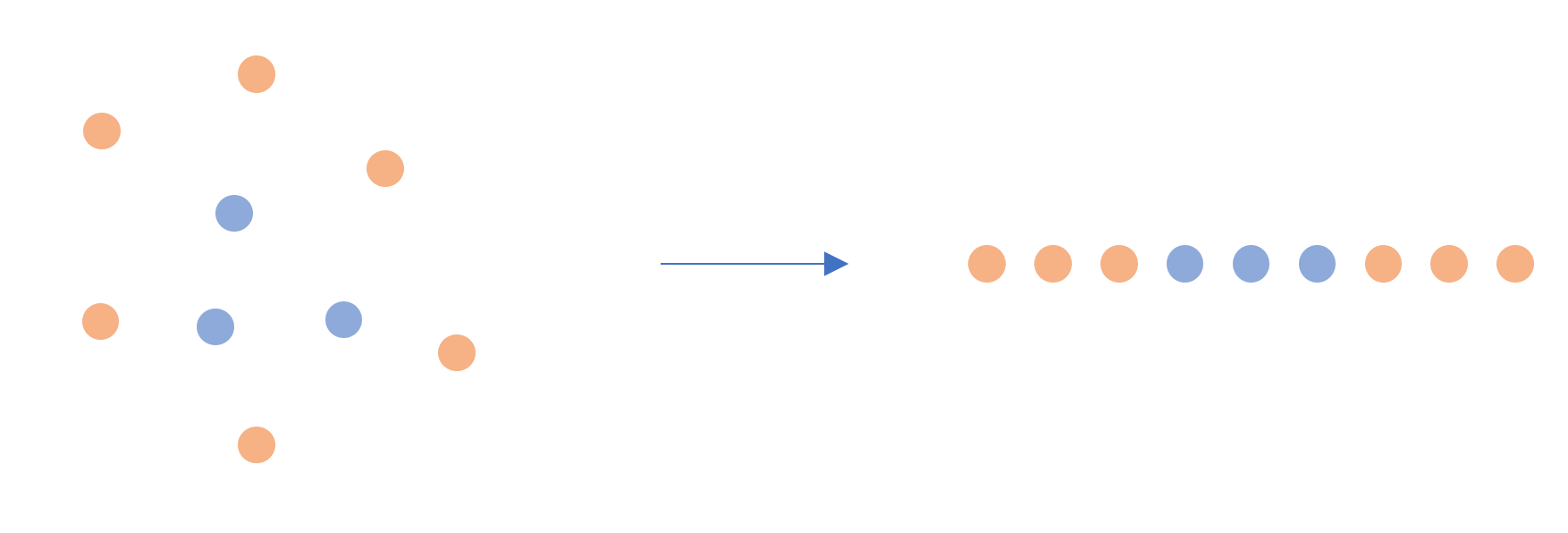이제 차원축소라는 목적으로 돌아와보자. 차원을 축소할 때 핵심은 데이터의 특성을 유지해야 한다는 것이다. 기존 차원에서 가까웠던 점들은 축소된 차원에서도 가까이 있어야 하고, 멀리 떨어져 있었던 점들은 똑같이 멀리 있어야 한다. 이는 곧 기존 차원에서의 정규분포가 축소된 차원에서도 비슷하게 유지되어야 한다는 것을 의미한다. 두 분포가 얼마나 유사한지 측정하는 방법이 있다면, 기존 차원의 정규분포와 축소된 차원의 정규분포 간의 유사도가 최대화되도록 차원을 축소하면 될 것이다.

수식으로 보기

$p_{j|i}$와 $q_{j|i}$ 정의하기

$d$차원 상의 데이터 $X$를 $p$차원으로 매핑한다고 해보자. 데이터 수는 $n$, 매핑된 데이터는 $Y$라고 하자. (즉 $X\in \mathbb{R}^{d\times n}$, $Y\in \mathbb{R}^{p\times n}$)

$d$차원 상에서 다음과 같은 $p_{j|i}$를 정의한다.

$p_{j|i}$는 $x_i$가 $x_j$를 이웃으로 선택할 확률을 의미한다. 직관에 부합하기 위해 $p_{i|i}$의 값은 0으로 설정되어 있다. 위 수식을 보면 다음과 같은 생각이 들 것이다.

1. 어디서 많이 본 형태인데?
   왠지 모르게 익숙한 형태이지 않은가? 그렇다! 정규분포의 PDF(확률밀도함수)에서 위 형태를 볼 수 있다.

   $f(x)=\frac{e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sigma\sqrt{2\pi}}$

   정규분포와 위 $p_{j|i}$가 어떻게 연관되어 있는 건지 이해하기 위해서, 위에서 보았던 그림을 다시 가져와보겠다.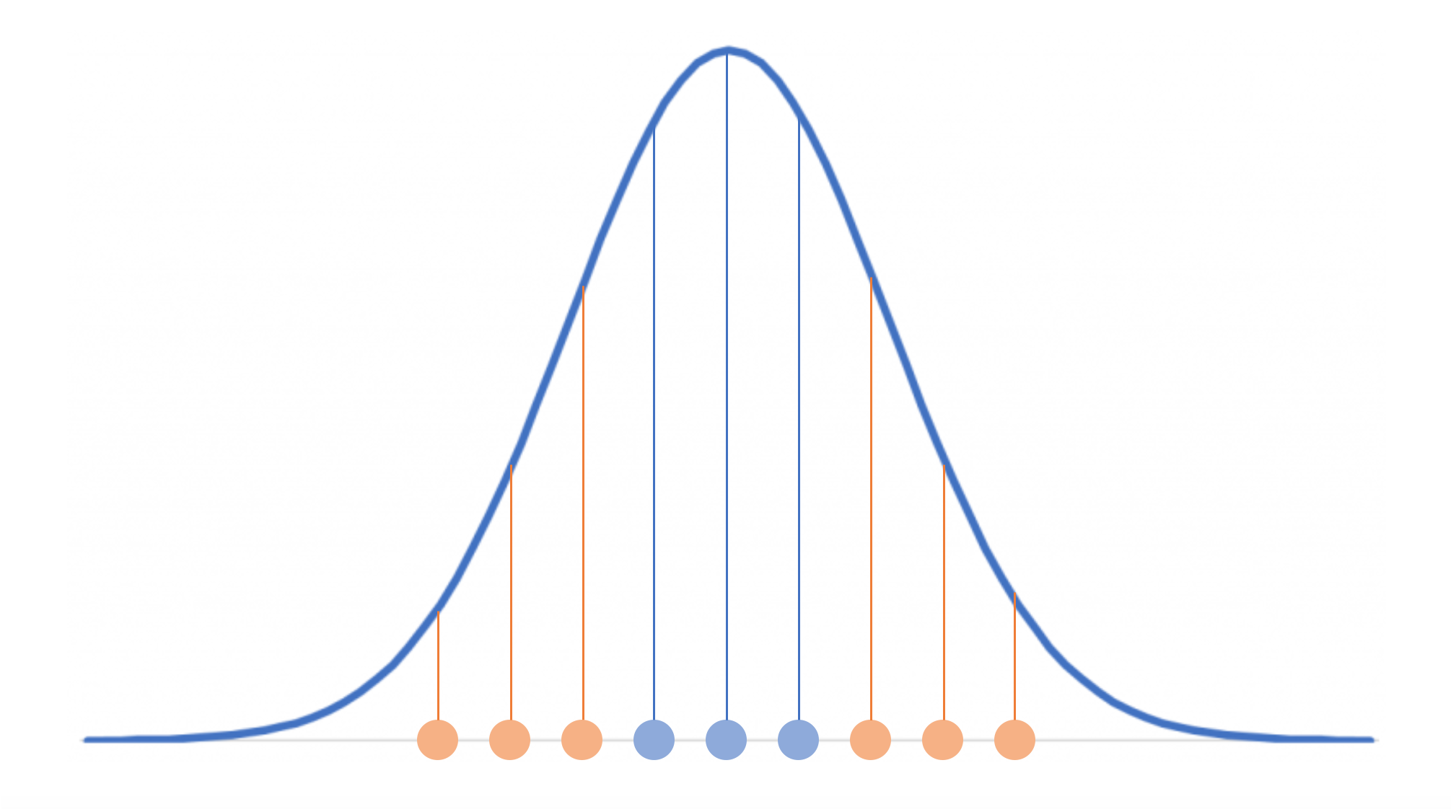$p_{j|i}$의 정의를 보면, 정규분포에서 $\mu$가 들어갈 자리에 $x_i$가 들어가 있다. 즉 위 그림에서 가운데에 위치한 평균(기준점)이 곧 $x_i$인 것이다. 정규분포에서 $x$가 들어갈 자리에 $x_j$가 들어가 있는 걸 보면, $x_j$는 우리가 관심이 있는 어떤 데이터 포인트(위 옅은 직선 상의 어떤 점)라고 할 수 있다. 다시 $p_{j|i}$의 정의를 가져와보자.

   $p_{j|i}=\frac{e^{\frac{-||x_i-x_j||^2}{2\sigma_i^2}}}{\displaystyle\sum_{k\neq i}{e^{\frac{-||x_i-x_k||^2}{2\sigma_i^2}}}}$

   $x_j$가 $x_i$에 가까울수록 분자가 커진다는 것은 자명한데, 위 그림을 보면 분자값이 어떻게 커지는지까지 쉽게 이해할 수 있을 것이다. 참고로 분모는, $x_i$가 다른 점들에 비해 $x_j$와 상대적으로 얼마나 가까운지를 말해주는 normalization 역할을 한다고 이해하면 된다.

2. conditional하다는 것은 $i$와 $j$를 바꾸면 값이 달라진다는 건가?
   그렇다. $p_{j|i}$와 $p_{i|j}$는 다른 값을 가질 수 있다. 이를 직관적으로 이해하기 위해서는 다음과 같은 예를 생각해보면 된다. $x_i$가 1이라는 반경 내에 100개의 점들이 존재하는 반면 $x_j$는 3이라는 반경 내에도 점들이 2-3개밖에 없다고 해보자. $x_i$ 입장에서 2만큼 떨어져 있는 점은 이웃이라고 보기 어려울 것이다. 반면 $x_j$의 경우는? 2만큼 떨어져 있어도 $x_j$에게는 엄연히 이웃이다. 만약 2만큼 떨어져 있는 그 점이 $x_i$라면, $x_j$ 입장에서 $x_i$는 이웃이지만 $x_i$ 입장에서 $x_j$는 이웃이 아니게 된다($p_{i|j}$ > $p_{j|i}$).

   ${\displaystyle\sum_{k\neq i}{e^{\frac{-||x_i-x_k||^2}{2\sigma_i^2}}}}$

   conditionality에 대해 약간의 추가 설명을 하기 위해 $p_{j|i}$의 분모를 가져와보았다. $x_i$의 경우 주변에 많은 점들이 가까이 있기 때문에, 위 값이 클 것이다. 반면 $x_j$의 경우 가까이 있는 점들이 별로 없기 때문에, $x_i$에 비해 상대적으로 위 값이 작을 것이다. 이 값으로 분자 즉 $e^{\frac{-||x_i-x_j||^2}{2\sigma_i^2}}$를 나눠주기 때문에, 주변 점들과의 거리에 상관없이 이웃의 범위를 각 점에 따라 유동적으로 설정할 수 있게 된다. 쉽게 말해, $x_i$ 입장에서 2번째 이웃 $x_{i_2}$와의 거리가 1인 반면 $x_j$ 입장에서 2번째 이웃 $x_{j_2}$와의 거리가 100이라고 하더라도, 위 분모로 인해 $p_{i_2|i}$의 값이 $p_{j_2|j}$의 값과 어느 정도 비슷해지는 것이다.

지금까지 $d$차원 상에서의 $p_{j|i}$를 살펴보았다면, 이제 $p$차원 상에서의 $q_{j|i}$에 대해 알아보자. $q_{j|i}$는 다음과 같이 정의된다.

$q_{j|i}$ 역시 $p_{j|i}$처럼 non-symmetric($q_{j|i}\neq q_{i|j}$인 경우가 존재)하다는 것을 알 수 있다. 또한 $p_{j|i}$에서의 논리를 그대로 끌고 오면, $q_{j|i}$가 $y_i$가 $y_j$를 이웃으로 선택할 확률을 의미한다는 것을 알 수 있다.

KL Divergence 적용하기

위에서 기본 아이디어를 설명하면서, 두 분포가 얼마나 유사한지 측정하는 방법이 있다면 기존 차원의 정규분포와 축소된 차원의 정규분포 간의 유사도가 최대화되도록 차원을 축소하면 된다고 설명하였다. 우리는 이제까지 $p_{j|i}$와 $q_{j|i}$를 정의하면서 $d$차원에서의 확률분포 하나와 $p$차원에서의 확률분포 하나를 마련해두었다. 이제 해야할 일은 두 확률분포의 유사도를 측정하는 방법을 찾는 것이다.

두 확률분포가 얼마나 비슷한지 파악하는 대표적인 방법 중 하나가 KL Divergence(Kullback-Leibler Divergence)이다. (아래 식에서 $b$는 2, $e$, 10 중 하나인 경우가 많다.)

KL Divergence에서의 divergence는 '발산'보다는 '차이'라고 해석하는 것이 정확하다. 즉 위 값은 $P$와 $Q$라는 두 확률분포가 얼마나 차이나는지를 보여주는 값이다(위 식은 이산확률변수에 대해서 정의한 KL Divergence 값이고, 연속확률변수에 대해서는 위 sigma 형식을 integral 형식으로 바꿔주면 된다). 위 식은 아래와 같이 바꿔쓸 수 있다.

하나의 항으로 표현된 것을 두 개의 항으로 나눈 것이다. 데이터사이언스에 익숙한 사람이라면 첫번째 항과 두번째 항 모두 익숙할 텐데, 각각 cross-entropy와 information entropy를 의미한다. 즉 KL Divergence는 cross-entropy에서 information entropy를 뺀 값이다. (정보 이론에서 말하는 entropy에 대해 알고 싶다면 이 글을 참고하자. 정보량을 '깜놀도'라고 표현하신 게 정말 적절하다는 느낌을 받았다.)

KL Divergence가 두 확률분포가 얼마나 다른지를 말해주므로, 우리는 차원축소의 cost function으로 KL Divergence를 활용할 수 있다. 쉽게 말해, KL Divergence 값이 최소화되도록 차원을 축소하는 것이다.

위 cost function에 근거하여 다음과 같은 상황들을 해석해보자.

1. $d$차원에서 서로 가까웠던 $x_i$, $x_j$가 차원축소 후 멀어져버린 상황
   $p_{j|i}$가 크고 $q_{j|i}$가 작다는 것을 의미한다. cost function에 대입하면 cost가 큰 상황이라는 것을 알 수 있다. 즉, 최적화가 잘 된다는 전제 하에 SNE는 기존 차원에서 가까웠던 점들이 차원축소 후 멀어지는 상황을 효과적으로 방지한다.

2. $d$차원에서 서로 멀리 떨어져 있었던 $x_i$, $x_j$가 차원축소 후 가까워져버린 상황
   $p_{j|i}$가 작고 $q_{j|i}$가 크다는 것을 의미한다. cost function에 대입하면 cost가 작은 상황이라는 것을 알 수 있다. 즉, 최적화가 잘 된다고 하더라도 기존 차원에서 멀리 떨어져 있었던 점들이 차원축소 후 가까워질 수 있다.

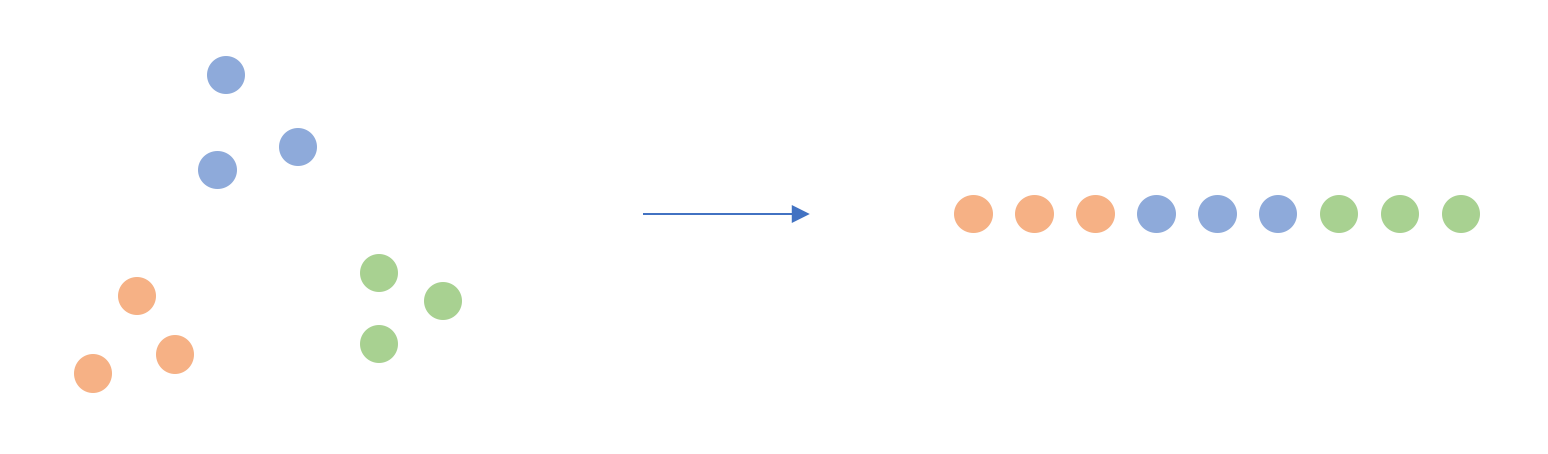쉽게 말해, SNE는 기존에 이웃이었던 점들을 차원축소 후에도 이웃으로 유지시키는 로직이다. 위 그림을 보면 2차원에서 파란색, 주황색, 초록색 점들은 각각 서로 가까이 모여 있었고, 차원축소 후에도 서로 모여있음을 확인할 수 있다. 하지만 파란색-주황색, 파란색-초록색, 주황색-초록색은 2차원에서 어느 정도 떨어져 있었음에도 불구하고 1차원에서는 가까워져 있다. 이렇게 기존 차원에서 멀리 떨어져 있었던 점들이 SNE에 의해서는 가까워질 수 있다.

그럼, t-SNE는?

t-SNE는 다음 두 가지 포인트에서 SNE와 다르다.

1. 비대칭성을 제거하였다.
2. Crowding problem을 핸들링한다.

하나씩 차례로 살펴보자.

비대칭성의 제거

SNE를 설명할 때 $p_{j|i}$와 $p_{i|j}$가 다를 수 있다는 것을 언급하였다. 하지만 t-SNE에서는 $p_{j|i}$의 정의를 다음과 같이 살짝 수정하여 $p_{j|i}=p_{i|j}$가 성립하도록 하였다.

식을 보면 $i$와 $j$의 위치를 바꿔도 값이 유지된다는 것을 알 수 있다. t-SNE를 소개한 논문에 따르면, 이렇게 대칭성을 부여할 경우 최적화에 드는 계산량을 줄일 수 있다. 여기서 $p_{ij}$의 정의를 그냥 $\frac{e^{\frac{-||x_i-x_j||^2}{2\sigma^2}}}{\displaystyle\sum_{k\neq l}{e^{\frac{-||x_l-x_k||^2}{2\sigma^2}}}}$(기존 정의에서 비대칭을 일으키는 요소들만 모두 제거한 식)로 설정하면 되지 않느냐라는 질문을 할 수 있는데, 논문에 따르면 $d$차원에서의 데이터 $x_i$가 다른 모든 점들과 멀리 떨어져 있는 외톨이 점일 경우 $p_{ij}$의 값이 모든 $j$에 대해 지나치게 작아져 최적화가 제대로 되지 않는다고 한다.

Crowding problem 핸들링

이미지 출처

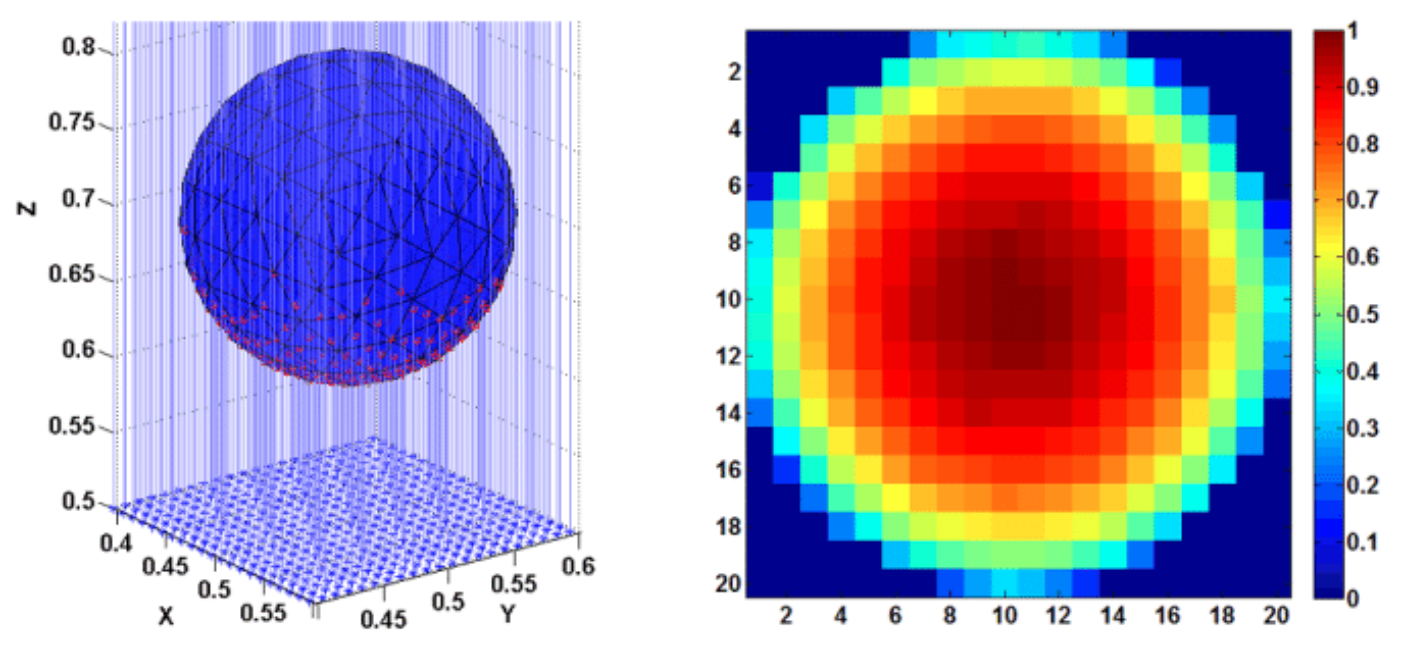
반구 표면에 일정한 간격으로 붙어 있는 3차원 데이터(왼쪽 사진에서 빨간 점)를 2차원으로 매핑한다고 생각해보자. 2차원 표면에 그대로 projection을 내리면, 가장자리의 데이터들은 듬성듬성하게 분포되는 반면 중앙의 데이터들은 상대적으로 조밀하게 몰릴 것이다(오른쪽 사진 느낌). 이렇게 차원축소를 거치면서 데이터들이 비정상적으로 몰리는 현상을 crowding problem이라고 한다.

차원축소 후에 데이터가 몰리는 게 문제라면, 데이터를 흩뜨려놓는 방안을 생각할 수 있을 것이다. t 분포가 바로 이 지점에서 등장한다. t 분포는 정규분포보다 상대적으로 두꺼운 꼬리를 가지고 있다. 쉽게 말해, 데이터가 상대적으로 고르게 퍼져 있는 느낌이다. 저차원에서 정의되었던 $q_{j|i}$에 이러한 t 분포의 성질을 적용한다면, 데이터가 몰리는 현상을 어느 정도 완화할 수 있을 것이다.

위 식은 자유도가 1인 스튜던트 t 분포의 성질을 반영하여 $q_{j|i}$를 재정의한 결과이다($p_{ij}$처럼 비대칭성이 제거된 것도 확인할 수 있다). 식을 보면 정규분포의 PDF 형태가 사라지고 cauchy distribution의 PDF 형태가 들어가 있다는 것을 볼 수 있다($Cauchy(0,1)\sim t(1)$). $q_{ij}$를 위와 같이 정의할 경우 crowding problem을 어느 정도 완화할 수 있을 뿐만 아니라, exponential 계산을 하지 않아도 된다는 점에서 computational advantage도 챙길 수 있다.

이후 이뤄지는 과정은 SNE와 동일하다. 새롭게 정의한 $p_{ij}$, $q_{ij}$를 가지고 cost function을 구성하고($KL(P||Q)$), cost를 최소화하는 방향으로 차원축소를 진행한다.

---

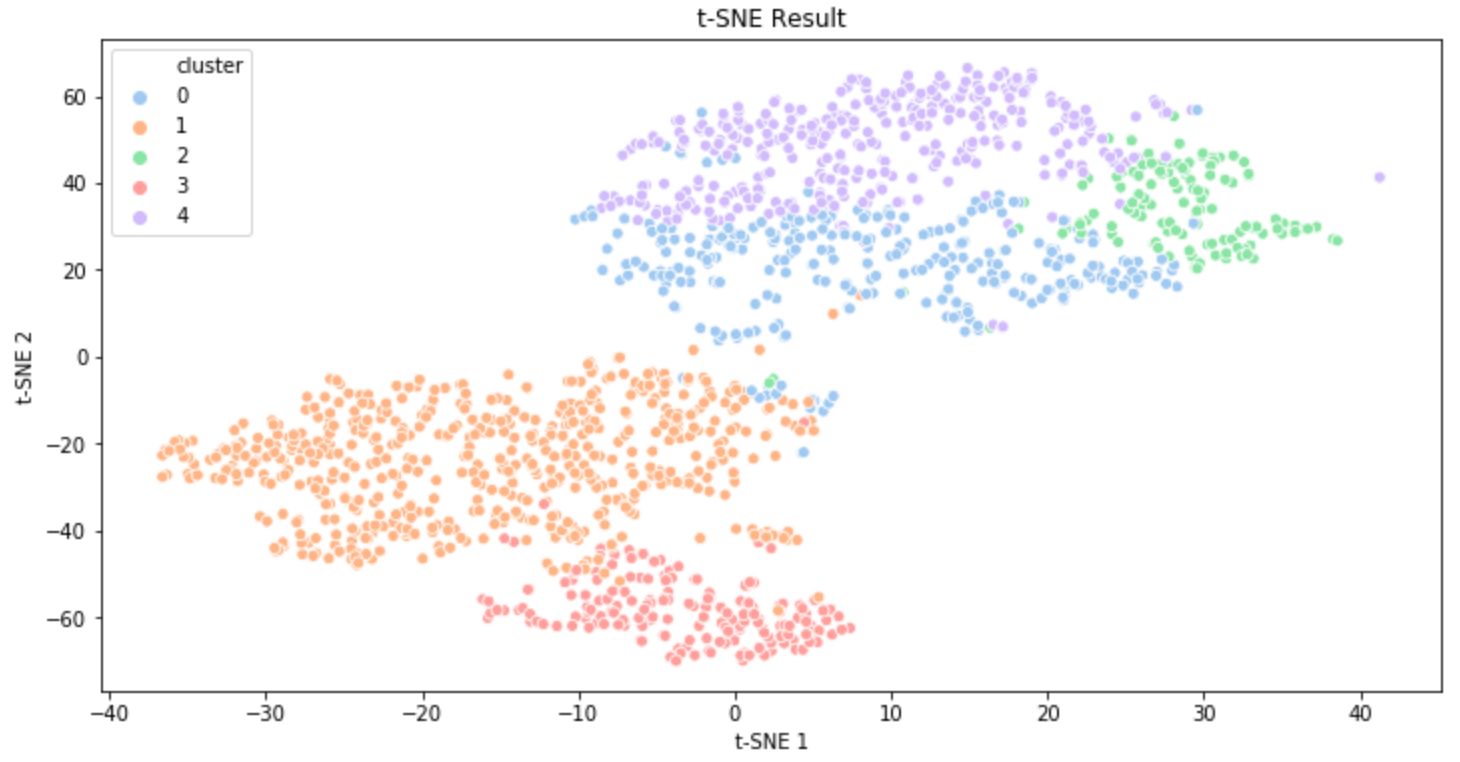
이번 글에서는 t-SNE의 원리를 알아보았다. 확률분포의 PDF가 활용돼서 그런지 다소 복잡한 수식이 들어가는데, 기본적인 원리는 나름 직관적인 편이다. 위 사진은 음악 데이터 클러스터링에 대해 t-SNE를 적용한 필자의 결과물인데, t-SNE 역시 PCA와 같이 파이썬 라이브러리로 쉽게 구현할 수 있으니 기회가 되면 파이썬으로 직접 한 번 구현해보도록 하자.