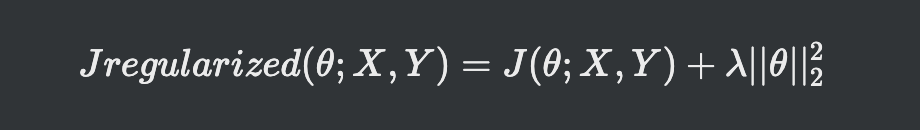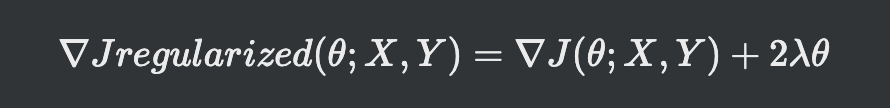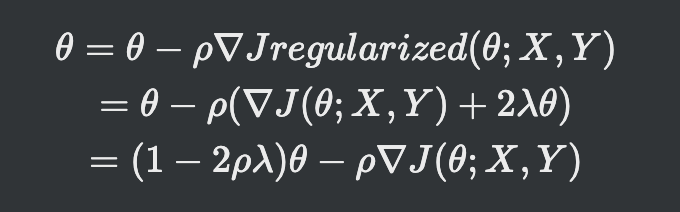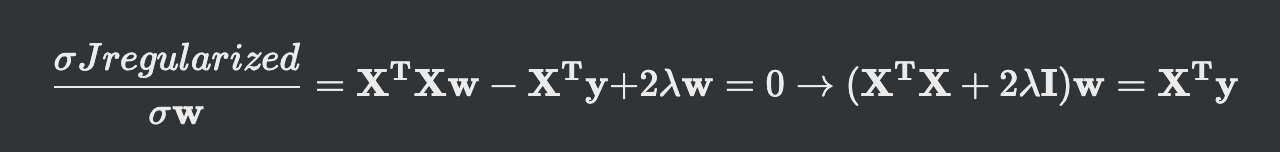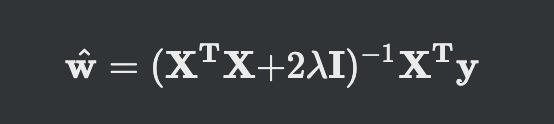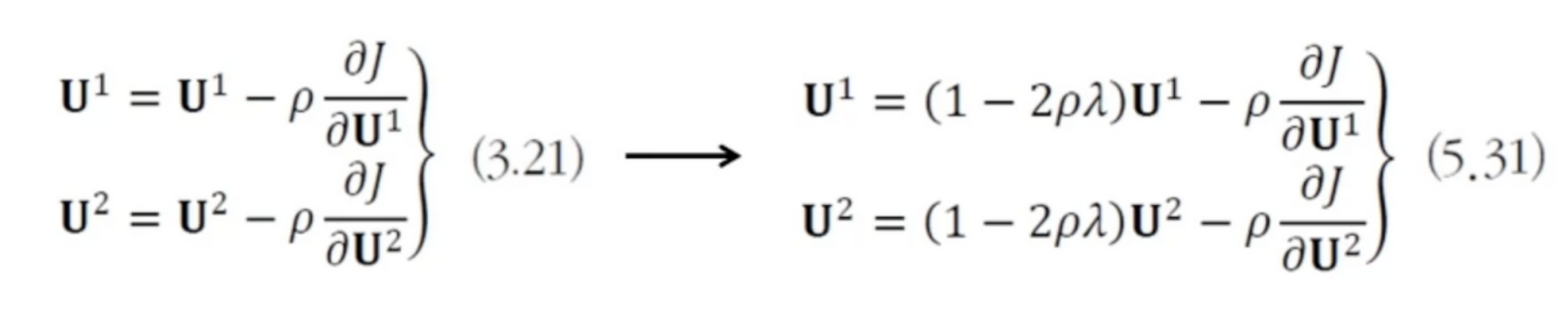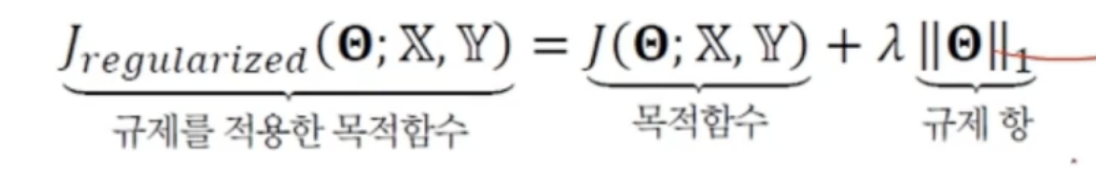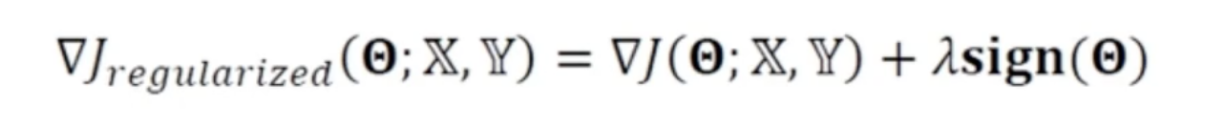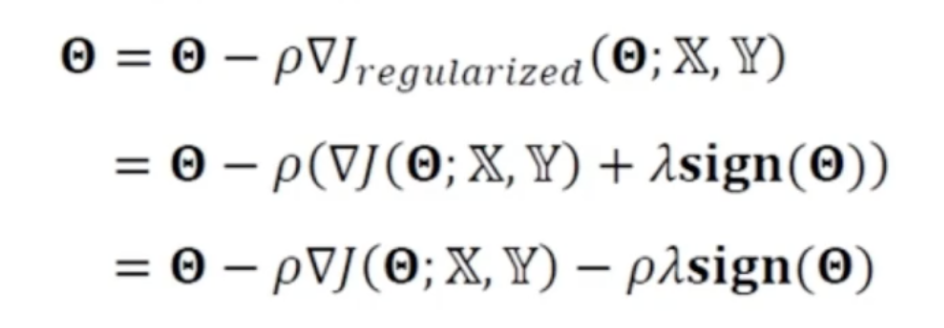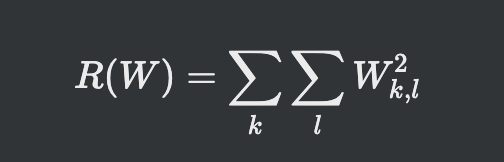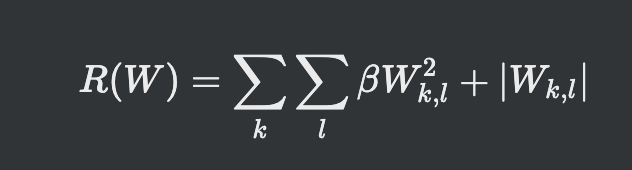규제항

• 규제항은 훈련집합과 무관하며, 데이터 생성 과정에 내재한 사전 지식에 해당
• 규제항은 매개변수를 작은 값으로 유지하므로 모델의 용량을 제한하는 역할
• 규제항 R(theta)로 L2놈이나 L1놈을 사용(큰 가중치에 벌칙, 작은 가중치 유지)

L2 norm

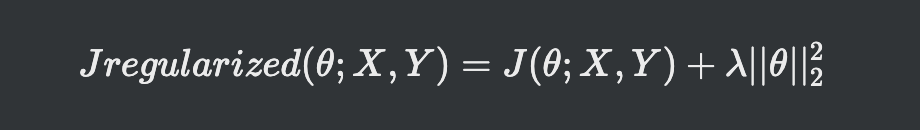
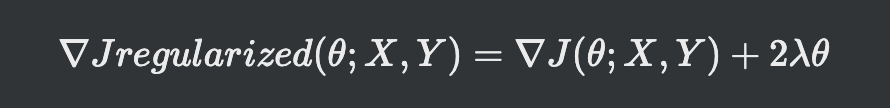
• 규제 항 R로 L2놈을 사용하는 규제 기법을 '가중치 감쇠(weight decay)라 부름
• 아래 역전파 과정에서 경사도를 계산하는 식이 아래 식

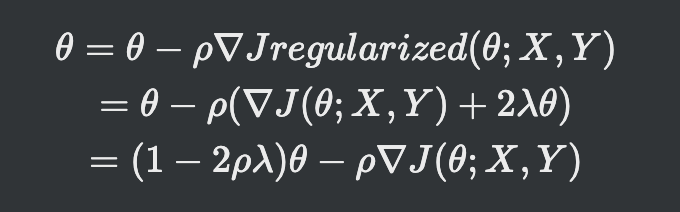
• 경사도를 경사도를 구하는 규제화된 경사도 진행양을 구하는 수식
• 람다가 0값으로 규제를 적용하지 않으면 원래식 쎼타 - 그래디언트가 됨
• (1- 2*학습률* 람다)를 원래 가중치에 곱해주는 형태

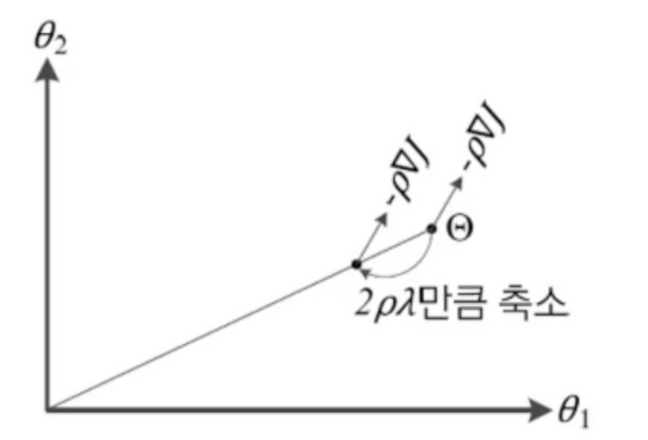
• 원래 진행해야 하는 쎼타값을 줄이고 그래디언트 만큼 이동하는 개념

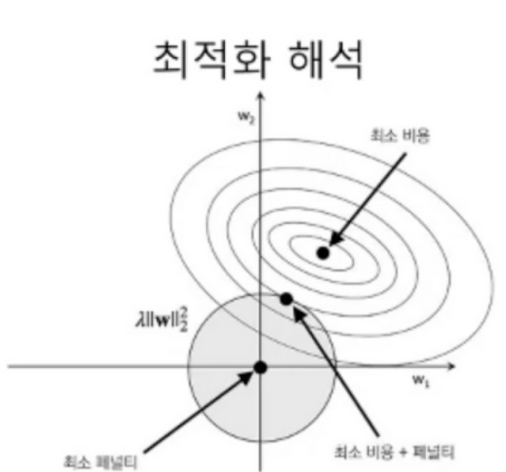
• L2 norm 은 원형적인 제한사항이 있으므로 위와 같은 형태가 됨

선형 회귀에 적용

• 원래 선형회귀의 목적함수에 가중치 L2norm을 더해주는 형태

• 위 목적함수를 미분하면 위와 같이 정리가 돼

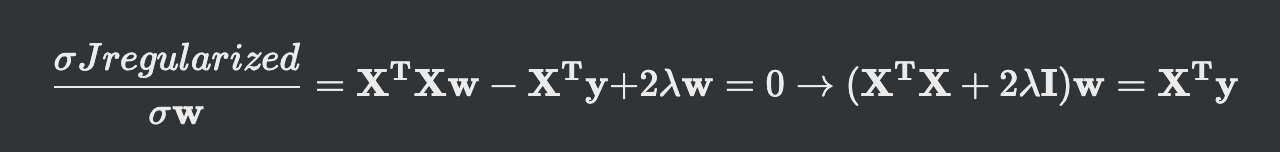
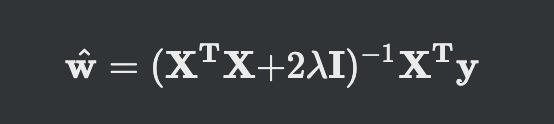
• 결국 최적화 가중치에 관한 식은 위처럼 정리가 돼
• 경사도가 0인 값에서 최적해가 나옴

MLP와 DMLP에 적용

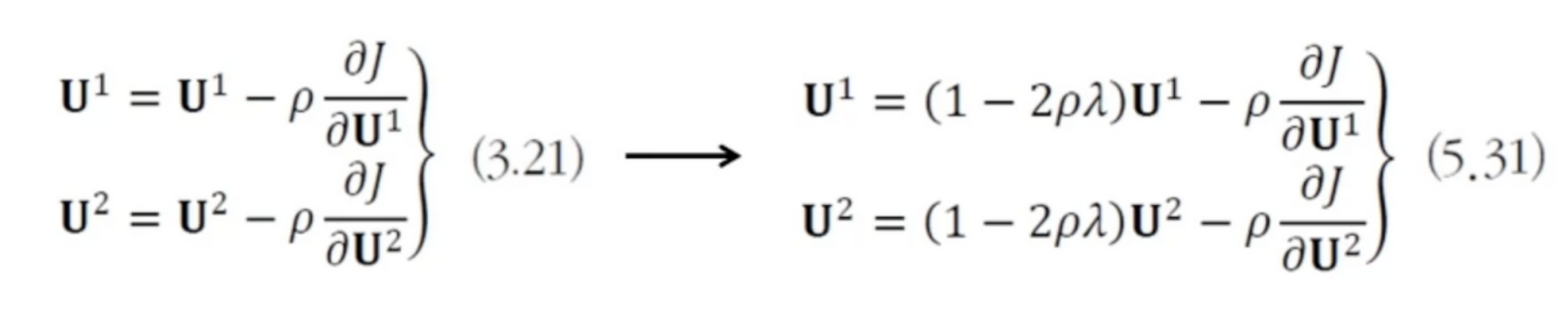
• 왼쪽이 원래 가중치 갱신 방법
• 오늘쪽에서 원래 있는 가중치의 양을 조절해서 진행 속도를 규제함

L1 NORM

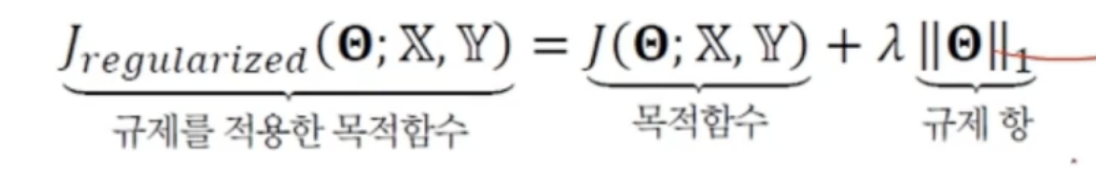
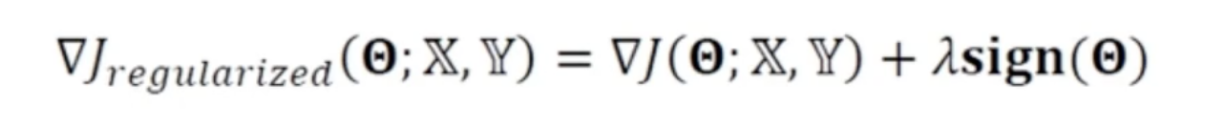
• 절대값을 활용하는 L1놈 같은 경우 미분하면 사인함수가 나오게 됨

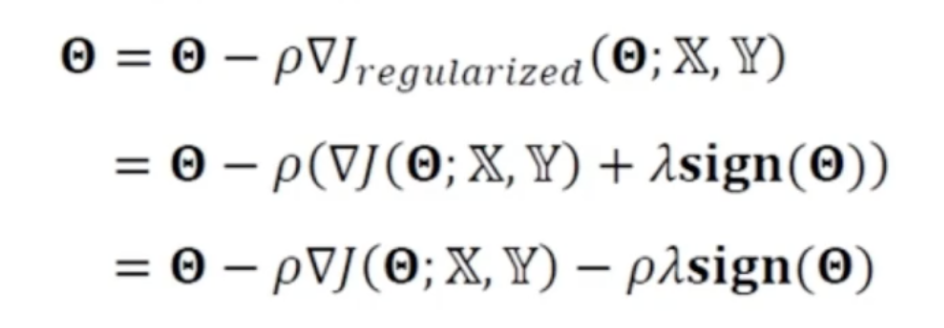
• 식을 정리하자면 매개변수 갱신은 사인값에 의해 정해지게 됨

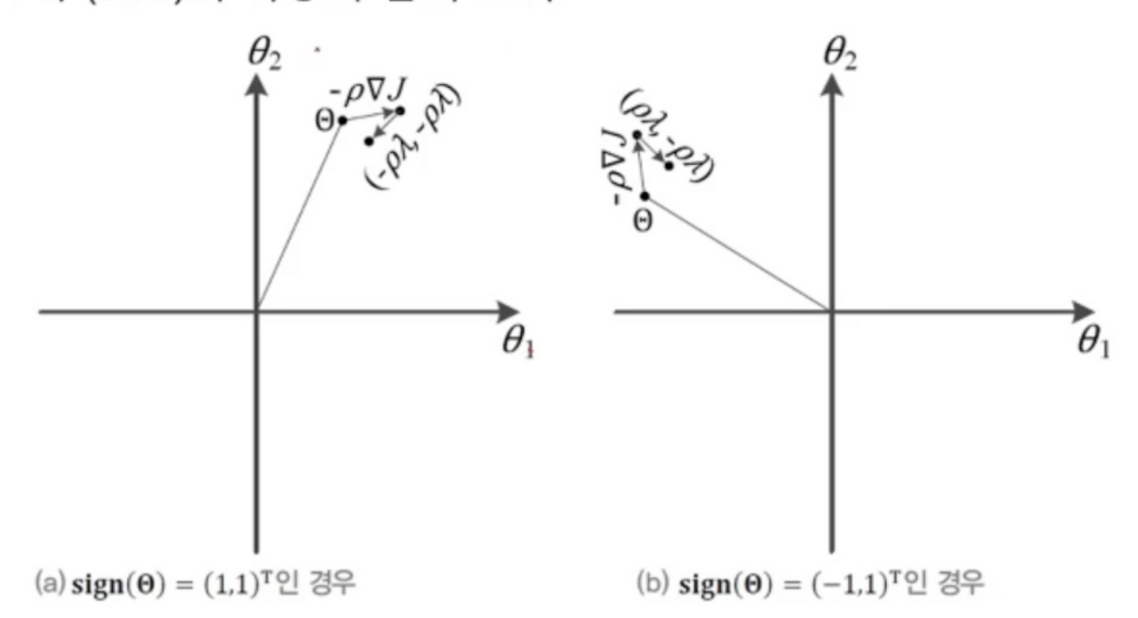
• 가중치가 회전하는 형태
• L1놈은 희소성 효과가 있음 가중치 w1에서는 0이되고 w2에서 1인 값으로 정해질 가능성 높음
• 0이 되는 매개변수가 많음

엘라스틱 넷 elastic net

• L2규제

• L1규제

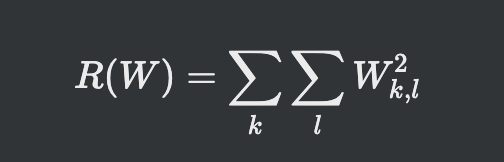
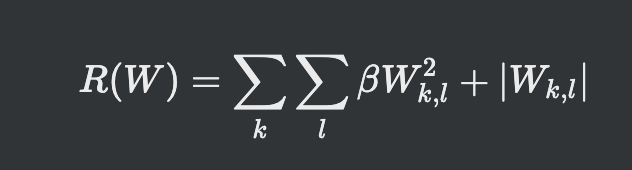
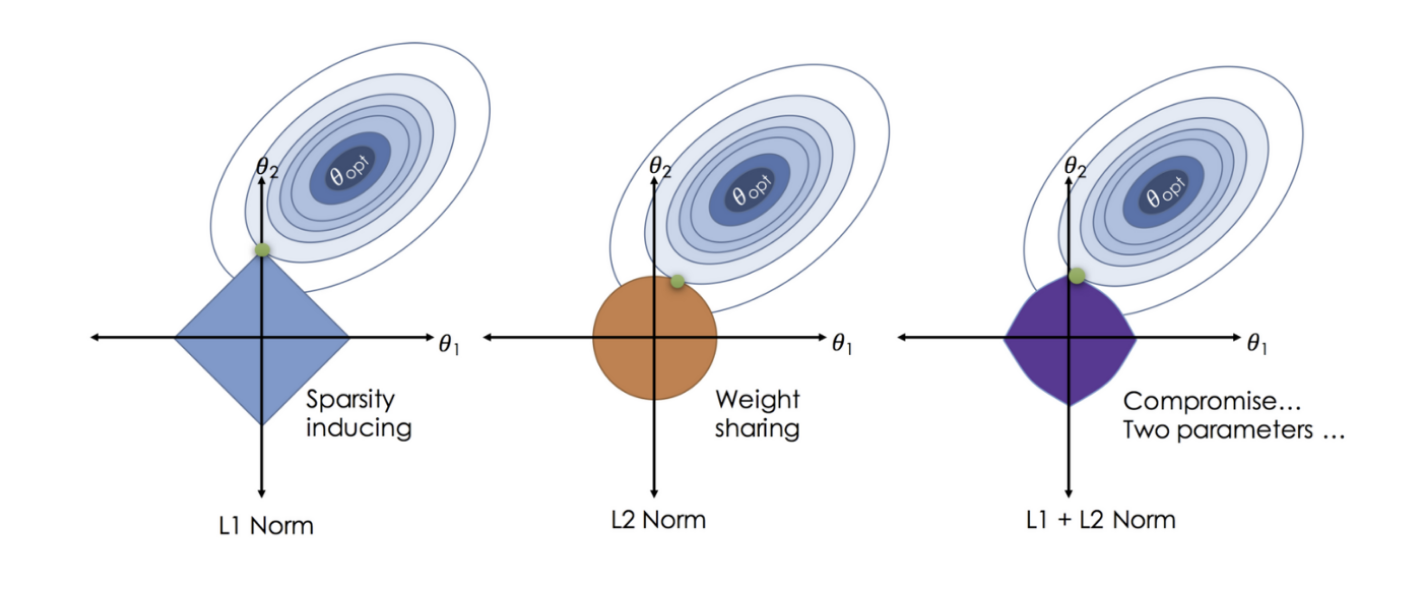
• L1 + L2 규제
• L1은 0이 되는 가중치가 많아지고
• L2는 전체적으로 적은량
• 엘라스틱은 골고루 적당한 양을 가짐