[NLP Paper Review] Transformer -1

✔️ Introduction

Seq2Seq는 RNN 계열의 모델을 사용해 sequential하게 데이터를 처리할 수 있어, 기존 DNN 모델보다 기계 번역에 유리하게 작용해왔습니다. 다만 이전 시점에서 정보를 연속적으로 받아 출력을 생성하는 방식은 몇 가지 문제가 존재했습니다.

1. sequential한 연산으로 병렬화가 되지 않는다.

2. context vector가 고정 차원이라 문맥에 손실이 발생한다.

3. long term dependency problem

위와 같은 문제를 해결하기 위해 ELMo나 bi-LSTM, Attention 등 여러 방법론이 제시되었고, 그 중 Attention을 기반으로 한 seq2seq는 2번과 3번의 문제를 다소 해결하였습니다. 하지만 구조 자체가 sequential한 연산을 요구하기에 효율적인 계산이 이뤄지지는 못했습니다. 따라서 논문에서는 transformer라는 Attention으로만 이뤄진 모델을 제안하여 병렬 처리를 가능하게 했습니다.

✔️ Model Architecture

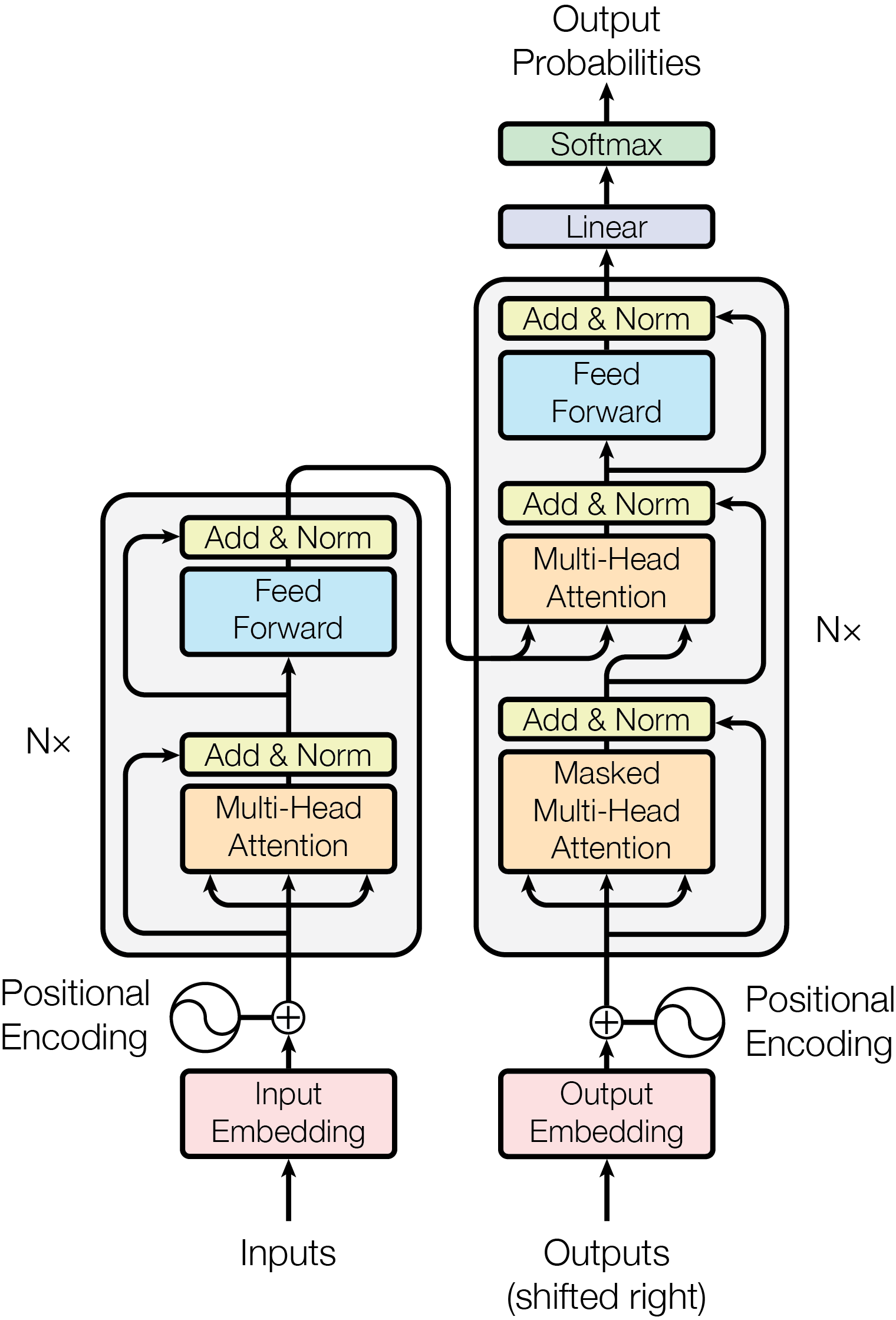모델 아키텍쳐는 기존 Seq2Seq에서 차용된 encoder & decoder 구조로 이뤄져 있습니다. 본격적으로 살펴보기 전에 논문에서 사용된 하이퍼 파라미터는 다음과 같습니다. 논문 내 나와있는 순서는 생략되어 있는 부분들이 있어서 input부터 output으로 이어지는 흐름대로 살펴보겠습니다.

🛠️ 하이퍼 파라미터

$d_{model} = 512$ (모델 차원)
$N = 6$ (레이어 수)
$h = 8$ (head 수)
$d_{ff} = 2048$ (Feed Forward Network 차원)

💡Embedding Layer

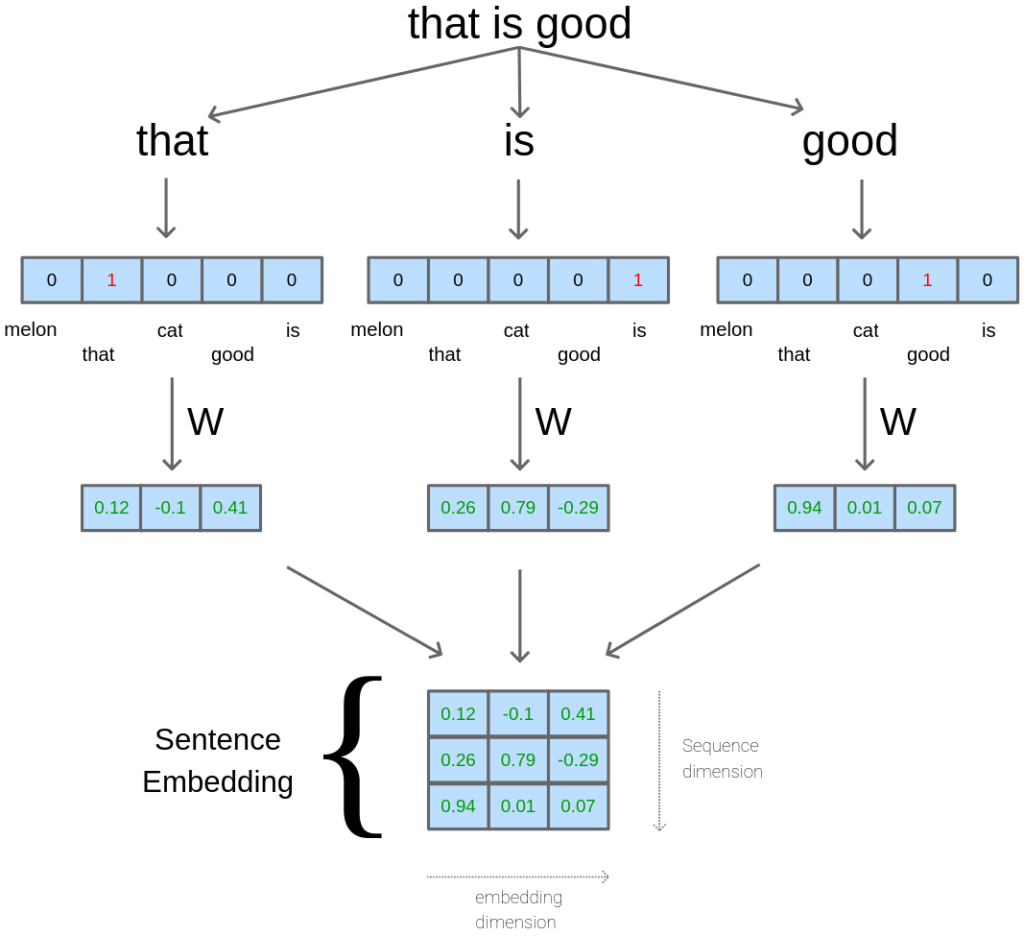
임베딩 레이어에서는 토큰들이 dense vector로 변환됩니다. 각 토큰 당 {1 x $d_{model}$} 크기의 랜덤 가중치 벡터로 변환되어 모델의 학습과 함께 학습됩니다.
이때, 모든 토큰 벡터들을 합한 {$n$ x $d_{model}$} 차원의 가중치 행렬은 encoder, decoder, 또 softmax 함수 전 선형 변환에서도 사용됩니다. 출력의 분산을 조정하기 위해서 $\sqrt{d_{model}}$로 스케일링해줍니다.

💡 Postional Encoding

transformer는 행렬 단위로 병렬 연산을 수행하다 보니, RNN 계열과 달리 입력 문장의 순서를 고려하지 못합니다. 이는 문장의 순서를 알 수 없기에 성능이 떨어지는 결과를 낳습니다. 따라서 논문에서는 임베딩 벡터 간의 위치 정보를 표현하기 위해 positional encoding을 사용하였습니다.

식은 다음과 같습니다.

$PE_{(pos, 2i)}=\sin(pos/10000^{2i/d_{model}})$
$PE_{(pos, 2i + 1)} = cos(pos / 10000^{2i / d_{model}})$

논문에서는 설명되어 있지 않지만 추가적으로 설명을 하면 다음과 같습니다.
좋은 positional encoding이기 위해서는 다음을 만족해야 합니다.

• 각 위치의 PE은 결정론적이어야 함
• 데이터의 내용, 길이와 관계 없이 PE는 동일
• 간격이 동일하면 거리는 동일해야함

몇 가지 방법들을 살펴보겠습니다.

🤔 simple indexing

$PE(a_i) = i$

각 위치의 인덱스를 사용하는 방법입니다. 이 경우, 입력이 길어질수록 i값이 커지기 때문에 한계가 존재합니다.

🤔 normalize indexing

$PE(a_i) = \frac{i}{T}$

값이 커지지 않게 simple indexing에 문장 길이로 나누어 0~1 사이 값으로 만드는 방법입니다. 하지만 데이터의 길이와 관계없이 동일하지 않으므로 한계가 있습니다.

🤔 binary indexing

simple indexing을 이진수로 표현하는 것입니다. 만약 위치가 7이라면 다음과 같습니다.

index 7 = 000111

하지만 0010에서 0011로 변화하는 것과 0011에서 0100으로 변화하는 것은 같은 간격임에도 거리가 다르기 때문에 적합하지 않습니다.

🤔 sinusoidal encoding

사인 함수를 활용하는 방식입니다. 사인 함수는 공역이 -1부터 1까지로 처리가 편하고 연속함수이므로 PE에 활용할 수 있습니다. 하지만 $sin(x + 2\pi m) = sinx$이므로 다른 위치여도 같은 값을 가질 수 있습니다. 때문에 주기를 $2\pi * 10000^\frac{2i}{d_{model}}$로 설정하여 차원 수 i에 따른 주기를 조절합니다. i값이 작을 때는 주기가 짧아져서 가까운 위치 차이를 구분하고, 클 때는 주기가 길어져 먼 거리의 위치 정보를 담습니다.
또한, i 위치에서의 PE를 선형 변환했을 때 다른 위치 j에서의 PE를 알 수 있다면 attention이 더 쉽게 위치에 대한 정보를 얻을 수 있습니다.

$PE_{pos + \Delta step} = PE_{pos} * T(\Delta step)$

이러한 translation 성질은 삼각함수의 회전 행렬(rotation matrix)로 표현이 가능합니다.
$\begin{bmatrix} \cos{(\theta+\phi)} \\ \sin{(\theta+\phi)} \end{bmatrix} = \begin{bmatrix} \cos{\phi} && -\sin{\phi} \\ \sin{\phi} && \cos{\phi}\end{bmatrix} \begin{bmatrix} \cos{\theta} \\ \sin{\theta}\end{bmatrix}$

따라서 PE는
$PE_{(pos, 2i)}=\sin(pos/10000^{2i/d_{model}})$
$PE_{(pos, 2i + 1)} = cos(pos / 10000^{2i / d_{model}})$

Positional Encoding값은 embedding vector와 더해져 attention의 입력으로 들어옵니다.

💡Multi-head Attention

self-attention

transformer에서는 self-attention이라는 개념을 사용합니다.

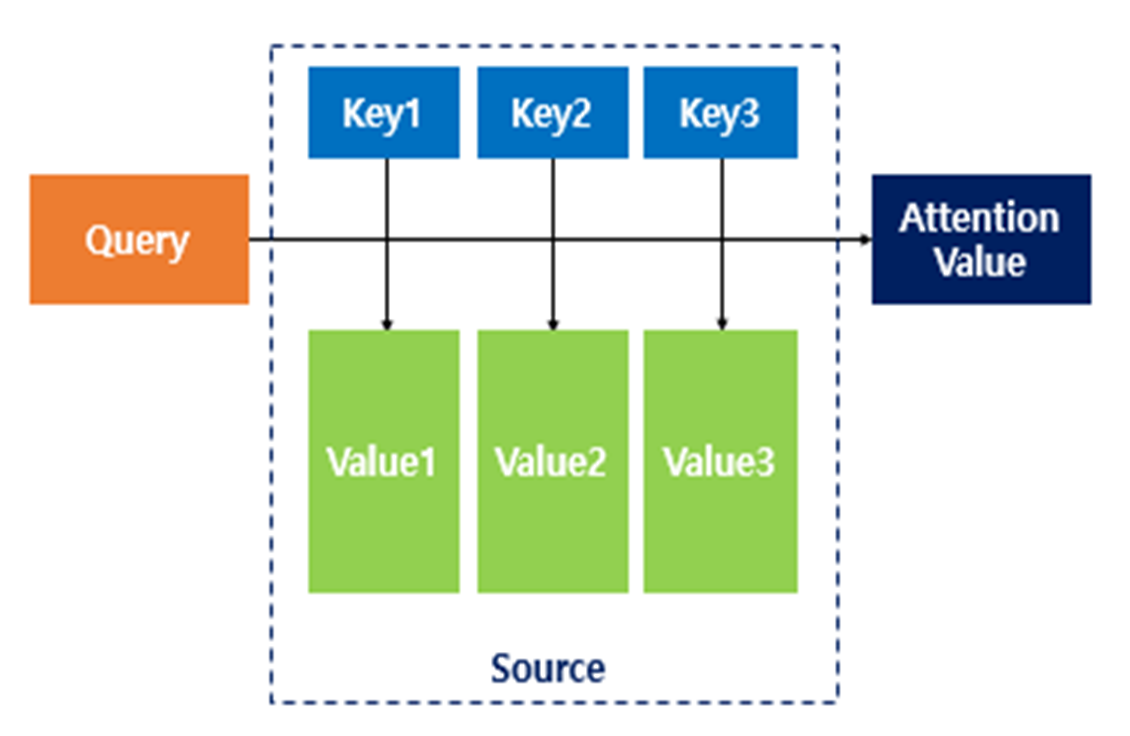
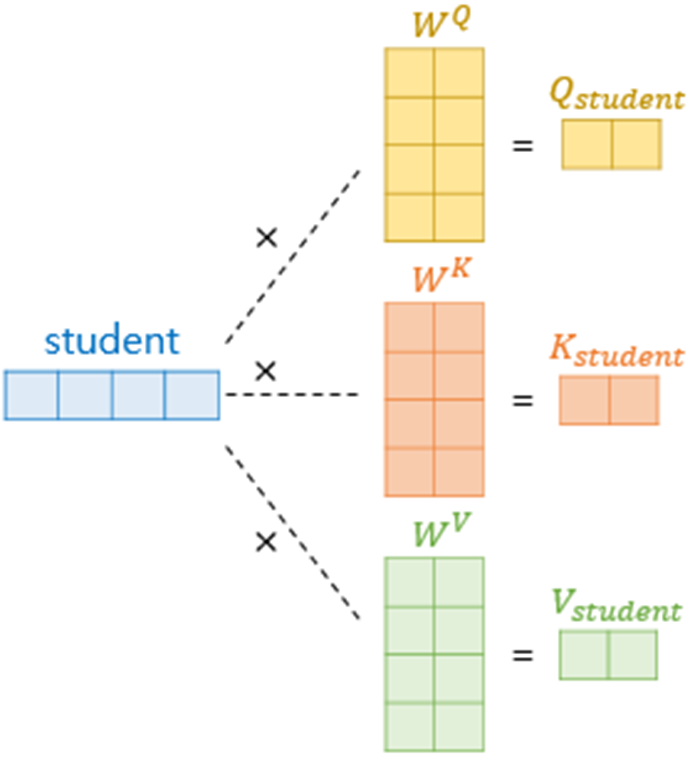
Q: 입력 문장의 모든 벡터
K: 입력 문장의 모든 벡터
V: 입력 문장의 모든 벡터

이처럼 자기 자신을 쿼리로 삼아 참조하는 attention 기법을 self attention이라고 합니다.

Multi-head Attention

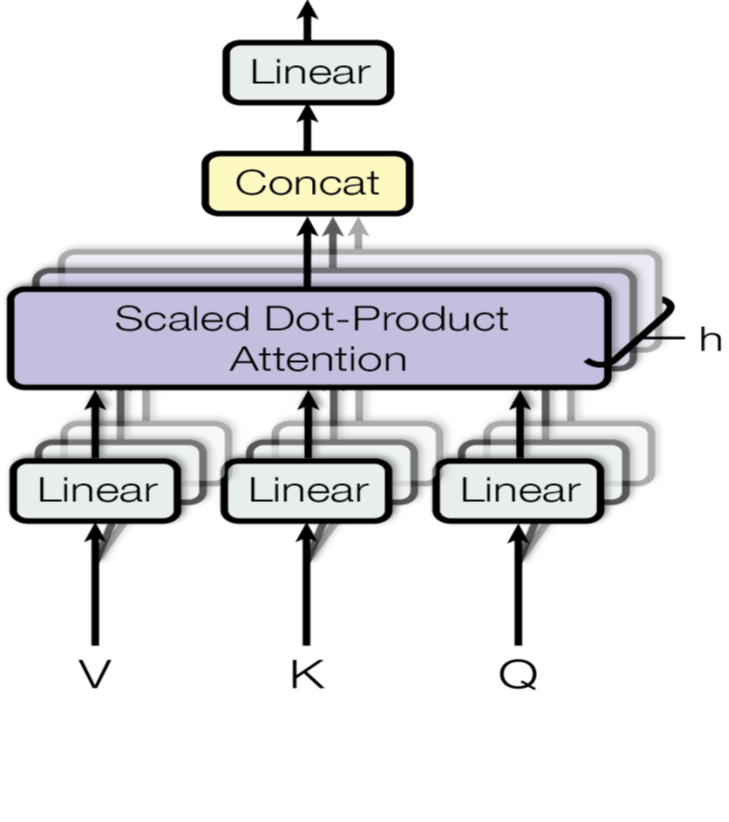multi-head attention은 입력을 여러 개의 head로 나누어서 각각 어텐션 연산을 진행한 후 concat하는 방식으로 이루어져 있습니다. 이를 위해 $d_{model}$ 차원으로 들어온 입력을 $d_{model} * (d_{model} / h)$ 크기의 가중치 $W$과 곱하여 $d_{model} / h$ 차원으로 만들어 줍니다.

Scaled-dot product

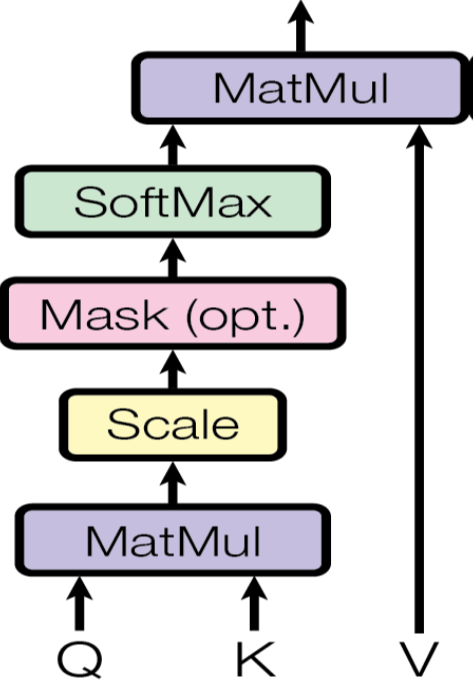선형변환된 Q, K, V는 scaled-dot product로 attention score를 계산하게 됩니다.

$Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$
($d_k$는 K의 차원)

이때, embedding layer와 비슷하게 $\sqrt{d_k}$로 스케일링을 해주는데 그 이유는 다음을 참조하길 바랍니다.
scaled-dot product에서 scailing을 하는 이유

연산이 완료된 head들은 concat되고, 선형 변환되어 최종 representation을 얻게 됩니다.

$MultiHead(Q, K, V) = Concat(head_1, ..., head_h)W^O$
$W^O \in \mathbb{R}^{hd_v * d_{model}}$

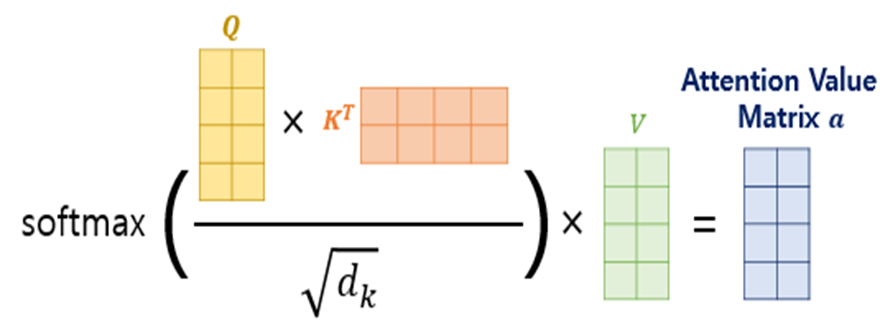
앞서 말했듯, transformer는 병렬로 연산하기에 행렬단위로 계산됩니다.

Application of Attention

Multi-head Attention은 transformer 내에서 다음과 같은 곳에 사용됩니다.

• encoder-decoder를 연결하는 레이어에서 K, V는 encoder의 입력이, Q는 decoder의 입력이 들어옵니다. (cross attention이라고도 합니다.)

• encoder 자체에도 multi-head attention layer가 들어가 있습니다.

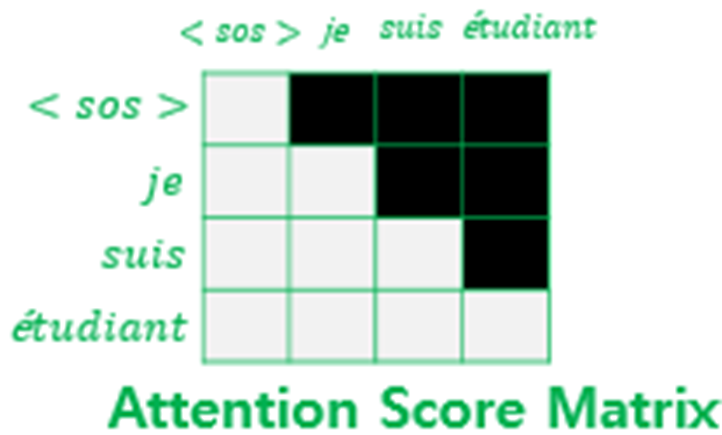
• decoder에서 self-attention을 사용하게 되면 미래 시점 위치의 토큰까지 디코더가 학습하게 됩니다. 이는 auto-regressive property를 해치는 것이므로 masking을 하여 미래 시점의 값들을 가려주게 됩니다.
  

💡 Add & Norm

Add & Norm은 각각 residual connection과 layer normalization을 말합니다.

Residual Connection

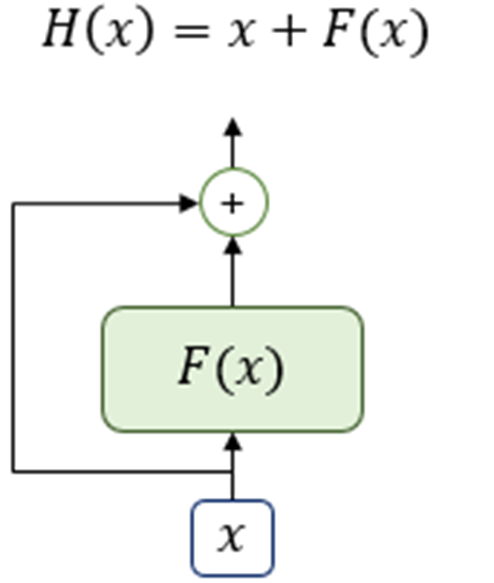
residual connection은 layer를 거친 후 입력과 출력을 더해주는 방식입니다. 이를 통해 학습이 진행되어도 값이 줄어들어 기존의 입력을 잃어버리는 일을 방지할 수 있게 되었습니다.

Layer normalization

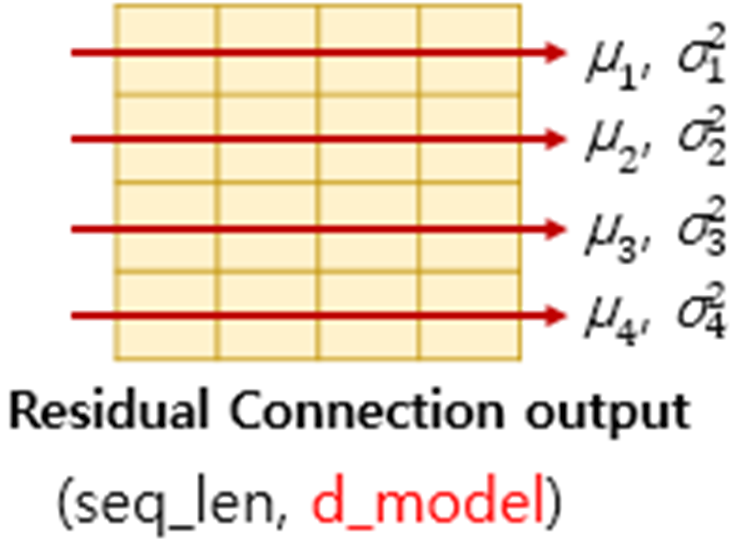
layer normalization은 행렬 내에서 열 방향으로 평균 및 분산을 구하고 정규화를 진행하는 것을 말합니다. 여기서는 $d_{model}$ 방향으로 정규화가 이뤄집니다.

💡 Position-wise Feed-Forward Networks

$FFN(x) = max(0, xW_1 + b_1)W_2 + b_2$

$W_1 = (d_{model}, d_{ff})$
$W_2 = (d_{ff}, d_{model})$

선형 변환을 해준 후 비선형 함수를 거칩니다. $d_ff$로 높은 차원에서 다시 $d_{model}$로 줄여가는 과정과 ReLU로 모델의 표현력을 높입니다.

💡 Flow

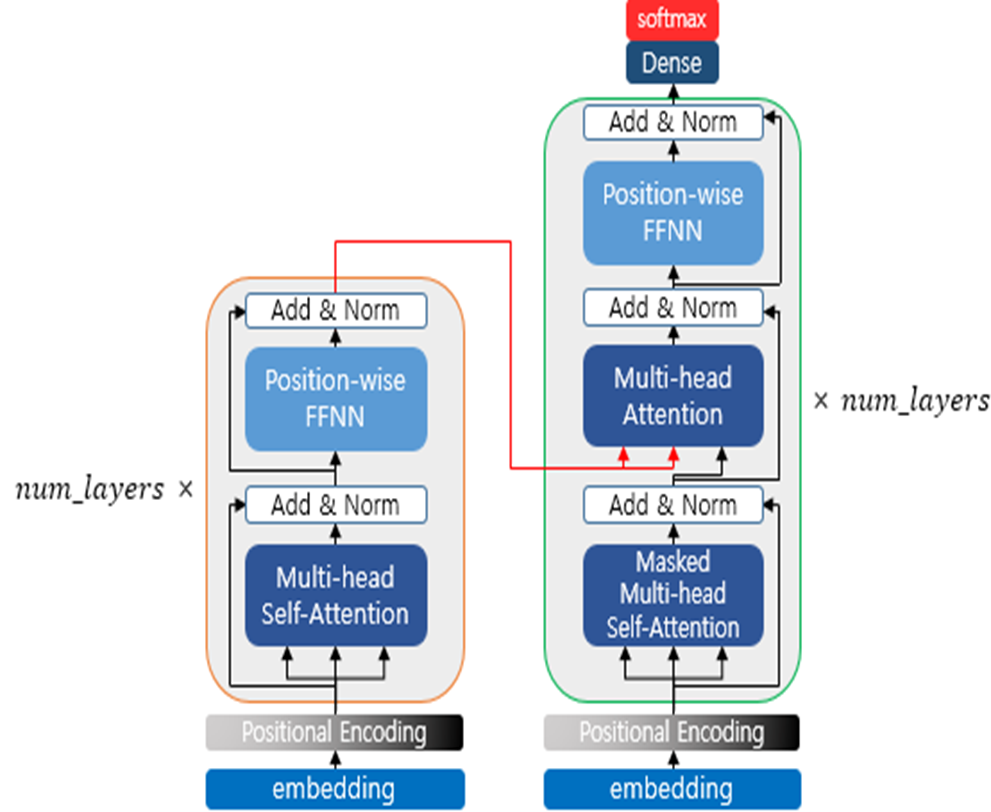
모델은 encoder와 decoder가 $N$개씩 존재합니다. 마지막 encoder에서 첫 번째 decoder로 K, V가 전달되고, 마지막 decoder에서 softmax를 거쳐 전체 토큰의 확률분포를 구하게 됩니다.

✔️ Why Self-Attention?

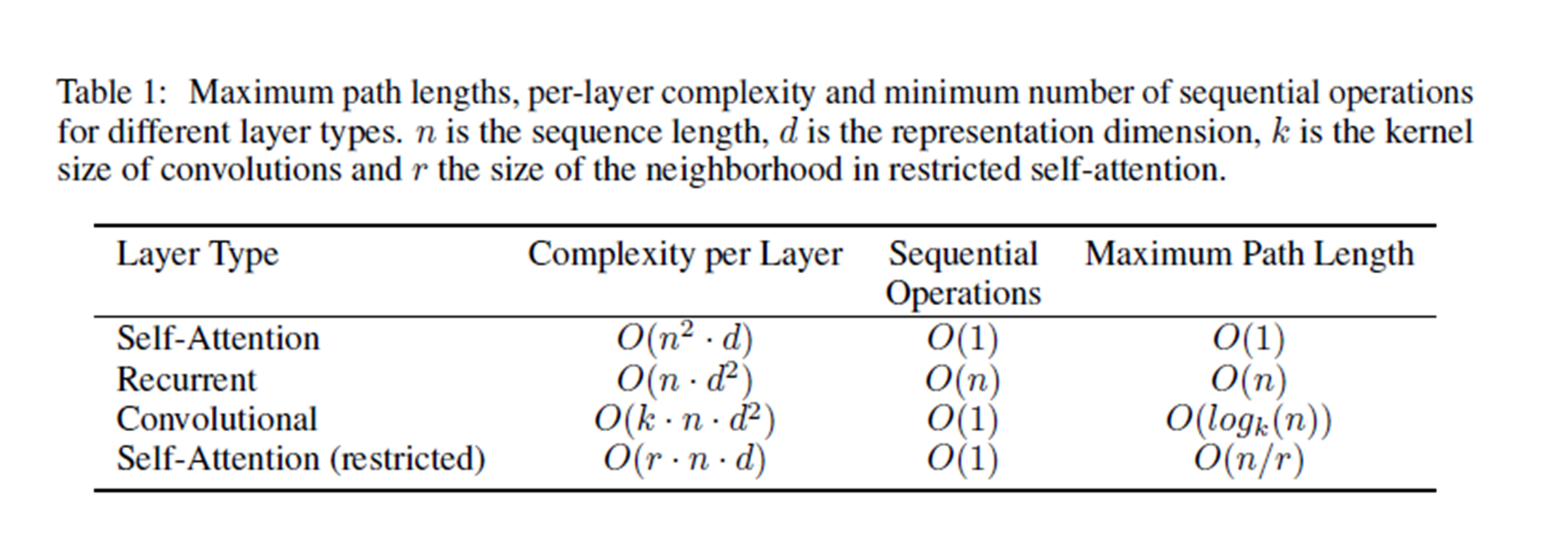
논문에서는 self-attention을 차용한 이유에 대해 세 가지 측면에서 설명합니다.

1. 레이어 당 계산 복잡도가 어느 정도인가

2. 병렬화될 수 있는 계산의 수(=sequential operation의 최소 수)

3. 시퀀스에서 떨어진 두 토큰이 영향을 주고 받기 위해 거쳐야 하는 네트워크 내 연산 수(= 최대 경로 길이)
   : 짧을 수록 gradient가 줄어들지 않으므로 학습에 유리함.