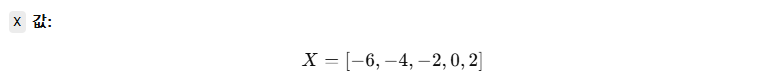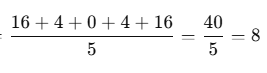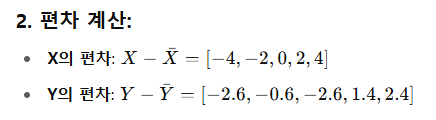공분산 (cov)의 개념
: 공분산(covariance)은 두 확률 변수 간의 관계를 나타내는 통계적 개념
두 변수의 값이 어떻게 함께 변하는지를 측정, 서로 양의 방향으로 변하는지, 음의 방향으로 변하는지, 또는 전혀 관계가 없는지를 알 수 있다.
Cov
cov 메서드는 결측값을 제외한 쌍별 공분산을 구하는 메서드입니다.
사용법
df.cov(min_periods=None, ddof=1)
min_periods: 공분산을 구할 최소 요소의 갯수 입니다. 요소의 갯수가 모자르면 NaN을 반환합니다.
먼저 기본적인 사용법 예시를 위해 5x2짜리 객체 3개를 생성하겠다.
col = ['X','Y']
data1 = [[-6,-3],[-4,-1],[-2,-3],[0,1],[2,2]]
data2 = [[7,-4],[4,-1],[2,0],[-1,3],[-4,9]]
data3 = [[3,-4],[3,-1],[3,0],[3,3],[3,9]]
df1 = pd.DataFrame(data=data1, columns=col)
df2 = pd.DataFrame(data=data2, columns=col)
df3 = pd.DataFrame(data=data3, columns=col)기본적인 사용법
df1은 좌표평면상에서 x가 증가할때 y도 증가하는 경향을 가집니다.
이때 공분산(cov)값은 0보다 크며 양의 상관관계라고 합니다.
df1에 대한 분석을 해보자면
pandas는 모집단 분산 공식이 아닌 표본 분산으로 계산한다.
데이터를 뜯어올때 일부만 뜯어올 수 있기 때문에 조금 더 정확한 계산을 위해 사용한다.
모집단 분산 : 편차 ^ 2 / n
표본 분산 : 편차 ^ 2 / (n - 1)
편차란 ?
평균값과 얼마나 떨어져있는 거리!
ex) 1.데이터 - 평균, 2.그 값 / n
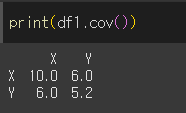
여기서 10.0은 x와 x의 분산 즉 자기 자신의 분산을 의미한다.
여기서 -2는 평균을 의미한다.
이 식에서 우리는 표준 분산을 하기 때문에 4로 나누어 40 / 4 = 10 결국 10이 나오게 된다.
마찬가지로 5.2는 y와 y의 분산 즉 y의 분산이다.
여기서 같은 값인 6.0은 x와 y의 공분산이다.
이런식으로 6.0이 나오게 된다.
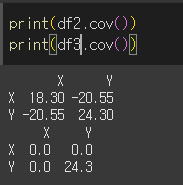
이렇게 df2, df3까지 함수를 써보면
이런 값이 나오게 된다.
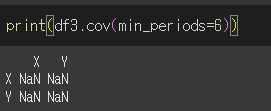
min_periods인수의 사용
min_periods인수는 공분산에 이용될 요소의 최소 갯수를 제한합니다.
이 숫자보다 요소의 수가 적을 경우 NaN을 반환합니다.
첨도 (kurt / kurtosis)의 개념
: 첨도란 데이터의 확률분포가 얼마나 뾰족한지를 나타내는 통계언어입니다.
사용법
df.kurt(axis=None, skipna=None, level=None, numeric_only=None, kwargs)
axis: 첨도를 구할 축을 지정합니다
skipna: 결측치를 무시할지 여부 입니다. 기본값은 True로 계산시 무시됩니다.
level: 멀티인덱스의 경우 레벨을 지정할 수 있습니다.
numeric_only: float, int, bool 형식만 포함할지 여부 입니다.
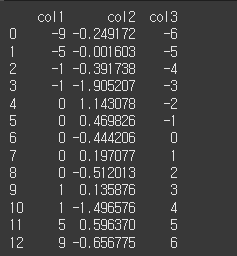
먼저 기본적인 사용법 예시를 위해 13x3짜리 객체를 생성하겠습니다.
l = [-9,-5,-1,-1,0,0,0,0,0,1,1,5,9] # leptokurtic(렙토커틱) : 중앙에 값이 많이 몰려 있어 꼬리가 두꺼운 뾰족한 분포.
m = np.random.normal(0,1,13) # mesokurtic(메조커틱) : 평균 0, 표준편차 1인 정규분포를 따르는 데이터(표준 첨도)
p = [-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6] # Platykurtic(플래티커틱) : 값이 고르게 퍼져 있음.
data = {"col1":l,"col2":m,"col3":p}
df = pd.DataFrame(data)
print(df)함수 사용
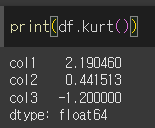
가운데가 뾰족한 경우(정규분포에 비해)
첨도 kurt는 0보다 크게 됩니다.
평균=0, 표준편차=1 인 정규분포에 근접하는 난수
첨도 kurt의 값은 0에 근접한 값이 출력됩니다.
뭉툭한(정규분포에 비해) 경우
첨도 kurt의 값은 0보다 작게 됩니다.
표준오차 (sem)의 개념
:표준 오차는 표본평균들의 표준편차로, 직관적으로 보면 추정값인 표본평균들과 참값인 모평균(표본평균의 평균)과의 표준차이 라고 할 수 있습니다.
사용법
sem(axis=None, skipna=None, level=None, ddof=1, numeric_only=None, kwargs)
axis: 첨도를 구할 축을 지정합니다
skipna: 결측치를 무시할지 여부 입니다. 기본값은 True로 계산시 무시됩니다.
level: 멀티인덱스의 경우 레벨을 지정할 수 있습니다.
ddof: 자유도를 표시합니다.
numeric_only: float, int, bool 형식만 포함할지 여부 입니다.
먼저 기본적인 사용법 예시를 위해 5x3짜리 객체를 생성하겠습니다.
a = [1,1,1,1,1]
b = [1,2,3,4,5]
c = [20,40,60,80,100]
data = {"col1":a,"col2":b,"col3":c}
df = pd.DataFrame(data)
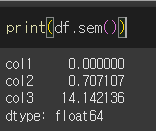
print(df)기본적인 사용법
col1의 경우 모든 요소가 같기 때문에 표본평균의 평균과 표본편균이 완벽하게 일치하여 표준오차가 없기 때문에 sem=0 을 반환하게 됩니다.
col2와 col3의 경우를 비교해보면 표준평균의 차이는 각 값들이 더 조밀한 col2가 더 작기 때문에 표준오차의 경우 표본평균의 표준편차도 더 작을수 밖에없습니다. 즉, col2의 sem값이 col3의 sem값보다 작습니다.
왜도(비대칭도) (skew)
: 왜도 또는 비대칭도 라고도 하며, 평균에 대해 최빈값이 얼마나 치우쳐져있는지를 나타내는 척도입니다.
왜도는 우측으로 치우칠수록 음의값, 좌측으로 치우칠수록 양의 값을 가집니다.
사용법
df.skew(axis=None, skipna=None, level=None, numeric_only=None, kwargs)
axis: 왜도를 구할 축을 지정합니다
skipna: 결측치를 무시할지 여부 입니다. 기본값은 True로 계산시 무시됩니다.
level: 멀티인덱스의 경우 레벨을 지정할 수 있습니다.
numeric_only: float, int, bool 형식만 포함할지 여부 입니다.
먼저 기본적인 사용법 예시를 위해 18x3짜리 객체를 생성하겠습니다.
a = [-5,-4,-3,-3,-2,-2,-1,-1,-1,0,0,0,0,0,1,1,1,2]
b = [-3,-2,-1,-1,-1,-1,0,0,0,0,0,0,1,1,1,1,2,3]
c = [-2,-1,-1,-1,0,0,0,0,0,1,1,1,2,2,3,3,4,5,]
data = {"col1":a,"col2":b,"col3":c}
df = pd.DataFrame(data)
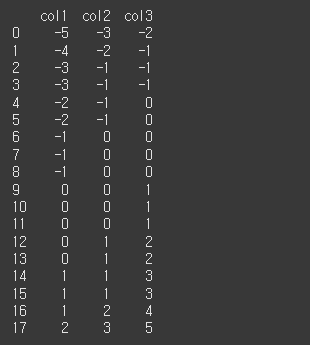
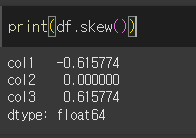
print(df)기본적인 사용법
col1의 경우 최빈값이 우측으로 치우쳐져 있기 때문에, 왜도값은 음수를 가집니다.
col2의 경우 대칭구조를 가지기 때문에 왜도값은 0이 됩니다.
col3의 경우 좌측으로 치우쳐져있기 때문에, 왜도값은 양수를 가집니다.
상관계수 (corr / corrwith)
피어슨 상관계수
두 변수 간의 선형 상관관계를 계량화 한 수치입니다.
코시-슈바르츠 부등식에 의해 +1과 -1사이의 값을 가집니다.
+1의 경우 완벽한 양의 선형 상관 관계, -1의 경우 완벽한 음의 상관관계,
0의 경우 선형 상관관계를 갖지 않습니다.
켄달 타우상관계수
두 변수들간의 순위를 비교해서 연관성을 계산하는 방식입니다.
스피어먼 상관계수
두 변수의 순위 값 사이의 피어슨 상관 계수와 같습니다.
사용법
df.corr(method='pearson', min_periods=1)
method: {pearson / kendall / spearman} 적용할 상관계수 방식입니다.
min_periods: 유효한 결과를 얻기위한 최소 값의 수 입니다. (피어슨, 스피어먼만 사용가능)
df.corrwith(other, axis=0, drop=False, method='pearson')
other: 동일한 이름의 행/열을 비교할 다른 객체입니다.
axis: {0 : index / 1 : columns} 비교할 축 입니다. 기본적으로 0으로 인덱스끼리 비교합니다.
drop: 동일한 이름의 행/열이 없을경우 NaN을 출력하는데, 이를 출력하지 않을지 여부입니다.
method: {pearson / kendall / spearman} 적용할 상관계수 방식입니다.
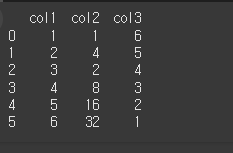
먼저 corr 메서드의 기본적인 사용법 예시를 위해 6x3짜리 객체를 생성하겠습니다.
col1 = [1,2,3,4,5,6]
col2 = [1,4,2,8,16,32]
col3 = [6,5,4,3,2,1]
data = {"col1":col1,"col2":col2,"col3":col3}
df = pd.DataFrame(data)
print(df)피어슨 상관계수
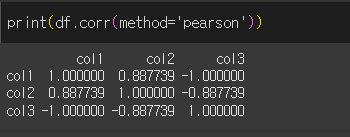
피어슨 상관계수의 경우 method='pearson'을 사용하며, 두 변수의 선형 상관계수를 의미합니다.
col1이 증가할 경우 col2는 대체로 증가하는 경향을 가지기에 0<p<1의 값을 가지며,
col1이 증가할 경우 col3은 완벽히 감소하기 때문에 p=-1의 값을 가집니다.
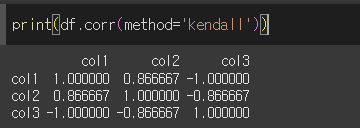
켄달-타우 상관계수
켄달-타우 상관계수는 두 순위간의 상관 계수를 의미합니다.
col1의 순위는 col2의 순위와 대체로 일치 하기에 0<p<1의 값을 가지며,
col1의 순위는 col3의 순위와 완벽히 반대이기 때문에 p=-1의 값을 가집니다
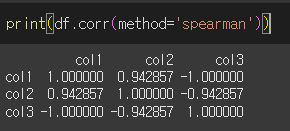
스피어먼 상관계수
스피어먼 상관계수는 두 변수의 순위의 피어슨 상관계수를 의미합니다.
corrwith
corrwith 메서드의 기본적인 사용법 예시를 위해 6x2짜리 객체 2개를 생성하겠습니다.
data1 = {"col1":[1,2,3,4,5,6],"col2":[1,4,2,8,16,32]}
data2 = {"col1":[6,5,4,3,2,1],"col3":[3,6,1,2,5,9]}
df1 = pd.DataFrame(data1)
df2 = pd.DataFrame(data2)
print(df1)
print(df2)기본적인 사용법
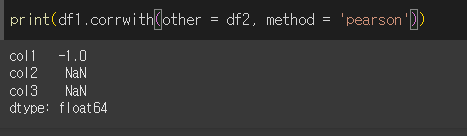
df1과 df2는 col1이라는 열을 갖지만 모두가 col2, col3을 갖진 않습니다.
이 상태에서 corrwith을 사용할 경우 col1에 대해서만 상관관계 계산이 진행됩니다.
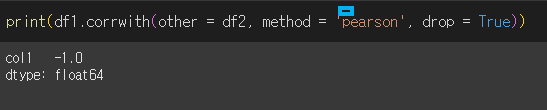
drop = True를 할 경우 쌍을 이루지 못하여 NaN을 반환한 열을 제외하고 출력합니다.