Optimization Algorithms

Optimization Algorithms

Mini-batch Gradient Descent

• Batch의 sample shape이 ($n_x, m$)이고 $m=5,000,000$이라 가정해보자.

  • 이제 5,000개의 sample씩 잘라서 mini-batch를 만들고, $\{t\}$ notation으로 1,000번을 반복하여 gradient를 구하는 방법을 나타내 볼 것이다.

• 기존 cost 구하는 공식과 regularization term $\lambda$이 합쳐진 값은 mini-batch를 한 번 순회하여 계산한 결과다.

  • Mini-batch 단위로 parameter $W$&$b$를 업데이트 하고, 이러한 과정을 $t$번 반복하면 "1 epoch"을 pass했다고 보는 것이다.

Understanding Mini-batch Gradient Descent

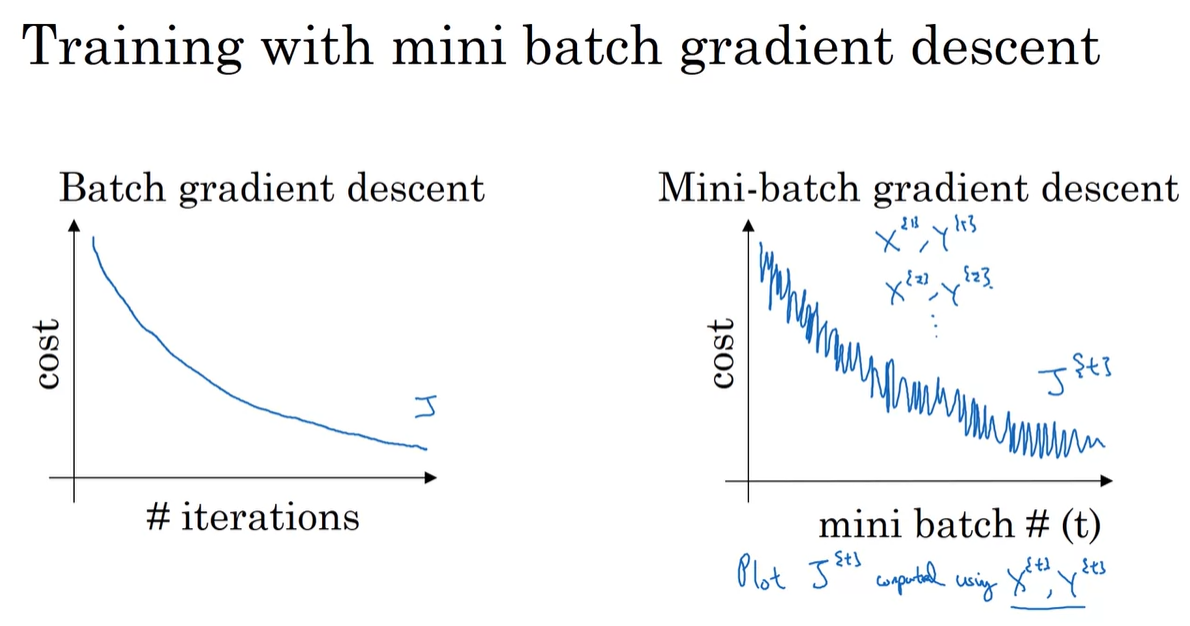
• Batch gradient descent와 Mini-batch gradient descent의 cost 변화량의 추이를 비교해보자.

  • Batch gradient descent에 비해 Mini-batch gradient descent가 진동이 잦다.

    • Mini-batch는 $t$개의 일부 sample만을 training set $X$, $Y$로 보기 때문에, 각 training set을 지날 때마다 loss의 분포가 다를 수 있기 때문이다.

• Mini-batch의 sample size를 $m$개라고 한다면, batch size가 1인 gradient descent는 Stochastic gradient descent라 한다.

  • Stochastic gradient descent는 vectorization으로 얻는 병렬 처리의 이점이 덜하다.

    • 즉, Lose speed up → 학습이 느리다.

  • Batch gradient descent는 하나의 iteration이 매우 느리다는 단점이 있다.

    • 따라서 1과 $m$ 사이의 값으로 training set을 구성하면, vectorization의 장점을 가질 수 있을 뿐더러 전체 set의 학습 결과를 기다릴 필요도 없다.

• 이제 우리는 이러한 가이드라인을 따르면 된다.

  • Training set이 매우 적을(small) 때에는 batch gradient descent를 활용한다.

  • Mini-batch size는 2의 제곱수를 따르는 것이 좋다. (CPU/GPU로 연산하기 때문)

    • Mini batch의 각 size는 CPU나 GPU의 memory(용량)에 따라 달라진다.

Exponentially Weighted Averages

• Exponentially Weighted Averages 혹은 Exponentially Weighted moving Average라 부르는 개념은 다음과 같은 예시로 설명 가능하다.

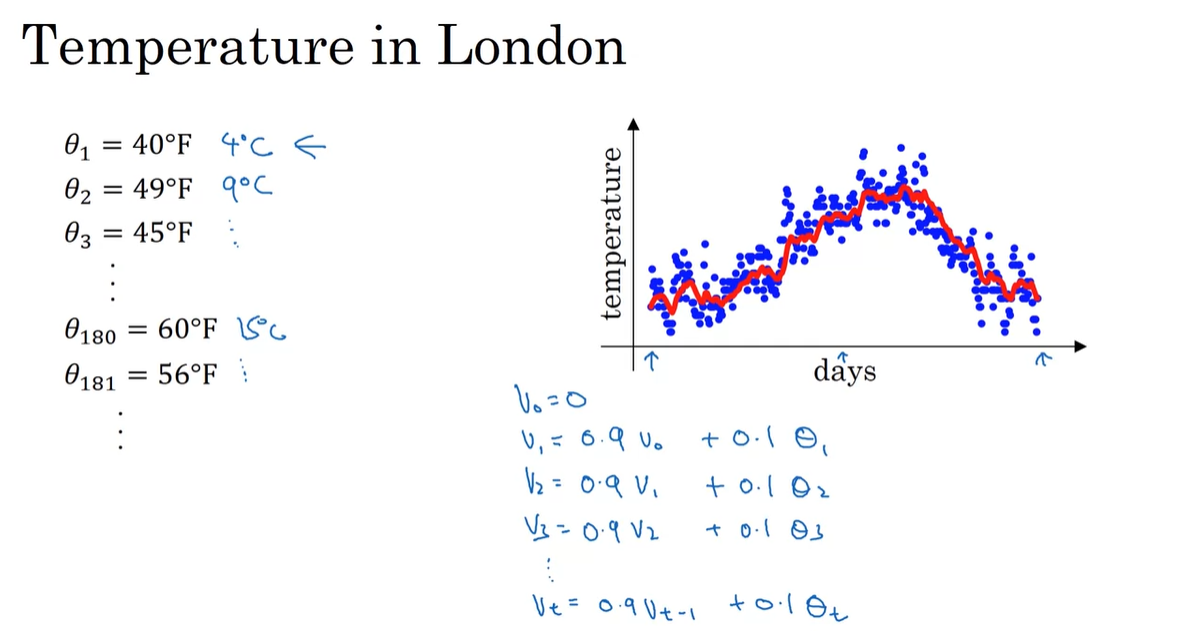
  • 날짜에 따른 London의 날씨 $\theta_{i}$가 주어진 상황에서 moving average를 계산하는 방법은 다음과 같다.

    $v_0 = 0$
    $v_1 = 0.9 v_0 + 0.1 \theta_1$
    $v_2 = 0.9 v_1 + 0.1 \theta_2$
    ...
    $v_t = 0.9 v_{t-1} + 0.1 \theta_t$

  • 0.9배의 previous value와 0.1의 오늘 날씨로 가중 평균을 구하는 것이다.

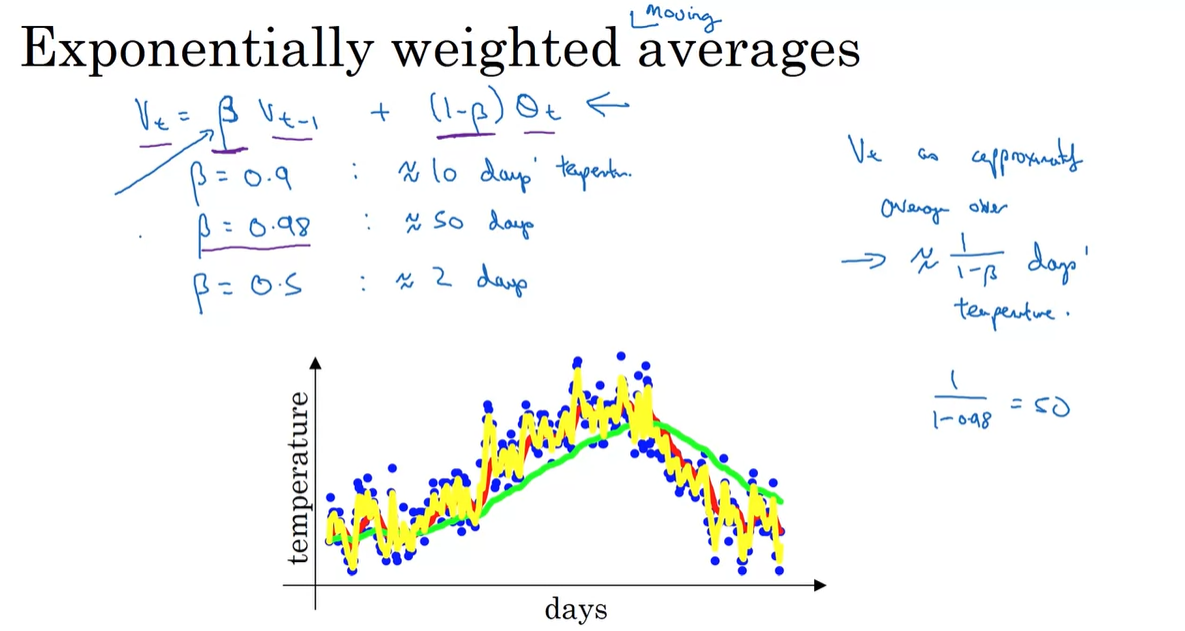
• Previous value에 얼마나 가중치를 둘 것인지를 결정하는 변수 $\beta$를 설정하여 일반화하면 다음과 같다.

  $v_t = \beta v_{t-1} + (1-\beta) \theta_{t}$

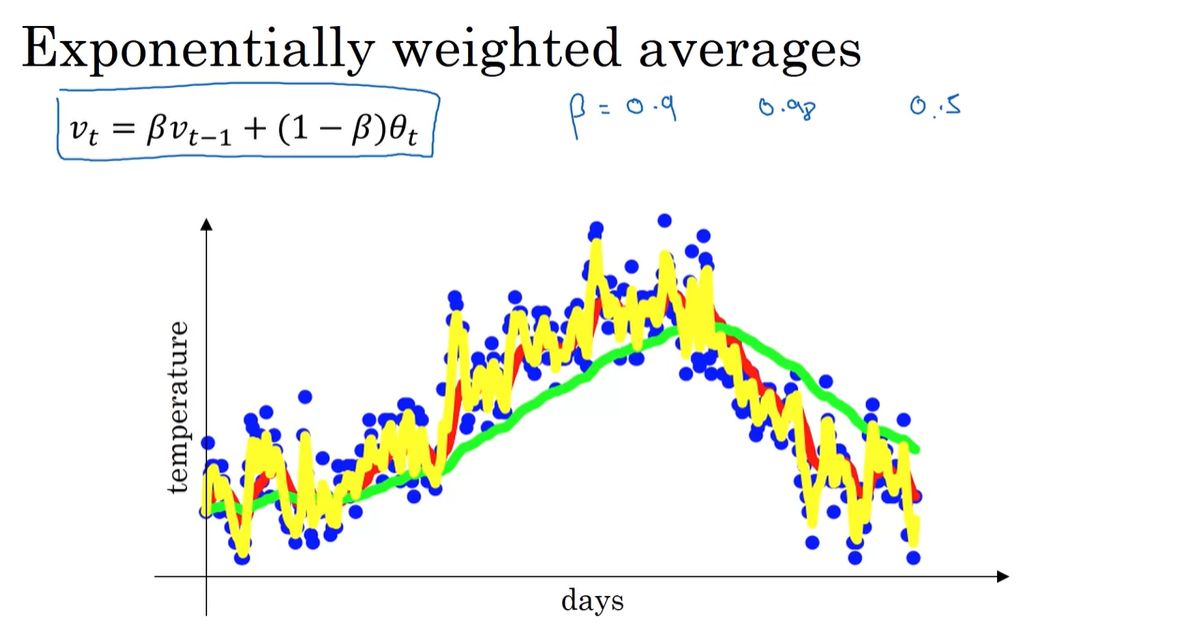
  • 이 때 $v_t$는 근사적으로 $\displaystyle \frac{1}{1-\beta}$일 간의 데이터만을 사용해 평균을 취하는 것과 같다.

    • if $\beta = 0.9$, $\displaystyle \frac{1}{1-0.9} \approx 10$ days → 빨간색 curve

    • if $\beta = 0.98$, $\displaystyle \frac{1}{1-0.98} \approx 50$ days → 초록색 curve

    • if $\beta = 0.5$, $\displaystyle \frac{1}{1-0.5} \approx 2$ days → 노란색 curve

  • 즉, $\beta$가 클수록 이전 값의 영향력을 더 높게 평가한다는 뜻이라고 해석하면 된다.

Understanding Exponentially Weighted Averages

• Exponentially Weighted Average의 수식은 다음과 같다.

  $v_t = \beta v_{t-1} + (1-\beta) \theta_{t}$

• $v_{100}$에서부터 reculsive하게 $\theta_{i}$에 관하여 정리하면 다음과 같이 수식이 전개된다.

  $v_{100} = 0.1 *\theta_{100} + 0.1 * 0.9 *\theta_{99} + 0.1 * (0.9)^2 \theta_{98} + ... + 0.1 * (0.9)^{99} \theta_{1}$

  • 이는 0.1을 기준으로 감소하는 함수와 data point $\theta$의 곱을 합한 값으로 이어진다.

  • 우리는 $\beta$를 알고 있으므로 $\beta^{\frac{1}{1-\beta}}$를 계산하면 항상 $\displaystyle \frac{1}{e} \approx 0.35$의 값을 얻는다.

    • if $\beta = 0.9$ → $0.9^{10} \approx 0.35 \approx \displaystyle \frac{1}{e}$

    • if $\beta = 0.9$ → $0.98^{50} \approx 0.35 \approx \displaystyle \frac{1}{e}$

  • 즉, $\displaystyle \frac{1}{1-\beta}$만큼의 일수가 지나면 기존 값의 1/3 정도의 값을 유지하다가 값이 확 떨어져, 해당 일수 이후의 날짜는 영향력이 크지 않다는 것을 의미한다.

  • $\epsilon = 1-\beta$ 로 두면 exponential의 정의에 의해 해당 정리가 더욱 명확해진다.

    • $(1 - \epsilon)^{\frac{1}{\epsilon}} = \displaystyle \frac{1}{e}$

• 이를 알고리즘으로 정리하면 아래와 같다.

  $v_0 = 0$ initialize
  Repeat {
  Get next $\theta_t$
  $v_\theta := \beta v_{\theta} + (1-\beta) \theta_t$
  }

  • 이와 같은 알고리즘은 $v_\theta$만을 메모리에 올려두고 계산하면 된다는 점이 장점이다.

Bias Correction in Exponentially Weighted Averages

• Exponentially Weighted Averages 알고리즘의 bias는 초기값 설정에 있다.

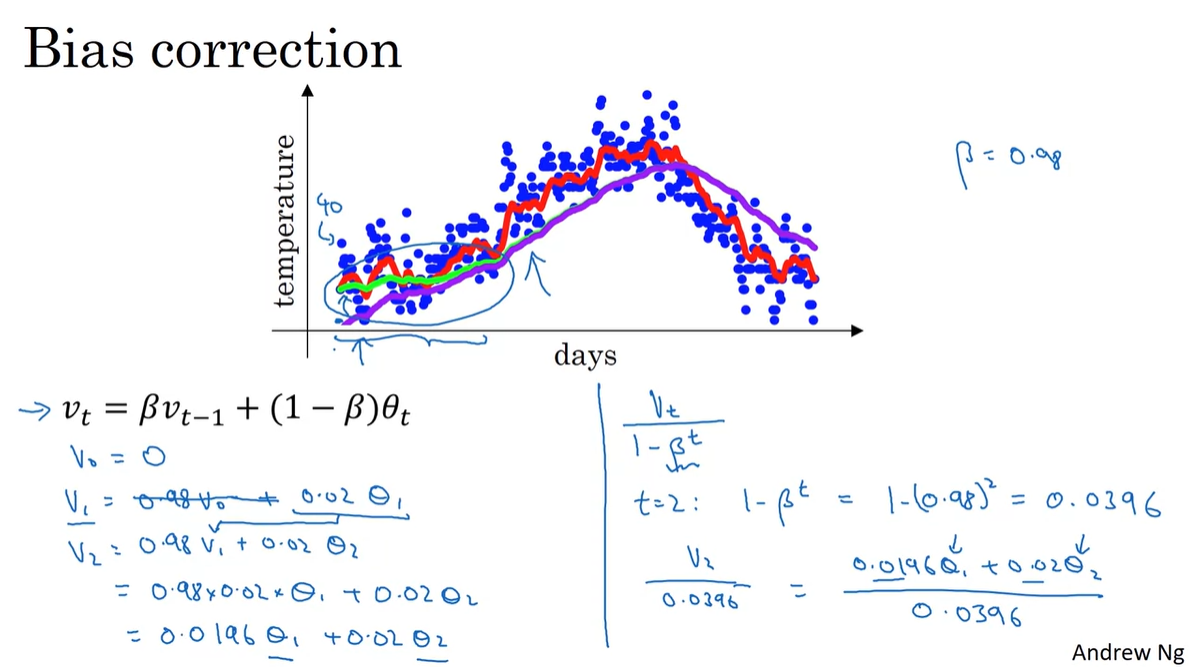
  • $v_0$를 0으로 설정하면 $v_1$은 결국 이전 값 없이 현재 값($\theta_1$)의 0.02만을 계산하게 된다.

  • 또한, 이렇게 계산된 $v_1$으로 $v_2$를 다시 계산한다면 이전 값($\theta_1$)의 영향력(0.0196)이 현재 값($\theta_2$)의 영향력(0.02)보다 훨씬 줄어들게 된다.

    • 이를 조정해주기 위해 $\displaystyle \frac{v_t}{1-\beta^t}$를 사용한다.

  • 예를 들어 $t=2$일 경우, $1-\beta^t$는 0.0396으로 계산되고, 이를 기존의 수식에다가 나눠주면 $0.0196/0.0396$과 $0.02/0.0396$으로 새로운 weight가 결정된다.

  • 만약 time step $t$가 더욱 커지게 되면 $\beta^t$가 0에 가까워져 해당 수식은 just $v_t$와 가까워지므로 초기값의 bias만 조정해주는 효과를 갖게 된다.

    • 아래 그래프에서 초록색 그래프가 기존 $v_t$이고, 보라색 그래프가 bias correction $\displaystyle \frac{v_t}{1-\beta^t}$를 나타낸다.

Gradient Descent with Momentum

• Gradient Descent시 아래와 같은 그림으로 학습이 이루어진다면 문제점은 "속도"가 너무 느리다는 점에 있다.

  • 우리가 원하는 바는 위 아래로 진동하는 부분이 slower되길 바라며, 좌우로 진동하는 부분은 faster하길 원한다.

    • 이를 위해 Momentum이라는 알고리즘이 등장했고, $v_{dW} = \beta v_{dW} + (1-\beta) dW$와 같은 수식의 추가로 학습이 가속화된다.

  • 물리학적으로 $v_{dW}$는 velocity를, $dW$는 accelator를, $\beta$는 fraction 값으로 취급하여 이해하는 편이 좋다.

    • 물리적으로 가속 운동을 할 때에는, 종단 속도에 도달하고자 한다면 fraction 항이 coefficient로 곱해지며 초기 속도 $v_0$와 가속도 $a$가 필요하기 때문이다.

• 일반적으로 $(1- \beta)$는 제외한 term으로 학습시키기도 한다.

  • 그러나 Andrew는 왼쪽의 정석적인 term으로 학습시키는 편을 추천하였다.

  • 또한, $\beta = 0.9$로 설정하였을 때 학습이 잘된다고 알려져 있다.

    • 이는 평균적으로 10 days 전의 value를 weighted average 취해주는 것이며, 이와 같은 방법으로 학습시키면 더욱 빠르고 정확한 학습이 가능하다고 한다.
      (Exponentially Weighted Average 참고)

RMSprop

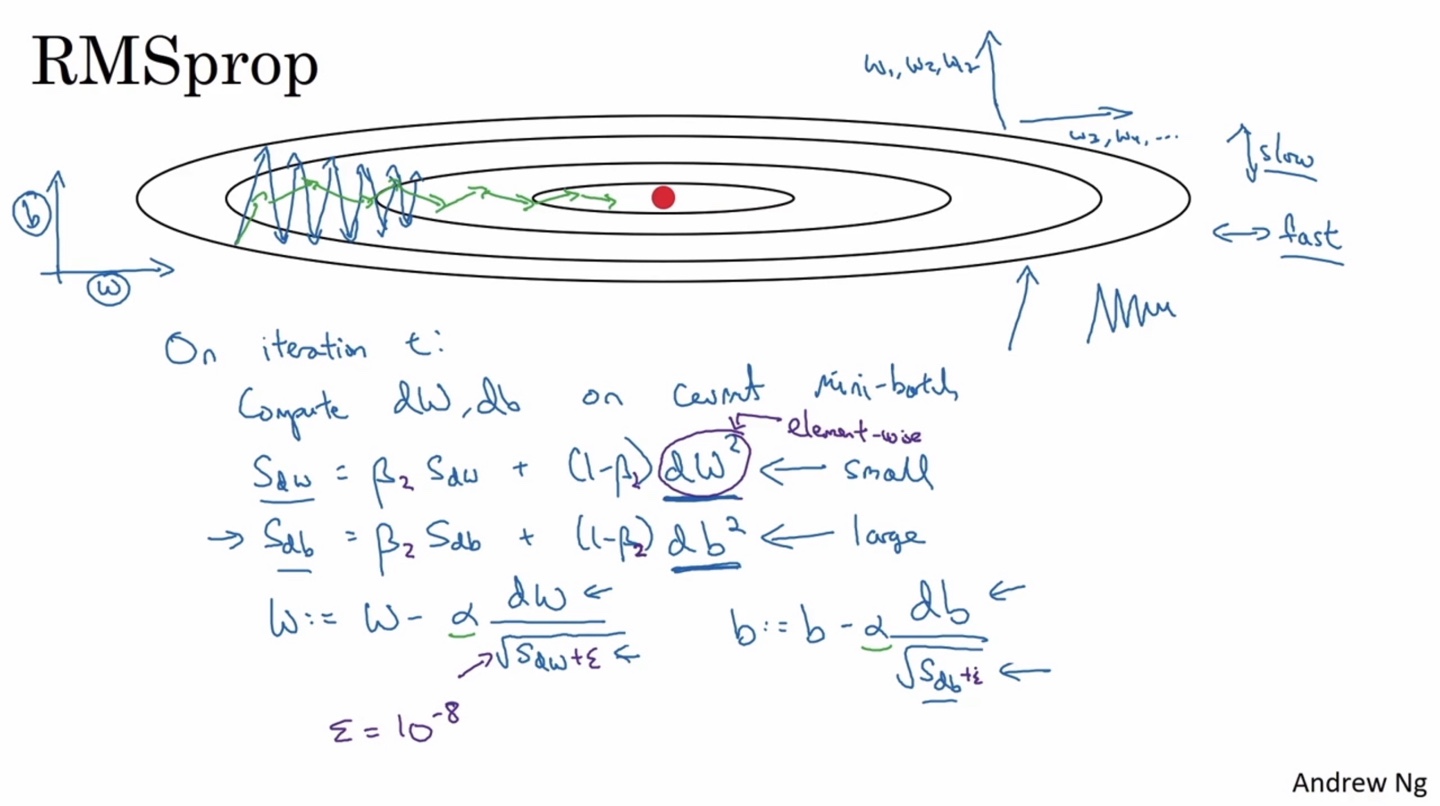
• 아직까지는 위 아래로 크게 진동하는 parameter의 수렴 속도는 느린 반면, 좌우로 짧게 진동하는 parameter의 수렴 속도는 빠르다는 문제점이 존재한다.

  • RMSProp은 현재의 mini-batch에 대해 다음과 같은 수식으로 gradient descent를 진행하여 위 문제를 해결하는 방법론 중 하나다.

    $S_{dW} = \beta_2 S_{dW} + (1-\beta_2) dW^2$
    $S_{db} = \beta_2 S_{db} + (1-\beta_2) db^2$

    $W := W -\alpha \displaystyle \frac{dW}{\sqrt{S_{dW} + \epsilon}}$ & $b := b -\alpha \displaystyle \frac{db}{\sqrt{S_{db} + \epsilon}}$

    • 이후에 나올 Adam 알고리즘의 Momentum term에 $\beta$가 다시 등장하기 때문에 $\beta_2$로 notation을 결정하였다.

  • 기존 Momentum 알고리즘과 비교한다면 paramerter term은 제곱 처리하고, 이전 값의 sqrt를 분모로 보내 진동의 정도(↑↓)에 반비례(↓↑)하도록 만든다.

    • 분모가 0이 되는 것을 방지하기 위해 매우 작은 숫자인 $\epsilon = 10^{-8}$을 더해 처리한다.

Adam Optimization Algorithm

• Adam 알고리즘은 Momentum과 RMSProp을 합한 방법론이다.

  • 아래와 같은 방식으로 작동하며 핵심 수식은 Momentum의 velocity term, RMSProp의 element-wise term, bias corrected, suppress oscilation term이다.

    $v_{dW} = \beta_1 v_{dW} + (1-\beta_1) dW$
    $v_{db} = \beta_1 v_{db} + (1-\beta_1) db$

    $S_{dW} = \beta_2 s_{dW} + (1-\beta_2) dW^2$
    $S_{db} = \beta_2 s_{db} + (1-\beta_2) db^2$

    $V_{dW}^{corrected} = v_{dW} / (1-\beta_1^t)$ & $S_{dW}^{corrected} = S_{dW} / (1-\beta_2^t)$
    $V_{db}^{corrected} = v_{db} / (1-\beta_1^t)$ & $S_{db}^{corrected} = S_{db} / (1-\beta_2^t)$

    $W := W -\alpha \displaystyle \frac{V_{dW}^{corrected}}{\sqrt{S_{dW} + \epsilon}}$ & $b := b -\alpha \displaystyle \frac{V_{db}^{corrected}}{\sqrt{S_{db} + \epsilon}}$

• 일반적으로 $\alpha$는 tuning 대상이며 $\beta_1$은 $0.9$, $\beta_2$는 $0.999$, $\epsilon$은 $10^{-8}$의 값을 갖는다.

  $\alpha$: need to be tune
  $\beta_1$: $0.9$
  $\beta_2$: $0.999$
  $\epsilon$: $10^{-8}$

  • Adam의 뜻은 Adaptive Moment Estimiation이다.

Learning Rate Decay

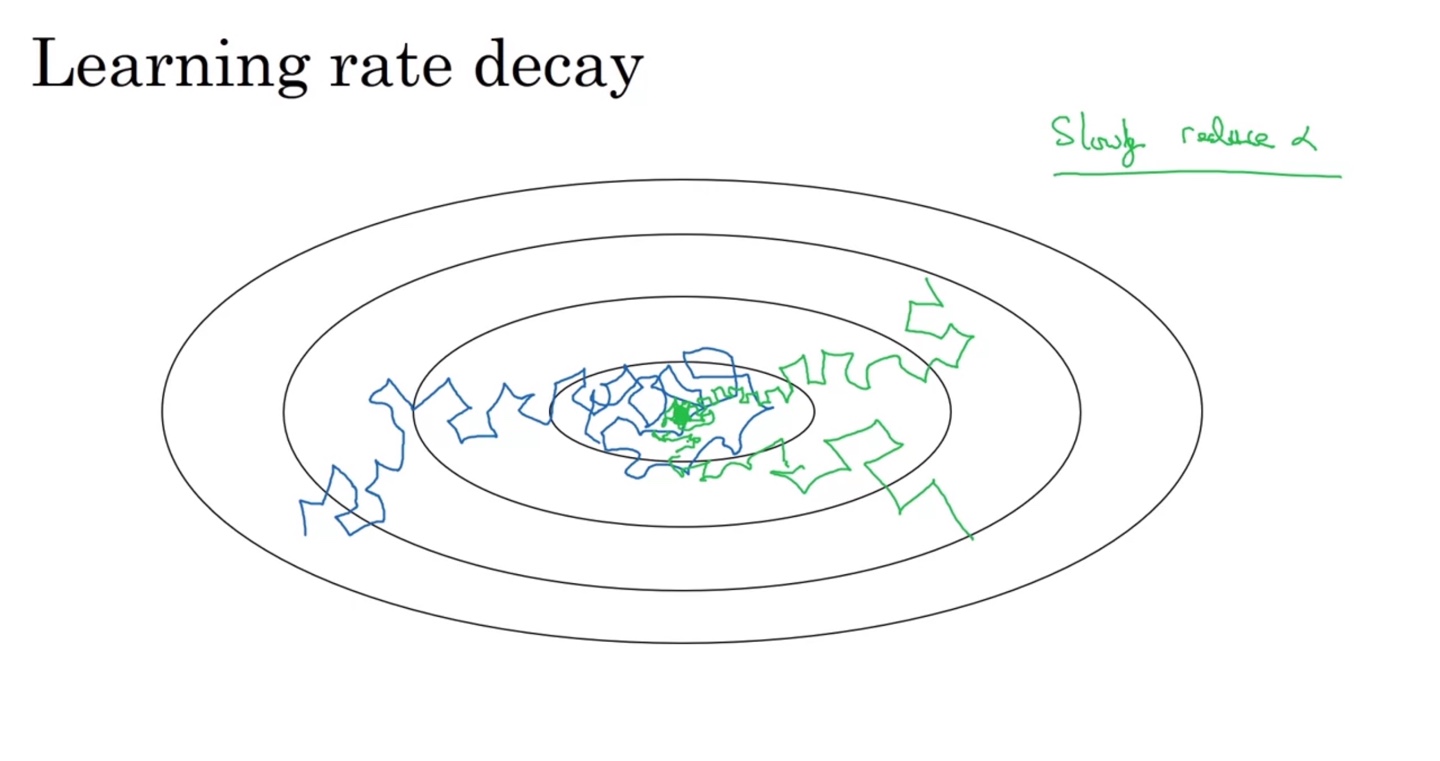
• Learning Rate는 학습이 진행될수록 decay되어야 큰 진동을 하지 않는다.

  • 따라서 학습이 진행되는 동안 lr이 감소하도록 만들어주는 것이 좋다.

• Epoch이 증가함에 따라 $\alpha$값이 작아지도록 만들려면 분모 term에 추가하는 편이 좋다.

  • 이렇게 hyperparameter를 설정해놓으면 learning rate가 점점 감소하게 되며, 학습이 진행될수록 섬세한 gradient descent가 가능해진다.

    $\alpha = \displaystyle \frac{1}{1+ decay\_rate * epoch\_num} \alpha_0$

• 그 외에도 여러 learning rate decay 방법론들이 있다.

  • Exponentially decay, $1/\sqrt{epoch\_num}$, discrete staircase 등의 방법들이 존재한다.

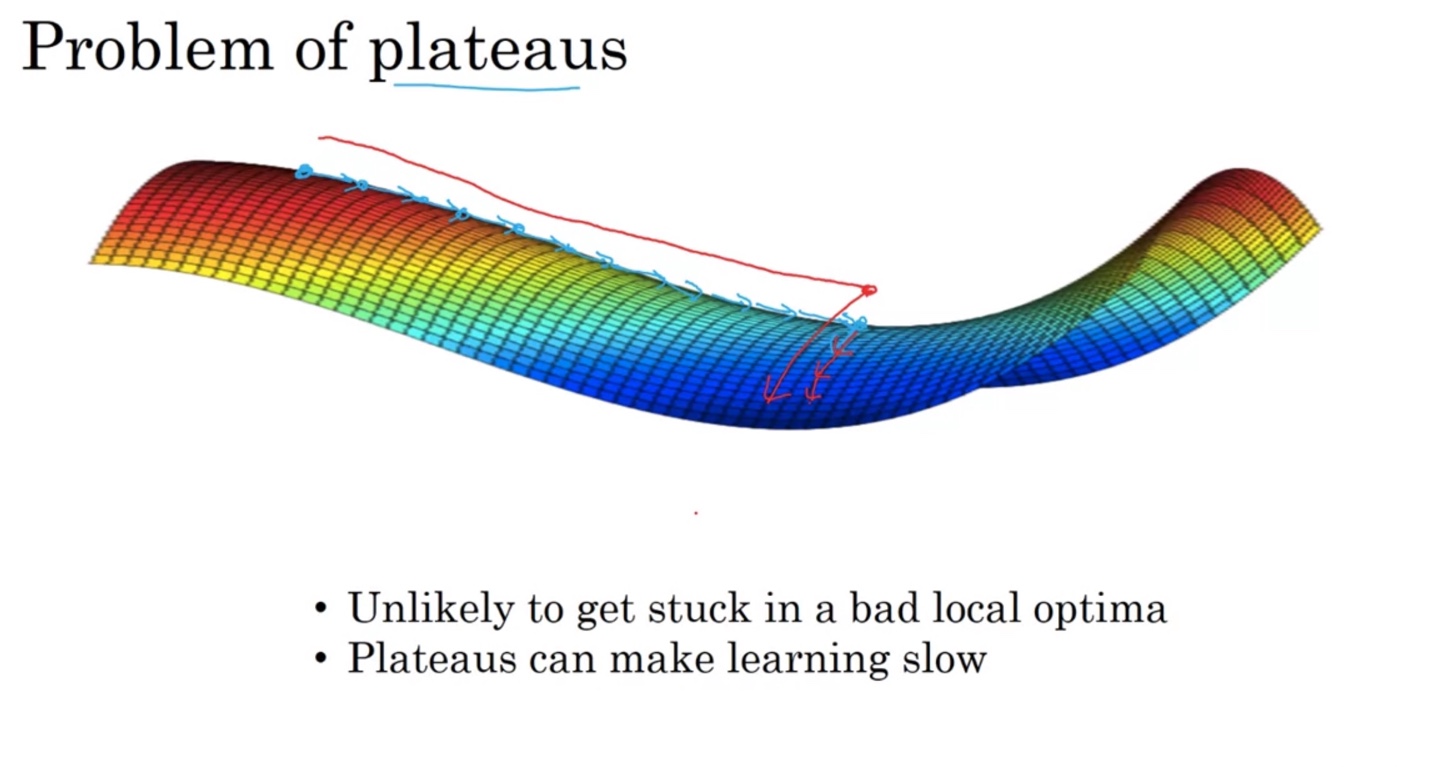
The Problem of Local Optima

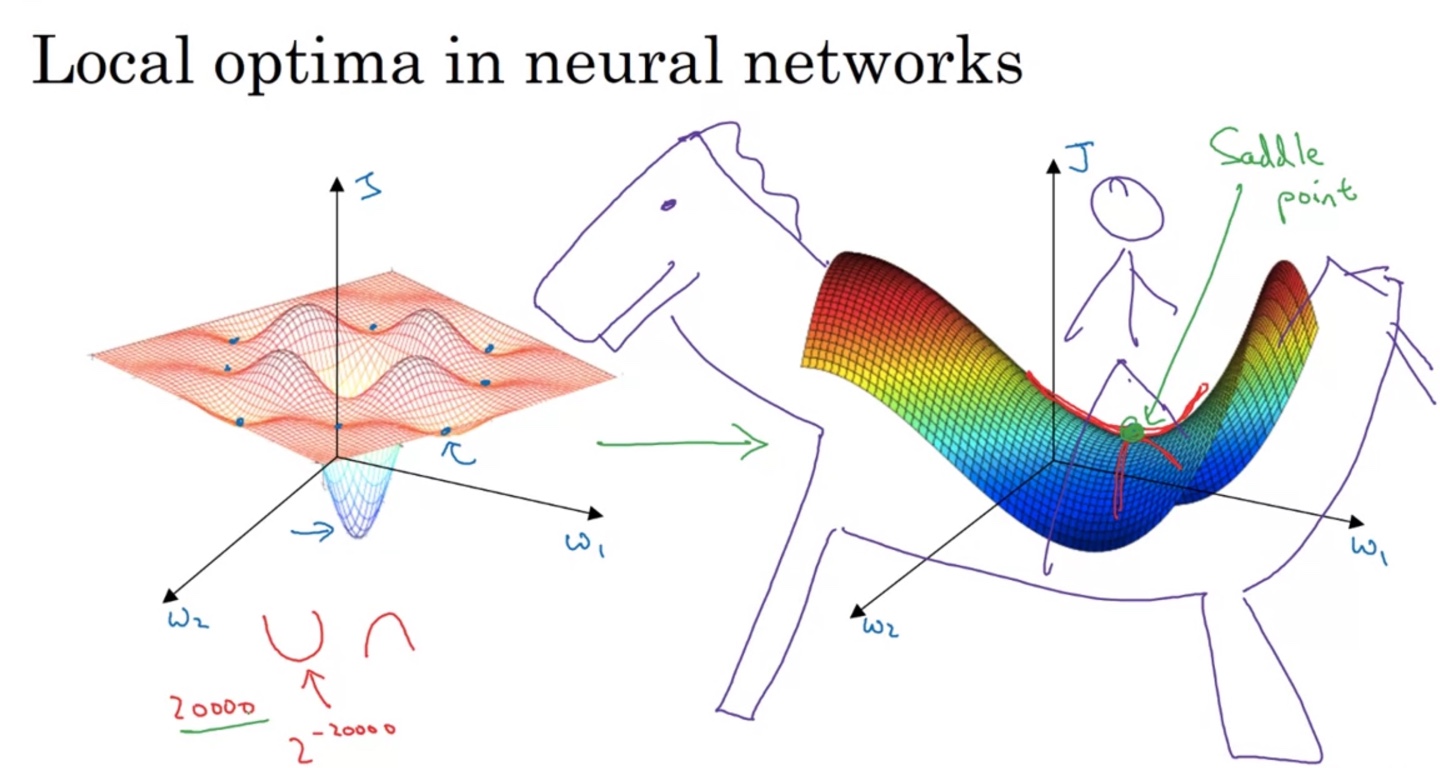
• Local Optima의 문제점은 Global Optima가 존재함에도 불구하고 학습을 멈추게 만드는 점에 있다.

  • 혹은 Saddle point라 불리우는 안장점에 parameter의 gradient descent가 더 이상 학습하지 않게 된다면 이 또한 문제가 된다.

    • 차원이 20,000개 정도 되는 공간에서는 어느 방향으로 움직여야 이 지점을 벗어날 수 있는지가 명확하지 않기 때문에 어려운 문제다.

• Loss surface가 plateaus(고원)의 형태를 띤다면 learning이 느려지기 때문에 문제가 있다.

  • Bad local optima에 갇혀(stuck)버릴 수 있는 불확실성이 존재하기 때문에, 이러한 문제가 일어날 수 있음에 주의를 기울여야 한다.

---

• 출처: [Coursera] Deep Learing Specialization