Practical Aspects of Deep Learning

Setting up your Machine Learning Application

Applied ML A highly iterative process

• 한 application이 다른 application에 곧바로 transfer 되는 것은 아니다.
• 각 분야에 맞는 things가 있고, iterative cycle을 통해 good choice를 찾게 되면 quick faster하게 만들 수 있다.

Train / Dev / Test sets

• Previous era (traditional ML)

  • train 70% / test 30% : all of them like 100-1000-10000
  • train 60% / dev 20% / test 20%

• Big data (in DL) : 1000000

  • train 98% / dev 1% / test 1% : 1% is 100000
  • train 99.5% / dev 0.4% / test 0.1% ← even more than 1 million data

Mismatched train/test distribution

• Mismatched distribution 상황

  • 만약 training set이 webpage에서 가져온 cat pictures고, dev/test set이 유저들이 app을 활용하며 올린 cat pictures라면,

    Dev와 Test set은 반드시 같은 distribution을 따라야 한다!

• 보통 "test" set이라 불렸던 set은 dev가 더 올바른 표현일 수 있으므로 dev라 칭하고자 한다.

Bias and Variance

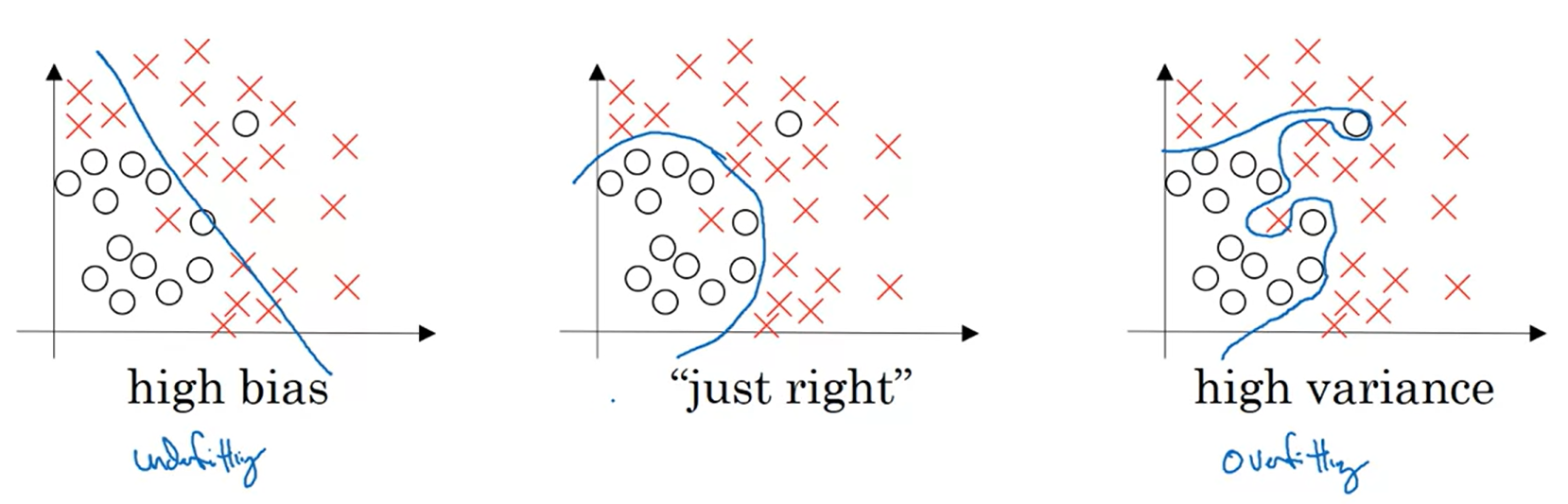
• 아래 그림과 같이 왼쪽처럼 모델이 너무 단순해서 분류 성능이 좋지 않으면 underfitting, 오른쪽처럼 너무 복잡해서 좋지 않으면 overfitting이라 한다.

  • 가운데와 같이 적절한 지점을 찾아 분류하는 모델을 학습시키는 것이 중요하다!

  

• 예를 들어, Cat classification을 수행한다고 하자.

  

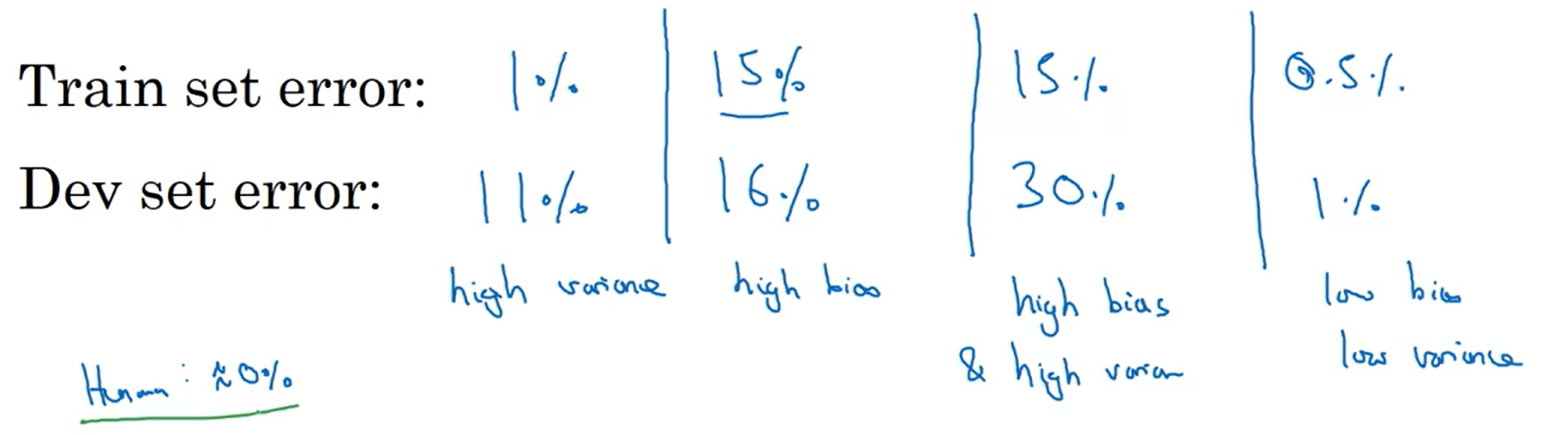
  • Human level performance가 0%일 때,

    • Train / Dev error가 1% / 11%일 경우 : high variance ← "overfitting"
    • Train / Dev error가 15% / 16%일 경우 : high bias ← "underfitting"
    • Train / Dev error가 15% / 30%일 경우 : high bias & high variance
    • Train / Dev error가 0.5% / 1%일 경우 : low bias & low variance

  • 정리해 보면

    • 첫 번째 상황은 overfitting, 두 번째 상황은 underfitting이다.
    • 맨 마지막 상황이 가장 best인 상황에 해당한다.
    • Variance가 높으면 Train 성능을 Dev(/Test) 성능이 따라가지 못한다는 뜻이고, Bias가 높으면 Train과 Dev(/Test) 모두 성능이 저평가되었다는 것을 뜻한다.

  • 만약, Human level performance가 15%일 때는

    • 기존 high bias라 판단했던 두 번째 상황이 좀 더 fit한 결과라고 봐도 무방하다.
    • Blurry image가 껴있는 상황에서 Optimal (Bayes) error를 측정했을 때 이와 같은 상황이 벌어질 수 있다.
    • 즉, 각 상황과 task에 맞는 performance를 잘 보고 판단하는 것이 중요하다.

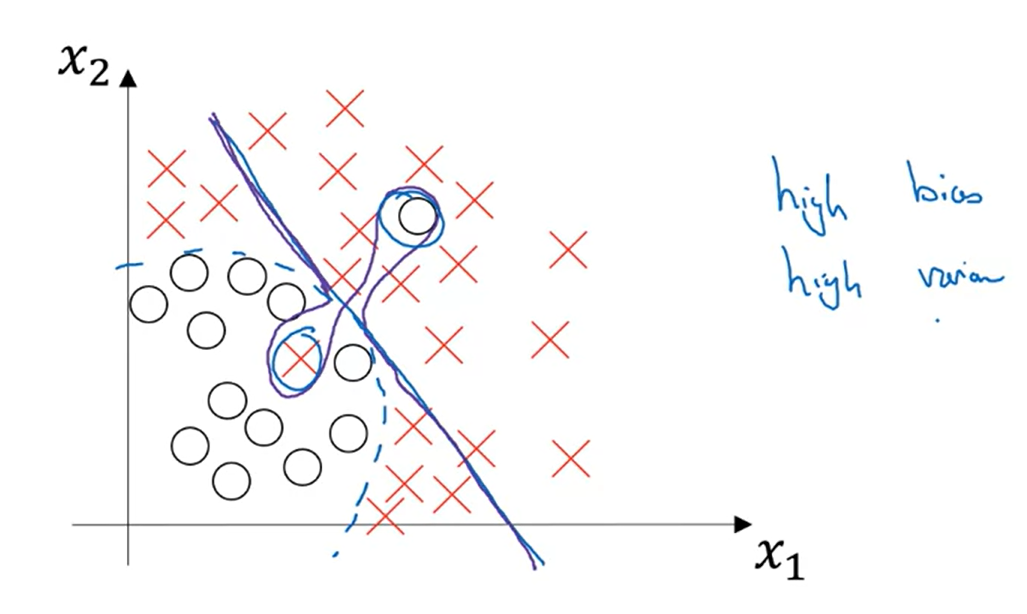
• High bias and high variance 상황은 어떤 것인지 보자.

  

  • 위 그림에서 보라색으로 표시된 부분이 high bias & high variance 상황이다.

  • 파란색으로 표시된 직선 분류기가 underfitting 상황이고, 보라색이 overfitting이다.

  • 즉, 훨씬 더 복잡한 curve function을 이루고 있고 특정 outlier들을 너무 많이 고려하는 유연성을 가지고 있다면 이런 문제가 발생할 수 있다.

  • 특히나 차원이 많아질수록 이 현상은 문제를 크게 만들 수 있으므로 주의하도록 하자!

Basic Recipe for Machine Learning

• Underfitting : What if? High bias? (training data performance)
  • Bigger network : layers ⇑
  • Train longer (NN architecture search) : epoches ⇑

↓ N (repeat)

• Overfitting : What if? High variance? (dev set performance)
  • More data
  • Regularization (NN architecture search) ← after next video

↓ N

• Done

---

• "Bias(↑↓) Variance(↓↑) trade off" : 서로 상반되는 영향을 끼친다!

• 'Bigger network' and 'More data' solved by appearing Deep learning

Regularizing your Neural Network

Regularization

• 일반적인 Logistic regresstion의 Cost function에서 더해지는

  • $\displaystyle \frac{\lambda}{2m} ||w||_2^{2}$ ← 이 항을 말한다.

• L2 norm으로 수식이 정리되기 때문에 L2 regularzation이라 하며,

  • L1 norm을 적용한 L1 regularization도 있다.

• $b$ parameter에 대하여 정규화 식을 적용할 수도 있지만 이는 생략한다.

  • $\lambda$는 일종의 parameter로서 $||W||_2^2$ norm의 scale을 조정한다.
  • $\lambda$를 프로그래밍 언어(python)으로 작성할 때 lambd로 쓰겠다.
    • 기존에 lambda라는 내장 함수가 존재하기 때문이다.

• Neural network 내에서는 layer들이 쌓여있기 때문에 notation이 다음과 같다.

  • $||W^{[l]}||_F^2 = \displaystyle \sum_{j=1}^{n^{[l-1]}} \sum_{i=1}^{n^{[l]}} (W_{ij}^{[l]})^2$ 참고로 아래 그림에 나와있는 것을 수정했다.

    • W의 shape은 $(n^{[l]}, n^{[l-1]})$, current layer $n^{[l]}$, previous layer $n^{[l-1]}$

  • 우리가 2 norm이라 부르는 것들은 관행적으로 Frobenius norm이라 한다.

• Regularization을 적용한 수식은 derivative될 때 $\displaystyle \frac{\lambda}{m} W^{[l]}$로 정리된다.

  • Gradient descent 시 $\partial W^{[l]}$ 이 항에 넣어주면 되며, 이를 정리하면 Regularization이 Weight decay의 역할을 한다는 것을 알게 된다.
  • Update 이후 $W$ 항의 변화가 $(1-\displaystyle \frac{\alpha \lambda}{m})W^{[l]}$로 정리되기 때문이다!

Why Regularization Reduces Overfitting?

• 그렇다면 왜 Regularization이 Overfitting을 방지한다는 것인가?

  • 기존 Cost function에 $\displaystyle \frac{\lambda}{2m} ||w||_2^{2}$ 항을 추가하면 weight decay 효과를 낼 수 있다는 것을 알게 되었다.

    • 즉, $W$의 원소 값을 줄일수록 overfitting을 방지할 수 있다는 직관을 얻을 수 있다.

  • 만약, $\lambda$ 항의 크기가 커지면 weight 항의 원소를 0에 가깝게 만들 수 있다.

    • 이는 hidden unit의 영향을 없애는 과정과도 같아진다.
    • 결국 몇몇 layer들의 영향만 가진 작고 단순한 신경망이 완성되는 것이다.

  • $\lambda$의 값을 크게 키울수록 신경망의 크기가 작아지면서 아래 그림과 같이 underfitting의 상황으로까지 이어질 수 있다.

    • 적절한 "just rignt" $\lambda$값을 찾는다면 좋은 성능을 가진 신경망이 완성될 것이다.

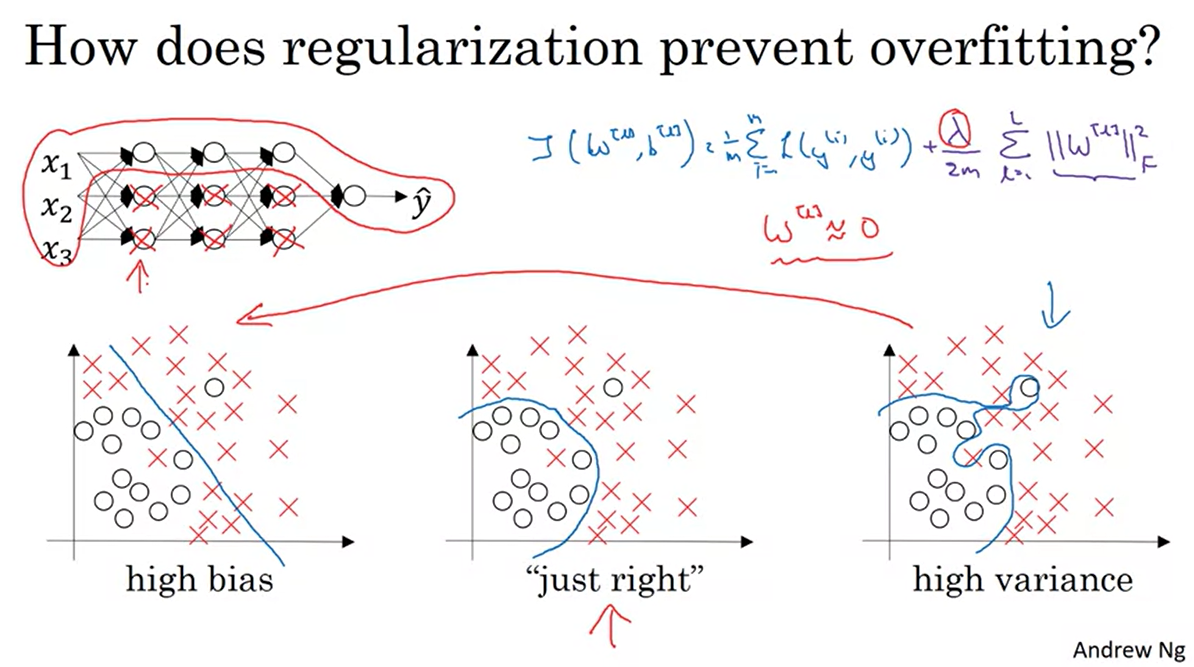
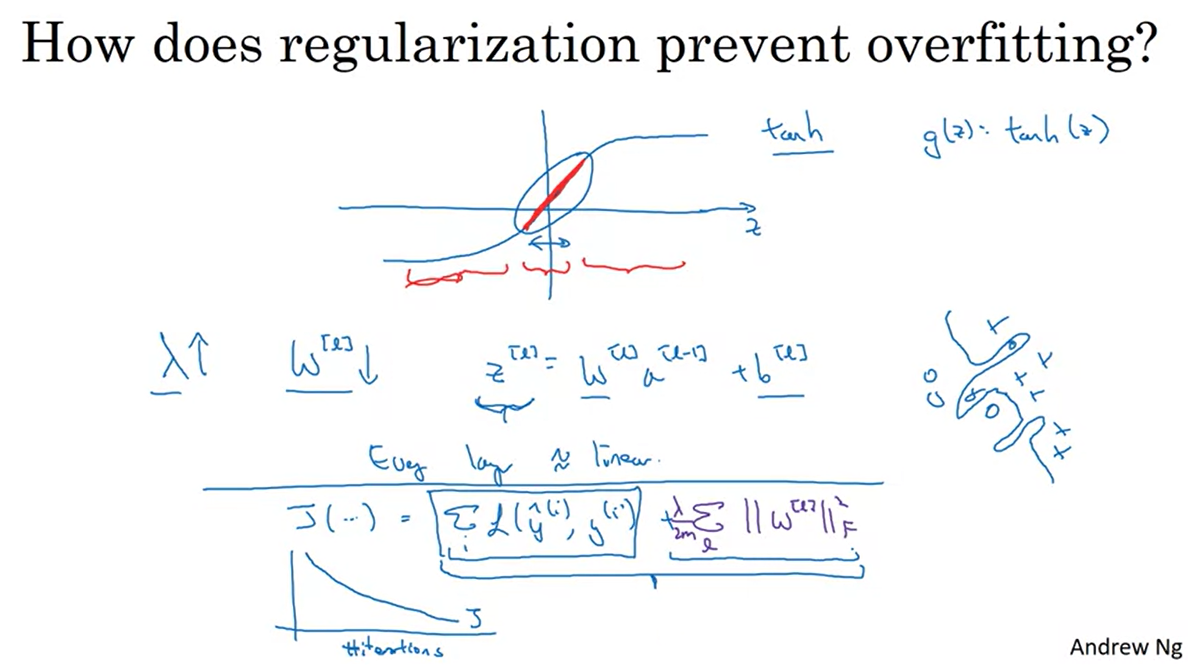
• 또 다른 예시를 살펴보자.

  • $tanh$ 함수와 같은 경우 0과 가까운 부분에서는 linear한 function 꼴을 갖지만, 그 외의 z가 너무 작거나 너무 큰 경우는 그렇지 않다.

    • Gradient 값이 미세해지면서 vanishing 문제에 빠질 수 있다.

  • $\lambda$의 크기를 키우면 weight $W$의 값도 줄어든다.

    • 모든 layer가 linear function이라면 $W$의 값이 작아질 때 $z$ 값도 작아진다.
    • 즉, z의 범위를 0에 가까운 값으로 보냄으로써 gradient update가 dynamic해질 수 있도록 만들 수 있는 것이다.

  • Debugging을 위해 plot 함수를 작성할 때에는 L2 panalty까지 추가한 Cost function을 그려야 한다.

    • 기존 Cost function만으로는 이제 단조로운 감소 함수가 만들어지지 않을 것이다.

Dropout Regularization

• Dropout이란 layer의 일부를 turn off하는 시스템이라고 이해하면 된다.

  • 0.5만큼의 prob.로 layer가 dropout된다고 가정하면, 아래 그림과 같이 4개의 layer중 2개의 layer만 남기고 forward & backward 영향력이 사라진다는 것을 뜻한다.

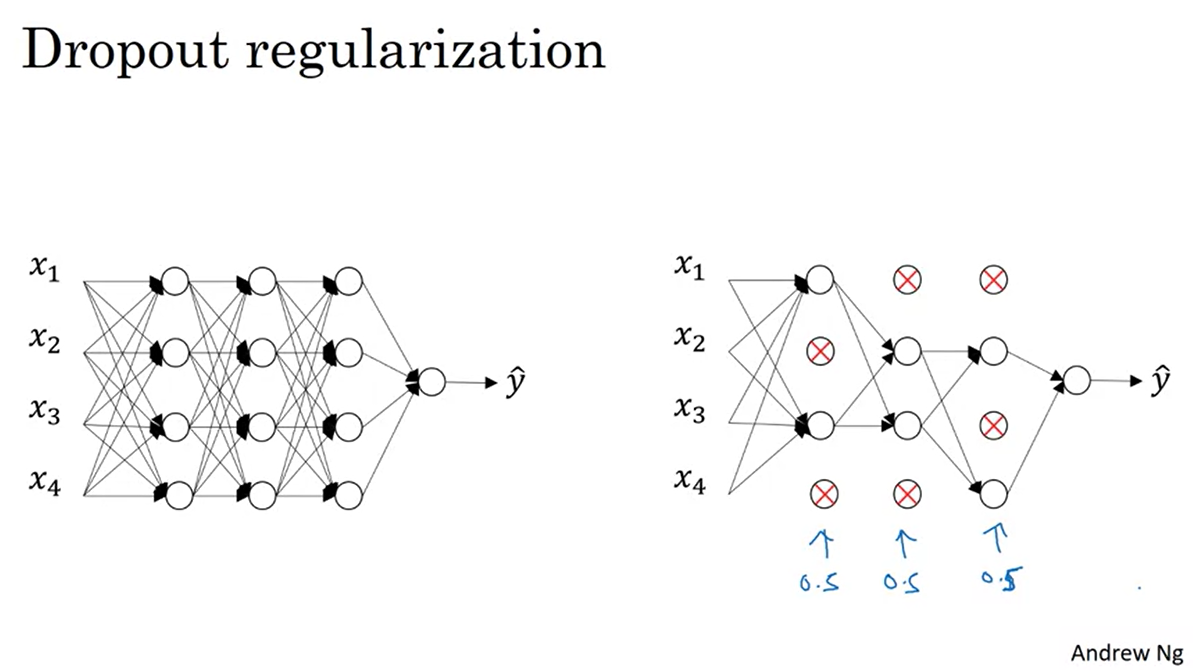
• Dropout을 코드로 구현할 때는 "Inverted dropout" 테크닉을 사용한다.

  • keep_prob 값을 0.8로 지정한다면 0.2 비율의 layer를 turn off한다는 것을 의미한다.
    • keep_prob보다 작은 값을 True로 설정하는 d3 배열을 지정하고 a3 layer와의 곱으로 0.8 비율의 layer만 남긴다.
    • 이 때, keep_prob으로 최종 결과값을 나눠주는 이유는 최종 layer a3의 실제 수치가 20%만큼 떨어졌다고 할 때, 정규화를 시켜주는 방법은 0.8을 나눠주는 것이기 때문이다.

• 만약 dropout이 없다면 layer가 깊게 쌓일 때 수치가 exploding하거나 vanishing하게 될 위험성이 있다.

  • 따라서 weight 수치를 안정화 시키기 위한 technique 중에 하나로 쓰인다.

Understanding Dropout

• 그렇다면 어째서 Dropout이 효과가 있는 것일까?

  • 직관적으로 말하자면, dropout은 gradient에 L2 panalty를 주는 것과 비슷한 효과를 가진다.
  • 몇몇 layer의 영향력을 꺼버림으로 인해 weights shrinking이 일어난다고 볼 수 있으며, Weights decay(L2) $\approx$ Shrink weights(Dropout)이기 때문이다.

• Dropout은 Computer Vision task에 매우 효과적이다.

  • 데이터의 수치값이 매우 많기 때문이며, 몇개의 layer를 꺼버림으로 인해서 여러 features의 영향력으로 분산시켜줄 수 있다는 장점이 있다.

• 또한, Dropout을 적용한 순간부터는 Cost function의 수치가 단조로울 수 없기 때문에 디버깅을 위해서라면 dropout을 끄고 plot하는게 좋다.

  • 이 때에는 keep_prob의 값을 1로 놓고 plot하면 된다.

Other Regularization Methods

• 지금까지 했던 모든 것들은 Overfitting을 방지하는 것이었다.

  • Data augmentation 기법 또한 데이터 수집 비용을 줄이고, 효과적으로 training할 수 있는 기법 중에 하나로 손꼽힌다.

    • 크게 Flip, Rotation, Shearing 기법들이 있다.

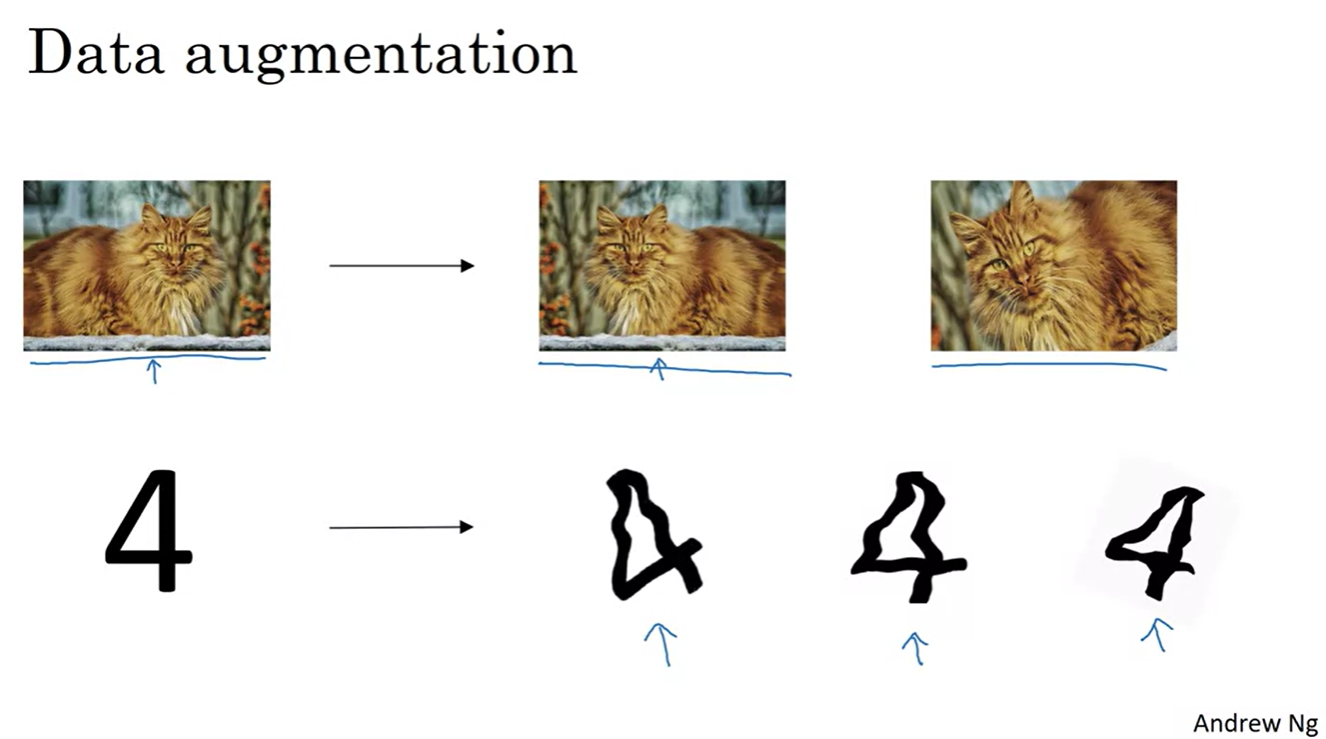
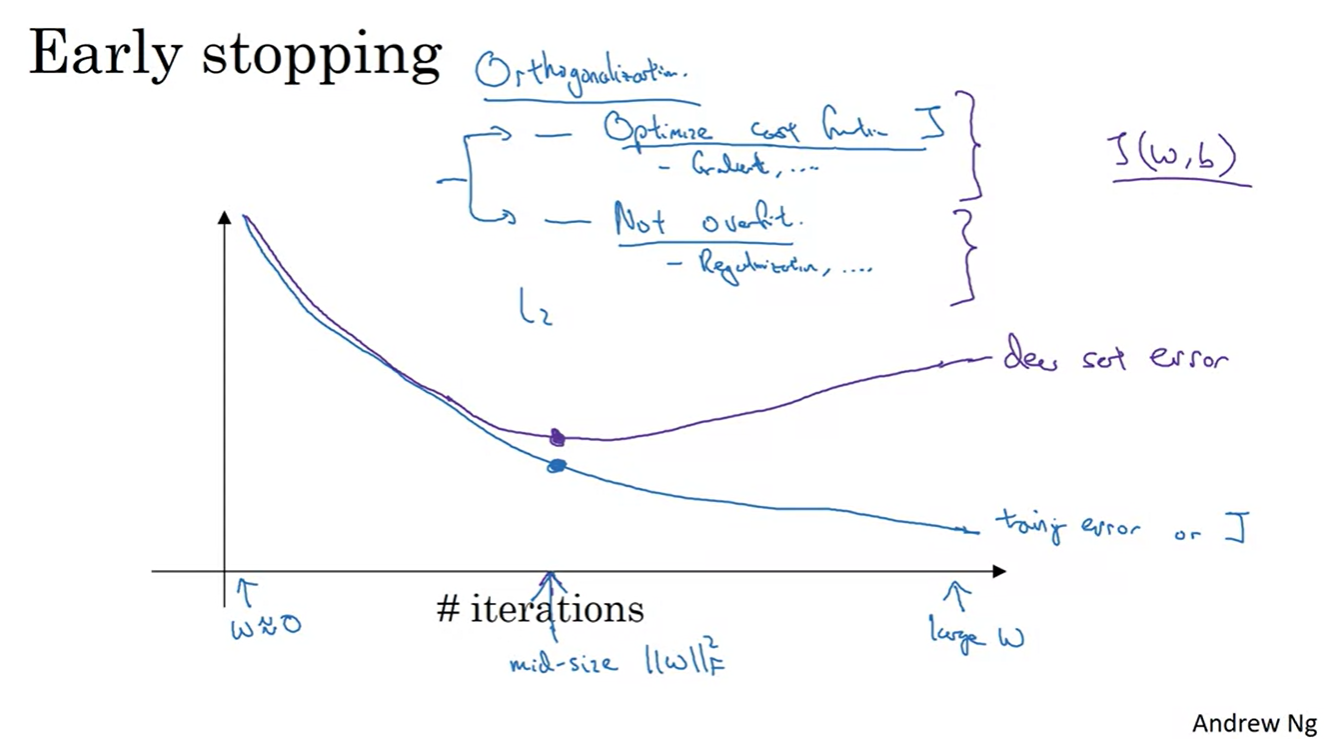
• Early stopping 기법 또한 Overfitting을 막는 방법 중에 하나다.

  • 만약 training error와 dev set error가 어느 순간을 기점으로 크게 차이가 나기 시작할 때, 훈련을 일찌감치 stop하는 기법이다.

    • 예를 들어, error의 원인이 weight가 계속 커지기 때문이라면 적당한 mid-size $W$일 때 훈련을 멈추는 것이다.

  • 그리고 Early stopping은 L2 norm panalty 기법에 비해서 계산 효율적인 방법론이라 할 수 있다.

    • 특별한 계산 없이 적당한 시점에 훈련을 멈춰주기만 하면 되기 때문이다.

• 우리가 지금까지 보았던 훈련 기법들은 크게 두 가지로 나눠볼 수 있었다.

  1. Cost function $J$를 optimizing하는 기법: Gradient descent, ...
  2. Overfitting을 방지하는 기법: Regularization, L2 norm...

• Andrew는 위의 두 가지 방법론이 Orthogonal한 성질을 가지고 있다고 했다.

  • 둘 중 하나만 고려해서 문제를 해결할 것이 아니라, 두 가지 영향력을 모두 고려했을 때 최적의 solution을 찾아낼 수 있다는 의미로 받아들이면 된다.

Setting Up your Optimization Problem

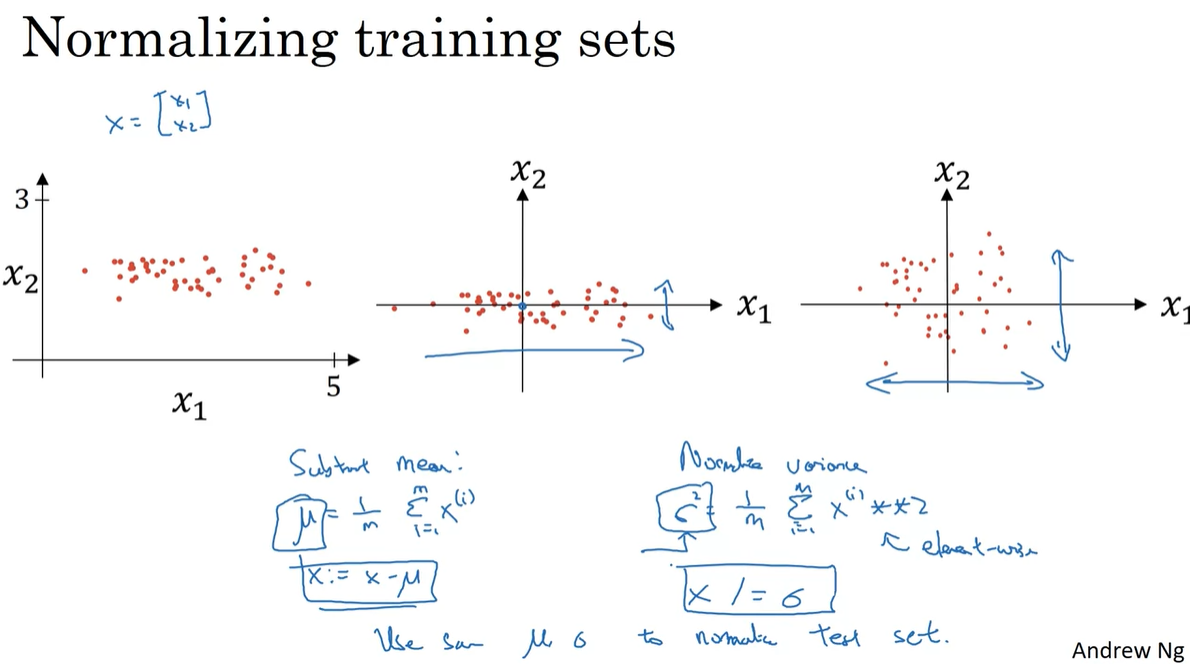
Normalizing Inputs

• Training data가 $X= \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix}$로 주어진 상황을 가정해보자.

  • Vector $X$의 mean $\mu$를 구하여 $X := X-\mu$로 업데이트 하자.

    • $\mu = \displaystyle \frac{1}{m} \sum_{i=1}^{m} x^{(i)}$

  • 이제 Variance $\sigma$를 구하여 $X /= \sigma$로 업데이트 한 결과가 맨 오른쪽 plot과 같다.

    • $\sigma^2 = \displaystyle \frac{1}{m} \sum_{i=1}^{m} x^{(i)} ** 2$ ← $x^{(i)} = orig \; x^{(i)} - \mu$

  • 이러한 과정을 Normalizing이라 한다.

    • 최종 plotting 결과, 데이터 분포가 중심에 많이 모이게 되었음을 알 수 있다.

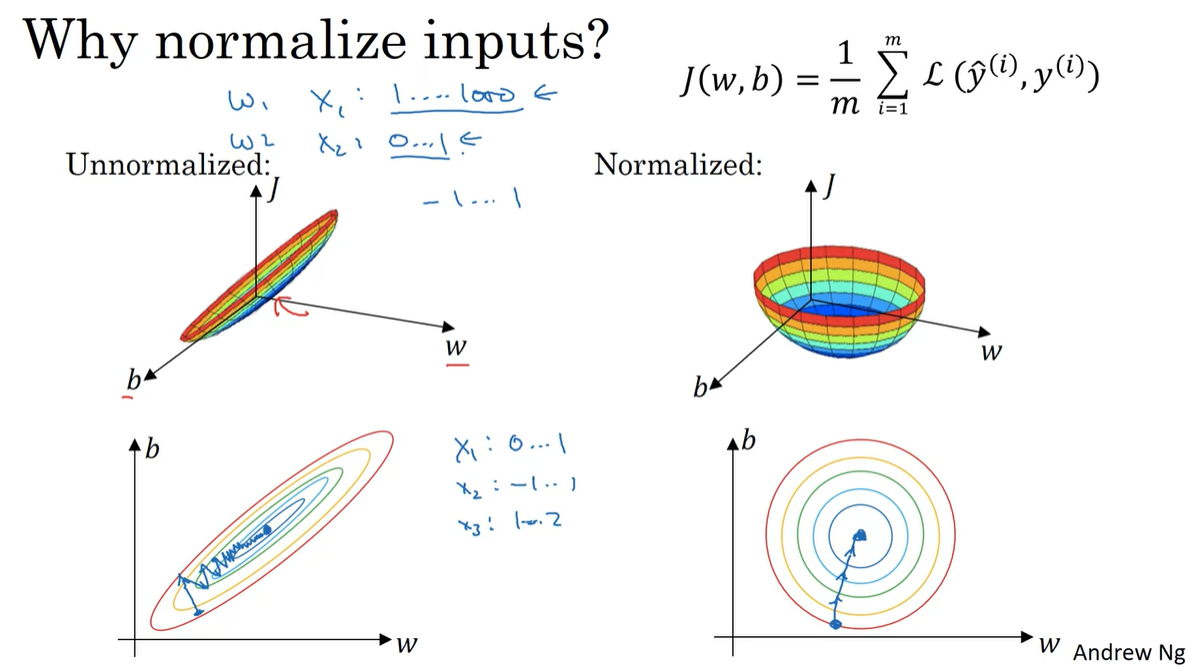
• 그렇다면 Normalizing은 왜 필요한 것일까?

  • Unnormalizing 상황에서의 cost function 그래프를 살펴보면 ex. $x_1=1 ... 1000$과 $x_2=0 ... 1$ 값의 분포 차이가 큰 이유로 weight $w$와 $b$ 분포가 다소 치우칠 수 있다.

  • 이러한 input을 Normalizing하면 Symmetric한 cost function을 얻을 수 있고, Unnormalizing 상황에 비해 bouncing하지 않는 매끄러운 학습이 이어진다.

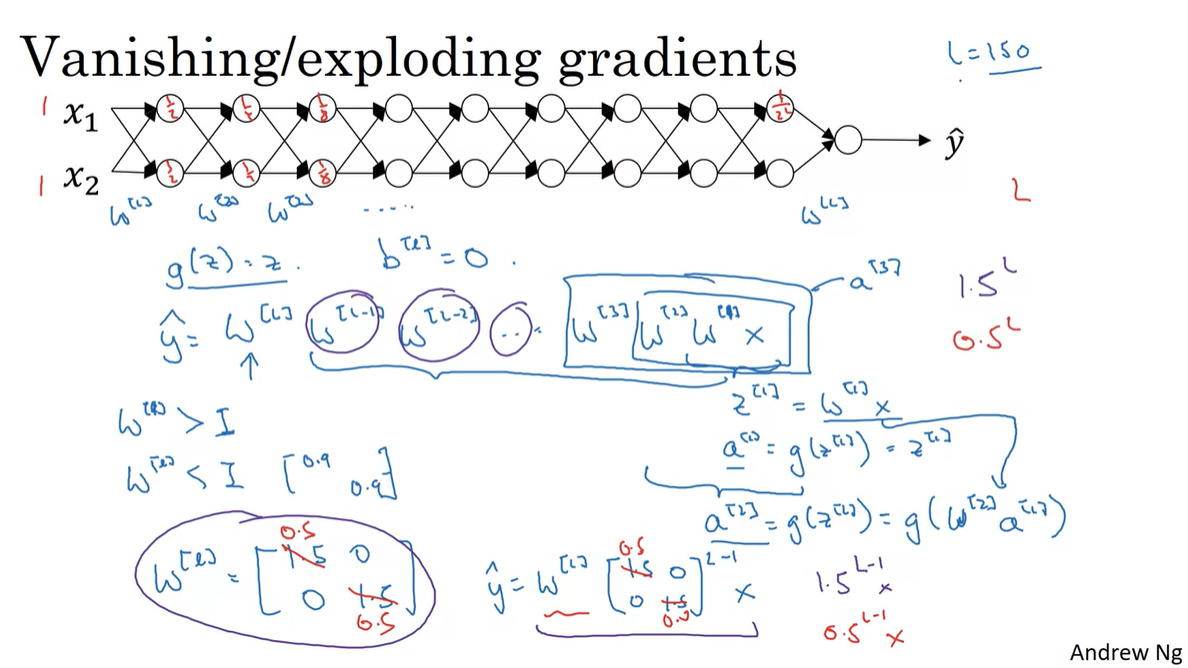
Vanishing / Exploding Gradients

• 만약 아래와 같은 deep layer로 쌓인 neural network가 존재한다고 해보자.

  • 추론값 $\hat{y}$은 weights $W$s와 input data $X$의 연쇄적인 곱으로 계산된다.

    • $\hat{y} = W^{[L]}W^{[L-1]} ... W^{[2]}W^{[1]}X$

  • 한 층마다 $W$가 곱해지고 나면, $Z = WX$는 activation function에 의해 $a = g(Z)$로 계산이 이어진다.

    • $W$의 한 value가 전부 $1.5$이거나 $0.5$일 때 $L=150$개라고 가정한다면, $1.5^{[L-1]}$나 $0.5^{[L-1]}$의 값은 매우 크거나 매우 작은 값을 갖게 된다.

    • Layer를 깊게 쌓으면 이러한 연산이 늘어나기 때문에, weight $W$의 원소가 1보다 클 때와 작을 때 모두 Exploding/Vanishing 문제를 일으킬 수 있다.

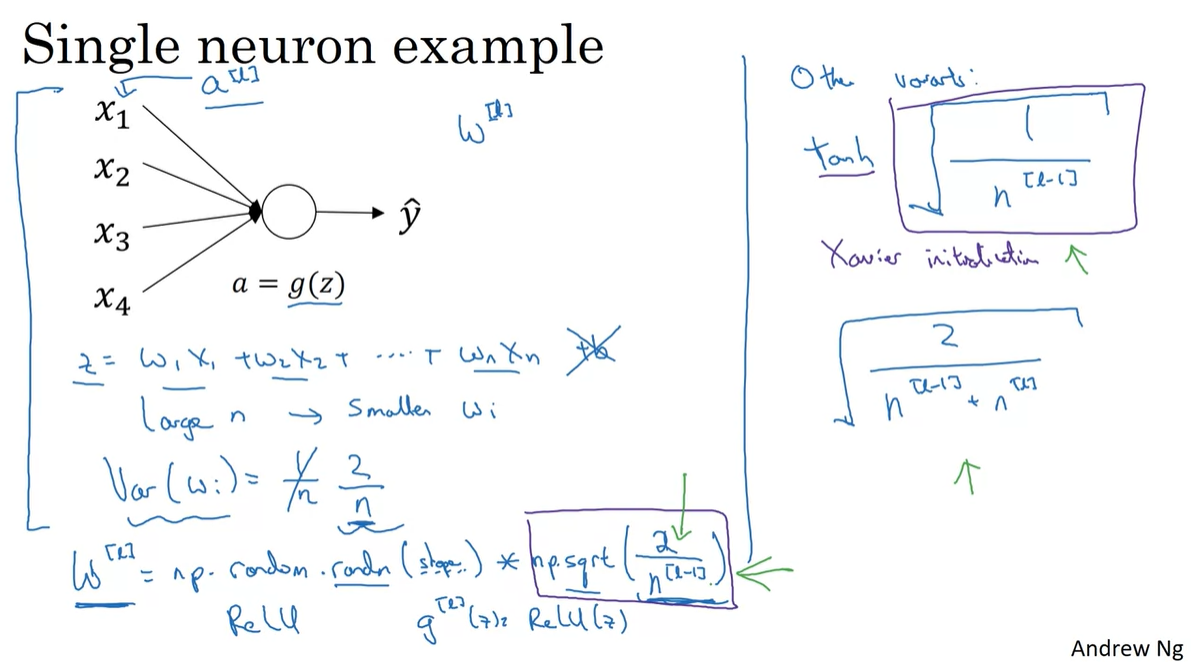
Weight Initialization for Deep Networks

• 한 layer를 통과하는 $z$값은 linear transform으로 엮인 $w_i x_i$의 합으로 정의된다.

  $z = w_1 x_1 + w_2 x_2 + ... + w_n x_n$

  • 만약 layer 개수 $n$이 늘어날 수록 $z$값은 커지기 때문에 $w$는 작은 value일수록 좋다.

    • 따라서 $w$의 분산을 $Var (w) = \displaystyle \frac{1}{n}$로 맞춰주는 initialize 방법을 주로 사용한다.

  • 코드로는 $W^{[l]} = np.random.randn(shape) * np.sqrt(\displaystyle \frac{1}{n^{[l-1]}})$을 사용한다.

    • Activation이 ReLU일 경우 $\displaystyle \frac{1}{n}$보다 $\displaystyle \frac{2}{n}$가 더 유효하다는 검증에 의해, $\displaystyle \sqrt{\frac{2}{n}}$를 대부분 사용한다.

    • Activation이 $tanh$라면 $\displaystyle \sqrt{\frac{1}{n^{[l-1]}}}$를 보라색 박스에 교체시켜 사용한다.

      ← Xavier initialization

    • Bengio 교수님과 그의 제자들이 쓴 논문에 의해 ReLU activation에서 $\displaystyle \sqrt{\frac{2}{n^{[l-1]} + n^{[l]}}}$가 곱해진 값이 더 유용하다고 검증한 바 있다.

      ← He initialization

Numerical Approximation of Gradients

• Gradient를 numerical하게 approximation하는 방법에 대해 소개한다.

  • 우리는 매우 작은 범위 내에 있는 $\epsilon$을 원래의 $\theta$에 $\pm$하여, { y축 값의 차이 / x축 값의 차이 }를 gradient라 정의한다.

  • Parameter Optimizing을 통해 계산한 $d\theta$와 numerical derivative로 계산한 $d\theta_{approx}$가 같아지는지 확인하기 위한 debugging 과정에 이러한 기법을 사용할 것이다.

  • $f'(\theta)$를 $\lim_{\epsilon \to 0} \displaystyle \frac{f(\theta + \epsilon) - f(\theta - \epsilon)}{2 \epsilon}$로 설정하면 $O(\epsilon^2)$의 compute 연산이

    들어가기 때문에 $\lim_{\epsilon \to 0} \displaystyle \frac{f(\theta + \epsilon) - f(\theta)}{\epsilon}$으로 계산하여 $O(\epsilon)$의 복잡도로 해결한다.

Gradient Checking

• Gradient Checking을 하기 위해서는 다양한 parameters를 $\theta$와 $d \theta$로 통합하는 과정이 필요하다.

  • ex. $W^{[1]}, b^{[1]}, ...$와 $dW^{[1]}, db^{[1]}, ...$를 하나의 큰 vector로 만들기 위해 concaternate한다.

• 각 항들(i)에 대해서 $10^{-7}$ 정도의 $\epsilon$값을 설정하여, Cost function의 gradient를 계산한 $d\theta_{approx}$를 구한다.

  • 이 값이 $d\theta$와 얼마나 차이가 있는지 알아보기 위해 $\displaystyle \frac{\begin{Vmatrix} d \theta_{approx} - d \theta \end{Vmatrix}_2}{\begin{Vmatrix} d \theta_{approx}\end{Vmatrix}_2 + \begin{Vmatrix} d \theta \end{Vmatrix}_2}$를 계산한다.

    • 만약 이 차이가 $10^{-7}$ 정도를 만족한다면 great, $10^{-3}$이면 worry라고 판단하도록 하여 gradient 계산이 잘 이루어지고 있는지 debugging하면 된다.

Gradient Checking Implementation Notes

• Gradient Checking 시 주의해야 할 점이 몇 가지 존재한다.

  • Training 시에 사용하지 말고 debugging 시에만 사용한다.

  • 만약 grad check 시 실패하였다고 뜬다면, bug를 찾아내기 위해 직접 $d \theta_{approx}[i]$와 $d \theta[i]$를 비교해보라.

  • Cost function에 Regularization 하는 것 또한 잊지 말아야 한다. ← $\lambda/2m$ ~ ...

  • Dropout과 함께 작업하지 말아야 한다. ← keep_prob을 1.0으로 설정한다.

  • Random initialization을 반복하며 training을 지속적으로 시도해보자.

Assignment

W1A1

Initialization

• Model differed by initialization

  • Zeros
  • Random
  • He

def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):
    """
    Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
    
    Arguments:
    X -- input data, of shape (2, number of examples)
    Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples)
    learning_rate -- learning rate for gradient descent 
    num_iterations -- number of iterations to run gradient descent
    print_cost -- if True, print the cost every 1000 iterations
    initialization -- flag to choose which initialization to use ("zeros","random" or "he")
    
    Returns:
    parameters -- parameters learnt by the model
    """
        
    grads = {}
    costs = [] # to keep track of the loss
    m = X.shape[1] # number of examples
    layers_dims = [X.shape[0], 10, 5, 1]
    
    # Initialize parameters dictionary.
    if initialization == "zeros":
        parameters = initialize_parameters_zeros(layers_dims)
    elif initialization == "random":
        parameters = initialize_parameters_random(layers_dims)
    elif initialization == "he":
        parameters = initialize_parameters_he(layers_dims)

    # Loop (gradient descent)
    for i in range(num_iterations):

        # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
        a3, cache = forward_propagation(X, parameters)
        
        # Loss
        cost = compute_loss(a3, Y)

        # Backward propagation.
        grads = backward_propagation(X, Y, cache)
        
        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)
        
        # Print the loss every 1000 iterations
        if print_cost and i % 1000 == 0:
            print("Cost after iteration {}: {}".format(i, cost))
            costs.append(cost)
            
    # plot the loss
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters

• Zero initialization

def initialize_parameters_zeros(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    parameters = {}
    L = len(layers_dims)            # number of layers in the network
    
    for l in range(1, L):
        parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1])) * 0.01  # 1-0
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

>>> W1 = [[0. 0. 0.]
		  [0. 0. 0.]]
	b1 = [[0.]
		  [0.]]
	W2 = [[0. 0.]]
	b2 = [[0.]]

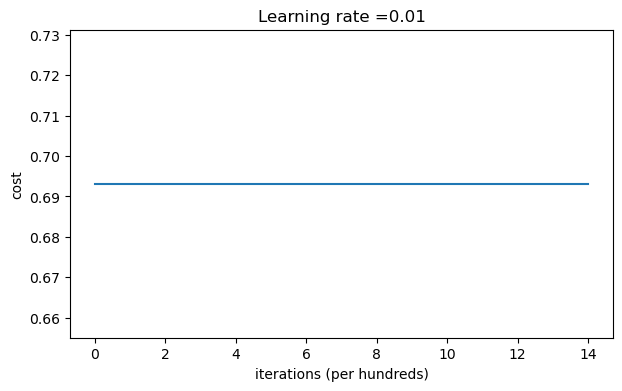
• 사실상 아주 작게 진동하는 그래프다.

  • Loss가 계속해서 0.6931.. 값을 나타내는 이유는 0 weights에 의해 $z=0$을 만들어버린 후, $a$가 계속적으로 0.5를 만족하기 때문에 생긴 결과다.

    • $a = ReLU(z) = max(0, z) = 0$

    • $\sigma(z) = \frac{1}{ 1 + e^{-(z)}} = \frac{1}{2} = y_{pred}$

    $\mathcal{L}(a, y) = - y \ln(y_{pred}) - (1-y) \ln(1-y_{pred})$

    • $\mathcal{L}(0, 1) = - (1) \ln(\frac{1}{2}) = 0.6931471805599453$

    • $\mathcal{L}(0, 0) = - (1) \ln(\frac{1}{2}) = 0.6931471805599453$

>>> Cost after iteration 0: 0.6931471805599453
	Cost after iteration 1000: 0.6931471805599453
	Cost after iteration 2000: 0.6931471805599453
	Cost after iteration 3000: 0.6931471805599453
	Cost after iteration 4000: 0.6931471805599453
	...

• Prediction 결과 두 경계선을 거의 구분하지 못한다.

>>> 
predictions_train = [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...]]
predictions_test = [[0 0 0 0 0 0 0 ...]]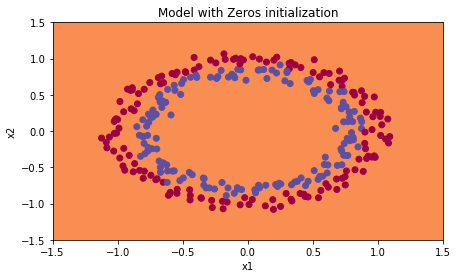

• Random Initialization

def initialize_parameters_random(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    np.random.seed(3)               # This seed makes sure your "random" numbers will be the as ours
    parameters = {}
    L = len(layers_dims)            # integer representing the number of layers
    
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * 10  # scaled by *10
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))

    return parameters

>>> W1 = [[ 17.88628473   4.36509851   0.96497468]
 		  [-18.63492703  -2.77388203  -3.54758979]]
	b1 = [[0.]
		  [0.]]
	W2 = [[-0.82741481 -6.27000677]]
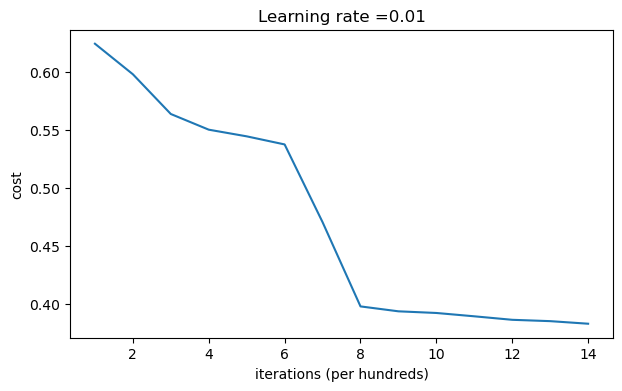
	b2 = [[0.]]

• Prediction 결과 안정적인 Loss curve를 가지게 되었음을 알 수 있다.

>>> Cost after iteration 0: inf
	Cost after iteration 1000: 0.6242305622140936
	Cost after iteration 2000: 0.5978835450878724
	Cost after iteration 3000: 0.5636222799576053
	Cost after iteration 4000: 0.5501000257265779
	...

• Boundary는 zero initialization보다는 향상되었다.

  

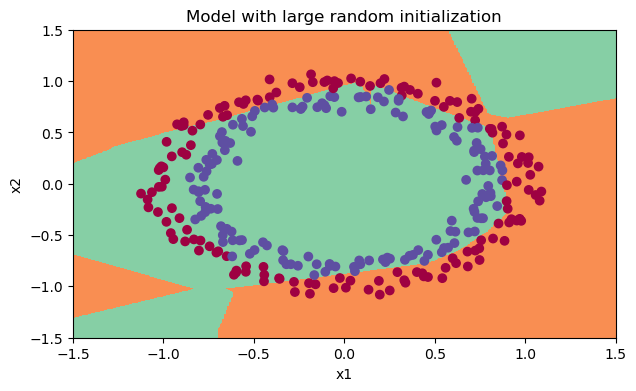
• He initialization

  • $\sqrt{\frac{2}{\text{dimension of the previous layer}}}$를 기대하기 때문에

    • $np.sqrt(2./layers_dims[l-1])$ 코드가 핵심이다.

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims) - 1 # integer representing the number of layers
     
    for l in range(1, L + 1):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * np.sqrt(2./layers_dims[l-1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
        
    return parameters

>>> W1 = [[ 1.78862847  0.43650985]
 		  [ 0.09649747 -1.8634927 ]
 		  [-0.2773882  -0.35475898]
		   [-0.08274148 -0.62700068]]
	b1 = [[0.]
		  [0.]
		  [0.]
		  [0.]]
	W2 = [[-0.03098412 -0.33744411 -0.92904268  0.62552248]]
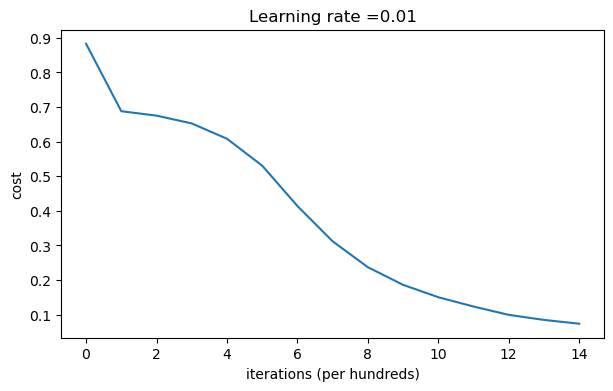
	b2 = [[0.]]

• Prediction 결과 가장 매끄럽다.

>>> Cost after iteration 0: 0.8830537463419761
	Cost after iteration 1000: 0.6879825919728063
	Cost after iteration 2000: 0.6751286264523371
	Cost after iteration 3000: 0.6526117768893807
	Cost after iteration 4000: 0.6082958970572938
	...

• Boundary 또한 매우 잘 형성되었음을 볼 수 있다.

  • 이러한 결과로 인해 알 수 있는 건 ReLU activation을 쓸 때 He initialization을 이용하는 것이 가장 적합하다는 점이다.

  

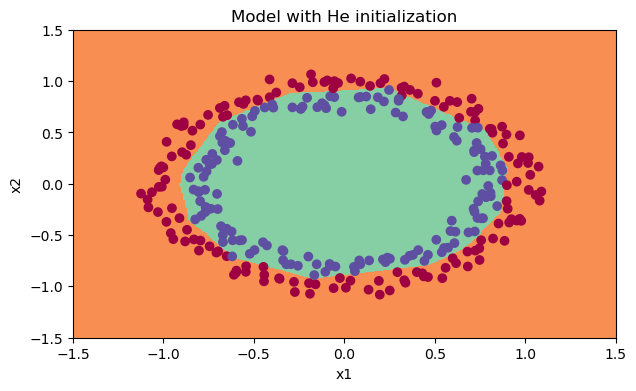
Regularization

• 아래와 같은 축구장에 두 팀을 배치하고, 우리 팀의 수비 진영을 확보하고 싶다.

  • 이러한 경계선(boundary)를 만들어주는 AI expert를 제작해보자.

  

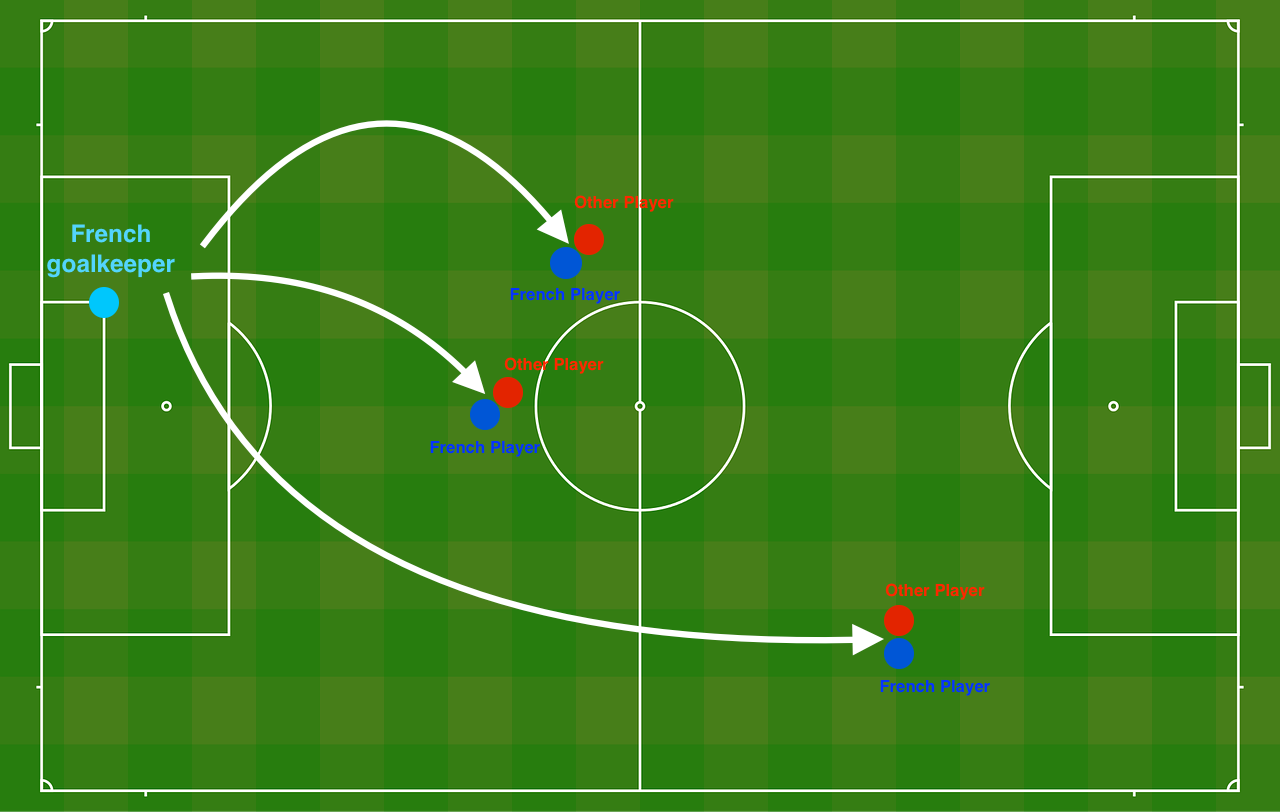
• Non-Regularized model

def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
    """
    Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
    
    Arguments:
    X -- input data, of shape (input size, number of examples)
    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples)
    learning_rate -- learning rate of the optimization
    num_iterations -- number of iterations of the optimization loop
    print_cost -- If True, print the cost every 10000 iterations
    lambd -- regularization hyperparameter, scalar
    keep_prob - probability of keeping a neuron active during drop-out, scalar.
    
    Returns:
    parameters -- parameters learned by the model. They can then be used to predict.
    """
        
    grads = {}
    costs = []                            # to keep track of the cost
    m = X.shape[1]                        # number of examples
    layers_dims = [X.shape[0], 20, 3, 1]
    
    # Initialize parameters dictionary.
    parameters = initialize_parameters(layers_dims)

    # Loop (gradient descent)

    for i in range(0, num_iterations):

        # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
        if keep_prob == 1:
            a3, cache = forward_propagation(X, parameters)
        elif keep_prob < 1:
            a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
        
        # Cost function
        if lambd == 0:
            cost = compute_cost(a3, Y)
        else:
            cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
            
        # Backward propagation.
        assert (lambd == 0 or keep_prob == 1)   # it is possible to use both L2 regularization and dropout, 
                                                # but this assignment will only explore one at a time
        if lambd == 0 and keep_prob == 1:
            grads = backward_propagation(X, Y, cache)
        elif lambd != 0:  # only regularization
            grads = backward_propagation_with_regularization(X, Y, cache, lambd)
        elif keep_prob < 1:  # only dropout
            grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
        
        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)
        
        # Print the loss every 10000 iterations
        if print_cost and i % 10000 == 0:
            print("Cost after iteration {}: {}".format(i, cost))
        if print_cost and i % 1000 == 0:
            costs.append(cost)
    
    # plot the cost
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('iterations (x1,000)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters

• Training 결과 안정적인 loss 커브는 달성했으나 boundary 양상은 다소 튀는 부분이 생겼다.

  

  

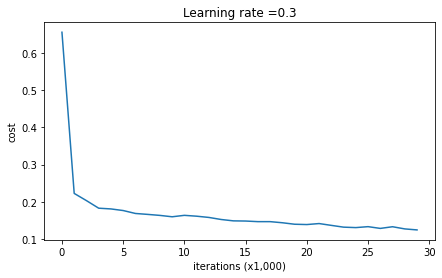
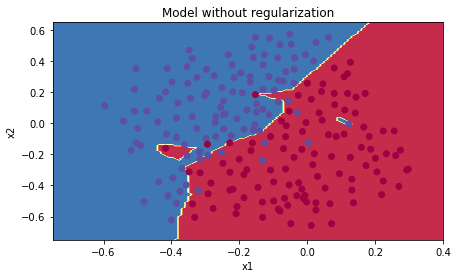
• Cost function에 L2 regularization term을 추가해보자.

  • $J_{regularized} = \displaystyle {-\frac{1}{m} \sum_{i=1}^{m} (y^{(i)} \log(a^{[L](i)}) + (1-y^{(i)})\log(1- a^{[L](i)}))}_\text{cross-entropy cost} + \displaystyle {\frac{1}{m} \frac{\lambda}{2} \sum_l \sum_k \sum_j W_{k,j}^{[l]2}}_\text{L2 regularization cost}$

def compute_cost_with_regularization(A3, Y, parameters, lambd):
    """
    Implement the cost function with L2 regularization. See formula (2) above.
    
    Arguments:
    A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    parameters -- python dictionary containing parameters of the model
    
    Returns:
    cost - value of the regularized loss function (formula (2))
    """
    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    W3 = parameters["W3"]
    
    cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost

    L2_regularization_cost = lambd/(2*m) * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
    
    cost = cross_entropy_cost + L2_regularization_cost
    
    return cost

• Backward propagation with regularization

  • $\frac{d}{dW} ( \frac{1}{2}\frac{\lambda}{m} W^2) = \frac{\lambda}{m} W$

def backward_propagation_with_regularization(X, Y, cache, lambd):
    """
    Implements the backward propagation of our baseline model to which we added an L2 regularization.
    
    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    cache -- cache output from forward_propagation()
    lambd -- regularization hyperparameter, scalar
    
    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y

    dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * (W3)
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims=True)
    
    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))

    dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * (W2)
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims=True)
    
    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))

    dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * (W1)
    db1 = 1./m * np.sum(dZ1, axis=1, keepdims=True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

• Regularization이 들어가야 학습이 더욱 안정적으로 일어나며 boundary 결과 또한 매끄럽다.

  

  

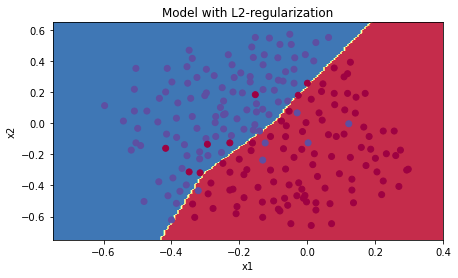
• Dropout이 포함된 코드를 살펴보자.

  • D = (D < keep_prob).astype(int)로 masking을 설정한다.

    • keep_prob을 0.8로 주면 20%의 node가 꺼지게 만든다는 것을 의미하며, 이를 기존 $X$에 곱해 $A = D * X$로 20% node를 masking한다.

• Forward propagation with Dropout

def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
    """
    Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
    
    Arguments:
    X -- input dataset, of shape (2, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape (20, 2)
                    b1 -- bias vector of shape (20, 1)
                    W2 -- weight matrix of shape (3, 20)
                    b2 -- bias vector of shape (3, 1)
                    W3 -- weight matrix of shape (1, 3)
                    b3 -- bias vector of shape (1, 1)
    keep_prob - probability of keeping a neuron active during drop-out, scalar
    
    Returns:
    A3 -- last activation value, output of the forward propagation, of shape (1,1)
    cache -- tuple, information stored for computing the backward propagation
    """
    
    np.random.seed(1)
    
    # retrieve parameters
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)

    D1 = np.random.rand(A1.shape[0], A1.shape[1])   # rand : 0~1 균일 분포, randn : 0~1 가우시안 정규 분포(대체로 0 주변)
    D1 = (D1 < keep_prob).astype(int)  # masked
    A1 = A1 * D1
    A1 /= keep_prob

    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)

    D2 = np.random.rand(A2.shape[0], A2.shape[1])   # rand : 0~1 균일 분포, randn : 0~1 가우시안 정규 분포
    D2 = (D2 < keep_prob).astype(int)  # masked
    A2 = A2 * D2
    A2 /= keep_prob

    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)
    
    cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
    
    return A3, cache

• Backward propagation with Dropout

def backward_propagation_with_dropout(X, Y, cache, keep_prob):
    """
    Implements the backward propagation of our baseline model to which we added dropout.
    
    Arguments:
    X -- input dataset, of shape (2, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    cache -- cache output from forward_propagation_with_dropout()
    keep_prob - probability of keeping a neuron active during drop-out, scalar
    
    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    
    m = X.shape[1]
    (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    dW3 = 1./m * np.dot(dZ3, A2.T)
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims=True)
    dA2 = np.dot(W3.T, dZ3)

    dA2 = D2 * dA2
    dA2 /= keep_prob

    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1./m * np.dot(dZ2, A1.T)
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims=True)
    
    dA1 = np.dot(W2.T, dZ2)
    dA1 = dA1 * D1
    dA1 /= keep_prob
    
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1./m * np.dot(dZ1, X.T)
    db1 = 1./m * np.sum(dZ1, axis=1, keepdims=True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

Gradient Checking

• Gradient를 수식적으로 표현하면 다음과 같다.

  • $\frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon}$

# GRADED FUNCTION: gradient_check

def gradient_check(x, theta, epsilon=1e-7, print_msg=False):
    """
    Implement the gradient checking presented in Figure 1.
    
    Arguments:
    x -- a float input
    theta -- our parameter, a float as well
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient. Float output
    """
    
    # Compute gradapprox using right side of formula (1). epsilon is small enough, you don't need to worry about the limit.
    theta_plus = theta + epsilon
    theta_minus = theta - epsilon
    J_plus = forward_propagation(x, theta_plus)
    J_minus = forward_propagation(x, theta_minus)
    gradapprox = (J_plus - J_minus) / (2 * epsilon) # () is necessary!!
    
    # Check if gradapprox is close enough to the output of backward_propagation()
    grad = backward_propagation(x, theta)  # real grad!

    numerator = np.linalg.norm(grad - gradapprox)  # None : frobenius norm
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)  # 'fro' is okay
    difference = numerator / denominator

    if print_msg:
        if difference > 2e-7:
            print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
        else:
            print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
    
    return difference

• N-dimentional Gradient checking은 for loop이 포함된다.

# GRADED FUNCTION: gradient_check_n

def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7, print_msg=False):
    """
    Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
    
    Arguments:
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3"
    grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters 
    X -- input datapoint, of shape (input size, number of examples)
    Y -- true "label"
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient
    """
    
    # Set-up variables
    parameters_values, _ = dictionary_to_vector(parameters)
    
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))
    
    # Compute gradapprox
    for i in range(num_parameters):
        
        # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
        theta_plus = np.copy(parameters_values)
        theta_plus[i] += epsilon
        J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(theta_plus))
        
        # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
        theta_minus = np.copy(parameters_values)
        theta_minus[i] -= epsilon
        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(theta_minus))

        # Compute gradapprox[i]
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
    
    # Compare gradapprox to backward propagation gradients by computing difference.
    numerator = np.linalg.norm(grad-gradapprox)
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
    difference = numerator / denominator

    if print_msg:
        if difference > 2e-7:
            print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
        else:
            print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")

    return difference

---

• 출처: [Coursera] Deep Learing Specialization