[DLS] Neural Networks and Deep Learning week 2

피망이·2023년 12월 1일

1st Course 1 Coursera Week 2

[DLS] Deep Learning Specialization

목록 보기

2/6

Logistic Regression as a Neural Network

Binaray Classification

귀여운 고양이 사진을 보고, 고양이인지(1) 아닌지(0) 판별하고 싶다.
이미지는 RGB의 color channels을 갖기 때문에 다음과 같은 형태로 컴퓨터에게 전달된다.
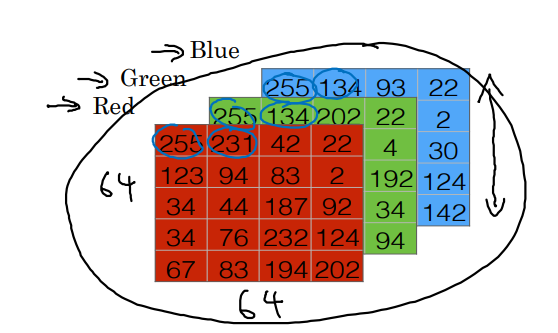
이를 squeeze하여 12288짜리 features가 담긴 하나의 열로 만든다.
- x가 샘플 하나이며, 정답 y로 mapping하는 작업을 거칠 것이다.
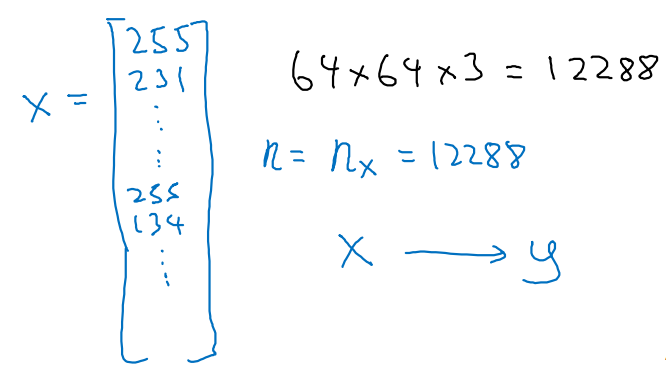
우리가 사용할 Notation은 다음과 같은 형태로 전개될 것이다.
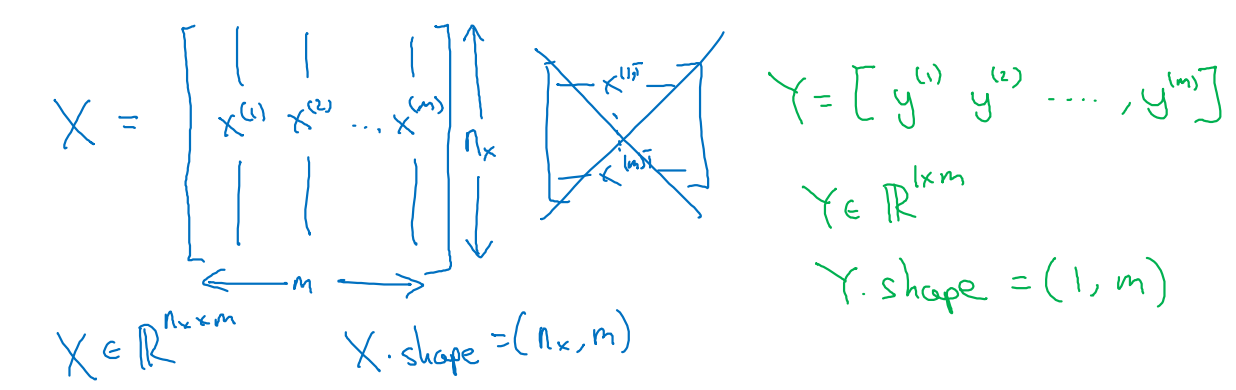
- m개의 training examples를 column을 기준으로 concat하여 training set X를 만든다.
  - 일부 Notation들은 x를 row를 기준으로 concat하기도 한다.
  - 우리는 column 기준 concat X를 사용할 것!
- 그러면 X.shape = (nx, m)의 형태일 것이며, 각각의 example들에 대한 정답 y는 Y.shape = (1, m)의 분포를 갖도록 만든다.

Logistic Regression

우리는 해당 사진(x)을 보고, 0과 1 사이의 y=1(고양이)일 확률을 계산할 것이다.
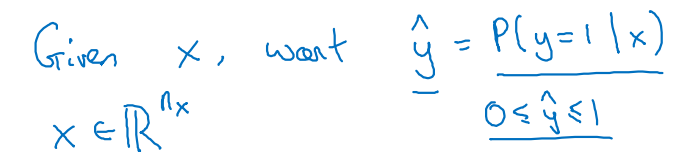
주어진 미션에 대한 파라미터들은 x를 y로 mapping할 w(nx개)와 b(1개)이다.
- sigmoid(σ) 함수를 씌워 0~1 범위를 갖는 추정값(yhat)을 계산한다.
sigmoid(σ) 함수의 특징은 z의 크기에 따라 달라진다는 점이다.
- x에 대한 선형 변환인 z) z가 크면 1로 판별, z가 작으면 0으로 판별

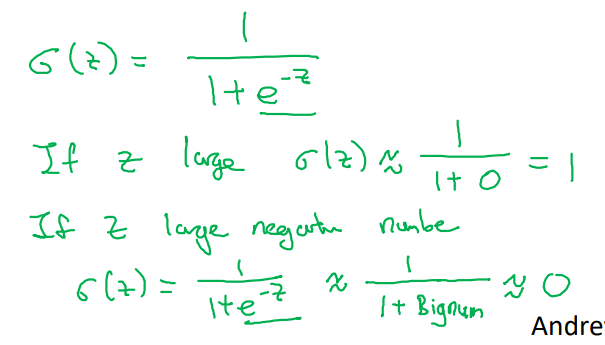
Logistic Regression cost function

example에 대한 subscript는 i로 표현할 예정이다.
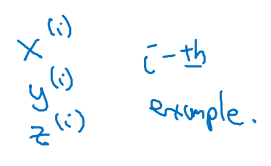
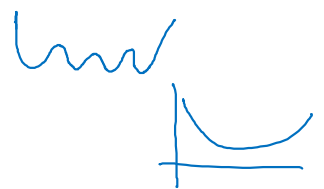
기존 선형 회귀에서 사용했던 Loss function을 Classification 문제에 적용하면 local optima에 빠지기 쉽다.
- 선형 회귀 Loss function) Squared Error: $L(\hat{y}, y) = \frac{1}{2} (\hat{y} - y)^2$
- 그림에서 위를 not convex, 아래를 convex라고 본다.
  - convex한 function을 재정의할 필요가 있음!
따라서 다음과 같은 형태의 Loss function을 사용할 것이다.
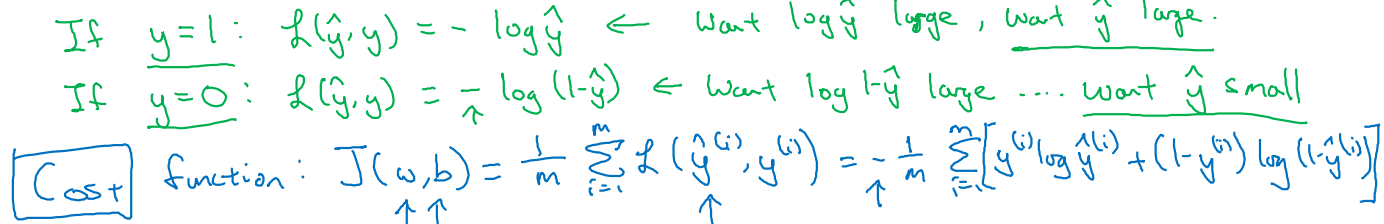
- Binary Cross Entropy: $L(\hat{y}, y)=-log(ylog \hat{y} + (1-y)log(1- \hat{y}))$
- 이 함수의 특징은 크게 두 가지 케이스로 나눠 볼 수 있다.
  1. y=1이라면, Loss는 $-log(\hat{y})$ 로 표현된다.
    $\Rightarrow$ Loss를 0으로 만들기 위해, $\hat{y}$ 을 sigmoid의 최댓값인 1로 만들어야 한다.
  2. y=0이라면, Loss는 $-log(1-\hat{y})$ 로 표현된다.
    $\Rightarrow$ Loss를 0으로 만들기 위해, $\hat{y}$ 을 sigmoid의 최솟값인 0으로 만들어야 한다.
  - 즉, label 예측이 틀렸을 때 더 큰 패널티를 줄 수 있는 특징으로 인해, MSE를 쓰는 것보다 BCE를 사용하여 추정하는 것이 더욱 효과적이다.
- 최종 Cost function은 parameter w와 b에 초점을 맞추어 전개한다.

Gradient Descent

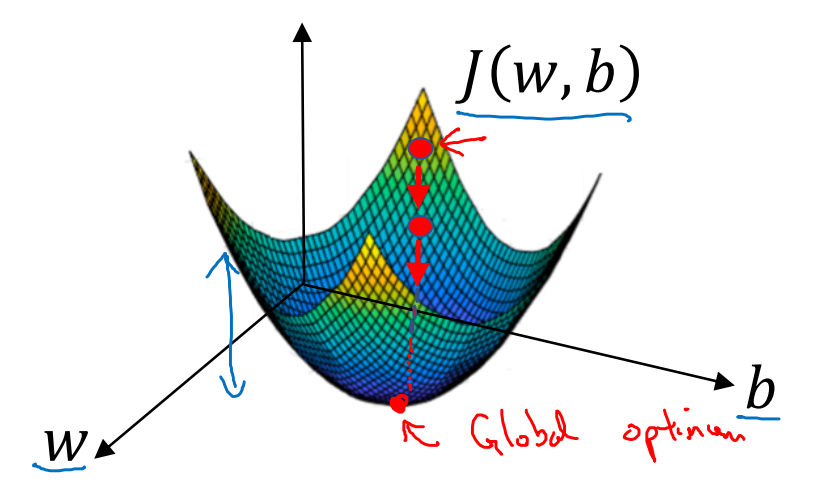
우리는 $J(w, b)$ 를 minimize하기 위한 parameter w와 b를 찾아야 한다.
- ←로 표현된 Initial point로부터 시작하여 down hill 작업을 거쳐 Global optimum으로 향하는 것이 Gradient Descent다.

이를 위해서는 derivative(미분)의 개념이 필요하다.
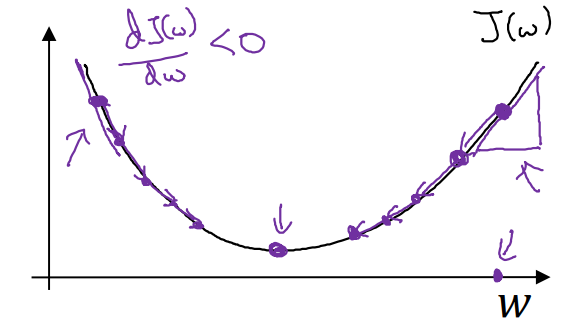
- 우리가 해결하고자 하는 objective function( $J$ )의 slope를 변수 w와 b에 대하여 미분한 값을 $\frac{\partial J}{ \partial w} = dw$ , $\frac{\partial J}{ \partial b} = db$ 로 표현하자.
- 아래와 같은 이차 함수의 꼴로 $J$ 가 표현된다면, minimize하기 위한 방향은 다음과 같다.
  - 기울기가 양수( $\frac{\partial J}{ \partial w} > 0$ )일 때, $w := w- \beta$ ( $w$ 가 작아져야)
  - 기울기가 음수( $\frac{\partial J}{ \partial w} < 0$ )일 때, $w := w+ \beta$ ( $w$ 가 커져야)
- learning rate( $\alpha$ )로 조정 민감도를 설정한 뒤 미분량( $dw$ , $db$ )을 포함한 최종 update 식은 다음과 같다.
  - $w := w - \alpha \; dw$
  - $b := b - \alpha \; db$

Derivatives

미분(Derivatives)이란 slope of the function이다.
- 1차 함수의 미분은 slope가 항상 동일하다.
  - ex. $f(a) = 3a$ , $\frac{df(a)}{da} = 3$
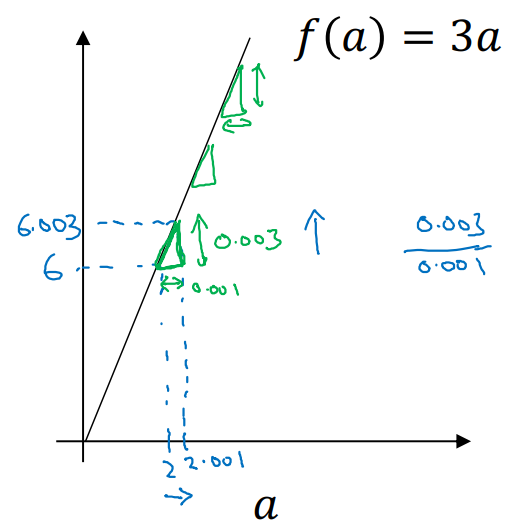
- a에 대한 어떤 값을 nudge(쿡 찌르다)하더라도 말이다.
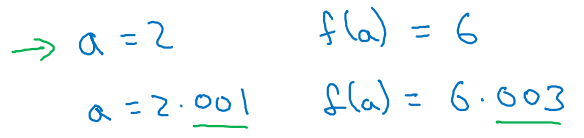
- 2차 함수의 미분은 각 a지점마다 기울기가 달라진다.
  - ex. $f(a) = a^2$ , $\frac{df(a)}{da} = 2a$
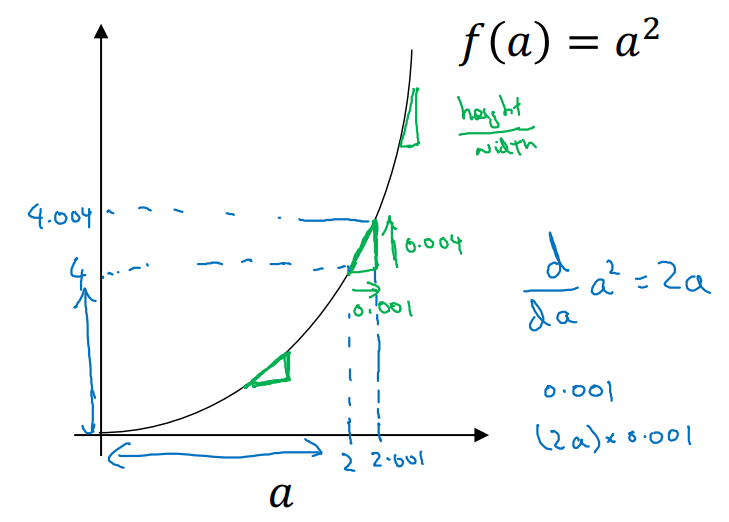
- 이외에도 다양한 derivative examples가 있다.

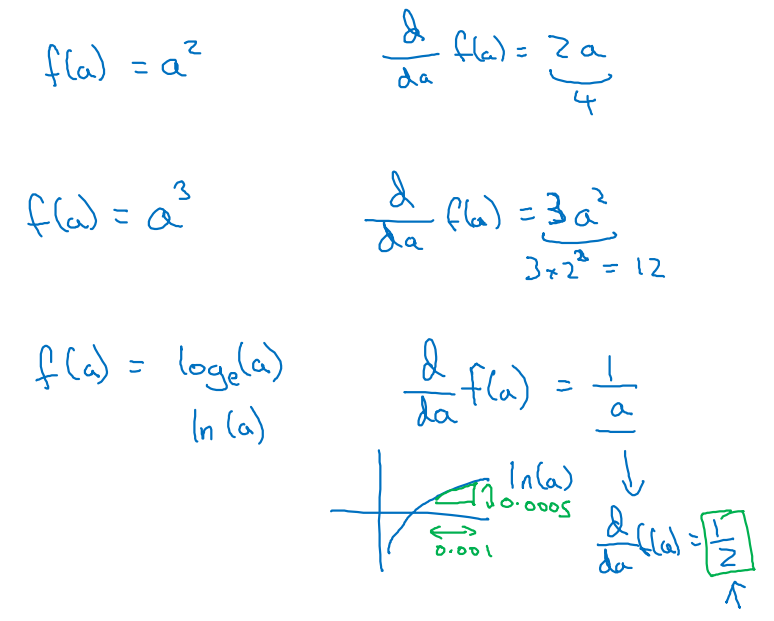
Computation Graph

Deep Learning의 계산 과정을 illustrating하는 graph에 대해 소개하고자 한다.
- w, b 뿐만 아니라 여러 parameter들이 연관된 cost function $J$ 를 시각화하는 방법을 알아보자.
예를 들어, $J(a, b, c) = 3(a+bc)$ 와 같은 함수가 정의되어 있다고 해보자.
- $bc = u$ , $(a+bc) = v$ , $3(a+bc) = J$ 라 하자.
- 각 parameters a, b, c를 initialize하여 아래와 같은 순서로 계산 과정을 visualizing하였다. (Propagation)
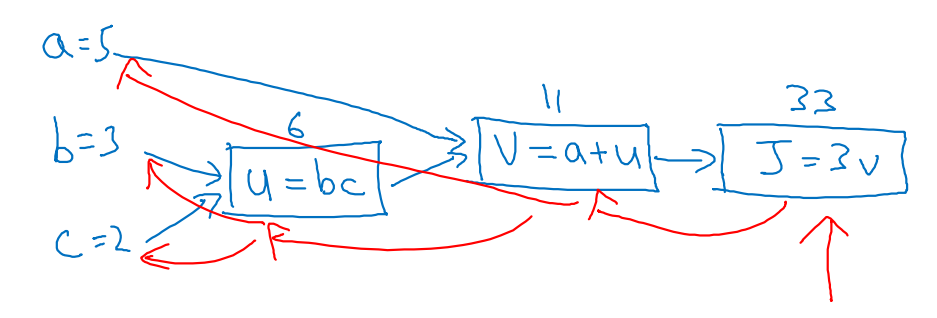
- 우리가 앞으로 해야할 일은 $J$ 의 미분값에 대하여 Gradient descenting을 통해 parameters을 update하는 것이다. (Backpropagation)

Derivatives with a Computation Graph

위 식에 따르면, $a → v → J$ 로 이어지는 과정을 통해 최종 cost $J$ 를 계산하였다.
- 이제, parameter a에 대한 업데이트를 진행하기 위한 수식을 정의해 보자.
  - $a := a - \alpha \; da$
$da = \frac{dJ}{da}$ 이므로, cost function $J$ 에 대하여 a로 미분한 값을 찾아야 한다.
- 즉, chain rule을 적용하여 $J → v → a$ 순서대로 미분을 전개한다.
- $\frac{dJ}{da}$ 을 구하기 위해(2), $\frac{dJ}{dv}$ (1)와 v에 대한 a 미분값 $\frac{dv}{da}$ (3)을 찾는 것이다.
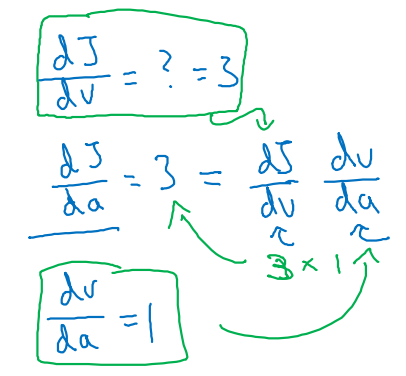
마찬가지로 parameter b에 대한 업데이트를 진행해 보자. (same as c)
- $J$ 를 구하기 위해 사용했던 계산 과정은 $b → u → v → J$ 였다.
- 따라서 $J → v → u → b$ 와 같은 과정으로 미분값을 찾아주어야 하며, 그 과정은 다음과 같다.
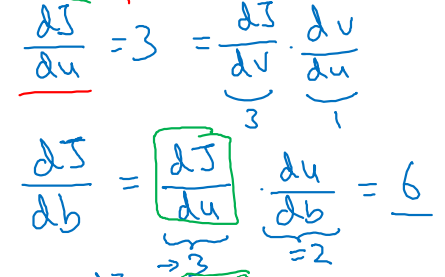
- $J$ 에 대한 직접적인 미분 $\frac{dJ}{dv}$ 과 v에 대한 u 미분값 $\frac{dv}{du}$ 로 $\frac{dJ}{du}$ 를 찾고 ( $J → v → u$ ),
  
  b에 대한 u 미분 $\frac{du}{db}$ 를 찾아 최종 $\frac{dJ}{db}$ 를 구한다. ( $u → b$ )
  - parameter b를 업데이트 한다. (same as c)
    - $b := b - \alpha \; db$
    - $c := c - \alpha \; dc$
이 모든 과정을 종합하여 나타내면 아래의 그래프와 같다. (Backpropagation)

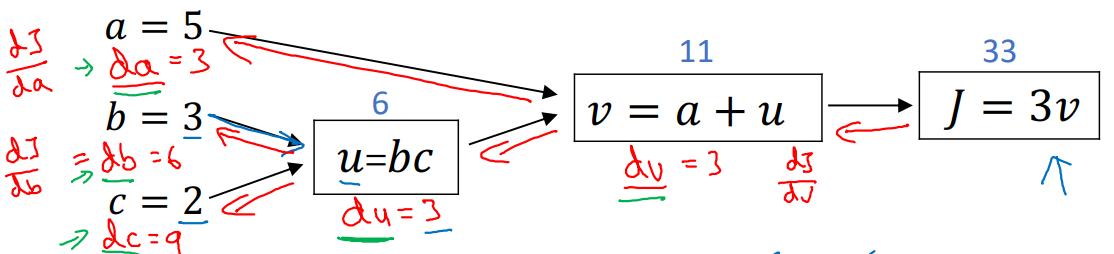
Logistic Regression Gradient descent

Logistic Regression의 수식은 다음과 같이 정리된다.
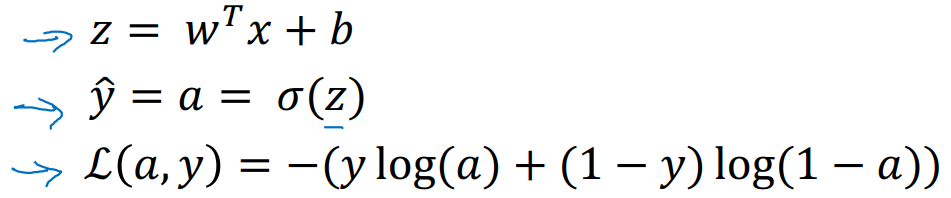
우리가 찾아야 할 parameters에 대한 Computation graph는 다음과 같다.
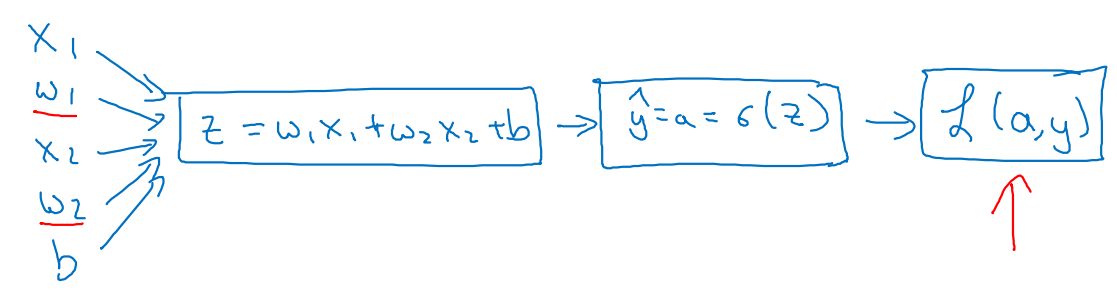
먼저, objective function(BCE) $L$ 에 대해 a로 미분하면 아래와 같이 전개된다.
- $da = \frac{dL(a, y)}{da} = -\frac{y}{a} + \frac{1-y}{1-a}$
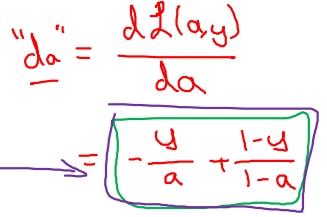
$L$ 을 $z$ 에 대한 미분으로 확장하면 아래와 같이 전개된다. (위에서 구한 $da$ 사용)
- $dz = \frac{dL}{dz} = \frac{da}{dz} \frac{dL}{da} = \frac{da}{dz} (-\frac{y}{a} + \frac{1-y}{1-a}) = (a-y) \;a (1-a)$
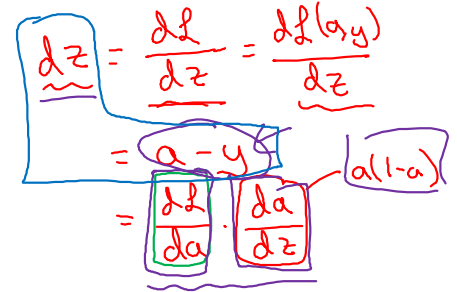
- parameters w1, w2, b에 대한 $L$ 의 미분값은 다음과 같이 정리된다.
  - $dw_1 = \frac{dL}{dw_1} = x_1 dz$ ,
  - $dw_2 = \frac{dL}{dw_1} = x_2 dz$ ,
  - $db = \frac{dL}{db} = dz$
- 이를 통해 최종 update를 구현한다.

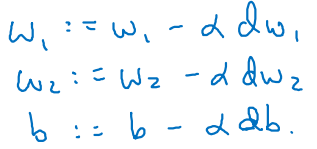
Gradient descenton m examples

Cost function $J$ 는 average of Loss function이다.
- m개의 training examples가 있으면 $\frac{1}{m}$ 으로 mean을 취해주어야 한다.
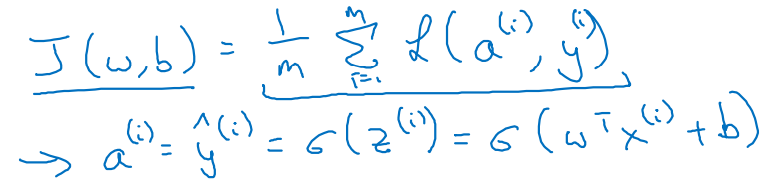
ith sample에 대한 Loss 미분값을 각각 전개하면 다음과 같이 $\Sigma$ 로 결합된다.
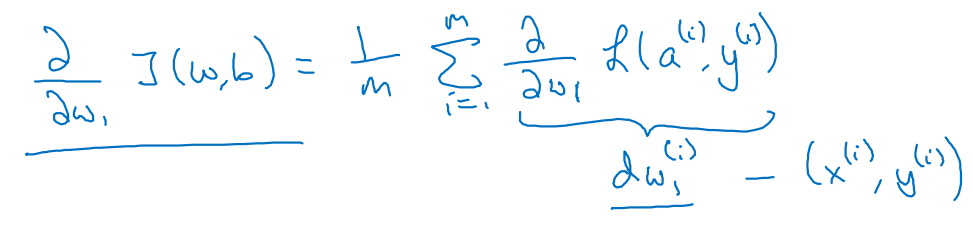
최종 parameters를 업데이트 하는 알고리즘은 다음과 같이 표현된다.
- $J=0$ 일 때, $dw_1$ 과 $dw_2$ , $db$ 가 모두 0이 되는 solution은 trivial solution이다.
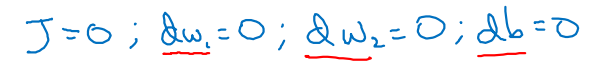
- 각 training example m개에 대하여 for loop을 돌며 calculation을 진행한다.
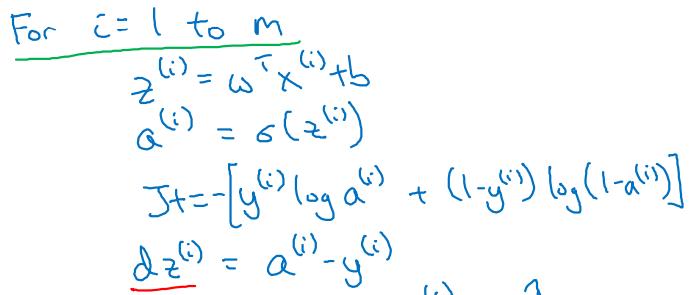
- 이 때, parameter update에 대한 부분은 ith notation을 적용하지 않는다.
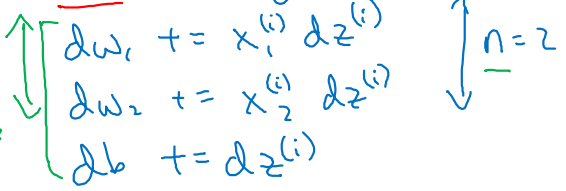
  - 그 이유는 우리가 처음에 input x(i)를 1차원 vector로 표현하였기 때문이고, 이로 인해 parameters 또한 vetorizing되어 계산 과정이 편리해졌다.
  - data의 size(n)에 따라 parameters 업데이트가 반복된다.
- m개의 examples에 대해 반복되었으므로, $\frac{1}{m}$ 을 곱함으로써 각각 averaging한다.

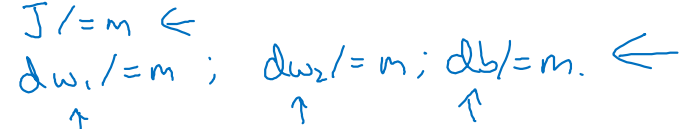
Python and Vectorization

Vectorization

w와 x가 nx에 대한 실수 차원에서 다음과 같이 정의된다고 하자.

non-vectorized / vectorized 형태를 python 코드로 표현하는 방법은 다음과 같다.
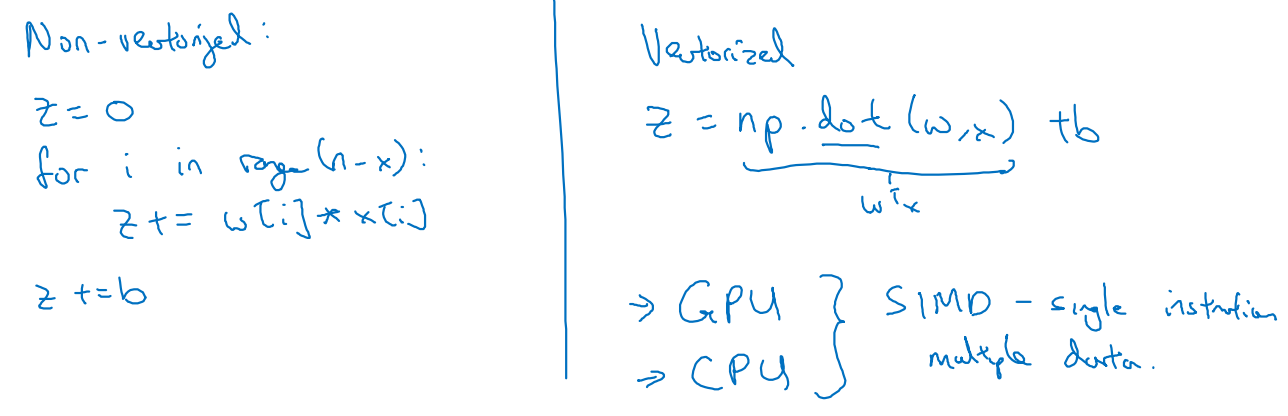
- numpy 라이브러리를 이용하여 vectorized된 matrix 형태로 dot을 적용하는 것이 non-vectorized 형태에서 for loop을 돌리는 것보다 더 빠르다.
  - 실습에 따르면 약 500배 가까이 더 빠르다는 것을 알 수 있었다.
- GPU를 사용하면 병렬(parallization) 컴퓨팅을 사용한다는 점에서 매우 효과적이고, CPU를 사용한다 하더라도 not so bad하다.

More vectorization Examples

$j$ 개의 labels을 분류하기 위해 $u = Av$ 와 같은 함수가 적용된다고 가정해보자.
- $u_i = \displaystyle \sum_{j} A_{ij} v_{j}$ 를 python 코드로 구현하는 방법은 크게
  
  1) 이중 for문을 사용하는 방법과
  2) numpy를 사용하는 방법으로
  
  나뉠 수 있다.
1) 이중 for문을 사용하는 방법
: label들이 담길 u 배열을 미리 0으로 initializing하여 지정해주어야 한다.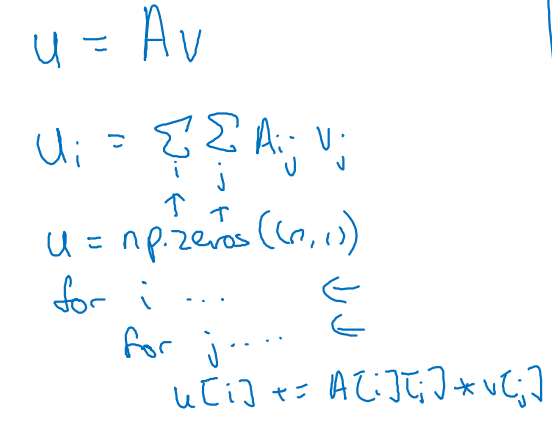

2) numpy를 사용하는 방법
: matrix dot product를 적용하는 것으로 표현하여 한 줄로 끝낸다. (승!)
v라는 배열 내부의 값에 전부 exp()을 씌워주기로 하자.
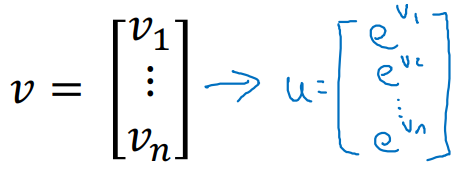
- 이 또한
  
  1) for loop를 돌며 각각의 값에 exp()를 취해주는 방법과
  2) numpy를 활용하여 broadcasting하는 방법이
  
  있다.
1) for loop으로 모든 값에 하나하나 exp()를 씌우는 방법

: 역시 마찬가지로, 정답이 담길 u 배열을 미리 지정해준다.

2) numpy를 사용하여 exp()을 broadcasting하는 방법 (승!)
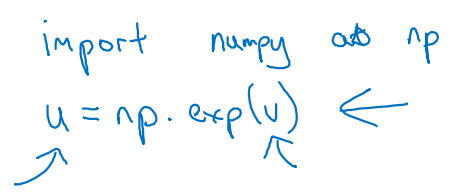
- 이외에도 log, abs, maximum etc.를 편리하게 이용할 수 있다.

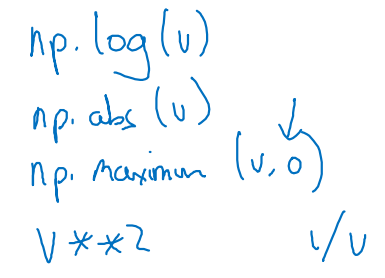
Vectorizing Logistic Regression

(nx, m)의 shape을 가지는 $X$ 를 parameters $W$ , $b$ 를 이용하여 선형 변환 해보자.
- $W^T X$ 의 matrix 형태는 다음과 같다.
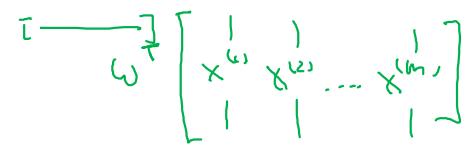
- (1, m)의 shape을 갖는 parameter $b$ 까지 더해진 최종 함수 $Z = W^T X + b$ 는 다음과 같이 표현된다.
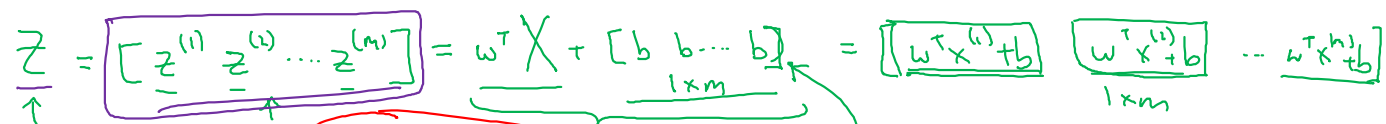
- 이를 코드로 표현하면 아래와 같고, sigmoid까지 적용한 matrix $A$ 또한 간단하게 표현할 수 있다.
  - Z = np.dot(W.T, X) + b
  - A = np.sigmoid(Z)
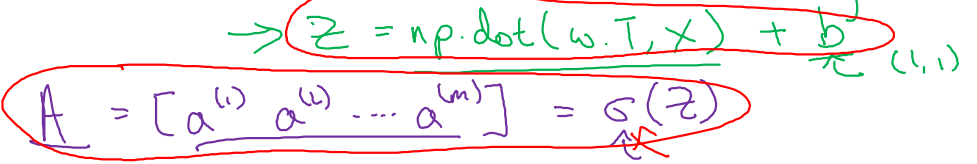
  - 이 때, $b$ 는 (1, 1)의 shape(즉, scalar)로 넣어 주어도 된다.
  - numpy에서 제공하는 broadcasting기법에 의해 (1, m)으로 extending되기 때문이다.

Vectorizing Logistic Regression’s Gradient Computation

$Z$ 에 대한 $d Loss$ 는 m개의 samples에 대하여 다음과 같은 matrix 형태를 갖는다.
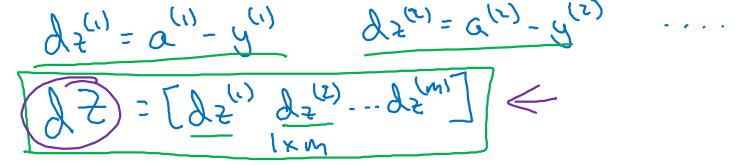
m개의 samples를 갖는 matrix $A$ 와 $Y$ 에 대하여 $Z$ 를 다시 표현하면 다음과 같다.
- $dZ = A - Y$
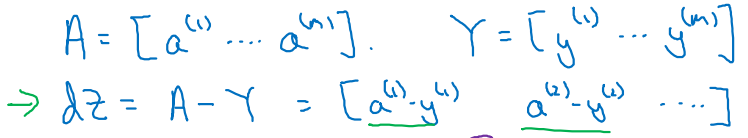
0으로 initialize 되어 있는 $dW$ 와 $db$ 값에 대해 다음과 같이 업데이트 하려 한다.
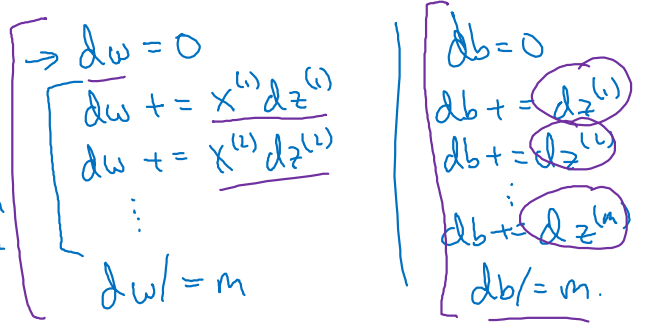
이를 matrix 형태로 표현하면 아래와 같이 간단한 matrix 연산으로 표현된다.
- $dW = \frac{1}{m} X dz^T$
- $db = \frac{1}{m} \displaystyle \sum_{i=1}^{m} dz^{(i)}$
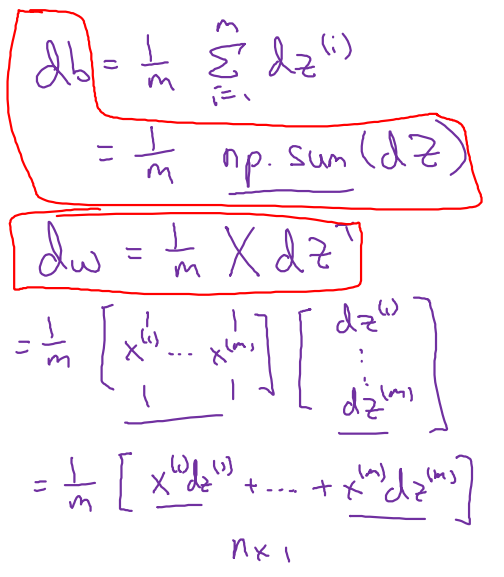
앞서, training examples m개에 대한 for loop으로 parameter들을 update하는 과정은 다음과 같았다.
- 하나의 ith example에 대하여 parameters w와 b가 nx개의 features에 각각 더해져 업데이트 되고 있는 것이다.
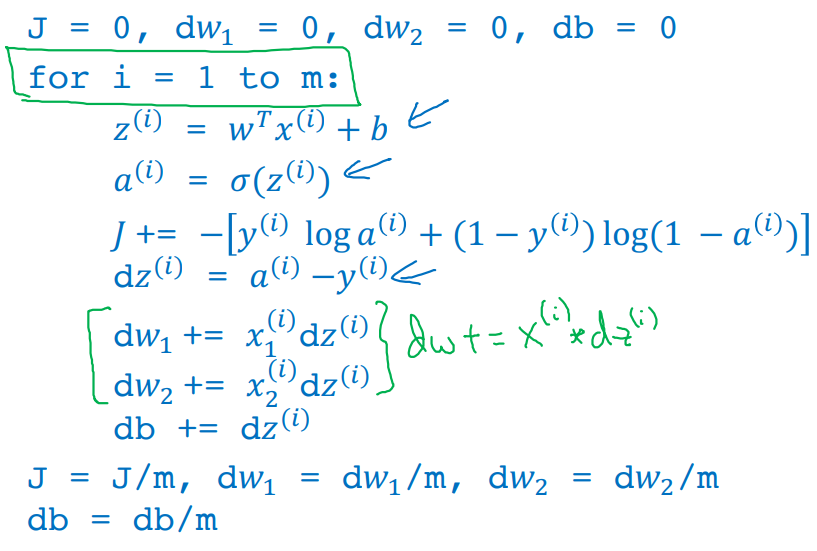
각 example을 1D vectorize하여 열을 기준으로 concat한 후 matrix 형태로 $X$ , $Z$ , $A$ , $Y$ 로 표현하고 나면,
- 다음과 같이 간단한 code를 작성함으로써 위의 작업을 대체할 수 있다.
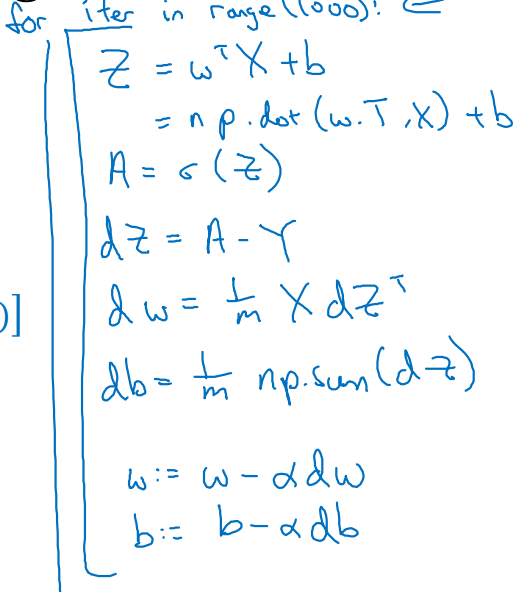
- 위 과정을 1000번의 epochs으로 묶어 parameters updating을 반복함으로써 효율적인 computation이 가능해진다.

Broadcasting in Python

matrix A를 행 따로, 열 따로 summation하는 방법은 다음과 같다.
- ex. 다음과 같은 예제 matrix A가 있을 때,
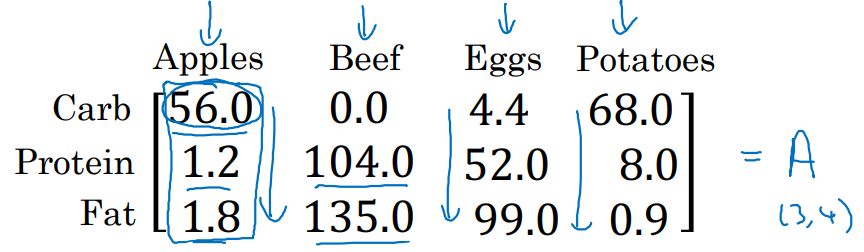
- A.sum(axis=0): A를 한 행만 남게끔 압축한다.
- A.sum(axis=1): A를 한 열만 남게끔 압축한다.
즉, 방향은 axis=0이 vertical, axis=1이 horizontal이다.

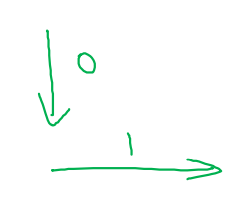
Broadcasting의 General Principle은 아래와 같다.
- ex. 아래와 같은 예제가 있을 때,
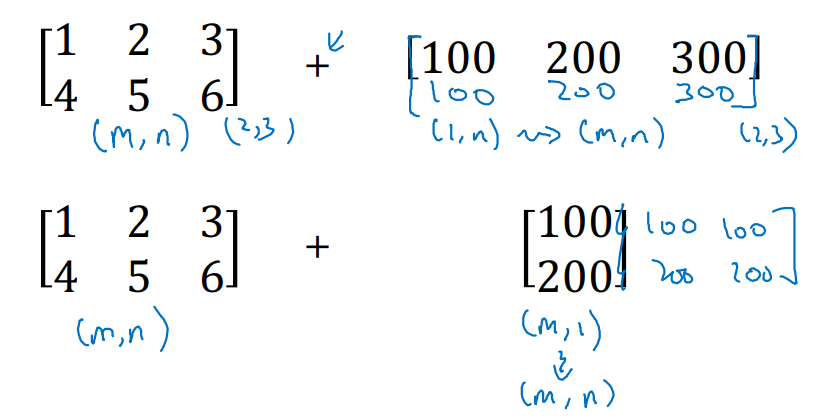
- (m, n)의 matrix에 (1, 1) scalar / (1, n) vector / (m, 1) vector 연산을 수행하면, 자동으로 (m, n) 형태의 matrix를 출력하게 된다.

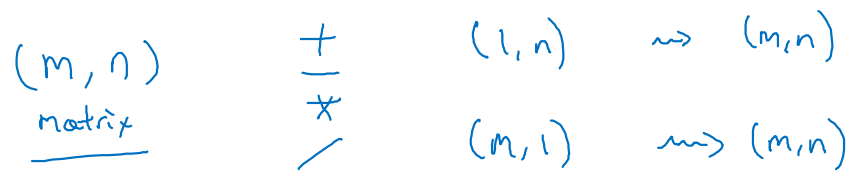
A Note on Python/Numpy Vectors

parameters를 initializing할 때 쓰일 vector를 지정하는 방법은
- np.random.rand() 함수를 사용할 것이다.
이 때, shape을 입력하는 칸에 쓸 notation은 다음과 같다.
- 1차원 vector를 표현할 때,
  - a = np.random.rand(5)와 같이 표현하지 않는다!
  - a = np.random.rand(5, 1)과 같이 표현해라.

Explanation of logistic regression cost function (Optional)

Logistic regression에서 활용된 cost function에 대해 자세히 알아보자.
- 우리는 주어진 input x에 대한 정답 추론 확률 $\hat{y}$ 을 알고 싶다.
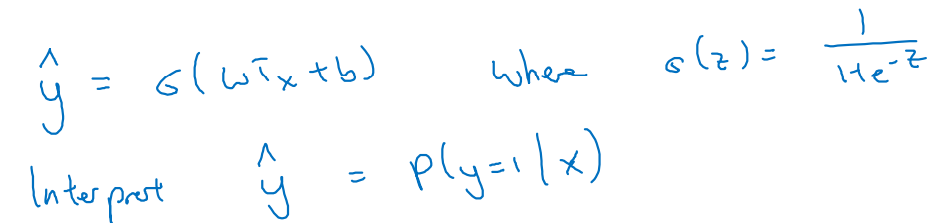
- Binary Classification이기 때문에 정답 y는 0과 1로 나뉠 것이다.
  - 정답 y=0 또는 y=1이 될 확률을 최대화하는 것이 최종 목표다!
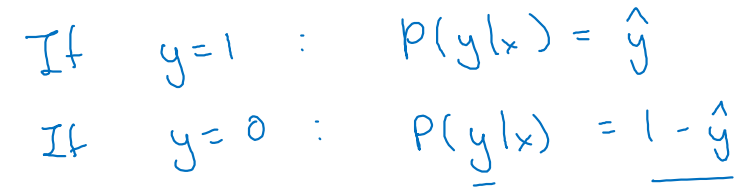
주어진 input x에 대한 두 확률을 합하여 정리하면 다음과 같이 표현된다.
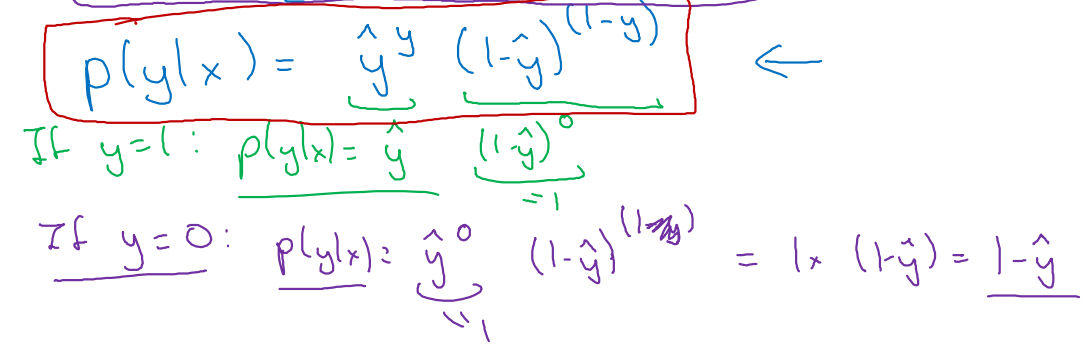
해당 확률에 단조 함수인(monotonically increasing) log function으로 묶으면, 다음과 같은 수식으로 전개된다.
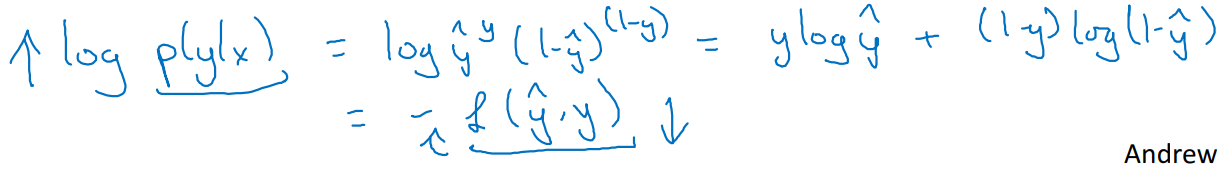
- 즉, 추정 확률을 최대화하는 작업이 Loss를 줄이는 일로 치환될 수 있는 것이다!
- log() 함수는 값이 커지더라도 크게 increasing하지 않는다(단조 함수)는 장점을 가지기 때문에 사용한다.
m개의 examples에 대하여 Cost function을 다시 유도해보자.
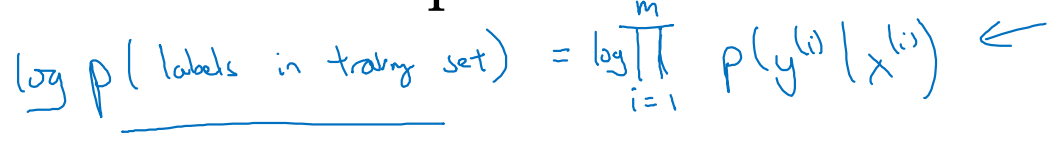
- m개의 training set 확률을 모두 곱하면 전체 확률이 된다.
- 값이 너무 커지지 않도록 log() 함수를 씌워주었다.
최종 확률을 maximizing하는 작업은 곧 Cost를 minimizing하는 작업과 같다.
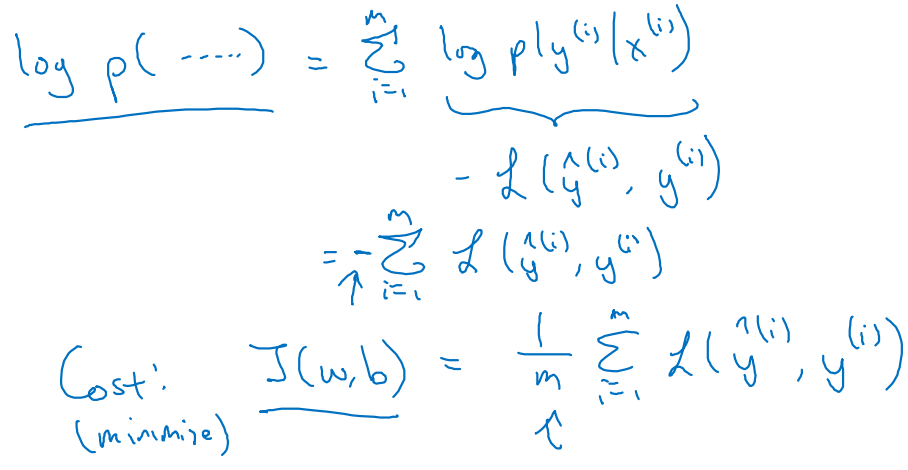
- 이러한 principle을 Maximum likelihood extimation(MLE)라 부른다.
  cf. MLE → Find out parameters(w, b) for increasing logP() !
출처: [Coursera] Deep Learning Specialization

Assignment

W2A1

Python Basics with Numpy

Sigmoid

def sigmoid(x):
    """
    Compute the sigmoid of x

    Arguments:
    x -- A scalar or numpy array of any size

    Return:
    s -- sigmoid(x)
    """
    
    s = 1 / (1 + np.exp(-x))
    
    return s

Sigmoid derivative

def sigmoid_derivative(x):
    """
    Compute the gradient (also called the slope or derivative) of the sigmoid function with respect to its input x.
    You can store the output of the sigmoid function into variables and then use it to calculate the gradient.
    
    Arguments:
    x -- A scalar or numpy array

    Return:
    ds -- Your computed gradient.
    """
    
    s = sigmoid(x)
    ds = s*(1-s)  # keep in mind, not just s(1-s)
    
    return ds

Image2vector

def image2vector(image):
    """
    Argument:
    image -- a numpy array of shape (length, height, depth)
    
    Returns:
    v -- a vector of shape (length*height*depth, 1)
    """

    v = image.reshape(image.shape[0] * image.shape[1] * image.shape[2], 1)  # (-1, 1)
    
    return v

>>> t_image = np.array([[[ 0.67826139,  0.29380381],
                         [ 0.90714982,  0.52835647],
                         [ 0.4215251 ,  0.45017551]],

                        [[ 0.92814219,  0.96677647],
                         [ 0.85304703,  0.52351845],
                         [ 0.19981397,  0.27417313]],

                        [[ 0.60659855,  0.00533165],
                         [ 0.10820313,  0.49978937],
                         [ 0.34144279,  0.94630077]]])

>>> image2vector(image) = [[0.67826139]
						   [0.29380381]
						   [0.90714982]
				  		   [0.52835647]
						   [0.4215251 ]
						   [0.45017551]
						   [0.92814219]
	  		  			   [0.96677647]
						   [0.85304703]
 						   [0.52351845]
 						   [0.19981397]
 						   [0.27417313]
						   [0.60659855]
 						   [0.00533165]
						   [0.10820313]
						   [0.49978937]
						   [0.34144279]
						   [0.94630077]]

Normalizing rows
For example, if $x = \begin{bmatrix} 0 & 3 & 4 \\ 2 & 6 & 4 \\ \end{bmatrix}\tag{3}$ then $\| x\| = \text{np.linalg.norm(x, axis=1, keepdims=True)} = \begin{bmatrix} 5 \\ \sqrt{56} \\ \end{bmatrix}\tag{4}$ and $x\_normalized = \frac{x}{\| x\|} = \begin{bmatrix} 0 & \frac{3}{5} & \frac{4}{5} \\ \frac{2}{\sqrt{56}} & \frac{6}{\sqrt{56}} & \frac{4}{\sqrt{56}} \\ \end{bmatrix}\tag{5}$

def normalize_rows(x):
    """
    Implement a function that normalizes each row of the matrix x (to have unit length).
    
    Argument:
    x -- A numpy matrix of shape (n, m)
    
    Returns:
    x -- The normalized (by row) numpy matrix. You are allowed to modify x.
    """
    
    x_norm = np.linalg.norm(x, ord=2, axis=1, keepdims=True)  # 2-norm = sqrt(x1**2 + x2**2 ...)
    x = x / x_norm  # normalized by row : axis=1

    return x

>>> x = np.array([[0, 3, 4],
              	  [1, 6, 4]])

>>> normalizeRows(x) = [[0.         0.6        0.8       ]
 						[0.13736056 0.82416338 0.54944226]]

Softmax

def softmax(x):
    """Calculates the softmax for each row of the input x.

    Your code should work for a row vector and also for matrices of shape (m,n).

    Argument:
    x -- A numpy matrix of shape (m,n)

    Returns:
    s -- A numpy matrix equal to the softmax of x, of shape (m,n)
    """
    
    x_exp = np.exp(x)
    x_sum = np.sum(x_exp, axis=1, keepdims=True)  # not np.sum(x)
    s = x_exp / x_sum
    
    return s

Vectorization

x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]

### VECTORIZED DOT PRODUCT OF VECTORS ###
tic = time.process_time()
dot = np.dot(x1,x2)
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")

### VECTORIZED OUTER PRODUCT ###
tic = time.process_time()
outer = np.outer(x1,x2)
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")

### VECTORIZED ELEMENTWISE MULTIPLICATION ###
tic = time.process_time()
mul = np.multiply(x1,x2)
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED GENERAL DOT PRODUCT ###
tic = time.process_time()
dot = np.dot(W,x1)
toc = time.process_time()
print ("gdot = " + str(dot) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")

>>> dot = 278
 ----- Computation time = 0.3806319999997143ms
outer = [[81 18 18 81  0 81 18 45  0  0 81 18 45  0  0]
		 [18  4  4 18  0 18  4 10  0  0 18  4 10  0  0]
		 [45 10 10 45  0 45 10 25  0  0 45 10 25  0  0]
		 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
		 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
		 [63 14 14 63  0 63 14 35  0  0 63 14 35  0  0]
		 [45 10 10 45  0 45 10 25  0  0 45 10 25  0  0]
		 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
		 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
		 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
		 [81 18 18 81  0 81 18 45  0  0 81 18 45  0  0]
		 [18  4  4 18  0 18  4 10  0  0 18  4 10  0  0]
		 [45 10 10 45  0 45 10 25  0  0 45 10 25  0  0]
		 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
		 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]]
 ----- Computation time = 0.17250400000001775ms
elementwise multiplication = [81  4 10  0  0 63 10  0  0  0 81  4 25  0  0]
 ----- Computation time = 0.08285399999996557ms
gdot = [16.30186898 29.01433709 20.08782052]
 ----- Computation time = 1.5292430000002355ms

L1 and L2 Loss

def L1(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L1 loss function defined above
    """

    loss = np.sum(abs(y-yhat))  # 1D : can be used sum(|[ ... ] - [ ... ]|)
    
    return loss

def L2(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L2 loss function defined above
    """
    
    loss = np.sum(np.dot(y-yhat, y-yhat))  # inner product, get **2
    
    return loss

W2A2

Logistic Regression with a Neural Network mindset

Dataset config

train_set_x shape: (209, 64, 64, 3)
train_set_y shape: (1, 209)
test_set_x shape: (50, 64, 64, 3)
test_set_y shape: (1, 50)

Reshape (Flatten)

train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T  # { row : 64*64*3, col : m_train }
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

train_set_x_flatten shape: (12288, 209)
train_set_y shape: (1, 209)
test_set_x_flatten shape: (12288, 50)
test_set_y shape: (1, 50)

Normalized

train_set_x = train_set_x_flatten / 255.  # normalized
test_set_x = test_set_x_flatten / 255.

General Architecture of the learning algorithm

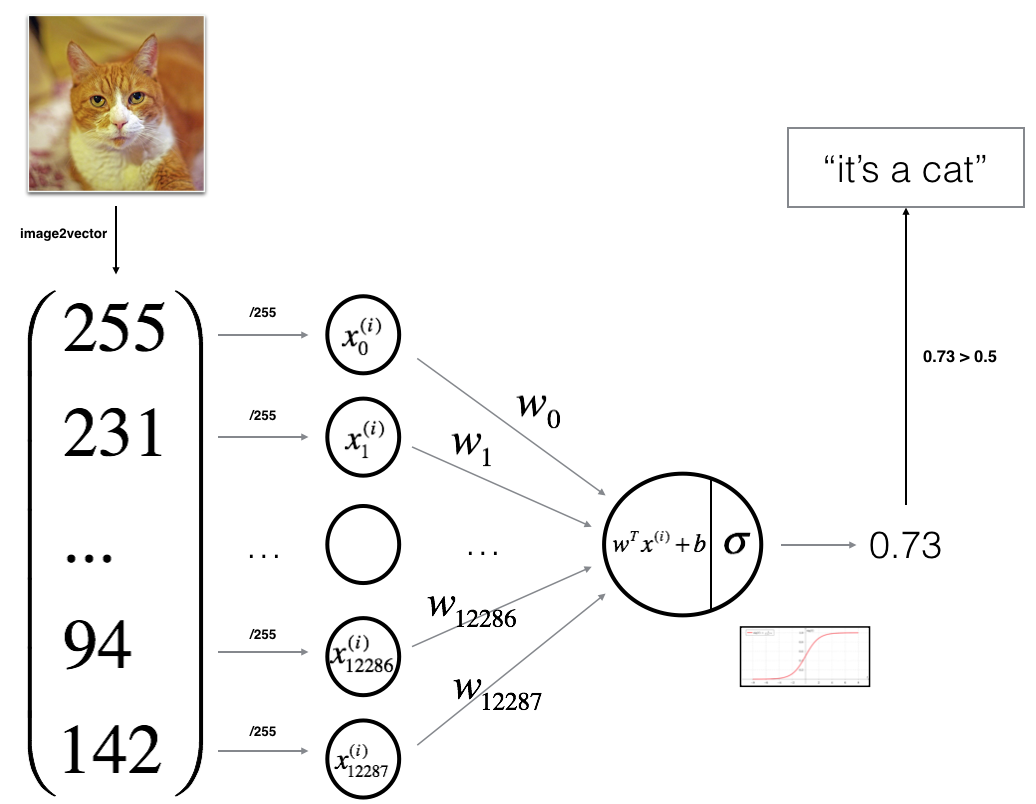
For one example $x^{(i)}$ :

z^{(i)} = w^T x^{(i)} + b \tag{1}

\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})\tag{2}

\mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})\tag{3}

The cost is then computed by summing over all training examples:

J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})\tag{6}

Initialize parameters (with 0)

def initialize_with_zeros(dim):
    """
    This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
    
    Argument:
    dim -- size of the w vector we want (or number of parameters in this case)
    )
    Returns:
    w -- initialized vector of shape (dim, 1)
    b -- initialized scalar (corresponds to the bias) of type float
    """

    w = np.zeros((dim, 1))  # not np.zeros(dim, 1) !
    b = 0.0

    return w, b

Forward propagation
- You get X
- You compute $A = \sigma(w^T X + b) = (a^{(1)}, a^{(2)}, ..., a^{(m-1)}, a^{(m)})$
- You calculate the cost function:
$J = -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)}))$
Back propagation
$\frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$ $\frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$

def propagate(w, b, X, Y):
    """
    Implement the cost function and its gradient for the propagation explained above

    Arguments:
    w -- weights, a numpy array of size (num_px * num_px * 3, 1)
    b -- bias, a scalar
    X -- data of size (num_px * num_px * 3, number of examples)
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)

    Return:
    grads -- dictionary containing the gradients of the weights and bias
            (dw -- gradient of the loss with respect to w, thus same shape as w)
            (db -- gradient of the loss with respect to b, thus same shape as b)
    cost -- negative log-likelihood cost for logistic regression
    
    Tips:
    - Write your code step by step for the propagation. np.log(), np.dot()
    """
    
    m = X.shape[1]
    
    # FORWARD PROPAGATION (FROM X TO COST)
    A = sigmoid(np.dot(w.T, X) + b)
    cost = -1/m * np.sum(Y * (np.log(A)) + (1-Y) * np.log(1-A))

    # BACKWARD PROPAGATION (TO FIND GRAD)
    dw = 1/m * np.dot(X, ((A-Y).T))
    db = 1/m * np.sum(A-Y)

    cost = np.squeeze(np.array(cost))

    grads = {"dw": dw,
             "db": db}
    
    return grads, cost

Optimization
- For a parameter $\theta$ , the update rule is $\theta = \theta - \alpha \text{ } d\theta$
- where $\alpha$ is the learning rate.

def optimize(w, b, X, Y, num_iterations=100, learning_rate=0.009, print_cost=False):
    """
    This function optimizes w and b by running a gradient descent algorithm
    
    Arguments:
    w -- weights, a numpy array of size (num_px * num_px * 3, 1)
    b -- bias, a scalar
    X -- data of shape (num_px * num_px * 3, number of examples)
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
    num_iterations -- number of iterations of the optimization loop
    learning_rate -- learning rate of the gradient descent update rule
    print_cost -- True to print the loss every 100 steps
    
    Returns:
    params -- dictionary containing the weights w and bias b
    grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
    costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
    
    Tips:
    You basically need to write down two steps and iterate through them:
        1) Calculate the cost and the gradient for the current parameters. Use propagate().
        2) Update the parameters using gradient descent rule for w and b.
    """
    
    w = copy.deepcopy(w)
    b = copy.deepcopy(b)
    
    costs = []
    
    for i in range(num_iterations):
        grads, cost = propagate(w, b, X, Y)  # check-up
        
        # Retrieve derivatives from grads
        dw = grads["dw"]
        db = grads["db"]
        
        # update rule
        w -= learning_rate * dw
        b -= learning_rate * db
        
        # Record the costs
        if i % 100 == 0:
            costs.append(cost)
        
            # Print the cost every 100 training iterations
            if print_cost:
                print ("Cost after iteration %i: %f" %(i, cost))
    
    params = {"w": w,
              "b": b}
    
    grads = {"dw": dw,
             "db": db}
    
    return params, grads, costs

Predict
- Calculate $\hat{Y} = A = \sigma(w^T X + b)$
- Convert the entries of a into 0 (if activation <= 0.5) or 1 (if activation > 0.5)

def predict(w, b, X):
    '''
    Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
    
    Arguments:
    w -- weights, a numpy array of size (num_px * num_px * 3, 1)
    b -- bias, a scalar
    X -- data of size (num_px * num_px * 3, number of examples)
    
    Returns:
    Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
    '''
    
    m = X.shape[1]
    Y_prediction = np.zeros((1, m))
    w = w.reshape(X.shape[0], 1)
    
    # Compute vector "A" predicting the probabilities of a cat being present in the picture
    A = sigmoid(np.dot(w.T, X) + b)  # (1, m)

    for i in range(A.shape[1]):
        # Convert probabilities A[0,i] to actual predictions p[0,i]
        if A[0, i] > 0.5 :
            Y_prediction[0,i] = 1
        else:
            Y_prediction[0,i] = 0
    
    return Y_prediction

Merge All Function

def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
    """
    Builds the logistic regression model by calling the function you've implemented previously
    
    Arguments:
    X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
    Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
    X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
    Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
    num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
    learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
    print_cost -- Set to True to print the cost every 100 iterations
    
    Returns:
    d -- dictionary containing information about the model.
    """
    
    w, b = initialize_with_zeros(X_train.shape[0])  # np.zeros((X_train.shape[0], 1)), 0.0
    params, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)  # {w-=, b-=}, {dw, db}, costs = [] / # be careful about num_ = 100 ,,,
    
    w = params["w"]
    b = params["b"]
    
    Y_prediction_train = predict(w, b, X_train)
    Y_prediction_test = predict(w, b, X_test)

    # Print train/test Errors
    if print_cost:
        print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
        print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))

    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test, 
         "Y_prediction_train" : Y_prediction_train, 
         "w" : w, 
         "b" : b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}
    
    return d

Training

logistic_regression_model = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=2000, learning_rate=0.005, print_cost=True)

>>> Cost after iteration 0: 0.693147
	Cost after iteration 100: 0.584508
	Cost after iteration 200: 0.466949
	Cost after iteration 300: 0.376007
	Cost after iteration 400: 0.331463
	Cost after iteration 500: 0.303273
	Cost after iteration 600: 0.279880
	Cost after iteration 700: 0.260042
	Cost after iteration 800: 0.242941
	Cost after iteration 900: 0.228004
	Cost after iteration 1000: 0.214820
	Cost after iteration 1100: 0.203078
	Cost after iteration 1200: 0.192544
	Cost after iteration 1300: 0.183033
	Cost after iteration 1400: 0.174399
	Cost after iteration 1500: 0.166521
	Cost after iteration 1600: 0.159305
	Cost after iteration 1700: 0.152667
	Cost after iteration 1800: 0.146542
	Cost after iteration 1900: 0.140872
	train accuracy: 99.04306220095694 %
	test accuracy: 70.0 %

# Plot learning curve (with costs)
costs = np.squeeze(logistic_regression_model['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(logistic_regression_model["learning_rate"]))
plt.show()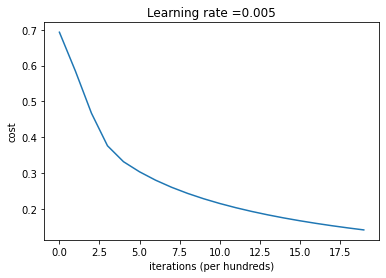

>>>

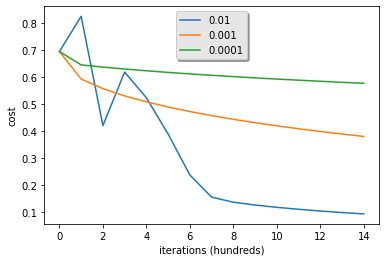
Choice of learninig rate

learning_rates = [0.01, 0.001, 0.0001]
models = {}

# for lr in learning_rates:
    # print ("Training a model with learning rate: " + str(lr))
    # models[str(lr)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=1500, learning_rate=lr, print_cost=False)
    # print ('\n' + "-------------------------------------------------------" + '\n')

for lr in learning_rates:
    plt.plot(np.squeeze(models[str(lr)]["costs"]), label=str(models[str(lr)]["learning_rate"]))

plt.ylabel('cost')
plt.xlabel('iterations (hundreds)')

legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()