Shallow Neural Network
Neural Networks Overview
-
Notation은 다음과 같이 쓸 예정이다.
- Each of X training set :
- # of Layer : , , ...

Neural Network Representation
-
2 layer NN에 대한 Architecture는 다음과 같다.
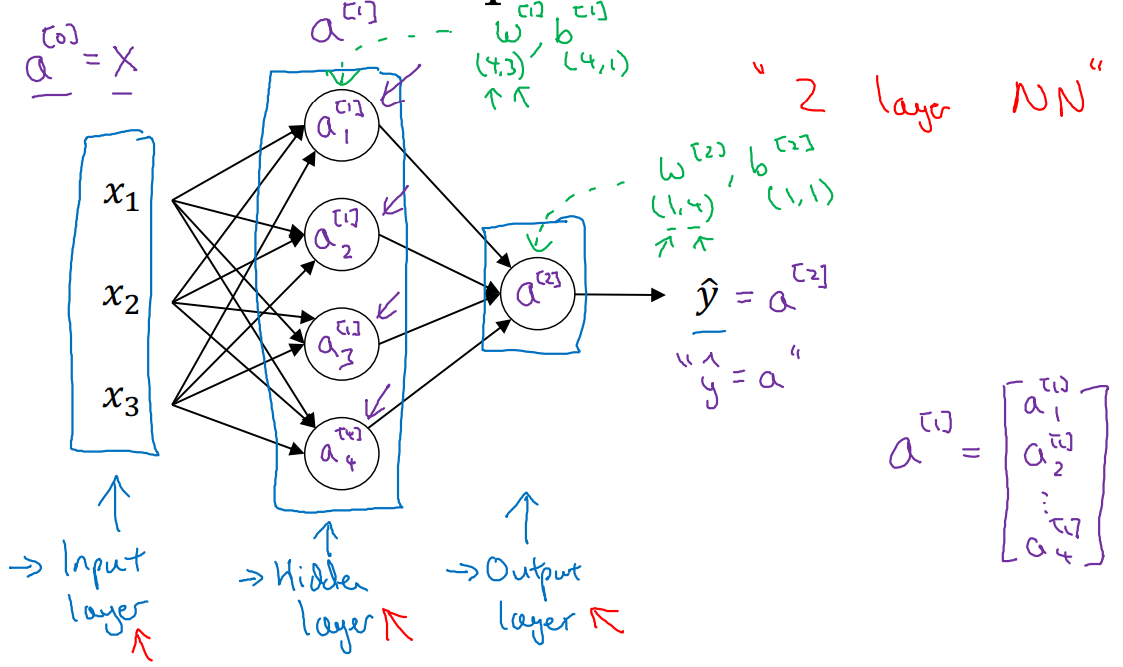
-
Input layer와 Output layer 사이에 존재하는 layer를 Hidden layer라 한다.
- Hidden layer는 observation(관측)되지 않는다.
- Input layer는 layer의 개수에 포함되지 않는다.
-
notation은 Activation까지 고려된 항이다.
-
각 layer마다 parameter(W, b)들이 독립적으로 존재하며, shape에 관해서는 이후에 알아볼 예정이다.
-
Computing a Neural Network’s Output
-
각 node 당 computation되는 과정이다.
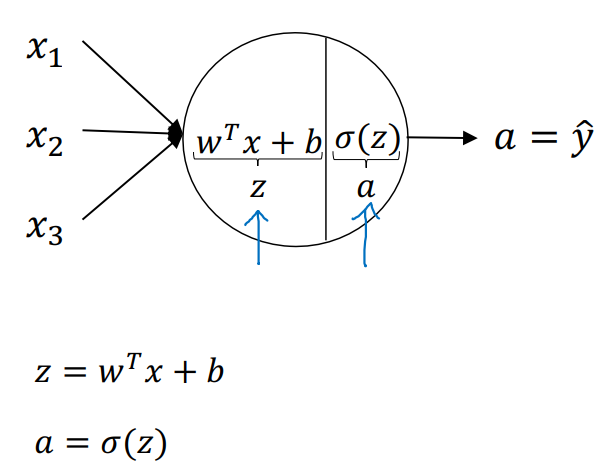
-
: 은 layer number, 는 node number in l layer로 지정한다면,
- 1 layer의 1st node와 1 layer의 2nd node 안에서 계산되는 과정의 예시이다.
- Notation에 주목하라.
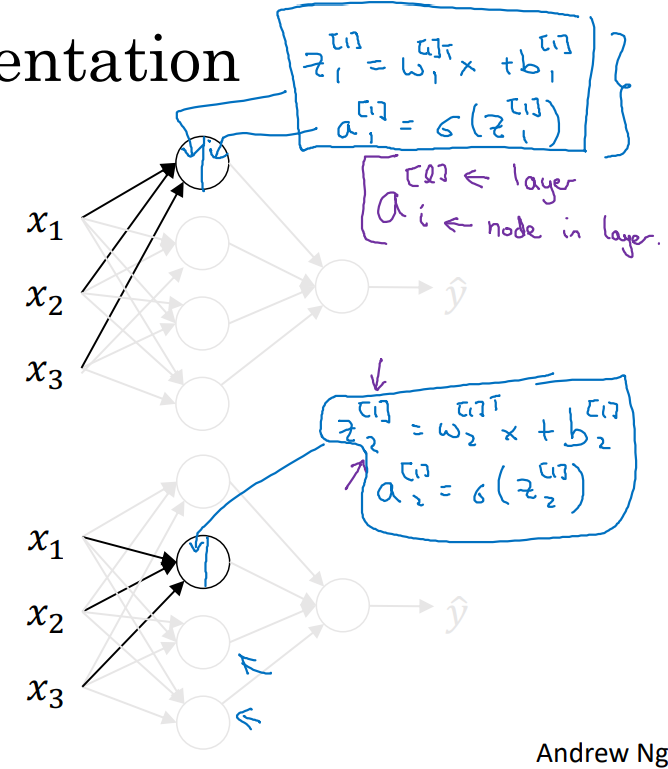
- 1 layer의 1st node와 1 layer의 2nd node 안에서 계산되는 과정의 예시이다.
-
선형 변환 의 계산 과정과 Activation 의 계산 과정을 행렬로 시각화 한 것이다.
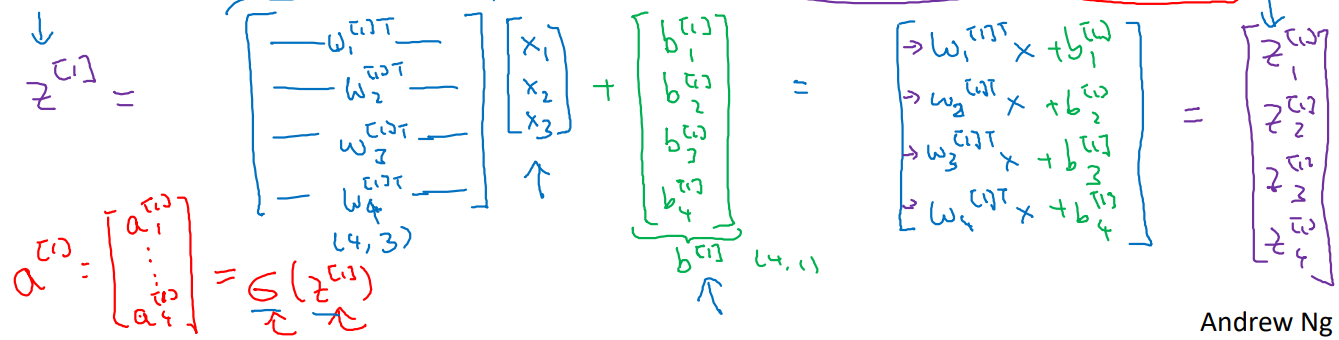
-
여기서 알 수 있는 점은 각 parameters의 shape이 아래와 같아야 한다는 점이다.
- 's shape = (next layer's # of nodes, previous layer's # of nodes)
- 's shape = (next layer's # of nodes, 1) <Broadcasting>
-
-
일반화하면 다음과 같이 정리될 수 있다.
- = 로 치환!

Vectorizing across multiple examples
-
우리가 정의한 input 의 matrix 형태는 다음과 같다.
- .shape = () = (hidden units, training examples)
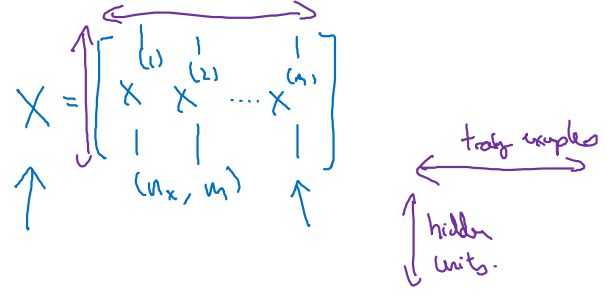
-
구해야 할 Calculating Process가 다음과 같을 때,
-
와 matrix의 형태 또한 column기준으로 stacking되어 아래와 같은 꼴로 표현되어 있을 것이다.
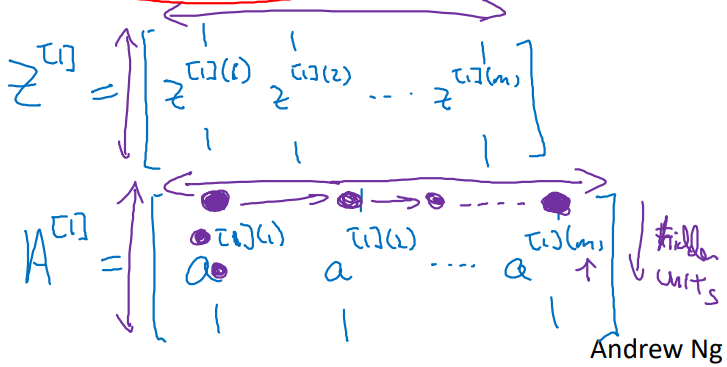
-
Explanation for vectorized implementation
-
Input data 에 대하여 parameter 와 로 linear transform한 를 구하는 과정이다.
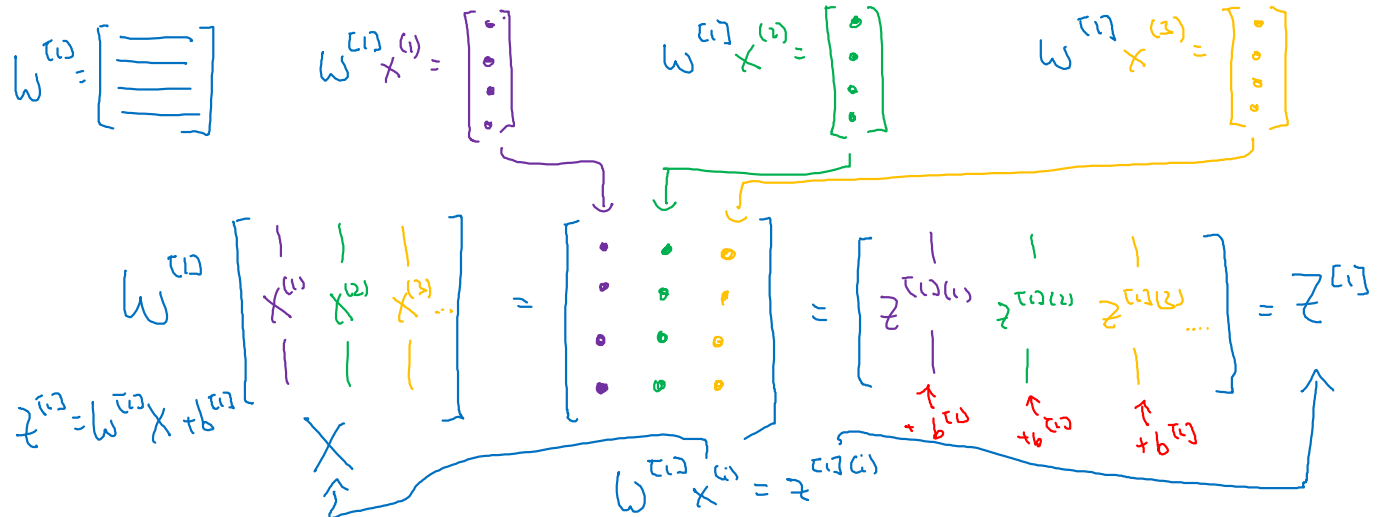
-
이렇게 matrix 형태로 stacking하여 계산하면 좋은 점은
- for loop으로 구현해야 할 과정의 불필요함을 해소해줄 수 있기 때문이다.
- 앞으로 우리는 각 samples를 vectorizing하여 계산 process에 적용할 것이다.
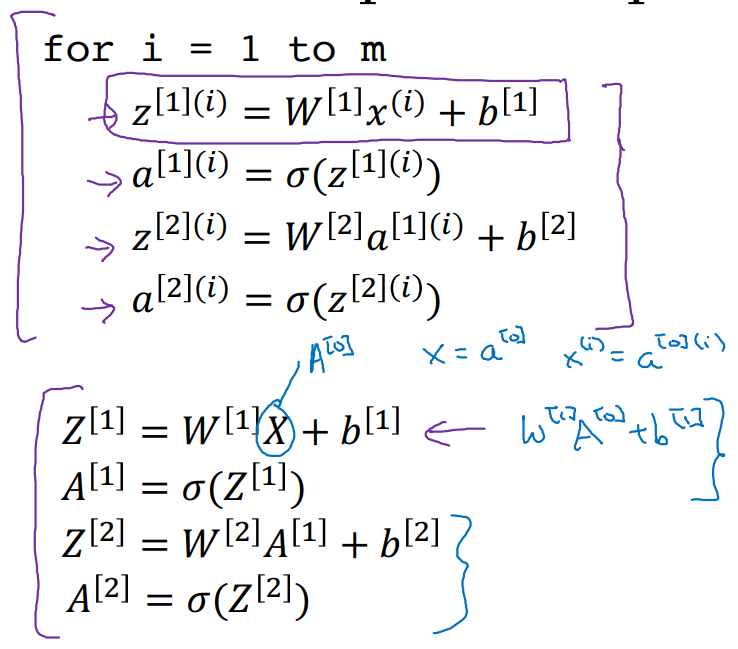
Activation functions
-
Notation
g()is non-linear function(비선형 함수), Here are more Candidates.-
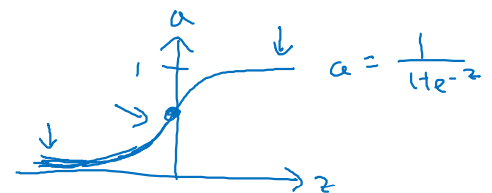
Sigmoid
- more familiar function
- 출력 범위는 (0, 1)이다. → data mean : 0.5
- Binary Classification의 출력값을 제외하곤 안 쓸 예정!
-
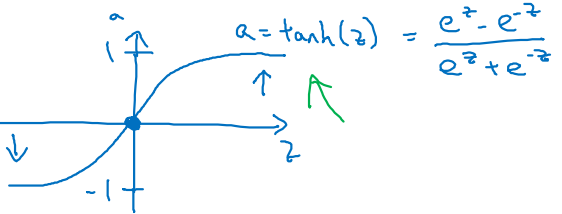
tanh (hyperbolic tangent)
- Sigmoid보다 효과가 좋다고 알려져 있다.
- 출력 범위는 (-1, 1)이다. → data mean : 0
- Zero-centerd output의 이점은 다음과 같다.
1) +/- 다양한 출력을 제공하여 모델이 더욱 빠르게 수렴할 수 있음
2) 평균이 0인 data에 한하여 더 빠르게 학습 ← data normalizing 때문
3) Gradient Vanishing 문제 감소 ← Sigmoid보다 출력 범위가 넓기 때문
-
But, Sigmoid와 tanh function의 단점은
- Gradient Vanishing : z값이 매우 크거나 매우 작을수록 gradient값이 매우 작아진다는 점이다.
- Learning slowly : parameter updating이 느려질 수 있는 문제가 있다.
-
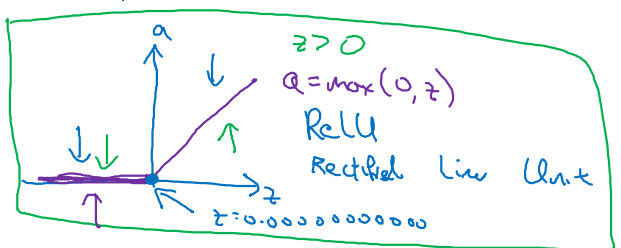
ReLU(Rectified Linear Unit)
- Very popular in Machine Learning
- Gradient when z>0 : 1, gradient when z<0 : 0
→ Gradient Vanishing 문제 완화! - z=0일 때의 gradient 값은 신경 쓸 필요 없다.
→ 완전히 0이 되는 일이 매우 드물기 때문 (0. 00000.. 값일 것)
-
But, ReLU function의 단점은 다음과 같다.
- 입력이 양수(+)인 경우에만 활성화되므로 효율적인 메모리 사용이 가능하지만,
입력이 음수(-)일 때는 해당 뉴런이 "dead"상태로 남아 영향력이 감소한다.
- 입력이 양수(+)인 경우에만 활성화되므로 효율적인 메모리 사용이 가능하지만,
-
이를 해결하기 위해 Leaky ReLU, Parametric ReLU, Exponential Linear Unit (ELU)와 같은 변종 ReLU 가족들이 나타났다.
-
Leaky ReLU
- 값은 주로 0.01
- 입력이 음수인 경우 작은 gradient를 갖게 만들어 좀 더 부드러운 출력을 생성하게 한다.

-
Parametric ReLU
- 를 학습 가능한 매개변수로 둔다.
- training 중에 업데이트 하여 데이터에 따라 적응적으로 기울기를 조절하게 만들 수 있다. → Leaky ReLU보다 좋은 성능
-
Exponential Linear Unit (ELU)
- 는 양수, 보통 1보다 작은 값을 가진다.
- ReLU나 Leaky ReLU보다 더 부드러운 함수 형태를 가진다.
→ 네트워크가 노이즈에 덜 민감하게 만들어줄 수 있다.
Why do you need non-linear activation functions?
-
-
What if the hidden layer would be linear function?
- 활성화 함수
g()를 Linear function()으로 놓고 전개하면 다음과 같다.- 마지막 줄에 주목하라.
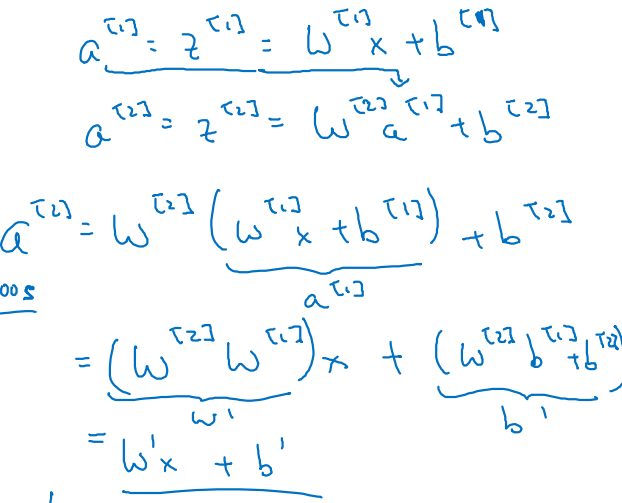
-
2개 이상의 linear function을 거쳐도 결국 하나의 linear layer를 거친 것과 같은 형태 ()를 갖는다.
- 여러 개의 linear layer로 deep neural network를 형성하는 것은 의미가 없다.
-
따라서, 우리는 다음과 같은 형태의 non-linear layer networks로 architecture를 구성할 것이다.
- 활성화 함수
g(): ReLU나 tanh 함수를 적용
- 활성화 함수
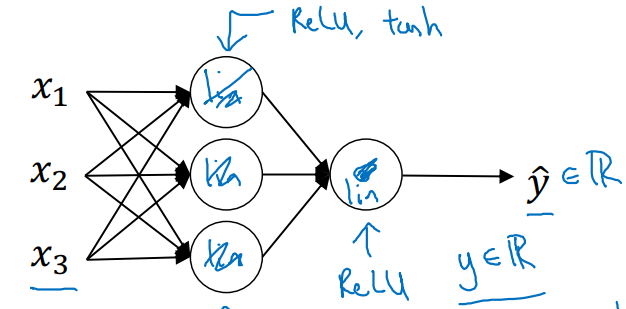
- 활성화 함수
Derivatives of activation functions
-
Sigmoid activate function
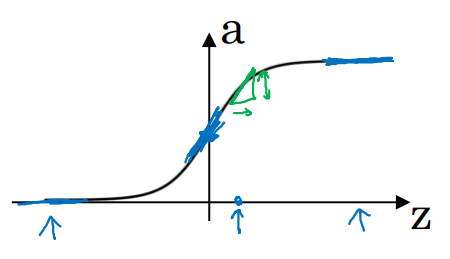
-
if z = 10)
-
if z = -10)
-
if z = 0)
-
-
tanh activate function
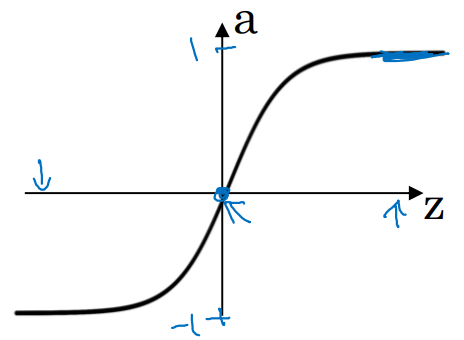
-
if z = 10)
-
if z = -10)
-
if z = 0)
-
-
ReLU activate function
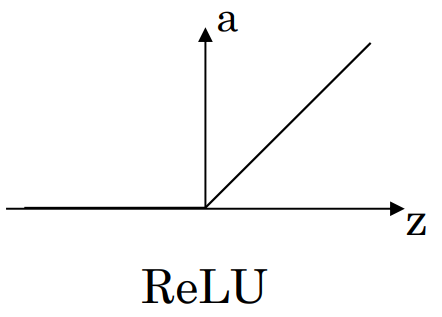
- Doesn't matter even
- 현실상 거의 불가능
- Doesn't matter even
-
Leaky ReLU activate function
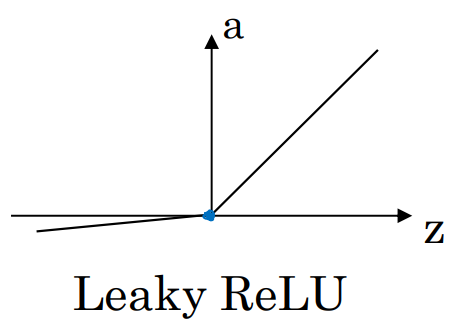
Gradient descent for neural networks
-
ex. 2 layers Neural Networks
- 네트워크 상에 존재하는 parameters와 이들의 shape을 확인해보자.
- .shape = (next layer's # of features, previous layer's # of features)
- .shape = (next layer's # of features, 1)
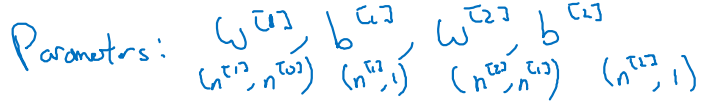
- 최적화 해야 할 (parameters에 대한) Cost function은 다음과 같다.
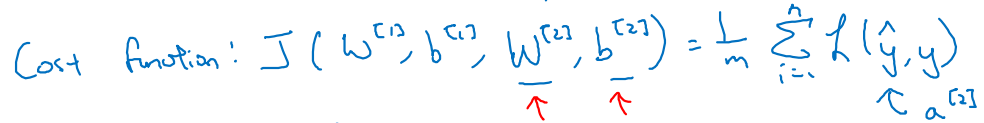
- 네트워크 상에 존재하는 parameters와 이들의 shape을 확인해보자.
-
Gradient descent의 학습 과정은 아래와 같다.
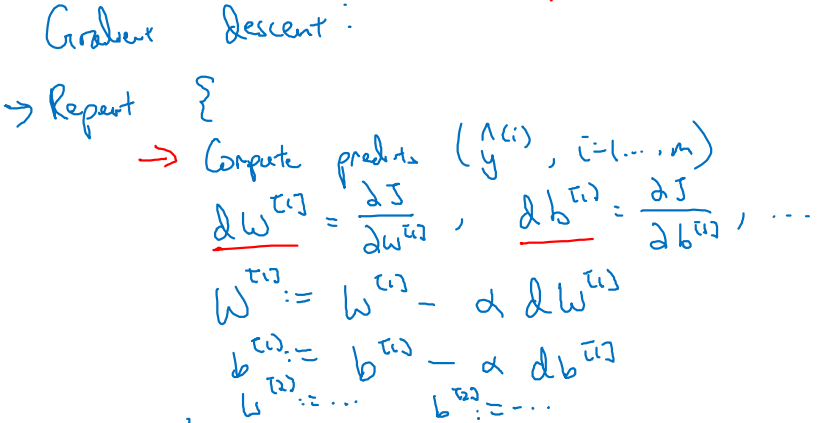
- 정답 추론값 을 구한다.
- 각 parameters에 대한 Cost 의 미분값을 구한다.
- 적절한 learning rate를 설정하여 parameters를 update한다.
- 반복...
-
을 구하기까지의 Forward propagation이다.
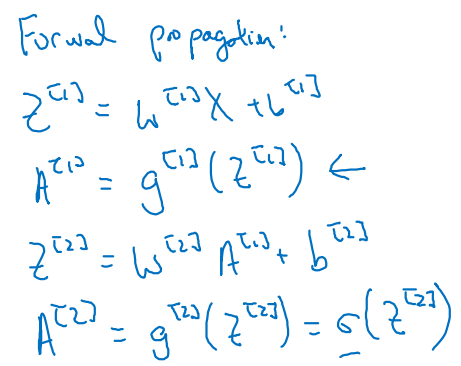
- 와 로 미분한 Cost 를 구하는 Backpropagation 과정이다.
keepdims = True로 놓으면 (4,)가 아닌 (4, 1)의 shape 형태를 유지한다.
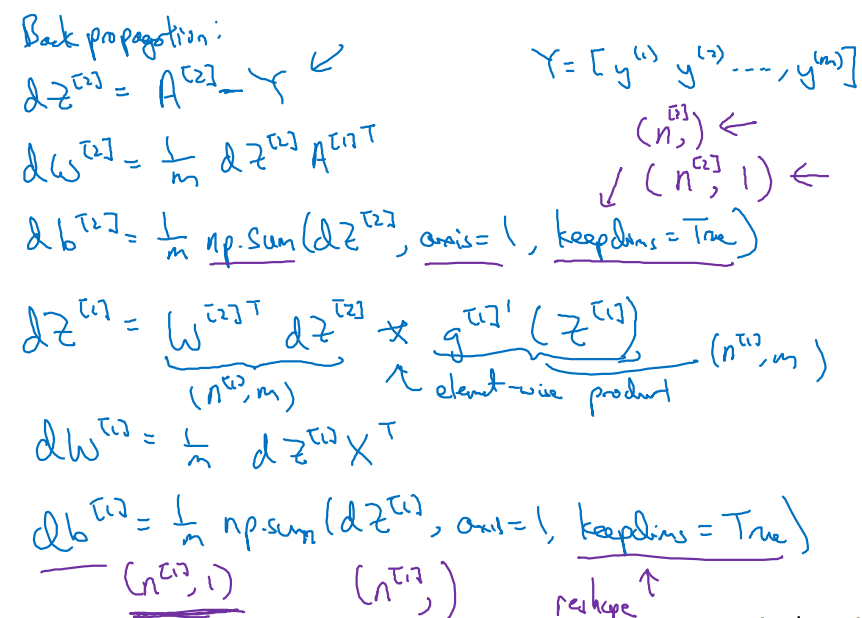
- Forward propagation 계산 식에서 봤다시피 Activation은 sigmoid 함수다.
- 해당 수식이 왜 이렇게 전개가 되는지는 다음 챕터를 통해 살펴보겠다.
- 와 로 미분한 Cost 를 구하는 Backpropagation 과정이다.
Backpropagation intuition (Optional)
-
Loss에 관한 미분 와 를 chain rule을 사용하여 전개해보자.
-
-
By
-
-
By
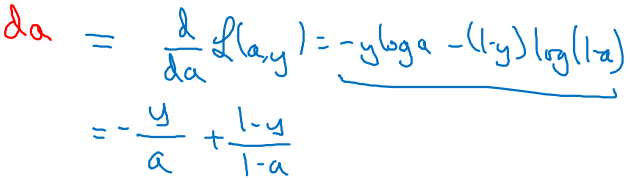
-
-
By
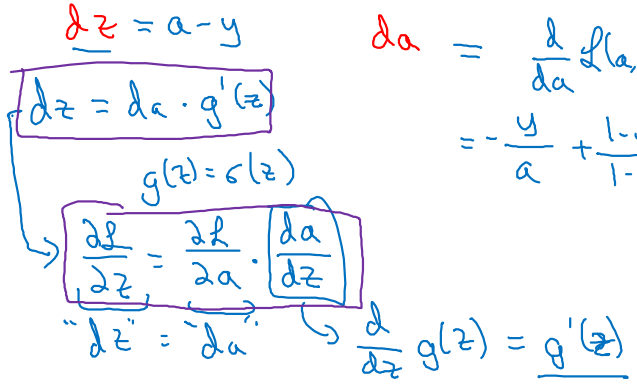
-
-
By
-
-
-
cf. )
→ →
-
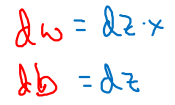
-
-
위의 전개 과정은 하나의 node에 대한 Backpropagation이었다.
- 같은 과정을 다른 node에 적용하면 term에만 차이가 있을 뿐 결과는 비슷하다.
- 가 들어갈 자리에 앞선 layer의 추론값 를 넣어주면 된다.
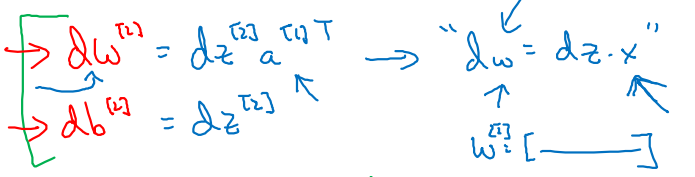
- 같은 과정을 다른 node에 적용하면 term에만 차이가 있을 뿐 결과는 비슷하다.
-
이를 바탕으로, 최종 parameter까지 연결되는 과정을 전개해보자.
-
-
By (transpose)
-
-
By < : sigmoid>
-
-
By
-
-
Summary of gradient descent
- 각 node별 gradient descent
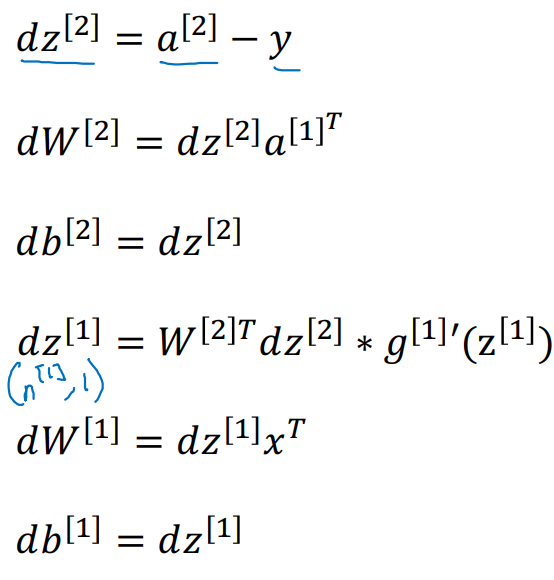
- 전체 행렬로 묶은 layer들의 gradient descent
- Training samples 개수인 m으로 평균 내어 주어야 한다.

Random Initialization
-
What happens if you initialize weights to zero?
- 다음과 같은 Architecture가 있다고 가정해보자.
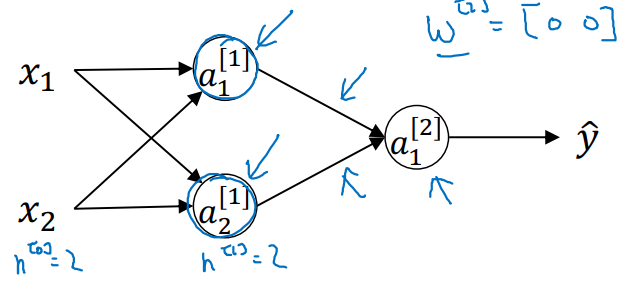
- 첫 layer의 parameter들을 0으로 초기화했다고 가정하면,

-
이러한 결과는
- Activation 이후의 결과를 모두 같게 만들어버린다.
- Backpropagation시 업데이트 될 parameter들의 diversity를 해친다.
→ 각 층의 가중치가 동일하게 업데이트 되므로

-
Parameter matrix의 행별 성분이 모두 같다면 해당 architecture는 symmetric 해진다.
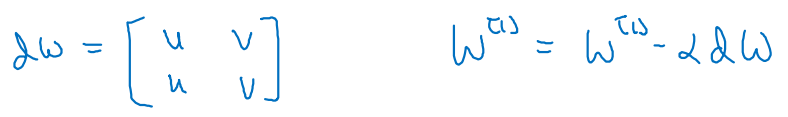
-
Network가 symmetric하다는 말은 (Bad)
- 가중치와 편향이 모두 동일한 값으로 설정되어 있다는 뜻이며,
- 학습 중에 각 층이 비슷한 기능을 수행하게 되어 모델의 표현 능력을 제한한다.

-
-
따라서 Random initialization을 채택한다.
- 코드로 나타내는 방법은 다음과 같다.
- 0.01의 small number를 곱해주는 이유는 gradient vanishing문제를 피하기 위해서다.
- tanh activate function을 예로 들면(아래 그림), 0에 가까운 값일수록(초록색) gradient는 dynamic하다.
- 반대로 100을 곱하게 되면(빨간색) gradient는 거의 0에 가까운 값이 되어 더이상 parameter updating이 진행되지 않는다.

-
더불어 Xavier(Glorot) 초기화나 He 초기화와 같은 방법론들이 있다.
-
Xavier(Glorot) 초기화
- 장점:
- 단점:
-
He 초기화
- 장점:
- 단점:
-
- 코드로 나타내는 방법은 다음과 같다.
Assignment
W3A1
Planar data classification with one hidden layer
-
Simple Logistic Regression
- 아래와 같은 Binary Classification task의 Planar dataset이 주어진다고 해보자.
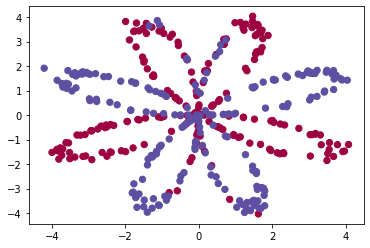
-
우리는 sklearn 패키지를 사용하여 쉽게 추론할 수 있다.
# Train the logistic regression classifier
clf = sklearn.linear_model.LogisticRegressionCV();
clf.fit(X.T, Y.T);- Plot decision boundary
# Plot the decision boundary for logistic regression
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
plt.title("Logistic Regression")
# Print accuracy
LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
'% ' + "(percentage of correctly labelled datapoints)") 
-
2 layer Neural Network model을 기획해보자.
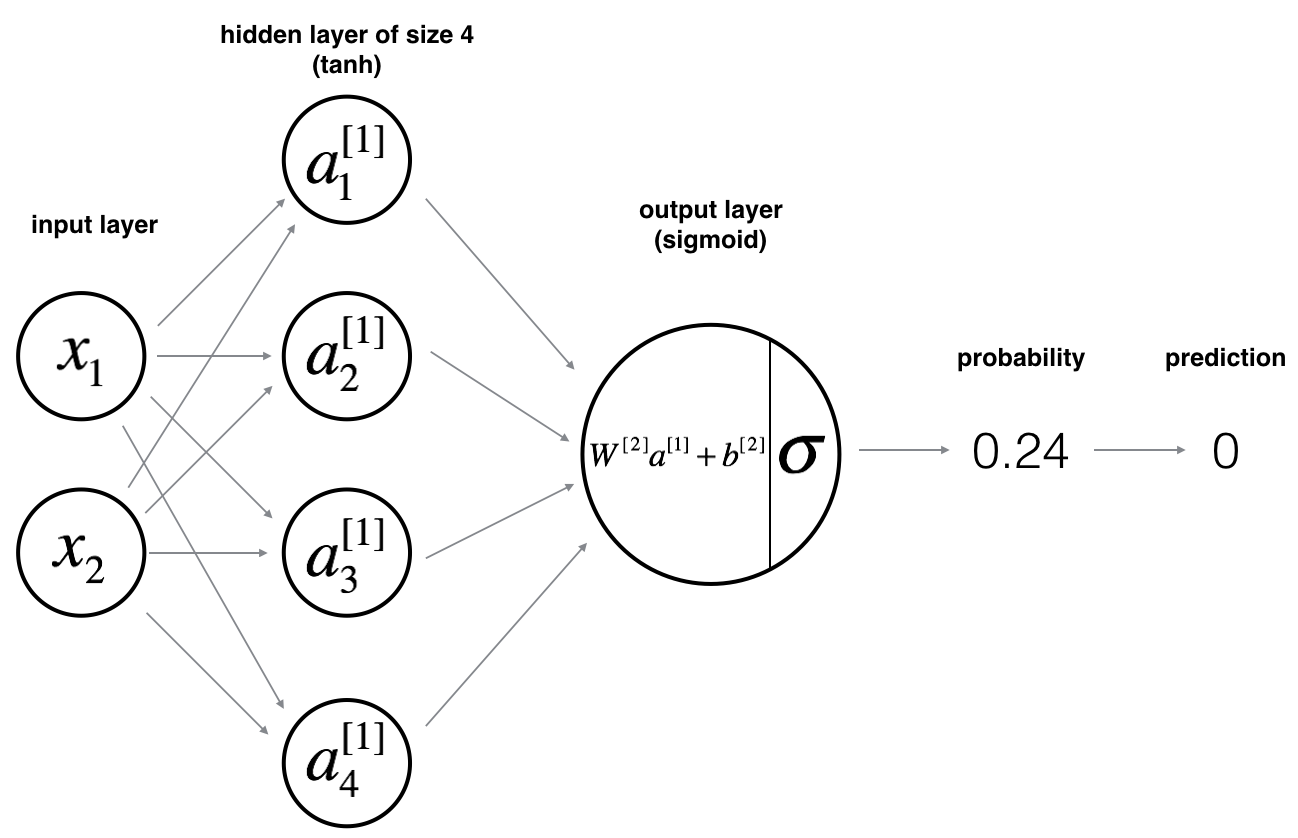
-
각 layer size를 결정하여 (n_x, n_h, n_y)의 형태로 손쉽게 가져다 쓰는 함수를 작성했다.
def layer_sizes(X, Y):
"""
Arguments:
X -- input dataset of shape (input size, number of examples)
Y -- labels of shape (output size, number of examples)
Returns:
n_x -- the size of the input layer
n_h -- the size of the hidden layer
n_y -- the size of the output layer
"""
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0] # 0 or 1 labels
return (n_x, n_h, n_y)- parameter matrix values를 initializing하는 함수를 작성했다.
- W는 random value * 0.01 값을 갖도록 만들었으며 b는 0으로 초기화했다.
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
params -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters-
아래의 수식에 따라 Forward Propagation을 구현하였다.
- 계산 완료한 값들은
cache에 넣어 backprop에 활용할 것이다! - 마지막 layer A2는 sigmoid()를 적용한 뒤의 출력값이다.
- 계산 완료한 값들은
def forward_propagation(X, parameters):
"""
Argument:
X -- input data of size (n_x, m)
parameters -- python dictionary containing your parameters (output of initialization function)
Returns:
A2 -- The sigmoid output of the second activation
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
"""
# Retrieve each parameter from the dictionary "parameters"
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1) # hidden layer
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2) # output layer
assert(A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache- Binary Cross Entropy Cost function을 구현하면 다음과 같다.
def compute_cost(A2, Y):
"""
Computes the cross-entropy cost given in equation (13)
Arguments:
A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
Returns:
cost -- cross-entropy cost given equation (13)
"""
m = Y.shape[1] # number of examples
# Compute the cross-entropy cost
logprobs = Y * np.log(A2) + (1-Y) * np.log(1-A2)
cost = -1/m * np.sum(logprobs) #cost = - (1/m) * (np.dot(np.log(A2), Y.T) + np.dot(np.log(1-A2), (1-Y).T))
cost = float(np.squeeze(cost)) # makes sure cost is the dimension we expect.
# E.g., turns [[17]] into 17
return cost- 아래의 수식에 따라 Backpropagation을 구현하였다.

def backward_propagation(parameters, cache, X, Y):
"""
Implement the backward propagation using the instructions above.
Arguments:
parameters -- python dictionary containing our parameters
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
X -- input data of shape (2, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
Returns:
grads -- python dictionary containing your gradients with respect to different parameters
"""
m = X.shape[1]
# First, retrieve W1 and W2 from the dictionary "parameters".
W1 = parameters['W1']
W2 = parameters['W2']
# Retrieve also A1 and A2 from dictionary "cache".
A1 = cache['A1']
A2 = cache['A2']
# Backward propagation: calculate dW1, db1, dW2, db2.
dZ2 = A2 - Y
dW2 = 1/m * np.dot(dZ2, A1.T)
db2 = 1/m * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = 1/m * np.dot(dZ1, X.T)
db1 = 1/m * np.sum(dZ1, axis=1, keepdims=True)
# YOUR CODE ENDS HERE
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads- Gradient 값이 저장되어 있는
graddictionary를 받아와 parameter 업데이트를 진행한다.- 기존 matrix를 deepcopy하여 저장해두고, 업데이트를 완료한 뒤 재저장한다.
def update_parameters(parameters, grads, learning_rate = 1.2):
"""
Updates parameters using the gradient descent update rule given above
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients
Returns:
parameters -- python dictionary containing your updated parameters
"""
# Retrieve a copy of each parameter from the dictionary "parameters". Use copy.deepcopy(...) for W1 and W2
W1 = copy.deepcopy(parameters['W1'])
b1 = copy.deepcopy(parameters['b1'])
W2 = copy.deepcopy(parameters['W2'])
b2 = copy.deepcopy(parameters['b2'])
# Retrieve each gradient from the dictionary "grads"
dW1 = grads['dW1']
db1 = grads['db1']
dW2 = grads['dW2']
db2 = grads['db2']
# Update rule for each parameter
W1 -= learning_rate * dW1
b1 -= learning_rate * db1
W2 -= learning_rate * dW2
b2 -= learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters- 위 함수들을 바탕으로 최종 nn_model()을 작성해보자.
cache에 A2도 들어있다.
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
"""
Arguments:
X -- dataset of shape (2, number of examples)
Y -- labels of shape (1, number of examples)
n_h -- size of the hidden layer
num_iterations -- Number of iterations in gradient descent loop
print_cost -- if True, print the cost every 1000 iterations
Returns:
parameters -- parameters learnt by the model. They can then be used to predict.
"""
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# Initialize parameters
parameters = initialize_parameters(n_x, n_h, n_y)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
# A2, cache = ...
# Cost function. Inputs: "A2, Y". Outputs: "cost".
# cost = ...
# Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
# grads = ...
# Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
# parameters = ...
A2, cache = forward_propagation(X, parameters)
cost = compute_cost(A2, Y)
grads = backward_propagation(parameters, cache, X, Y)
parameters = update_parameters(parameters, grads, learning_rate = 1.2)
# Print the cost every 1000 iterations
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters-
우리는 Binary Classification 문제를 해결하려 했기 때문에 sigmoid() 출력값인 A2를 정답 probability(확률)으로 이용한다.
- A2가 0.5 초과면 label 1, 0.5 이하면 label 0으로 정답 추론값을 뽑아낸다.
def predict(parameters, X):
"""
Using the learned parameters, predicts a class for each example in X
Arguments:
parameters -- python dictionary containing your parameters
X -- input data of size (n_x, m)
Returns
predictions -- vector of predictions of our model (red: 0 / blue: 1)
"""
# Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.
A2, cache = forward_propagation(X, parameters)
predictions = (A2 > 0.5) # A2 : 추론된 확률
return predictions- 이제 모델에 데이터를 넣어 predict를 진행해보자.
# Build a model with a n_h-dimensional hidden layer
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
# Plot the decision boundary
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
>>> Cost after iteration 0: 0.693162
Cost after iteration 1000: 0.258625
Cost after iteration 2000: 0.239334
Cost after iteration 3000: 0.230802
Cost after iteration 4000: 0.225528
Cost after iteration 5000: 0.221845
Cost after iteration 6000: 0.219094
Cost after iteration 7000: 0.220661
Cost after iteration 8000: 0.219409
Cost after iteration 9000: 0.218485 
-
Accuracy는 아래와 같은 수식과 code로 전개된다.
- Y와 predictions 간의 TP 유사도와 TN 유사도를 구한다.
- (TP + TN)를 전체 데이터로 나누어 정답을 맞힌 비율을 판단한다.
# Print accuracy
predictions = predict(parameters, X)
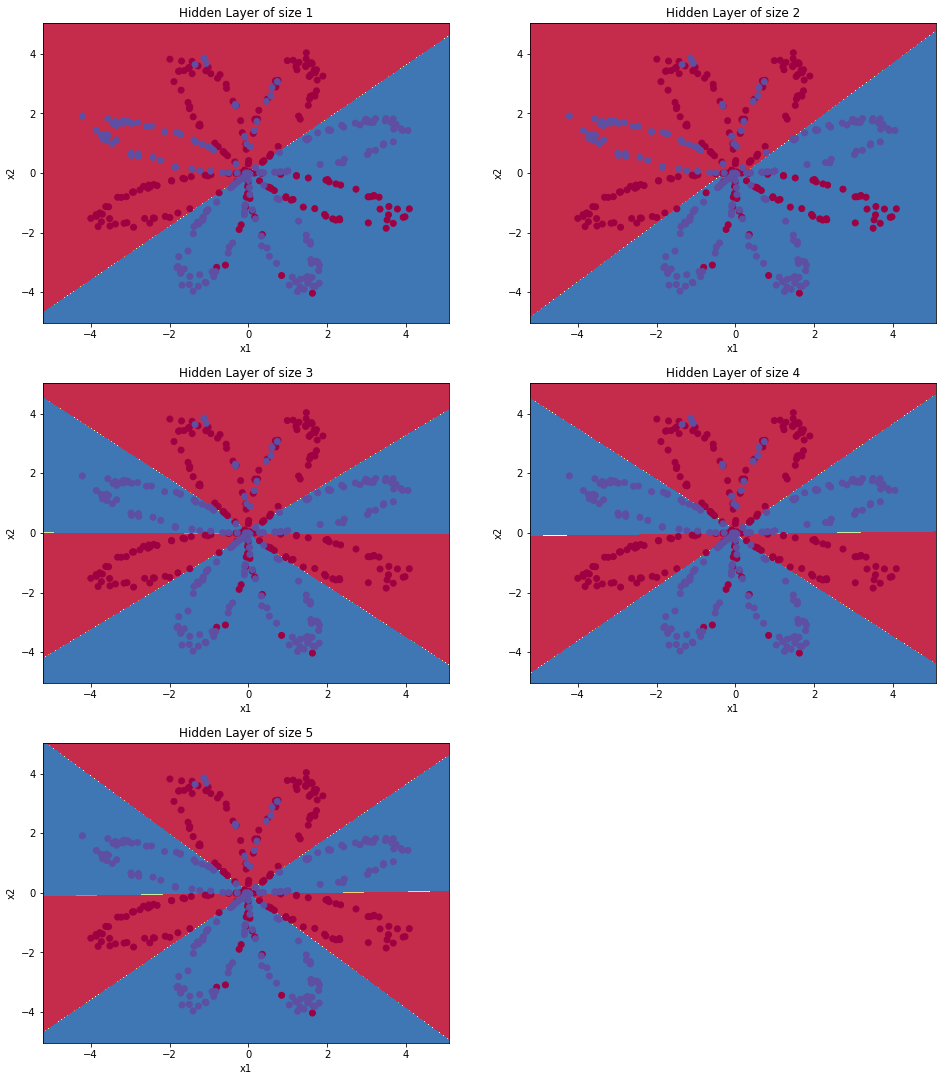
print ('Accuracy: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')- Hidden layer size를 늘려가면서 plot한 결과를 살펴보자.
- layer가 깊어질수록(deep) 분류 성능이 높아져가는 것을 시각화하였다.
# This may take about 2 minutes to run
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5]
# you can try with different hidden layer sizes
# but make sure before you submit the assignment it is set as "hidden_layer_sizes = [1, 2, 3, 4, 5]"
# hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y,predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size)*100)
print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))