Lecture 14: Location, Scale, and LOTUS

Properties of Normal Distribution

• $Z \sim N(0, 1)$

• CDF $\Phi$

• $E(Z) = 0$

• $Var(Z) = E(Z^2) = 1$

• $E(Z^3) = 0$

  • $\int_{-∞}^{∞} z^3 \displaystyle \frac{1}{\sqrt{2 \pi}} e^{-z^2/2} dz$ (odd fn)
  • "3rd moment"

• $- Z \sim N(0, 1)$ (symmetry)

  • Let $X = \mu + \sigma Z$, $\mu \in \R$ (mean, location), $\sigma > 0$ (SD, scale)

  • Then we say $X \sim N(\mu, \sigma^2)$

    • $E(X) = \mu$

    • $Var(\mu + \sigma Z) = \sigma^2 Var(Z) = \sigma^2$

      • $Var \ge 0$; $Var(X) = 0$ if and only if $P(X=a) = 1$ for some $a$

      • $Var(X) = E((X-EX)^2) = EX^2 - (EX)^2$

      • $Var(X+c) = Var(X)$

      • $Var(cX) = c^2 Var(X)$

      • $Var(X+Y) \ne Var(X) + Var(Y)$ in general, not linear
        [equal if $X$, $Y$ are indep.]

      • $Var(X+X) = Var(2X) = 4Var(X)$

    • Standardization(표준화) : $Z = \displaystyle \frac{X-\mu}{\sigma}$

      • Simple and Useful transformation!

      • 단위를 제거할 수 있으므로 무차원 변환하여 해석 가능

Find PDF of $N(\mu, \sigma^{2})$

• CDF :

  $P(X \le x) = P(\displaystyle \frac{X-\mu}{\sigma} \le \displaystyle \frac{x-\mu}{\sigma})$

  $= \Phi (\displaystyle \frac{x-\mu}{\sigma})$
  

• Derivative of CDF : PDF!

  $= \displaystyle \frac{1}{\sigma \sqrt{2 \pi}} e^{-(\displaystyle \frac{x-\mu}{\sigma})^2/2}$

  • 합성함수 미분 : $\displaystyle \frac{1}{\sigma} \Phi' (\displaystyle \frac{x-\mu}{\sigma})$

• $-X = -\mu + \sigma(-Z) \sim N(-\mu, \sigma^2)$

  • Later we'll show : if $X_j \sim X_j \sim N(\mu_j, \sigma_j^2)$ indep.
  • $X_1 + X_2 \sim N(\mu_1 + \mu_2, \sigma_1^2, \sigma_2^2)$
  • $X_1 - X_2 \sim N(\mu_1 - \mu_2, \sigma_1^2, \sigma_2^2)$

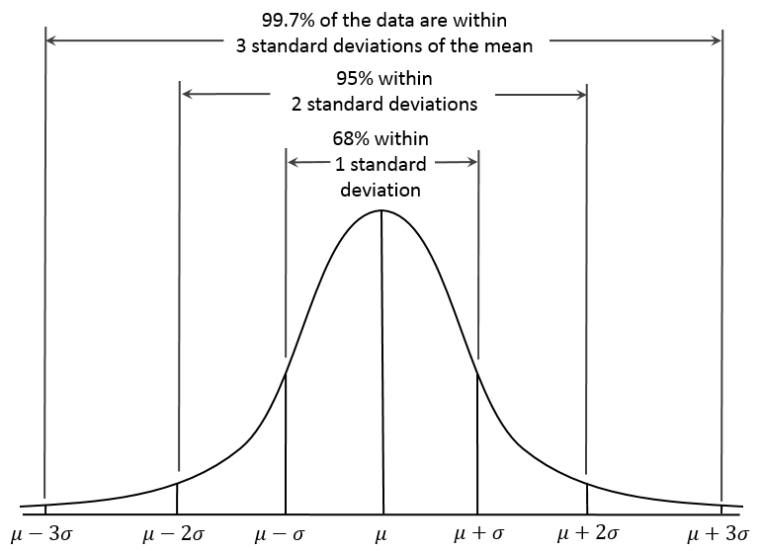
• 68-95-99.7% Rule, $X \sim N(\mu, \sigma^2)$

  • $P(|X-\mu| \le \sigma) \approx 0.68$
  • $P(|X-\mu| \le 2\sigma) \approx 0.95$
  • $P(|X-\mu| \le 3\sigma) \approx 0.99.7$

  

Calculations of Poission Distribution

Prob.	$P_0$	$P_1$	$P_2$	$P_3$	...
$X$	$0$	$1$	$2$	$3$	...
$X^2$	$0^2$	$1^2$	$2^2$	$3^2$	...

• $E(X) = \sum_{x} x P(X = x)$

• $E(X^2) = \sum_{x} x^2 P(X = x)$

• $X \sim Pois(\lambda)$

  • $E(X) = \lambda$

  • $E(X^2) = \displaystyle \sum_{k = 0}^{∞} \displaystyle \frac{k^2 e^{-\lambda} \lambda^k}{k!}$

    • $\displaystyle \sum_{k=0}^{∞} \displaystyle \frac{\lambda^k}{k!} = e^{\lambda}$

    • $\lambda \displaystyle \sum_{k=1}^{∞} \displaystyle \frac{k \lambda^{k-1}}{k!} = \lambda e^{\lambda}$ (Derivative)

    • $\displaystyle \sum_{k=1}^{∞} \displaystyle \frac{k \lambda^{k}}{k!} = \lambda e^{\lambda}$

    • $\displaystyle \sum_{k=0}^{∞} \displaystyle \frac{k^2 \lambda^{k-1}}{k!} = \lambda e^{\lambda} + e^{\lambda} = e^{\lambda}(\lambda+1)$ (Derivative again)

  • $E(X^2) = e^{-\lambda} e^{\lambda} \lambda (\lambda+1) = \lambda^2 + \lambda$

  • $Var(X) = \lambda^2 + \lambda - \lambda^2 = \lambda$

    • 평균과 분산이 같다!

Find $Var(X)$, $X \sim Bin(n, p)$

• $X = I_1 + ... + I_n$, $I_j$ $\sim i.i.d. Bern(p)$

  • $X^2 = I_1^2 + ... I_n^2 + 2 I_1 I_2 + 2 I_1 I_3 + ... 2 I_{n-1}I_{n}$

  • $E(X^2) = nE(I_1^2) + 2 \begin{pmatrix}n\\2\\ \end{pmatrix} E(I_1 I_2)$ [indicator of succession both trials 1, 2]

    $= np + n(n-1)p^2 = np + n^2 p^2 - np^2$

    $\Rightarrow Var(X) = np - np^2 = np(1-p) = npq$, $q=1-p$

Prove LOTUS for discrete sample space

• Show $E(g(X)) = \displaystyle \sum_{x} g(x) P(X=x)$

• $\displaystyle \sum_{x} g(x) P(X=x)$ [grouped] $= \displaystyle \sum_{s \in S} g(X(s)) P(\{s\})$ [ungrouped] (Pebble World)

  • $\displaystyle \sum_{x} \displaystyle \sum_{S: X(s) = x} g(X(s)) P(\{s\})$ [Definitely]

    $= \displaystyle \sum_{x} g(x) \displaystyle \sum_{S: X(s) = x} P(\{s\})$

    $= \displaystyle \sum_{x} g(x) P(X=x)$ [Sum of the pebbles mass]

---

• 출처 : Statistics 110, boostcourse