Lecture 15: Midterm Review

Coupon colletor(toy collector)

• n toy types, equally likeyly, Find expected time $T$ (i.e. # toys) until have complete set.

  • n 가지 장난감을 모아야 전체를 모은다고 할 때, 장난감 전부를 모으는 데까지 걸리는 시간 T(뽑아야 하는 장난감 수)의 기댓값을 구하시오.

    • $T = T_1 + T_2 + ... + T_n$
    • $T_1$ = (time until 1st new toy) = 1
    • $T_2$ = (additional time until 2nd new toy)
    • $T_3$ = (... 3rd)

  • $T_1$ = 1, $T_2 - 1 \sim Geom(\displaystyle \frac{n-1}{n})$, ...

    • $T_2$ is probability of new one that would not be the same as $T_1$ item.

  • $T_j - 1 \sim Geom(\displaystyle \frac{n-(j-1)}{n})$

  • $E(T) = E(T_1) + ... + E(T_n)$

    • At Geometry distribution with 1(1st term), $E(X) = 1+ \displaystyle \frac{q}{p} = \displaystyle \frac{1}{p}$

  • $E(T) = 1 + \displaystyle \frac{n}{n-1} + \displaystyle \frac{n}{n-2} + ... +\displaystyle \frac{n}{1} = n(1 + \displaystyle \frac{1}{2} + \displaystyle \frac{1}{3} + ...)$

    $\approx n log n$ for large n

Universality

• $F(x_0) = \displaystyle \frac{1}{3}$

  $P(F(X) \le \displaystyle \frac{1}{3})$

  $= P(X \le x_0)$

  $= F(x_0) = \displaystyle \frac{1}{3}$, $F(X) \sim Unif(0, 1)$

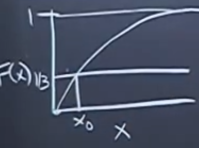
• Logistic distribution

  $F(x) = \displaystyle \frac{e^x}{1 + e^x}$

  $U \sim Unif(0, 1)$,

  $F^{-1}(U) = log \displaystyle \frac{U}{1-U}$ is logistic.

Symmetry

• Let $X$, $Y$, $Z$ be i.i.d. positive r.v.s.

  • Find $E(\displaystyle \frac{X}{X+Y+Z}) = E(\frac{X}{X+Y+Z}) = E(\frac{Z}{X+Y+Z})$ (symmetry)

    • $E(\displaystyle \frac{X}{X+Y+Z}) + E(\frac{X}{X+Y+Z}) + E(\frac{Z}{X+Y+Z})$ (linearity)

      $= E(\displaystyle \frac{X+Y+Z}{X+Y+Z}) = 1$

      $\Rightarrow E(\displaystyle \frac{X}{X+Y+Z}) = \frac{1}{3}$

LOTUS

• $U \sim Unif(0, 1)$, $X=u^2$, $Y=e^{X}$, Find $E(Y)$ as an integral.

  • $E(Y) = \int_{0}^{1} e^{x} f(x) dx$, $f(x)$ is PDF of $X$

    • CDF: $P(U^2 \le x) = P(U \le \sqrt{x}) = \sqrt{x}$ if $0 < x < 1$

    • $f(x) = \displaystyle \frac{1}{2} x^{-1/2}$, $x \in (0, 1)$

  • Better way: $E(Y) = \int_{0}^{1} e^{u^2} du$

Practice

• $X \sim Bin(n, p)$, find distribution of n-X.

  • PMF: $P(n-X=k) = P(X=n-k) = \begin{pmatrix}n\\n-k\\ \end{pmatrix} p^{n-k} q^{k} = \begin{pmatrix}n\\k\\ \end{pmatrix} q^{k} p^{n-k}$

  • Story: $n-X \sim Bin(n, q)$, by swapping "success" and "failure"

Poisson distribution

• Example: # emails I get in time $t$ is $Pois(\lambda t)$

  • Find PDF(or CDF) of $T$, time of 1st email.

• $P(T > t) = P(N_t = 0)$ with $N_t$ = (# emails in [0, $t$])

  • $e^{-\lambda t} (\lambda t)^0 (0)! = e^{-\lambda t}$

  • CDF is $1- e^{-\lambda t}$, $t > 0$

• 출처 : Statistics 110, boostcourse