Lecture 18: MGFs Continued

Expo MGF

• $X \sim Expo(1)$, find MGF, moments

  cf. 물리학에서의 관성 모멘트와 분산이 관련이 있음

  • MGF: $M(t) = E(e^{tx}) = \int_{0}^{∞} e^{tx} e^{-x} dx = \int_{0}^{∞} e^{-x(1-t)} dx = \displaystyle \frac{1}{1-t}$, $t < 1$

    • $\int_{0}^{∞} e^{-ax} = \displaystyle \frac{1}{-a} e^{-ax} \biggr|_{0}^{∞} = \frac{1}{a}$

  • Derivative: $M'(0) = E(X)$, $M''(0) = E(X^2)$, $M'''(0) = E(X^3)$, ...

    • $|t| < 1$, $\displaystyle \frac{1}{1-t} = \sum_{n=0}^{∞} t^n$ (taylor expansion)

    • $\displaystyle \sum_{n=0}^{∞} n! \frac{t^n}{n!} \Rightarrow E(X^n) = n!$

  • $Y \sim Expo(\lambda)$, let $X = \lambda Y \sim Expo(1)$,

    • so $Y^n = \displaystyle \frac{X^n}{\lambda^n} \Rightarrow E(Y) = \frac{n!}{\lambda^n}$

Standard Normal MGF

• Let $Z \sim N(0, 1)$, find all its moments.

  • $E(Z^n) = 0$ for n odd by symmetry.

  • MGF: $M(t) = e^{t^2/2} = \displaystyle \sum_{n=0}^{∞} \frac{(t^2/2)^n}{n!} = \sum_{n=0}^{∞} \frac{t^{2n}}{2^n • n!} = \sum_{n=0}^{∞} \frac{t^{2n} (2n!)}{(2n!) \;2^n • n!}$

  $\Rightarrow E(Z^{2n}) = \displaystyle \frac{(2n!)}{2^n • n!}$ $\begin{cases} n=1 \Rightarrow {E(Z^2) = 1 = 1} \\ n=2 \Rightarrow {E(Z^4) = 3 = 1 • 3} \\ n=3 \Rightarrow {E(Z^6) = 1 • 3 • 5 = 15} \\ \end{cases}$

Poission MGF

• $X \sim Pois(\lambda)$

  • $E(e^{tx}) = \displaystyle \sum_{k=0}^{∞} e^{tk} e^{-\lambda} \lambda^{k}/k! = e^{-\lambda} e^{\lambda e^t} = e^{\lambda(e^t - 1)}$

• Let $Y \sim Pois(\mu)$ indep. of $X$, Find distribution of $X+Y$.

  • Multiply MGFs: $M_X M_y = e^{\lambda (e^t-1)} e^{\mu(e^t-1)} = e^{(\lambda + \mu)(e^t-1)}$

    $\Rightarrow X+Y \sim Pois(\lambda + \mu)$

  • Counterexample) if $X$, $Y$ dependent:

    • $X=Y \Rightarrow = X+Y = 2X$ is not Pois. since even

    • $E(2X) = 2\lambda$, $Var(2X) = 4\lambda$ increasing! (is not Pois)

Joint Distribution (결합 분포)

• $X$, $Y$ r.v.s

  • joint CDF

    $F(x, y) = P(X \le x, Y \le y)$

  • joint PMF

    $P(X=x, Y=y)$

  • marginal CDF

    $P(X \le x)$ is marginal dist. of X.

  • joint PDF(continuous)

    $f(x, y)$ such that $P((x, y) \in B) = \iint_{B} f(x, y) dxdy$

  • independence

    $X$, $Y$ indep. if and only if $F(x, y) = F_X(x)F_Y(y)$

    Equiv. to
    $P(X=x, Y=y) = P(X=x)P(Y=y)$ (discrete)
    $f(x, y) = f(x) f(y)$ all $x$, $y \in R$

• Getting marginal distribution (주변 분포)

  • $P(X=x) = \sum_{y} P(X=x, Y=y)$ discrete

    $f_Y(y) = \int_{-∞}^{∞} f_{X, Y} (x, y dx)$

• Example

  • X, Y Bernulli

  	Y=0	Y=1
  X=0	$\displaystyle \frac{2}{6}$	$\displaystyle \frac{1}{6}$	$\displaystyle \frac{3}{6}$
  X=1	$\displaystyle \frac{2}{6}$	$\displaystyle \frac{1}{6}$	$\displaystyle \frac{3}{6}$
  ----	----	----	----
  	$\displaystyle \frac{4}{6}$	$\displaystyle \frac{2}{6}$

• They are independent.

  • all of $P(X=0)$ * all of $P(Y=0)$ $= \displaystyle \frac{4}{6} • \frac{3}{6}$

    $\Rightarrow P(X=0, Y=0) = \displaystyle \frac{2}{6}$

  

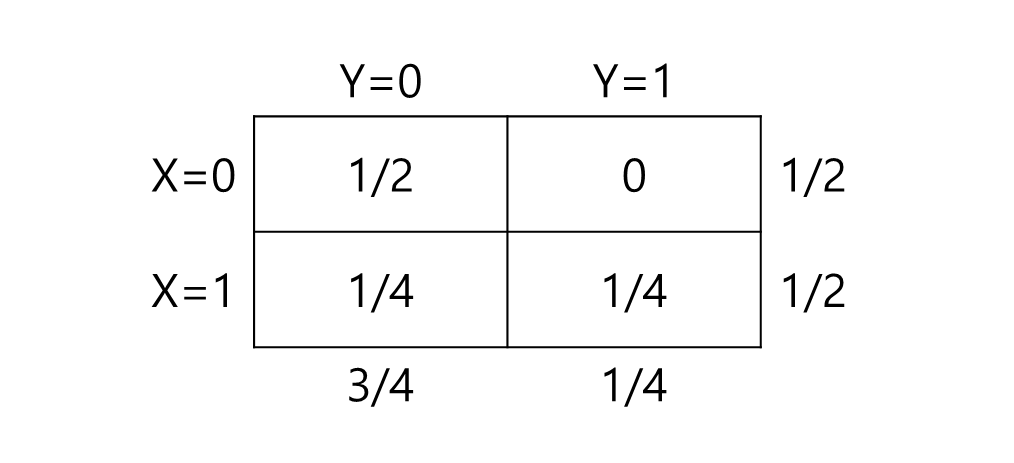
• This one is dependent.

  • all of $P(X=0)$ * all of $P(Y=1)$ $= \displaystyle \frac{1}{2} • \frac{1}{4}$

    $\nRightarrow P(X=0, Y=1) = 0$

Examples

• Ex1. Uniform on square $\{(x, y): x, y \in [0, 1]\}$

  

  • joint PDF const. on the square,

    $\begin{cases} 0, {outside} \\ c, {0 \le x \le 1}, {0 \le y \le 1} \\ 0, {otherwise} \\ \end{cases}$

  • Integral is area, $c = \displaystyle \frac{1}{area} = 1$

    • marginal: $X$, $Y$ are indep. Unif(0, 1)

• Ex2. Uniform in disc, $\{x^2 + y^2 \le 1\}$ ← 제약 조건식으로 인해 독립이 아님!

  

  • joint PDF

    $\begin{cases} \displaystyle \frac{1}{\pi}, {x^2 + y^2 \le 1} \\ 0, {otherwise} \\ \end{cases}$

  • $X$, $Y$ Dependent

    • Given $X=x$, $- \sqrt{1-x^2} \le y \le \sqrt{1-x^2}$

• 출처 : Statistics 110, boostcourse