Lecture 8: Random Variables and Their Distributions

Binomial distribution Bin(n, p)

• $X ~ Bin(n, p)$

1. Story: X is # of successes in n independent Bern(p) trials

   • Bern(p) p: prob. success

2. Sum of indicator random variables(지시 확률 변수): $X = X_1 + X_2 + ... + X_n$,

   $X=P(match)=\begin{cases} 1, & {if\; jth\; trial\; successes} \\ 1, & {otherwise} \\ \end{cases}$

   $X_1,\; ... \; X_n$ i.i.d (indep. identically distribution) Bern(p)

3. PMF(Prob. Math Function, 확률 질량 함수): $P(X=k) = \begin{pmatrix}n\\k\\ \end{pmatrix} p^k q^{n-k}$, $q = 1-p$

R.V.s (Random Variables)

• There is a sample space:
  

  • $X=7$ is an event.

• CDF(Cumulative Distribution Function, 누적 분포 함수)

  • $X \le x$ is an event.

  • $F(x) = P(X \le x)$

  • then F is the CDF of X

PMF(for discrete r.v.s)

• Discrete: possible values $a_1, a_2, ... , a_n$ or $a_1, a_2, ...$

• PMF: $P(X=a_j)=p_j$ for all j

  • $p_j \ge 0$, $\displaystyle \sum_{j} p_j = 1$

• PMF of Binomial distribution

  • $P(X=k) = \begin{pmatrix}n\\k\\ \end{pmatrix} p^k q^{n-k} = (p+q)^n = 1^n = 1$, by Binomial Thm.

    • $k \in \{0, 1, 2, ... n\}$

• $X ~ Bin(n, p)$, $Y ~ Bin(m, p)$ indep. \Rightarrow $X+Y ~ Bin(n+m, p)$

  1. Immediate from story: successes of nth and mth trials

  2. $X_1,\; ... \; X_n$, $Y_1,\; ... \; Y_n \Rightarrow X+Y = \displaystyle \sum_{j=1}^{n} X_j + \displaystyle \sum_{j=1}^{n} Y_j$

     :sum of n+m i.i.d. Bern(p) $\Rightarrow$ Bin(n+m, p)

  3. $P(X+Y=k) = \displaystyle \sum_{j=0}^{k} P(X+Y=k \; | \; X=j) P(X=j)$

     $= \displaystyle \sum_{j=0}^{k} P(Y=k-j \; | \; indep.) \begin{pmatrix}n\\j\\ \end{pmatrix} p^j q^{n-j}$

     $= \displaystyle \sum_{j=0}^{k} \begin{pmatrix}m\\k-j\\ \end{pmatrix} p^{k-j} q^{m-k+j} \begin{pmatrix}n\\j\\ \end{pmatrix} p^j q^{n-j}$

     $= \displaystyle \sum_{j=0}^{k} \begin{pmatrix}m\\k-j\\ \end{pmatrix} \begin{pmatrix}n\\j\\ \end{pmatrix} p^j q^{n-j} p^k q^{m+n-k}$

     → VanderMonde: $\begin{pmatrix}m+n\\k\\ \end{pmatrix}$

Example

• 5 card hand, find distribution(PMF or CDF) of # aces

  • Lex $X = (number \; of \; aces)$

• Find $P(X=k)$. This is 0 except if $k \in \{0, 1, 2, 3, 4\}$.

  • Assume: Not Binomial

  • $P(X=k) = \frac{\begin{pmatrix}4\\k\\ \end{pmatrix} \begin{pmatrix}48\\5-k\\ \end{pmatrix}} {\begin{pmatrix}52\\5\\ \end{pmatrix}}$ for $k \in \{0, 1, 2, 3, 4\}$

  • Like(Same as) the elk problem.

  

• Have b black, w white marbles. Pick simple random sample of size n.

  • Find dist. of (# white marbles in sample)

  • $P(X=k) = \frac{\begin{pmatrix}w\\k\\ \end{pmatrix} \begin{pmatrix}b\\n-k\\ \end{pmatrix}}{\begin{pmatrix}w+b\\n\\ \end{pmatrix}}$ , $0 \le k \le w$, $0 \le n-k \le b$

  • Hypergeometric(초기하 분포): sampling without replacement

    → we do not get a binomial because trials are not indep.(dep!)

  • This is difference between Binomial(복원 추출) and Hypergeometric(비복원 추출)

  • $\displaystyle \sum_{k=0}^{w} P(X=k) = \frac{1}{\begin{pmatrix}b+w\\n\\ \end{pmatrix}} \displaystyle \sum_{k=0}^{w} \begin{pmatrix}w\\k\\ \end{pmatrix} \begin{pmatrix}b\\n-k\\ \end{pmatrix} = \frac{1}{\begin{pmatrix}b+w\\n\\ \end{pmatrix}} \begin{pmatrix}b+w\\n\\ \end{pmatrix} = 1$ by VanderMonde.

CDF

• Form of distribution $P(X \e x)$

  • Continuous
    

  • Discrete
    

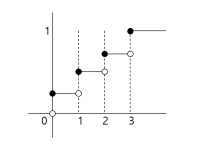
• CDF 참고할 만한 문서 : CDF의 정의

• CDF 참고할 만한 강의 → CDF의 미분 = PDF(확률 밀도 함수), PDF의 적분 = CDF

• 출처 : Statistics 110, boostcourse