Linear Classifier
Loss Function
- 불량성을 정당화할 수 있는 방법
Optimization
- 가능한 모든 W의 공간을 정의하여, 가장 덜 나쁜 W를 찾는 과정
General form
- 학습 데이터 x와 정답 레이블 y를 비교하여 Loss fuction에 대응하는 값을 평균내는 과정

Loss function for CV
SVM
-
다소 이상한 꼴일 수 있다.
-
정답 레이블 점수가 잘못된 레이블의 점수보다 크거나 같으면
0 -
정답 레이블 점수가 잘못된 레이블의 점수보다 작다면
sj - si +1

-
hinge loss : 그래프 모양

- cat, car, frog 카테고리에 대한 점수를 계산 -> 전체 평균 내기
- car 카테고리는 정답 레이블 값이 매우 높기 때문에 Loss가 0이 된다.
- 전체 레이블에 대해 평균낸 값이 5.27정도로 나왔다면, 이는 "5.27 정도의 잘못된 추론을 하고 있다"라고 해석할 수 있다.


+1의 의미 : W에 대한 공간을 확장하면 의미 없어진다.
-
Q1. What happens to loss if car scores change a little bit?
- Loss will not change : 0
- car score는 이미 충분히 높기 때문에 loss가 한 번 0으로 판명되면 그 이후로도 0이다.
-
Q2. What is the min/max possible loss for SVM?
- min : 0 / max : infinity(∞)
- hinge loss form으로부터 예상해보면, score가 음수에 가까울수록 무한대가 된다.
-
Q3. At initialization W is small so all s ~ 0, What is the loss?
- class number - 1
- 1 + 1 + 0 + 1 + ... : 정답 레이블을 제외하고 1이 더해질 것이기 때문이다.
- 디버깅 전략으로 쓰기이기도 한다.
-
Q4. What if the sum was over all classes?
- 정답 레이블을 제외하지 않고 합산하면 어떻게 되나?
- 매번 1씩 증가하게 될 것이다. ->
sj - si(0) + 1 - 따라서 정답 레이블 점수를 빼주는 작업은 최소 손실이 0이 될 수 있게 만드는 핵심 형태였다는 것을 알 수 있다.
-
Q5. What if we used mean instead of sum?
- 별 차이 없다.
- 차이를 상수로 조정하는 일이므로
-
Q6. What if we used squared form? : ()^2
- 달라질 것
- hinge loss는 미세한 차이에 별로 신경쓰지 않는 반면, squared loss는 틀린 값의 가중치를 더 많이 두는 방법이므로 추론에 예민한 상황일 때 사용한다.
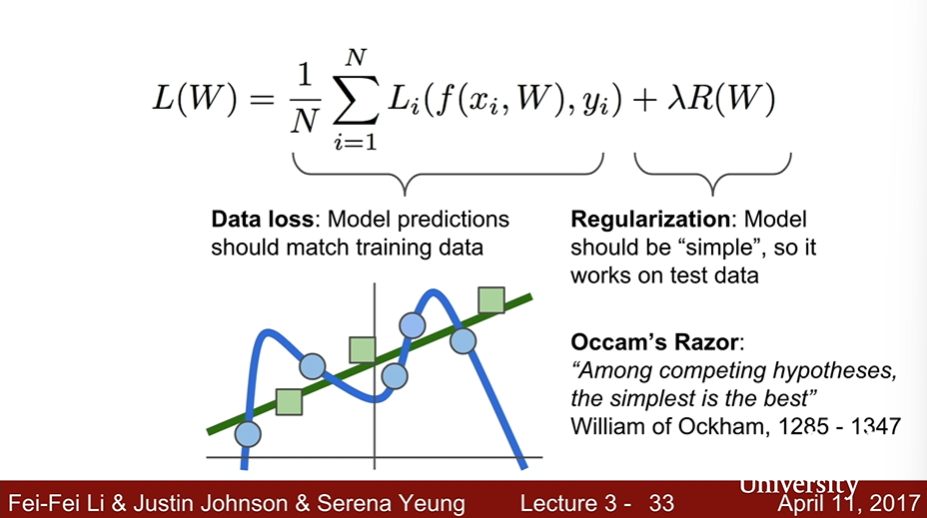
Multiclass SVM : Example code
def L_i_vectorized(x, y, W):
scores = W.dot(x)
margins = np.maximum(0, scores - scores[y] + 1)
margins[y] = 0
loss_i = np.sum(margins)
return loss_iRegularization : Overfitting 방지
- train data set에만 잘 fitting된 추론은 좋지 않다.
- 광범위한 추론이 가능하게끔 만들기 위해서가 정규화를 진행하는 이유이다.
- In common use
- L2 normalization that weight decay : 분산되는 효과를 줌
- L1 normalization : 행렬 W의 희소성을 장려한다.

Softmax Classifier
Multinormial Logistic Regression
- 로그를 사용하는 이유는 최대화가 쉽기 때문이다.
- softmax 함수에 sum을 취하고 이를 확률화하여 로그에 -를 취해주면 정답에 가까울수록 값이 작아지는 함수를 기록할 수 있다. -> Loss function!!

- for example

Q1. What is the min/max possible loss L_i
- min : 0 / max : infinity(∞)
- if softmax() explained as probability is equel to 1, loss is definitely 0!!
- 확률이 0과 1이 될 수 있게 만드는 score는 무엇일까?
- 거의 -무한대(∞), 무한대(∞)에 가까워야한다.
- 다행히도 컴퓨터의 숫자는 유한하기 때문에, 이러한 문제까지 갈 일은 없다.
Q2. Usually at initialization W is small so all s ~ 0. What is the loss?
- -log(1/C) = logC : C는 클래스 개수
- exp(0) ~ 1이기 때문에 -log(1 / 1+1+ ... 1)
- 마찬가지로 디버깅 방법 중 하나이다.
Softmax vs. SVM
-
SVM는 올바른 클래스의 점수를 잘못된 클래스의 점수보다 크게 만드는 것에 관심이 있다.
- 학습 데이터를 흔들어도 0의 loss가 바뀌지 않는 것처럼 올바른 클래스의 점수가 바뀌지 않는다.
- 추론을 진행하면 할수록 학습 데이터에 관심을 갖지 않는다.
-
Softmax는 확률 질량을 1로 유도하려고 한다.
- 올바른 클래스에 점점 더 많은 확률 질량을 쌓아가며 개선하는 방법이다.
Recap
Supervised learning
- get score : linear classifier
- get loss function : ex. SVM, Softmax ...
- regularization

- Deeplearning : 매우 복잡한 f를 정의하는 것
Optimization
Gradient Descent
# Vanilla Gradien Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_grad # perform parameter update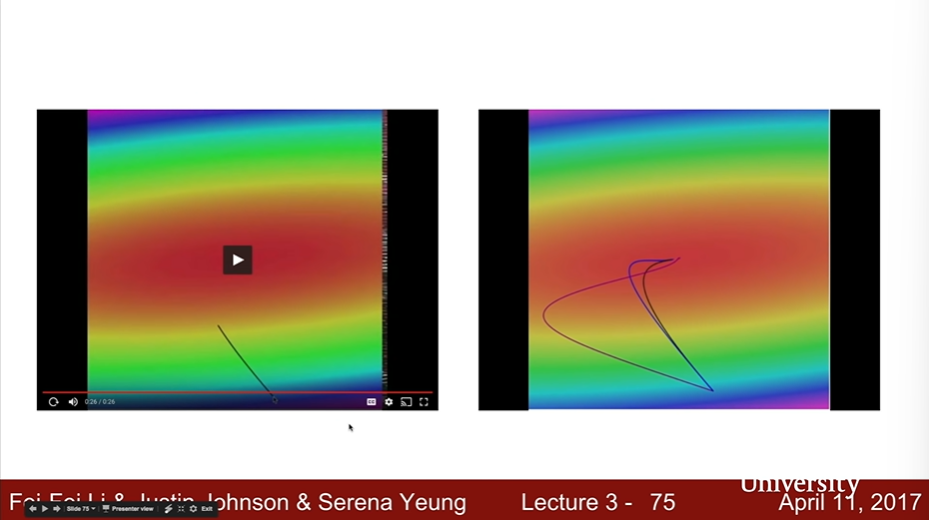
- black : Gradient Desecent
- blue : Momentum
- red : Adam
Stochastic Gradient Descent (SGD)
- Using minibatch!
# Vanilla Gradien Descent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -step_size * weights_grad # perform parameter update
http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/
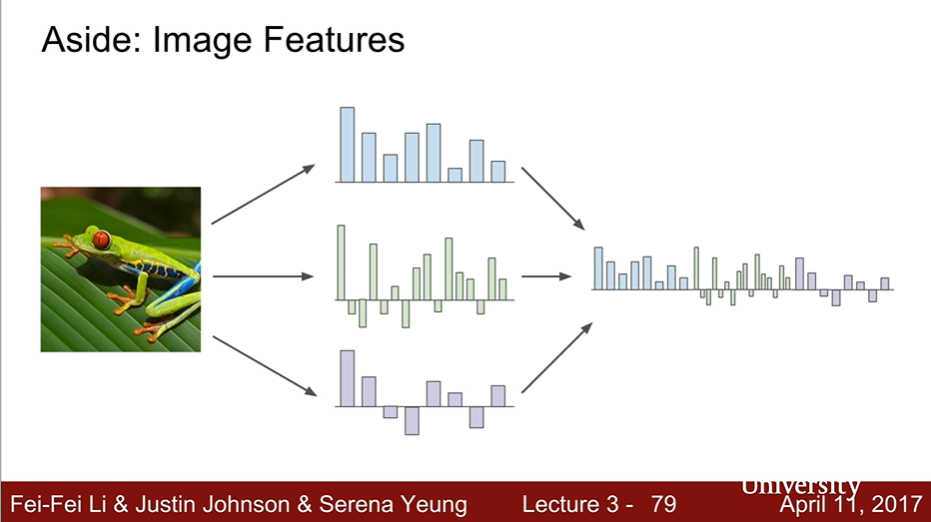
Image Features
- 이미지 픽셀을 입력받아 RGB 신호를 feature로 추출하고, 이를 concat하여 선형 분류기에 넣는다.
- 이 방법은 그리 좋지 않다.
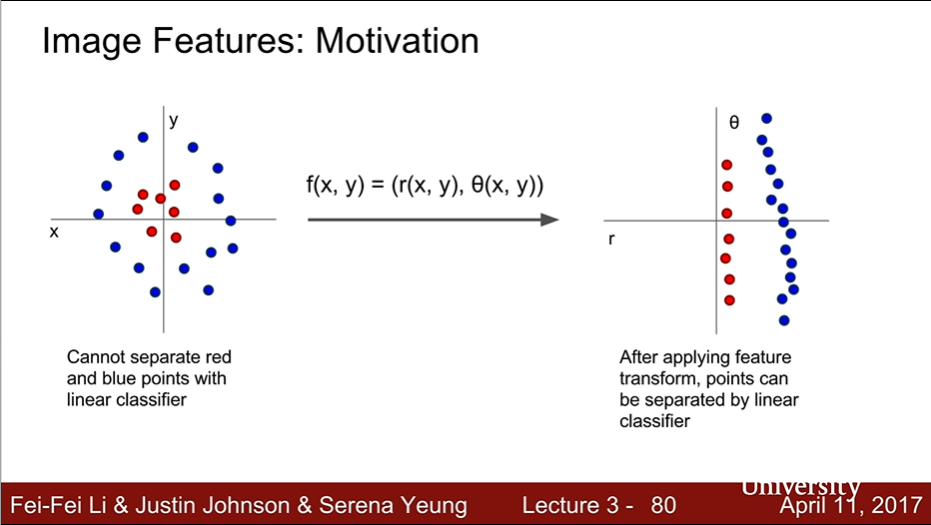
- Motivation
- 선형 분류기로 해결할 수 없는 문제들은 어떻게 할까?
- ex. 극좌표로 feature transform 한다.
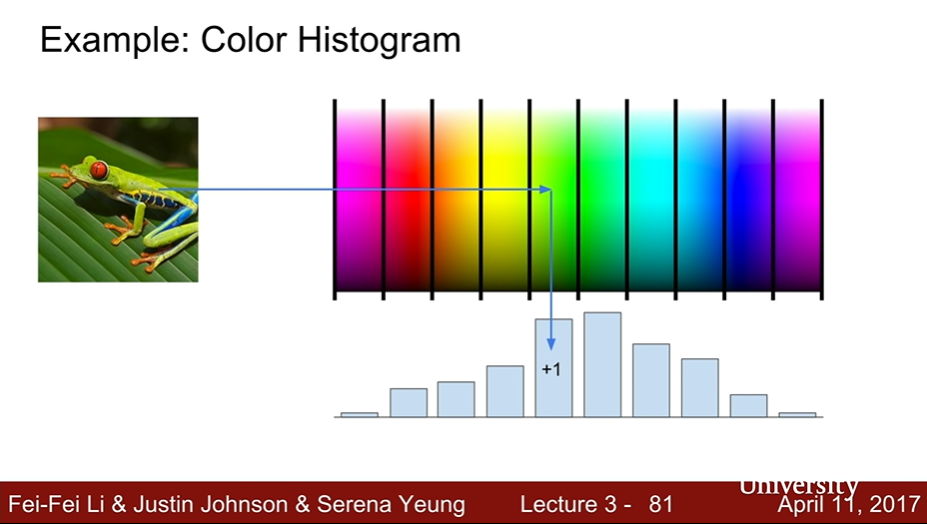
- Example : Color Histogram
- 어떤 color들이 많은지 feature vector화 한다.
- Example : Histogram of Oriented Gradients(HoG)
- 인간이 사물을 하는 인식하는 방법에서 착안, edge를 찾고 픽셀을 나누어 encoding하는 방법이다.
- 자연어 처리 된 codebook과 비교하여 유사도를 판단하는 방법으로서 꽤나 오래된 특징 표현 기법 중 하나이다.

- Clustering patch (like using k-means)
- codebook : visual words

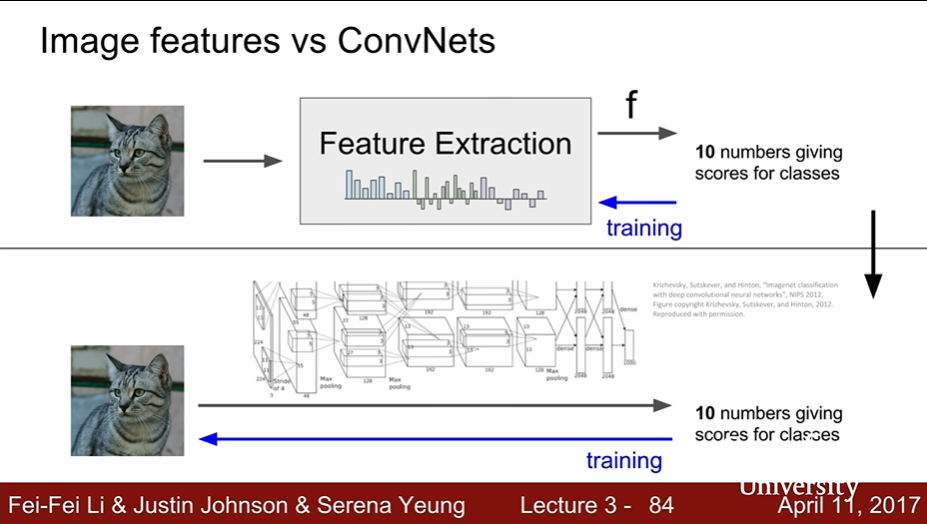
- Image features vs ConvNets
- CNN : 데이터에서 feature를 바로 추출한다는 점만 간편해졌을 뿐 이전 feature 추출 방법과 내용은 일치함
[출처] CS 231n | Stanford University school of Engineering
