[MMD] Calculus for Machine Learning and Data Science Week 1
Derivatives and Optimization
Lesson 1 - Derivatives
Machine Learning Motivation
- 아래와 같이 bedroom의 수에 따라 집의 가격이 결정되는 문제를 다룬다고 해보자.

- Machine Learning으로 할 수 있는 일은 아래와 같은 table의 관계를 예측하여 9개의 bedroom을 가진 집 가격을 알아내는 과정이라고 할 수 있다.

-
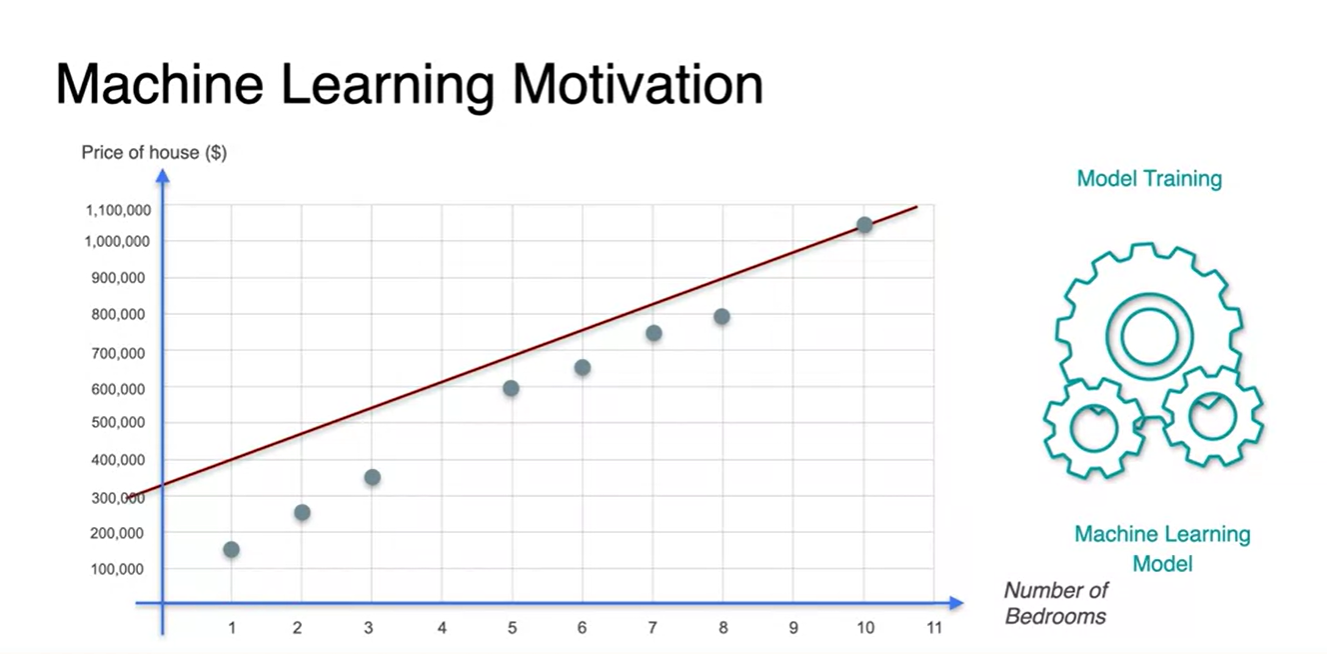
각 데이터 점들을 plot하여 나타내보자.
-
아래처럼 놓여진 데이터들의 관계를 설명하는 선형 분류 문제를 풀고자, 다양한 직선들을 estimation하는 과정을 거친다.
-
이 때, 모든 데이터 분포를 일반화하여 잘 설명할 수 있는 하나의 직선을 찾는 것이 machine learning의 동작 원리다.
-
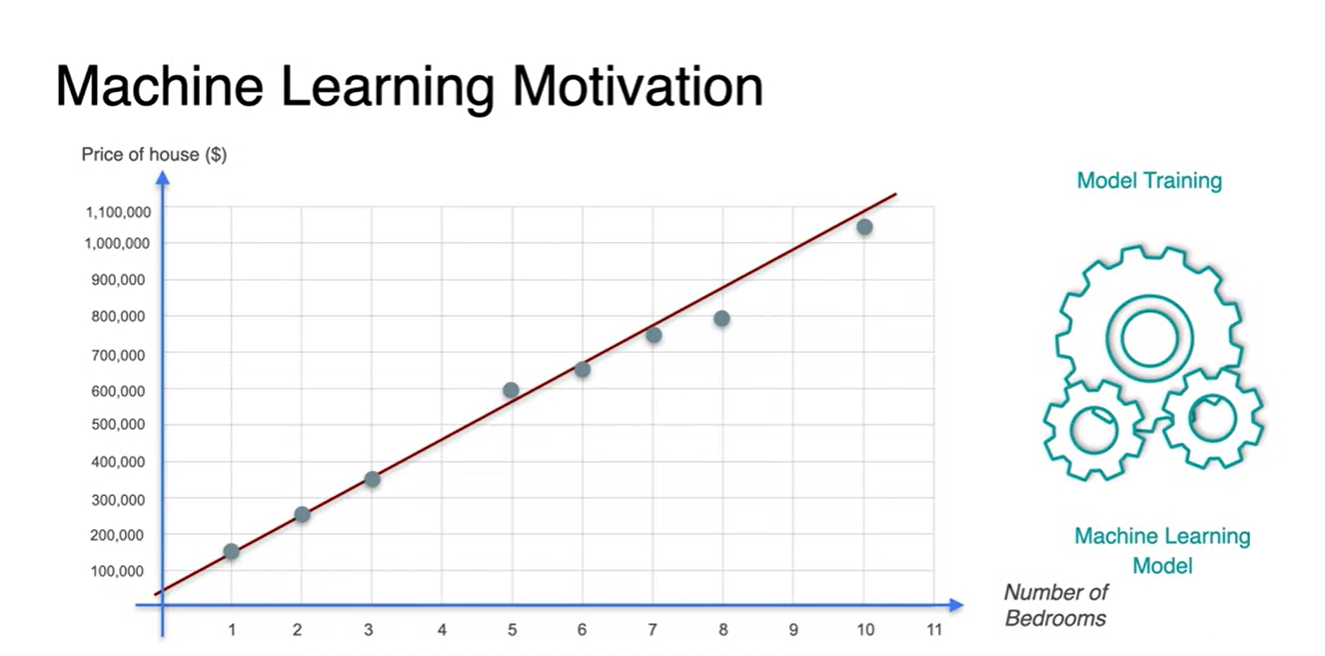
- 이후 우리가 training한 Linear Regression 모델로, 알고자 하는 9개의 bedrooms 집 가격을 예측하여 정답을 취한다.
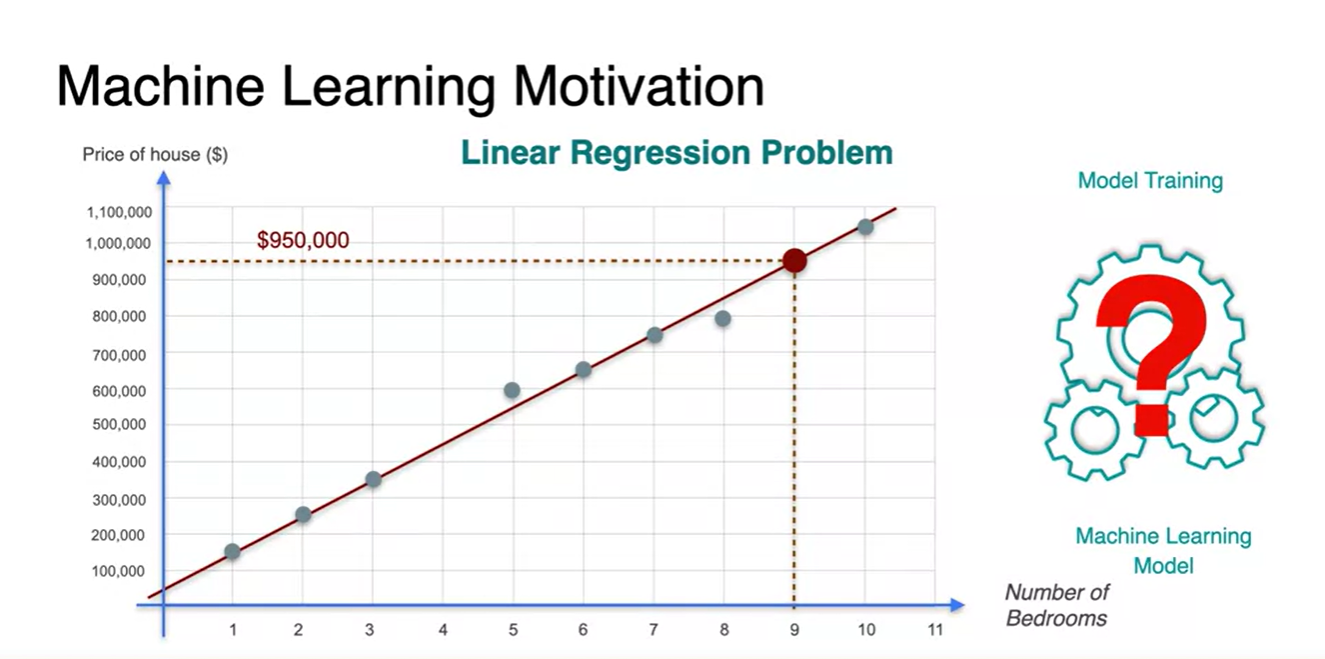
-
예를 들어, 외계인의 언어가 다음과 같이 단어의 등장 횟수를 표로 정리할 수 있고 그 때의 기분이 두 분류로 나뉜다고 해보자.
- 이러한 분류 문제를 Sentiment analysis(감성 분석)이라고 한다.

-
만약 아래와 같이 직선을 예측했다면 완벽하게 training되었다고 볼 수 없다.
- 정답에 따라 적절하게 분류하지 못했기 때문이다.
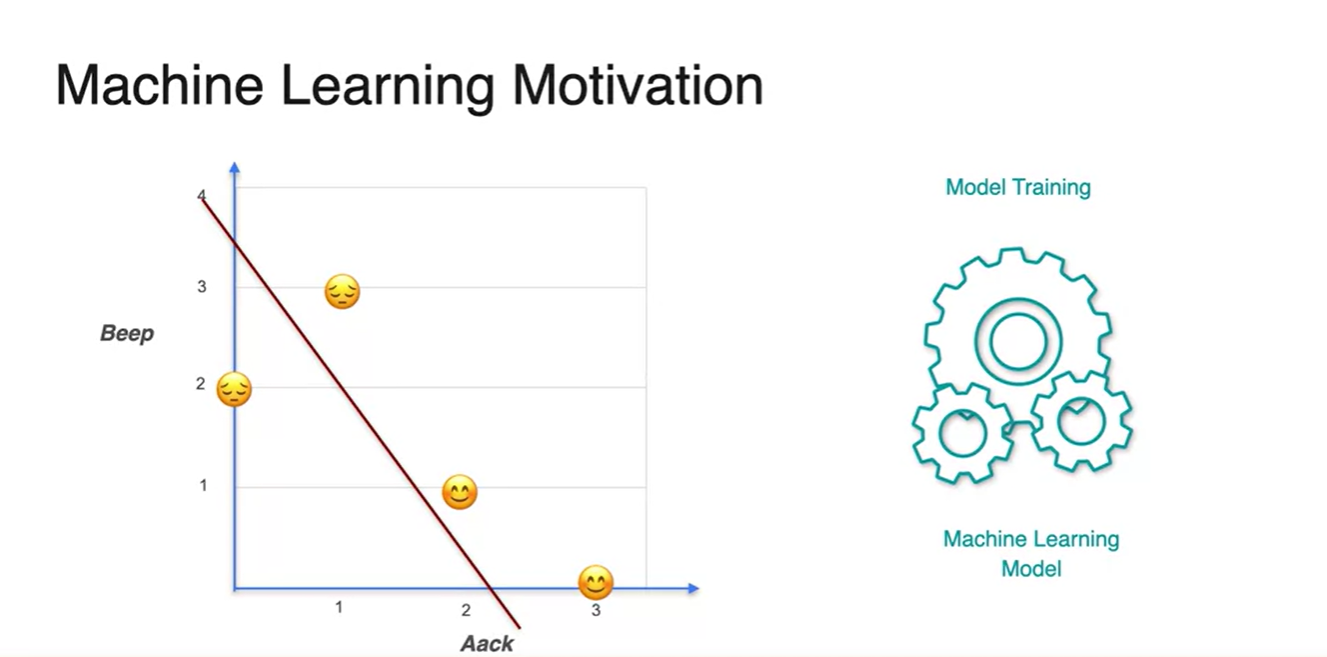
- 머신러닝은 위 그래플를 올바른 정답으로 교정하기 위한 작업이라 할 수 있다.
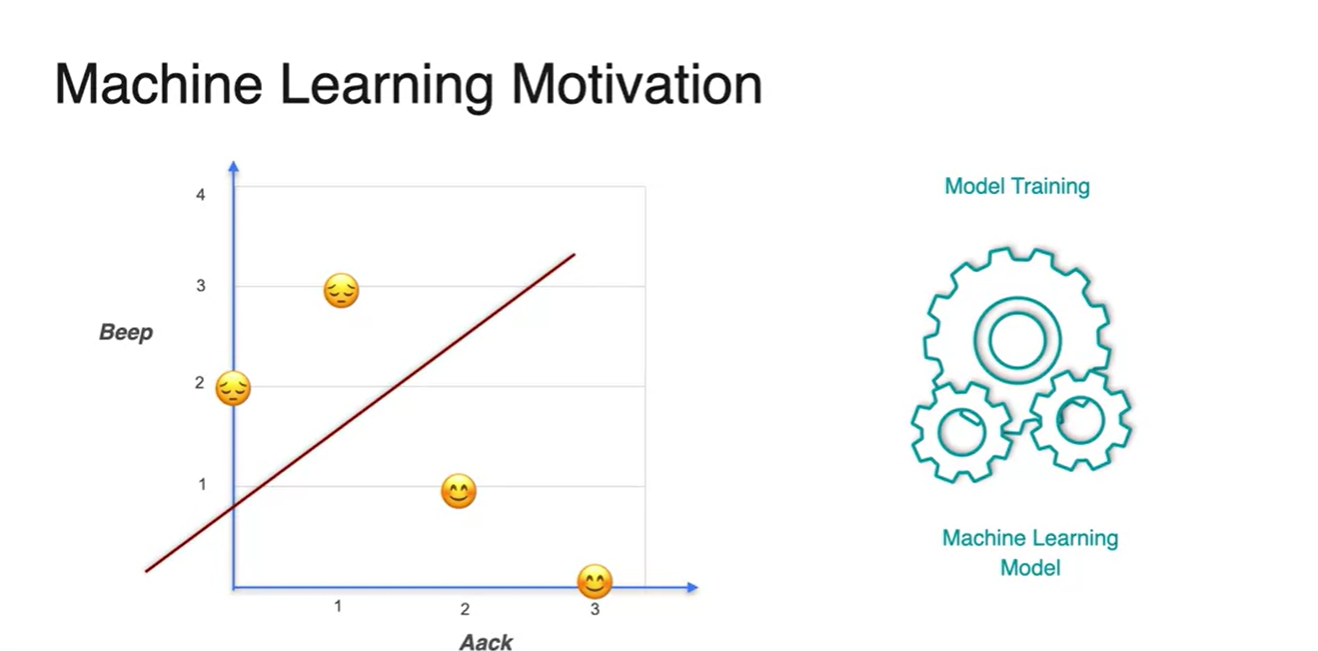
- 그렇다면 모델은 어떻게 이러한 분포를 완벽하게 구분지을 수 있을까?
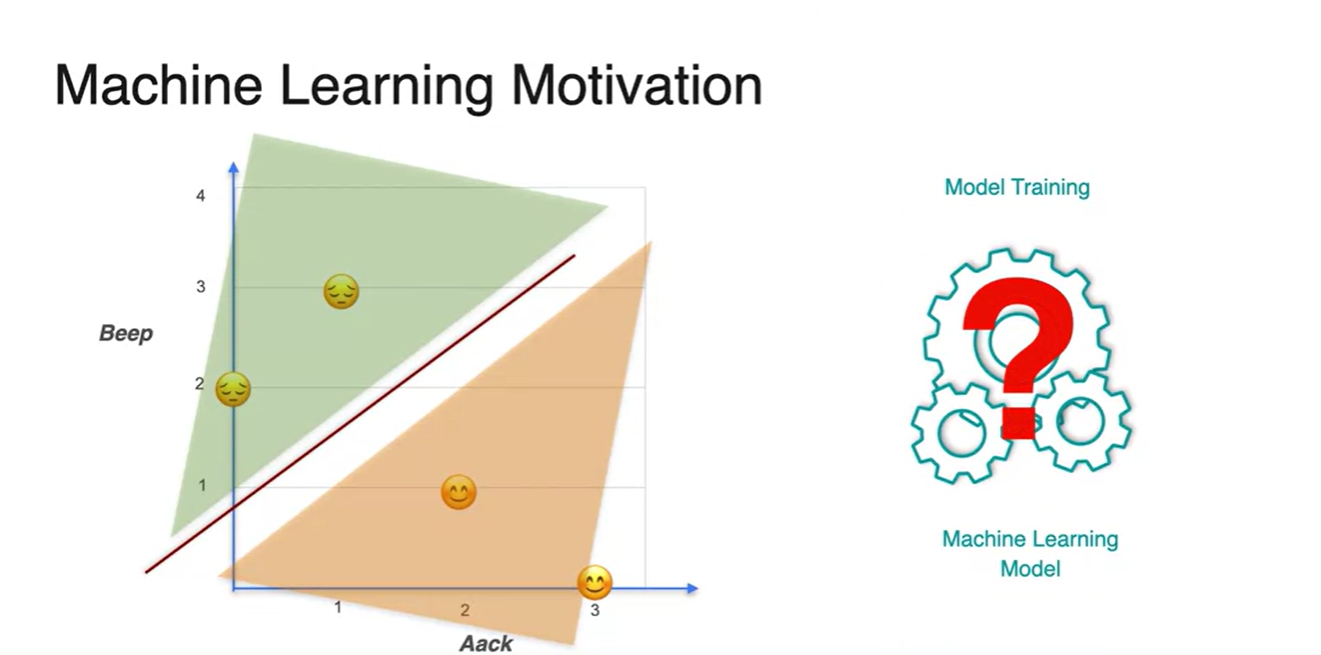
-
Model을 training하기 위해 필요한 개념을 아래에 정리하였다.
- Linear Regression 뿐만 아니라 Classification task에서도 같은 concept을 적용할 수 있을 것이다.
Introduction to Derivatives - Part 1
- 물리에서 속력(velocity)이란 거리(distance)를 시간(time)으로 나눈 값으로 나타낼 수 있다.
-
만약, 시간 단위를 아래 table과 같이 쪼개서 시간에 따른 거리 정보를 기록했다고 해보자.
- 이 차의 속력은 constant speed를 가지는가?

-
정답은 No다.
-
10-15초 간격의 거리 변화와 15-20초 간격의 거리 변화가 다르기 때문이다.
- 즉, 같은 시간 변화량 기준의 거리 변화량이 일정하지 않다!
-

- 이번에는 12.5초에서의 자동차 속력을 확정지을 수 있는가?
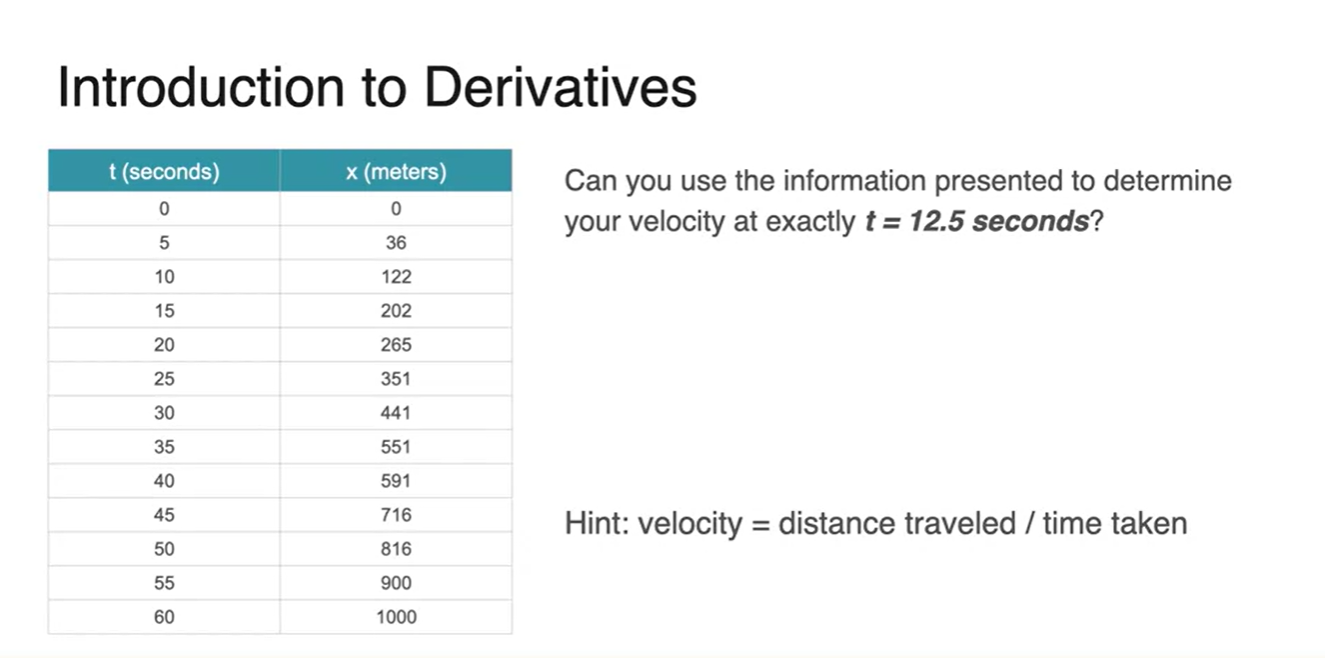
-
정답은 No다.
-
아래의 정보만 가지고서는 12.5초일 때의 정확한 speed를 결정지을 수 없다.
- 10-15초 사이의 거리 변화량은 두 지점의 Average(평균 속도)를 나타낼 뿐이지, 해당 지점의 실제 순간 속도를 나타내는 것이 아니기 때문이다.
-
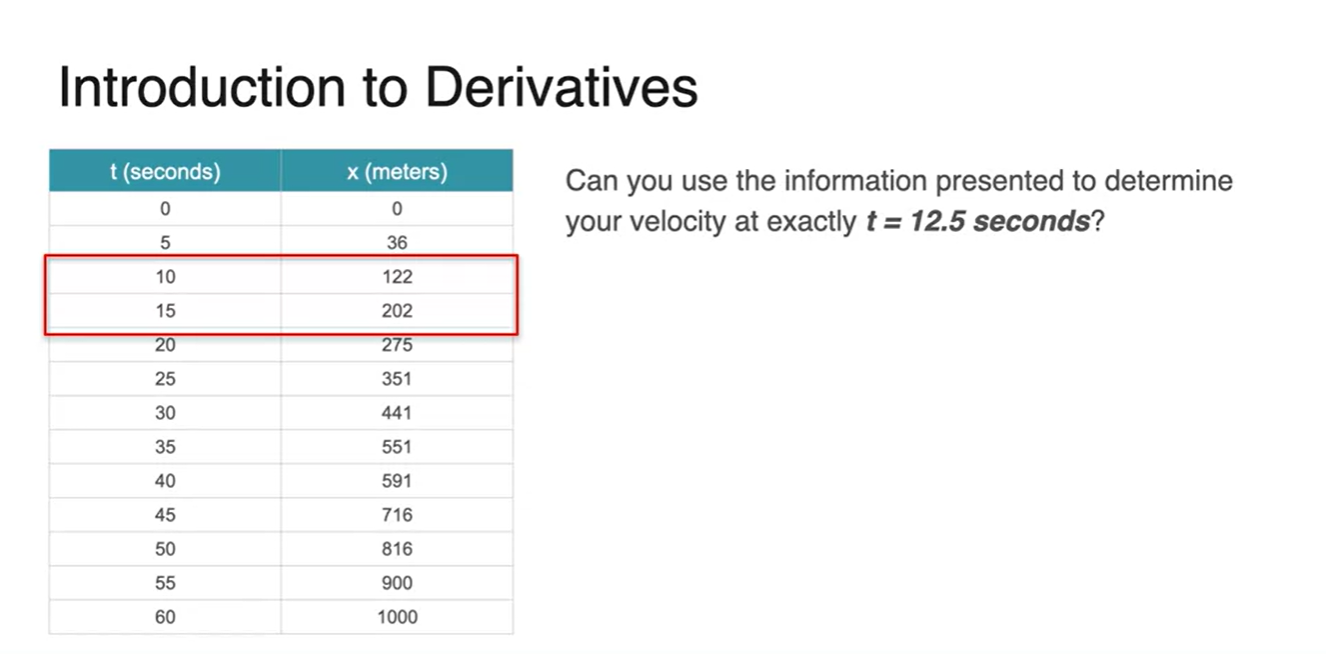
-
Slope란 두 지점의 평균 속도를 의미한다.
- 의미적으로는 x축으로 달려간 거리(run)로 상승 정도(rise)를 나눈 값으로 해석한다.
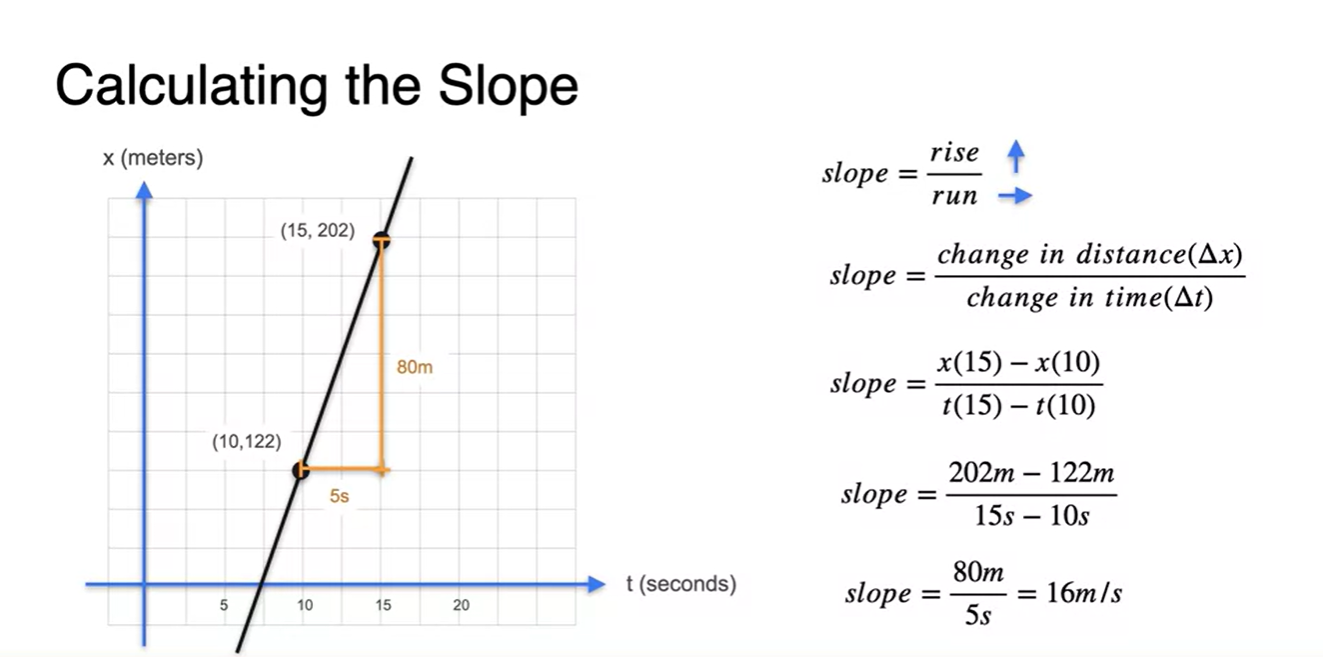
-
만약, 시간의 범위가 조금 더 촘촘하여 12초와 13초에서의 움직임 거리를 알 수 있다면 어떨까?
- 12.5초의 순간 속도를 알기 위한 estimation이 조금 더 정확해질 것이다.

-
아래와 같은 방식으로 12.5초의 순간 Slope를 estimation한다.
- 여전히 정확하지는 않지만, 아까보다는 15m/s에 가깝다고 얘기할 수 있을 정도라고 할 수 있다.

Derivatives and tangents
-
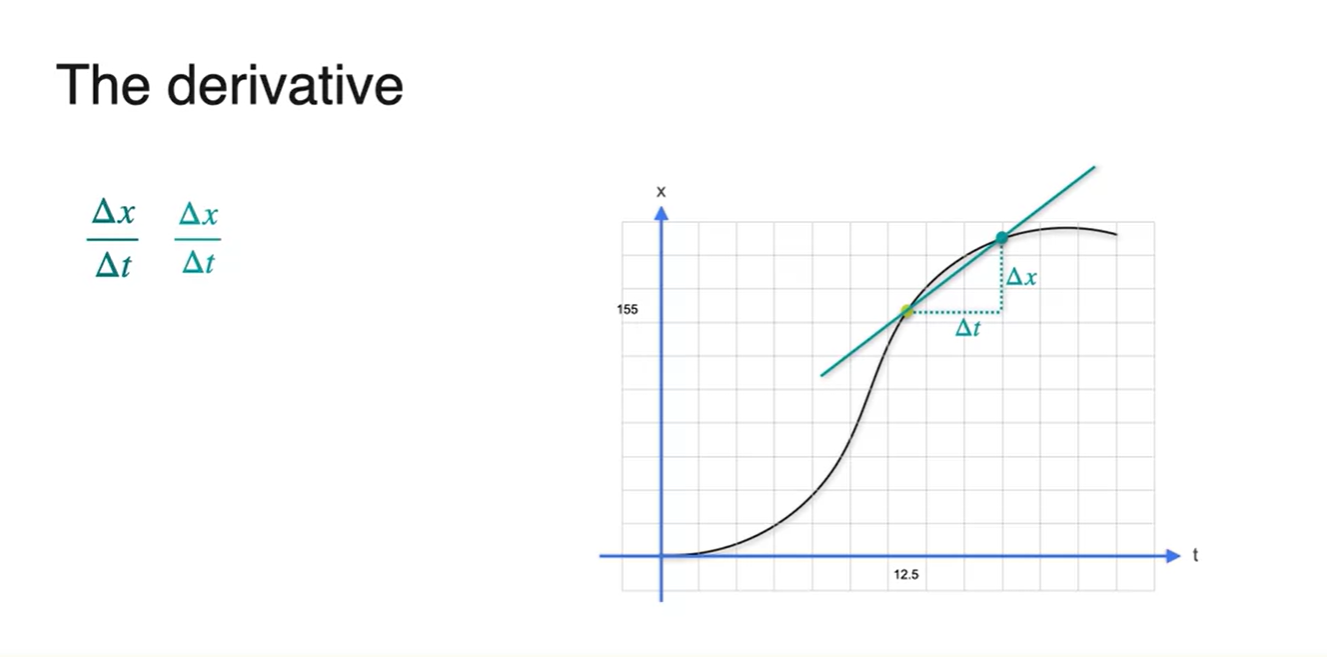
아래와 같이 12.5초일 때의 속도를 구하는 과정을 살펴보자.
- 특정 어느 지점과의 평균 변화량을 계산하여 slope를 계산하였다.
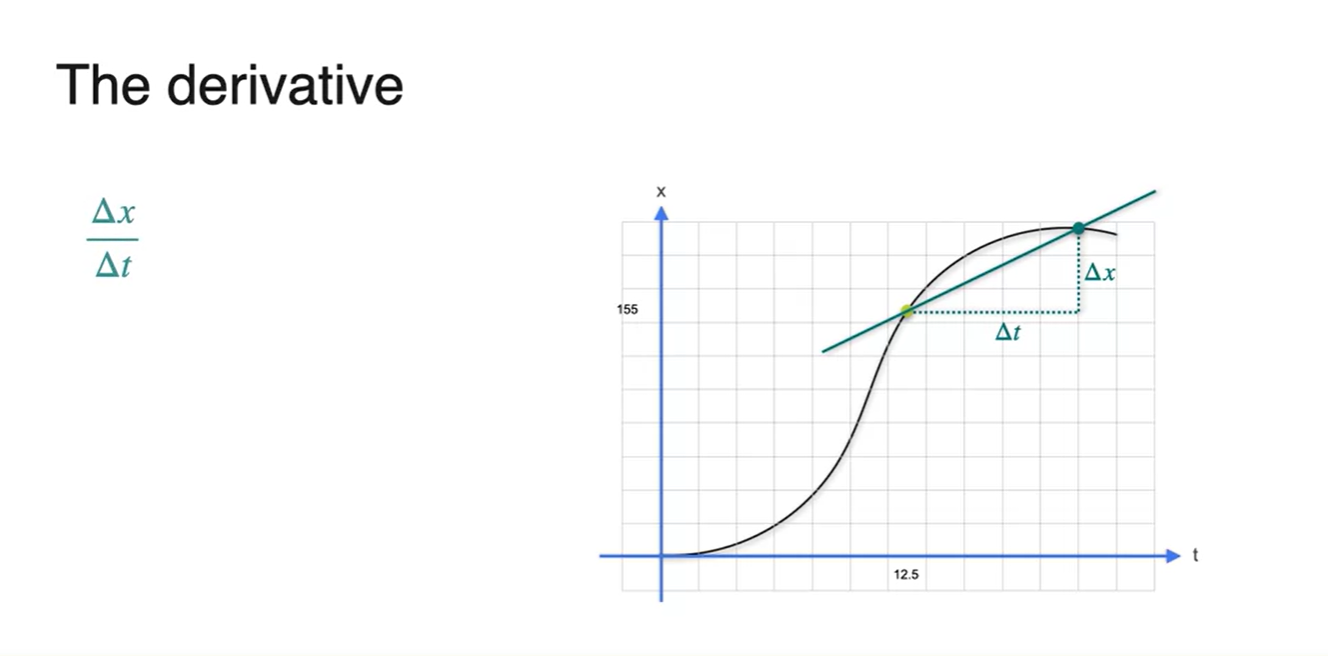
-
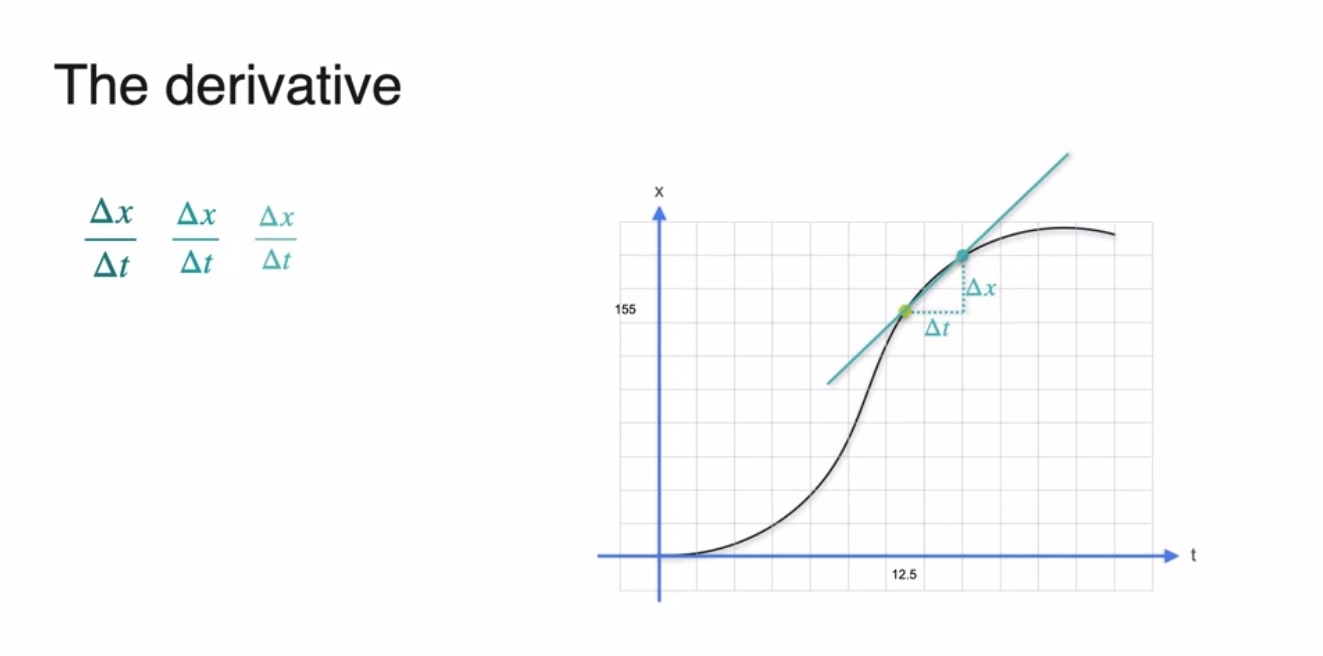
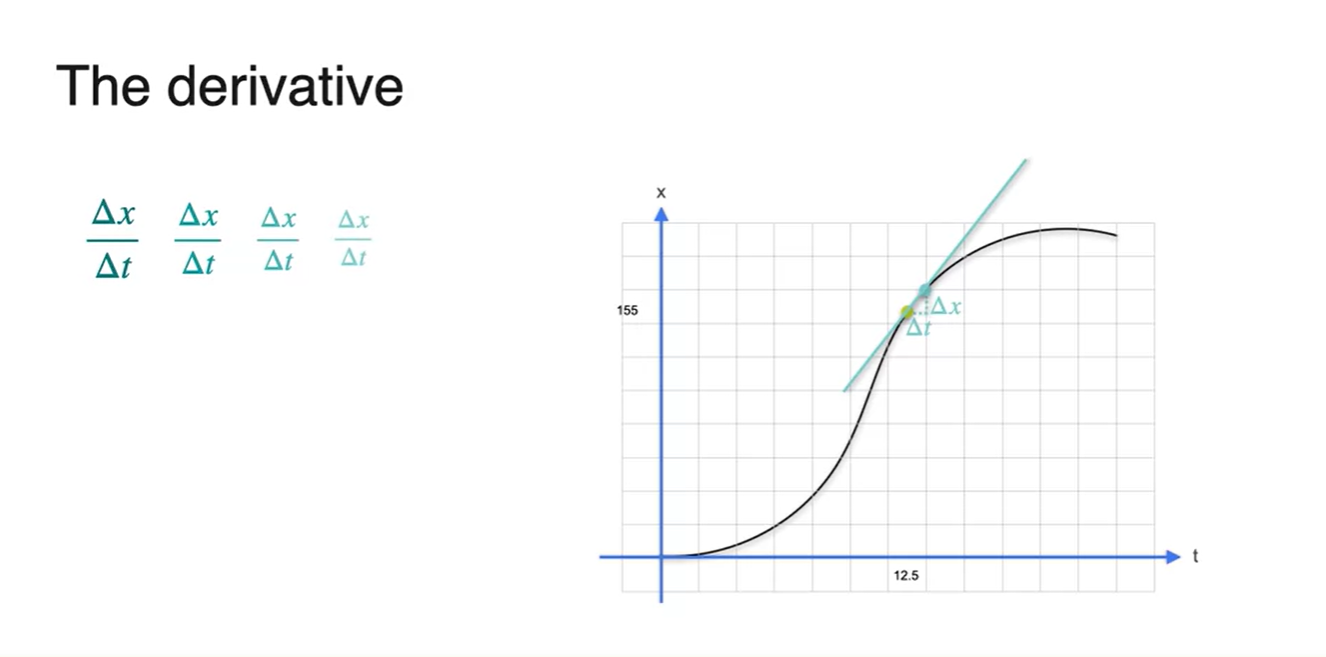
두 점 사이의 거리를 좁혀보면 slope(기울기)가 조금 더 변화된 것을 알 수 있다.
- 두 지점 사이의 거리를 계속해서 좁히다 보면 12.5초에서의 순간 속도와 거의 값이 동일해진다.
-
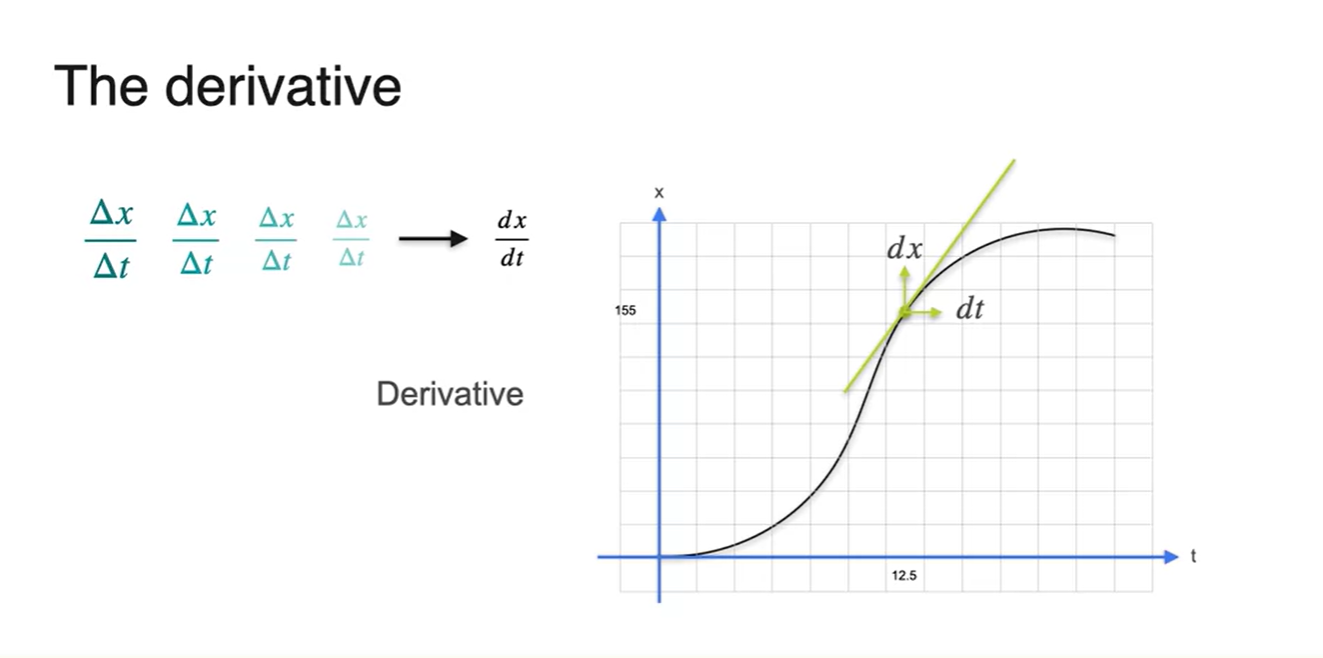
결론적으로 12.5초에서의 순간 속력을 구하기 위해서는
- 를 구해야 한다.
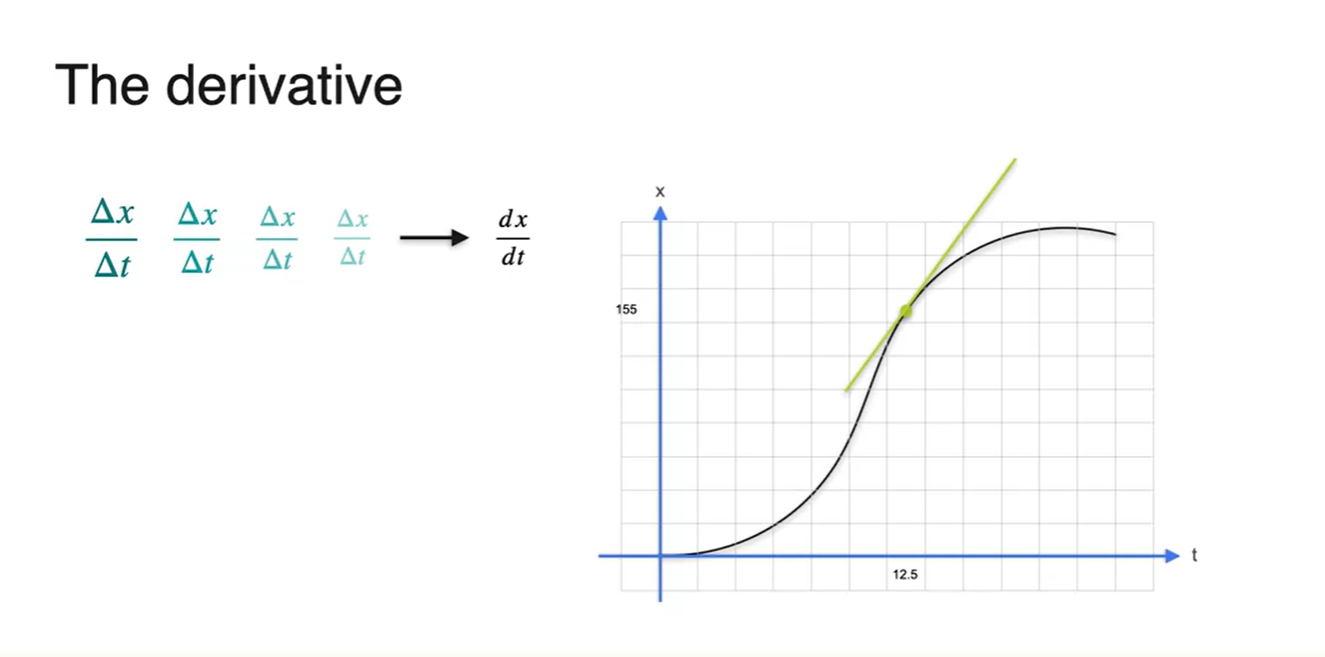
-
"The Slope of the tangent at the particular point"
- 이 개념이 바로 Derivative인 것이다.
Slopes, maxima and minima
-
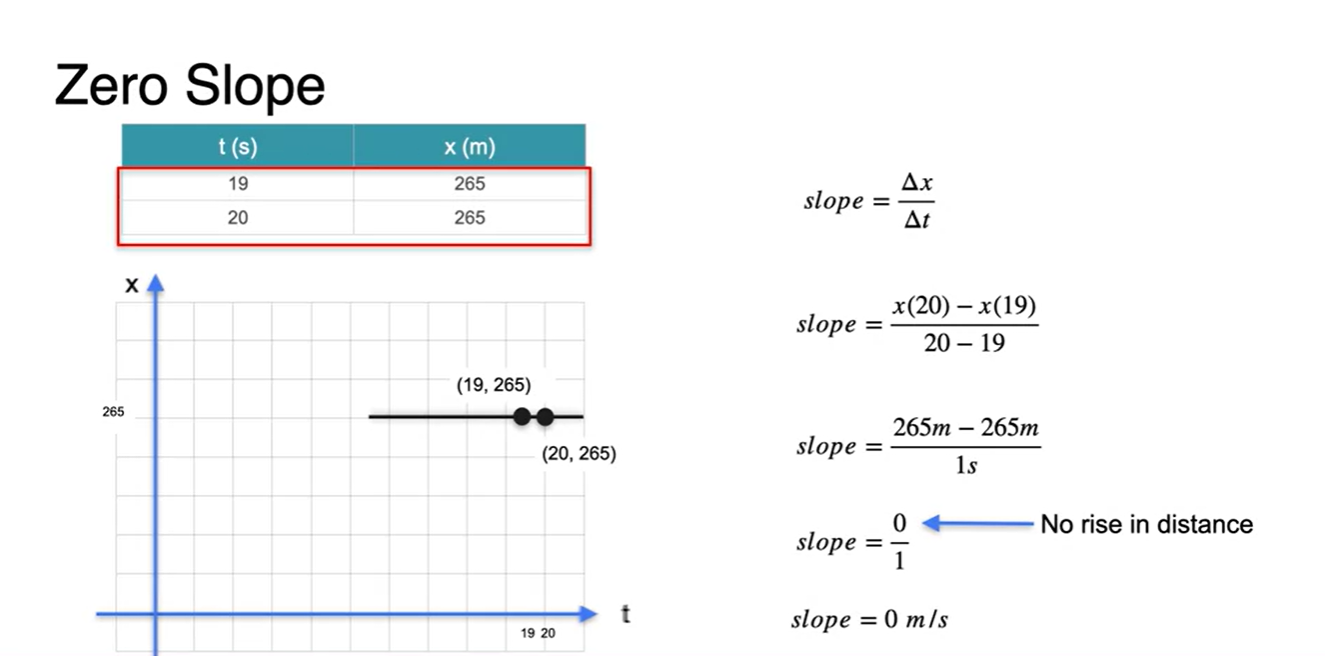
아래와 같이 19초와 20초 distance가 변하지 않는 table이 주어졌다고 해보자.
- 이와 같은 상황의 Slope는 zero 값을 갖는다.
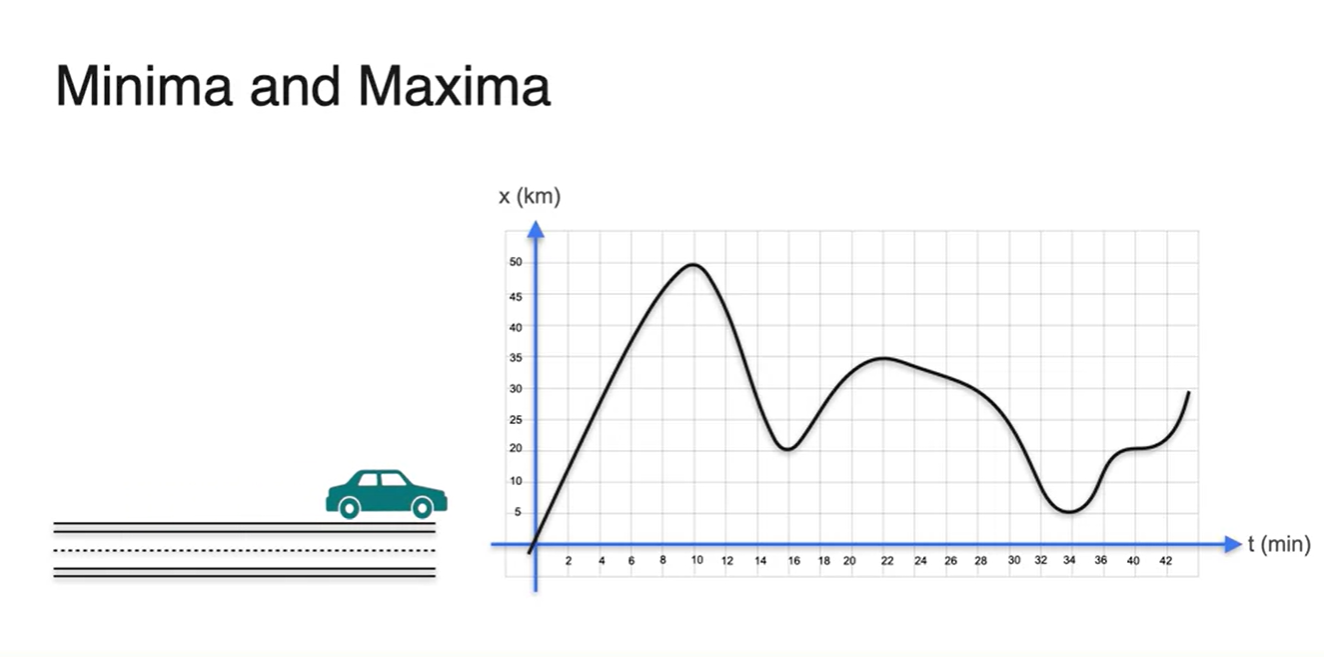
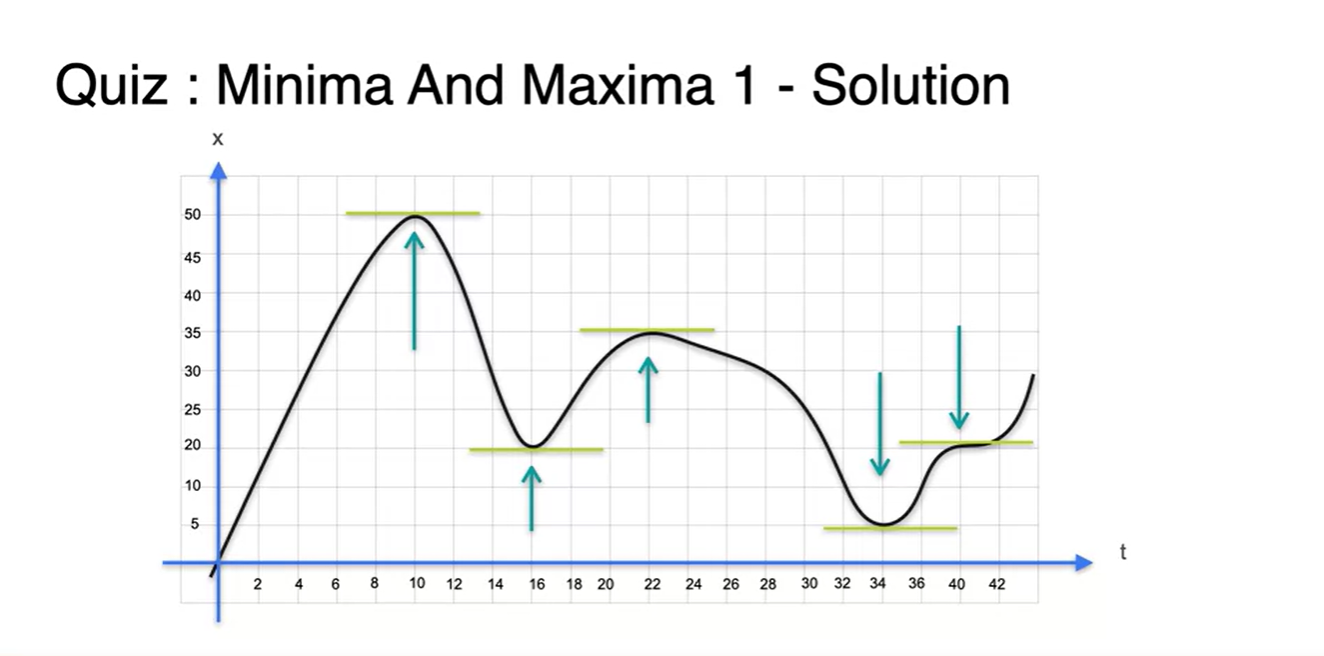
- 자동차의 시간에 따른 위치 변화가 다음과 같이 펼쳐졌다고 해보자.
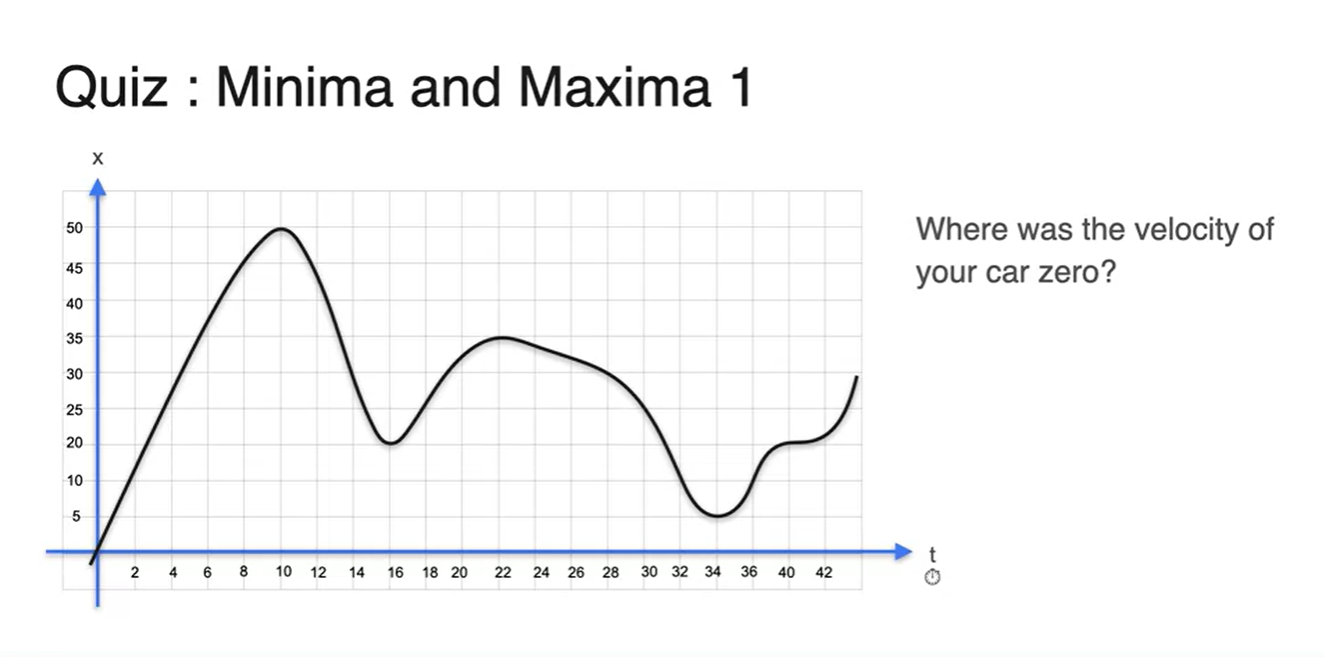
- 이 차의 속력이 0이 되는 순간의 시간은 몇 초인가?
-
정답은 Slope가 horizontal한 모든 지점이다.
- t = 10s, 16s, 22s, 34s, 40s가 정답이다.
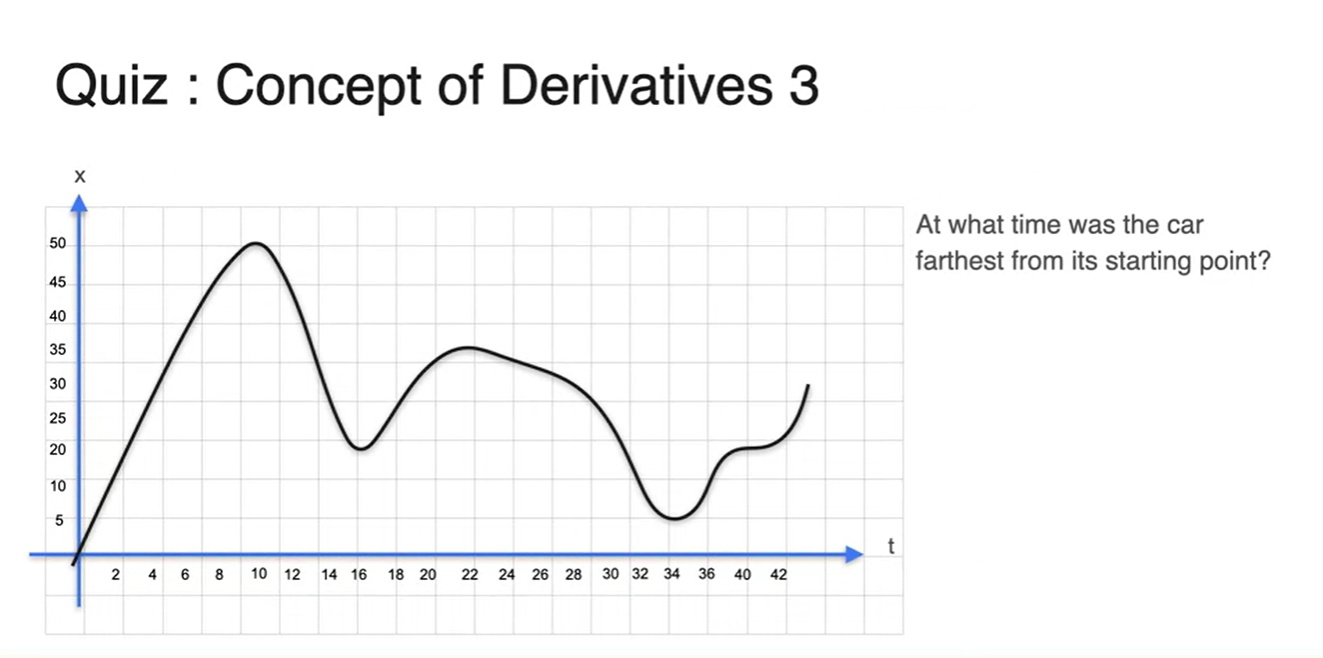
- 자동차가 staring point로부터 가장 먼 지점은 어디인가?
-
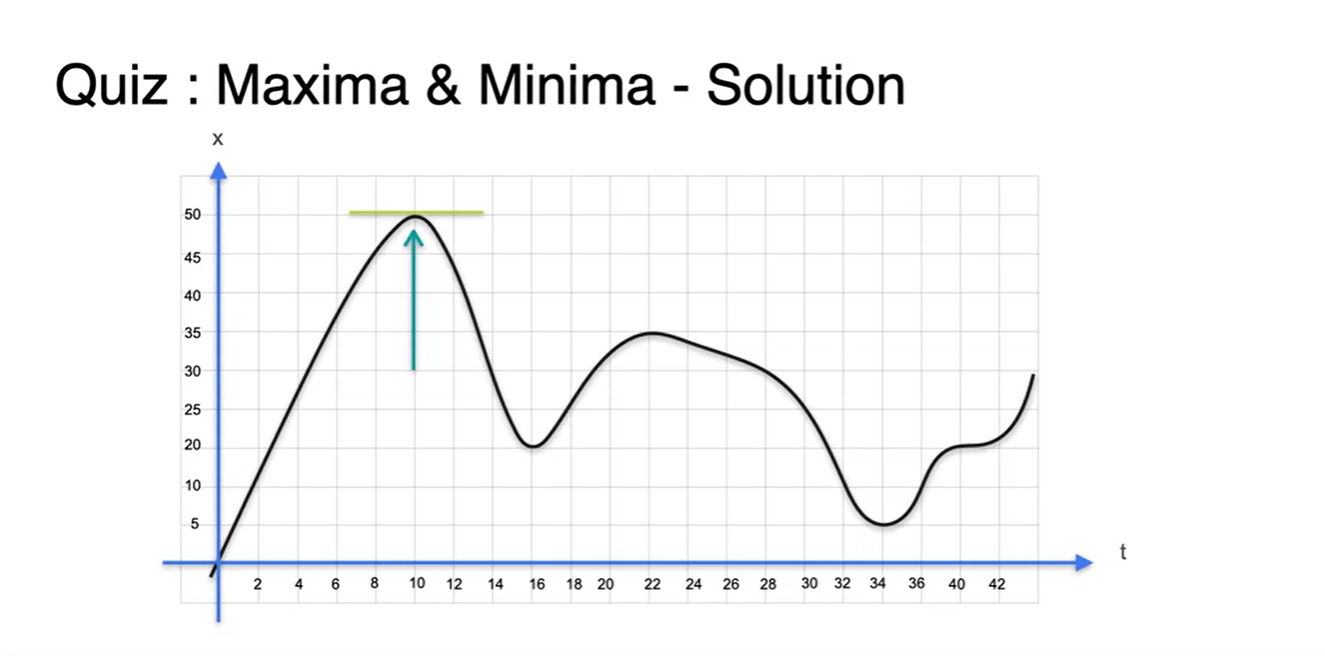
놀랍게도 slope가 0이었던 지점 중에 maximum point가 존재한다.
- 이는 최댓값과 최솟값을 구하기 위해 slope가 0인 지점을 먼저 찾고, 그 이후 최대 & 최소를 구하는 과정으로 estimation할 수 있다는 것을 의미한다.
Derivatives and their notation
- 앞에서 시간에 따른 거리 변화를 로 표현한다고 했다.
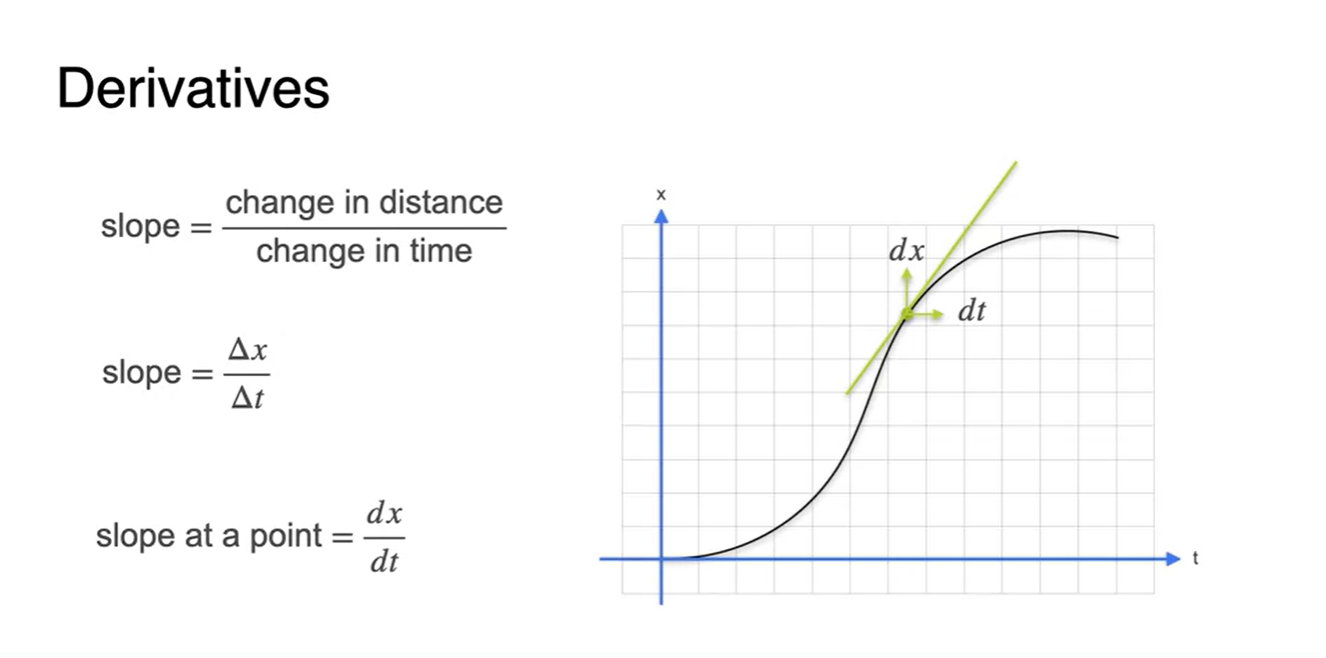
-
변수와 변수로 바꾸어 적용하면 로 표현할 수 있게 된다.
- 2차원 평면 상에서는 이 notation을 일반적으로 사용한다.
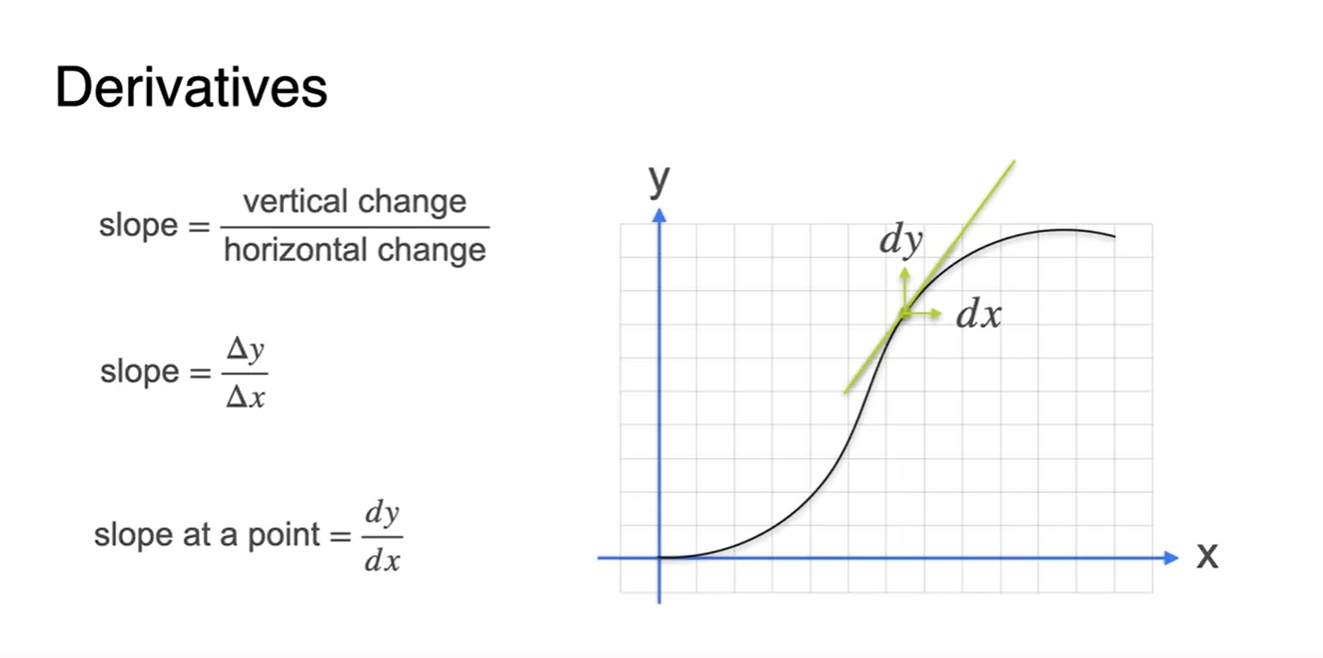
-
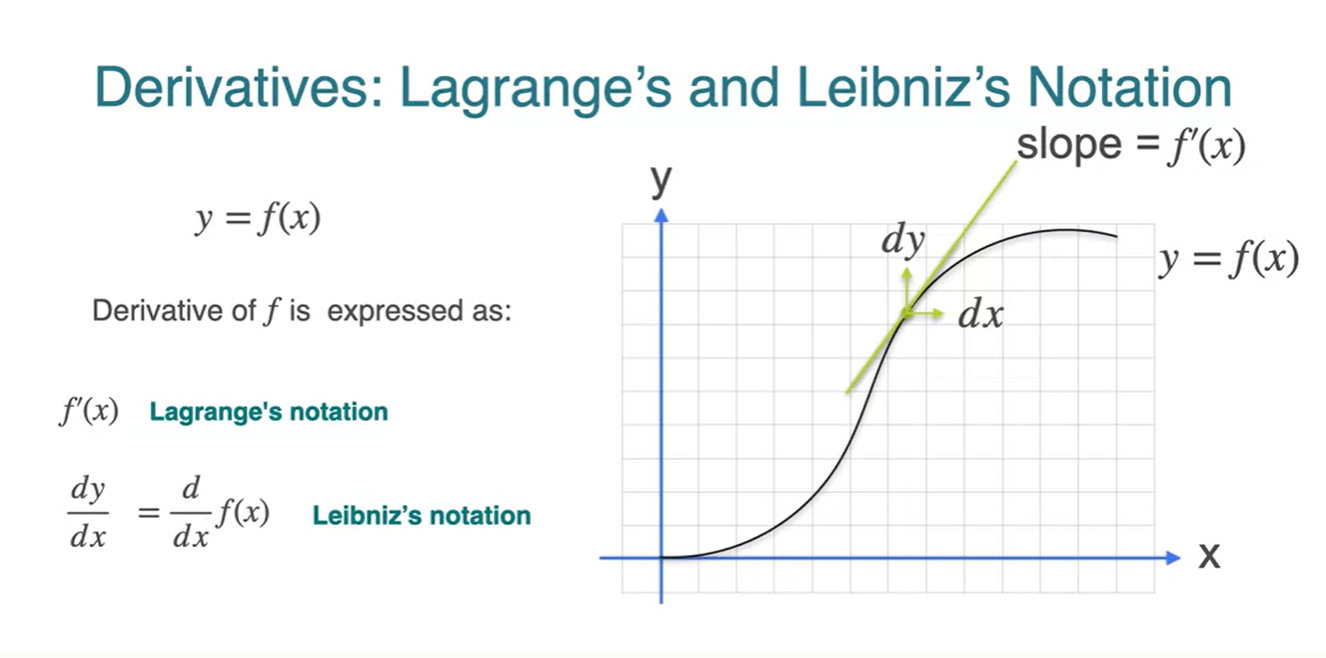
미분에 대한 수식을 표현하는 방법이 아래와 같이 두 가지가 있다.
-
Lagrange's notation :
-
Leibniz's notation :
-
Some common derivatives - Lines
-
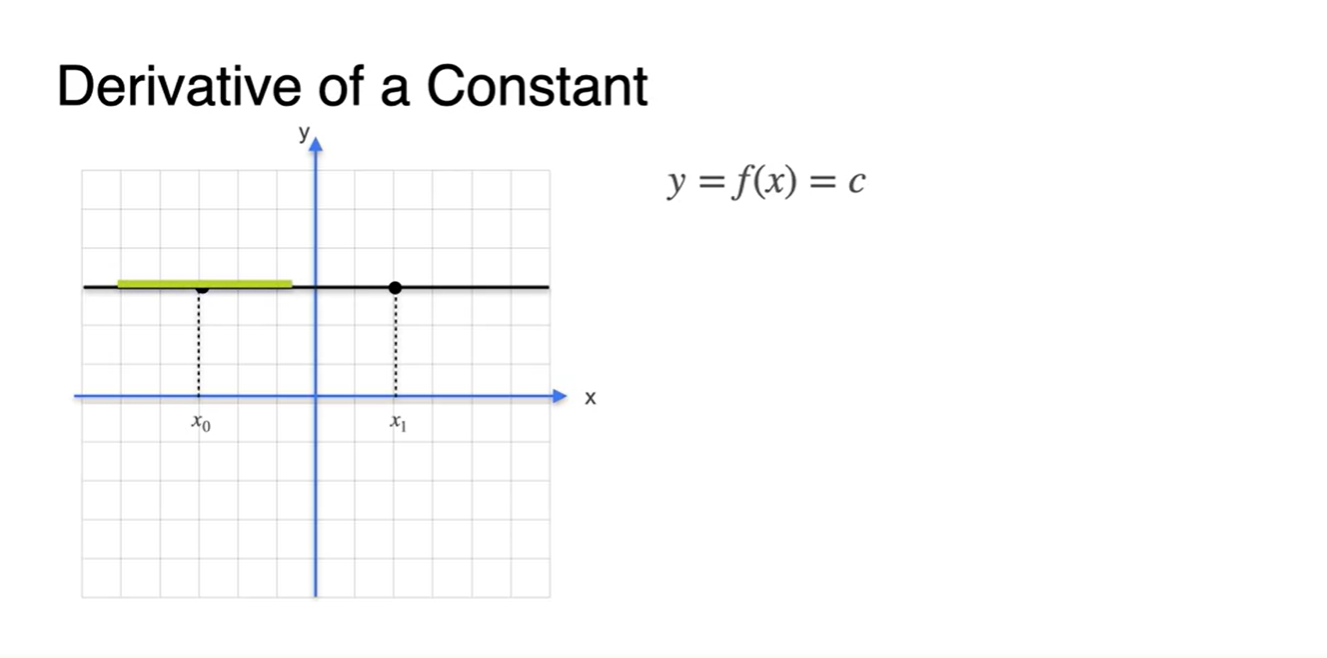
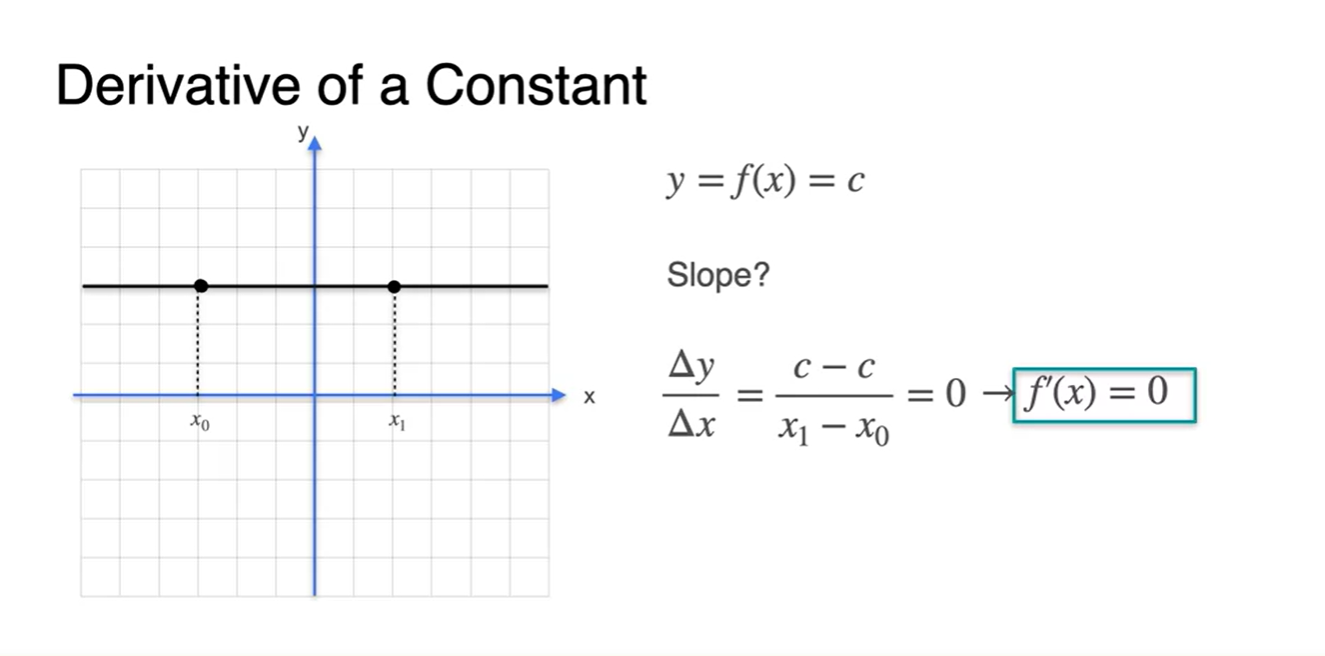
Constant 함수의 derivative는 0이다.
- Slope를 계산해보면 어느 점에서나 0의 값을 가진다는 것을 알 수 있다.
-
함수의 derivative는 얼마일까?
- 멀리 떨어진 두 지점의 Slope를 계산해보면 가 나온다.
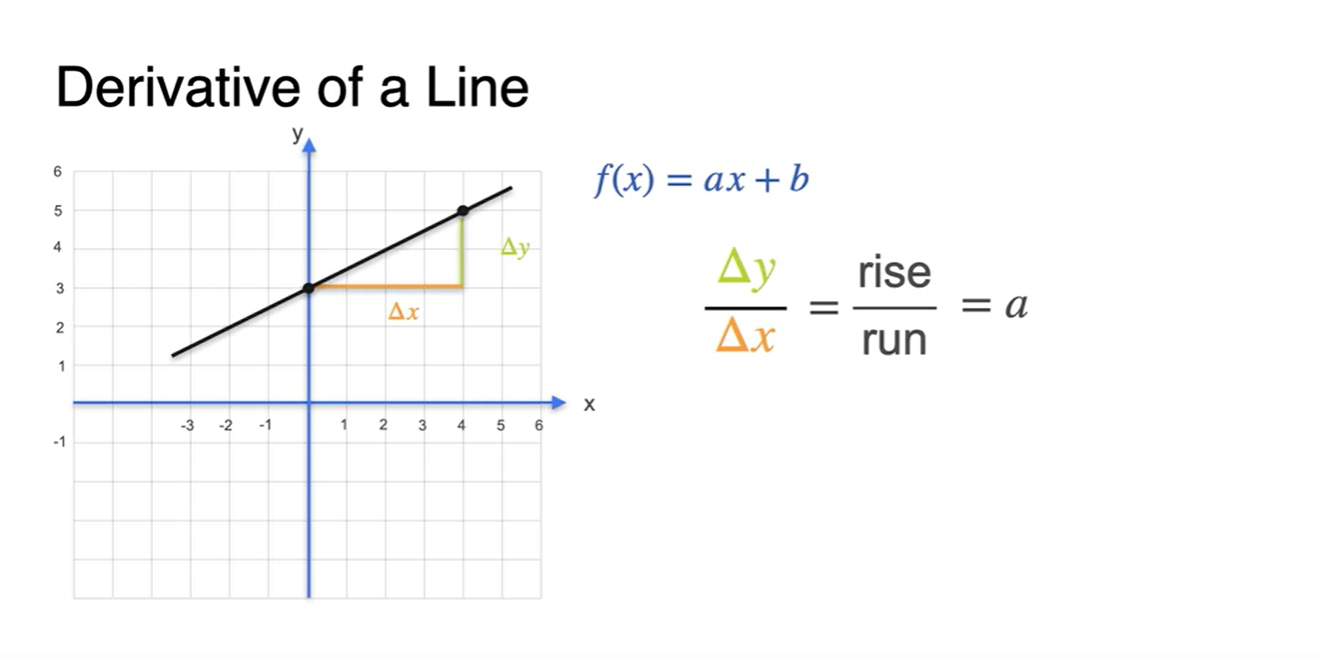
- 원점에서 매우 가까운 두 점의 slope를 계산해도 같은 값이 나온다.
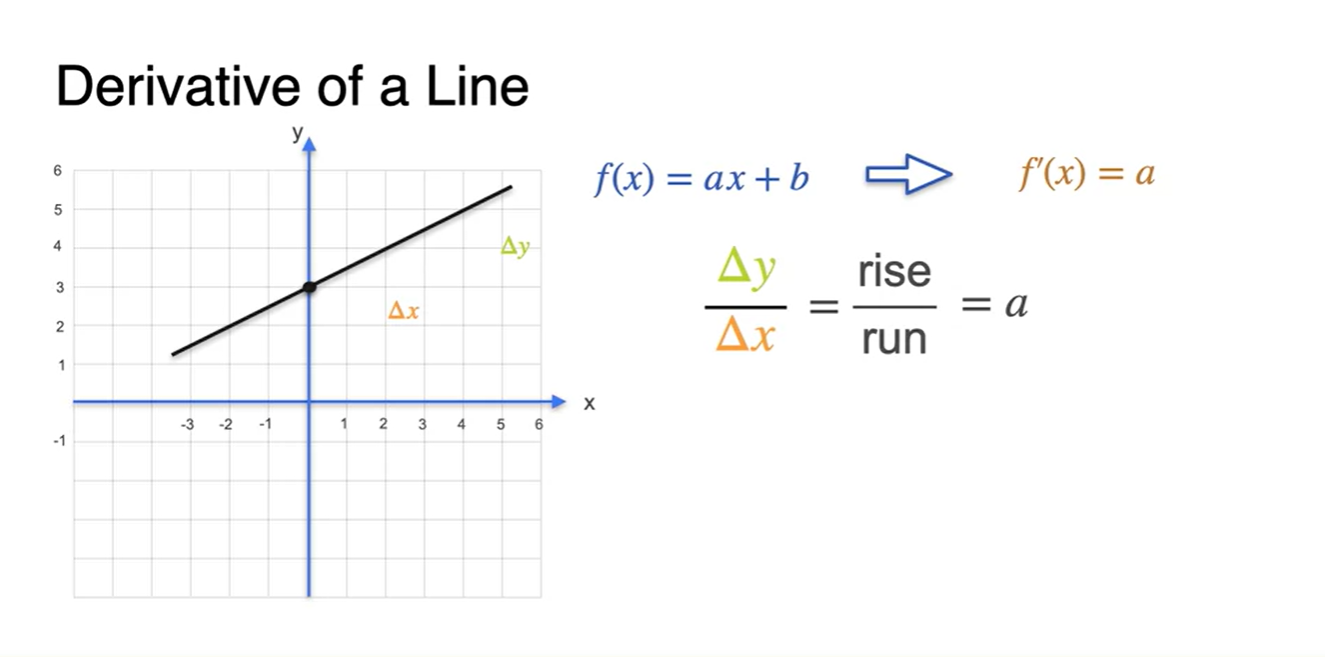
-
를 더한 만큼의 변화량이 추가되어 좌표로 표현되었기 때문에
- slope를 계산해보면 대부분의 값이 소거되었음을 알 수 있다.
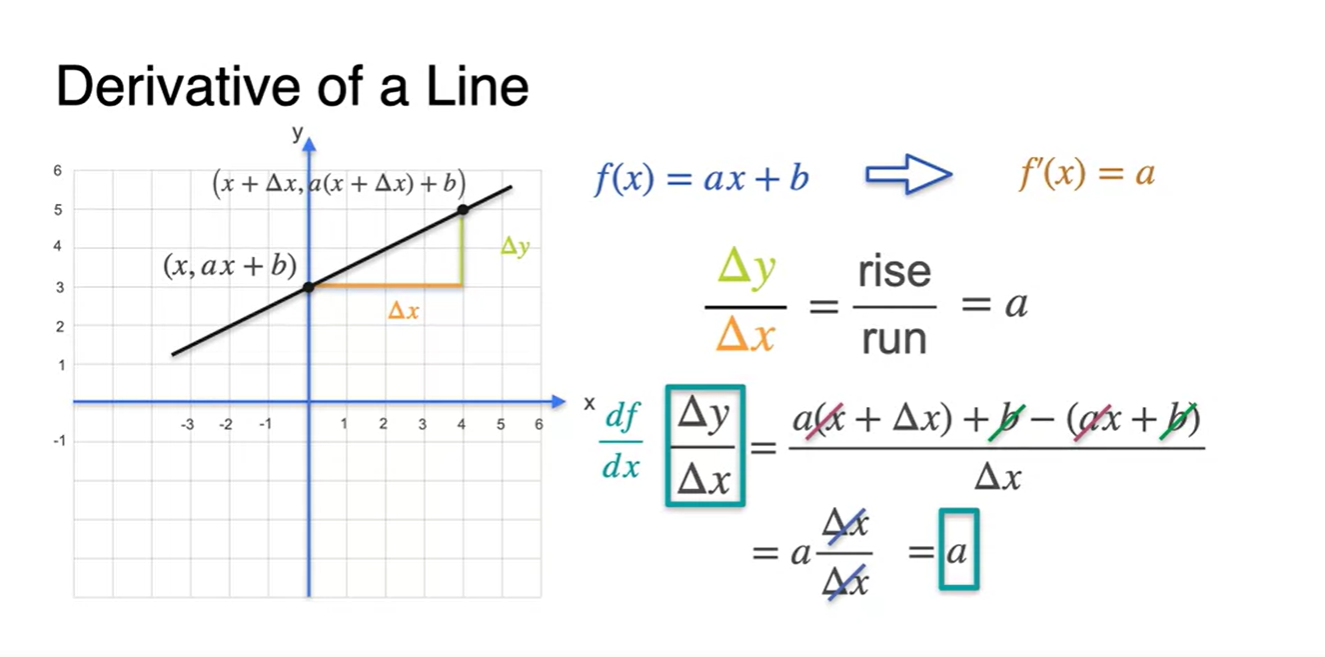
Some common Derivatives - Quadratics
-
이번에는 2차 함수의 derivative을 살펴보자.
- Slope는 그래프의 순간 기울기이므로 파란색 line과 같이 그려질 것이다.
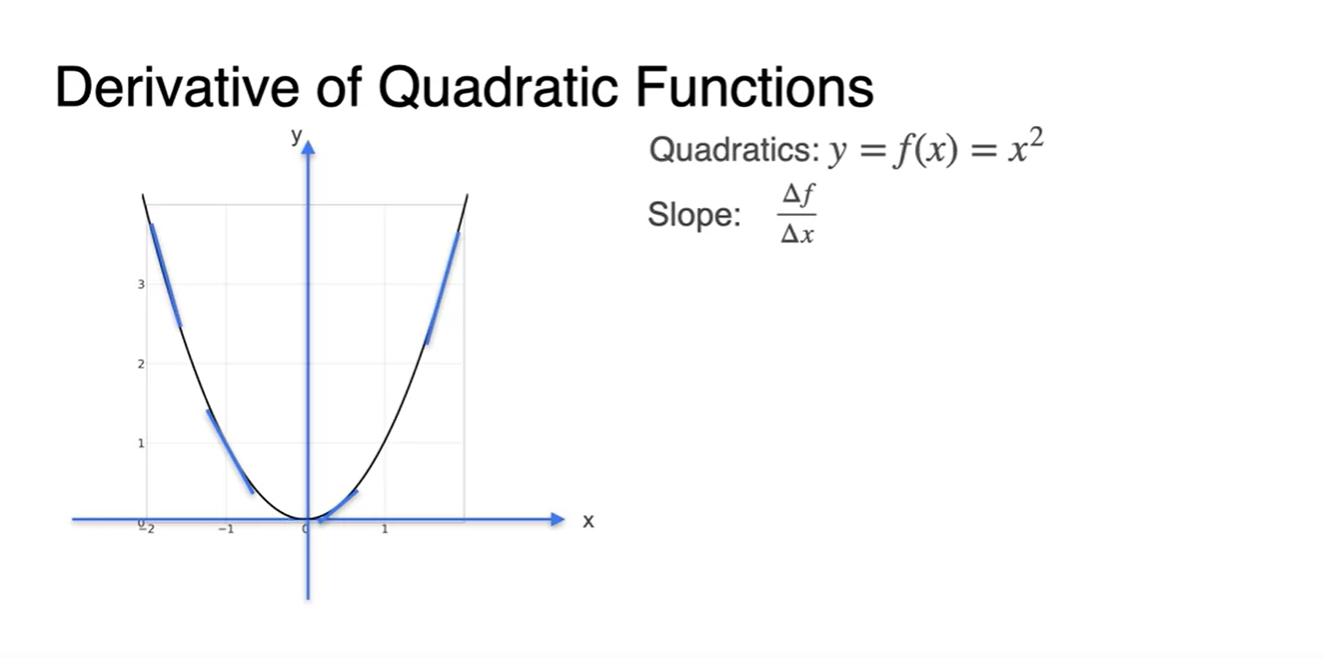
-
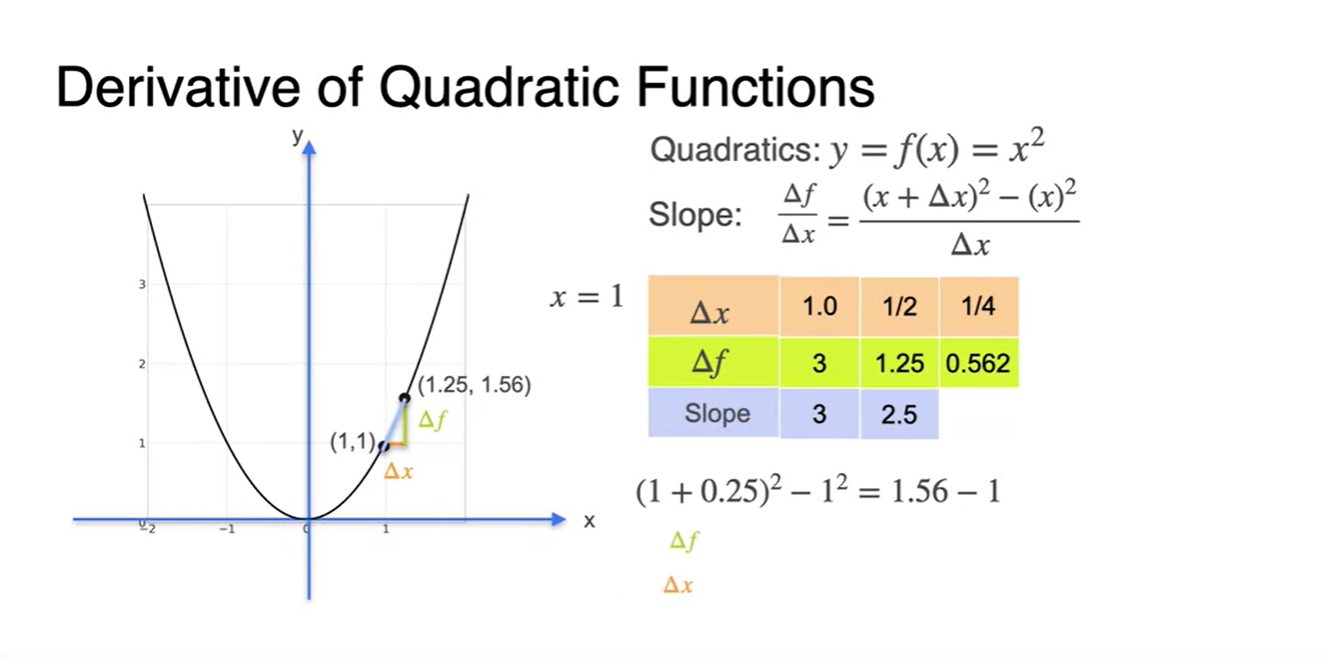
가 1인 slope를 구하면
- 를 로 나눠준 결과와 같다.
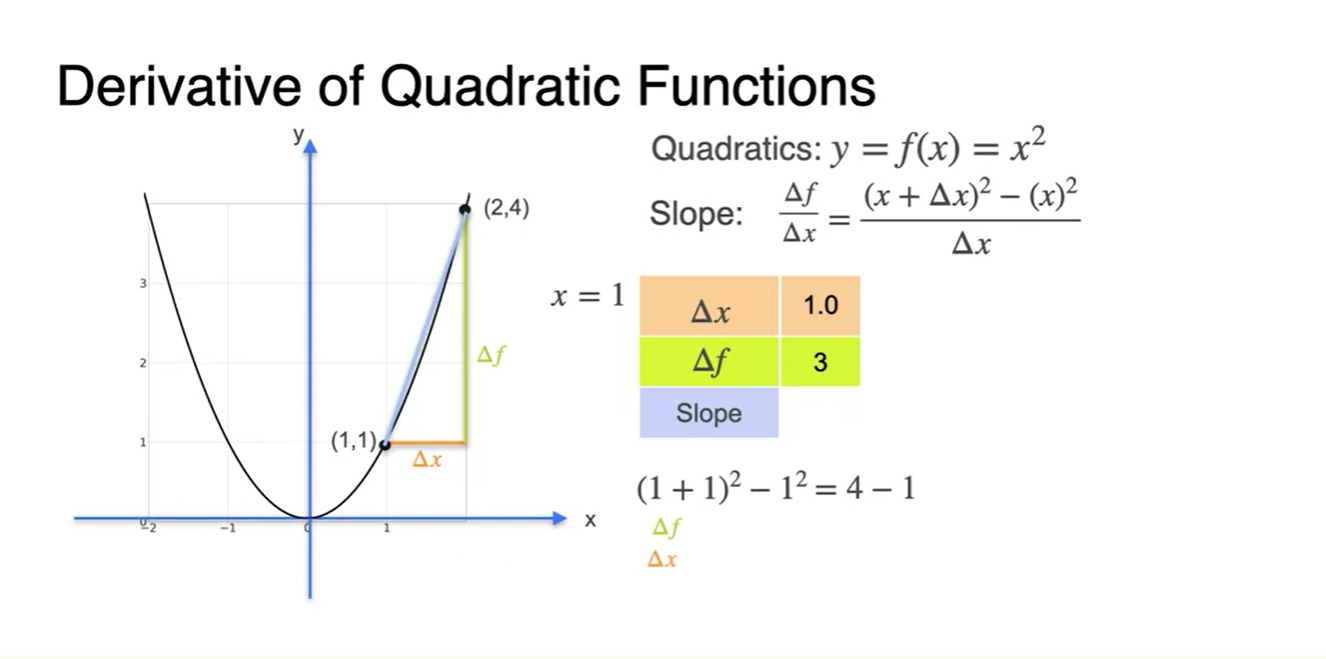
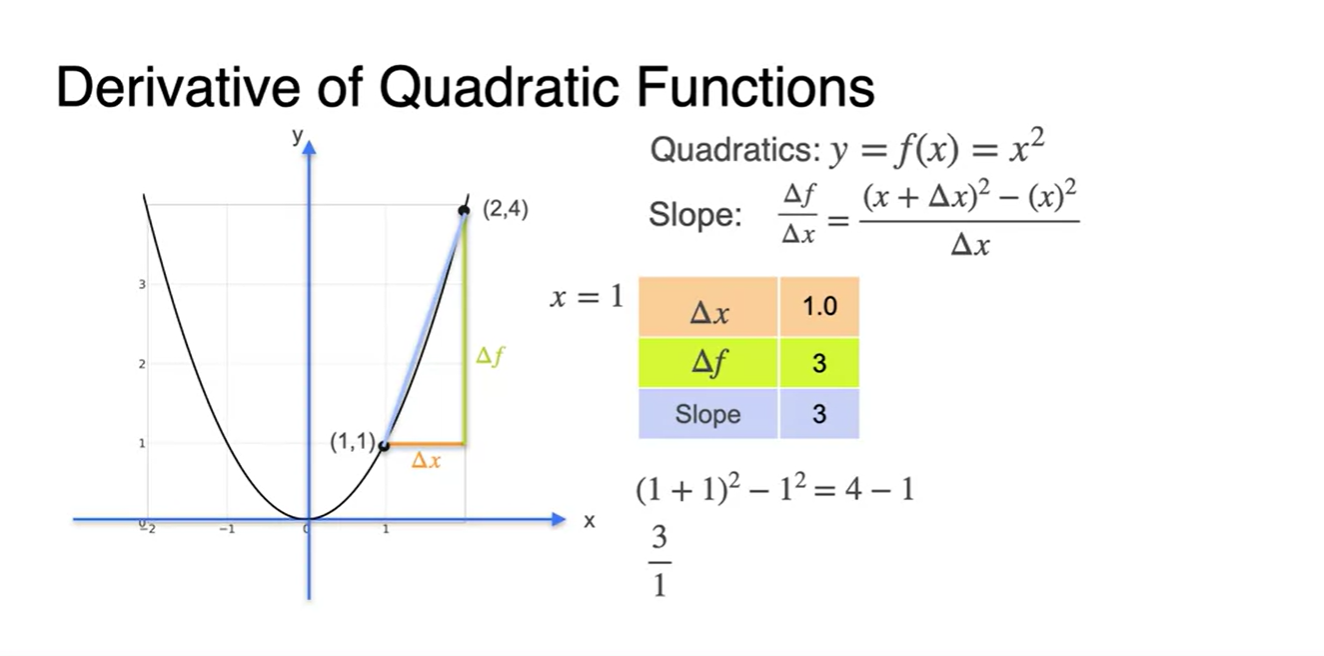
-
를 1/2로 범위를 줄이면
- slope 계산 값은 2.5가 되었다.
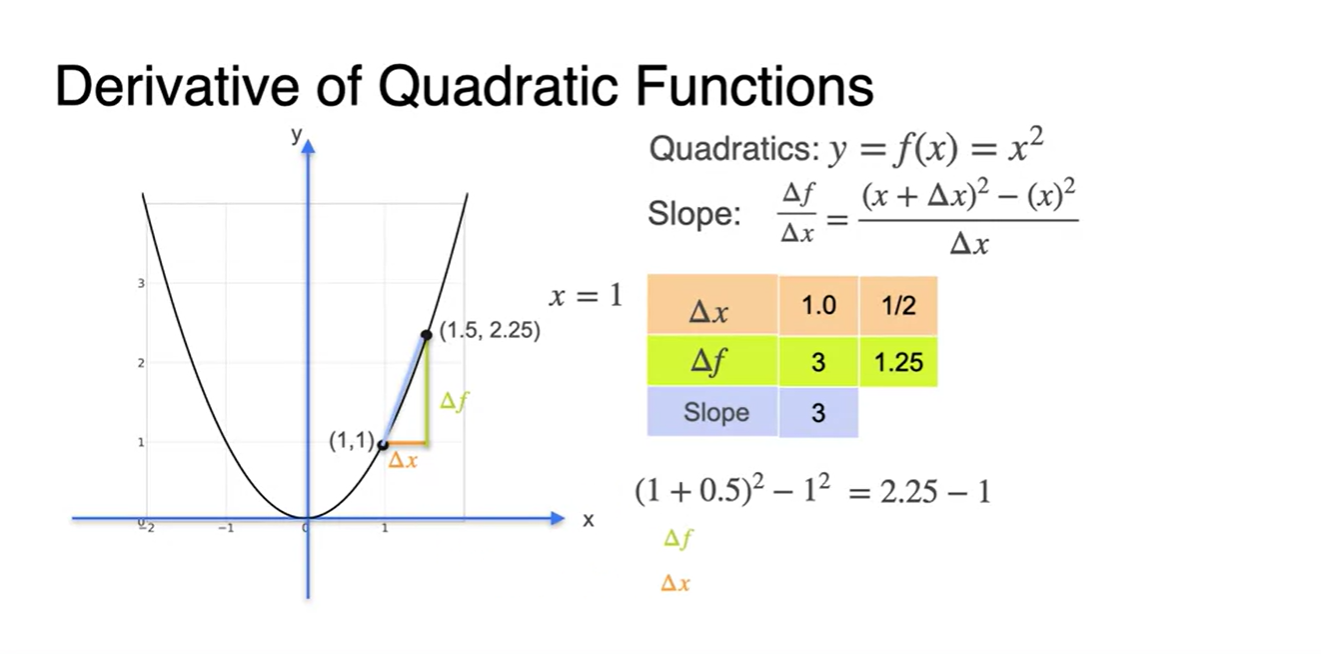
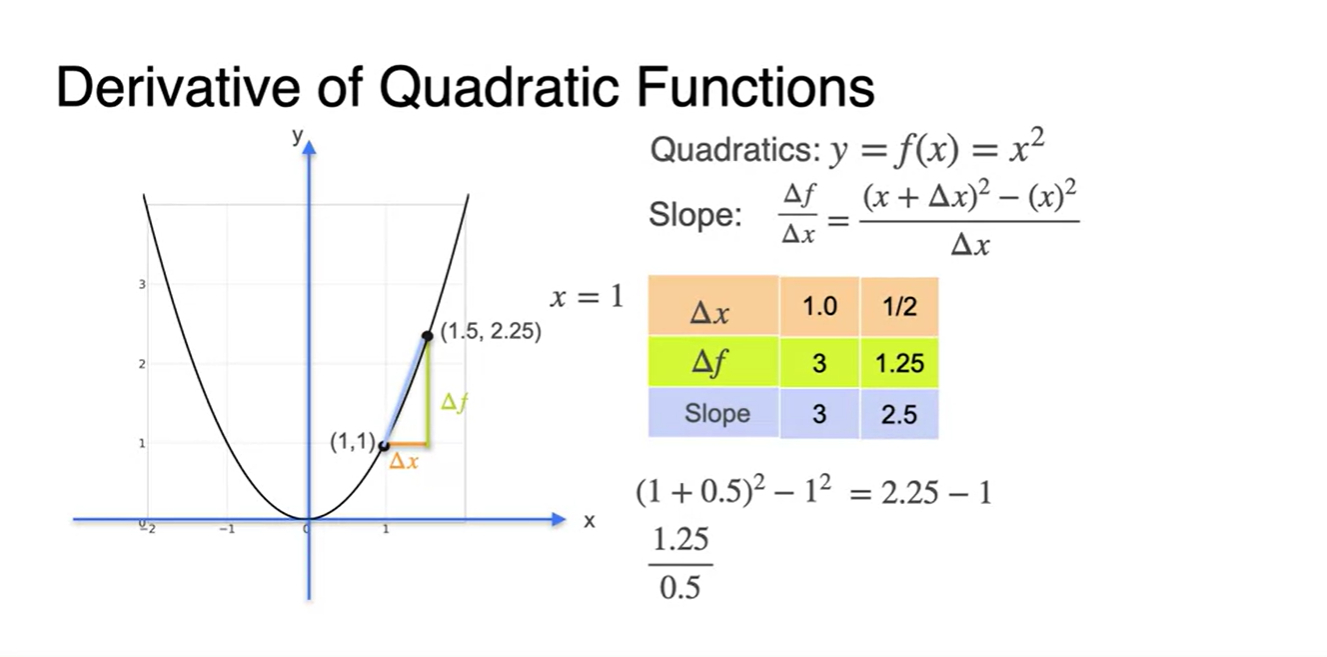
-
를 1/4로 범위를 더욱 줄이면
- slope 계산 값은 2.25다.
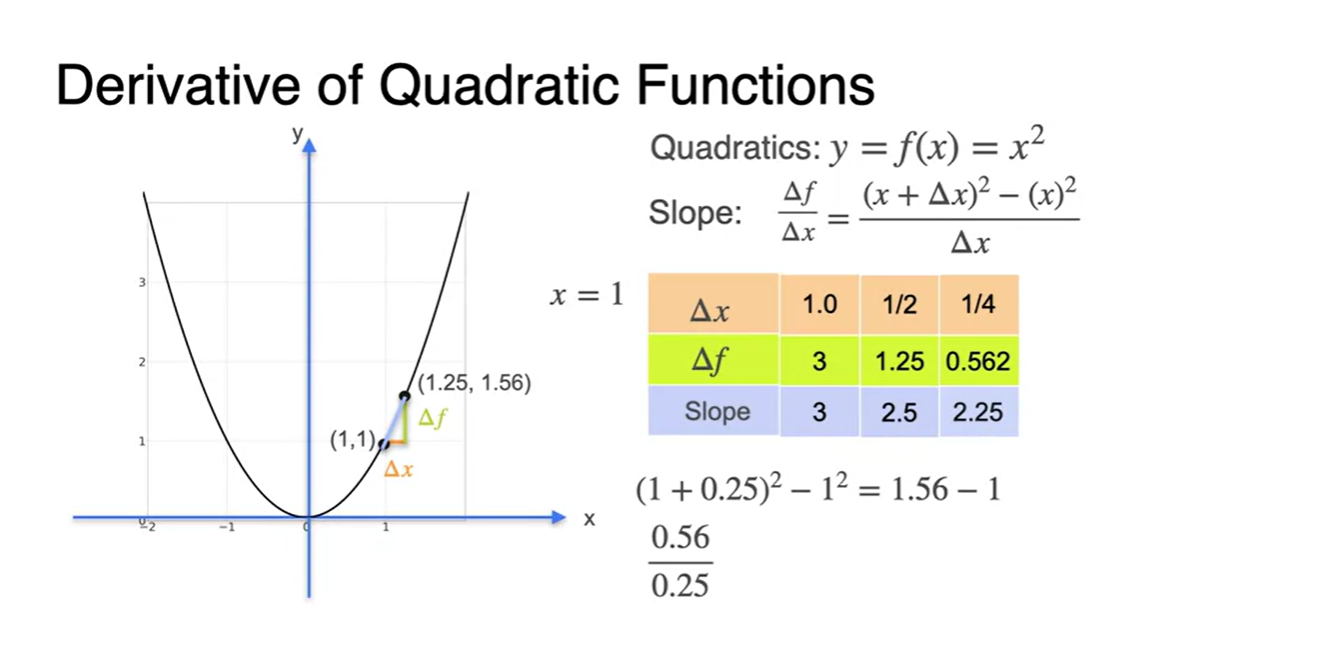
-
계속해서 를 줄여가며 derivative를 계산하면 점점 2에 수렴하게 되는 것을 알 수 있다.
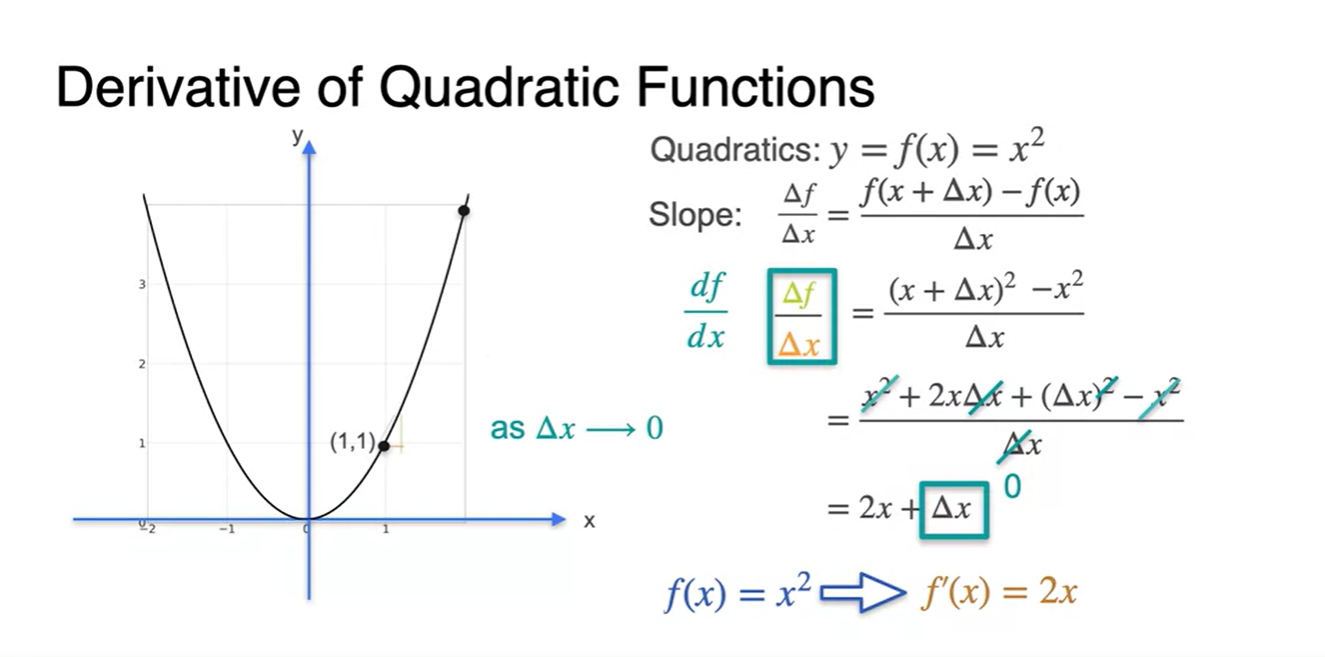
- 의 수식으로 전개될 수 있다.
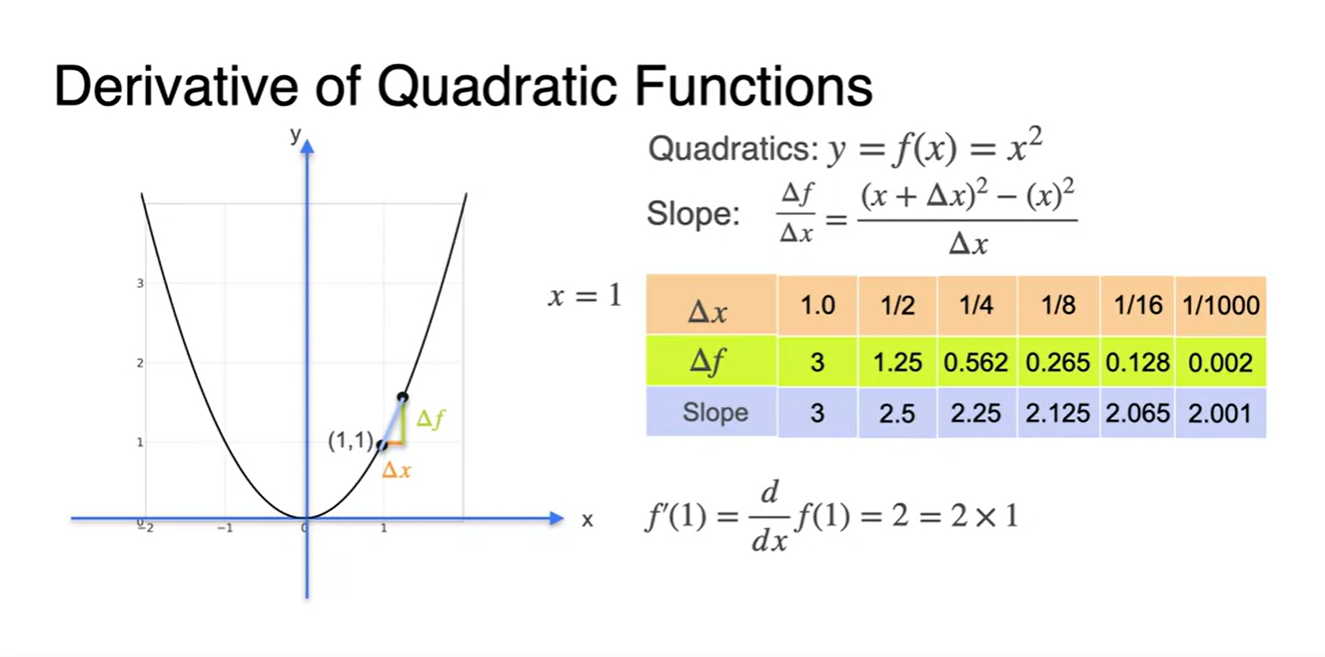
- 아래와 같이 가 포함된 수식으로 나타낸다면 로 정리될 수 있다.
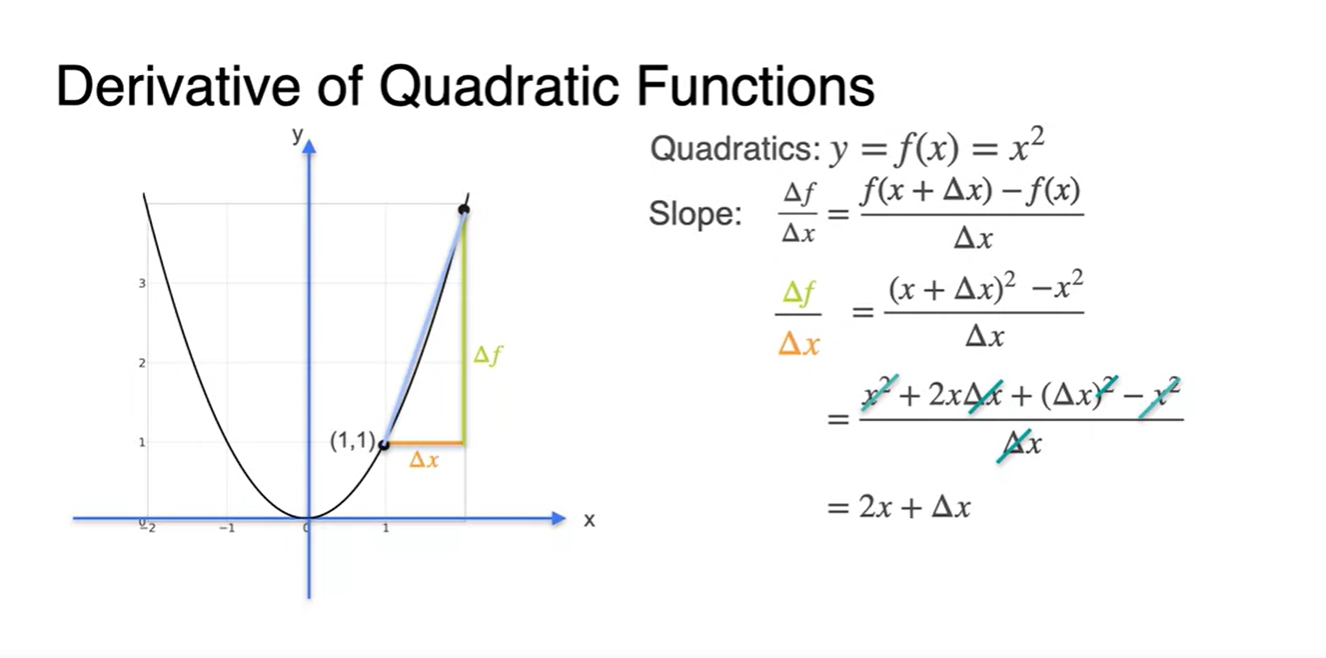
-
을 만족한다면 derivative 최종 수식은 로만 정리된다.
- 따라서 로 정리될 수 있다.
Some common derivatives - Higher degree polynomials
-
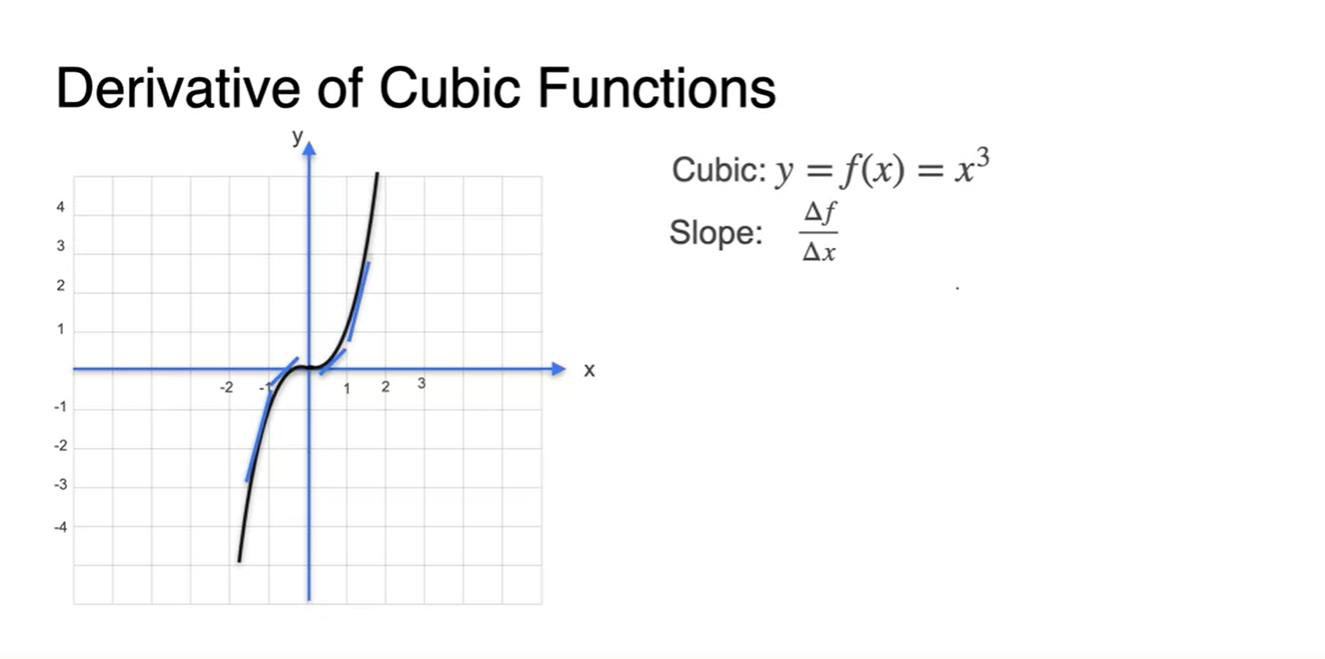
이제 고차원 다항 함수의 derivative를 구해보자.
- 마찬가지로 slope는 순간 미분인 파란색 lines와 같다.
-
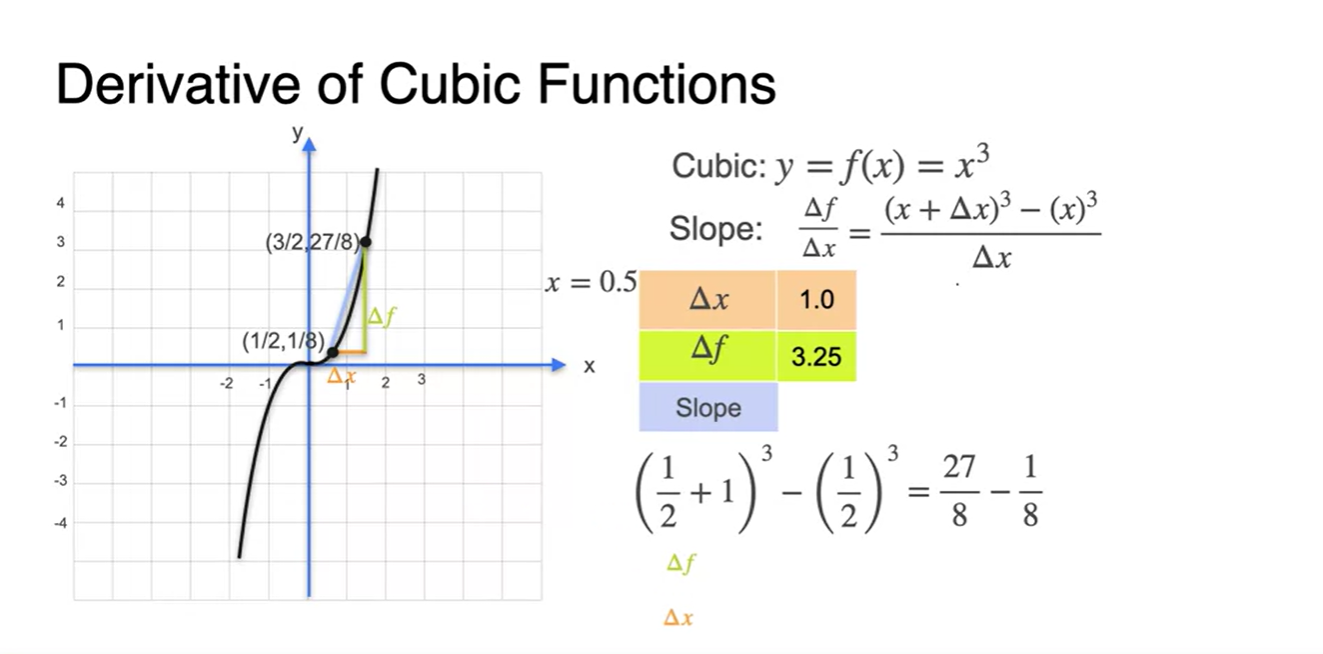
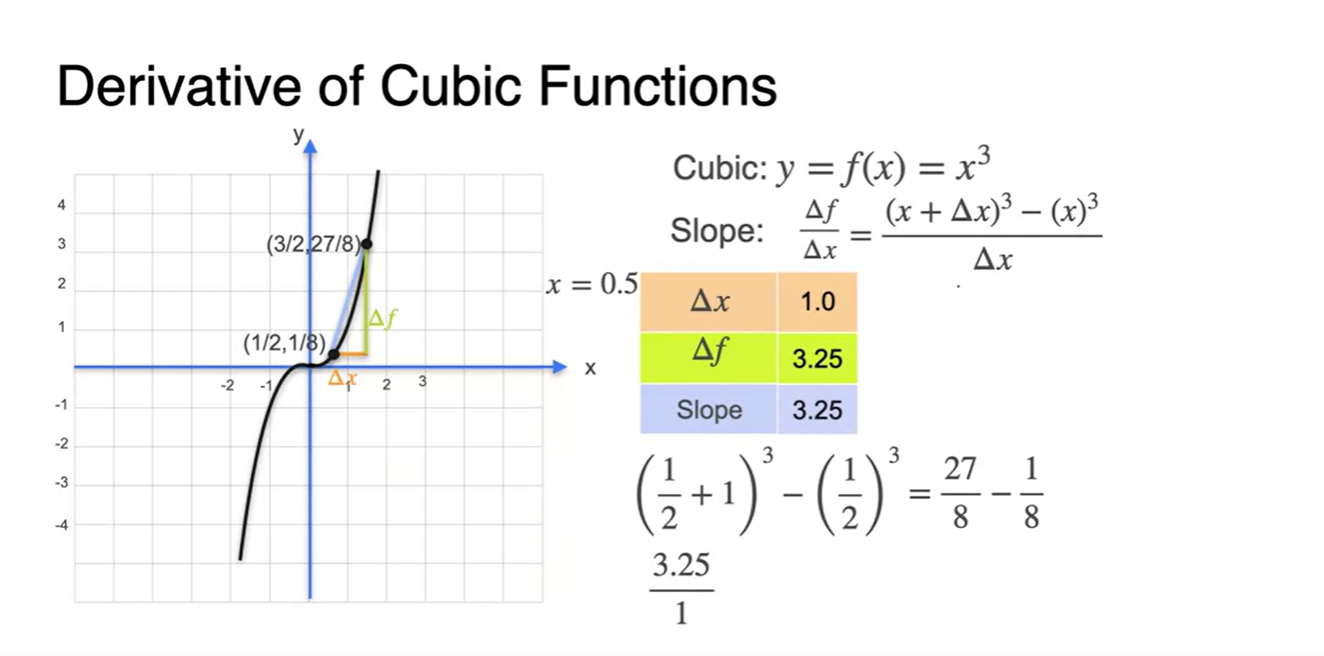
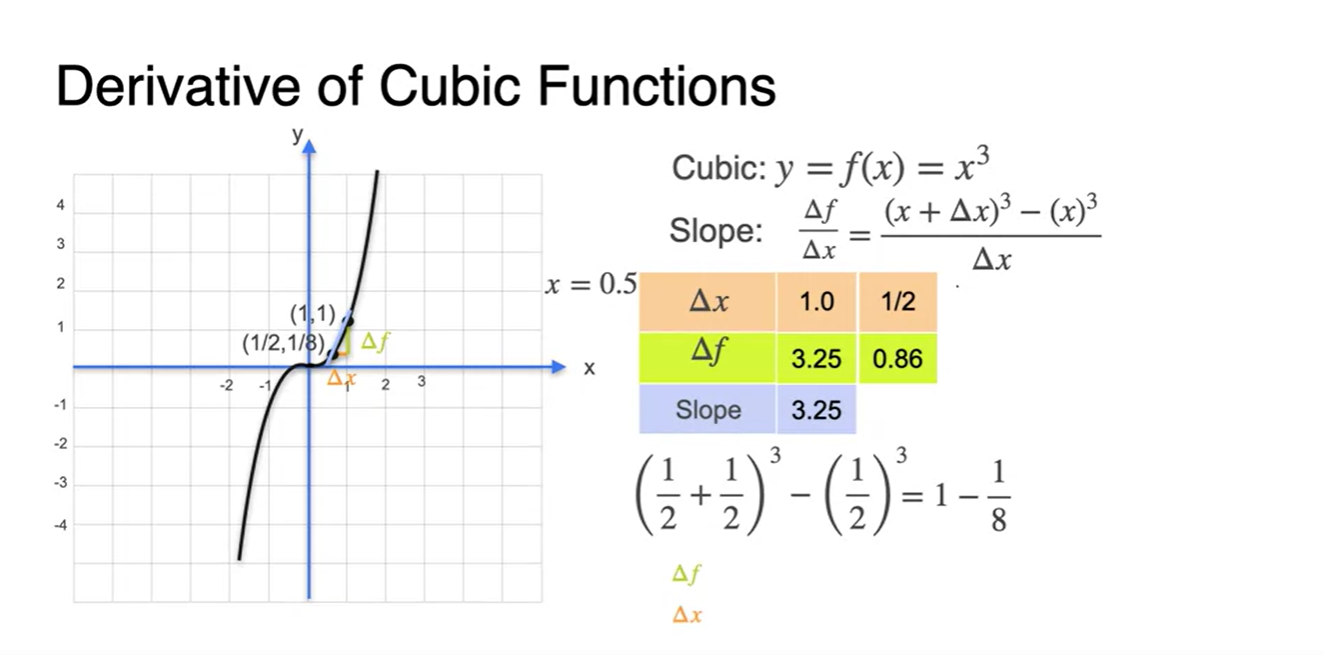
가 1인 slope를 구하면
- 를 로 나눠준 결과와 같다.
-
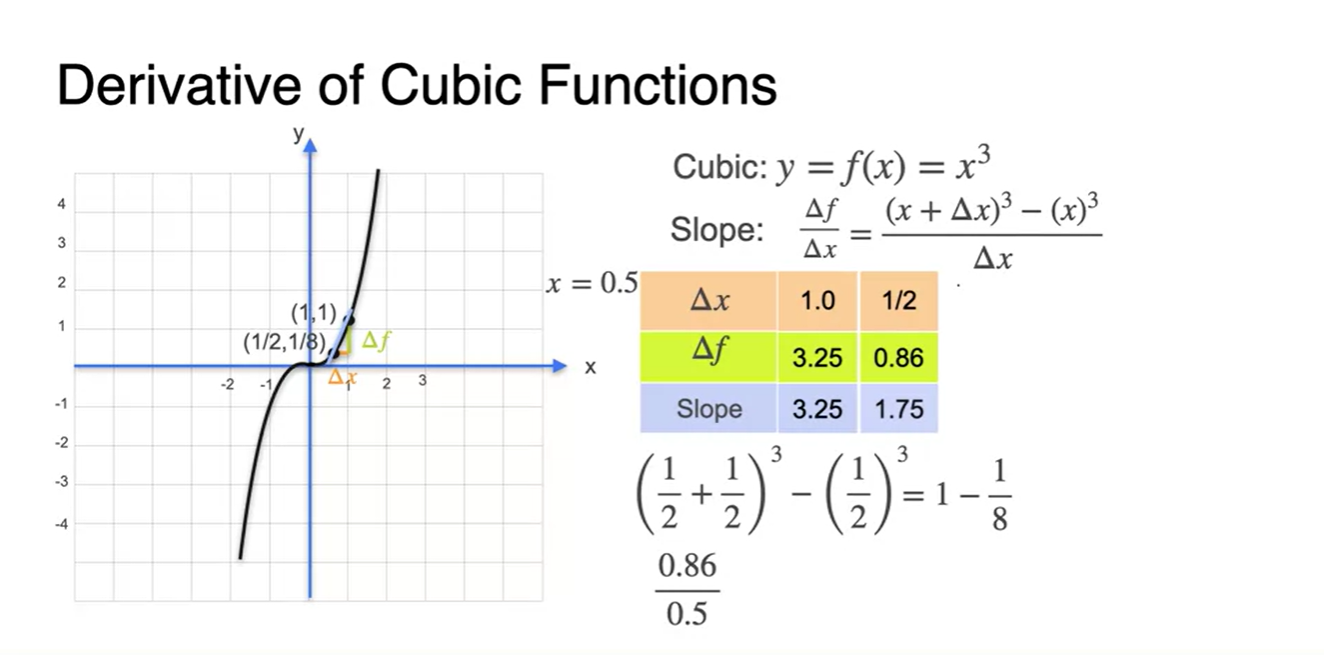
를 1/2로 범위를 줄이면
- slope 계산 값은 1.75가 되었다.
-
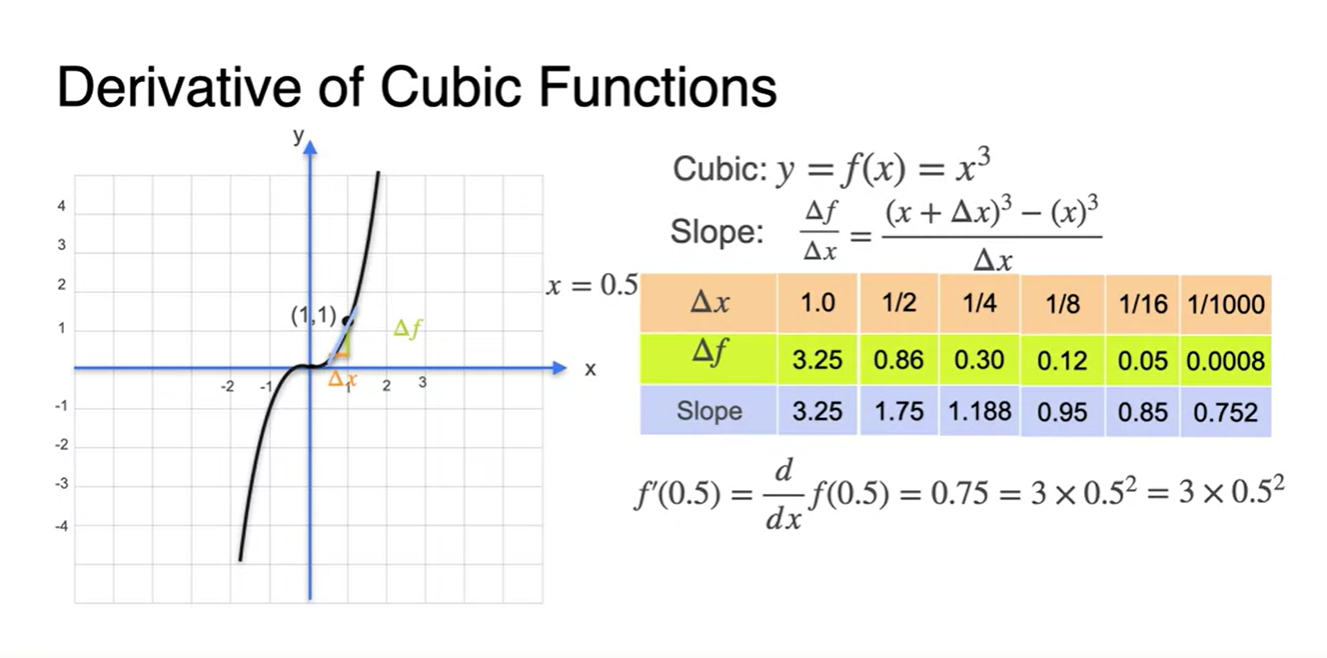
의 범위를 한없이 줄이면
- slope 계산 값은 0.75로 수렴하고, 값과 같음을 알 수 있다.
- 아래와 같이 가 포함된 수식으로 나타낸다면 으로 정리될 수 있다.
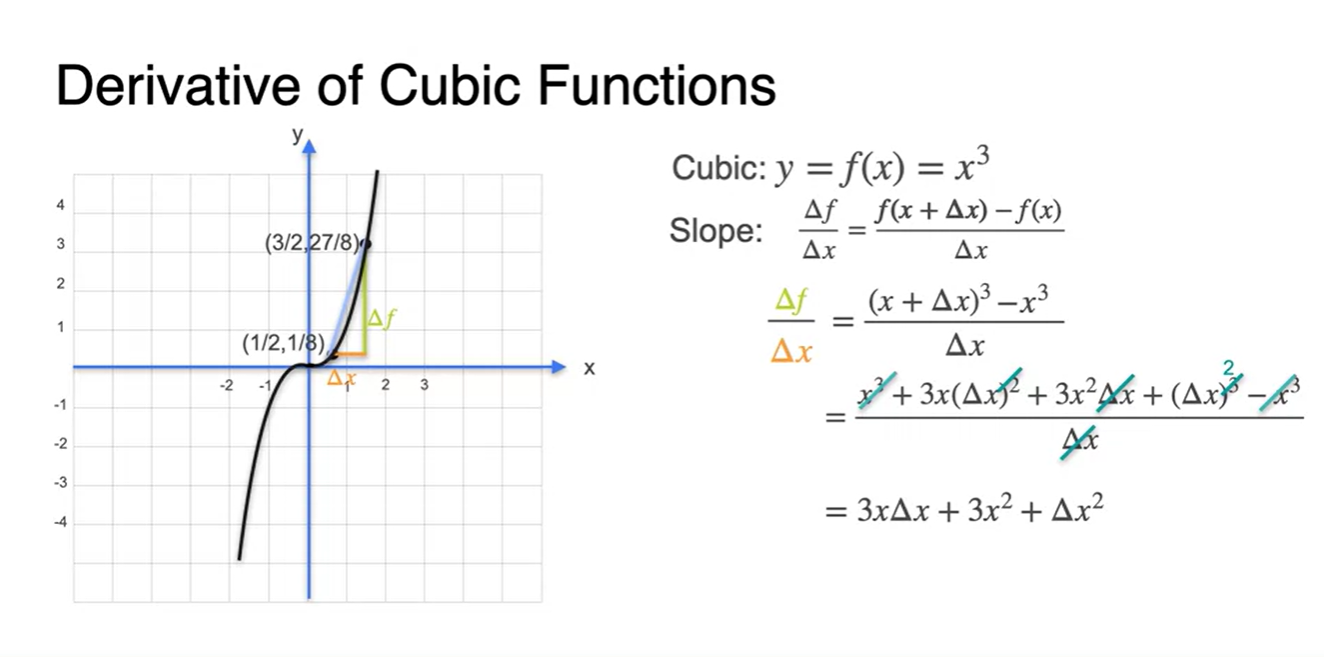
-
을 만족한다면 derivative 최종 수식은 로만 정리된다.
- 따라서 로 정리될 수 있다.
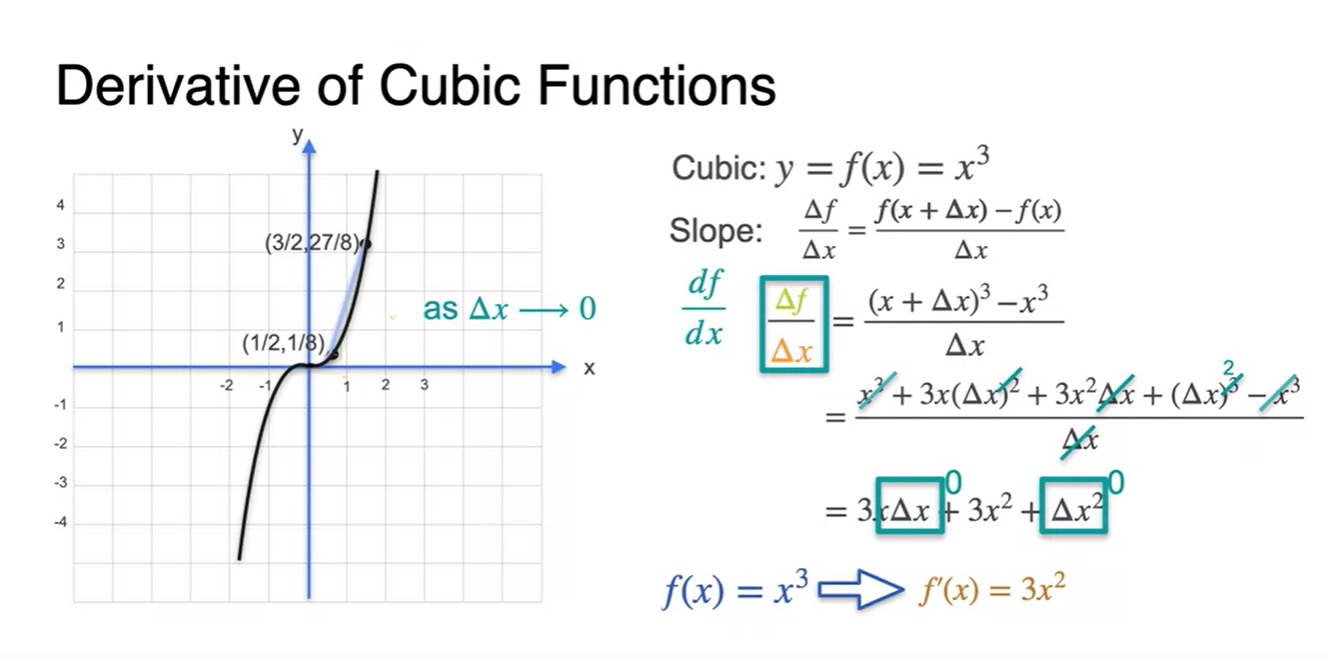
Some common derivatives - Other power functions
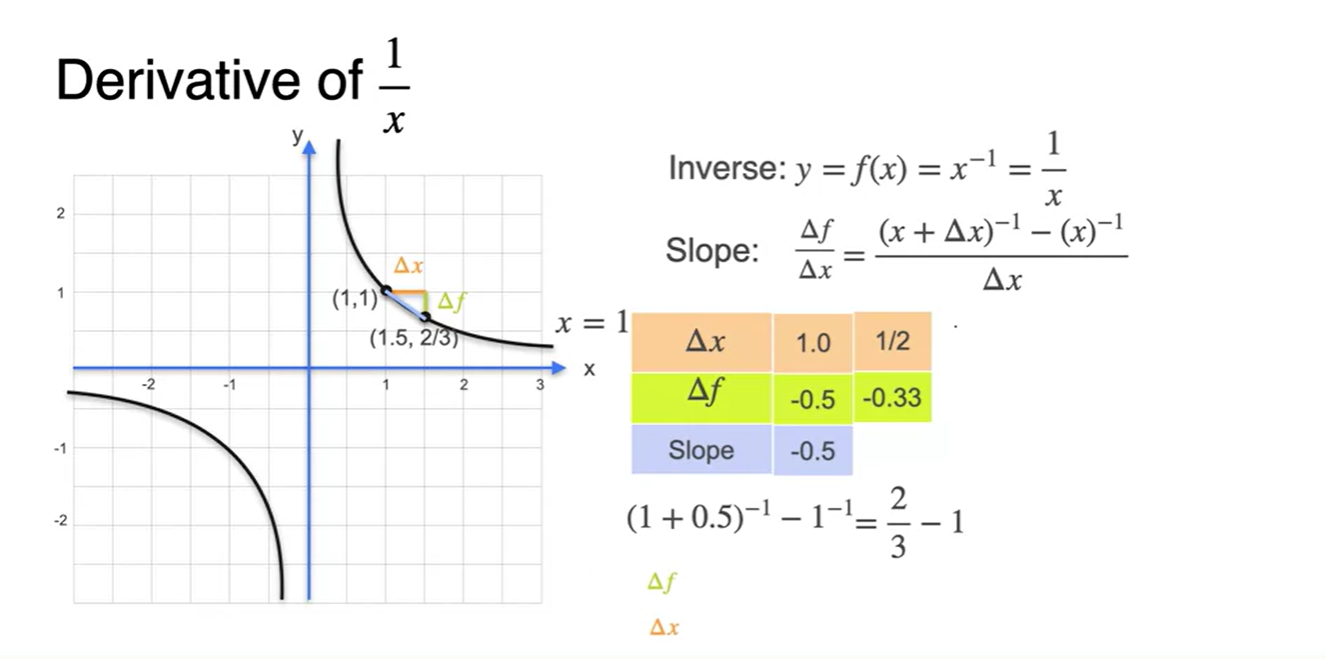
- 이번에는 또 다른 제곱항을 갖는 의 함수를 derivative해보자.
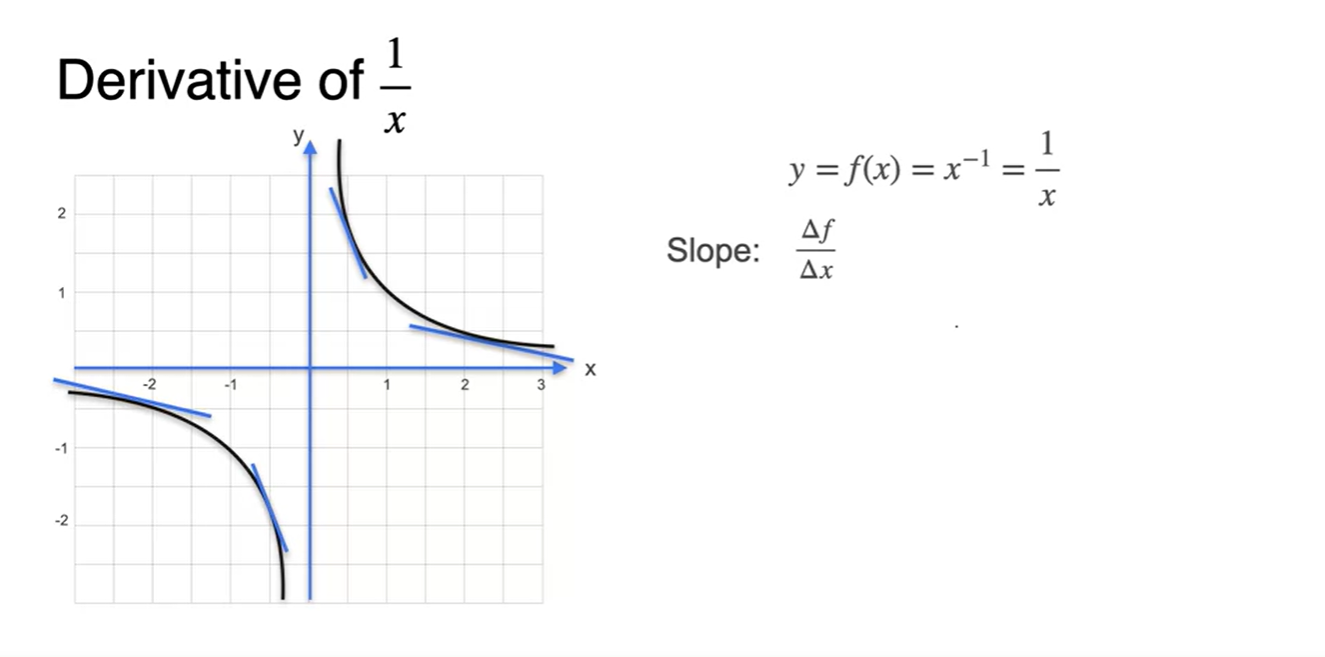
-
가 1인 slope를 구하면
- 를 로 나눠준 결과와 같다.
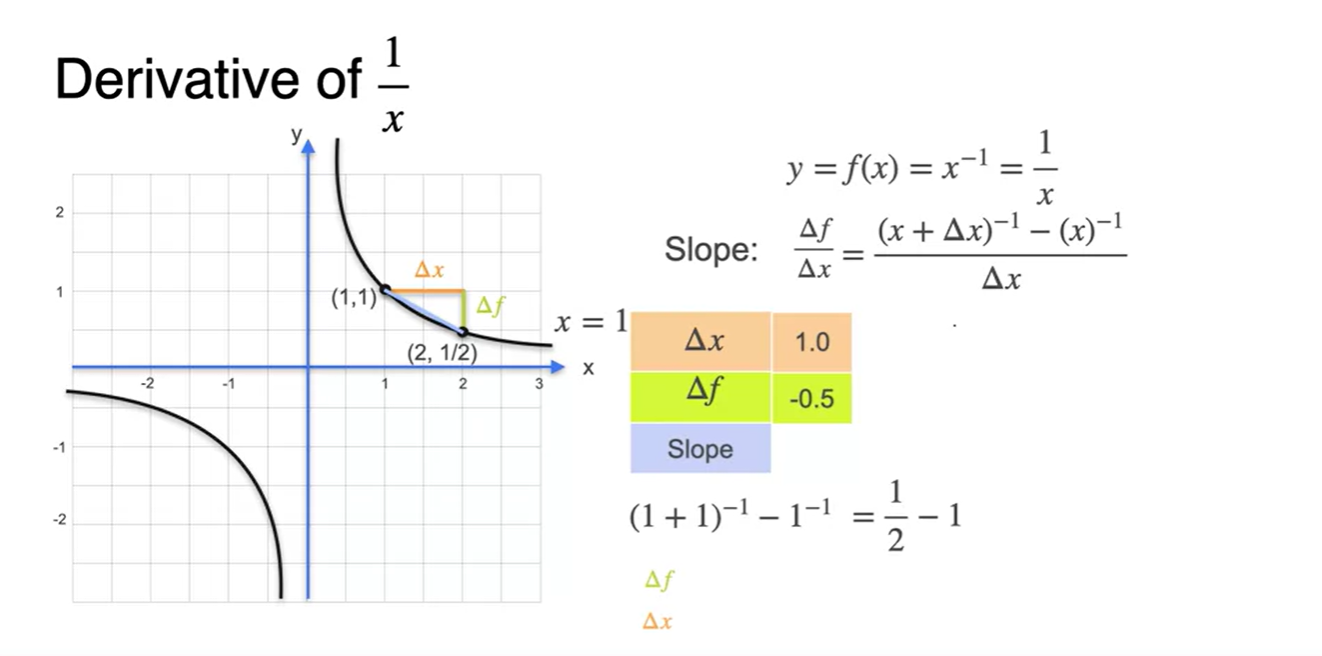
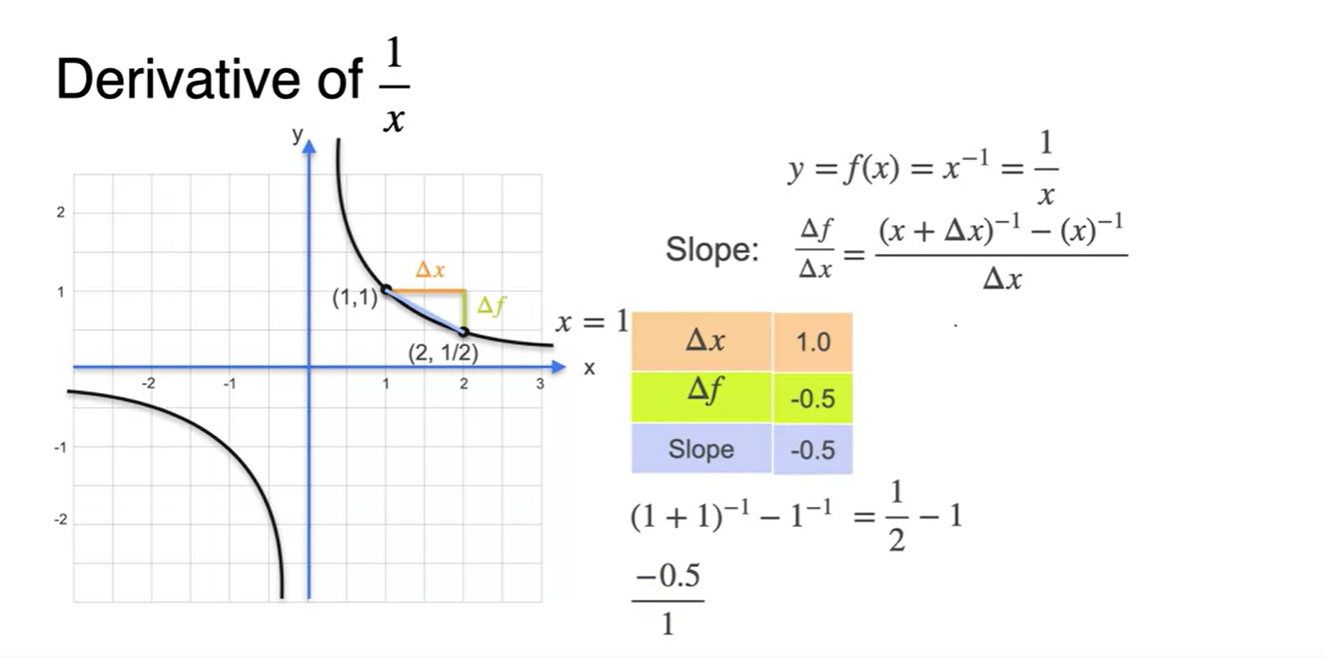
-
를 1/2로 범위를 줄이면
- slope 계산 값은 -0.67이 되었다.
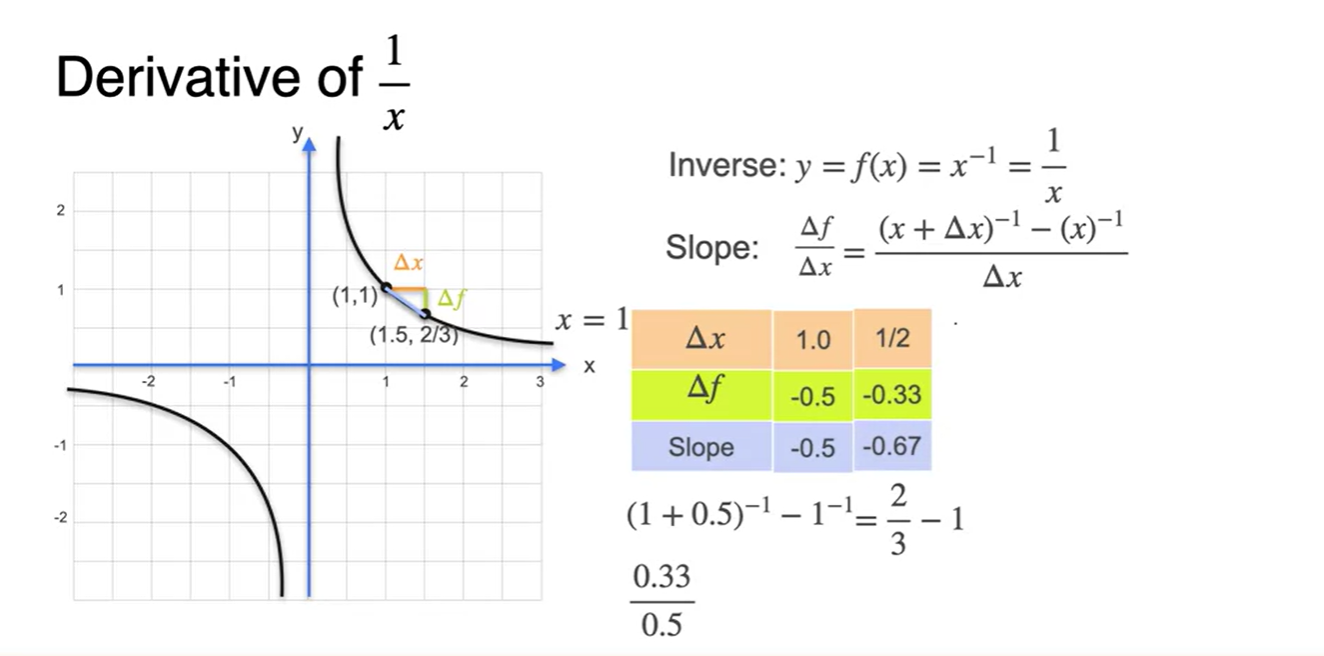
-
의 범위를 한없이 줄이면
- slope 계산 값은 -0.999로 수렴하고, 값과 같음을 알 수 있다.
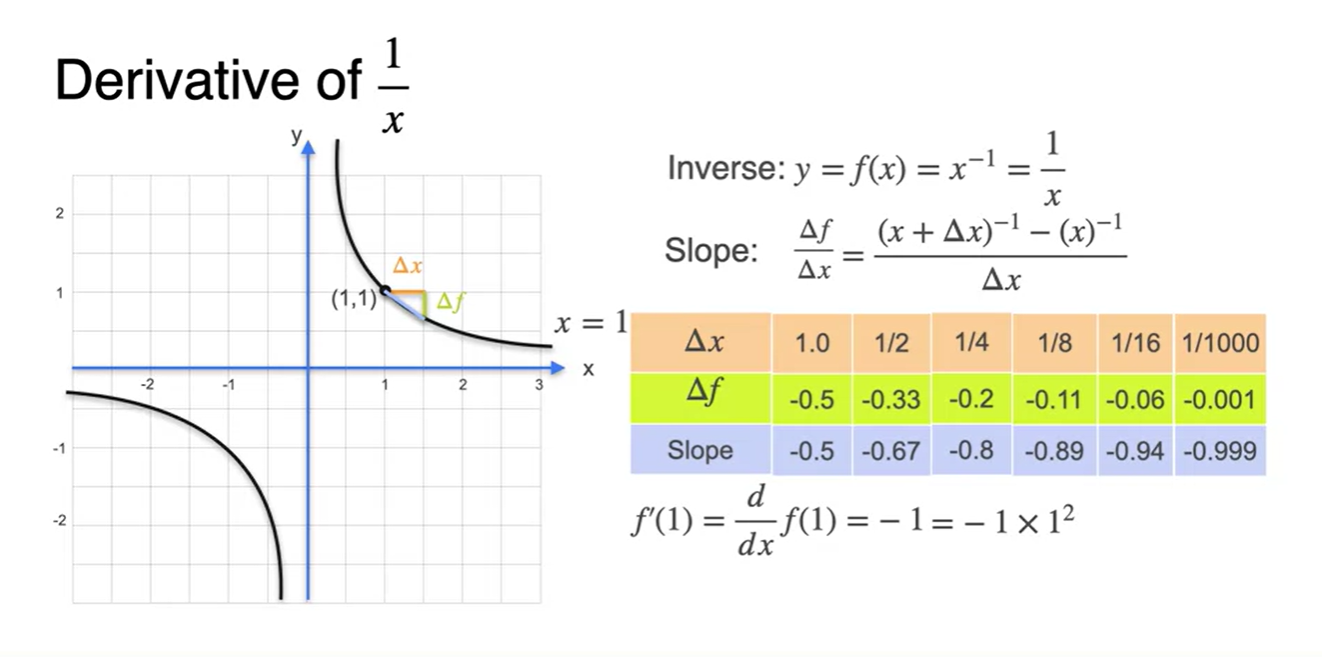
-
을 만족한다면 derivative 최종 수식은 로만 정리된다.
- 따라서 로 정리될 수 있다.
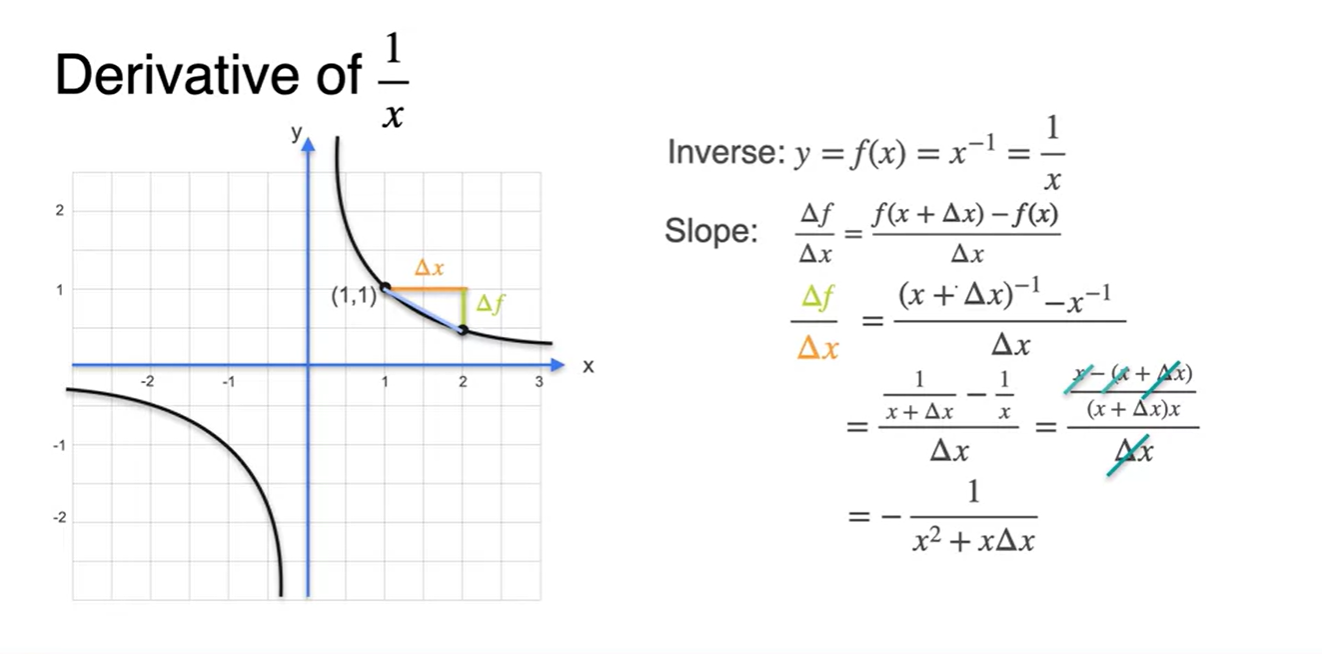
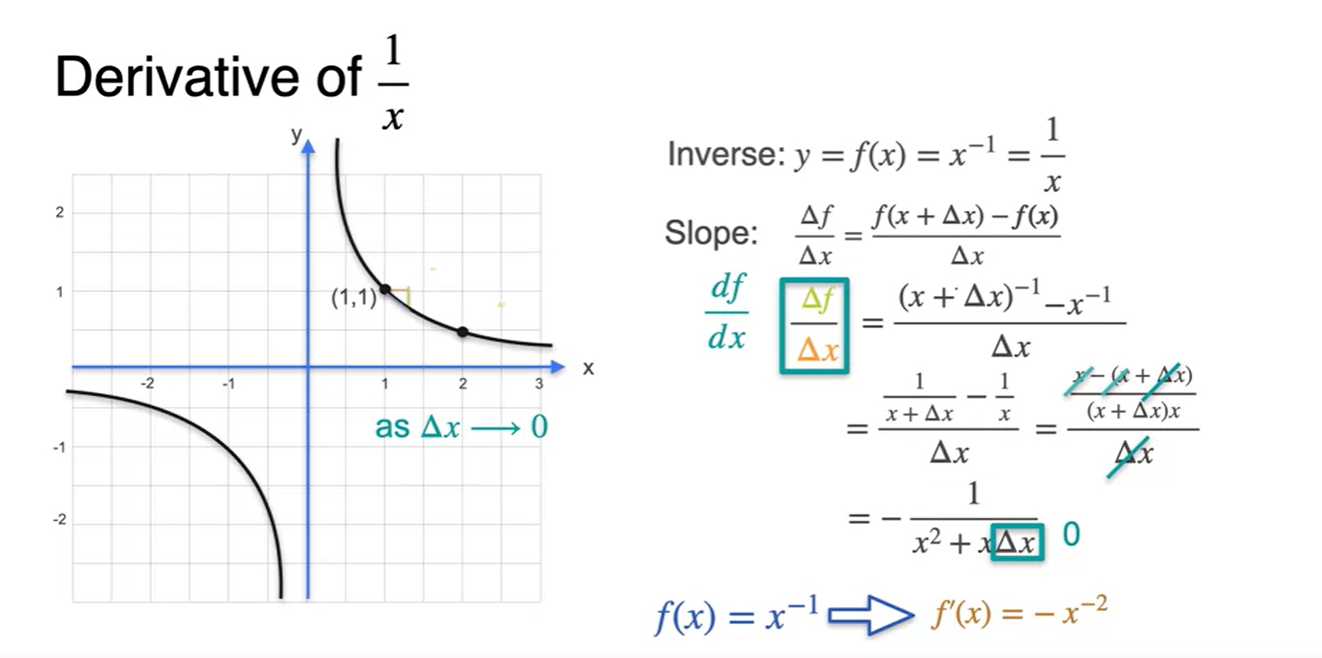
-
그러므로 다음과 같이 derivative 수식을 일반화할 수 있다.
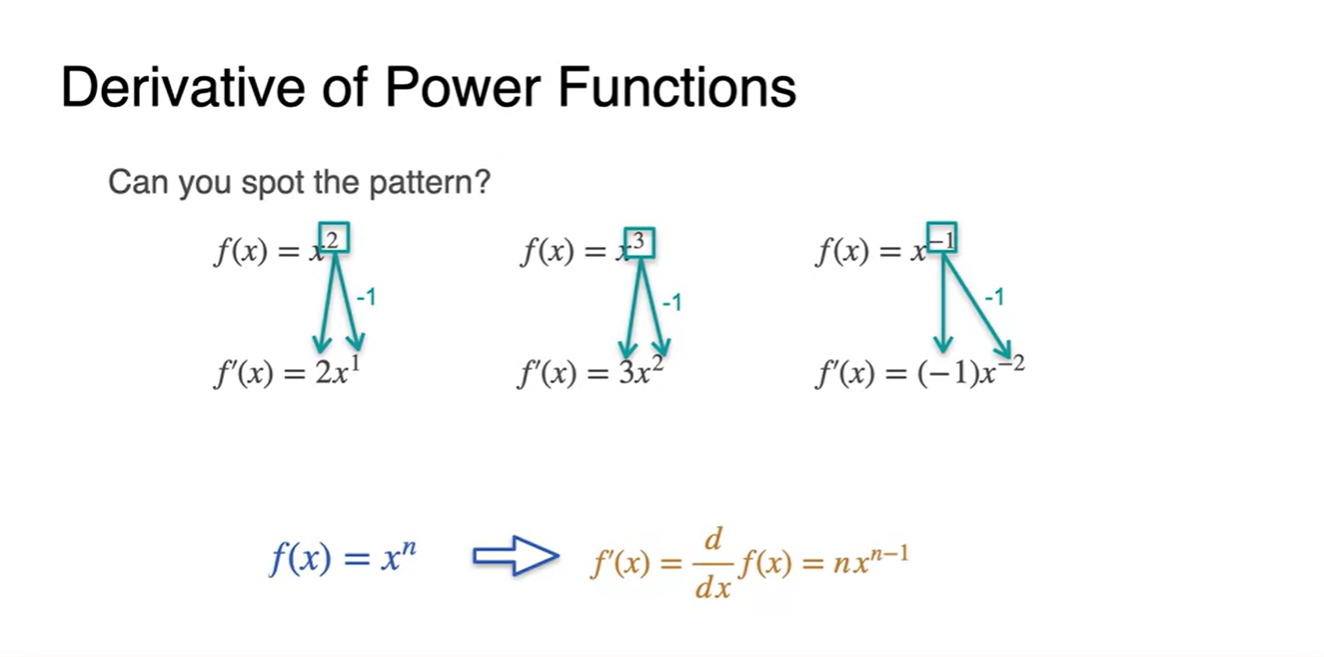
The inverse function and its derivative
-
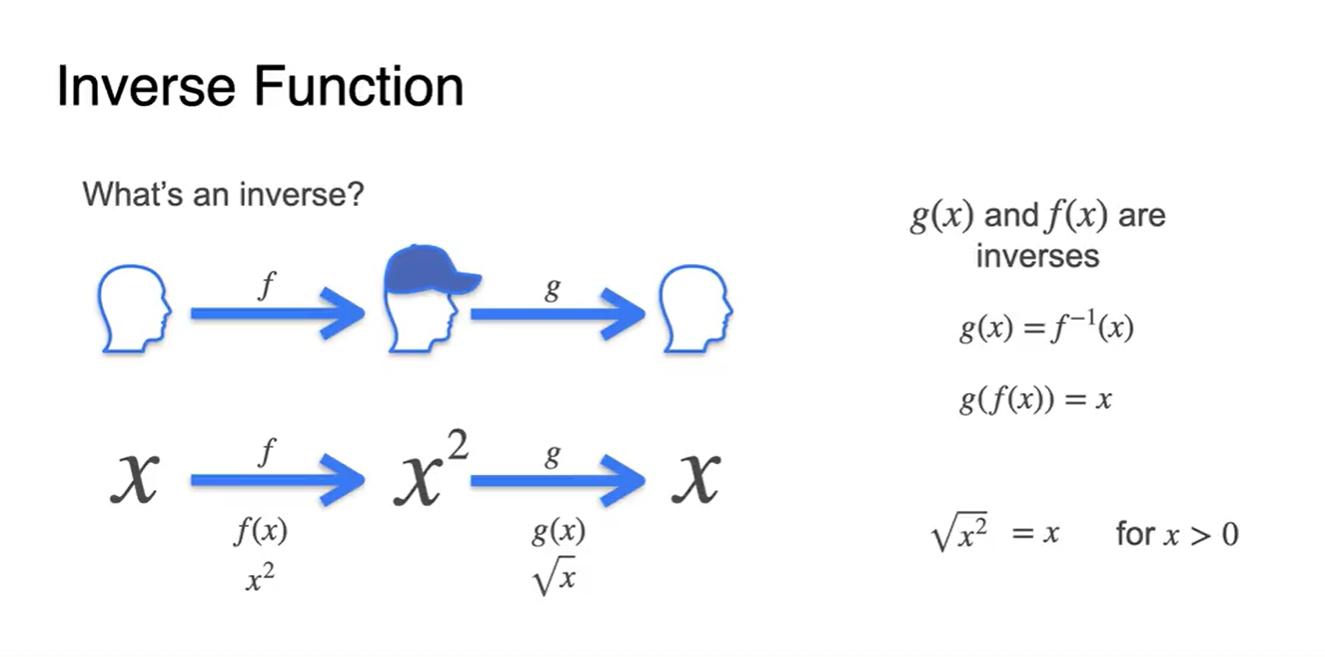
Inverse란 했던 일을 다시 되돌리는 것을 말한다.
- function을 모자에 비유한다면 함수와 함수는 모자를 썼다 벗었다 하는 관계라고 할 수 있다.
- 수식으로는 , 그리고 로 표현한다.
-
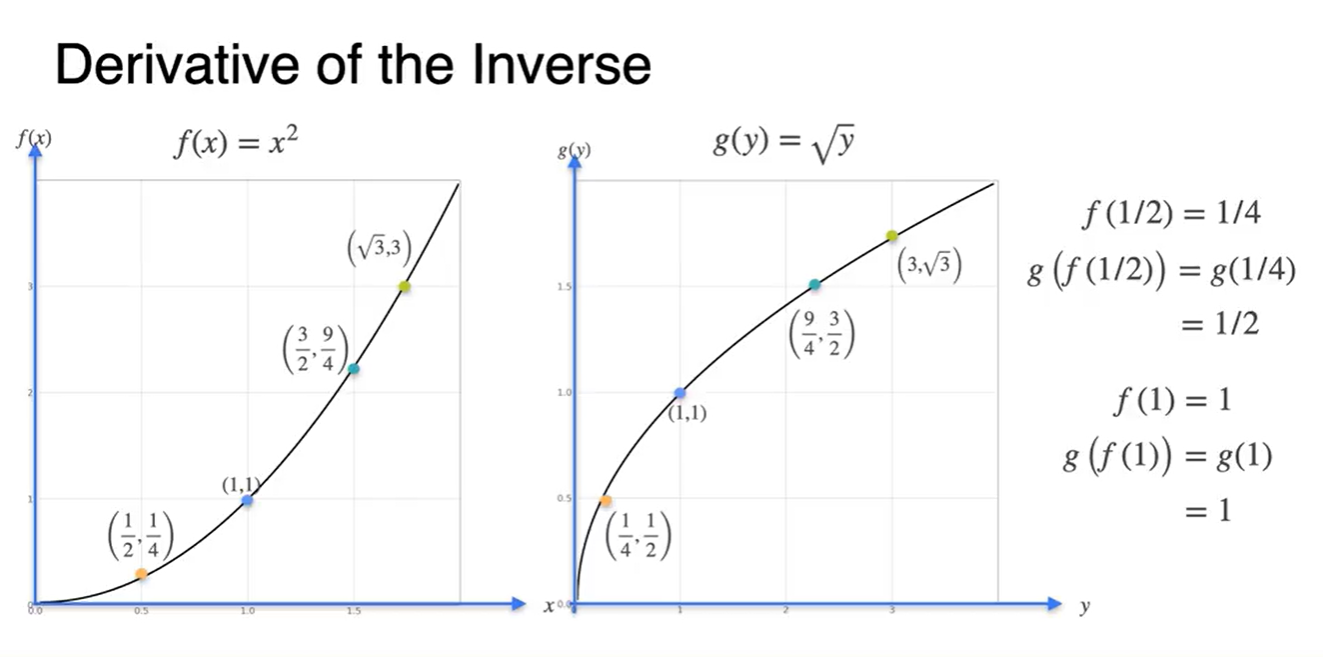
함수에 값을 집어 넣어보자.
-
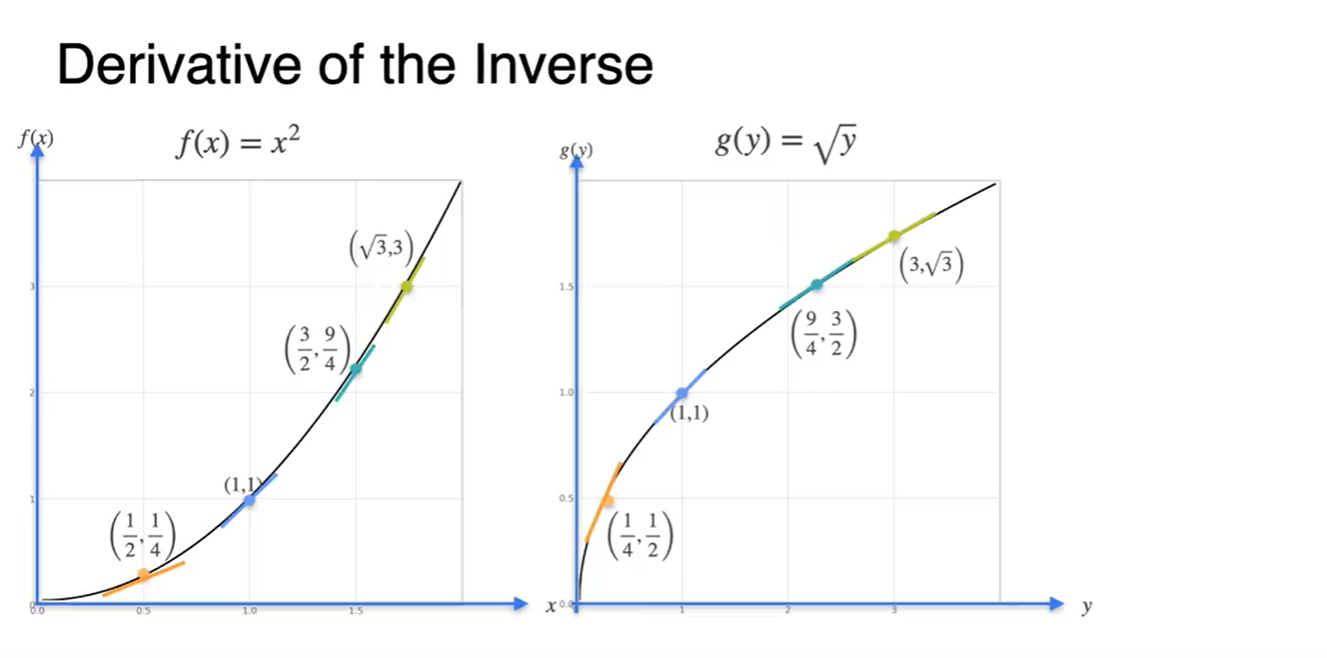
각각의 값을 좌표로 확인해보면, 와 의 값이 서로 바뀌어 있는 관계의 함수라는 것을 알 수 있다.
- ex. → ,
-
-
각 함수의 미분 또한 대칭 관계다.
- 함수의 미분은 증가(+) 함수, 함수의 미분은 감소(-) 함수다.
-
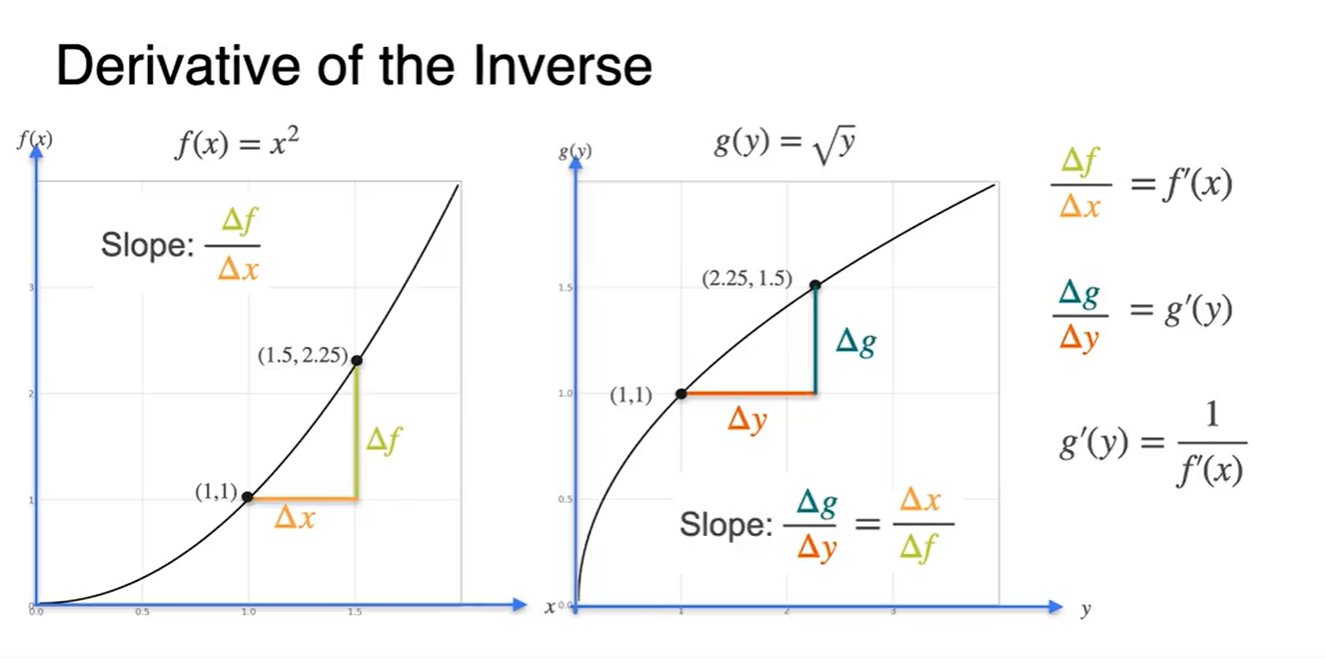
함수의 derivative는 로, 함수의 derivative는 로 정리된다.
- 이므로, , 즉 와 역수 관계다.
-
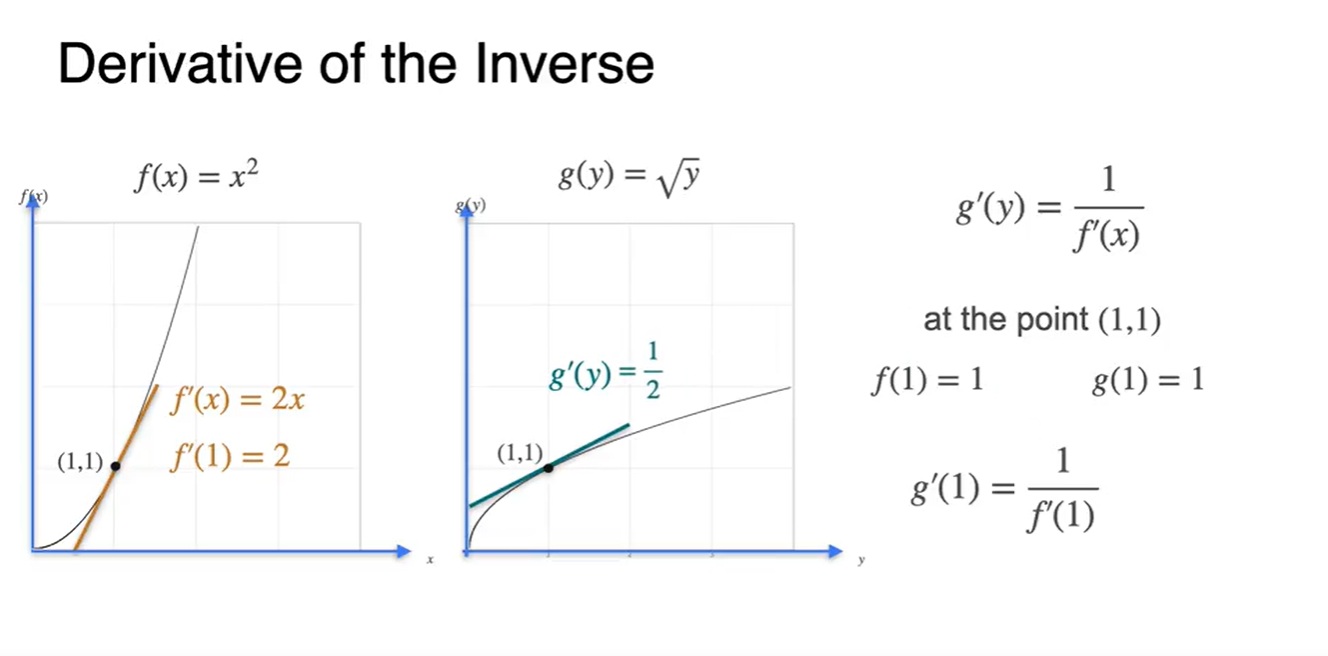
(1, 1)의 점을 대입해보자.
-
에 을 대입하면
-
에 를 대입하여
- 서로 역수 관계다.
-
-
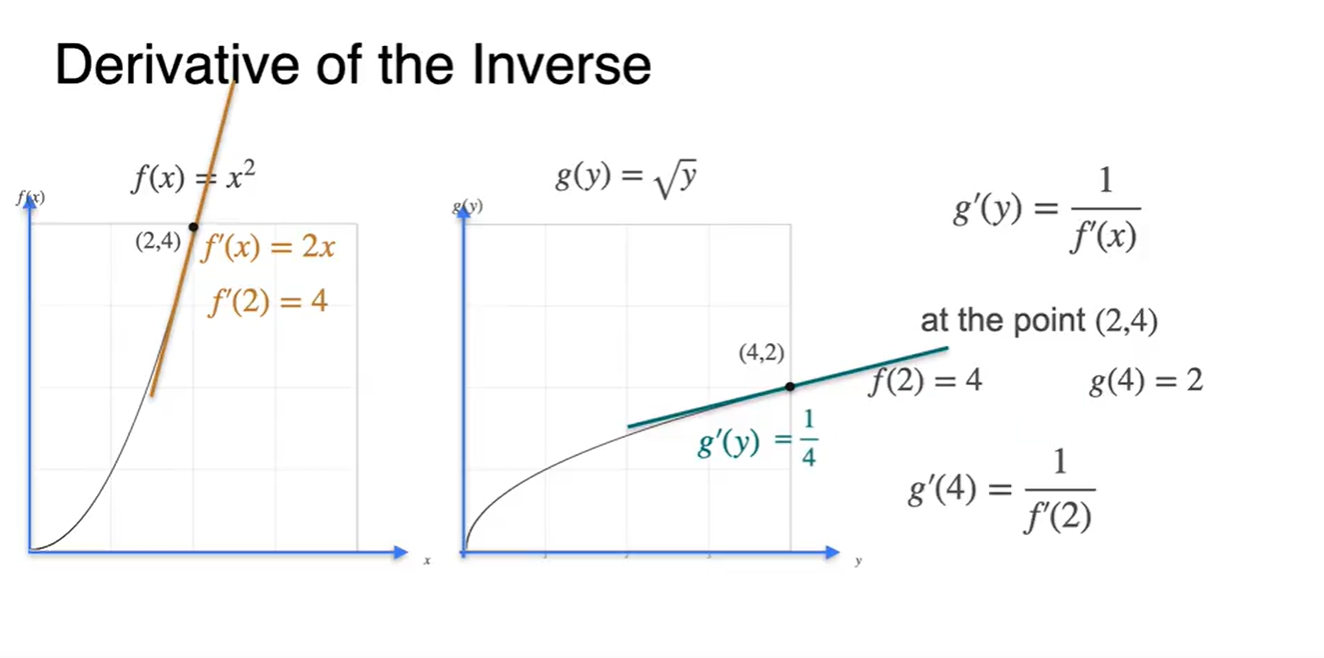
(2, 4)의 점을 대입해보자.
-
에 을 대입하면
-
에 를 대입하여
- 서로 역수 관계다.
-
Derivative of trigonometric functions
-
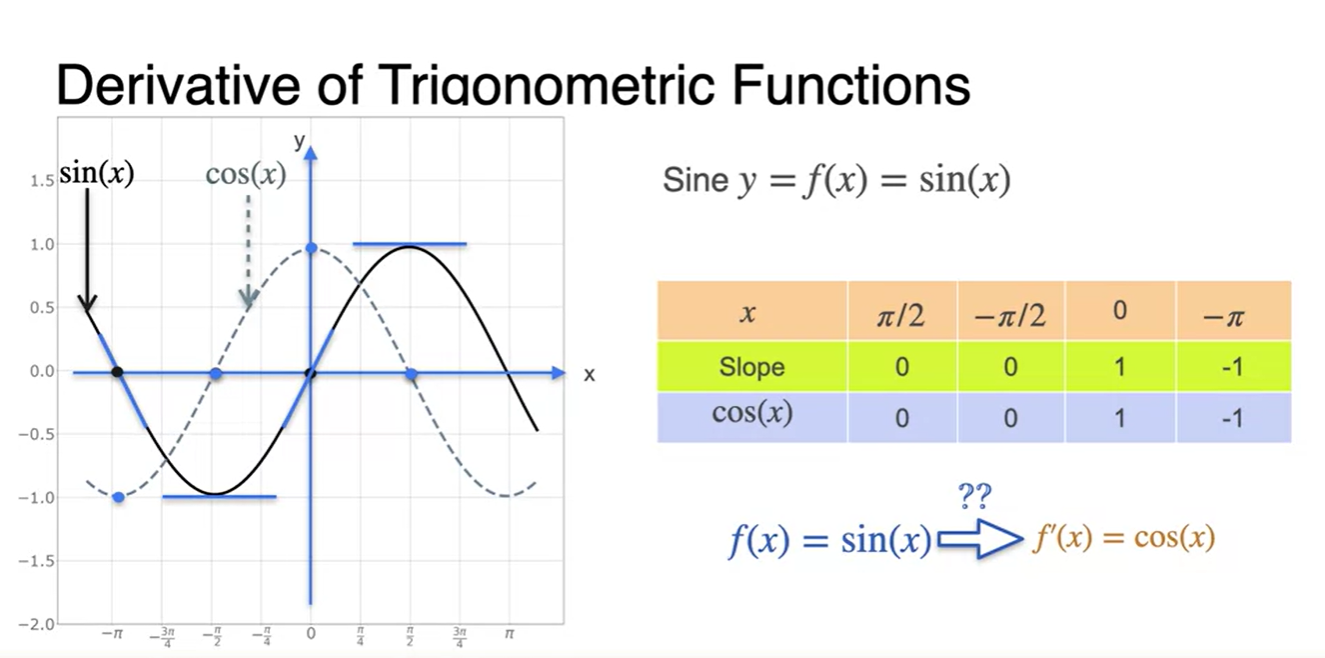
이번에는 , 함수를 미분해보자.
-
의 값에 따른 slope of 과 의 값을 비교해보면 놀랍게도 같다.
-
의 미분이 라는 것을 알 수 있다.
-
-
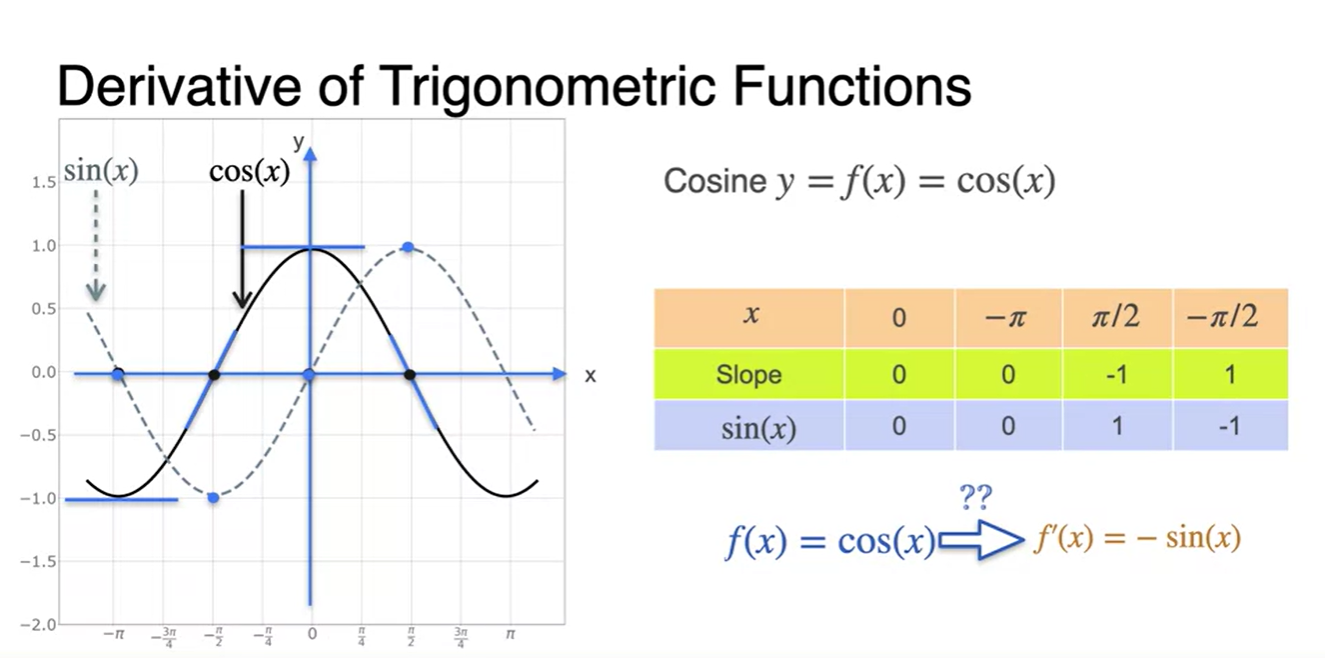
마찬가지로, slope of 과 는 모든 지점에서 같은 값을 가진다.
-
의 미분이 라는 것을 알 수 있다.
-
-
, 의 미분 수식이 어떻게 정리될 수 있었는지를 살펴 보자.
-
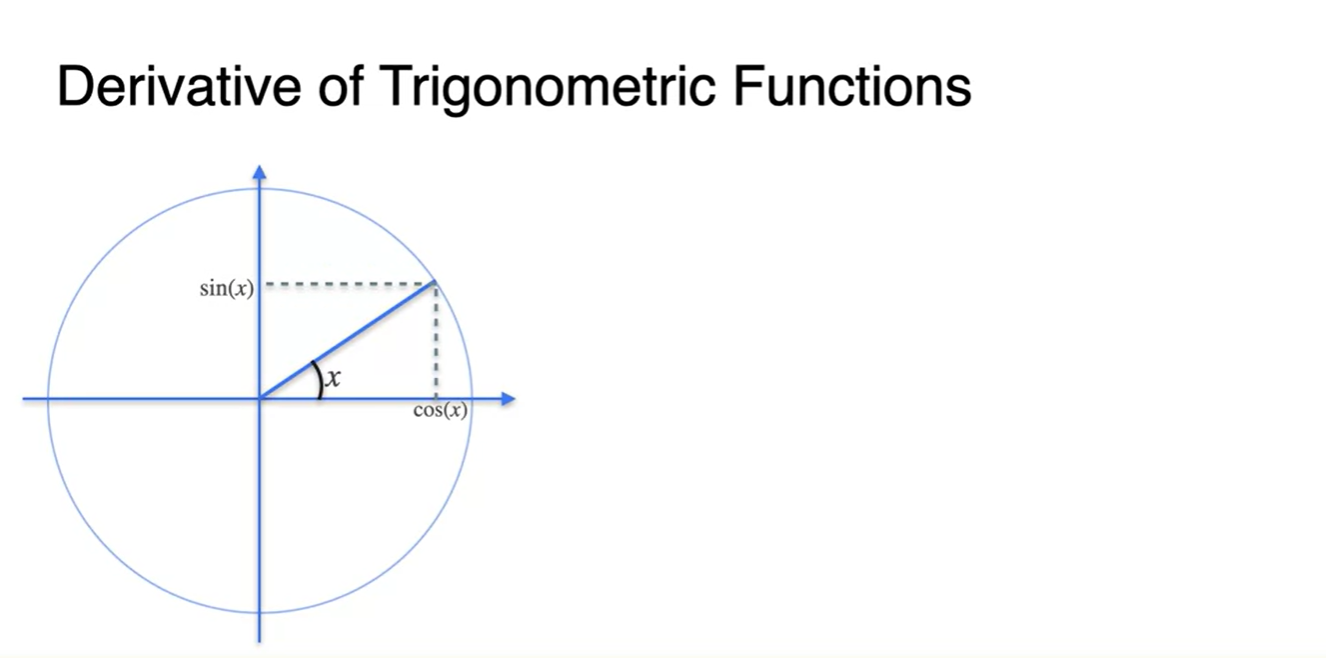
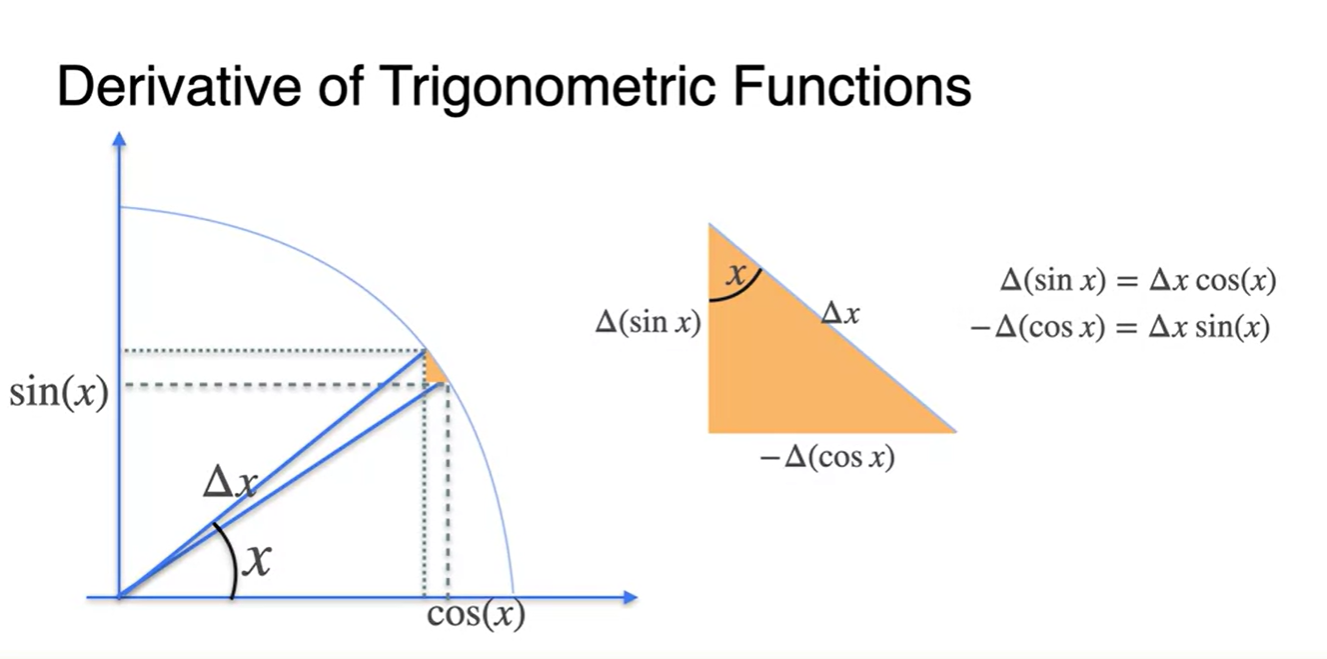
다음 그림과 같은 원형 좌표계에서는 가 특정 어떤 각도일 때, 와 는 x축 projection, y축 projection 좌표이다.
- (, )
-
-
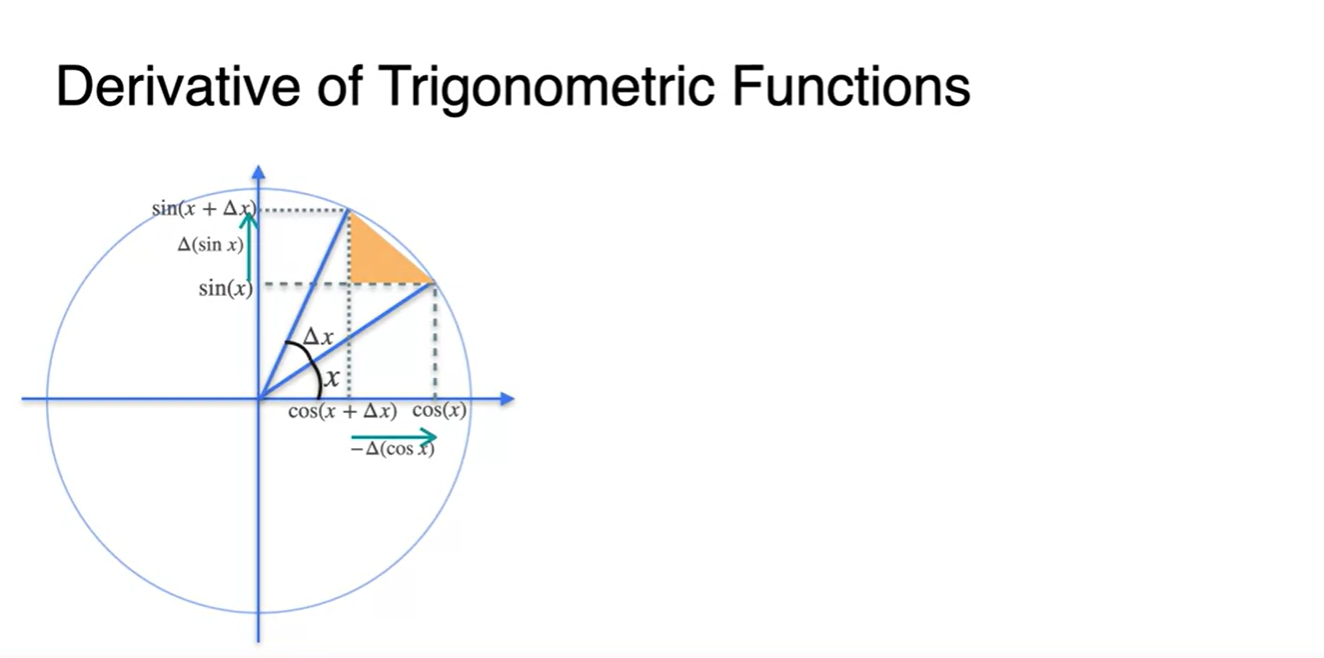
만큼의 각도를 더 움직였다고 해보자.
-
이 때, 기존 x 좌표는 줄어들고 y 좌표는 커짐을 알 수 있다.
- x축 변화량 :
- y축 변화량 :
-
-
삼각형 모양을 가져와 보자.
-
직각 삼각형의 윗 각도를 라고 할 때, 와 는 다음과 같이 정리된다.
-
-

-
이제 원의 반지름이 1이고, 가 매우 작은 범위에 있다고 가정해보자.
-
자리가 로 근사되어, 위에서의 빗변 가 가 된다.
- 닮음 정리 이용 :
- , when
-
-
따라서 정리하면 다음과 같다.
-

Meaning of the Exponential (e)
-
는 식이 이 무한대로 보내졌을 때, 2.718...의 값으로 수렴하는 상수다.
- 라면 미분한 함수도 같은 함수임이 큰 특징이다.
- 주로 과학이나 이자(interest) 문제에서 사용된다.

-
당신이 $1를 가지고 있다고 해보자.
-
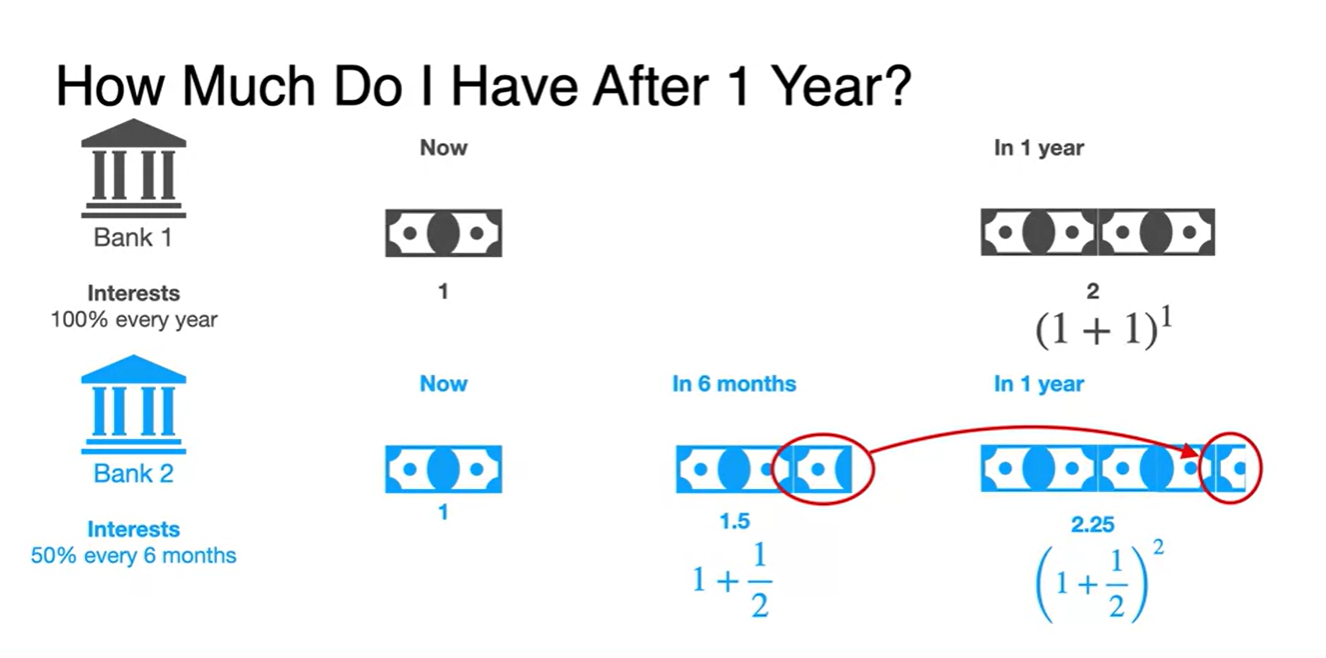
Bank1은 1년에 100%의 이자를 주겠다고 하며
Bank2는 6개월에 50%, Bank3는 4개월에 33.3%의 이자를 주겠다고 한다. -
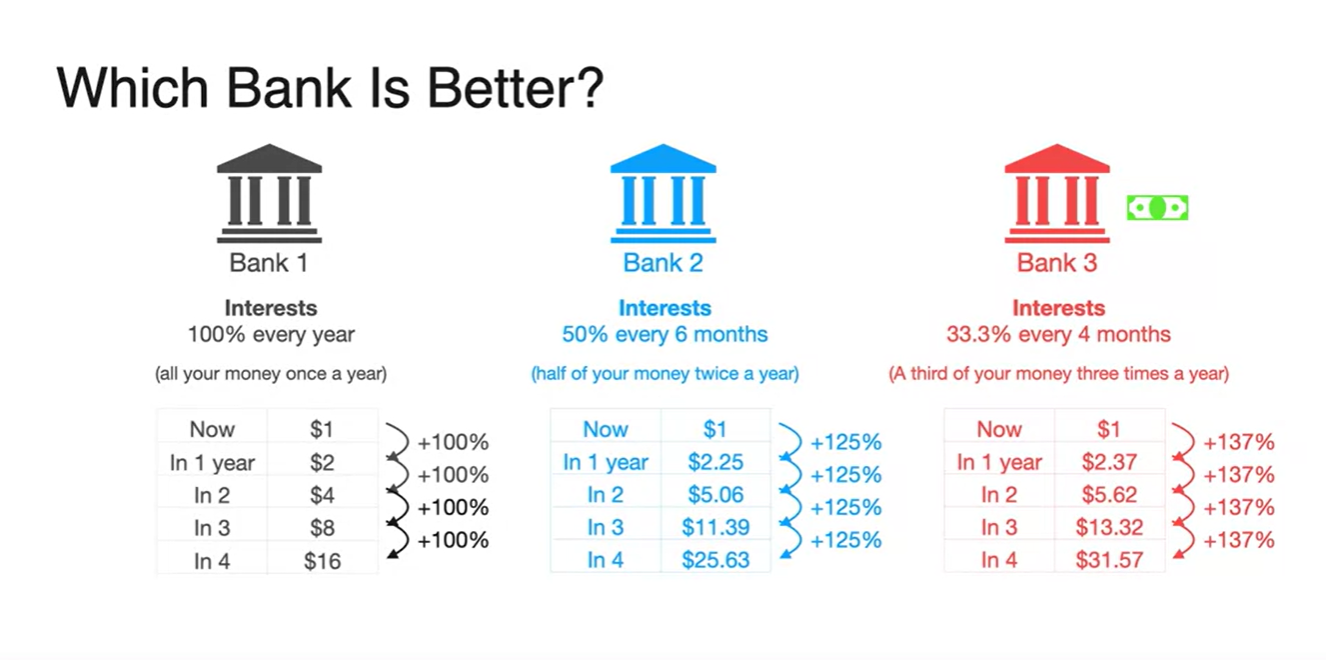
어느 은행에 넣어야 이자를 더 많이 받을 수 있을까?
- 놀랍게도 정답은 Bank3이다.
-

-
Bank1에 $1를 넣으면 1년 뒤에는 의 이자를 받는다.
- Bank2에 $1를 넣으면
6개월 뒤에는 , 1년 뒤에는 의 이자를 받는다.
- Bank2에 $1를 넣으면
-
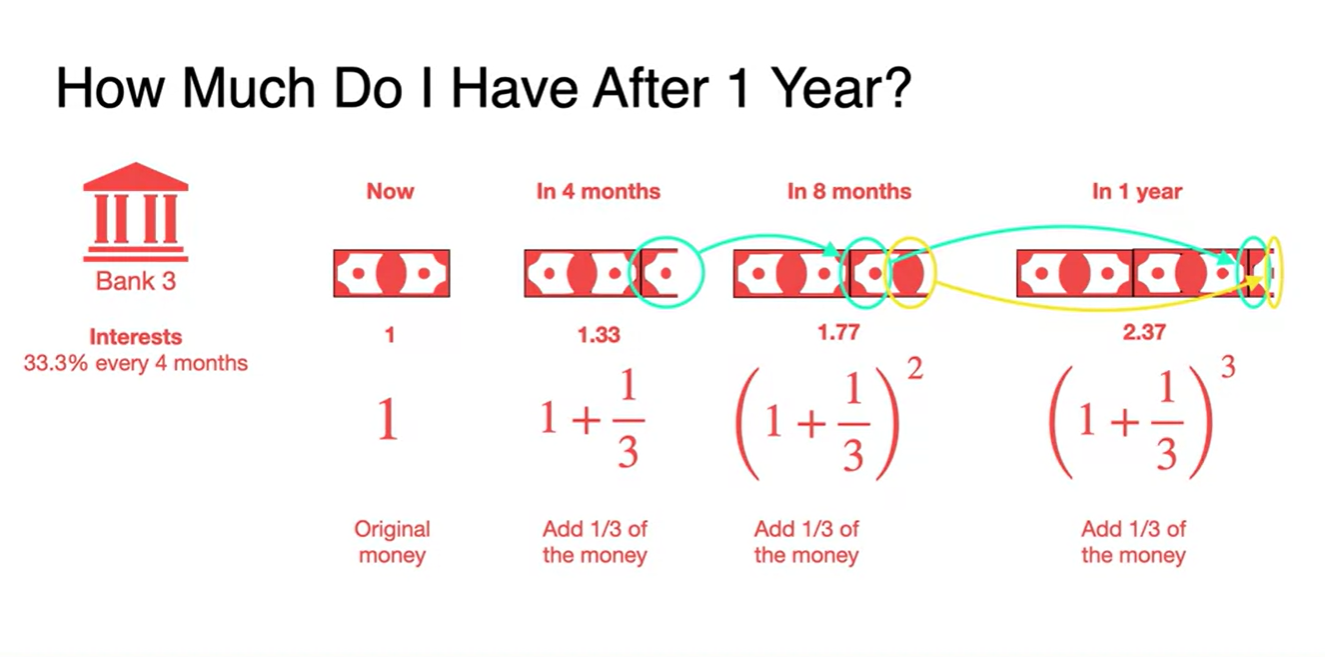
Bank3에 $1를 넣으면 1년 뒤에는 의 이자를 받는다.
"Your money is making your money."
- 미리 받은 이자가 증식하여 짭짤한 돈이라도 계속 붙기 때문이다.
-
일종의 "복리의 마법"이다.
- 소급이라도 달라붙은 돈을 복리로 계속 갖다 붙이면 결과적으로 1년에 137%의 이자를 받는 셈이 되는 것이다.
-
일반적인 수식으로 정리하면 money + interest다.
-
money : + interest :
-
원금 1에 의 이자를 더한 값을 n제곱배 해주기 때문이다.
-
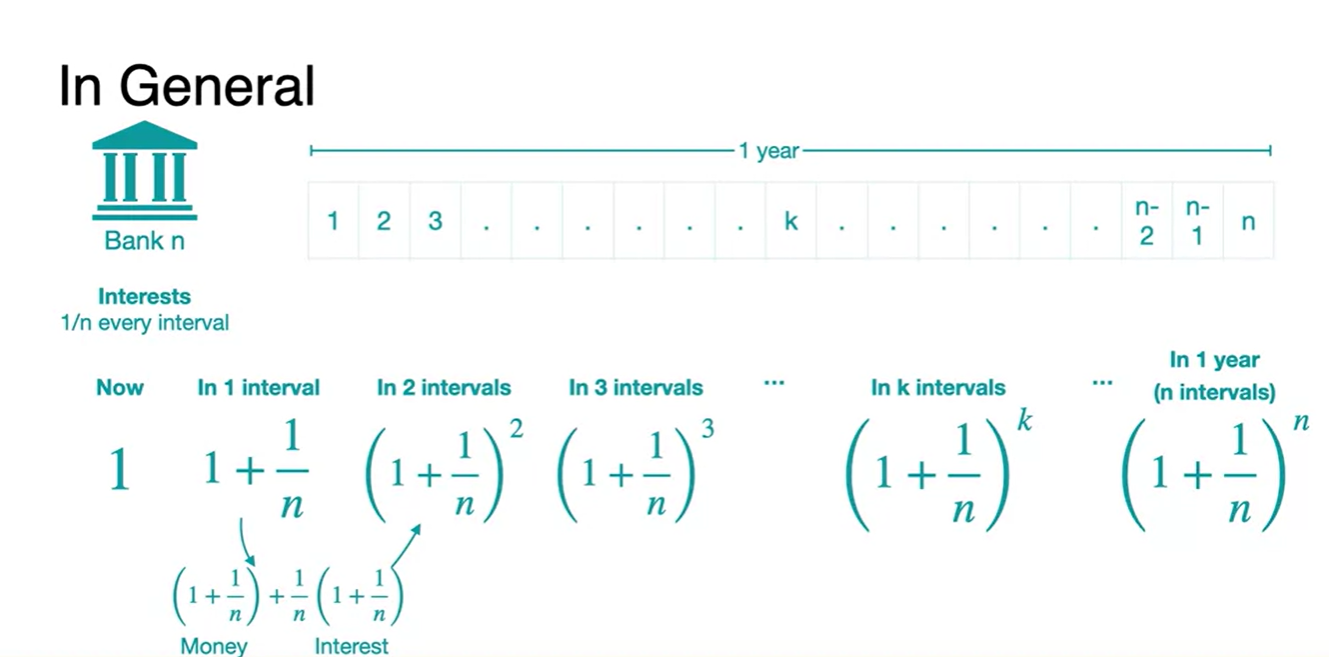
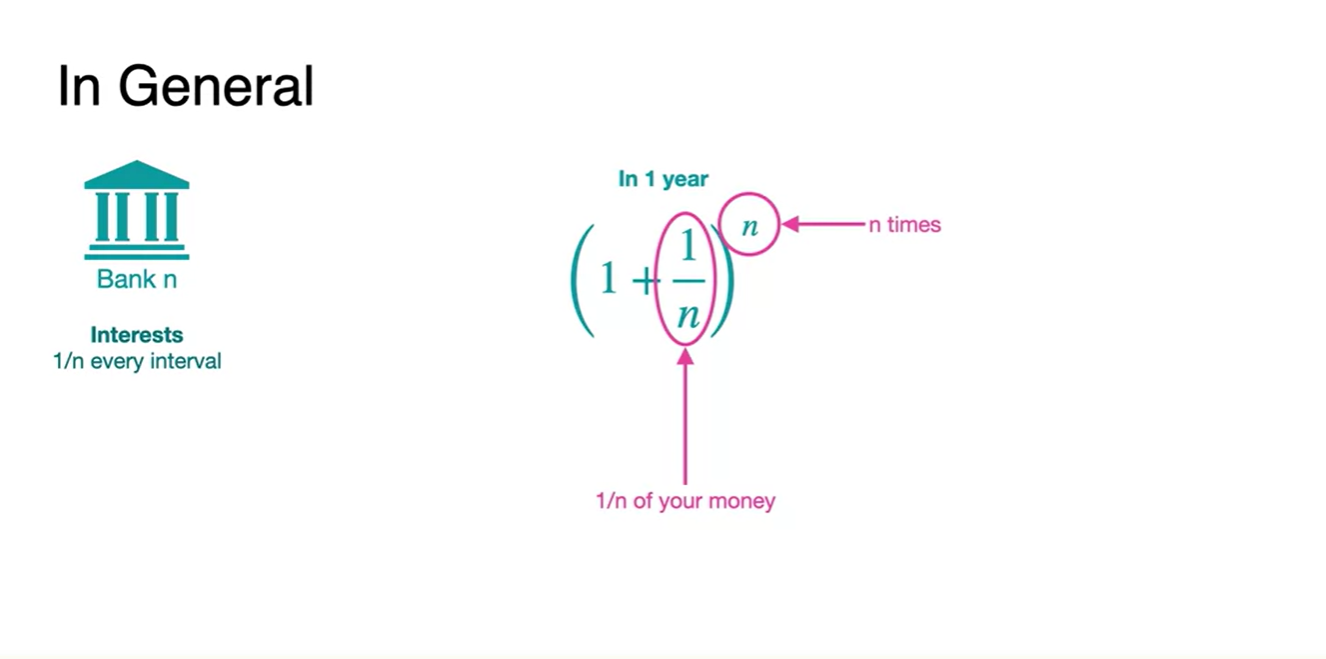
-
무수히 많은 은행에다가 원금 $1을 예치했다고 해보자.
- 마지막 은행에서 1년에 받는 이자는 얼마인가?

-
정답은 다.
-
이 숫자는 2.718...에 수렴한다고 하며, 기호로는 라고 쓴다.
- 의 의미는 interest(이자)에 가깝다.
-


The derivative of e^x
-
의 derivative는 다.
- 는 Slope of the function이 자기 자신이라는 흥미로운 성질이 있다.
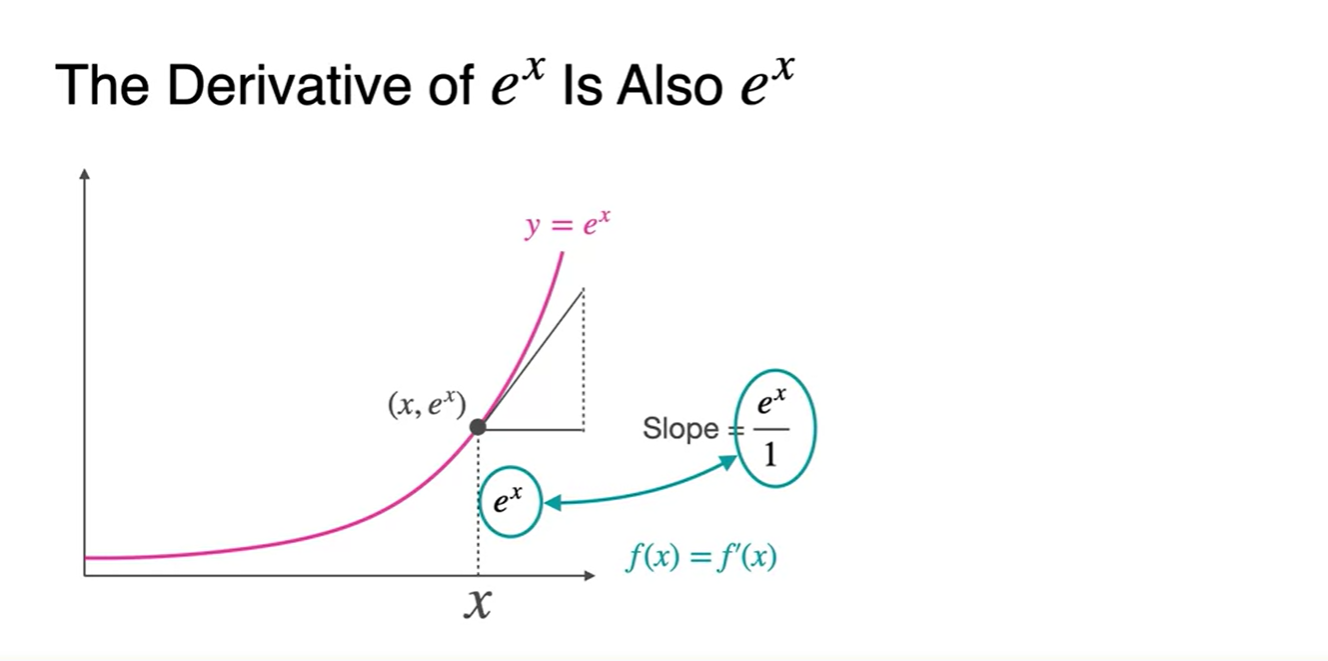
- 에 1과 1/2을 대입하여 slope를 구해보자.
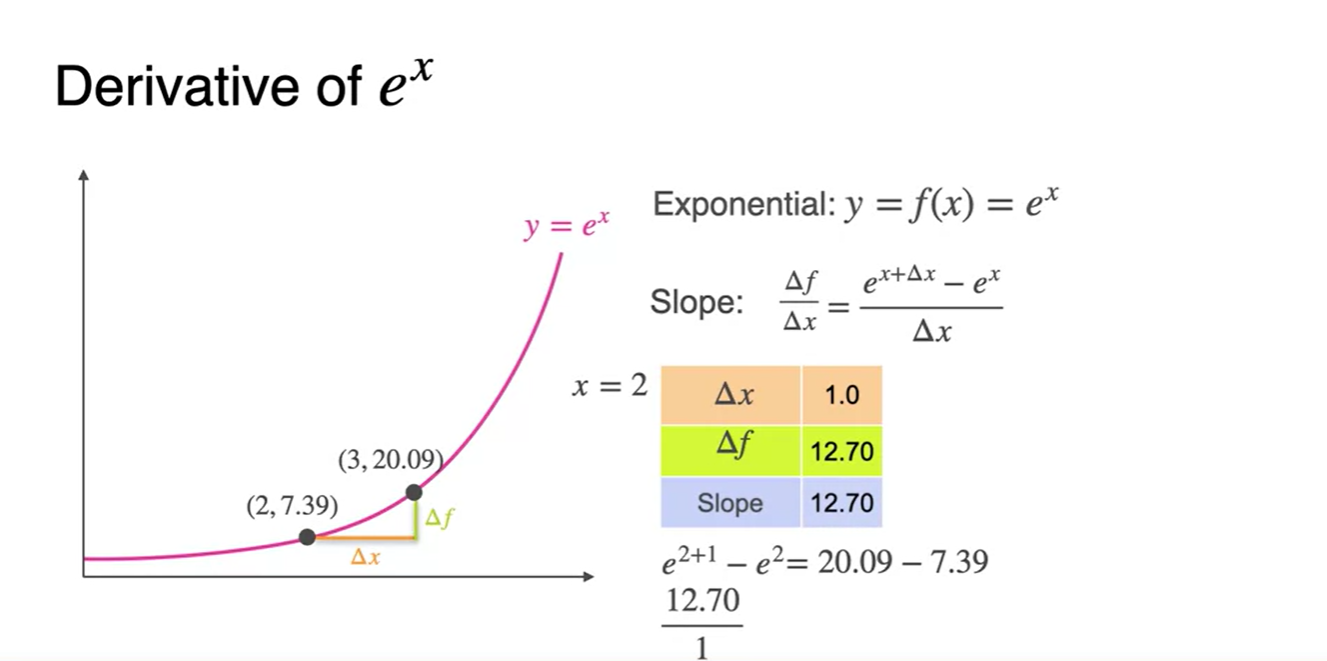
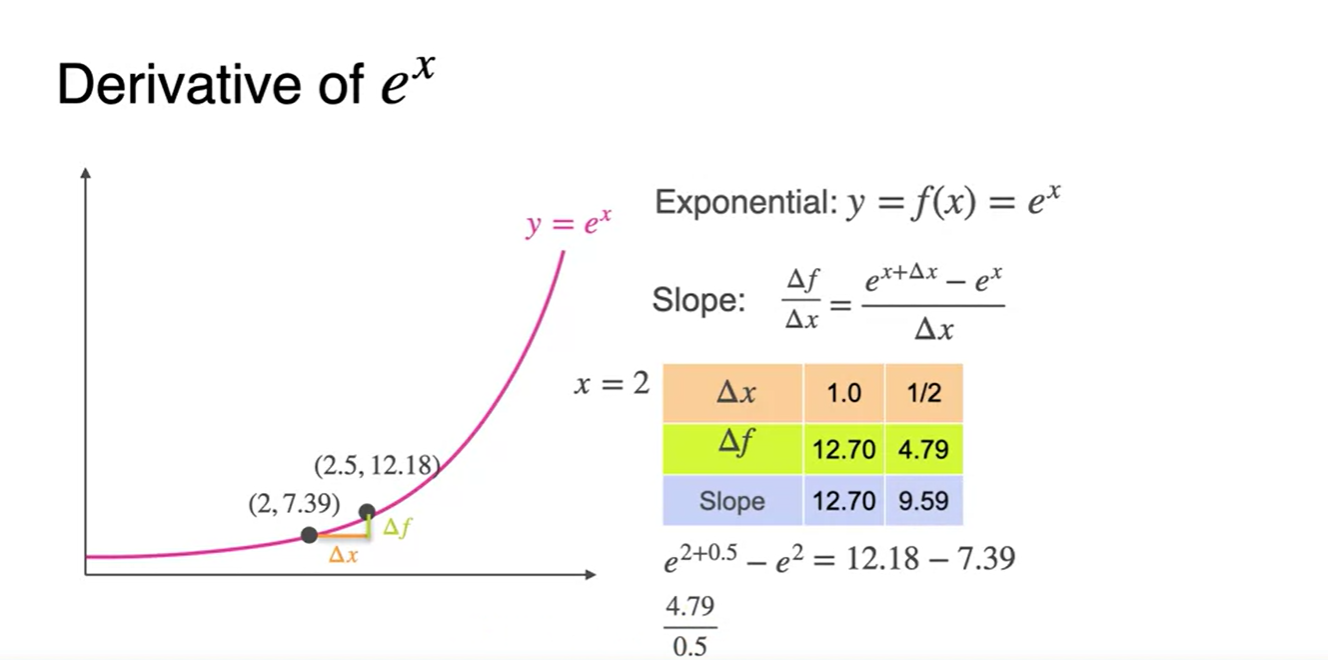
-
가 1/1000로 매우 작다고 가정하여 slope를 구해보자.
- 놀랍게도 기존 점의 y좌표 즉, 가 2일 때 의 값으로 수렴한다.
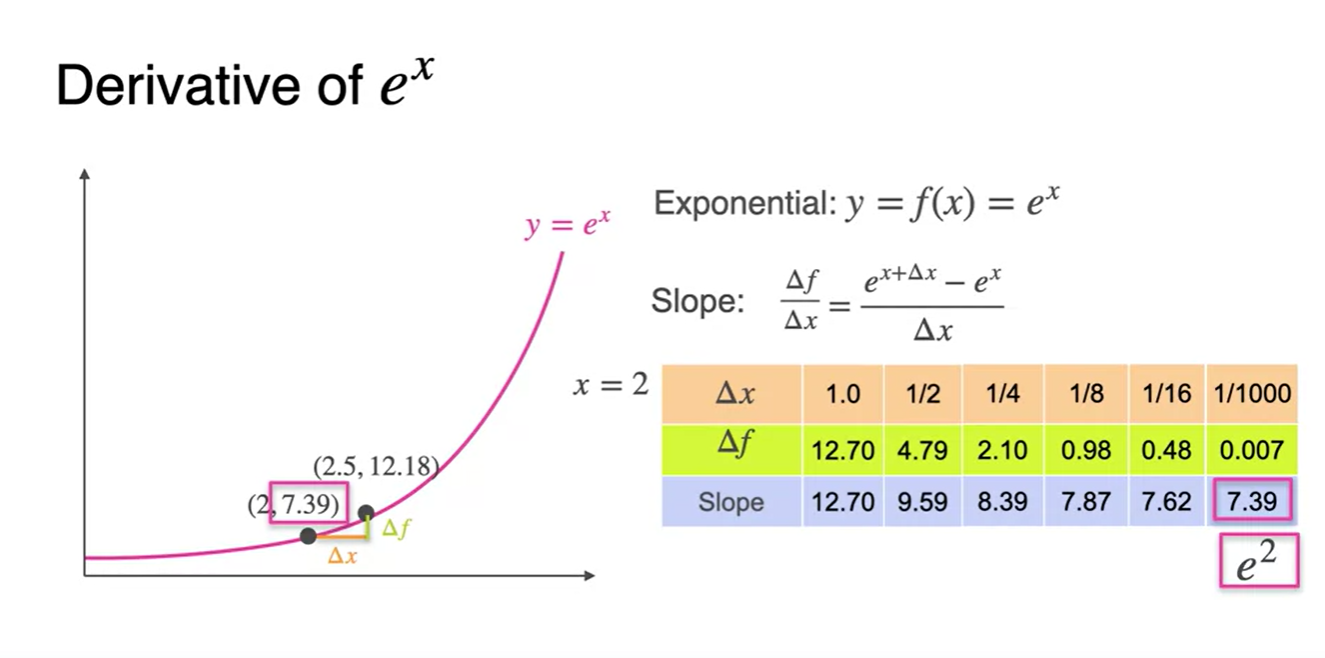
The derivative of log(x)
-
함수는 와 어떤 관계를 가지는지 알아보자.
-
의 거듭 제곱에 값을 올리면 x가 나온다.
- 이며 임을 미루어 보아 서로 역함수 관계라는 것을 알 수 있다.
-
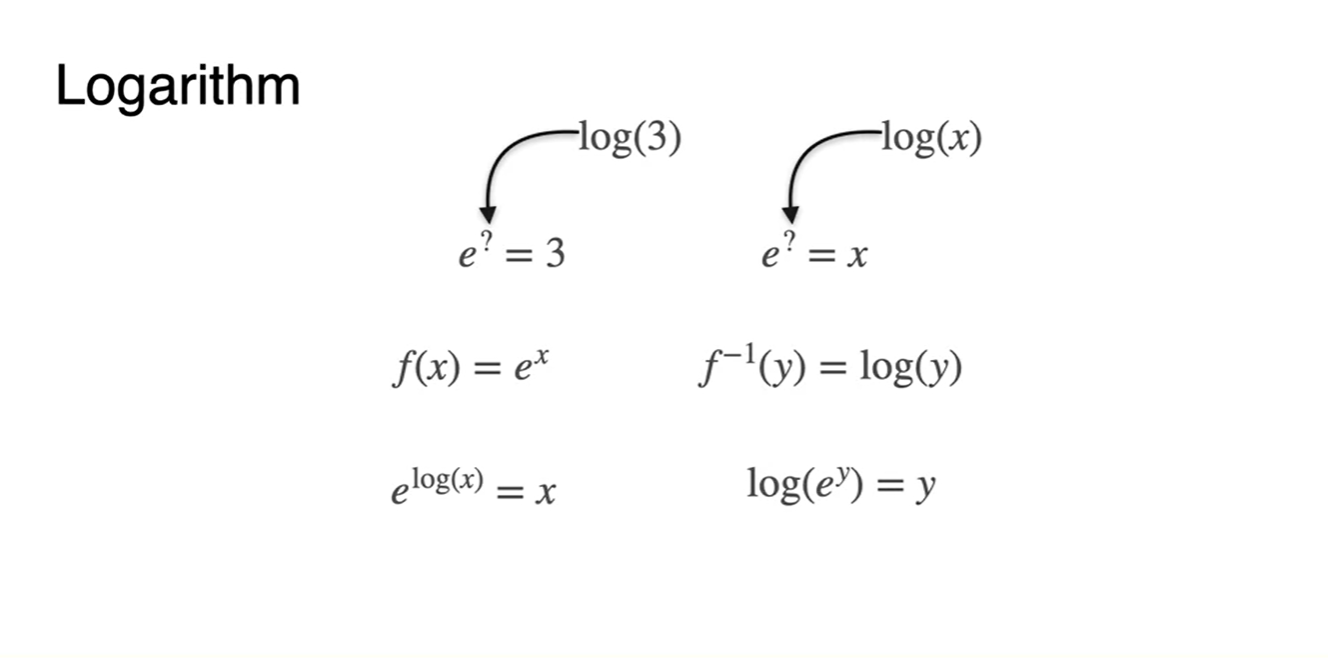
-
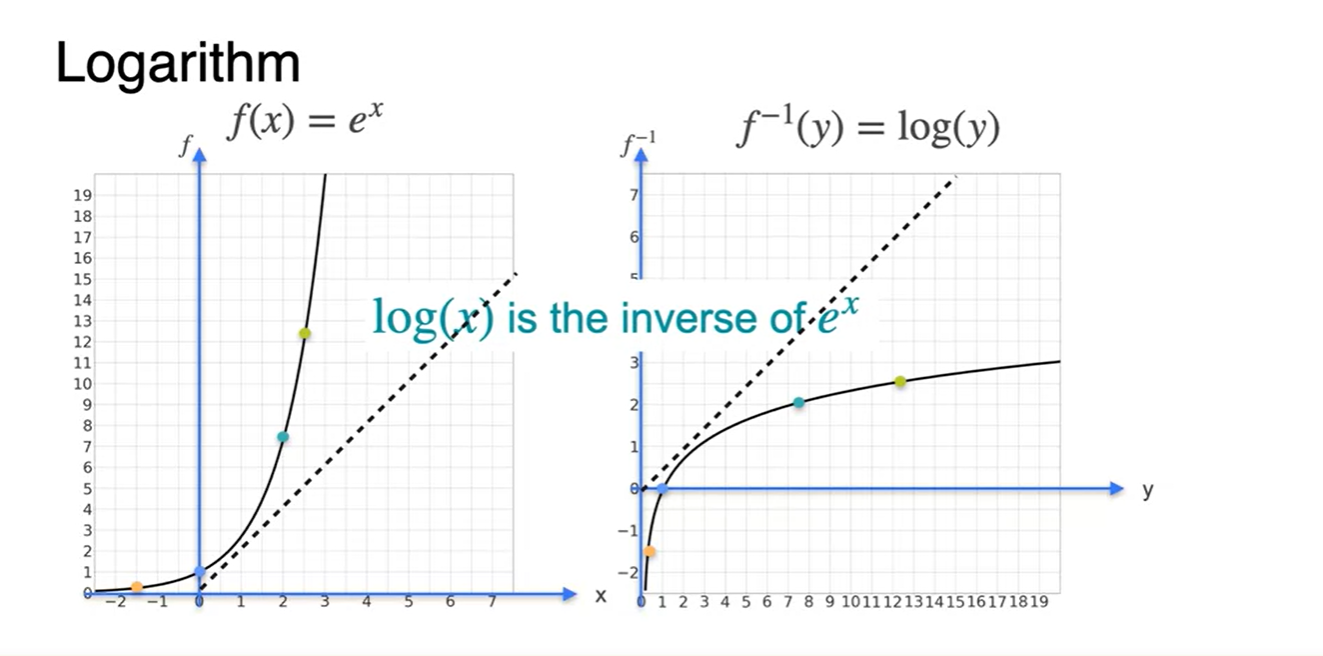
와 함수 그래프를 살펴보자.
- 대칭을 이루고 있으므로 서로 역함수(inverse) 관계임을 알 수 있다.
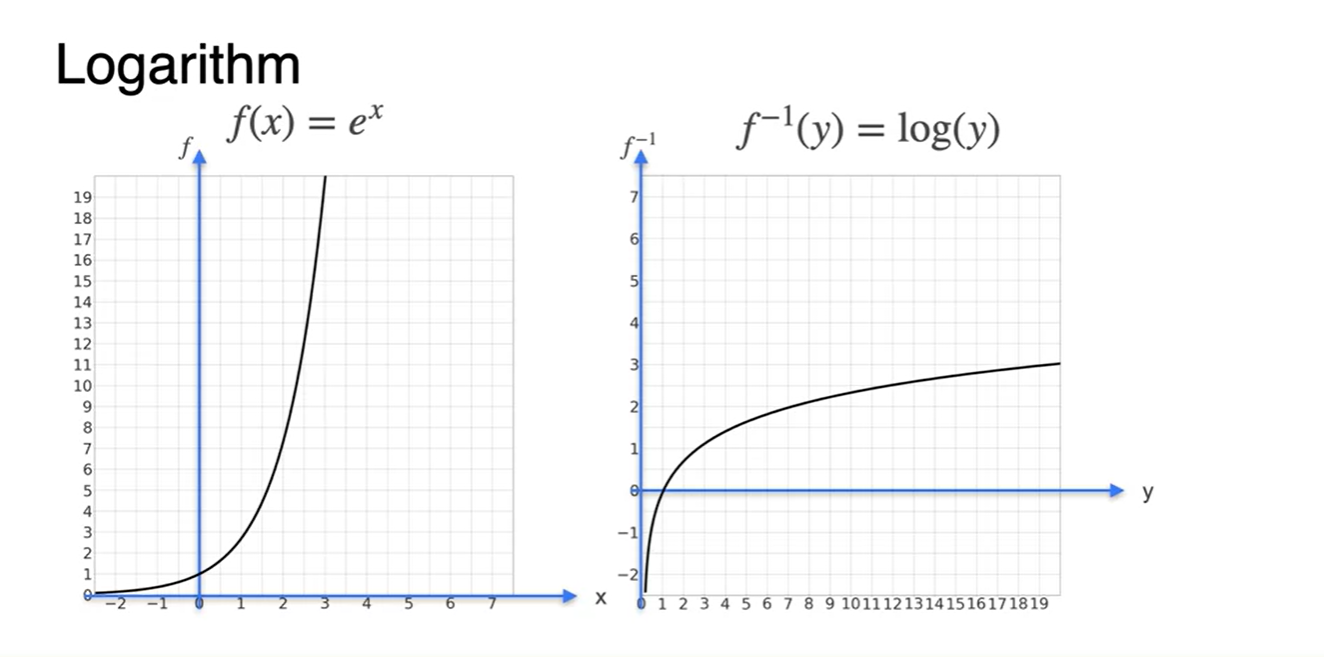
-
함수의 미분을 로부터 유도해보자.
- 핵심은 변수 y로 정리된 함수의 미분이 라는 것이다.

Existence of the derivative
-
Differentiable 함수와 Non-differentiable 함수를 구별해보자.
-
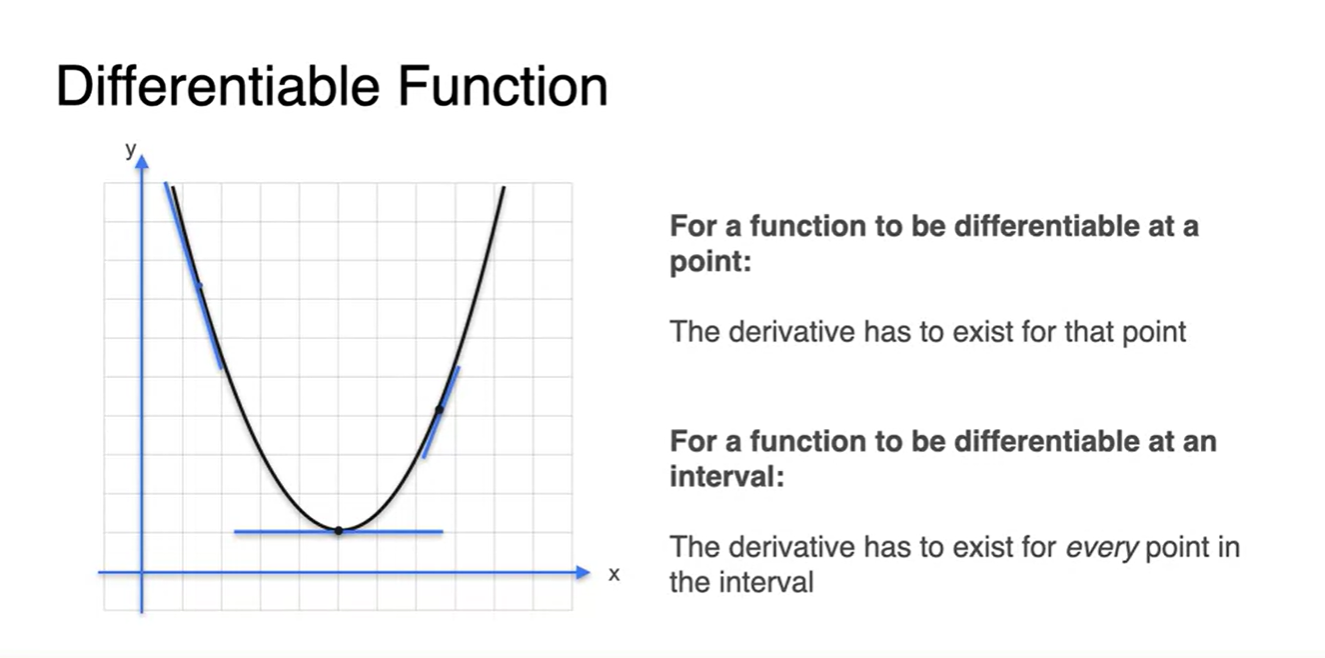
아래와 같은 function은 구간 내에 정의된 "interval"한 모든 지점에서 미분 가능하다.
- 조건은 1. 연속 함수이면서 2. 뾰족하지 않은 함수다.
-
-
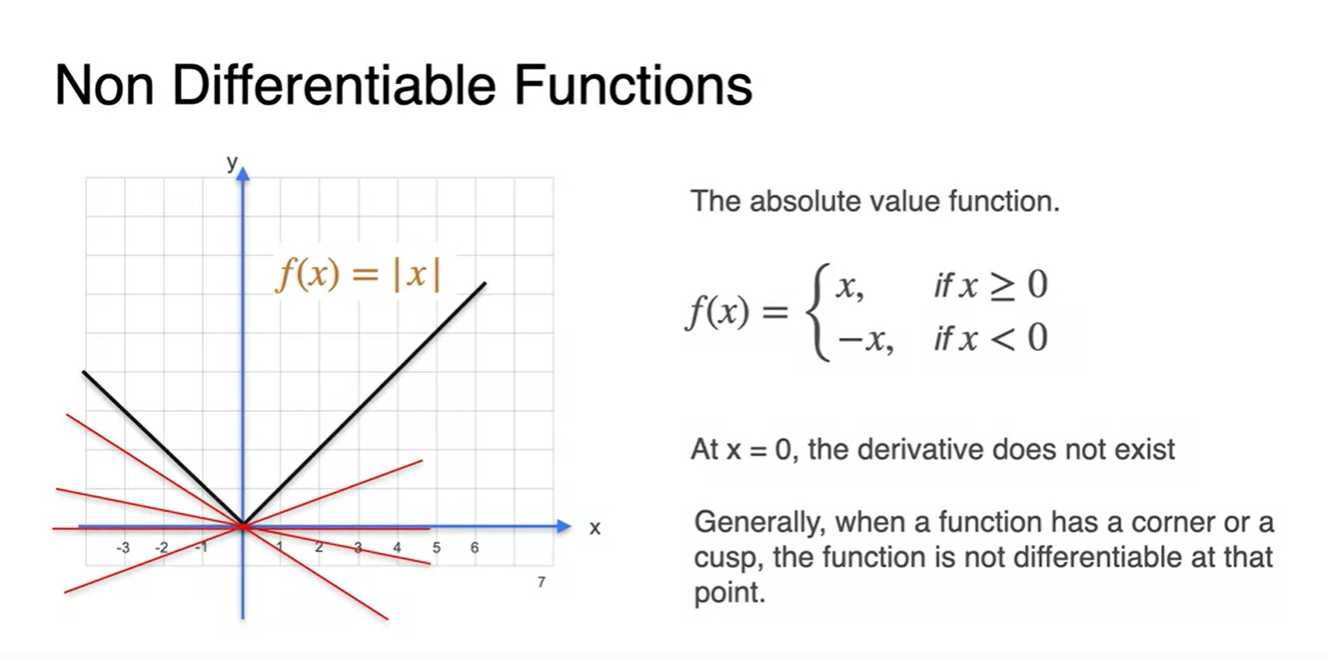
의 그래프를 그려보자.
-
지점에서는 어떠한 방식으로 미분하여도 같은 tangent(기울기)가 나오지 않는다.
- 따라서 미분 불가능하다.
-
-
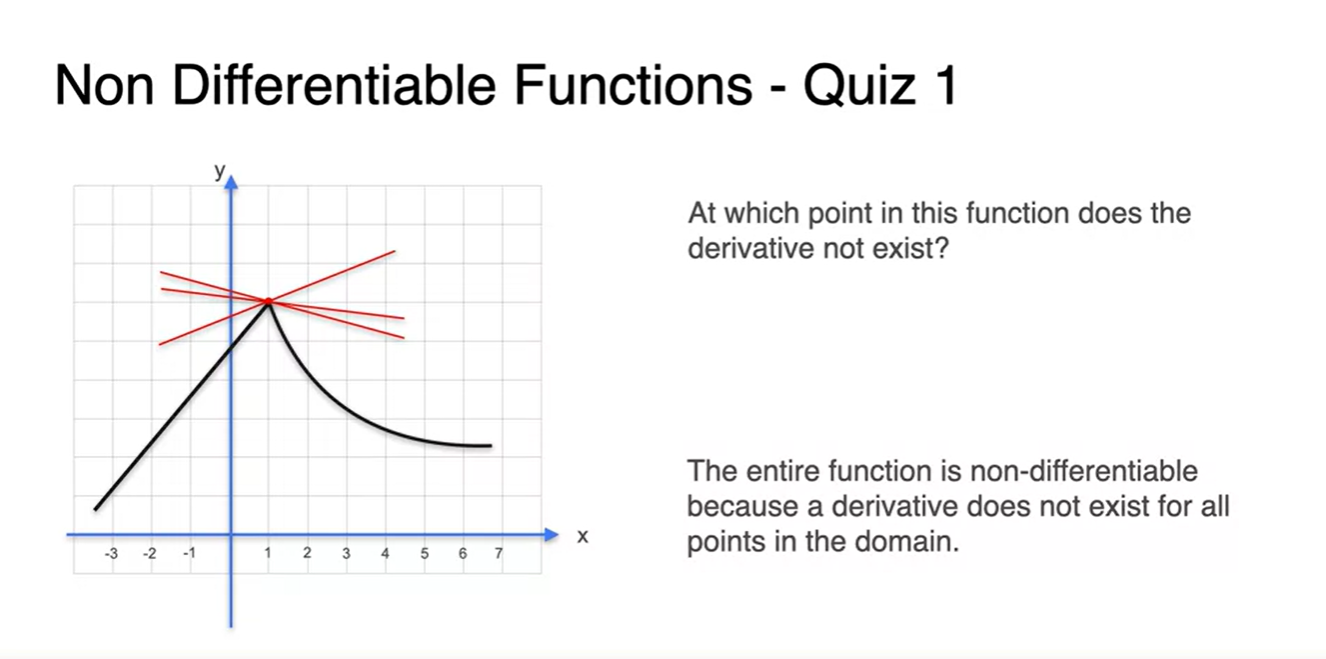
아래와 같은 function에서도 마찬가지다.
- 애초에 뾰족한 지점()이 존재하면 미분이 불가능하다.
-
아래 함수 처럼 에서 연속되지 않는 function이라면 어떨까?
- 이 함수 역시 어떤 slope를 기울기라고 정의내릴 수 없기 때문에 미분 불가능하다.
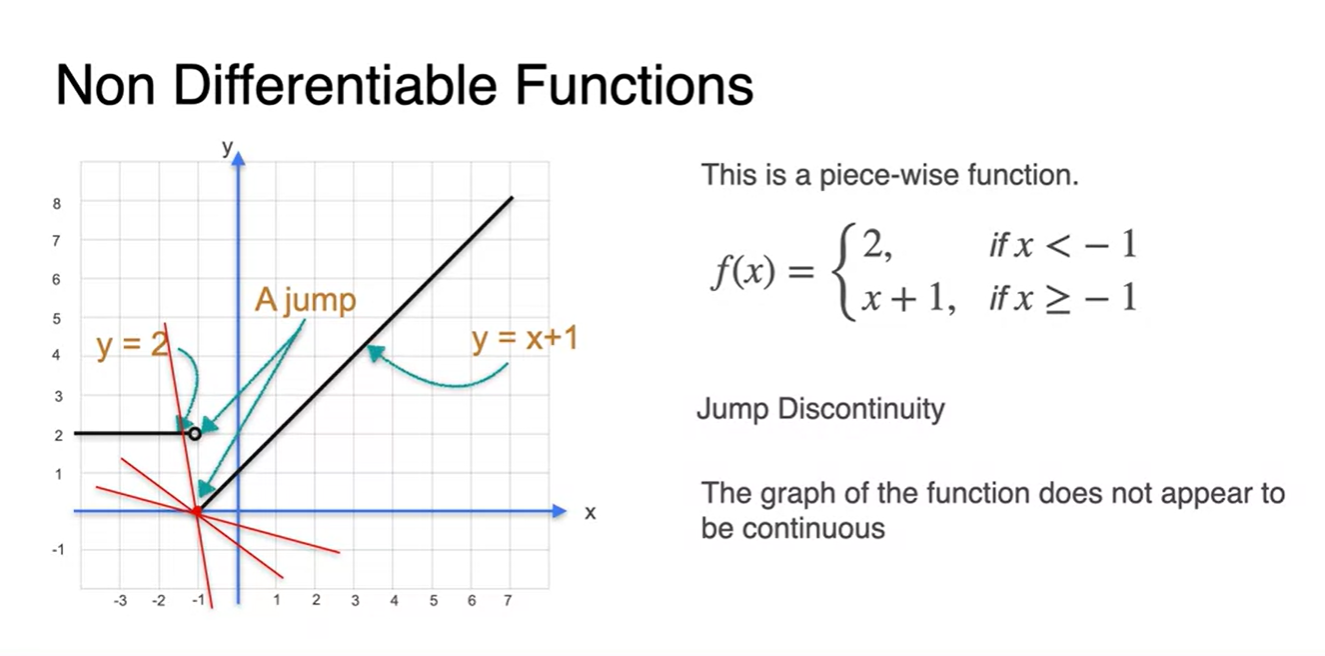
-
마지막으로 의 함수는 미분 가능할까?
-
지점을 보면 slope가 무한대로 정의됨을 알 수 있다.
- 따라서 이 또한 미분 불가능하다.
-
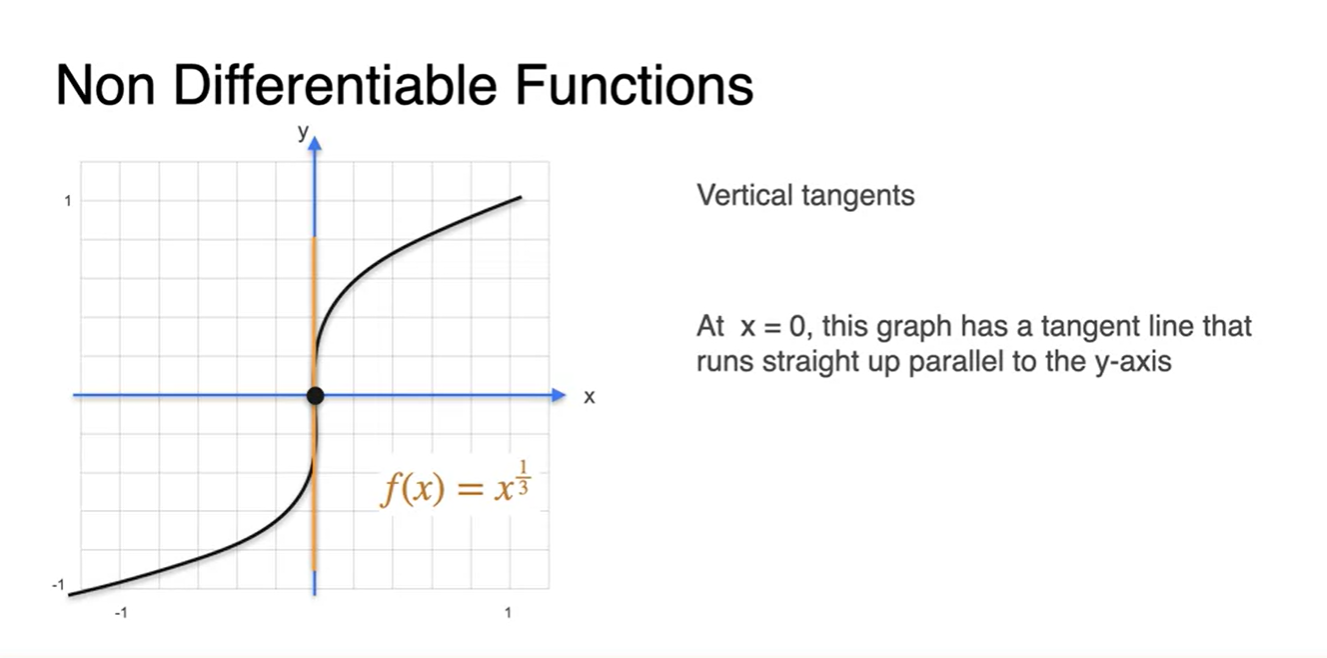
-
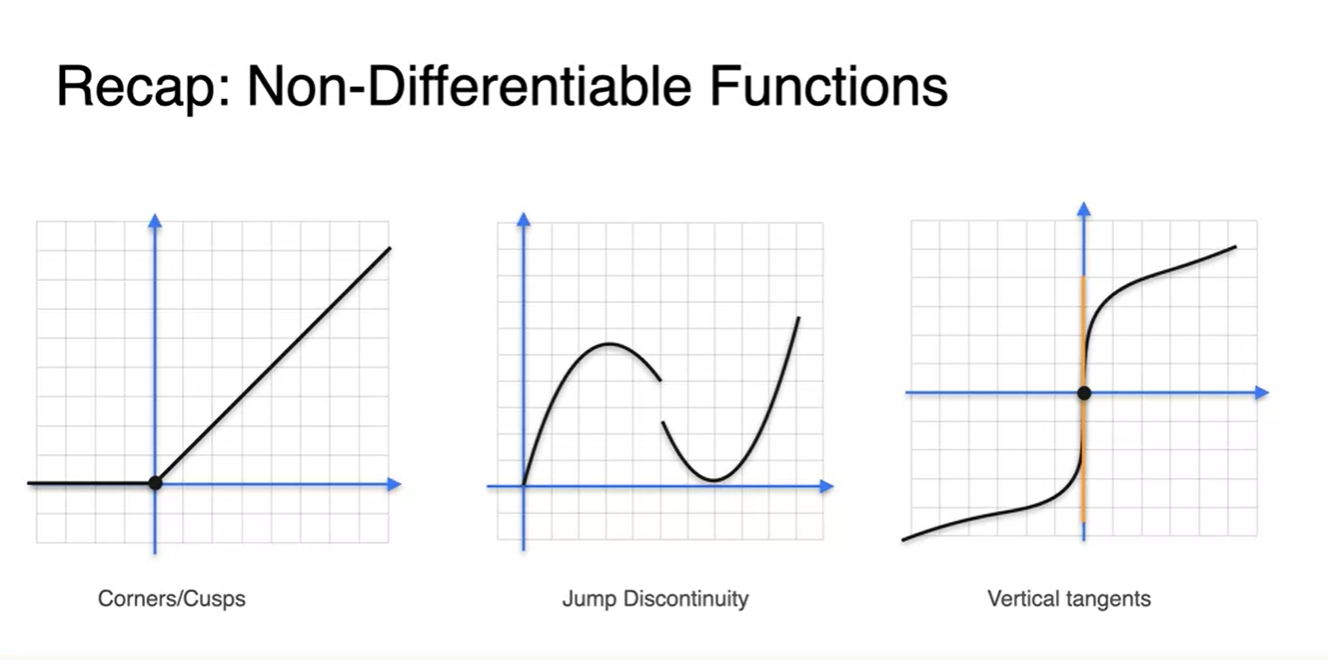
정리하자면 아래와 3가지 같은 상황에서 미분이 불가능하다.
- 뾰족한 지점이 존재하거나
- 연속하지 않은 함수이거나
- 기울기가 ∞인 지점이 있을 때
Properties of the derivative: Multiplication by scalars
-
Derivative의 성질에 대해 알아보자.
- ex. 식 같은 scalar배 관계를 가진 와 가 있을 때, 각 함수의 미분 또한 배수 관계다.

-
과 의 그래프를 살펴보자.
- 에서와 에서의 secant line(평균 변화율)을 계산하면 상수배 만큼의 차이를 가지는 걸 알 수 있다.
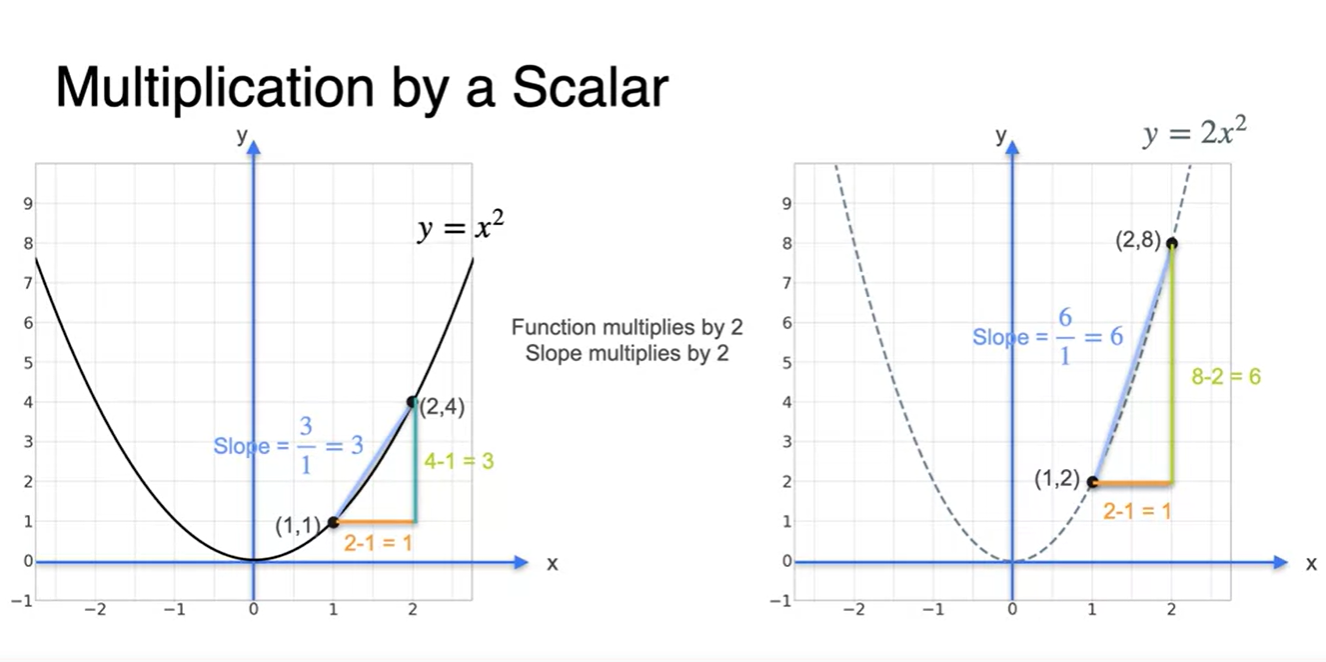
- 정리하자면, 함수의 tangent line(순간 변화율) 또한 와 같다.
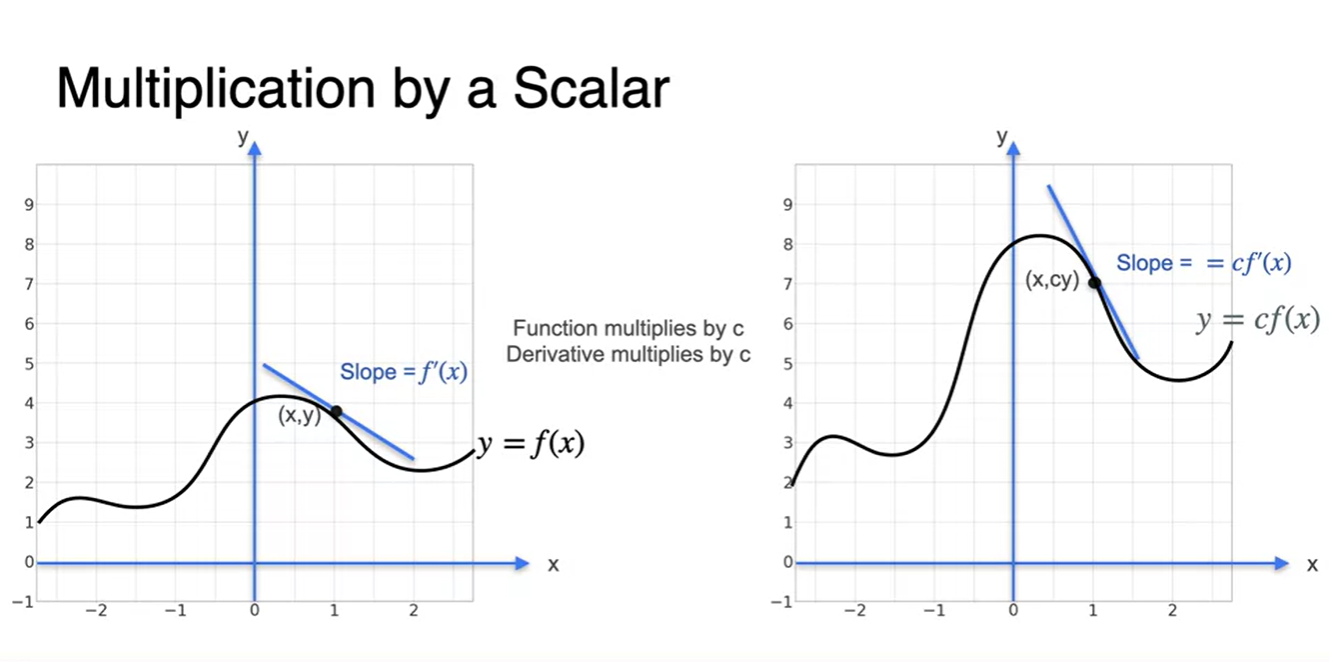
Properties of the derivative: The sum rule
- Derivative의 두 번째 성질은 함수의 덧셈 또한 선형적으로 미분이 가능하다는 점이다.
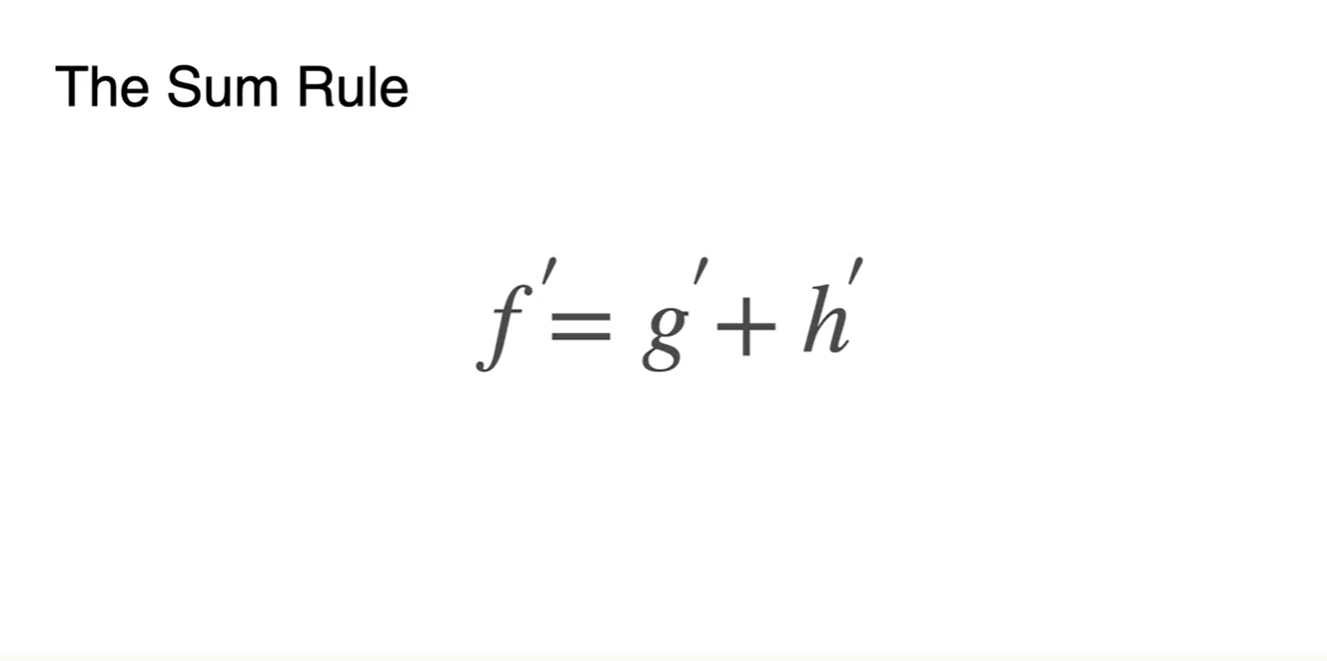
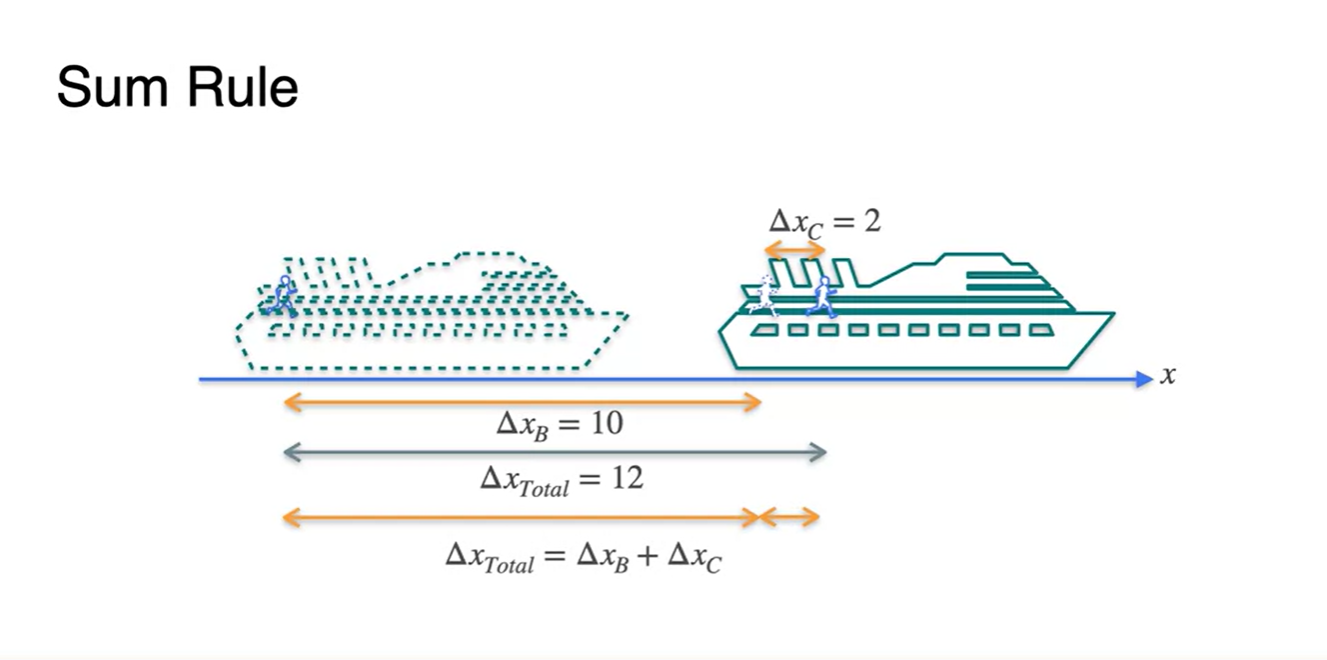
-
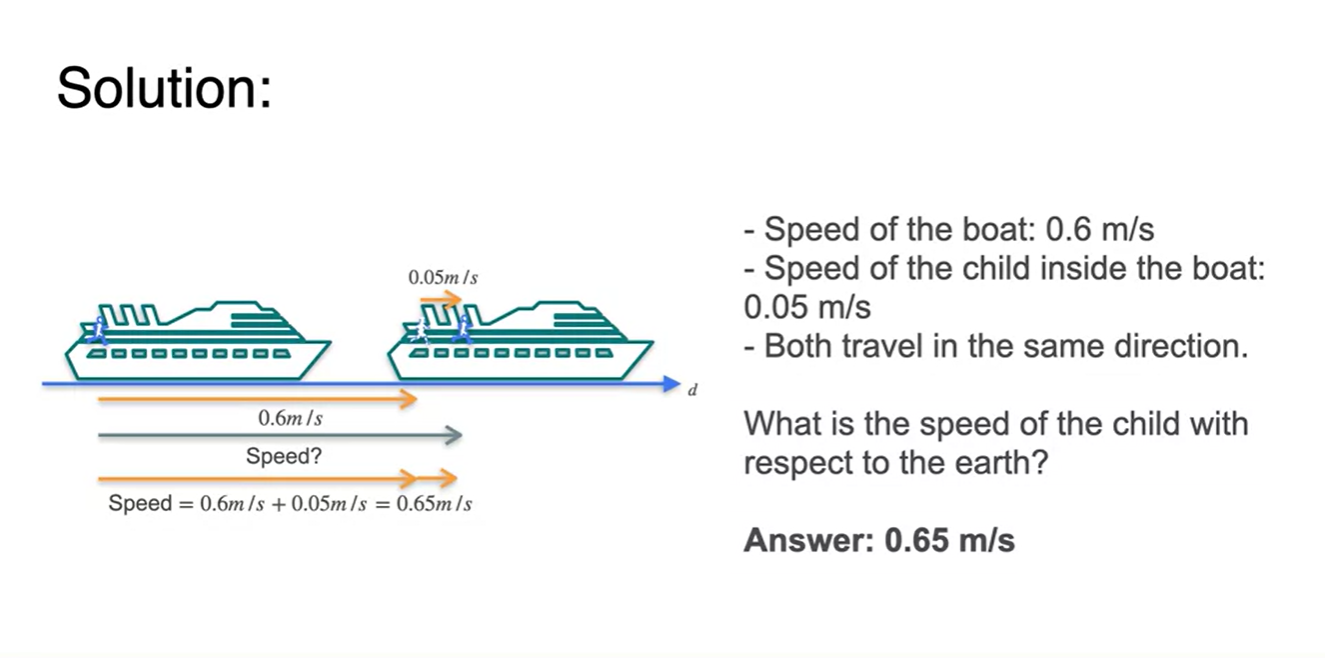
배의 움직인 거리()와 배에 올라탄 사람의 움직인 거리()가 각각 2와 10이라고 하자.
- 지구에서 보았을 때 배에 올라탄 사람의 움직인 전체 거리()를 계산해보면, 각 거리의 합() 12라는 것을 알 수 있다.
-
그렇다면 배와 사람의 속도가 주어졌을 때, 지구에서 본 배 위에 올라탄 사람의 (상대)속도는 얼마일까?
- Speed of the child with respect to the earth?
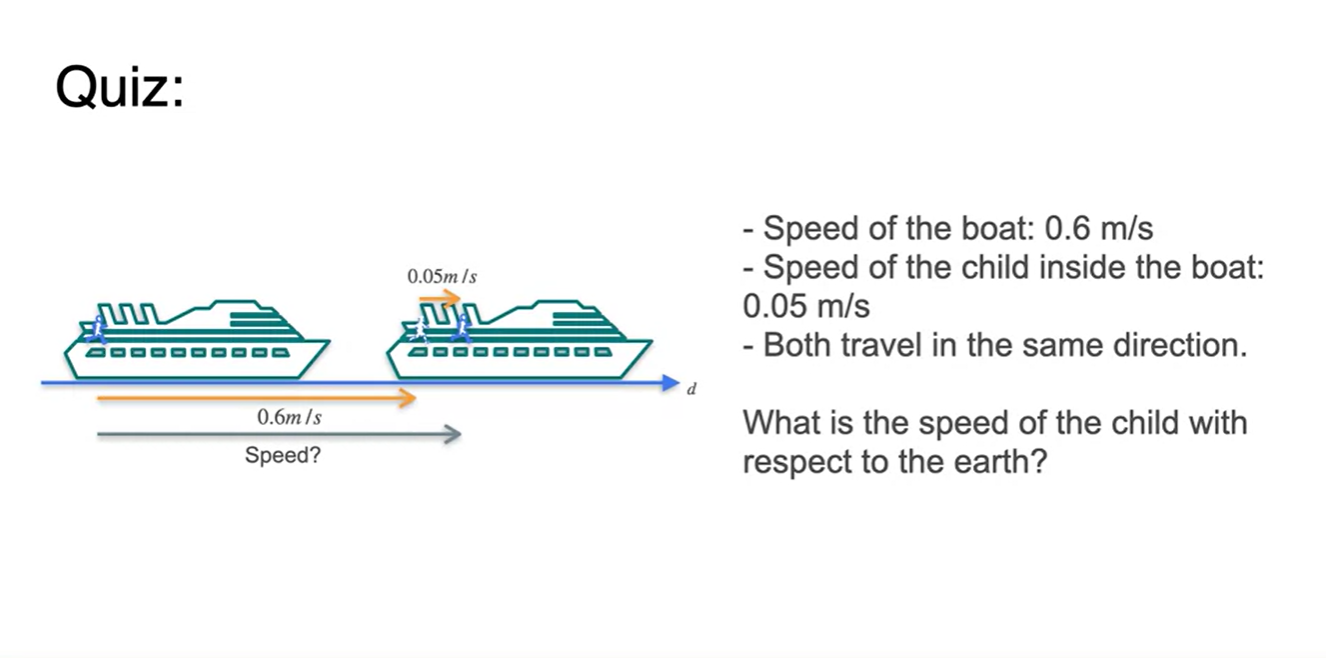
- 정답은 각 사물의 속도를 선형적으로 더한 값이다.
-
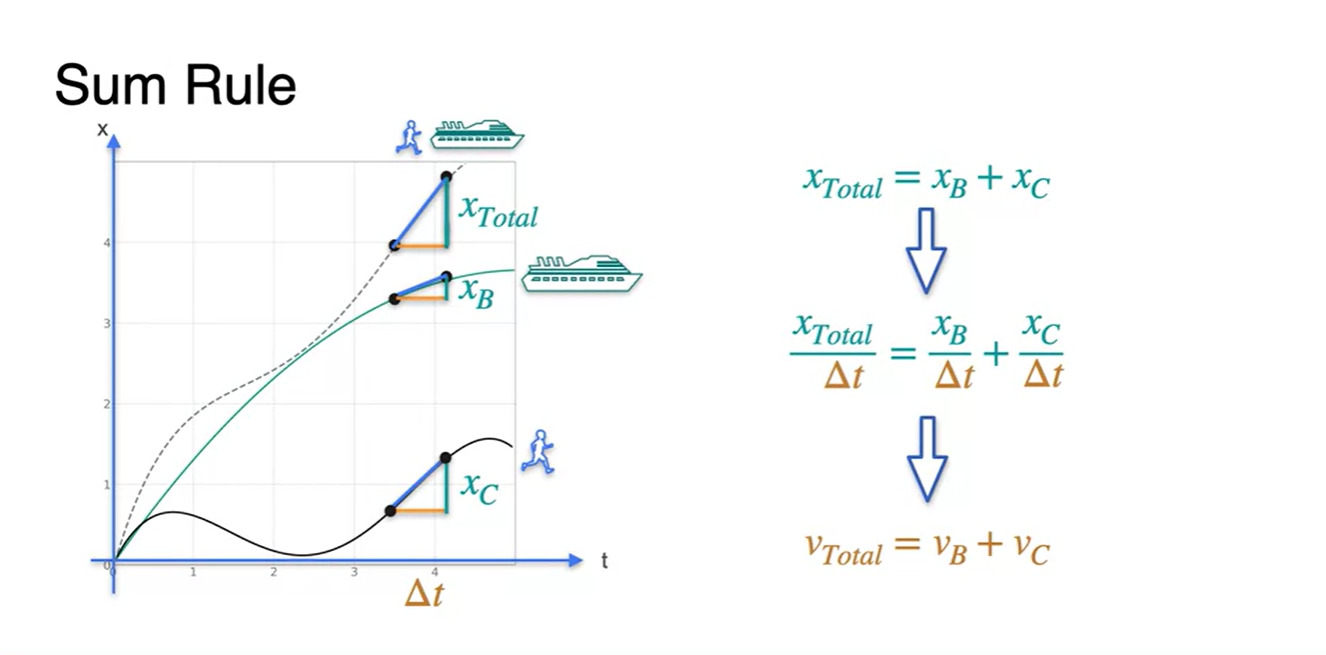
수식을 통해 정리해보자면, 각 거리의 합이 전체 거리이듯
- 로 나눈 값 또한 선형적인 속도()의 합으로 나타난다.
-
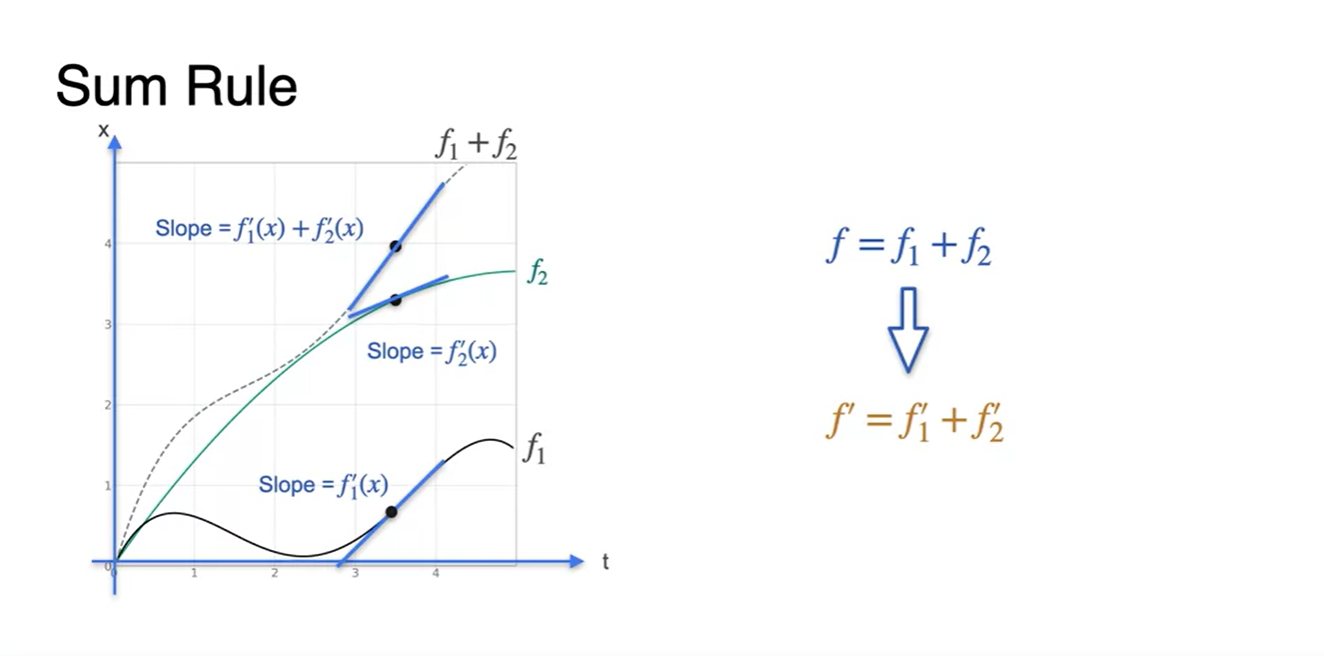
따라서 여러 함수를 합한 전체 함수의 derivative는 각 derivative의 합이다.
- 다시 말해, 각 함수의 미분 합으로 전체 함수의 미분을 구할 수도 있다.
Properties of the derivative: The product rule
-
Derivative의 또 다른 성질 중에 하나는 product 함수일 때 드러난다.
-
함수가 있을 때, 함수의 미분은 이다.
- 강의에서는 귀엽게도 hammar로 내리치는 비유를 했다.
-
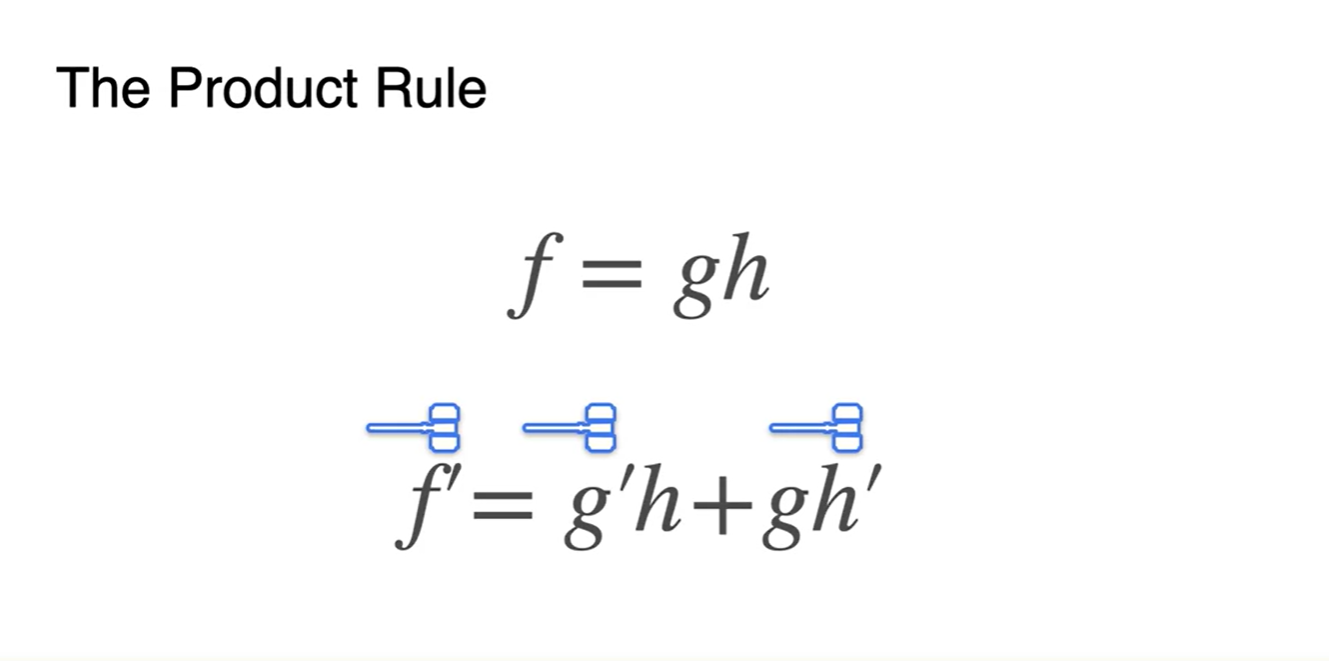
-
두 인부가 집을 짓는다고 가정해보자.
-
가로와 세로를 각각 맡아 시간에 따라 벽돌을 쌓아나간다고 할 때, 각 변이 완성되는 함수는 와 로 시간()에 따라 나타낼 수 있다.
-
집이 지어지는 전체 면적은 두 함수의 곱으로 표현할 수 있으며, 로 수식이 전개된다.
-
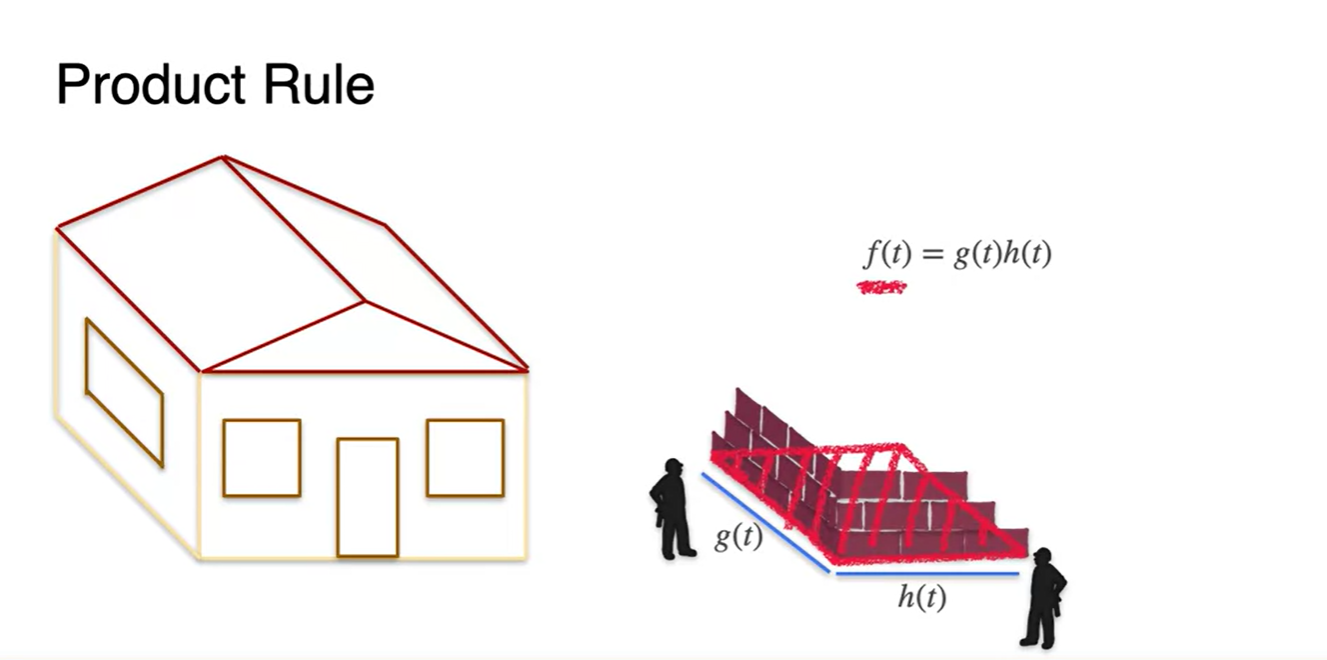
-
그렇다면 에 따른 각 변과 전체 면적의 변화율은 어떻게 변할까?
-
면적 에 대하여 에 따라 달라지는 면적은 총 세 개의 직사각형이다.
- , , 다.
-
이를 시간에 따른 변화()로 나누어 아주 작은 범위의 시간으로 보내면(), 로 표현 가능해진다.
-
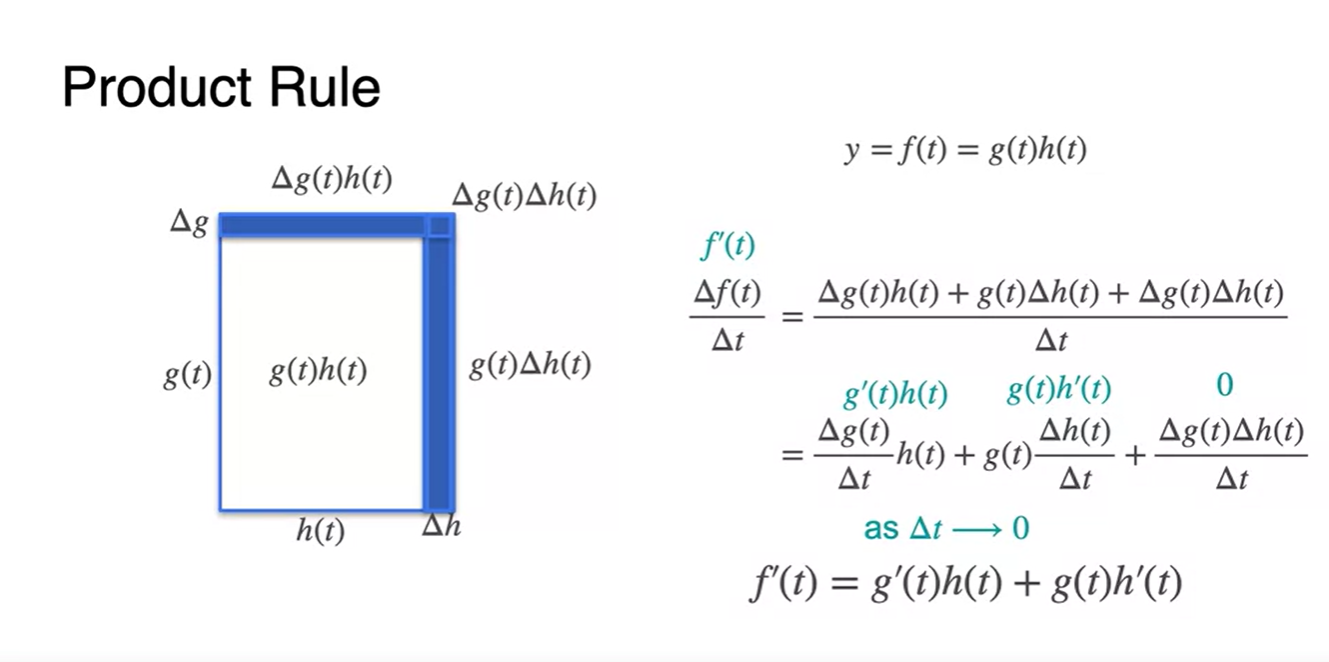
Properties of the derivative: The chain rule
-
Derivative의 마지막 성질에 대해 알아보자.
-
와 같은 composition(합성) 함수를 공통 변수 로 미분하면
- 수식으로 정리된다.
-
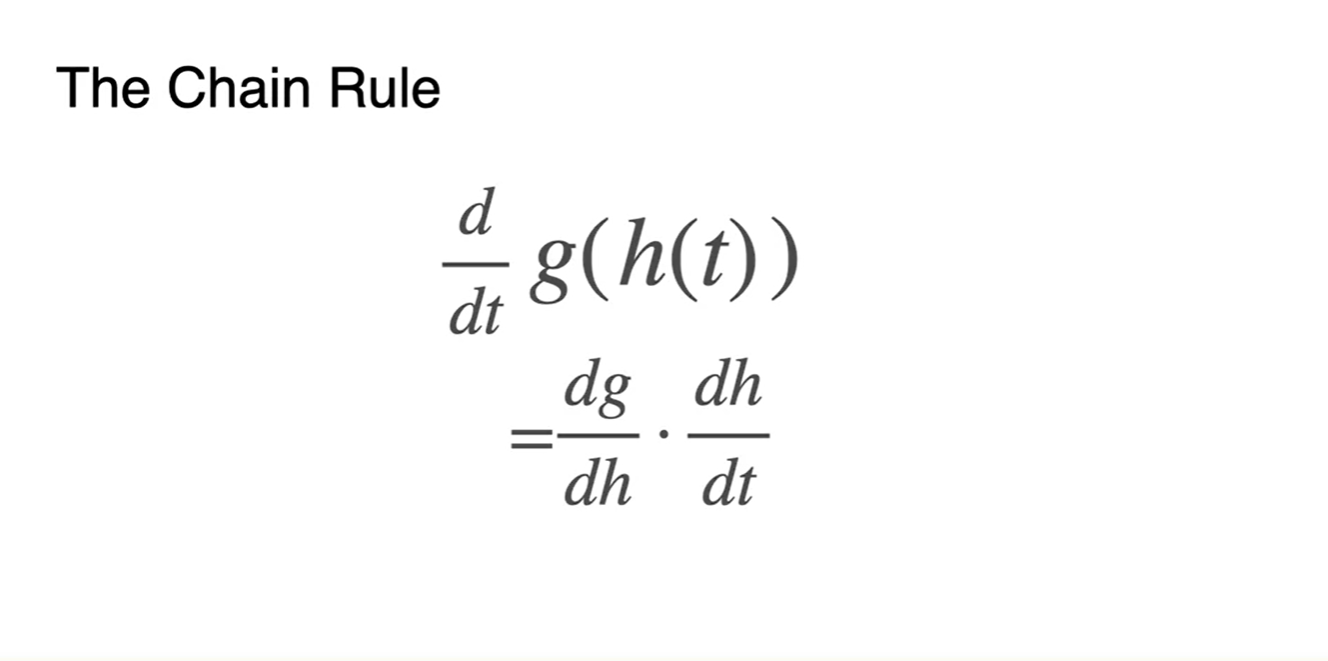
-
함수가 바깥에 한 번 더 씌워져 있어도 비슷하다.
- 식으로 정리된다.
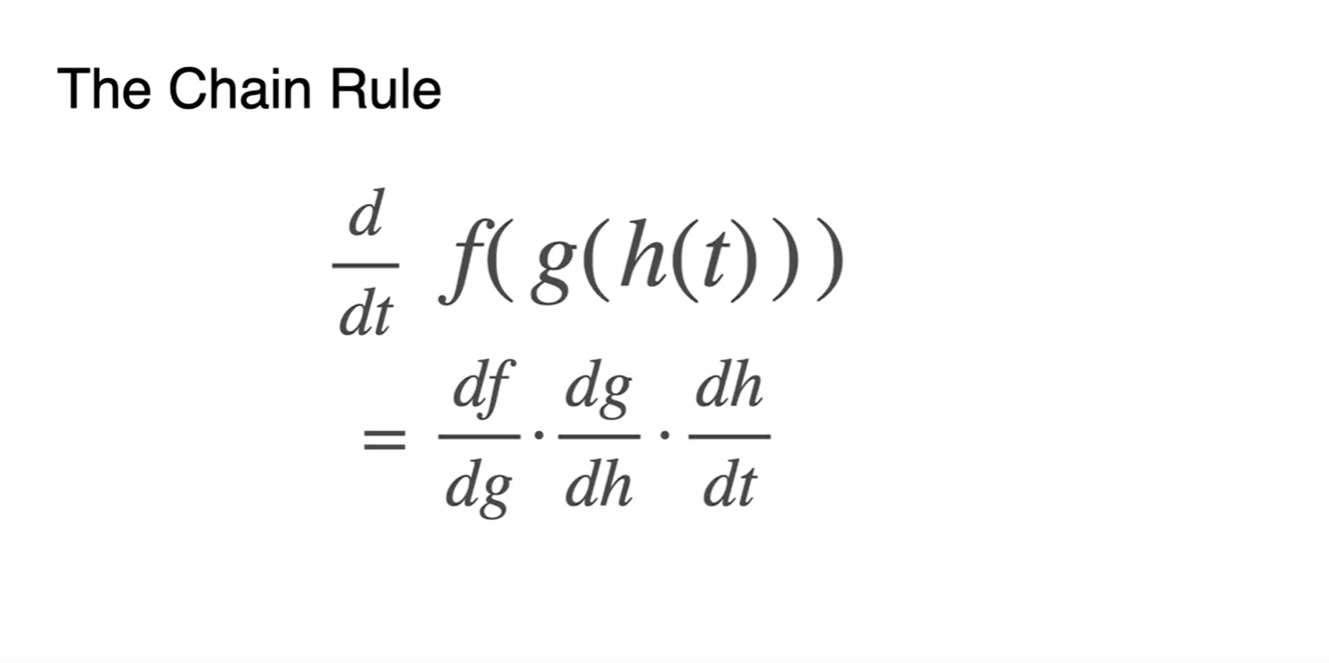
-
Lagrange 미분 표현식으로 정리하면 아래와 같다.
- 함수를 여러 번 합성했다면 겉껍질 → 속껍질 순으로 미분해주면 된다.
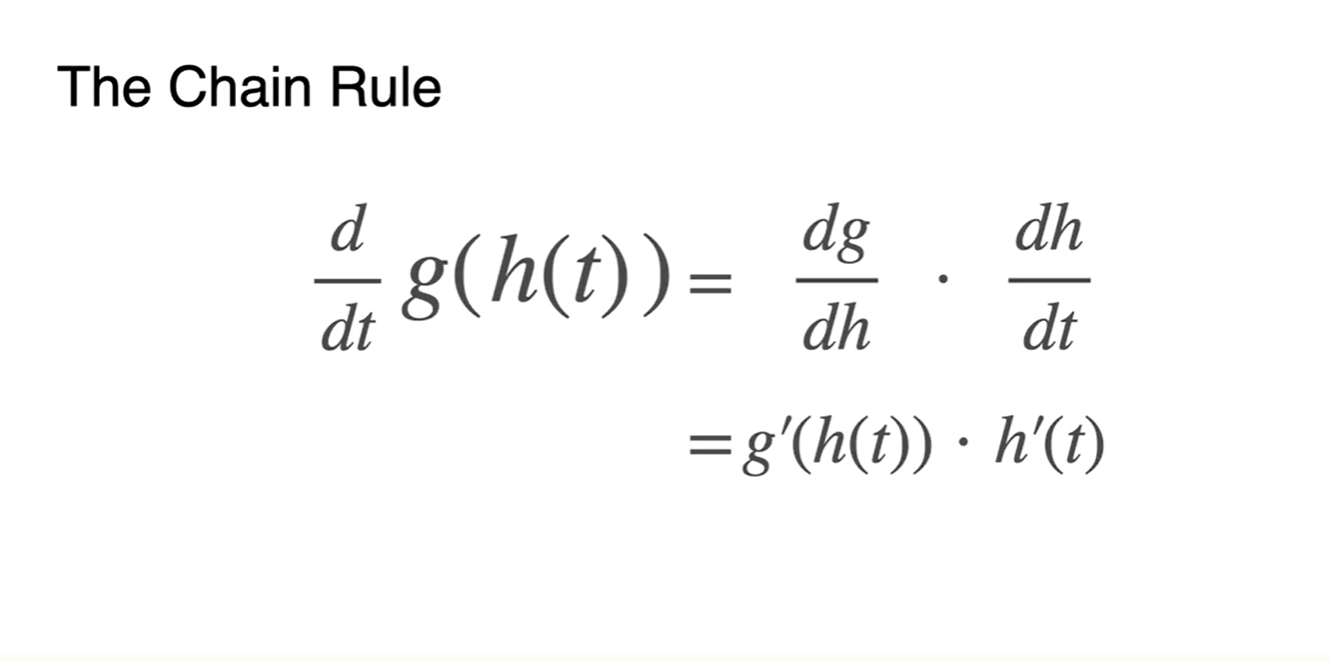
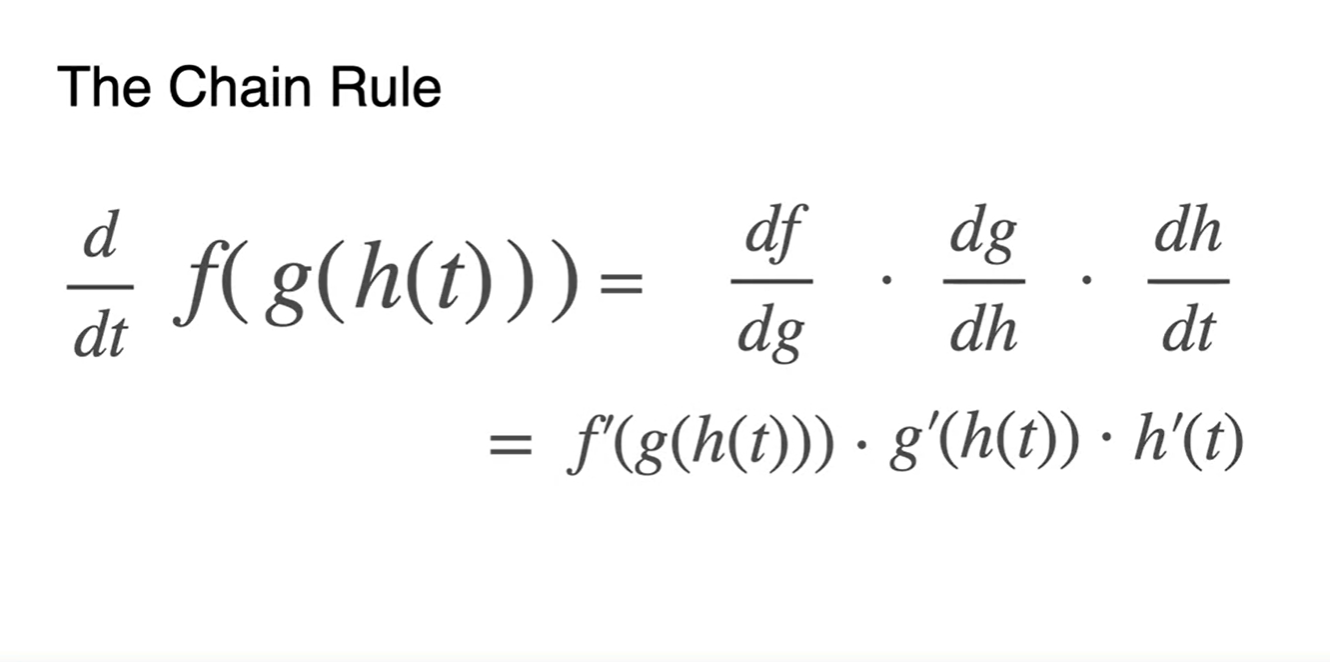
-
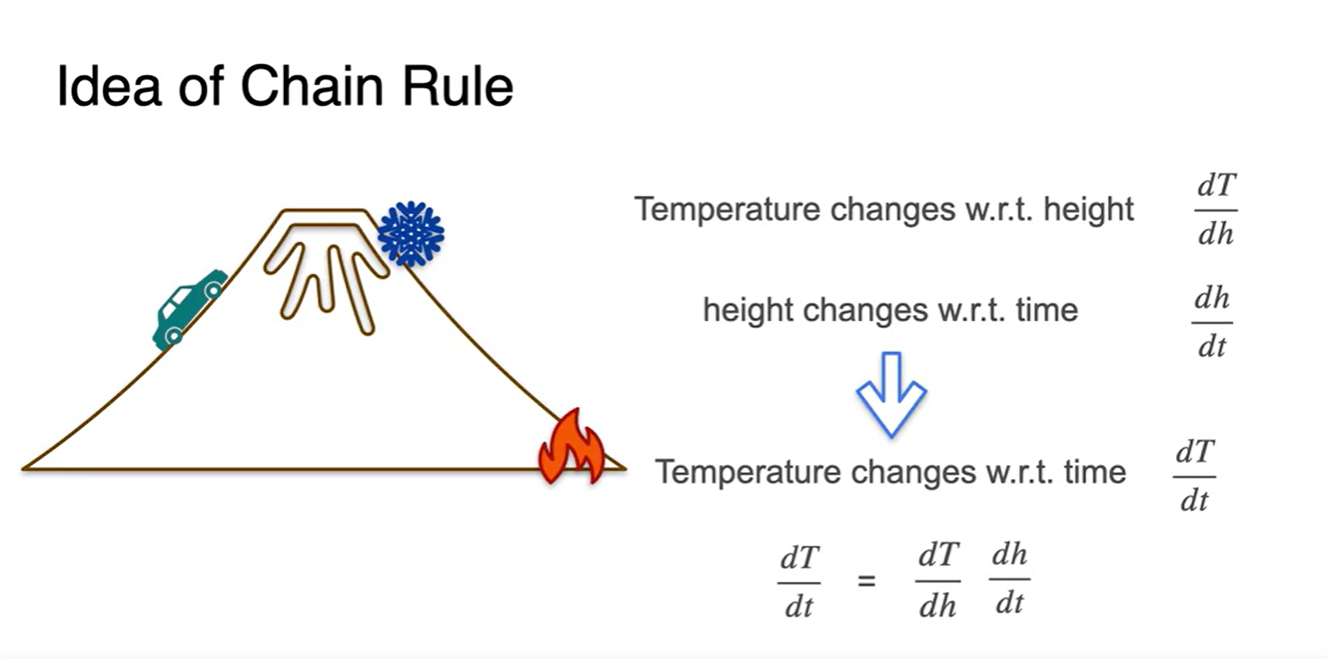
예를 들어, 자동차가 산을 오르며 느끼는 온도 변화를 생각해보자.
-
산의 온도 차이는 높이(h)에 따라 변하는 함수고, 산을 오르는 자동차의 움직임 변화는 시간(t)에 따라 달라지는 함수다.
- 각 함수의 변화율을 수식으로 나타내자면 , 로 나타낼 수 있다.
-
그렇다면 자동차에 타고 있는 사람이 느끼는 시간(t)에 따른 산의 온도 변화(T)율은 어떻게 표현할까?
- 로 chain rule을 적용하여 나타낼 수 있을 것이다.
-
-
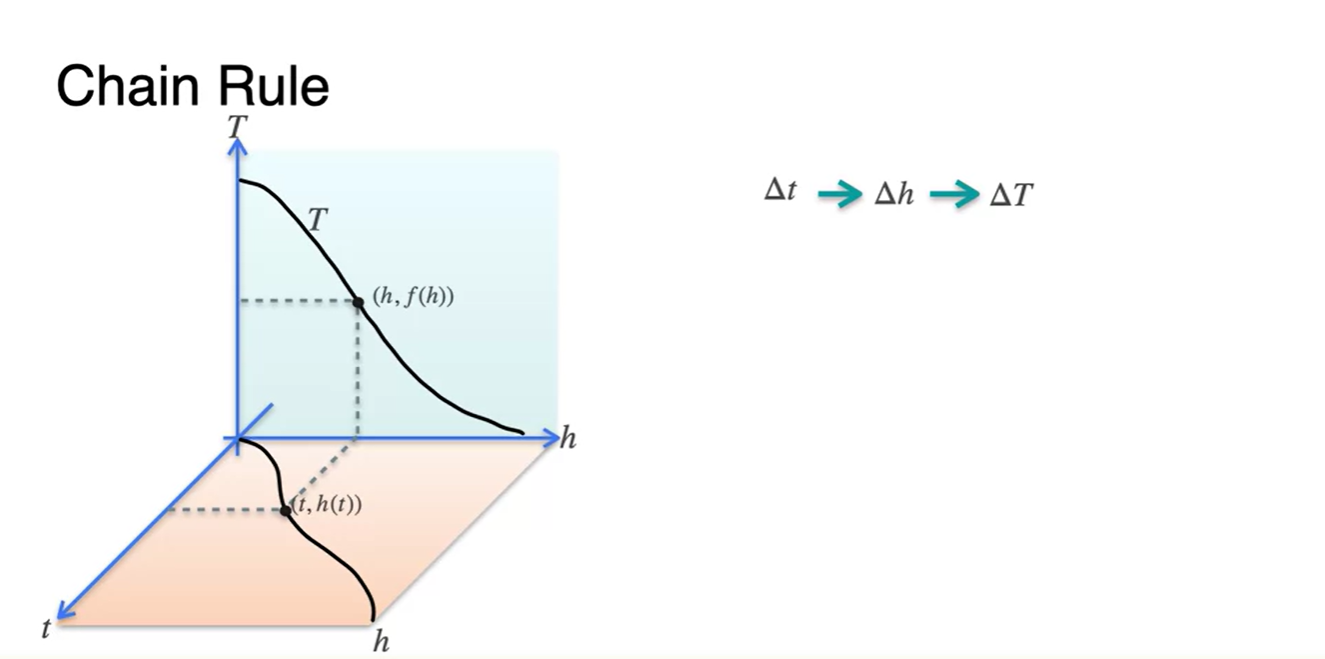
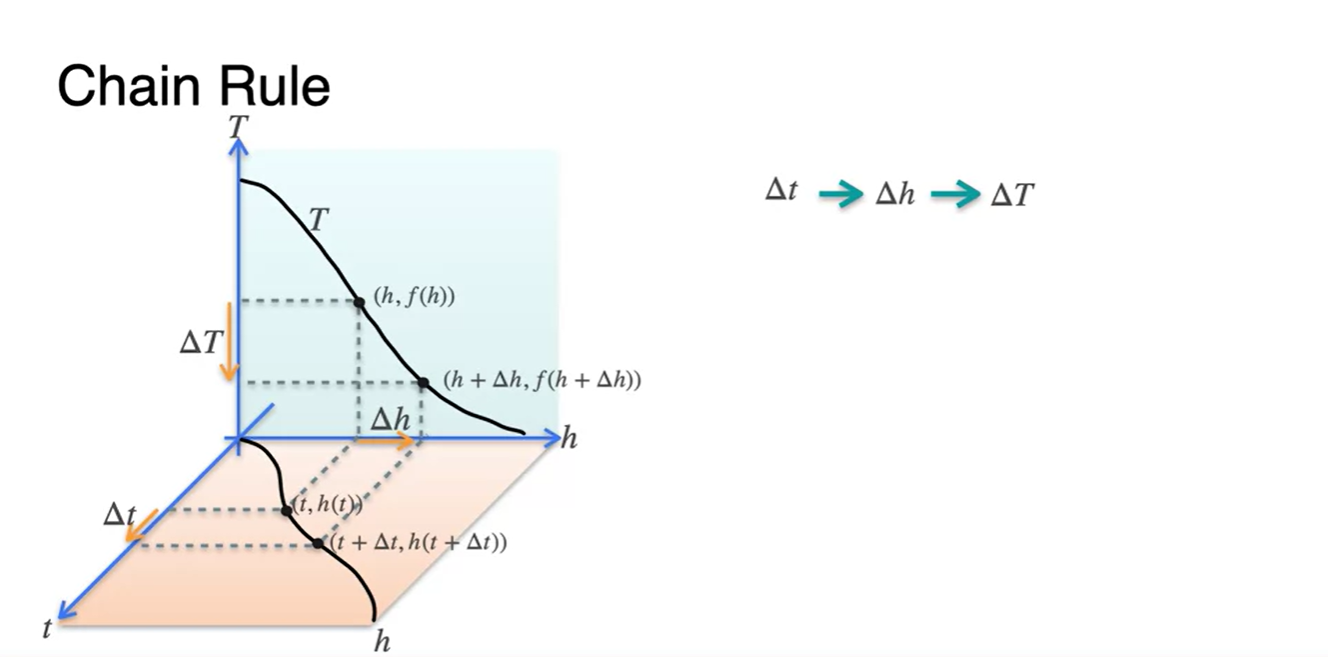
이러한 함수를 plot한다면 어떻게 그려질까?
- 아래 평면에 그려지는 함수는 시간(t)에 따른 높이(h) 변화율이다.
- 옆 평면에 그려지는 함수는 높이(h)에 따른 온도(T) 변화율이다.
-
우리가 알고 싶은 변화율은 시간(t)에 따른 온도(T) 변화율이므로,
- 중간 다리 역할을 하는 높이(h)를 기준으로 변화율을 기록하면 아래 그림과 같이 변화하는 움직임을 살펴볼 수 있다.
-
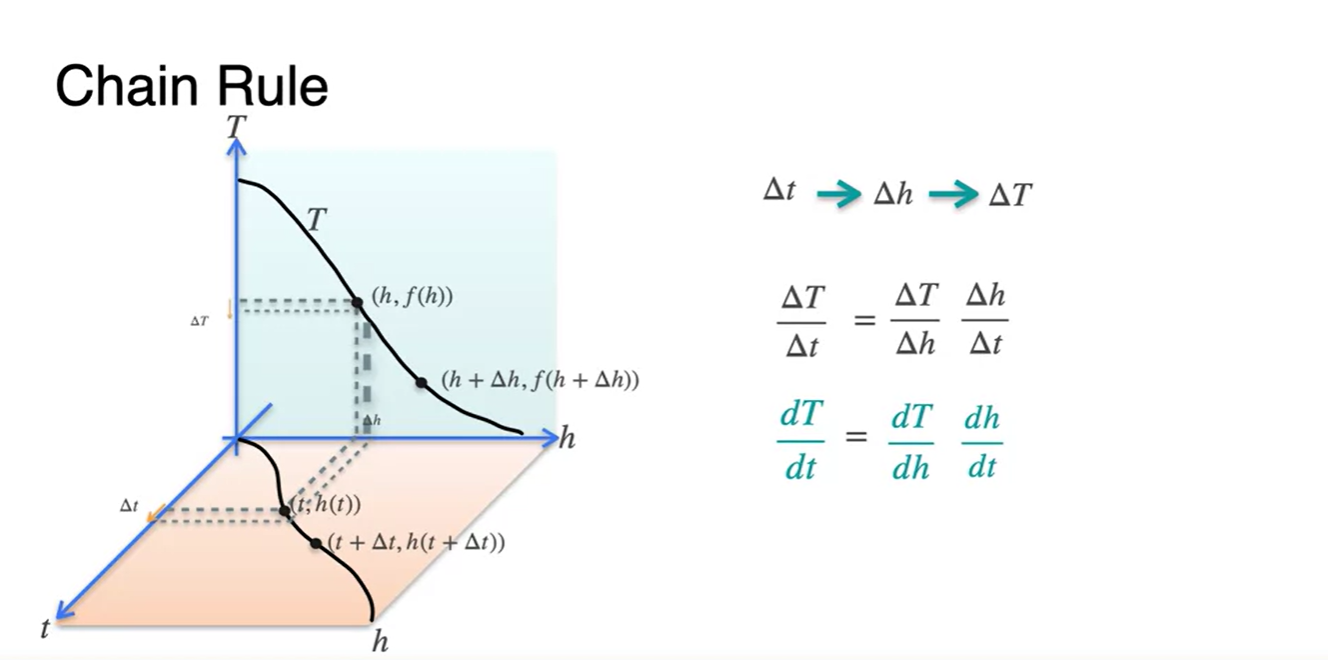
이를 수식으로 표현하면 로 표현할 수 있다.
- 변수들끼리 연결된 형태의 함수라면 chain rule을 이용하여 미분이 가능하다.
Optimization
Introduction to optimization
-
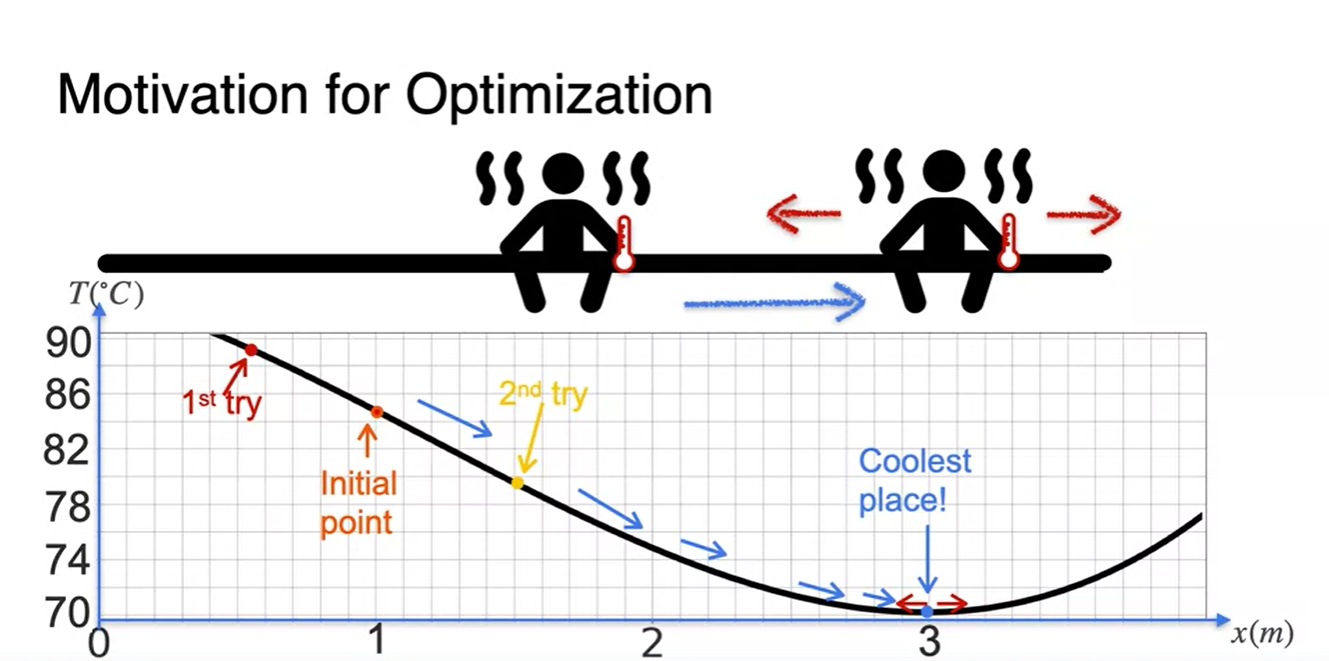
매우 뜨거운 사우나 벤치에 앉아 있다고 해보자.
- 너무 더워서 현재 온도보다 차가운 지점을 향해 가려고 한다.
-
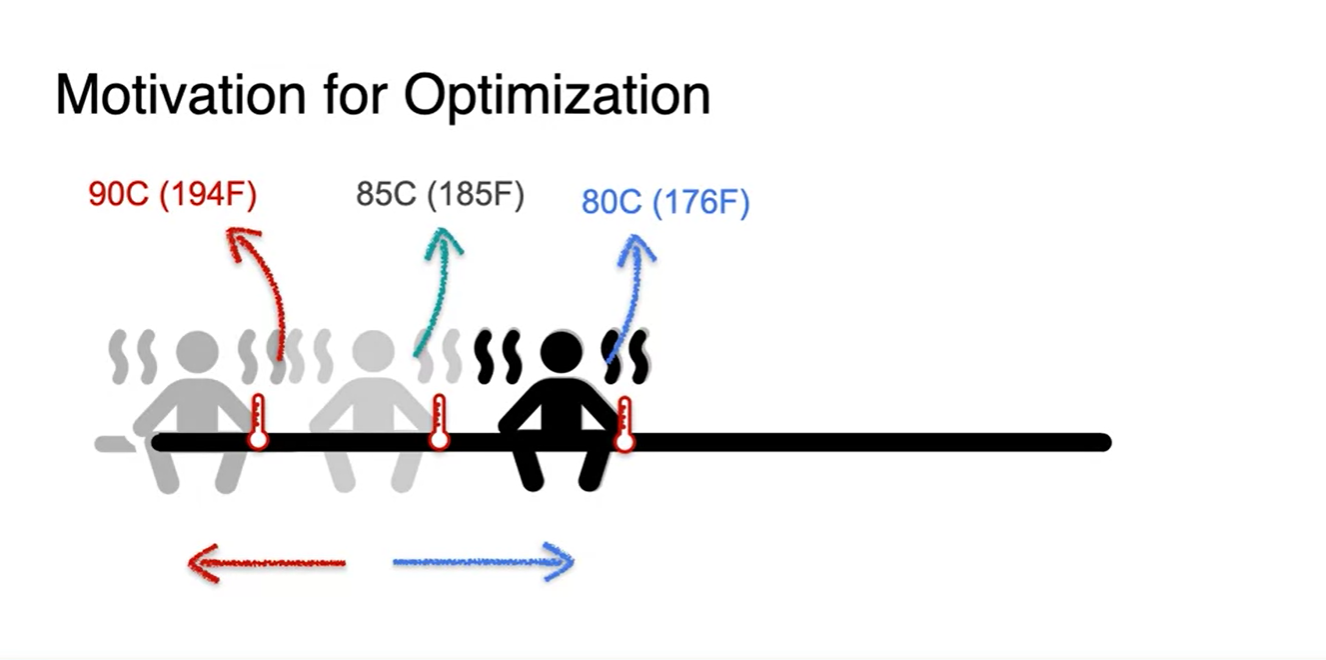
왼쪽으로 갔더니 온도가 더 높아졌고, 오른쪽으로 갔더니 온도가 낮아졌다.
- 이를 바탕으로 온도의 최솟값을 찾겠다고 한다면 자연스레 어디로 향하게 되는가?
-
정답은 오른쪽일 것이다.
- 오른쪽으로 향해가다가 특정 어느 지점에서 온도가 다시 높아지기 시작했다면 가장 차가운 지점은 어디인가?
- 바로, 온도가 높아지기 시작하는 직전 point의 온도일 것이다.
-
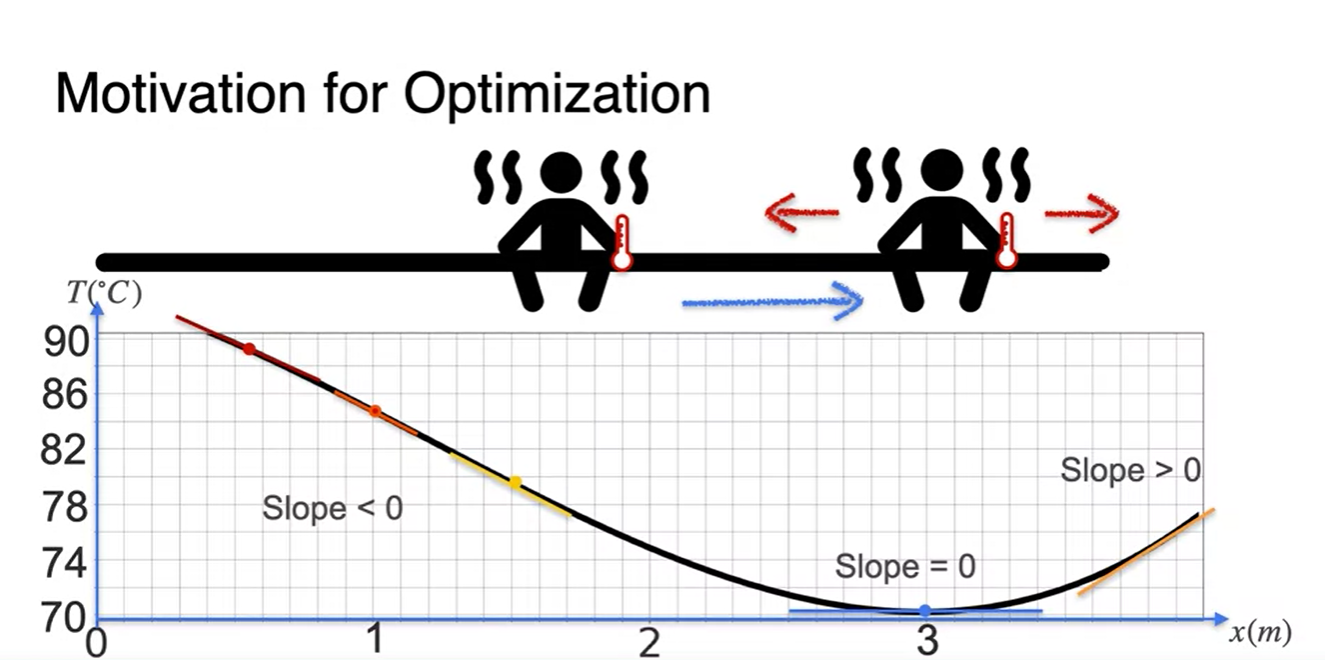
이를 기울기로 표현하면 첫 지점으로부터 차가운 지점으로 향해가는 동안의 slope는 < 0이 된다.
- 가장 차가운 지점에서 slope는 0이었다가, 다시 뜨거워지기 시작하면서 slope가 > 0의 값을 갖게 된다.
-
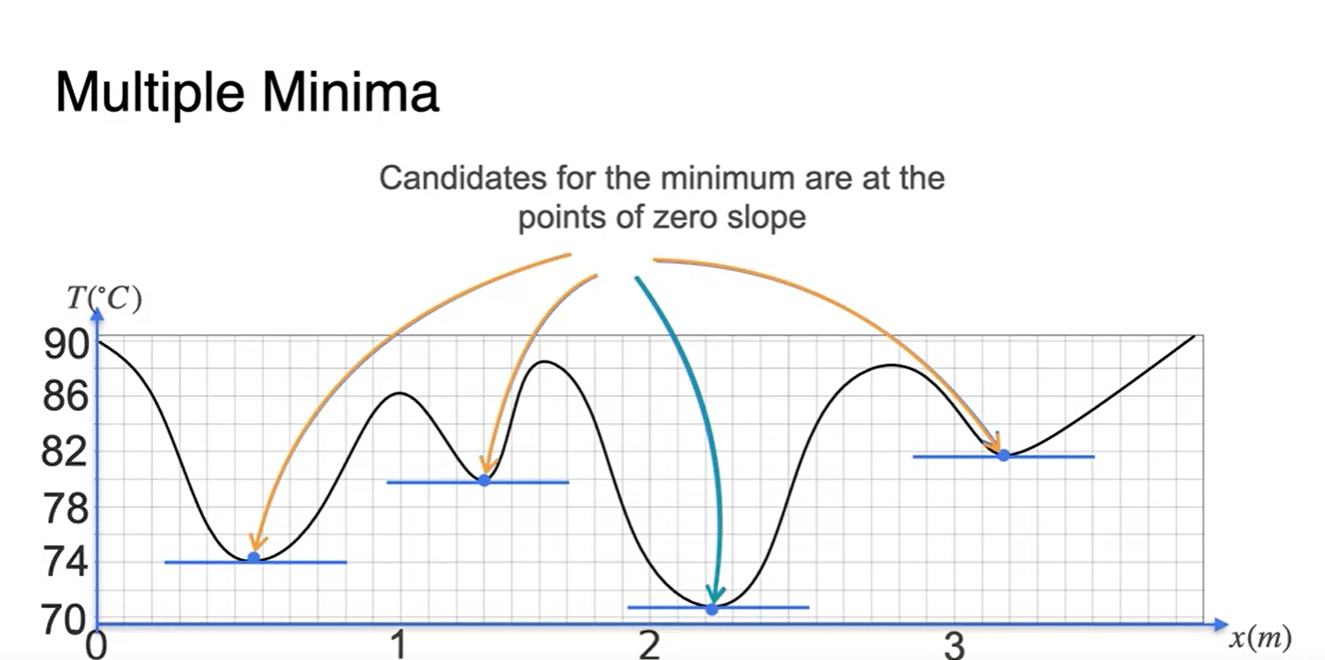
만약 아래와 같이 최저값을 많이 가지고 있는 함수라면 zero slope 후보는 많아진다.
- 이 중 가장 최저값을 찾아야 하는 것이 머신러닝에서의 핵심이라고 할 수 있다.
Optimization of squared loss - The one powerline problem
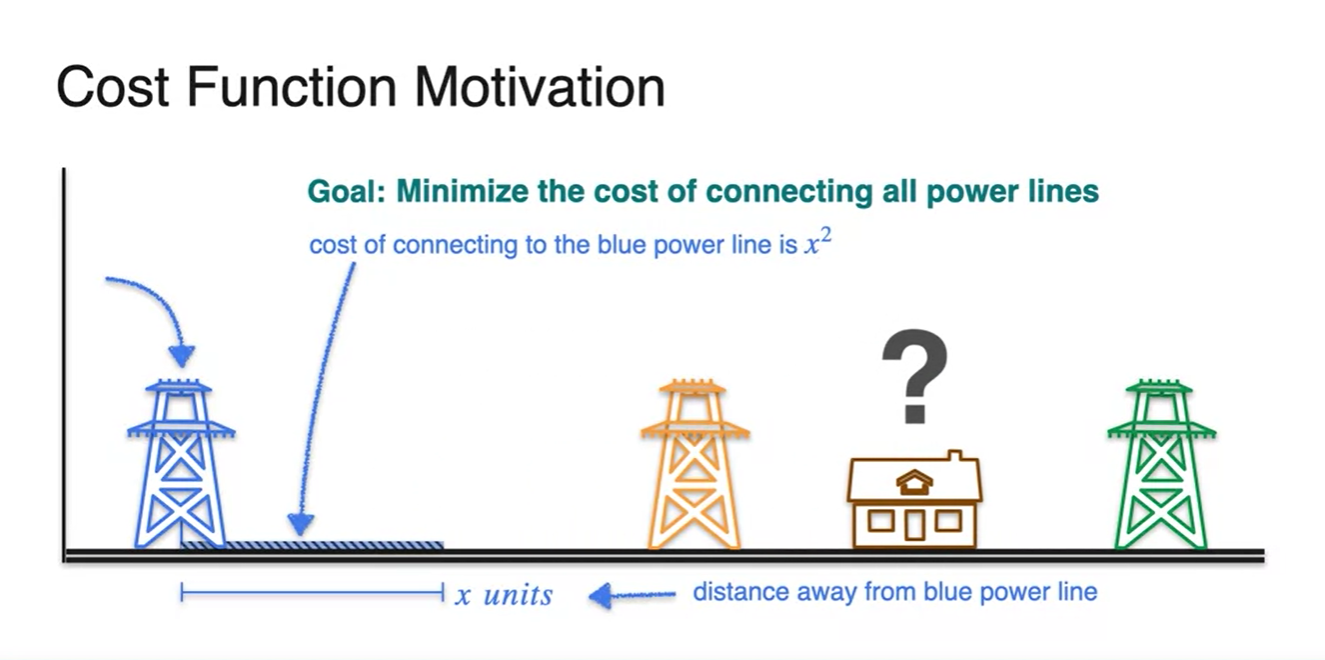
- 아래 그림과 같이 전력선과의 거리가 최소가 되는 지점에 집을 짓는다고 가정해 보자.

-
전력선과의 거리가 이고, power line을 설치하는데 드는 비용이 이라면
- 우리가 해야할 일은 비용 의 값을 최소로 만드는 것이다.
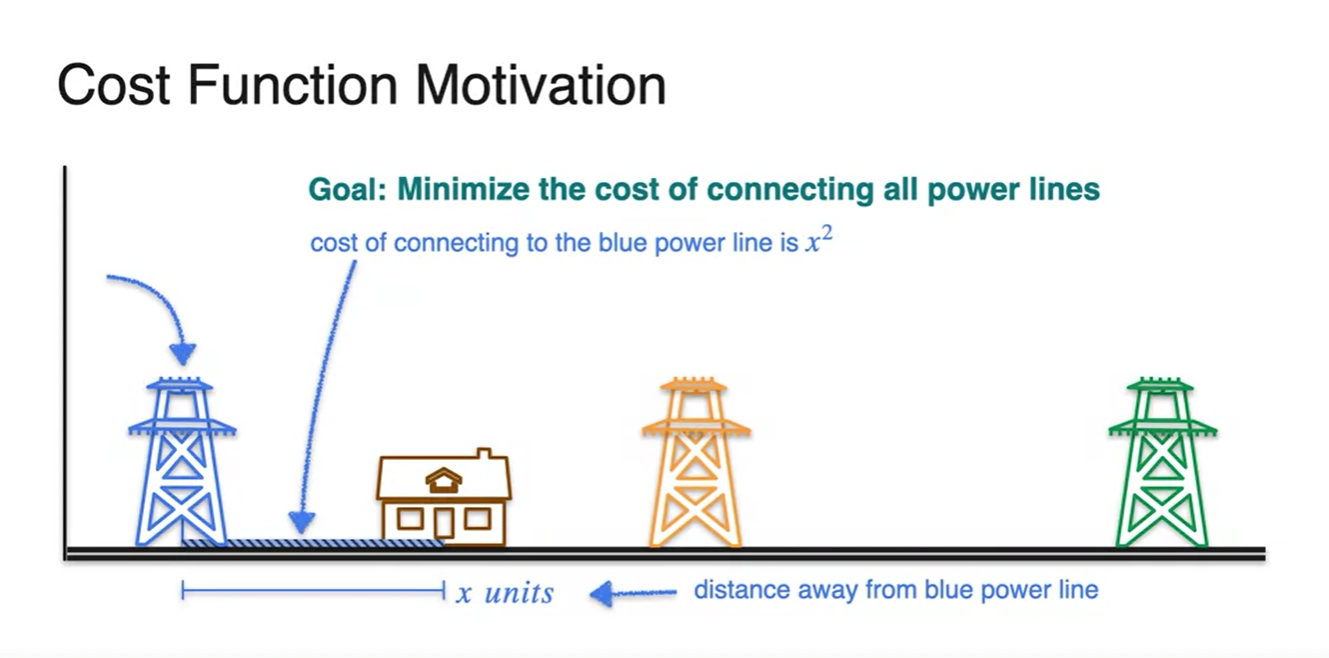
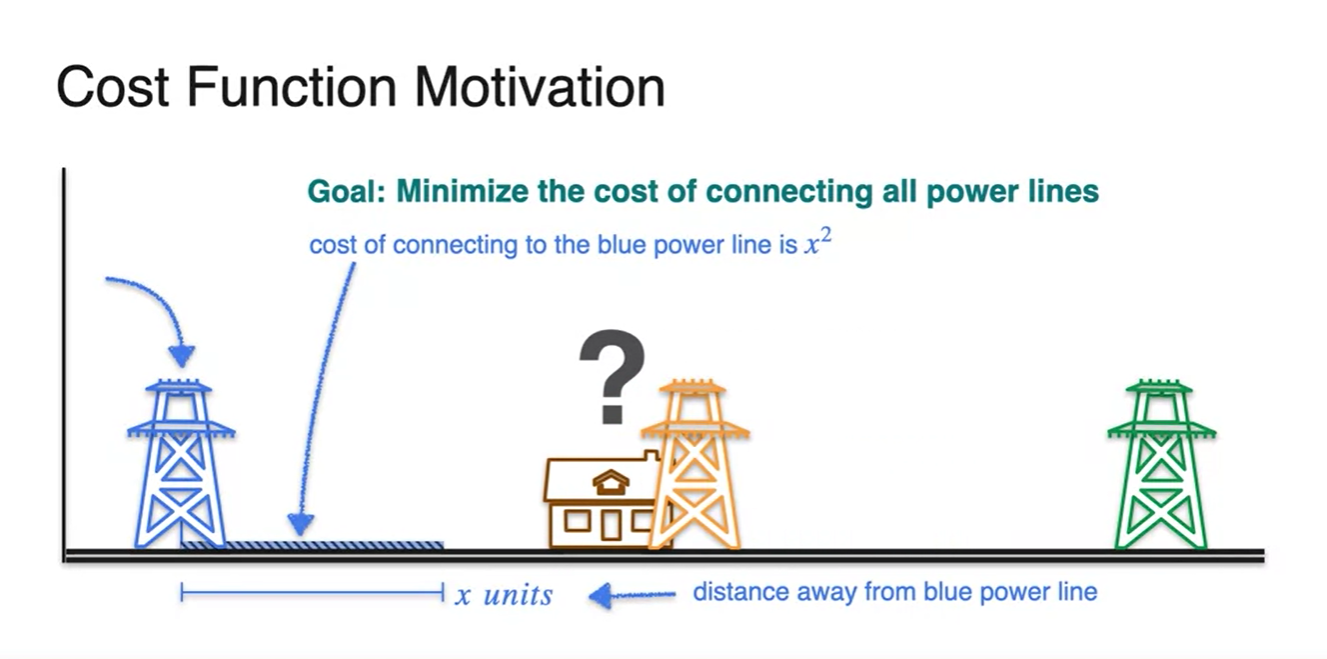
- 과연 집을 어디에 설치해야 할까?
-
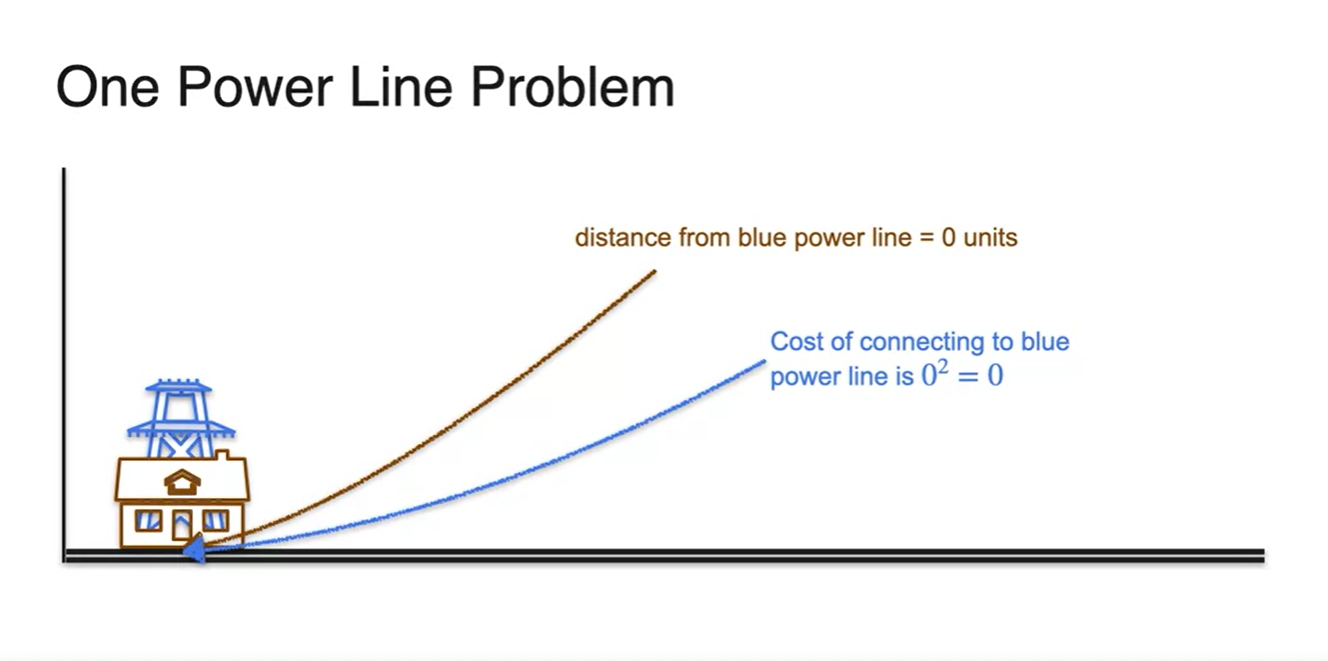
Power line이 하나 있다면 전봇대의 위치와 같은 곳에 설치해야 할 것이다.
- 이 때가 이며, cost 이 최소가 되는 지점이기 때문이다.
Optimization of squared loss - The two powerline problem
-
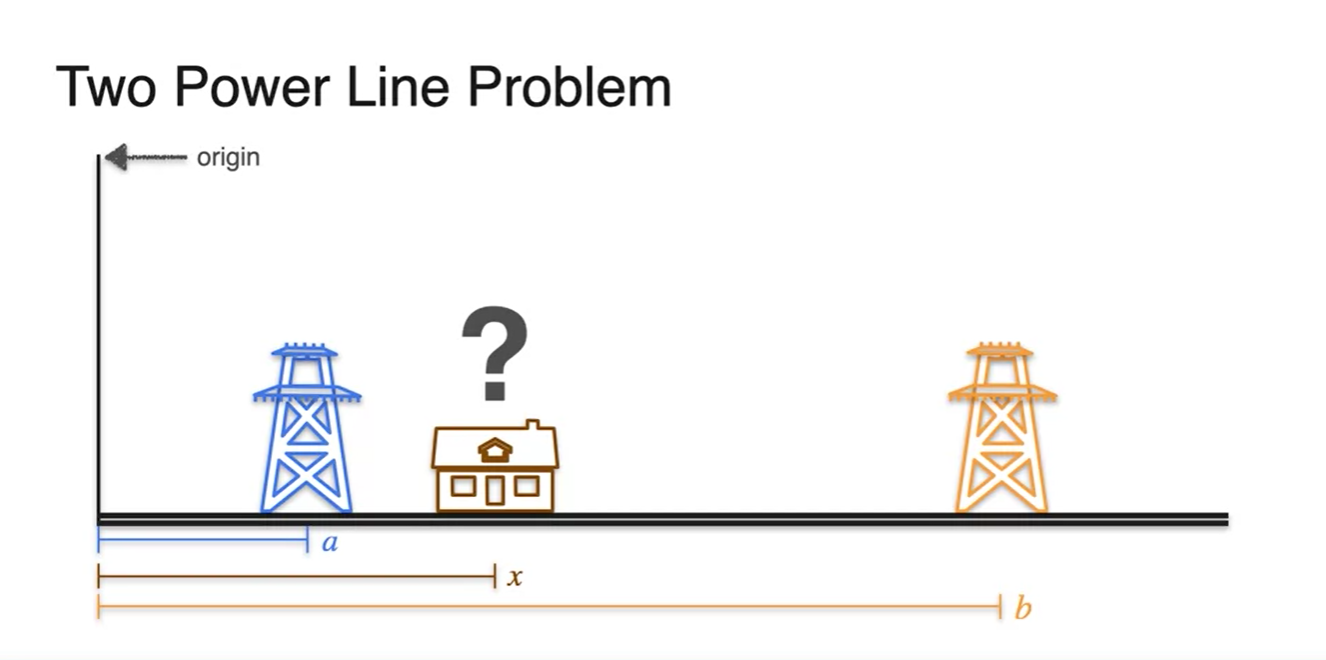
전봇대가 두 개라면 어떨까?
- 원점을 origin으로 하여 거리를 차례대로 , , 라고 놓아보자.
-
집과 전봇대 사이의 거리는 각각 , 로 정의될 것이며
- power line을 설치하는 데 드는 비용은 , 으로 정의된다.
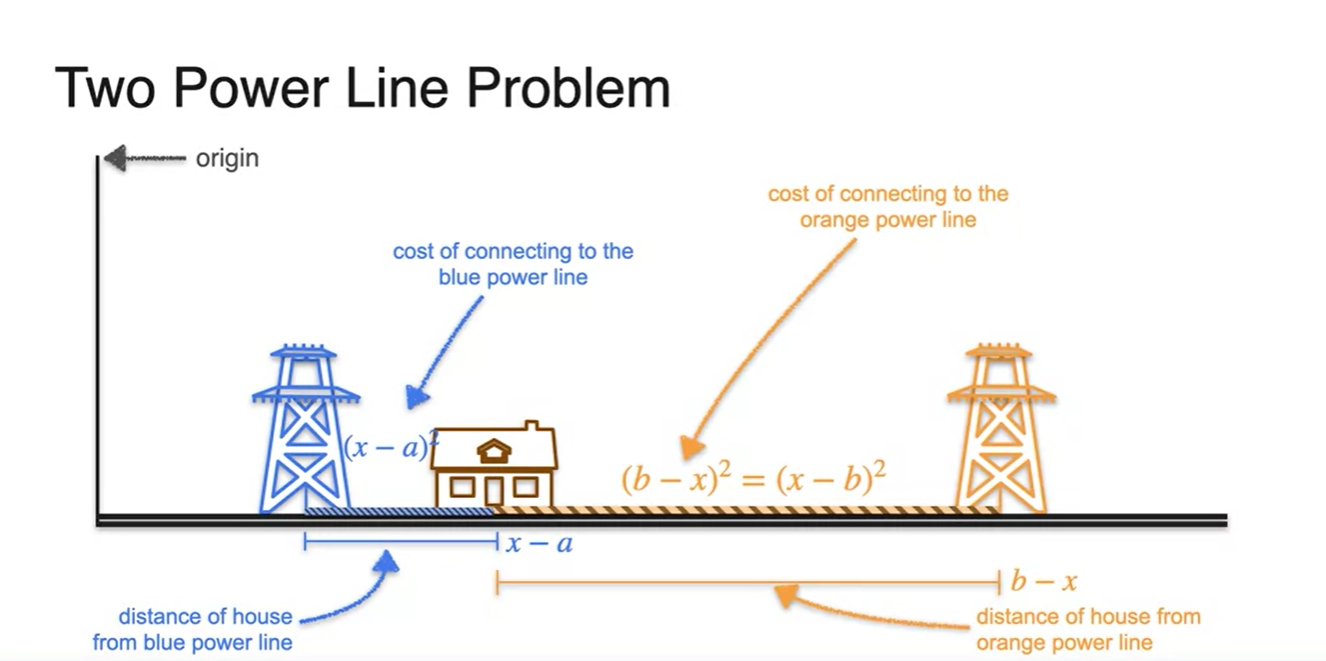
-
우리는 최종적으로 를 최소화 하는 데에 목적을 두고
- 이러한 식을 cost function이라 정의하여 이를 minimize하는 를 찾도록 하자.
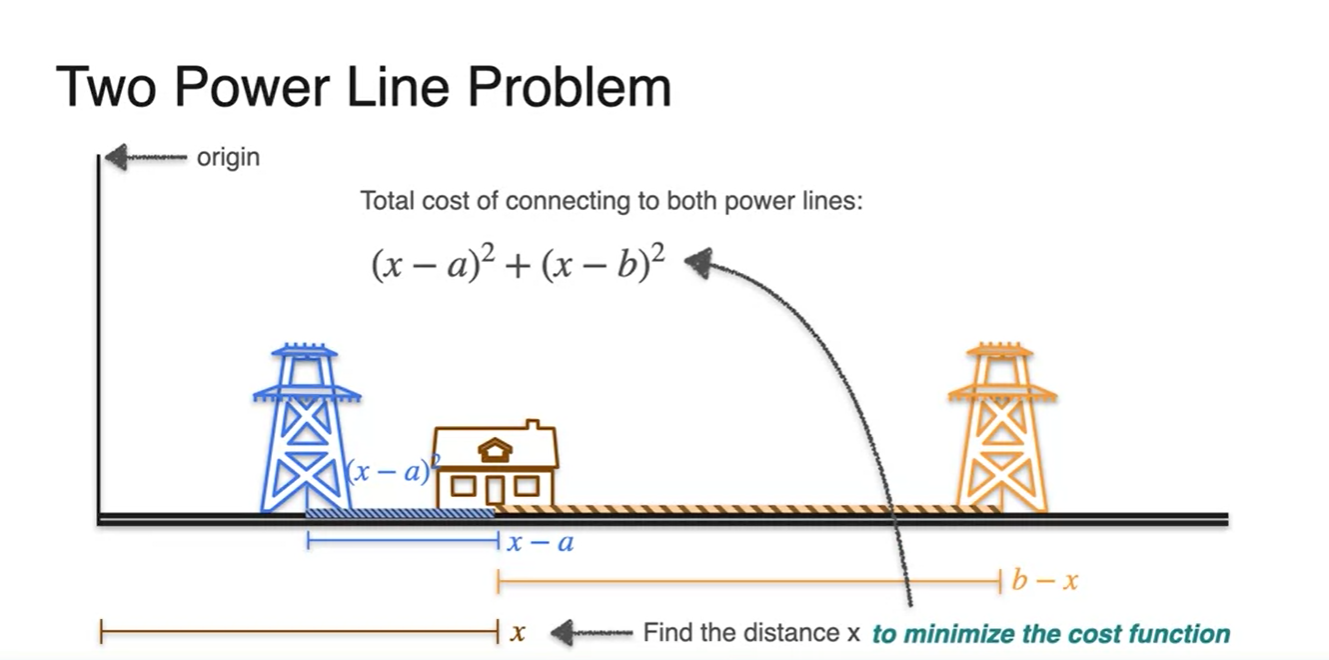
-
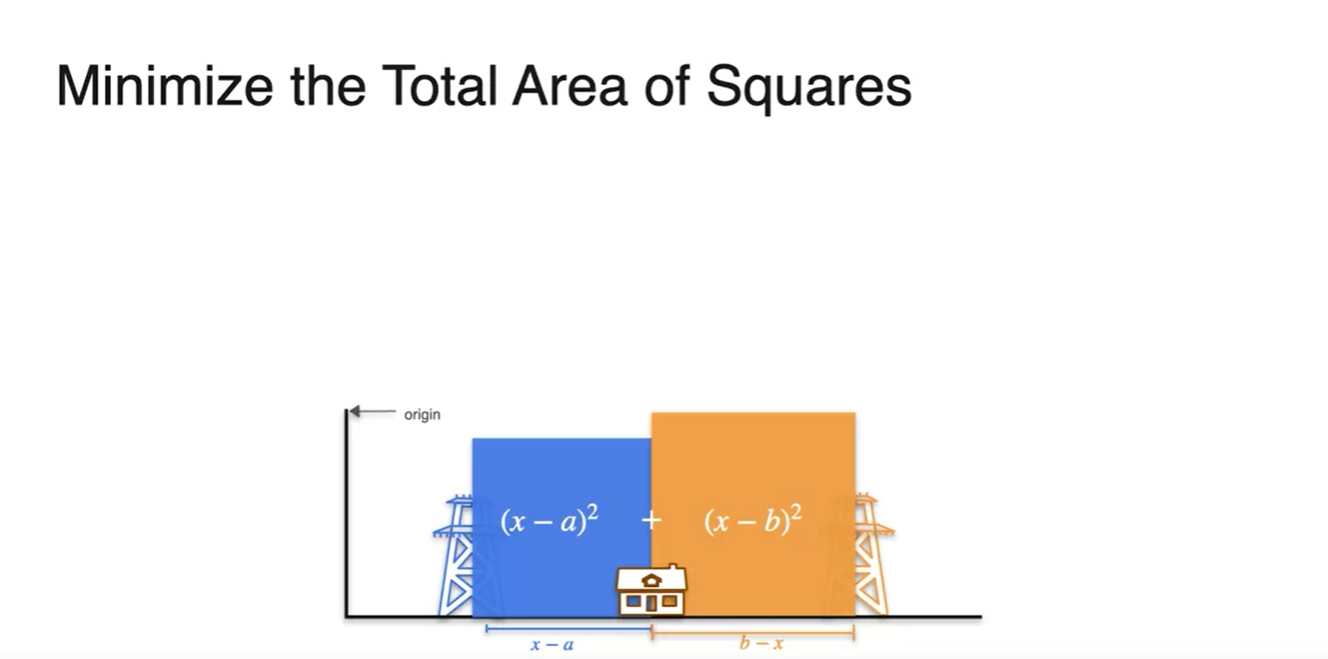
어쩌면 우리는 정답을 알고 있다.
- 두 전봇대 사이의 중점에 집을 지으면 된다는 점을 말이다.
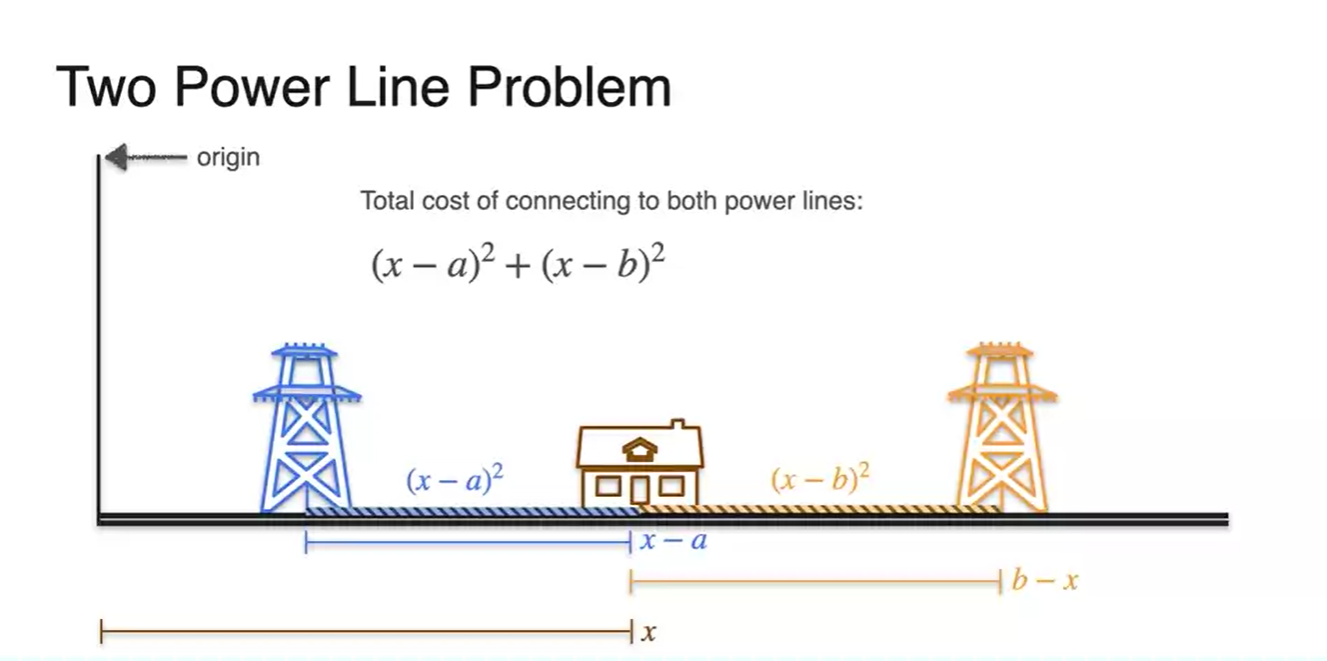
-
Graphical하게 표현해보면 과 는 각각 두 전봇대 사이의 거리가 한 변인 면적에 해당한다.
- 최종 cost function은 두 면적을 더한 수식이 되는 것이다.
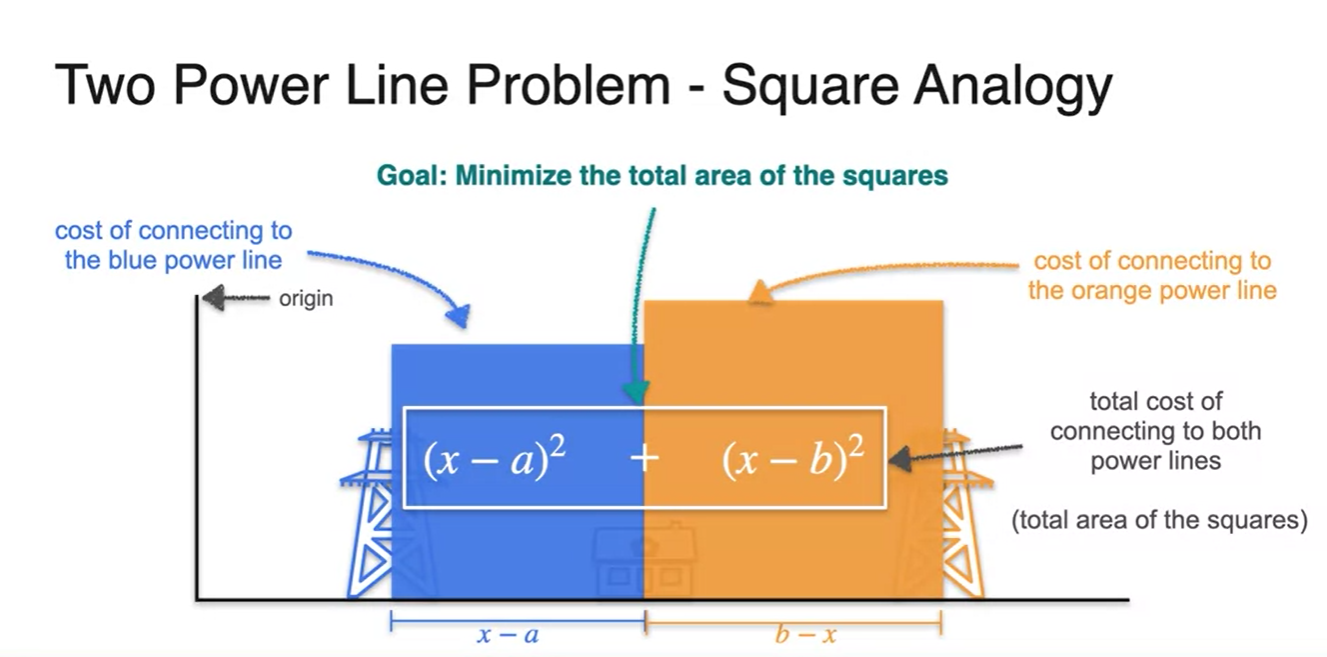
-
집이 너무 왼쪽으로 치우쳐져 있다면 면적이 훨씬 클 것이고,
- 집이 너무 오른쪽으로 치우쳐져 있다면 면적이 훨씬 클 것이다.
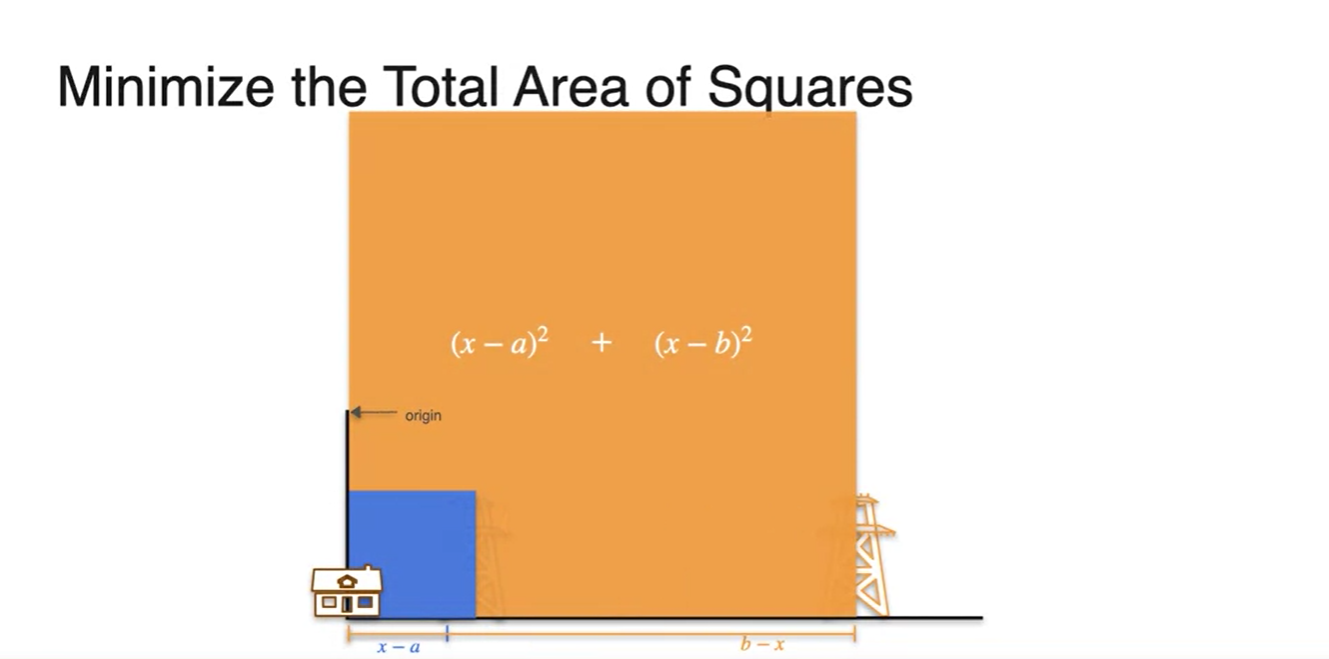
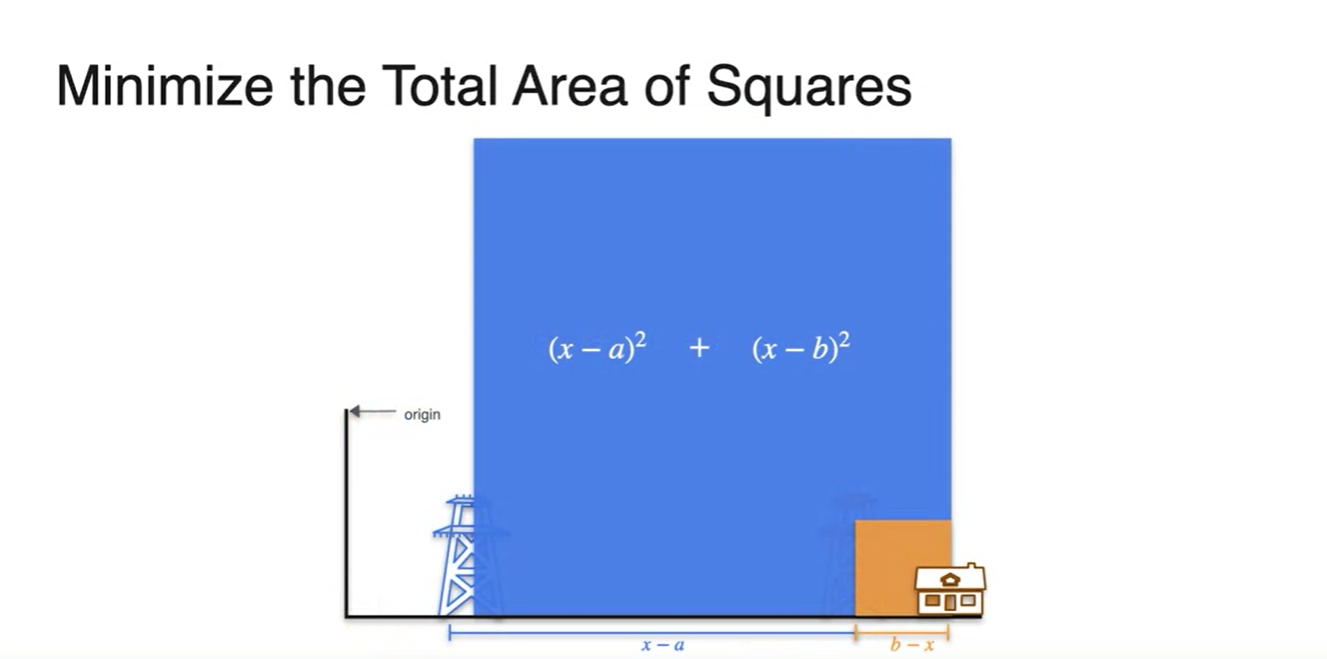
- 따라서 두 면적의 최솟값은 당연하게도 가 중점을 지나야만 한다.
-
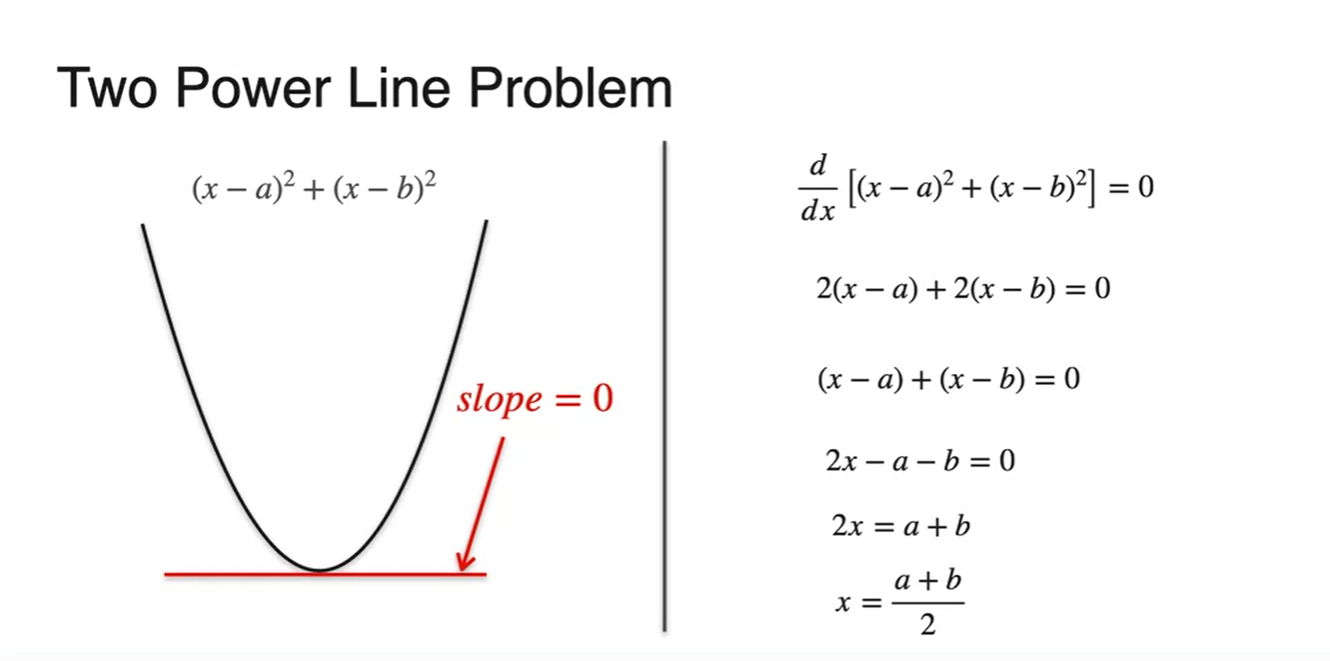
이를 좀 더 수식적으로 표현해보자.
-
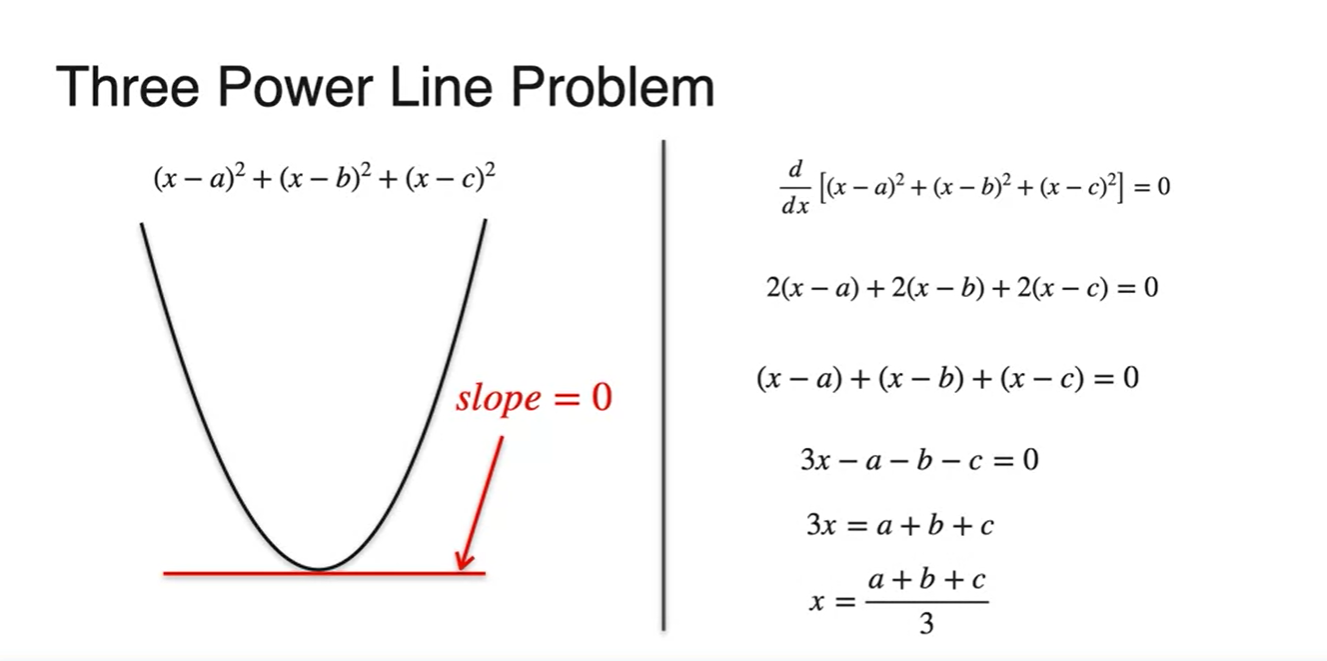
우리는 함수 를 minimize하는 지점을 찾아야 하므로 slope가 0인 지점을 찾아야 한다.
-
이는 이 cost function 의 derivative, 가 0이 되는 값을 찾는 것이며 가 정답이다.
-
Optimization of squared loss - The three powerline problem
-
전봇대가 3개라면 어떨까?
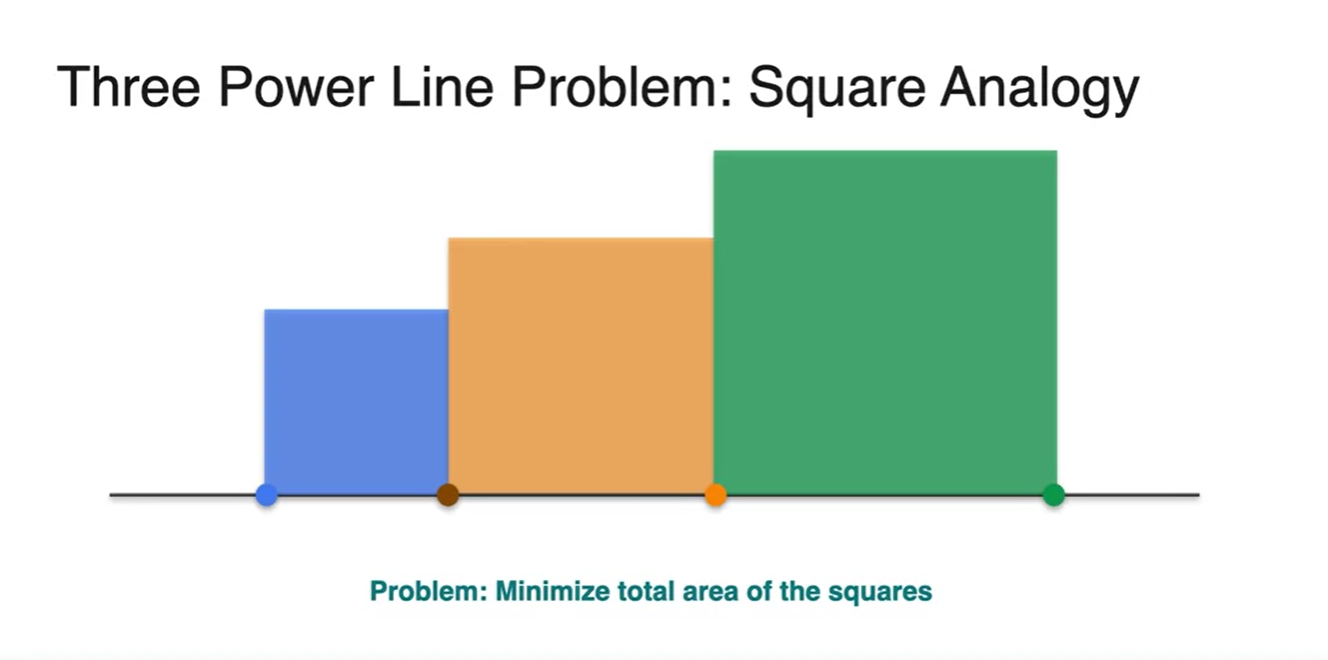
- 마찬가지로 각 거리는 , , 이며, 각 제곱의 합을 minimize해주는 것이 우리의 목표가 된다.
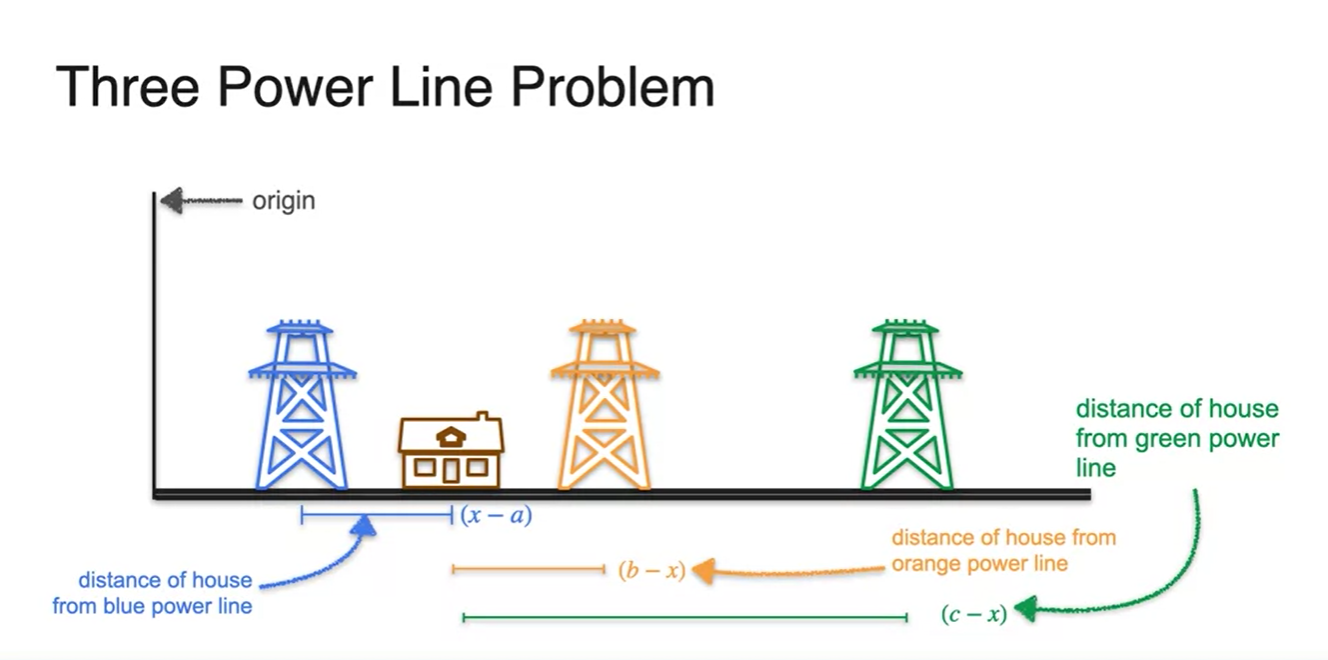
- 각 area의 합이 최소가 되는 지점 는 어디일까?
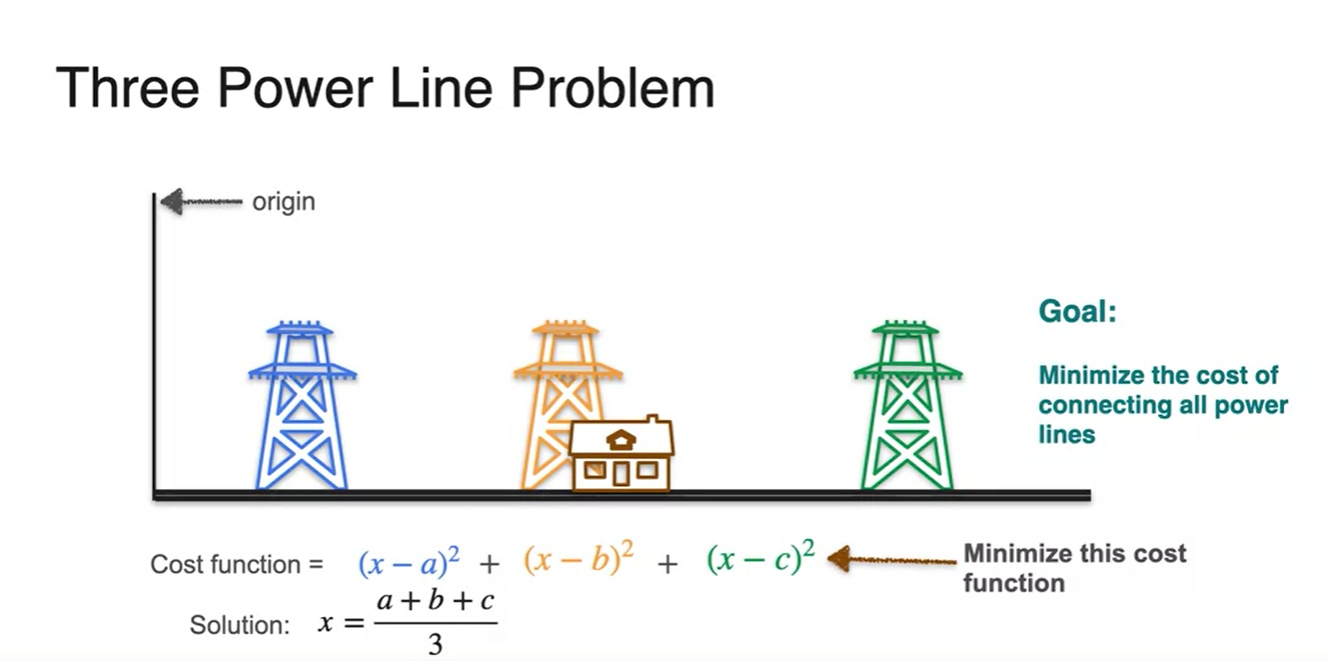
- 정답은 이다.
-
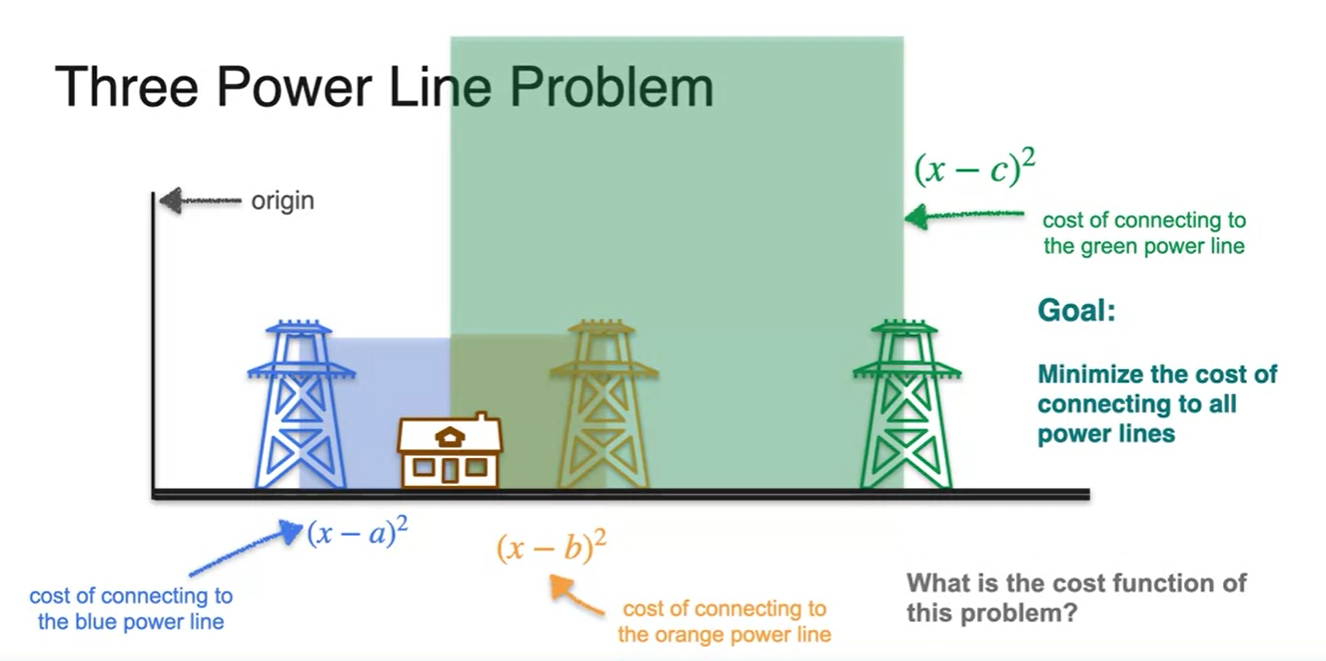
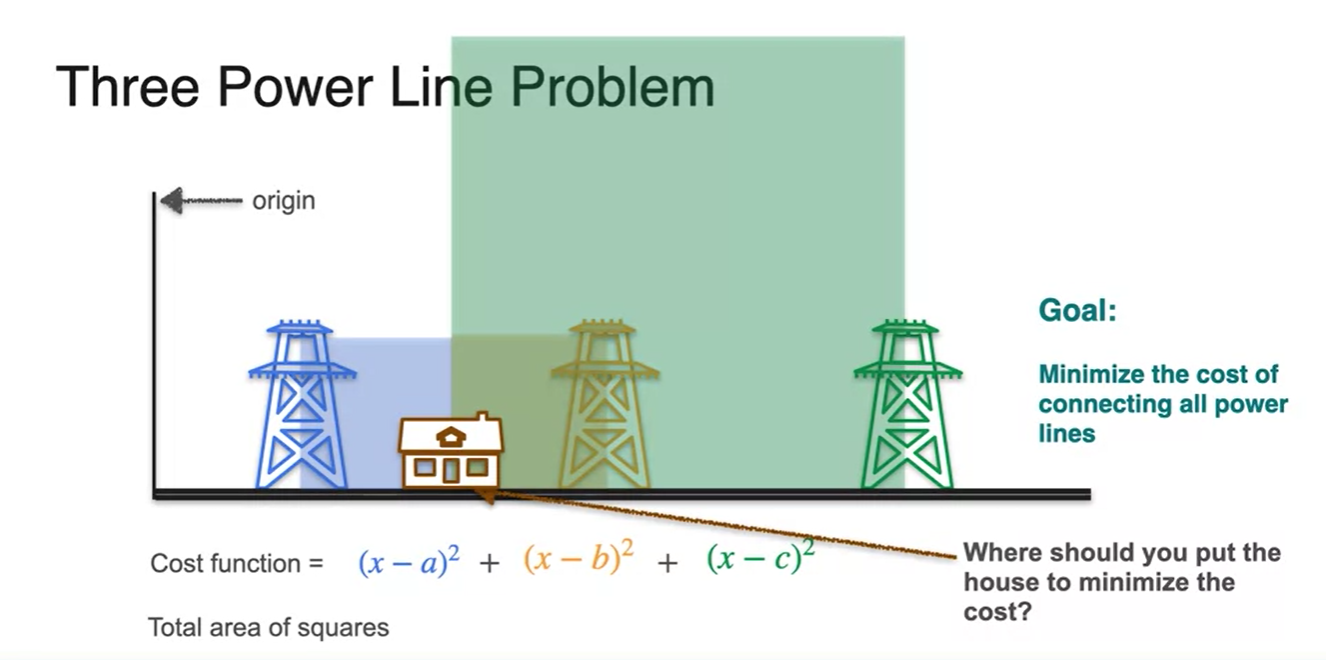
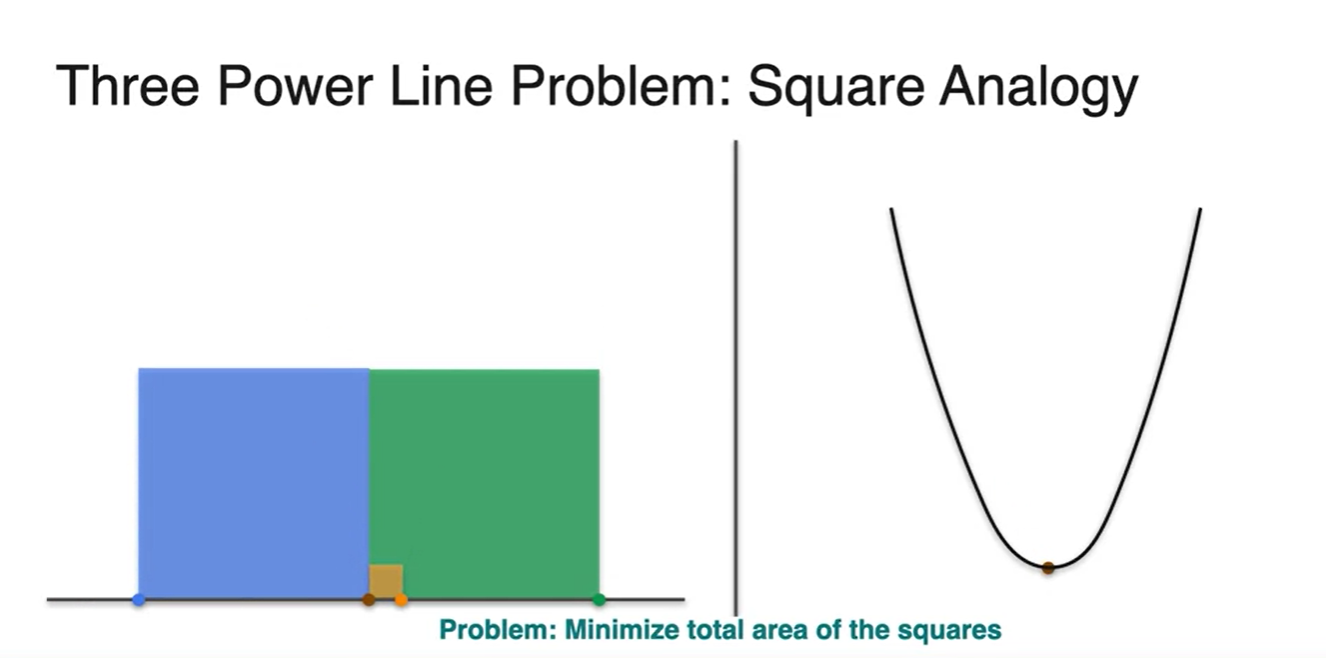
Graphical하게 표현하면 각 이차함수의 합이 cost function임을 알 수 있고,
- 각 수식의 합은 역시 마찬가지로 검은색 line과 같은 이차 함수 형태를 띤다.
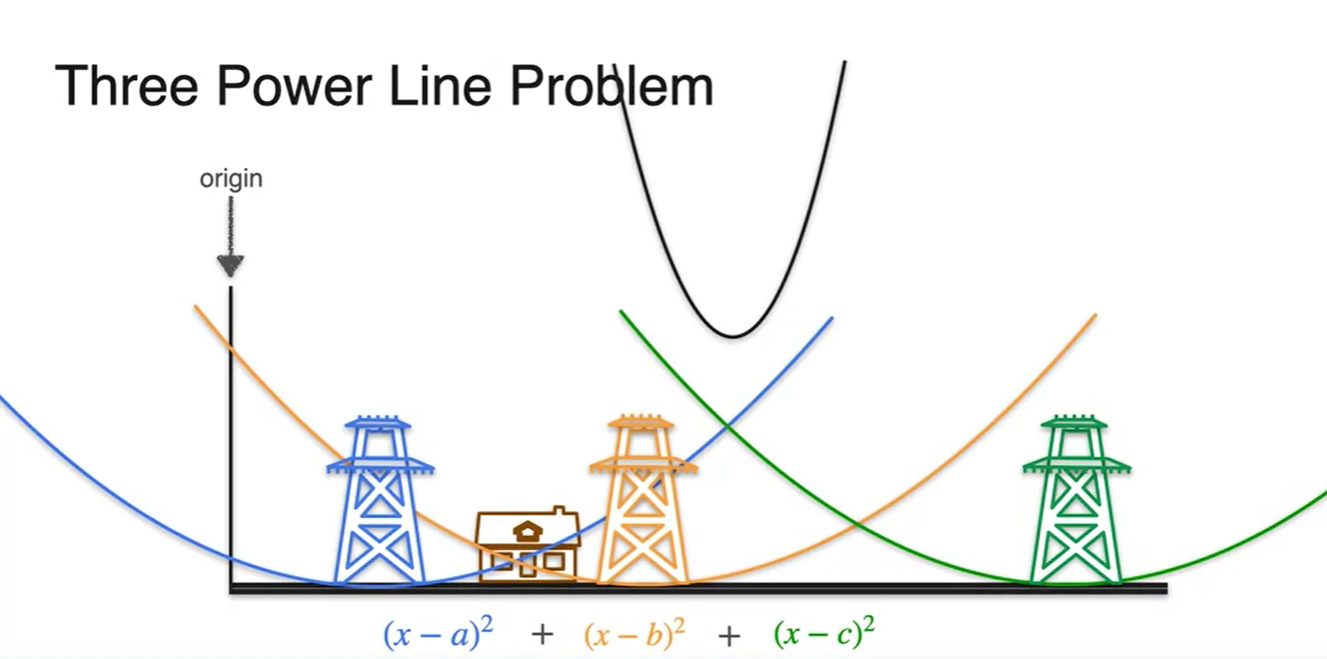
- 로 미분하여 slope가 0이 되는 지점을 찾아보면 정답을 알 수 있다.
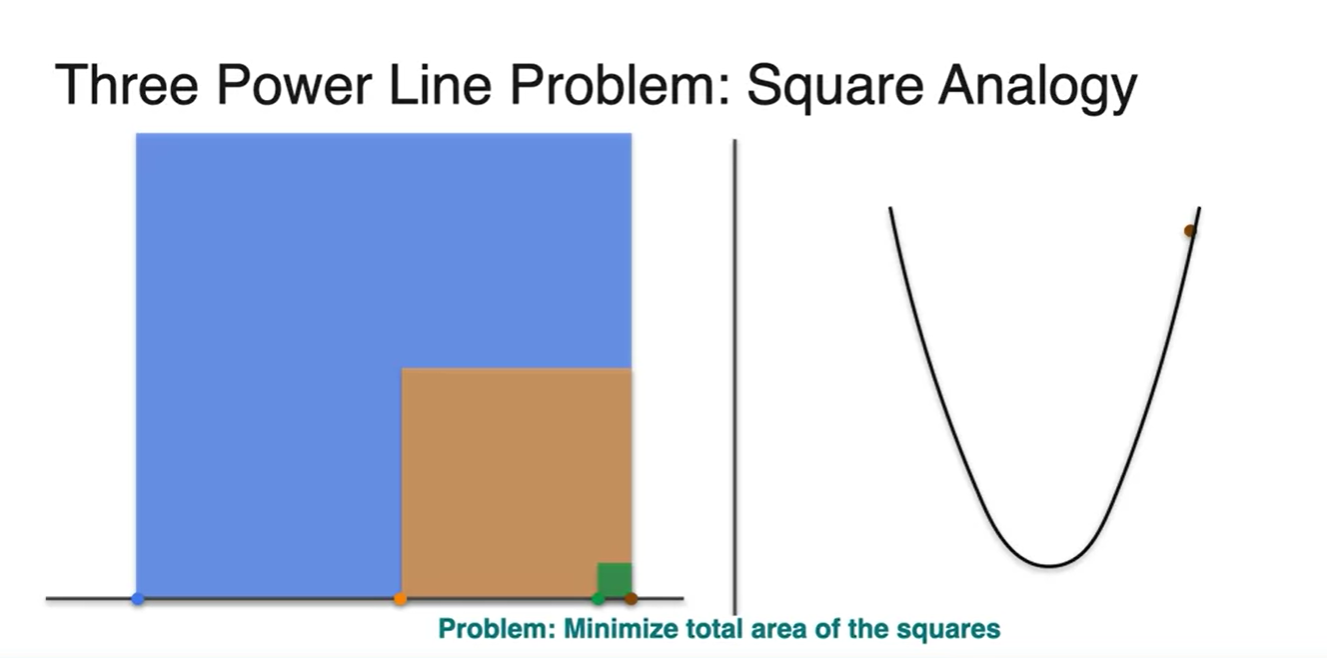
- 지금까지 우리는 각 squares의 합을 minimize하는 Square Analogy로 최적의 값을 추정해 보았다.
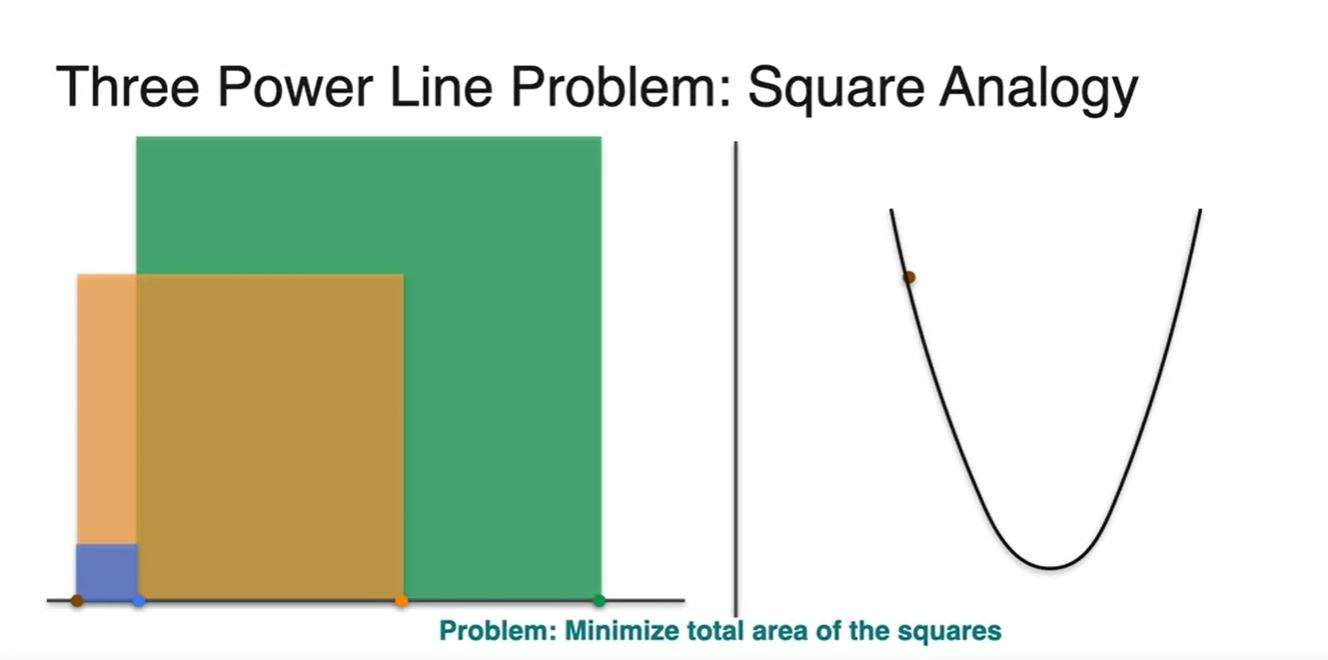
- 의 값에 따른 square area의 면적과 그래프 위의 점을 비교해보자.
-
data point의 개수가 개일 때로 일반화하면
-
cost function은 각 distance 제곱의 합이며 solution은 distance의 합을 평균낸 것이라고 할 수 있다.
-
이는 실제 머신러닝 optimization에서 매우 중요한 개념으로 차지할 예정이다.
-
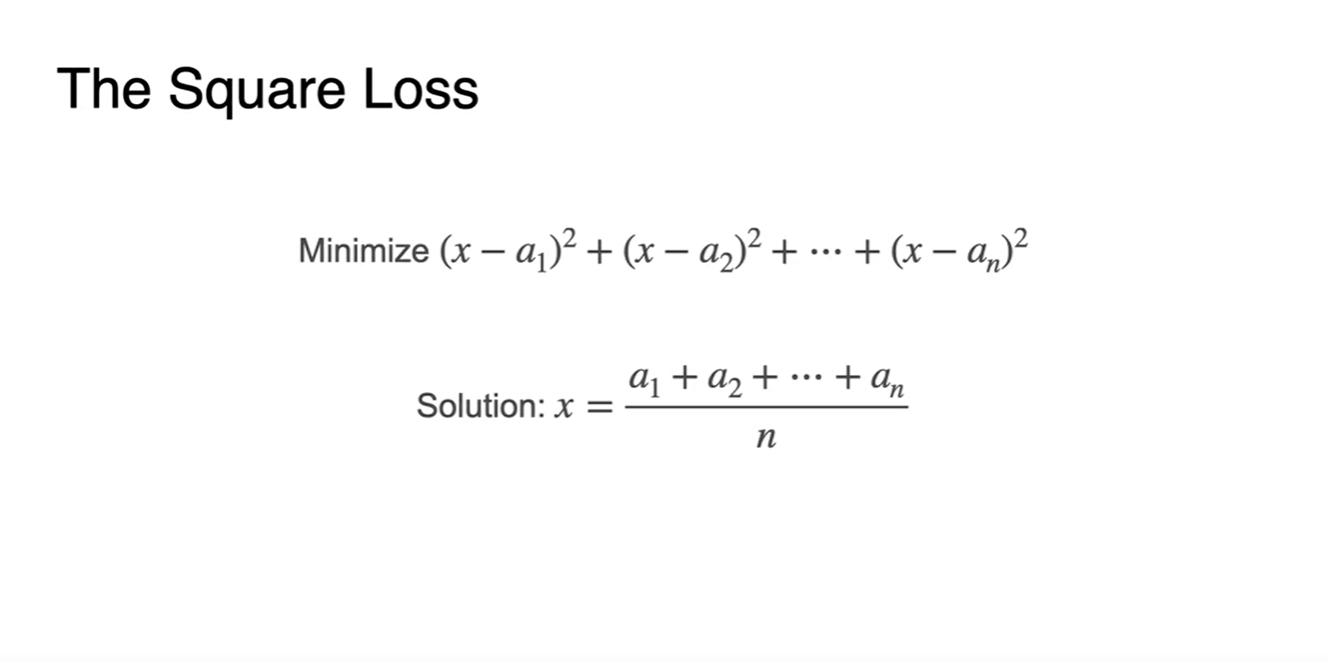
Optimization of log-loss - Part 1
-
세 가지 버전의 Coin 확률 set이 있다고 하자.
- H가 많이 나올수록 이긴다고 할 때, 이 중 가장 이길 수 있는 확률이 높은 조합은 무엇인가?

-
정답은 Coin 3 조합이다.
- 10번의 동일한 횟수로 던졌다고 할 때, 가장 큰 확률이 여러 번 나타난 최종 확률 곱이 가장 크기 때문이다.
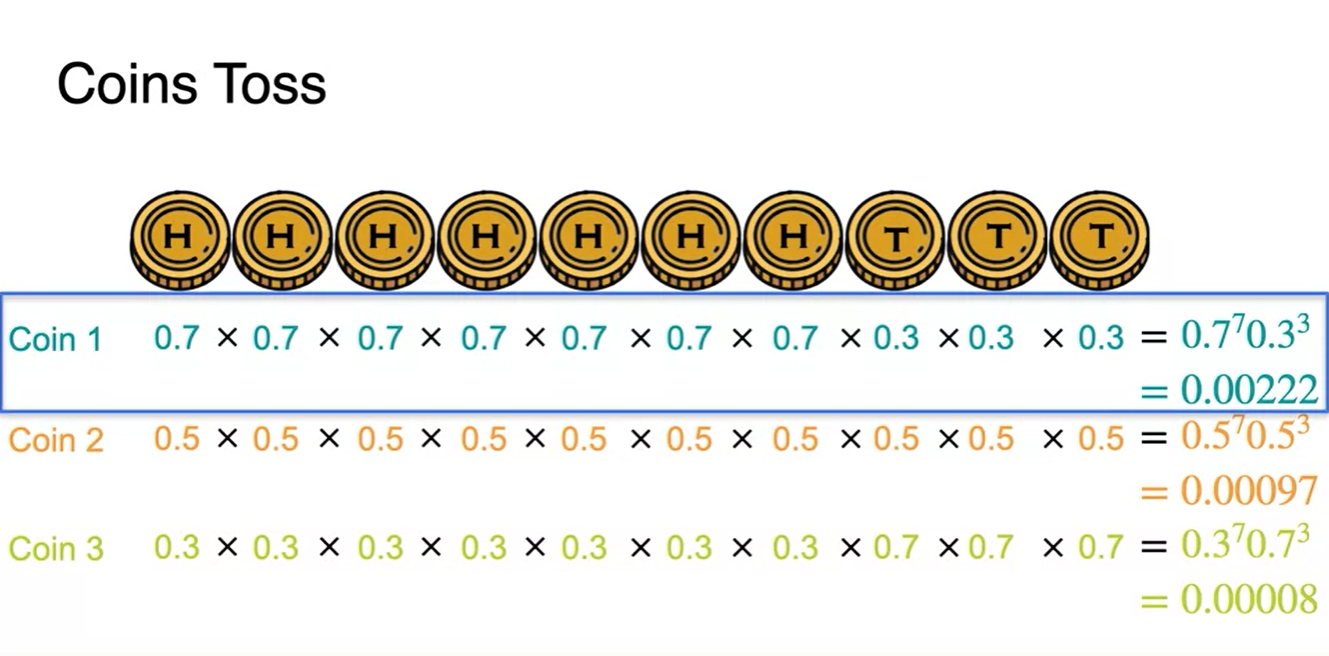
-
H가 나올 확률을 , T가 나올 확률을 라고 하자.
- 그러면 우리가 이길 수 있는 확률은 일 것이며, 우리의 목표는 이 확률 수식을 maximize하는 문제가 된다.

-
확률 를 변수로 하여 해당 수식의 최댓값을 찾기 위해 미분해보자.
-
Product rule과 Chain rule을 적용하여 찾은 확률 후보 는 0, 1, 그리고 0.7 이렇게 세 가지다.
-
그러나 일 때나 일 때에는 전체 maximize function이 0이 되므로 최대를 만족하지 않는다.
- 따라서 정답은 이다.
-


-
Maximize function 를 그냥 미분하지 말고, 를 씌운 뒤 미분해보자.
- 미분 이후의 최댓값 parameter 수치는 로 동일하며, 함수로 scaling 해주고 난 뒤의 미분이 훨씬 간편해 진다는 것을 확인할 수 있다.
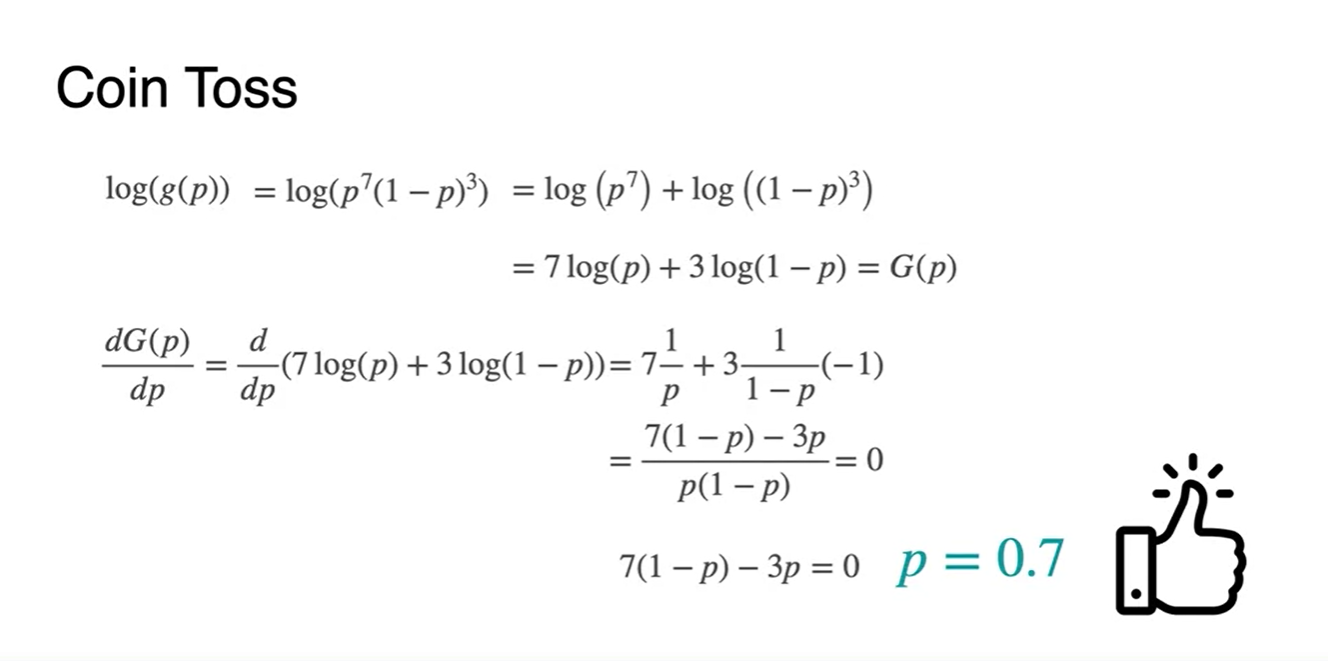
-
우리가 앞으로 하게 될 일은 이러한 maximize 함수 에 -를 붙여 minimize하는 작업이 된다.
- 이 방법론이 바로 Maximize Log-Likelihood Estimation(MLE)가 되는 것이다.
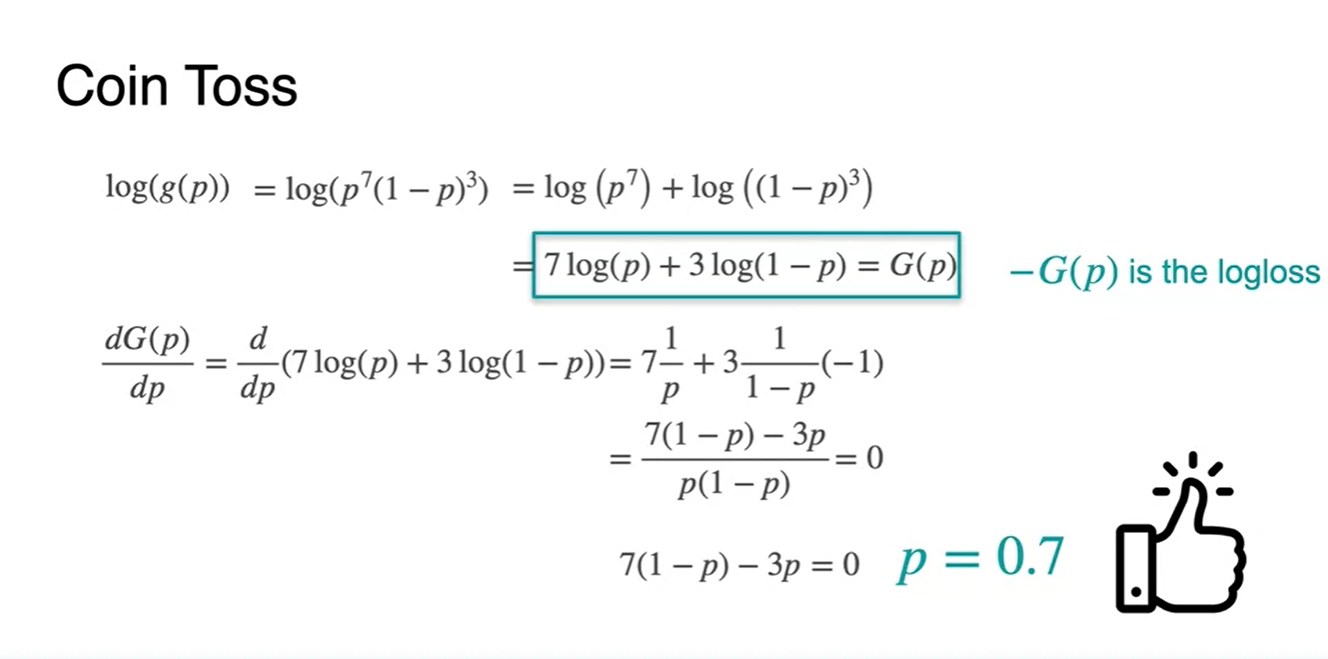
Optimization of log-loss - Part 2
-
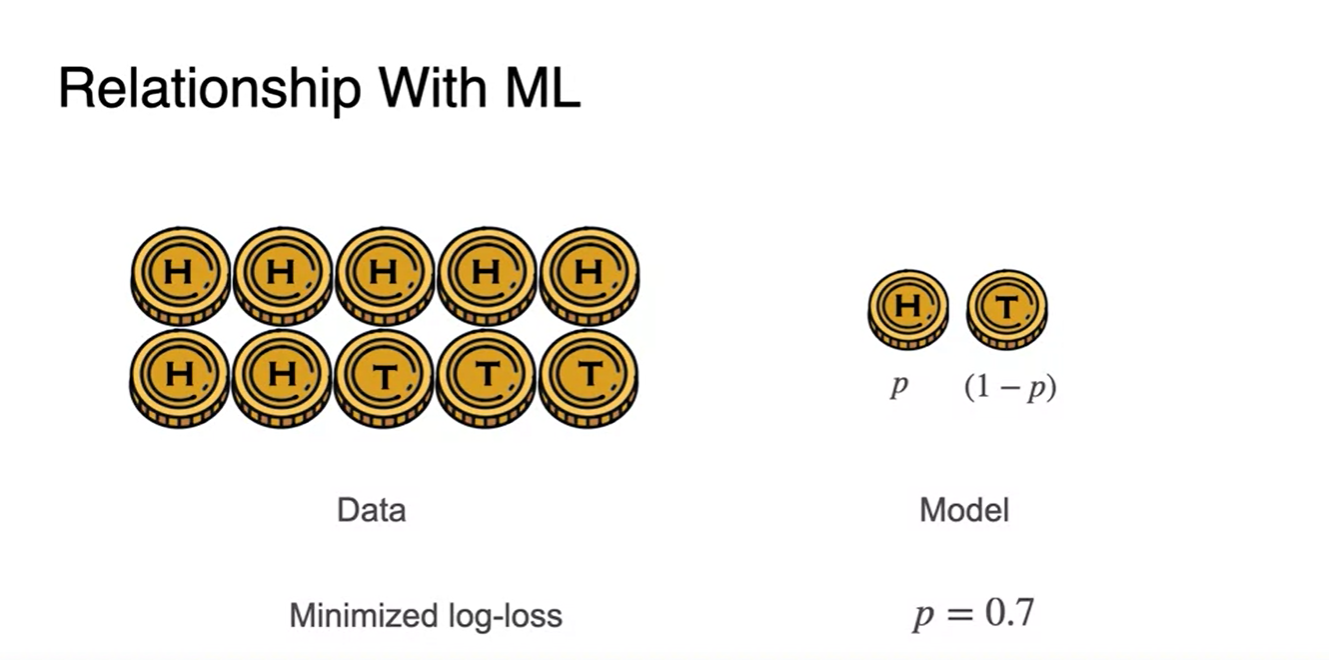
왼쪽에 놓인 coin들의 분포가 Data이고, Model은 각 data point가 발현되는 확률을 모델로 한다고 해보자.
- 우리가 해야할 일은 log-loss를 줄이는 일이며 그 결과, 가장 그럴듯한(최대화) 모델을 만들기 위해서는 이어야 한다는 정답을 얻었다.
-
그렇다면 어째서 log 함수여야 하는가?
-
아래와 같이 data 분포가 다양해진다면 cost function은 각 확률 값들을 모두 곱한 값이 된다.
-
곱셈의 미분은 product rule을 적용해야 해서 매우 복잡하다.
- 따라서 곱셈을 덧셈으로 바꿔줄 수 있는 log 함수를 사용하는 것이 훨씬 간편하고 계산 효율적이다.
-

-
뿐만 아니라 확률값은 항상 0과 1사이의 값을 가지므로 매우 tiny한 값이라는 특징이 있다.
- 이 때문에 계속해서 곱해주는 것보다 더해줌으로써, 컴퓨터가 계산 가능한 범위에 놓아주려는 의미가 있다.

