[MMD] Calculus for Machine Learning and Data Science Week 2
Week 2 - Gradients and Gradient Descent
Lesson 1 - Gradients
Introduction to Tangent planes
-
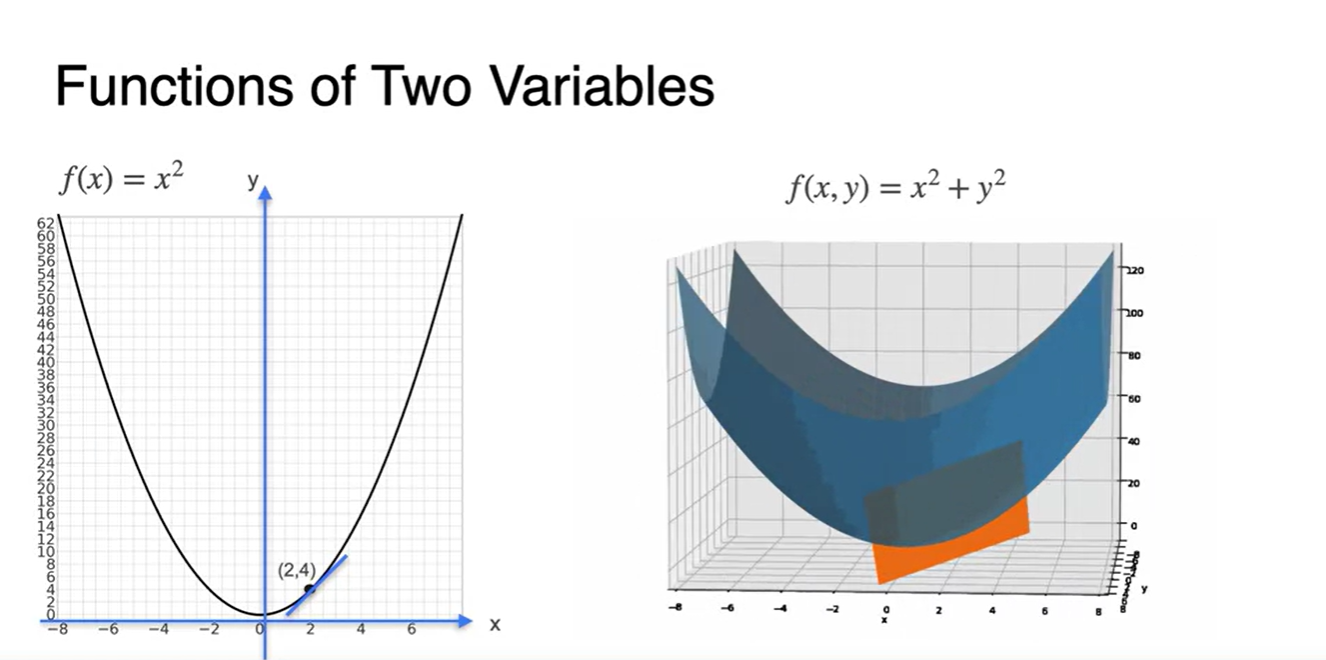
의 그래프에서 (2, 4)를 지나는 tangent line을 그리면 왼쪽 그림과 같았다.
- 의 그래프는 오른쪽 그림과 같이 3차원 공간에 펼쳐지고, (2, 4)를 지나는 tangent function은 line이 아닌 plane으로 형성된다는 점을 알 수 있다.
-
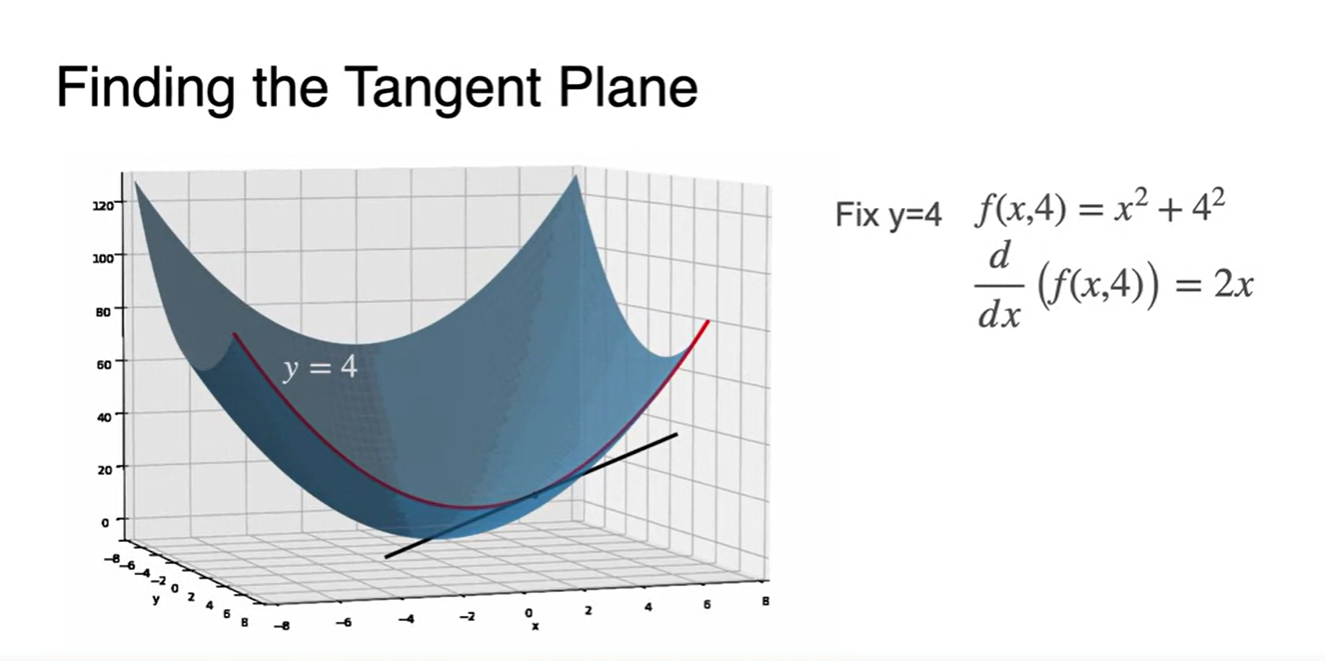
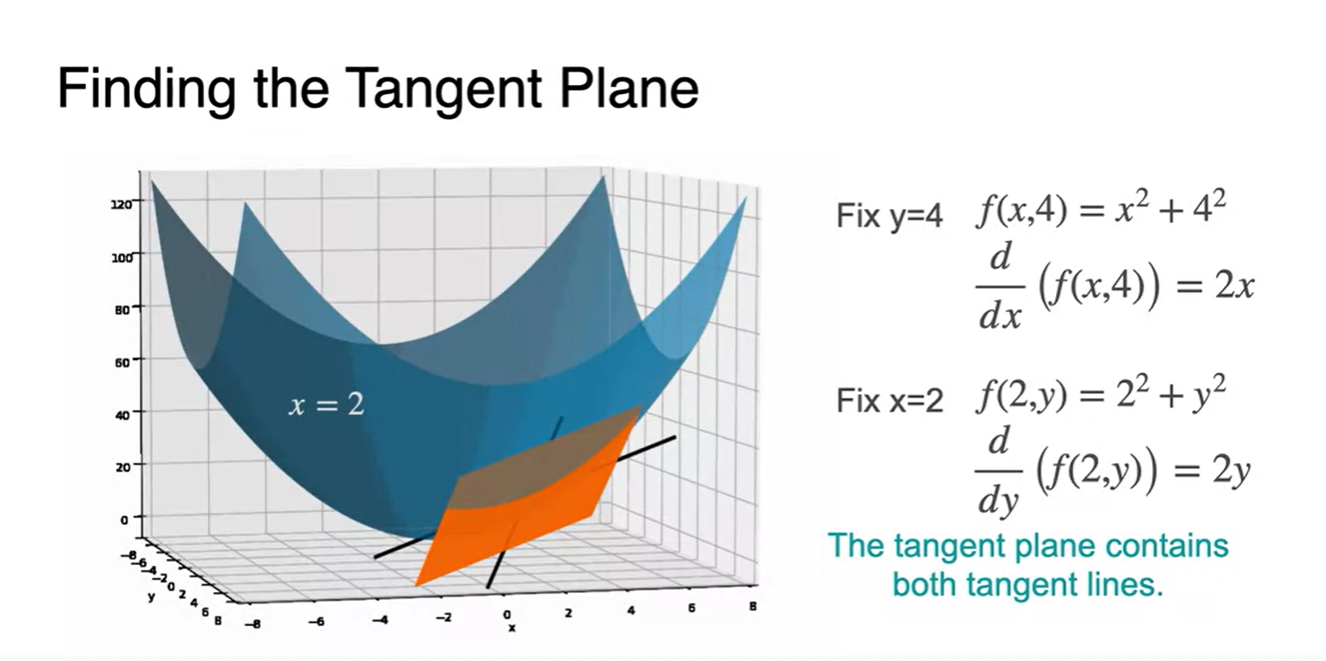
Tangent Plane을 찾는 방법은 다음과 같다.
-
로 결정한 공간은 parabolic line이 되며 이 때의 derivative는 로 표현된다.
-
로 결정된 공간 역시 parabolic line이 형성되며 이 때의 derivative는 다.
-
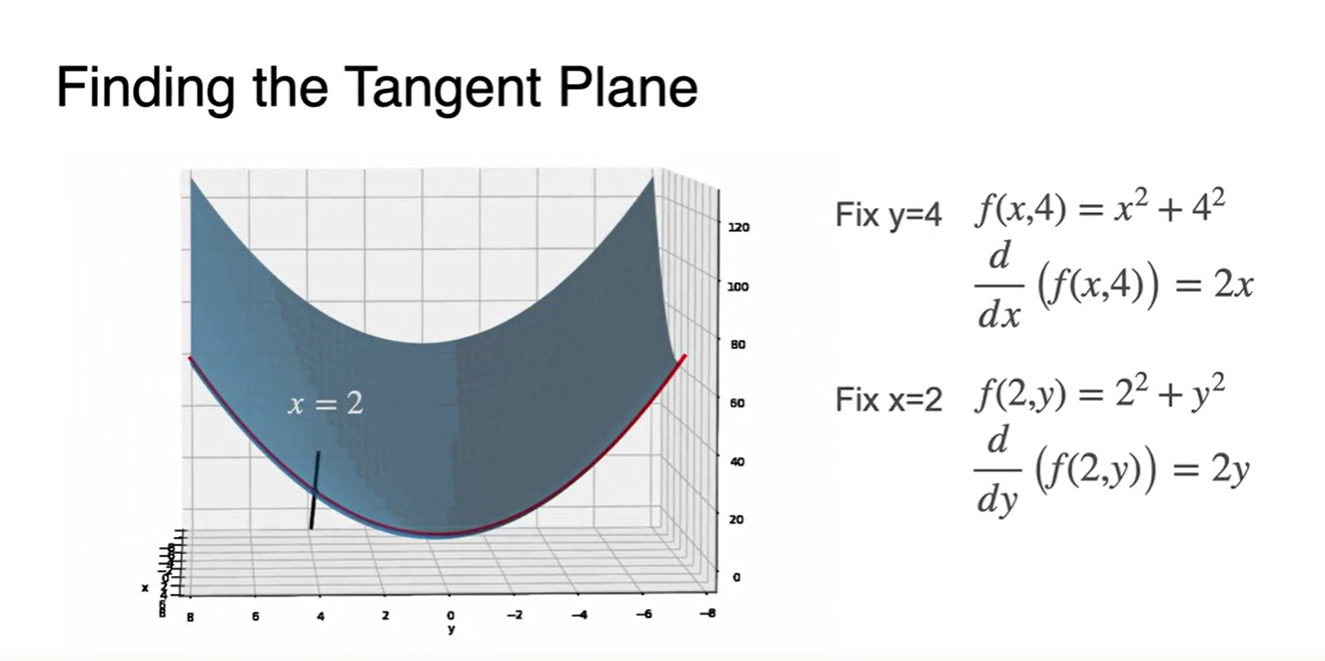
- 그러면 이제 두 선이 교차하는 plane을 찾을 수 있으며 이를 tangent plane이라 한다.
Partial derivatives - Part 1
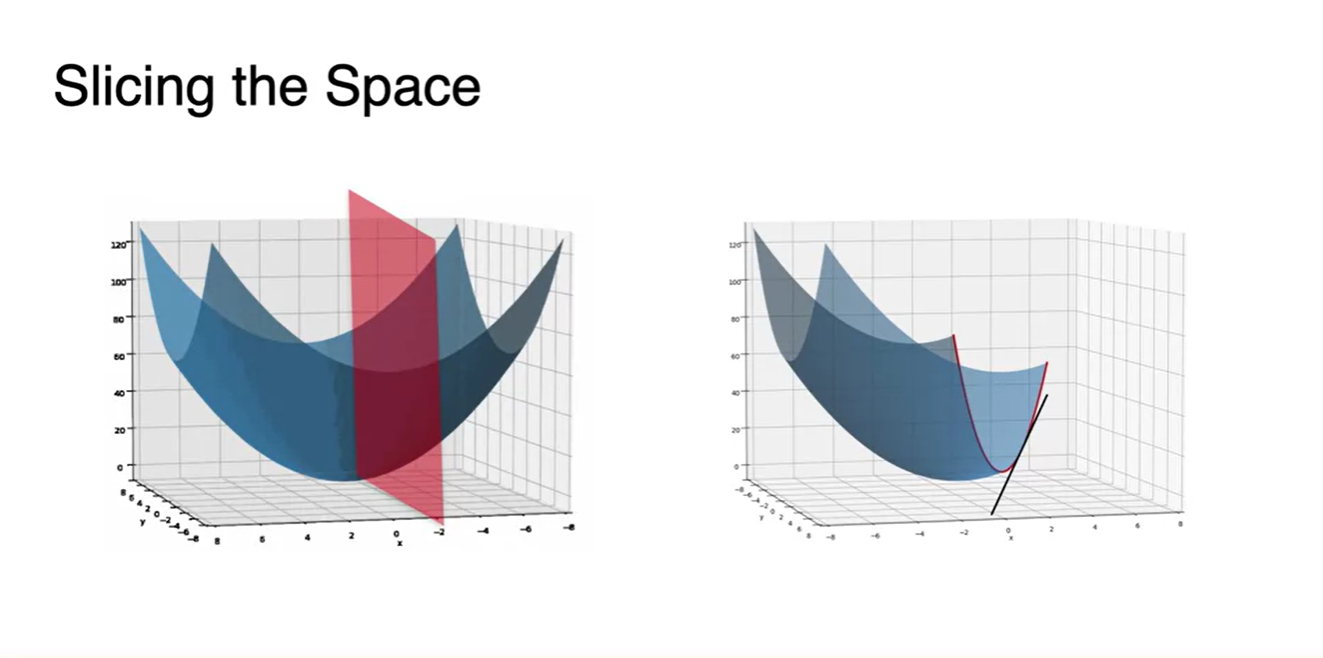
- Plane을 Slicing하는 방법은 특정 값을 constant로 지정하는 것이었다.
-
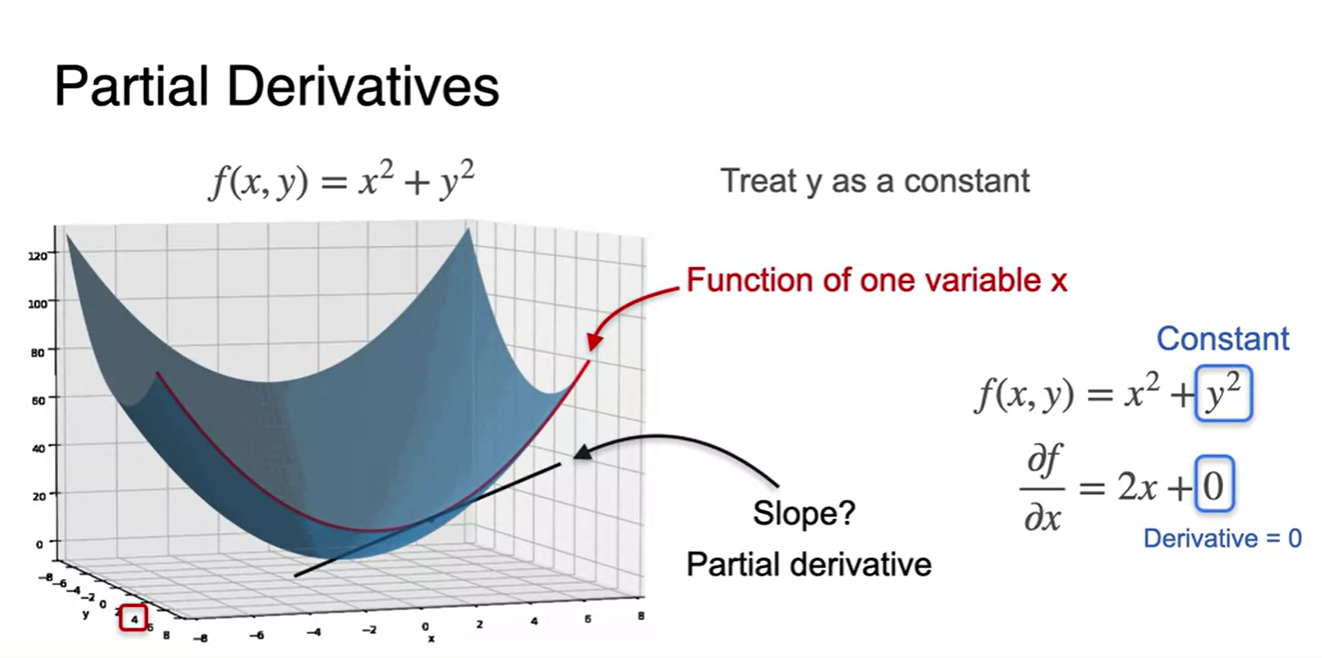
어떠한 값을 constant로 취급했을 때, function은 변수 에 대해서만 관련 있어지는 것을 확인할 수 있었다.
- Partial Derivatives(slope)는 다른 변수들을 constant로 취급했을 때의 미분을 가리키며 기호로는 로 쓴다.
- 변수가 와 2개만 존재할 때, partial derivatives는 아래 그림과 같이 두 개로 나뉠 수 있다.
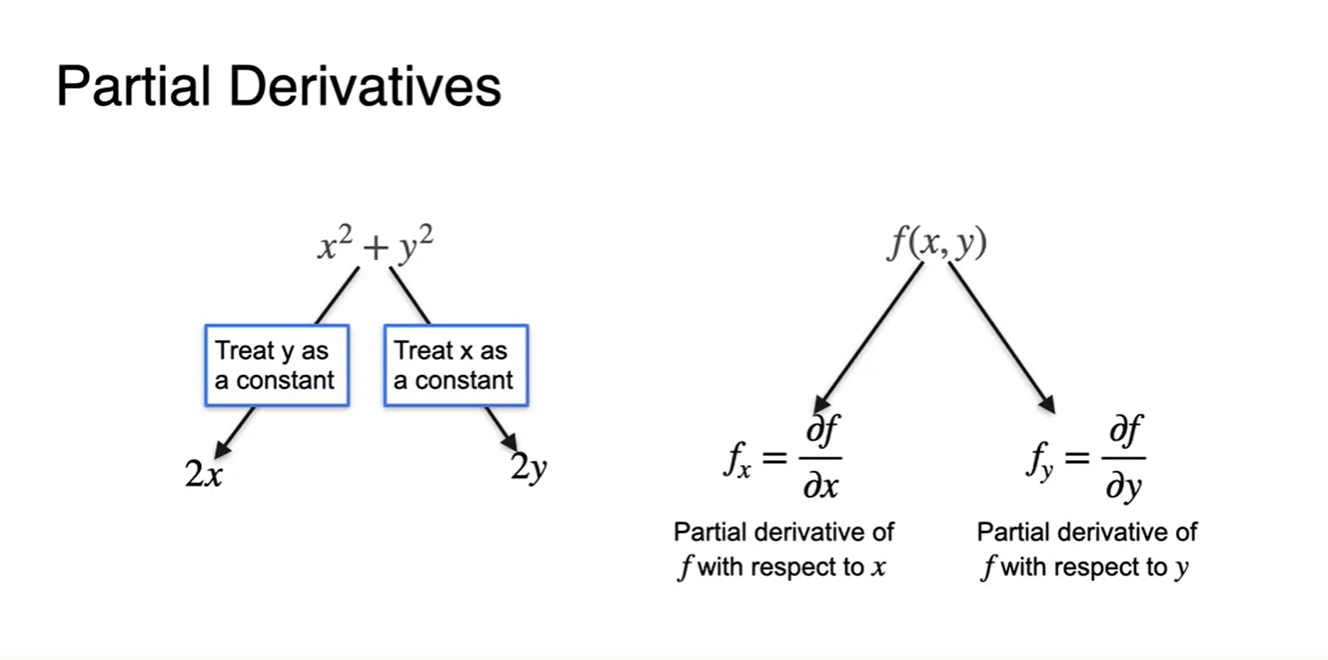
- Notation은 다음과 같이 & 로 표현하며 우리는 각각의 변수에 따른 편미분 값을 찾아야 한다.

-
우리는 두 가지 step을 밟을 수 있다.
- Derivative 변수 를 제외한 모든 변수를 constant로 취급한다.
- 기존의 normal한 방법을 그대로 사용하여 변수를 미분한다.
-
위의 방법론을 적용한 와 는 각각 와 다.


-
, 가 곱해진 형태의 function 또한 다른 변수를 masking하여 편미분한다.
- 차례로 를 constant로 두었을 때의 상황이랑 를 constant로 두었을 때의 상황을 편미분 한 결과다.


Gradients
-
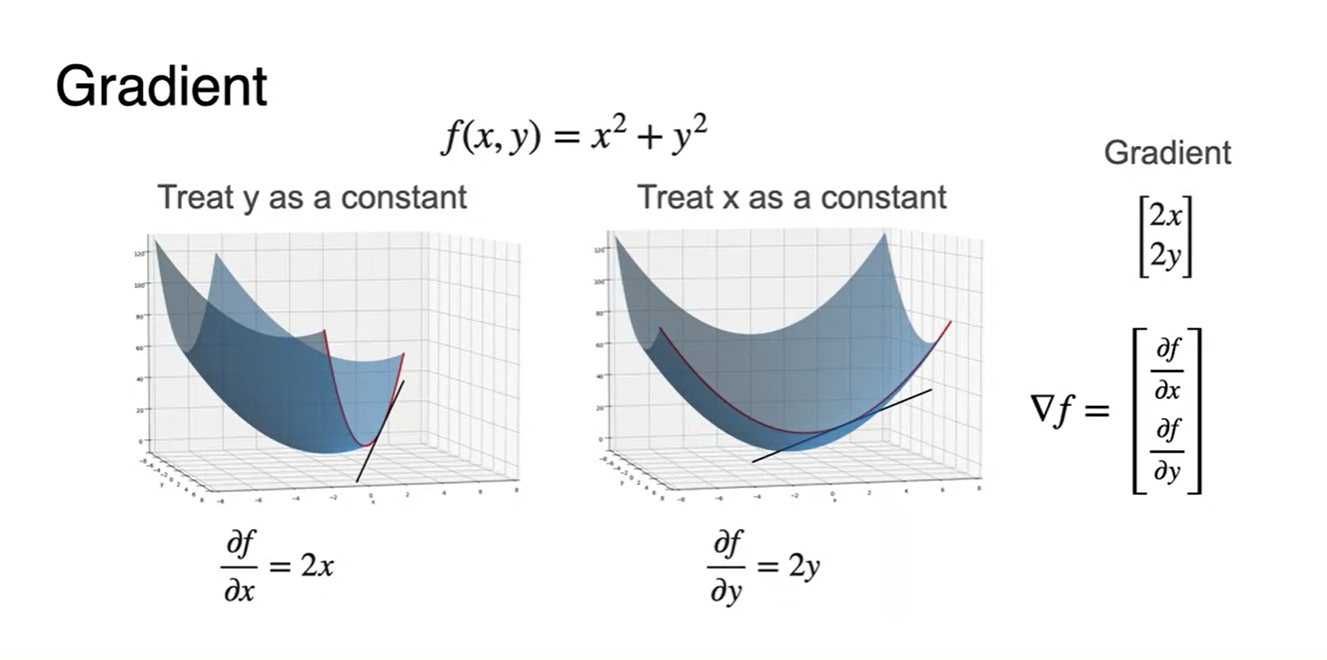
의 function을 변수별로 편미분하여 나타내면 하나의 긴 vector 꼴로 concaternate하여 나타낼 수 있다.
- 17변수가 있다면 17 길이의 vector로 표현하는 것이다.
-
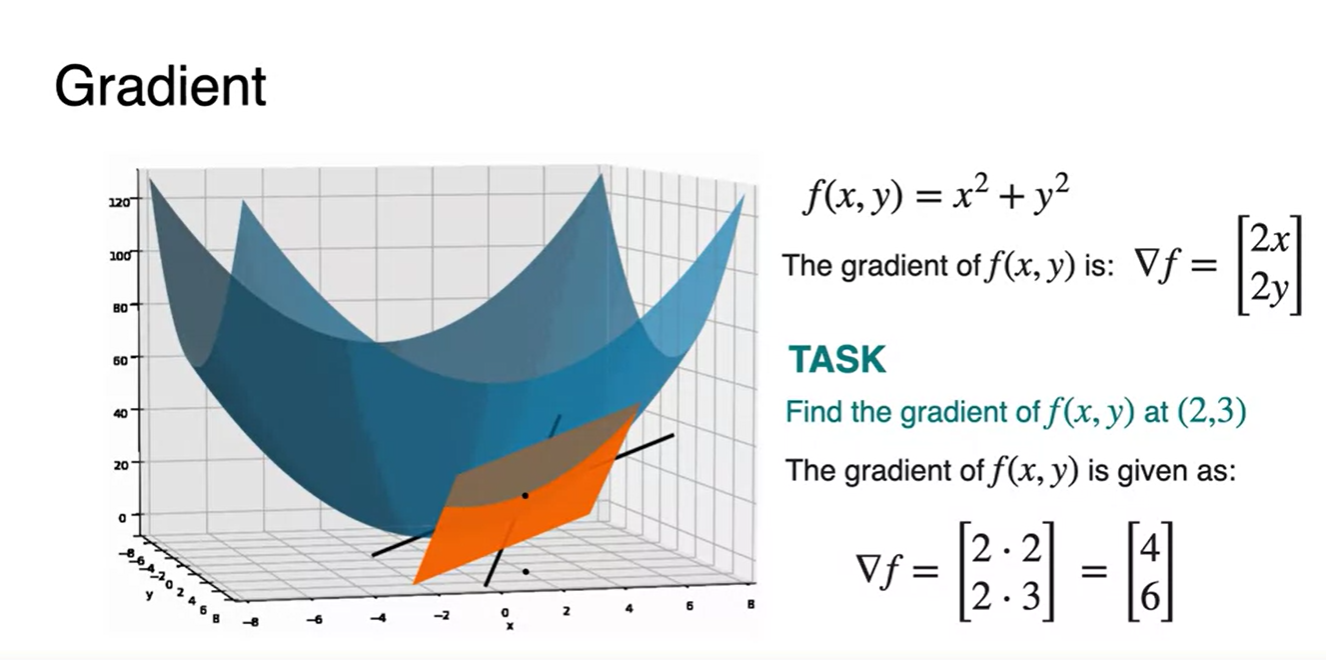
(2, 3) 지점에서의 gradient를 구하는 방법은 각 변수별로 편미분 한 와 를 대입하는 것으로 해결할 수 있다.
- Gradient의 의미는 말 그대로 경사진 정도를 방향과 크기로 나타내는 것이다.
Gradients and maxima/minima
-
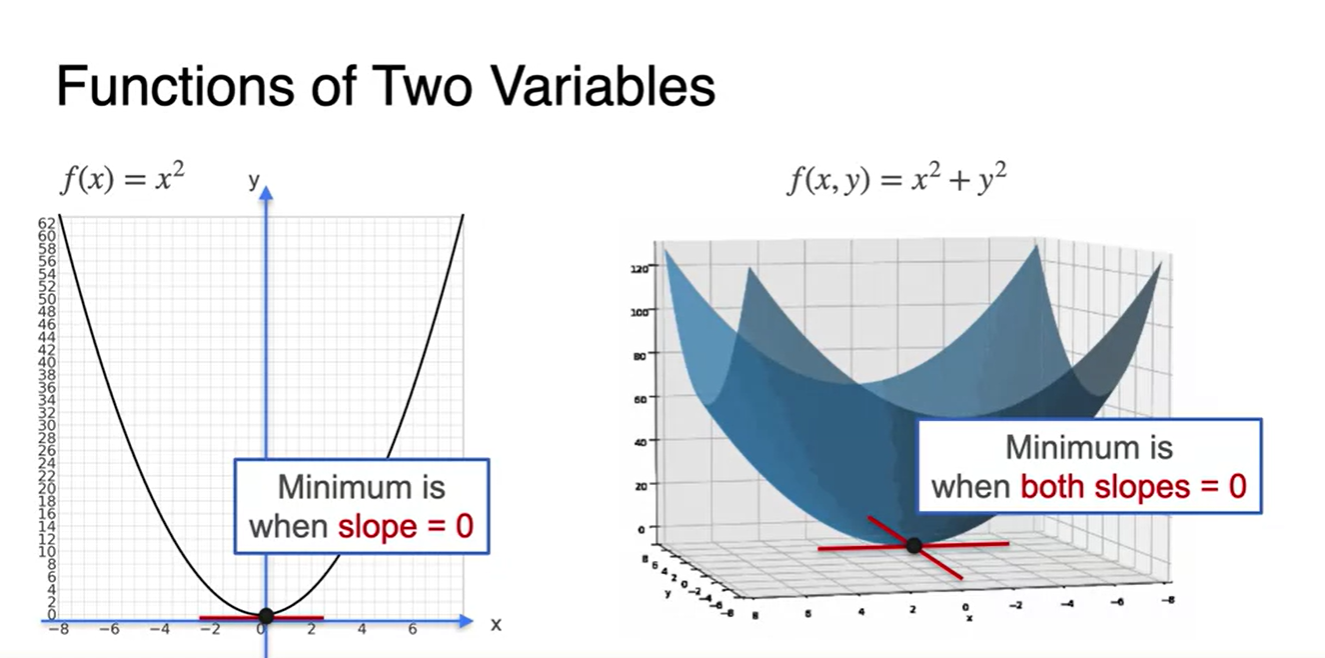
왼쪽 그림과 같은 변수가 하나인 function을 minimize하는 방법은 slope를 0으로 만드는 를 찾는 일이었다.
- 오른쪽 그림은 두 변수의 function으로 확장한 버전이며, 이 또한 slope를 0으로 만드는 와 를 찾는 일이 핵심이다.
-
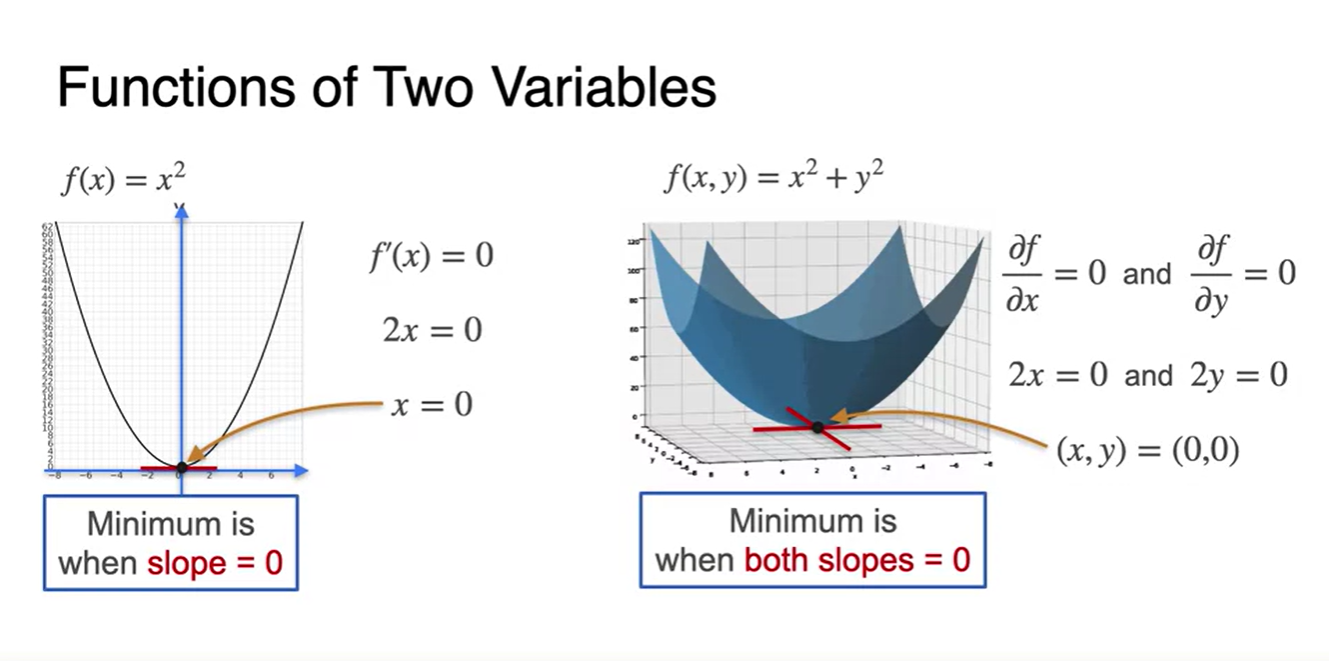
따라서 각 변수별로 편미분하여 각각의 derivative function이 0이 되는 와 를 찾아야 한다.
- 이러한 slope를 찾는 과정이 바로 전체 함수를 minimize하는 값을 찾아가는 과정이라고 볼 수 있다.
Optimization with gradients: An example
-
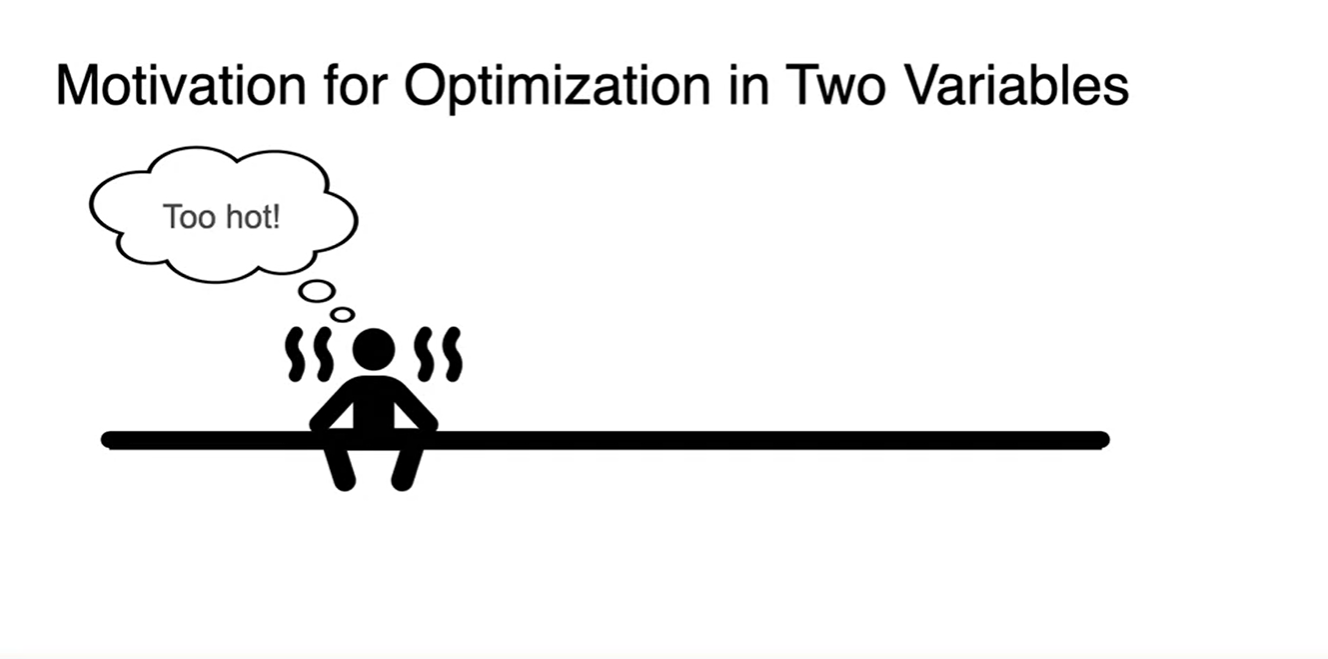
이전에 예시로 들었던 Sauna 문제를 생각해보자.
- 우리는 이 공간 내에서도 가장 차가운 지점을 찾아가야만 한다.
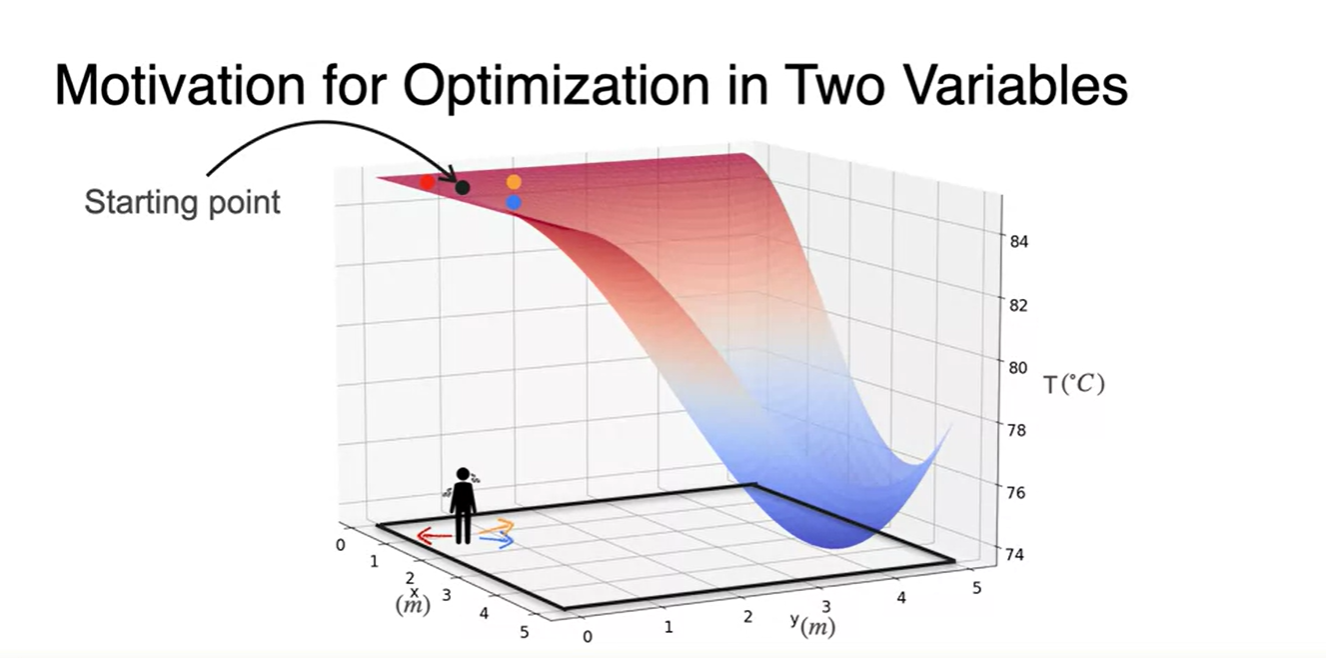
-
Starting point가 아래와 같이 여러 개라고 하면 여러 direction으로 뻗어나갈 수 있다.
- 다양한 direction들을 고려해보고, 결국 찾아가게 되는 방향의 경로는 점점 마지막 그림과 같다.
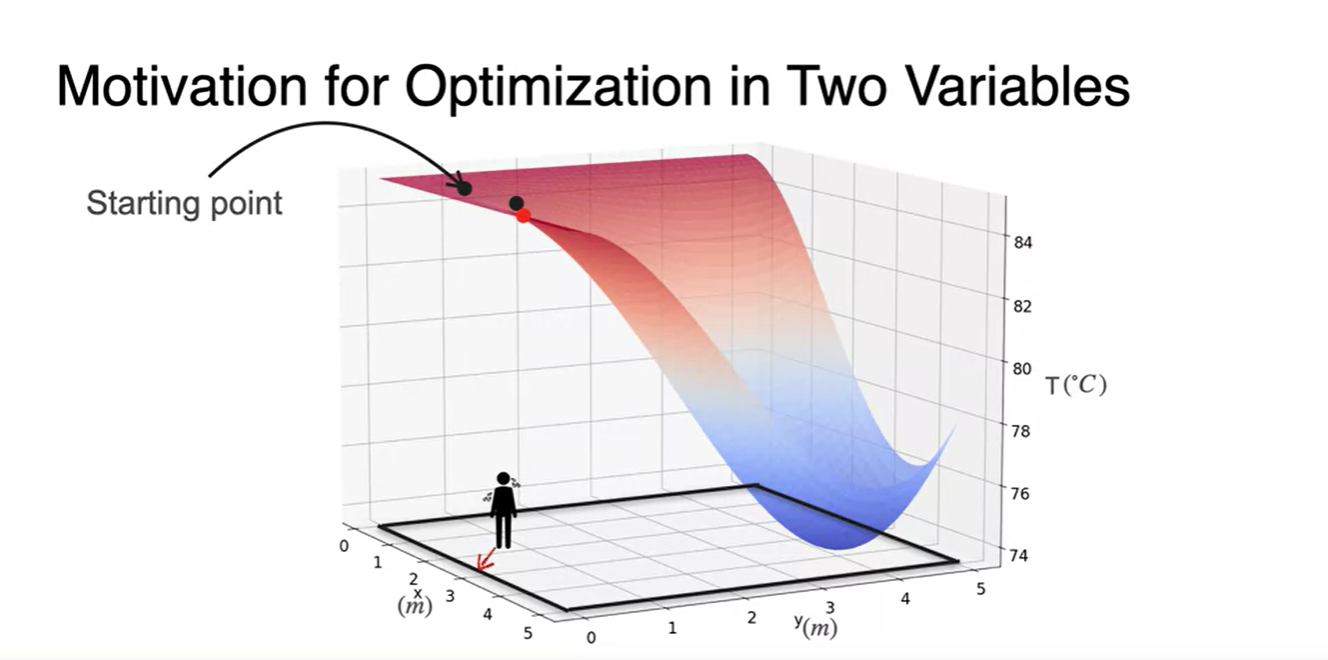
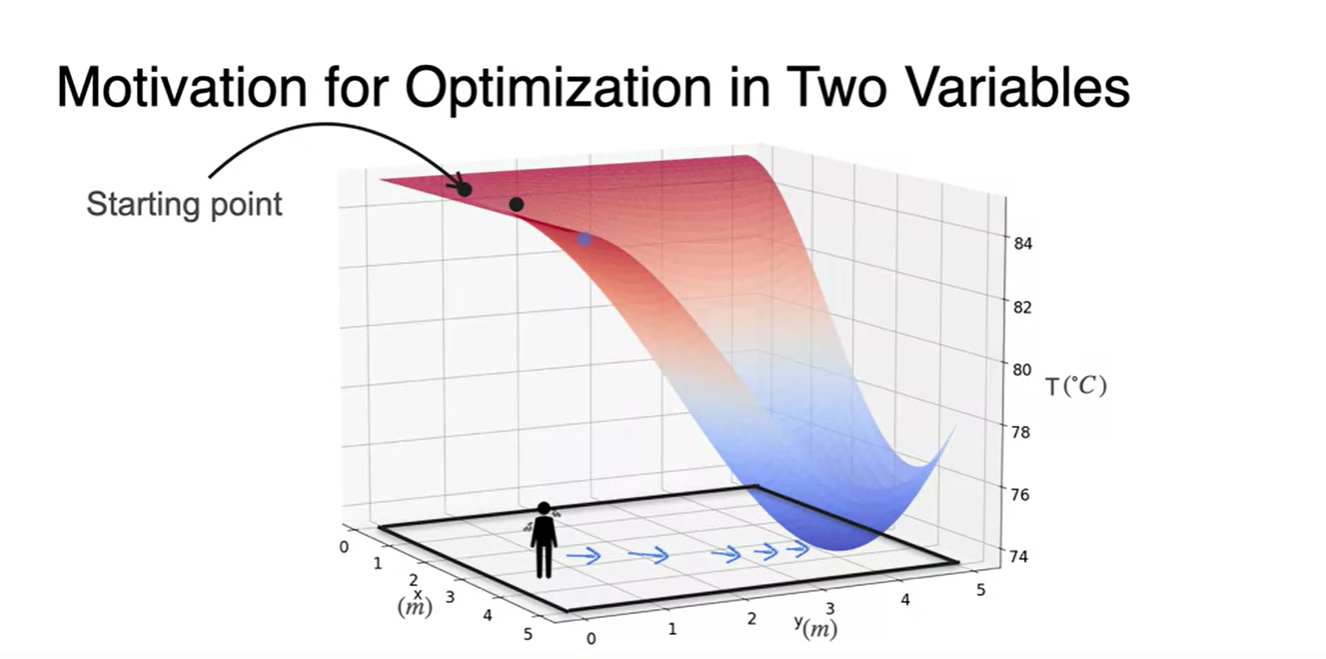
- 즉, 각 변수의 편미분을 0으로 만드는 (x, y) 지점이 해당 function의 최소 지점이다!
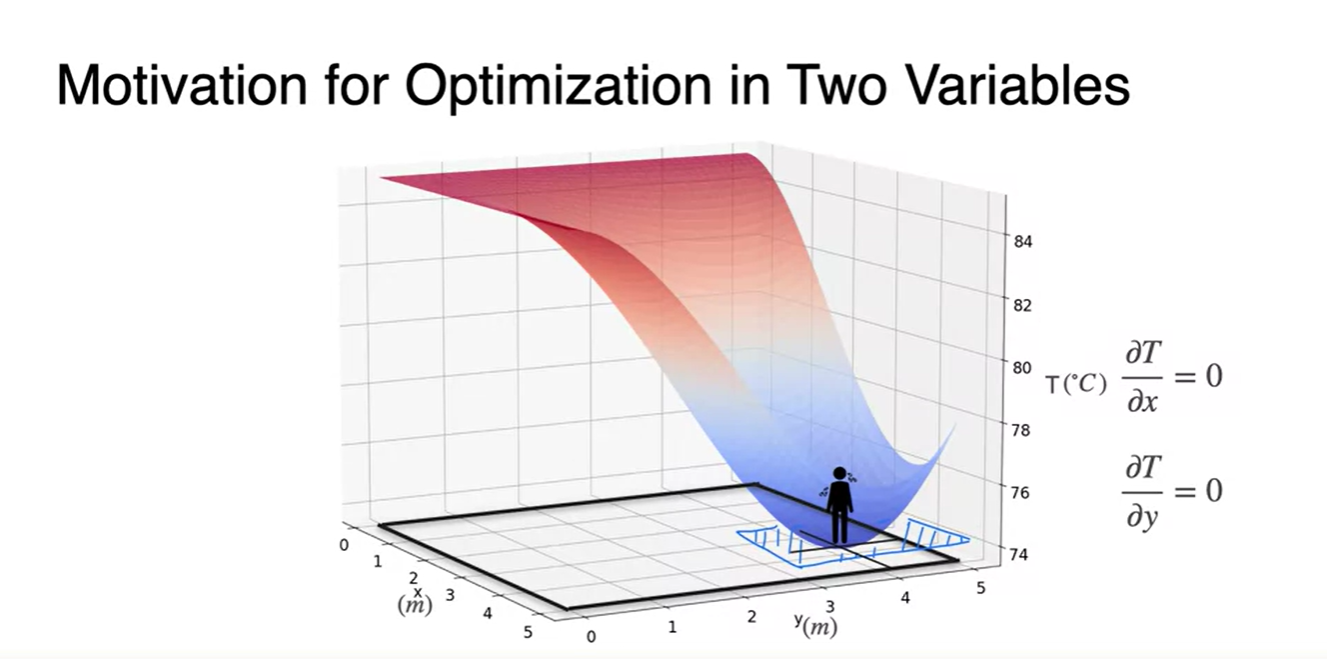
-
이 그래프의 function 꼴은 사실 매우 복잡하다.
- 와 변수로 각각 편미분 해보라.
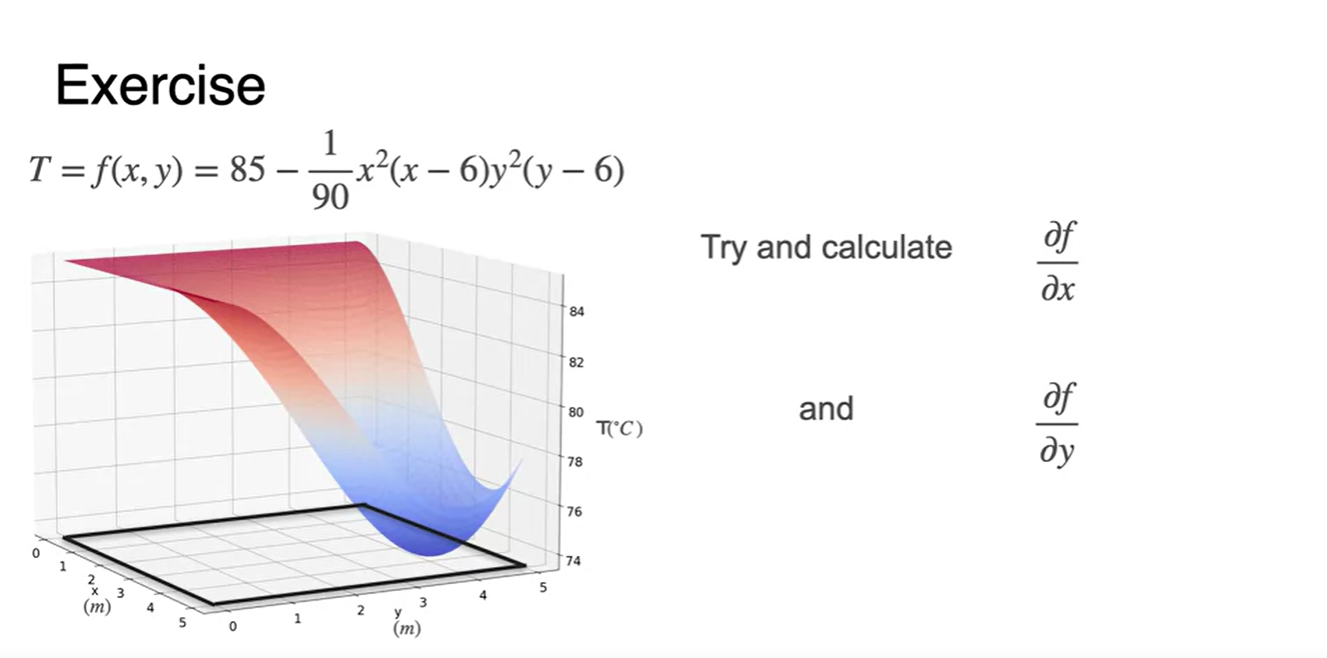
- 함수의 편미분을 0으로 만드는 최종 와 후보는 다음과 같다.
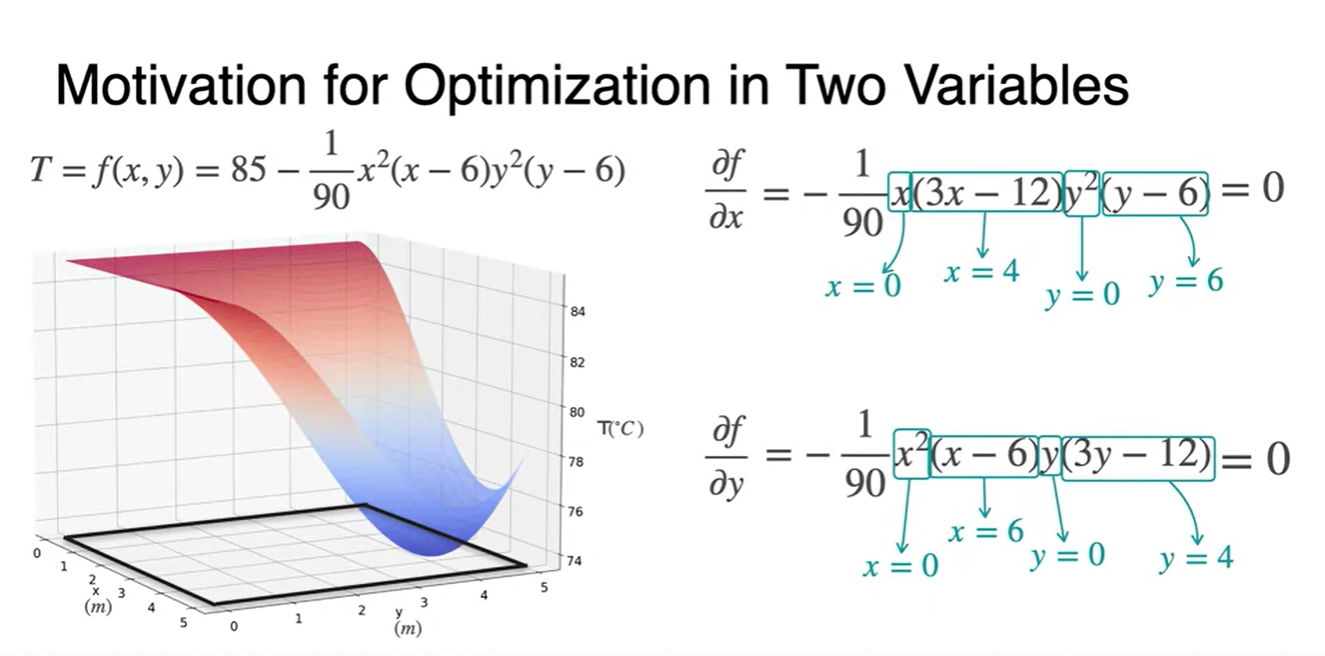
-
우리가 찾은 후보군들에 대해서 모든 가능한 조합을 만들어보고, 각 점을 대입해보라.
- 이 function을 minimum하게 만드는 (4, 4) 단 하나로 결정되었다는 것을 알 수 있다.
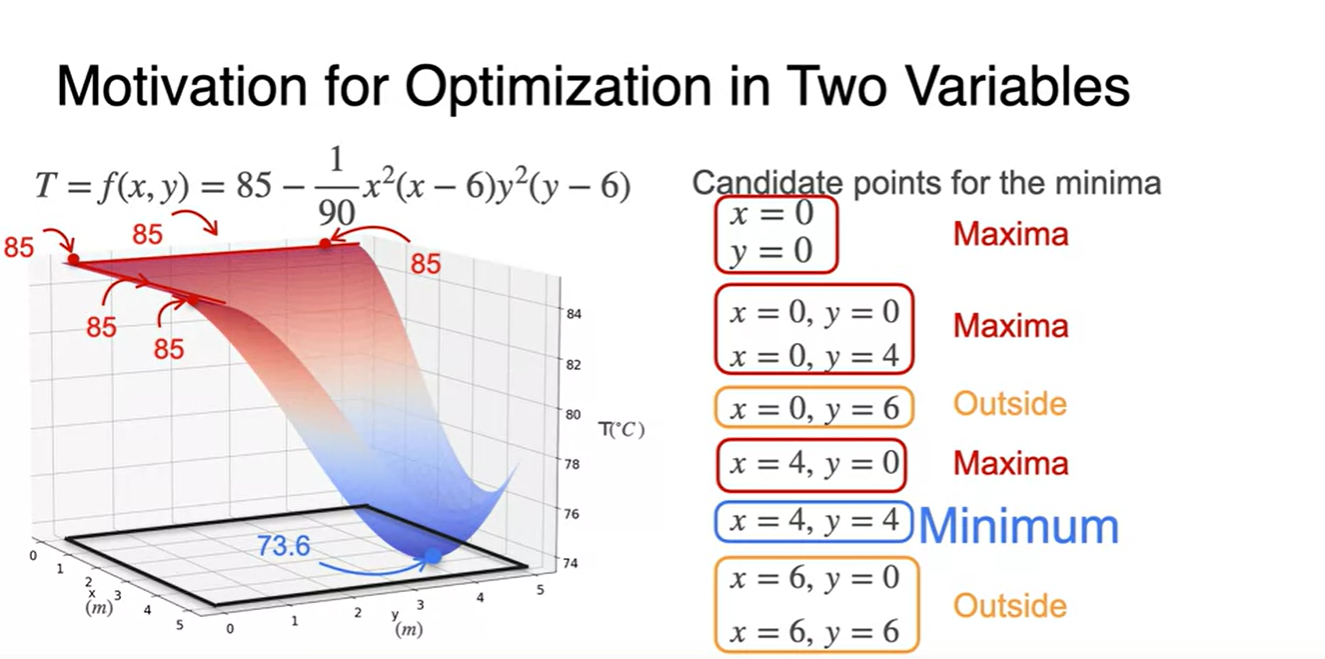
Optimization using gradients - Analytical method
-
세 전봇대의 좌표가 (1, 2), (2, 5), (3, 3)으로 주어진다고 해보자.
-
Linear Regression은 data point들의 연관성을 가장 잘 설명하는 하나의 line을 찾는 일이다.
- 이 수식이 weight와 bias를 포함한 이다.
-
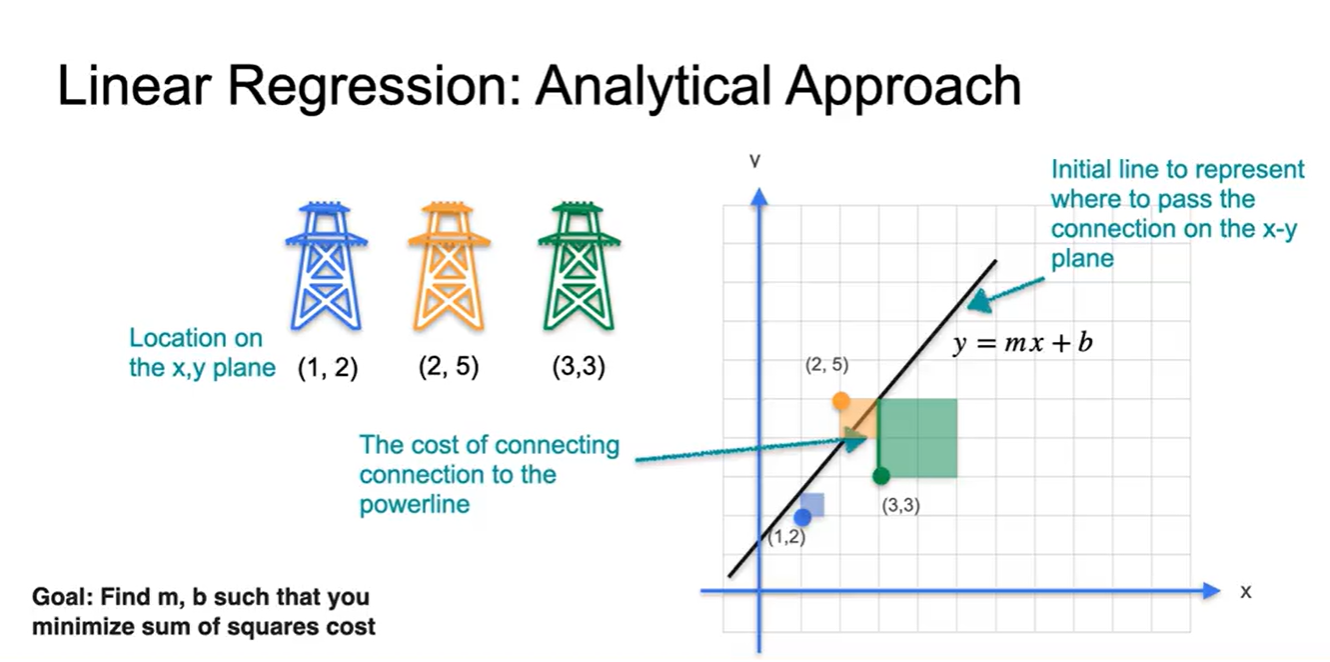
-
Data point의 좌표와 Linear Regression으로 예측한 line의 좌표를 고려해보자.
-
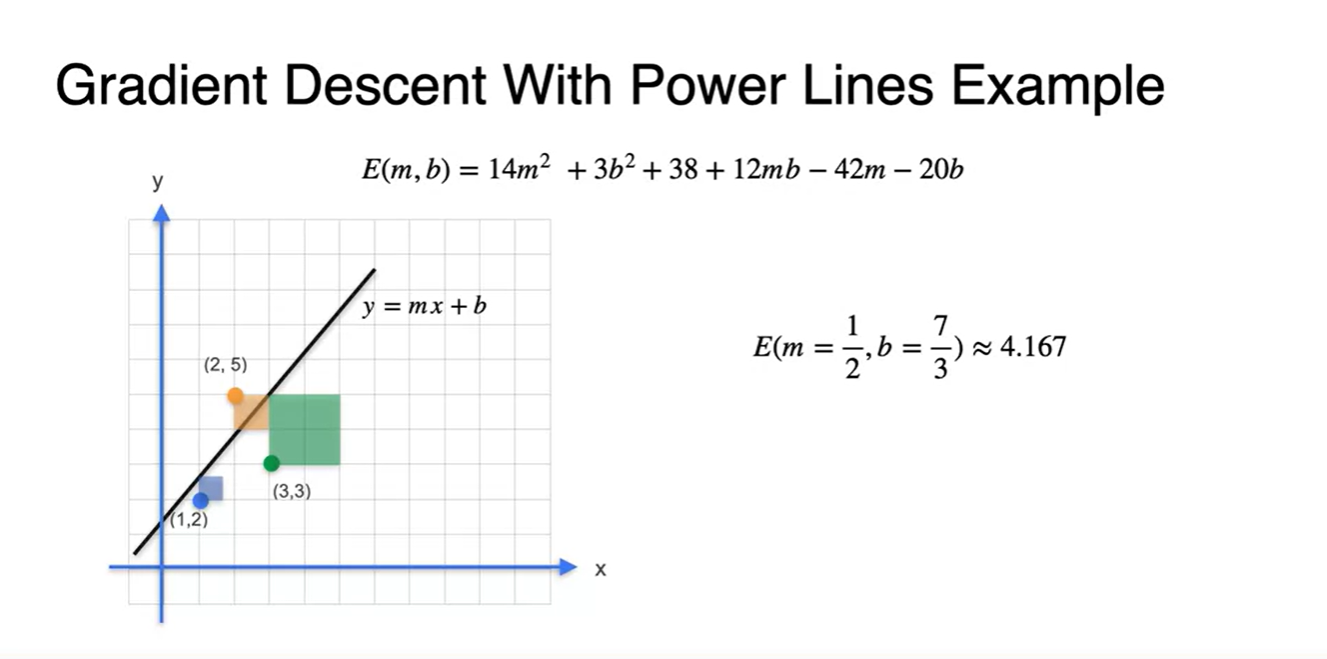
(두 값의 차이)의 제곱을 기하학적으로 표현해보면 아래와 같은 사각형의 합이 된다.
- 우리가 미분해야 할 Error function은 라는 것을 알 수 있다.
-
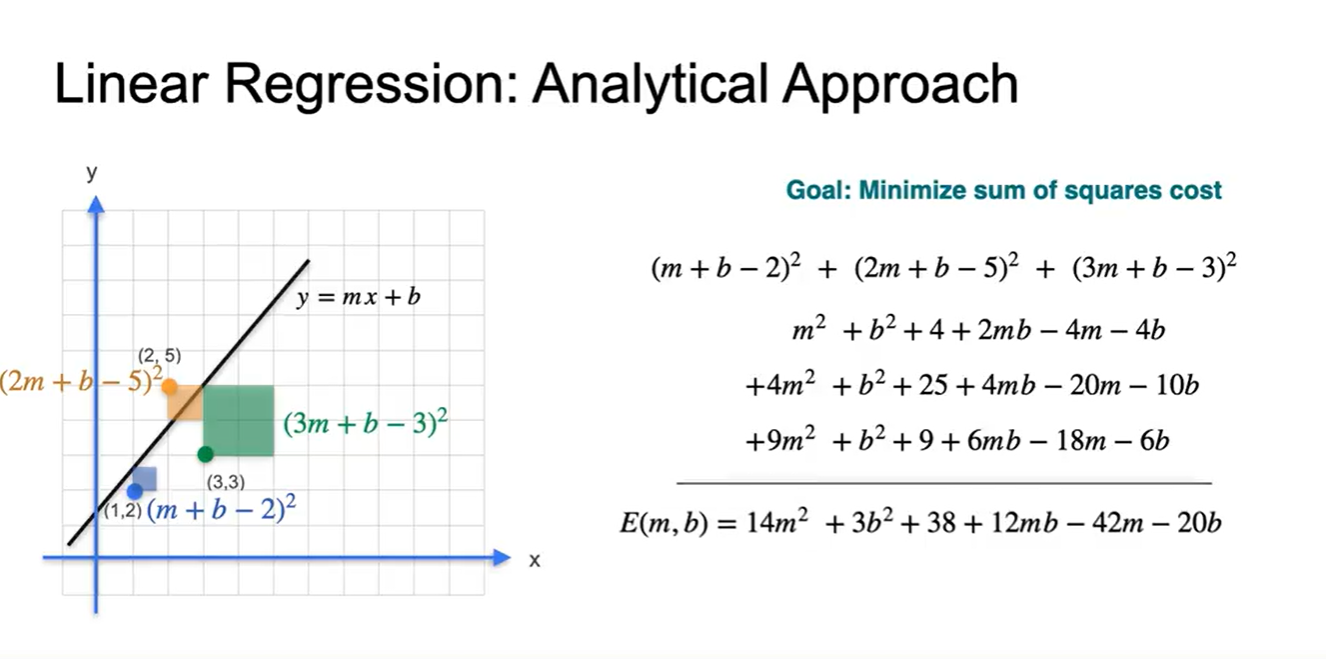
- 각 변수로 편미분하면 어떤 값을 가질지 계산해보자.
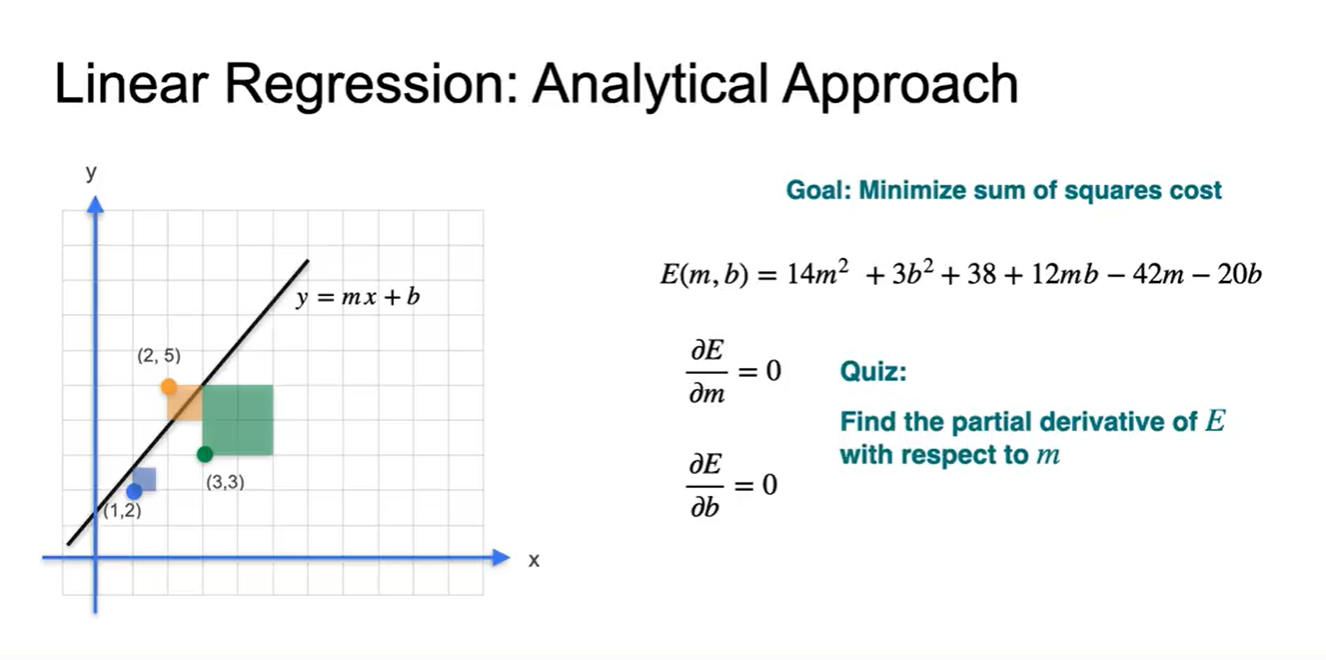
- 해당 slope 각각을 0으로 만드는 과 의 값은 얼마일까?
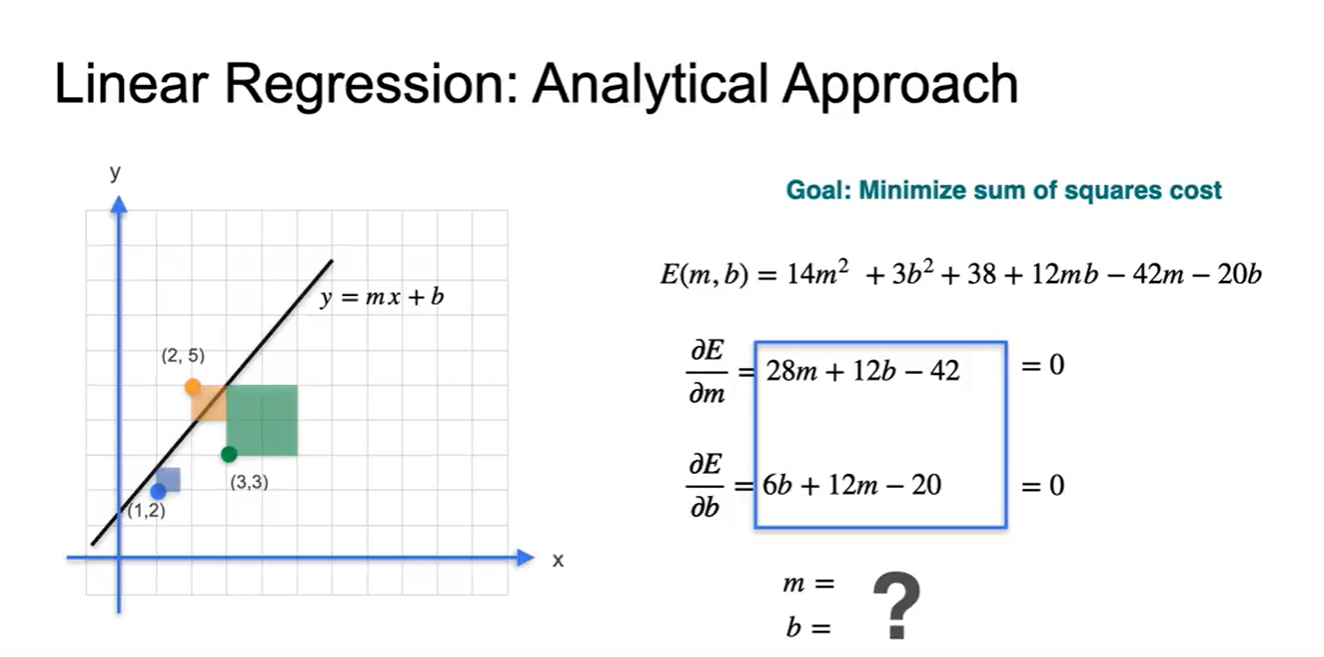
- 두 수식을 연립하여 조건을 만족하는 과 는 와 이다.
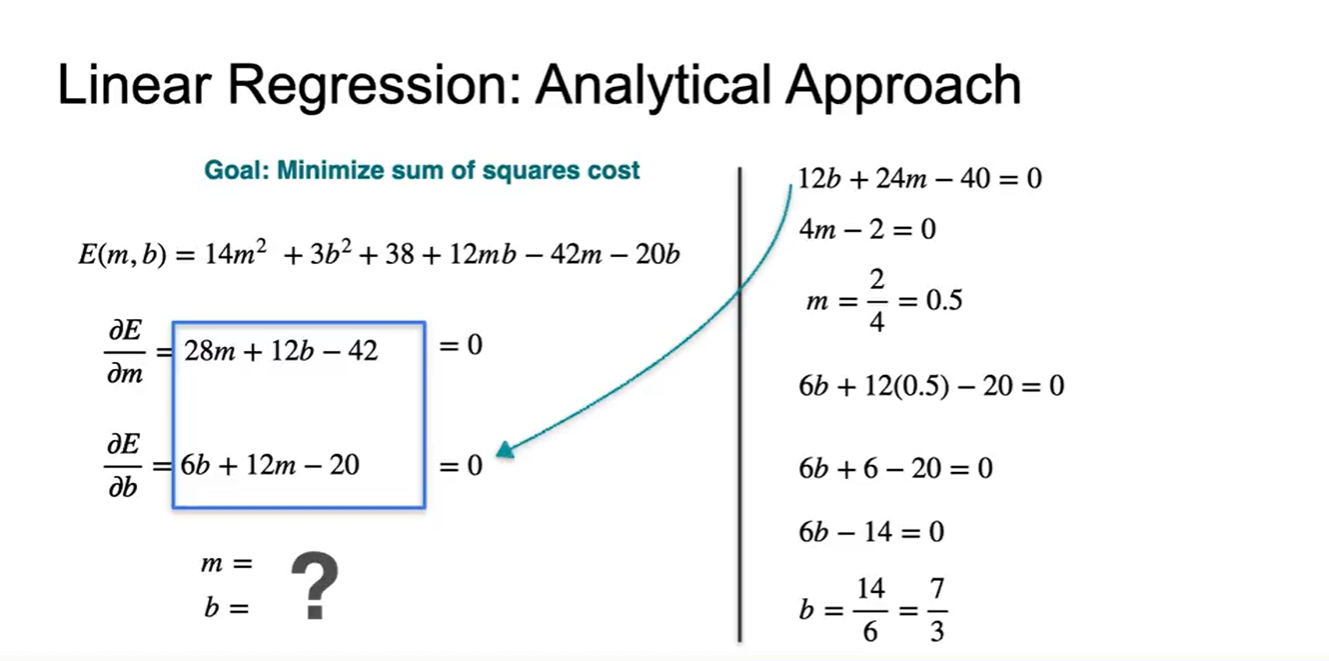
- (, )을 대입하여 나타낸 Error 값은 4.167이다.
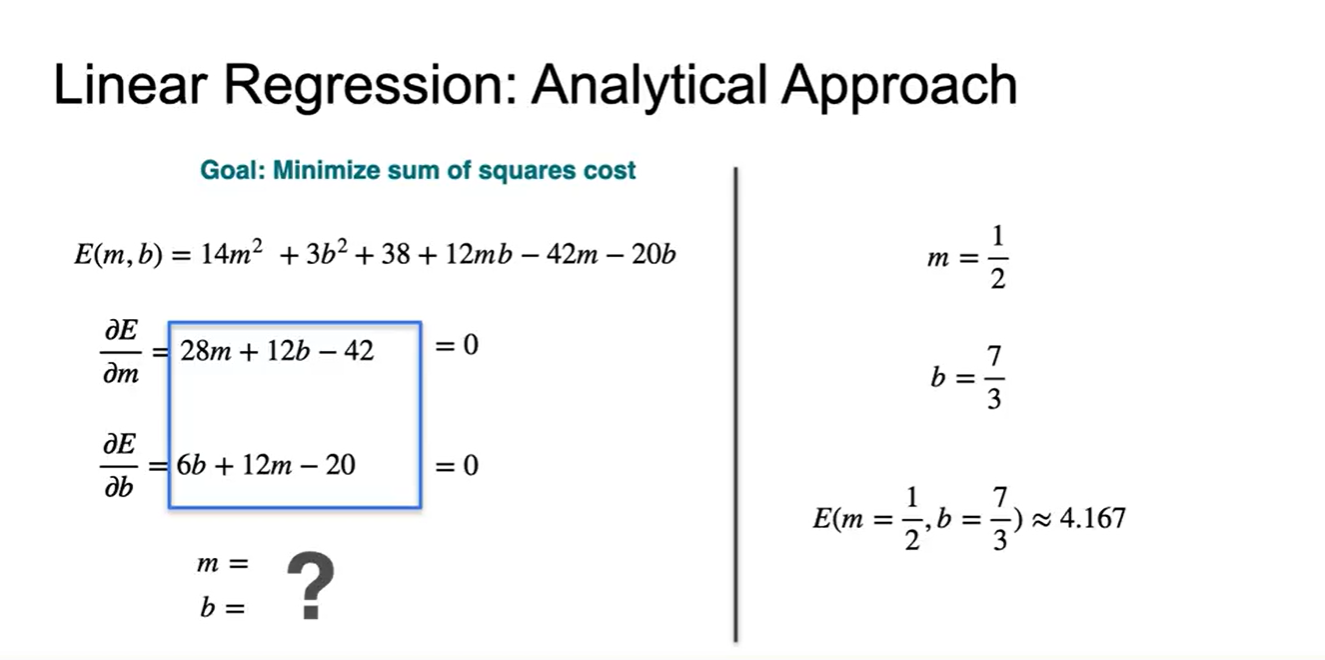
- 그림으로 표현해보면 해당 값의 square 넓이가 가장 최소인 것을 알 수 있다.
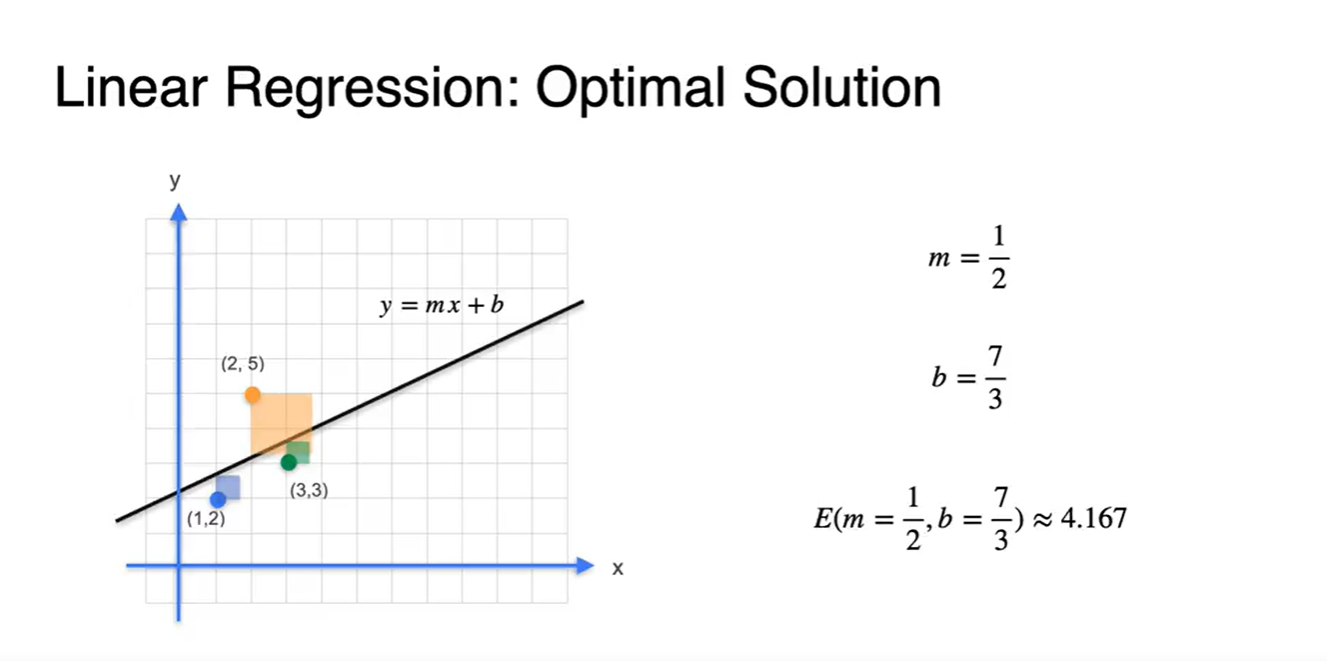
-
그렇다면 이러한 과 값은 어떻게 찾을 것인가?
- Gradient Descent가 해결해 줄 것이다.

Lesson 2 - Gradient Descent
Optimization using Gradient Descent in one variable - Part 1
-
1 variable을 갖는 function에서의 Gradient Descent가 무엇인지를 얘기해보자.
-
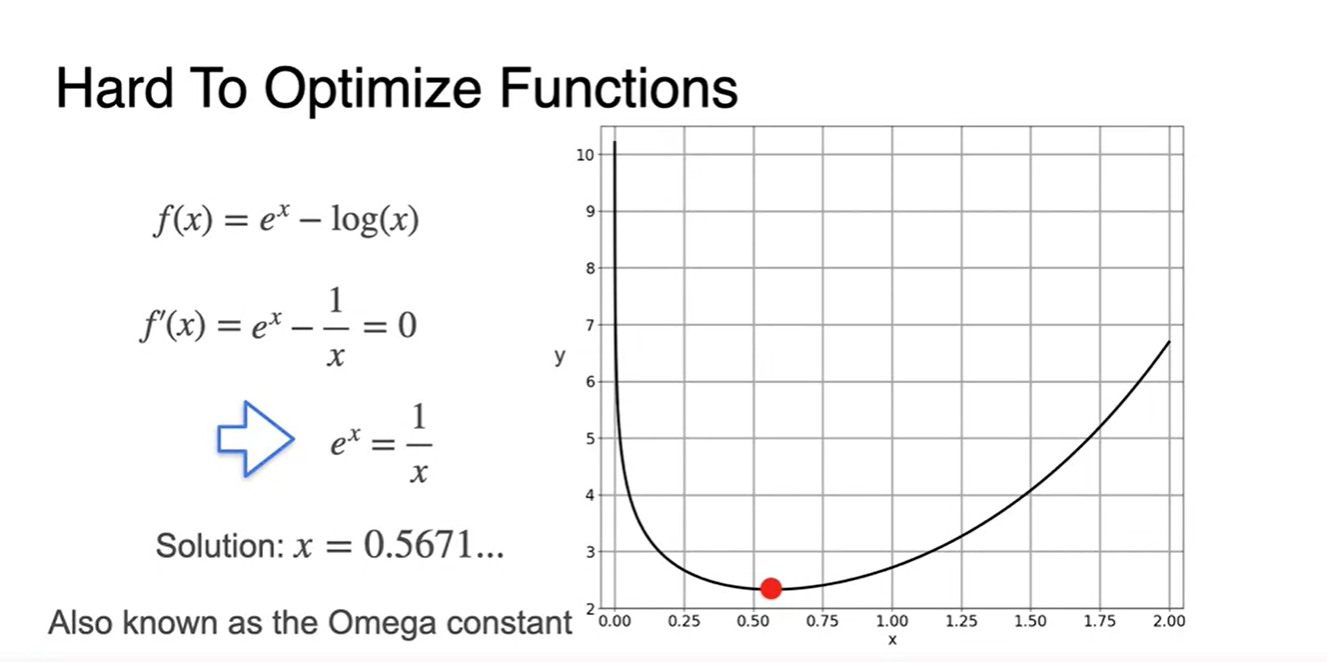
의 그래프가 아래와 같은 smooth한 function으로 정의되었다.
-
Minimum인 값은 어디인가?
- 미분 함수 인 곳일 것이다.
-
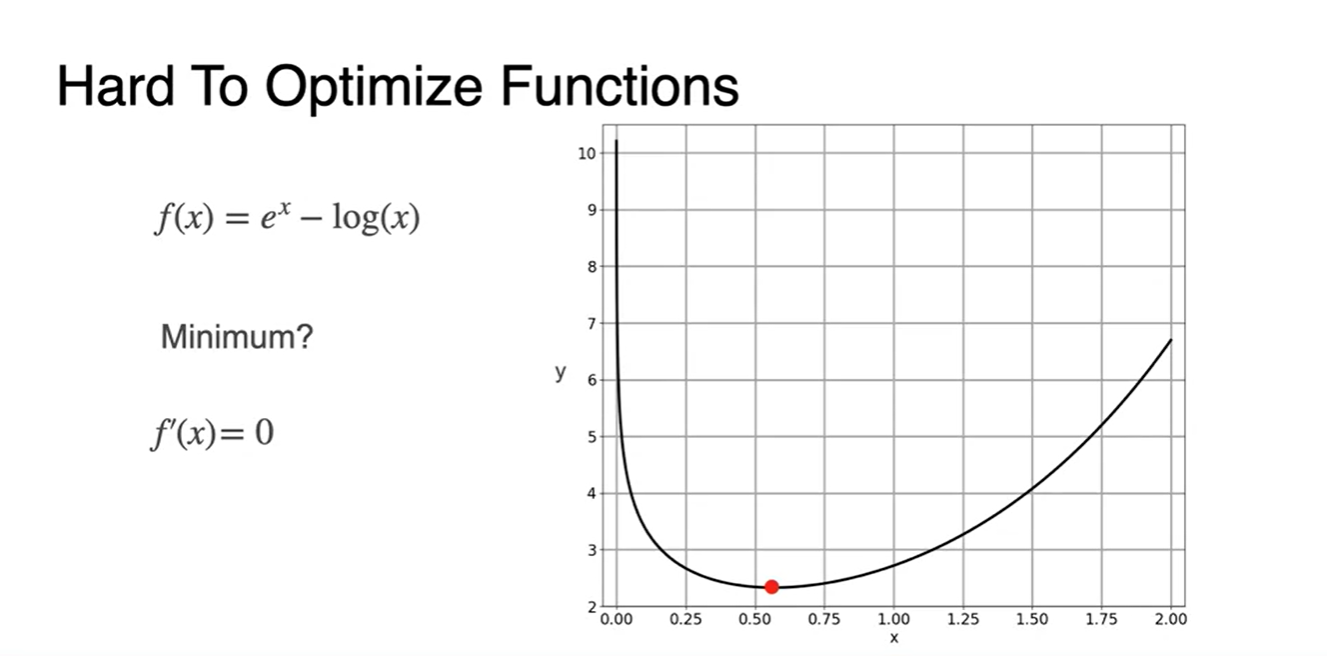
-
의 derivative 가 0인 지점은 일 때이고, 이 지점에서 전체 함수가 최소인 지점을 갖는다.
- 이 상수(constant)를 Omega constant라고 부른다고 한다.
-
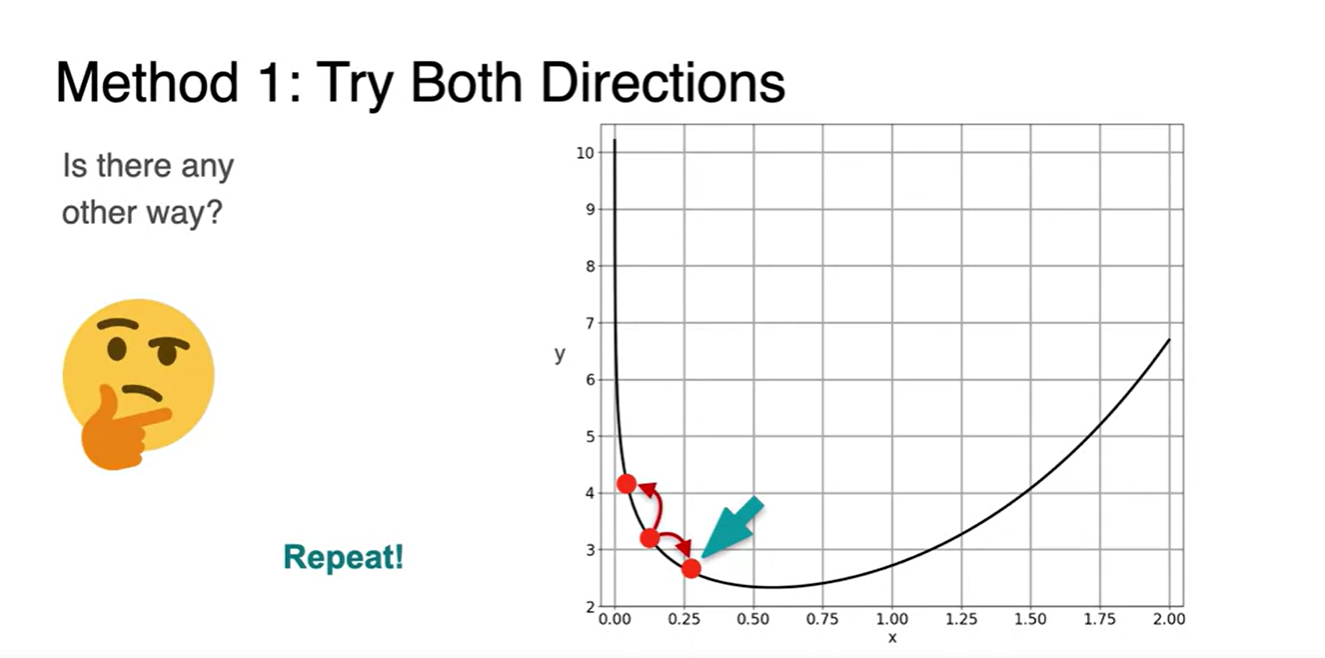
다른 방법으로 minimum을 찾아가는 방식이 있을까?
- 한 지점을 잡고, 점을 옮겨가면서 최소인 값을 찾는 방법은 어떤가?
- 여러 점을 옮겨다니며 이전보다 작아진 지점을 찾고, 이를 반복(repeat)한다면?
-
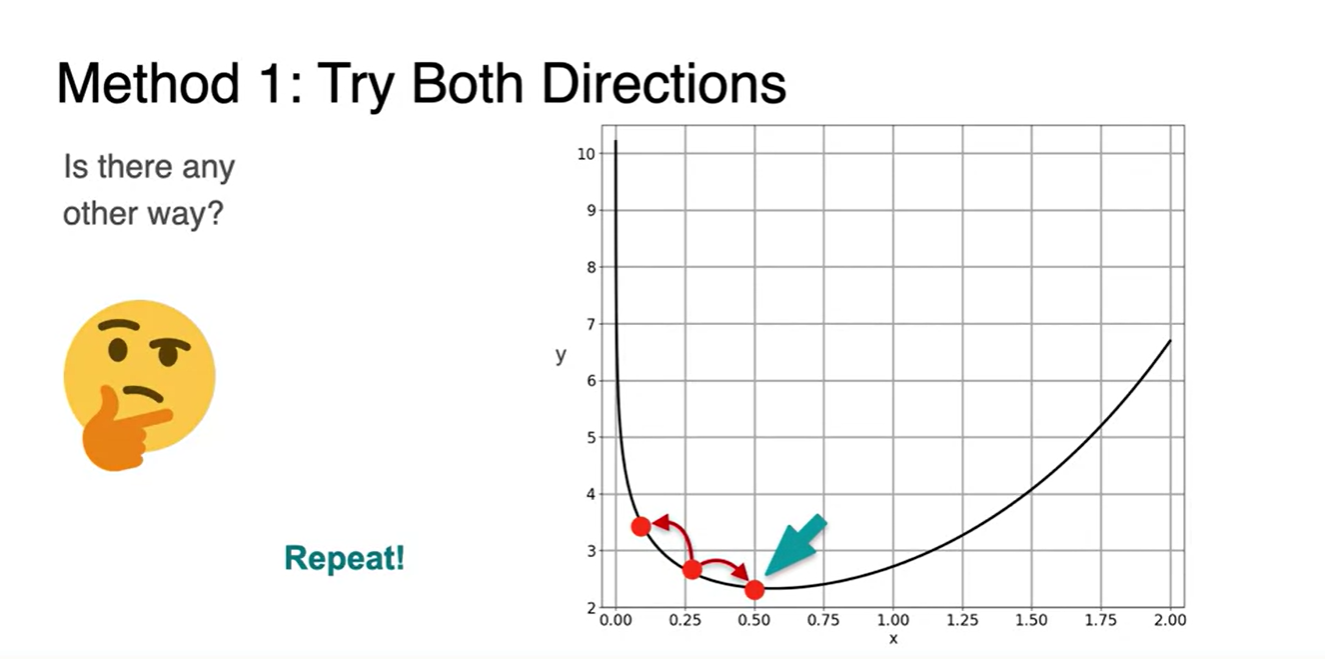
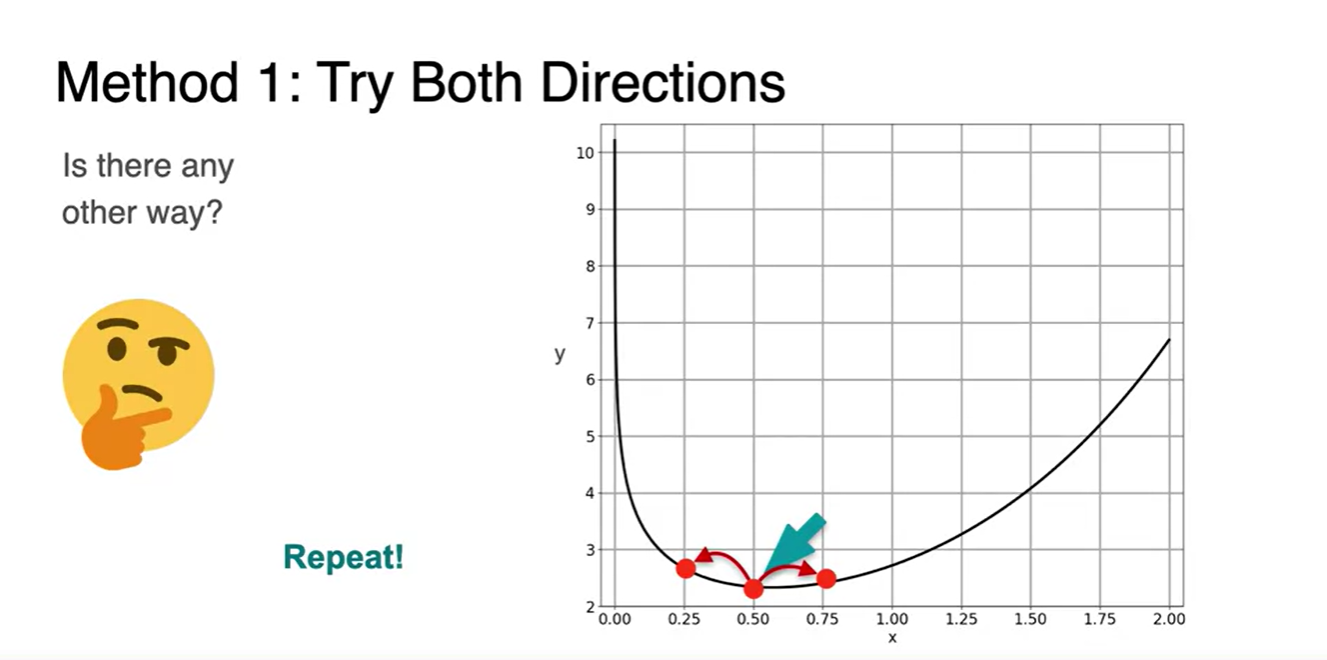
여러 step을 반복하다 보면 최소 지점을 찾게 될 수 있지 않을까?
- 이 지점을 찾아나가는 방법이 Gradient Descent이며, "step"은 곧 learning rate를 가리킨다.
- learning rate의 의미는 아래와 같다.
Ensure that the "steps" are small enough.
- learning rate의 의미는 아래와 같다.
- 이 지점을 찾아나가는 방법이 Gradient Descent이며, "step"은 곧 learning rate를 가리킨다.
Optimization using Gradient Descent in one variable - Part 2
-
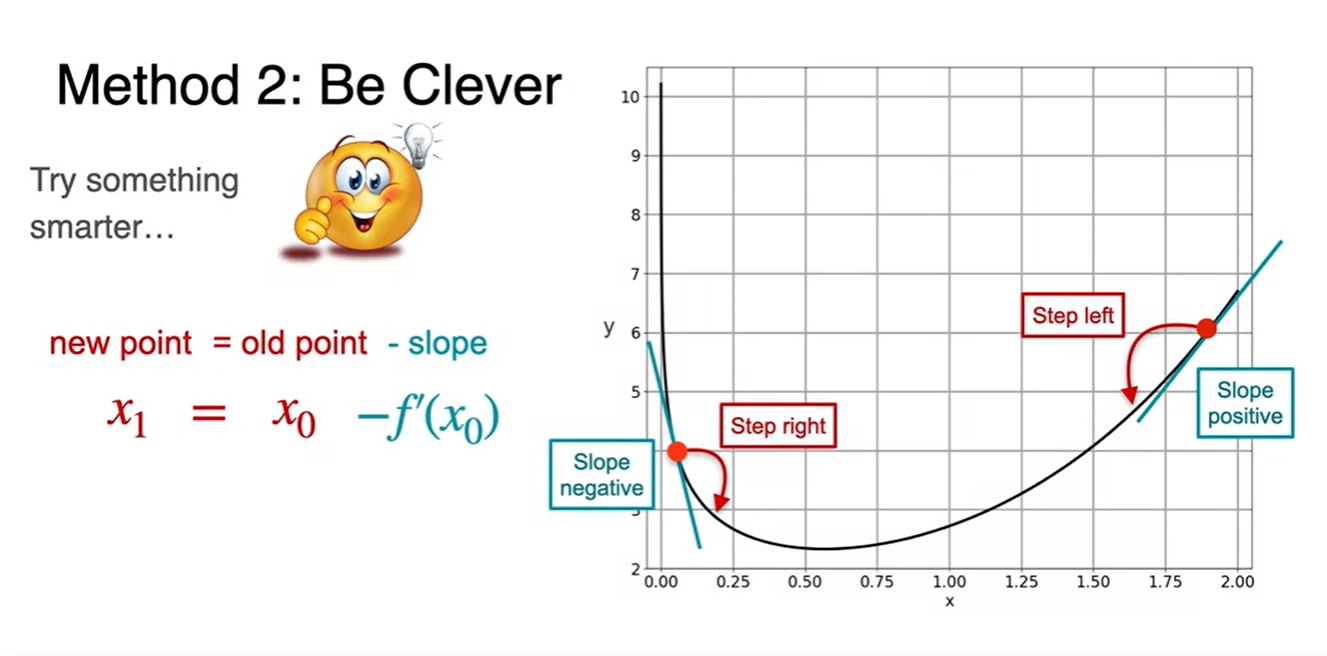
Slope의 부호에 따라 step을 어디로 가야할지 생각해보자.
-
Negative slope을 갖는다면 left로 향해야 하고, Positive slope을 갖는다면 right로 향해야 한다.
- 그렇다면 새로운 point는 로 계산되면 된다!
-
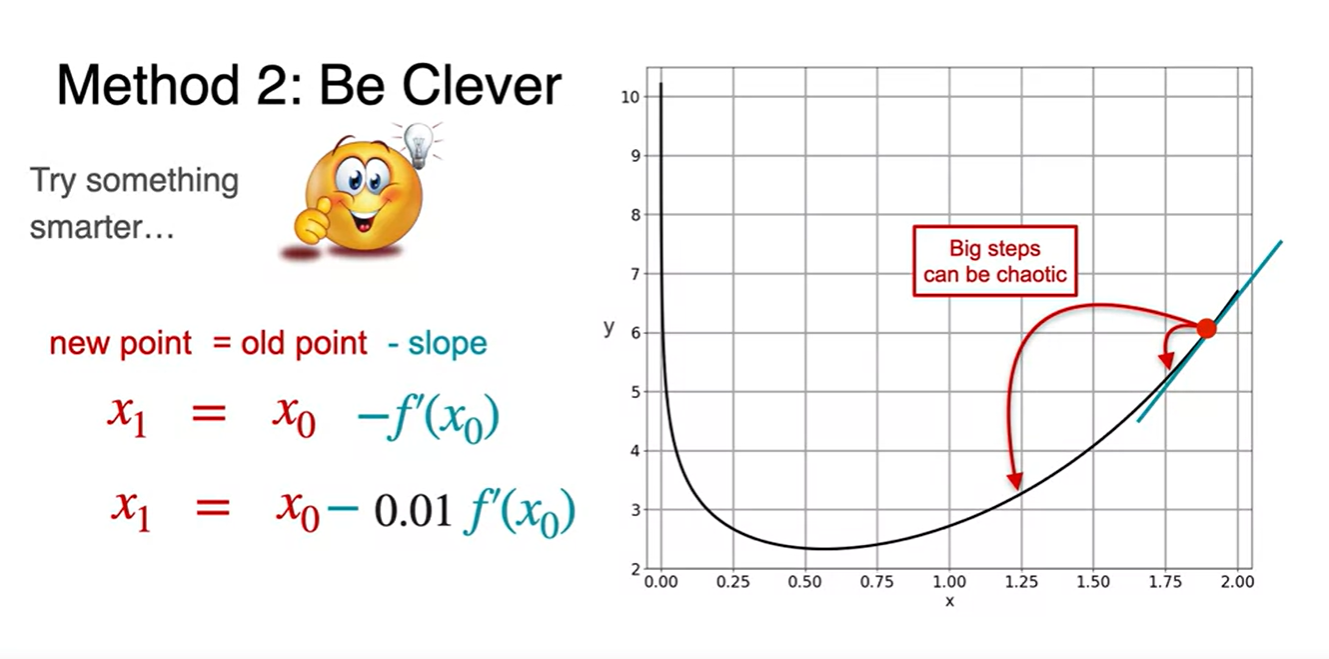
-
이 때 매우 큰 step으로 update된다면 값이 크게 뛸 수 있다. (chaotic)
- 따라서 0.01과 같은 매우 작은 learning rate를 곱해주어 적당한 양으로 step이 update될 수 있도록 만든다.
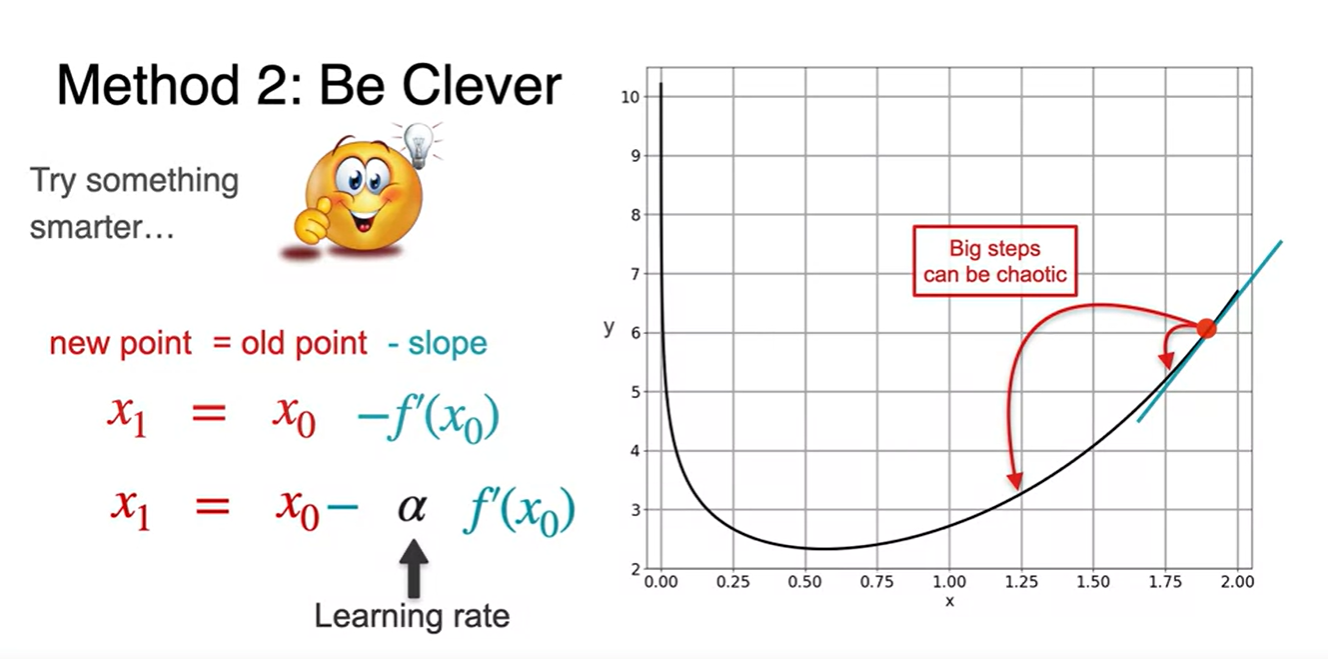
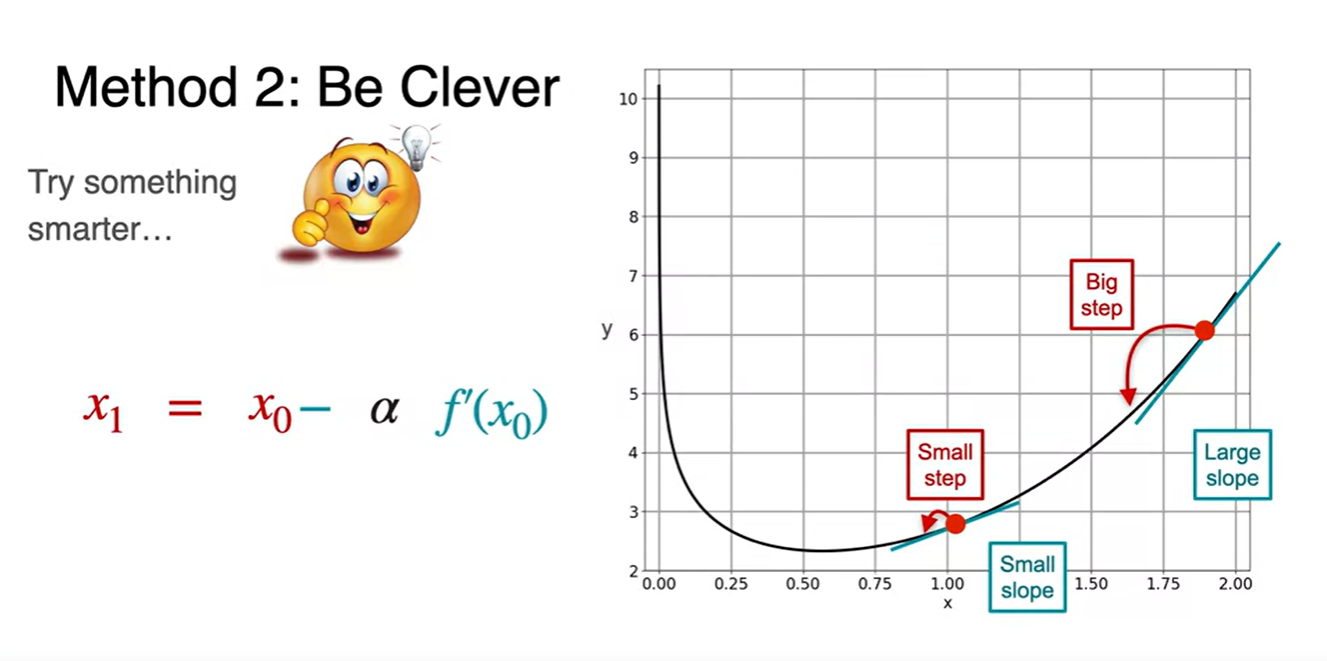
- 이러한 과정을 여러 번 반복하는 작업이 Gradient Descent다.
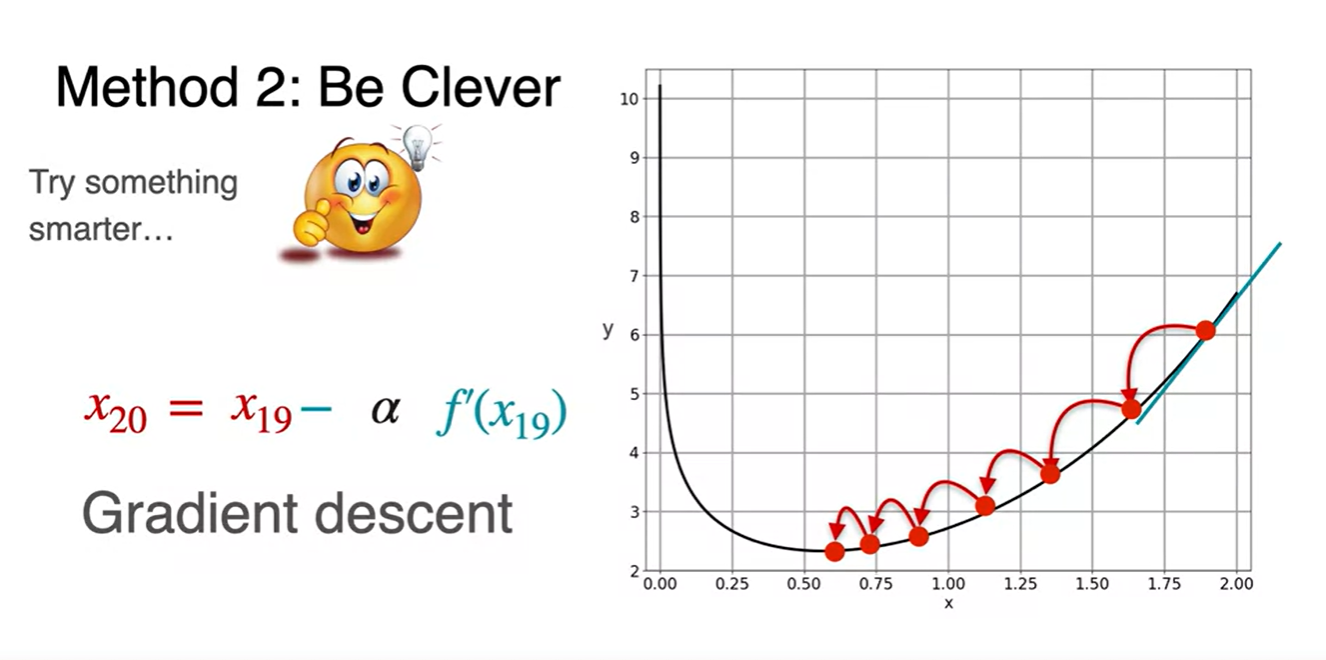
-
이를 알고리즘으로 표현하면 아래와 같다.
- learning rate를 정의하고, starting point 를 정한다.
- 다음 값을 업데이트 하기 위한 점화식 을 세워 대입한다.
- 2번 step을 반복해가면서 진정한 minimum 지점을 찾는다.

-
예시로 몇 가지 점들을 대입해 보자.
- slope를 구하여 gradient descent 식에 대입하면 다음과 같은 minimum 을 찾아갈 수 있게될 것이다.
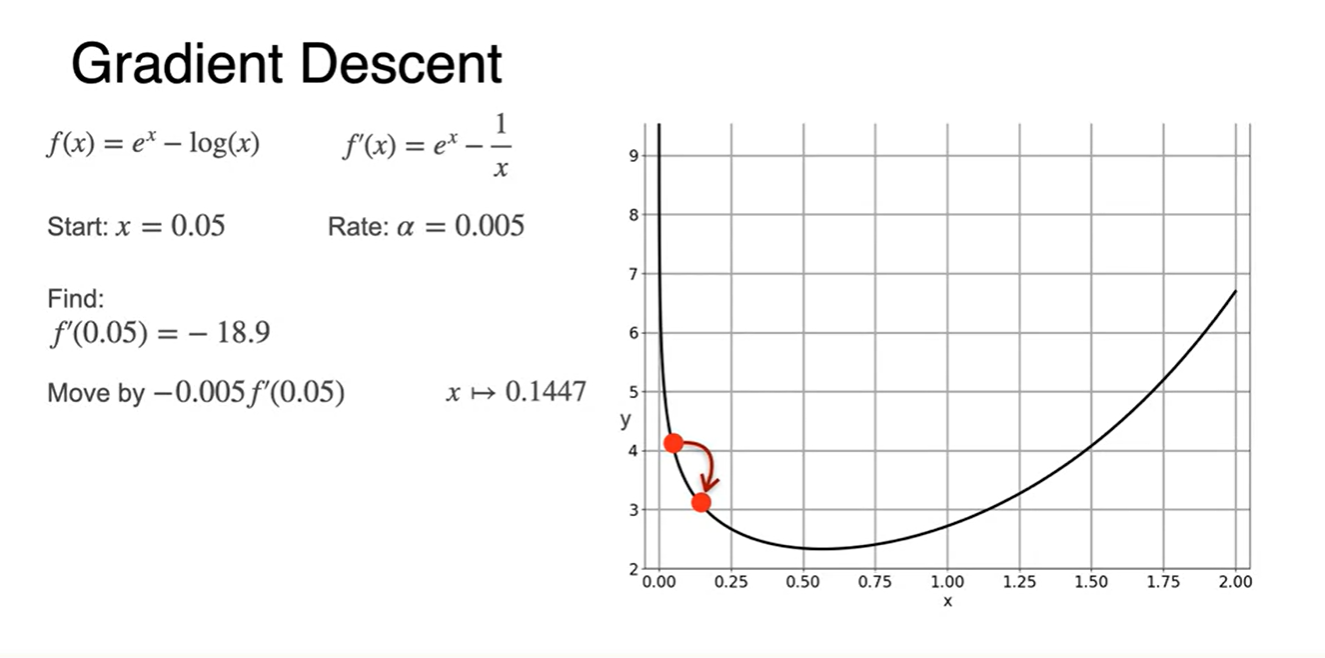
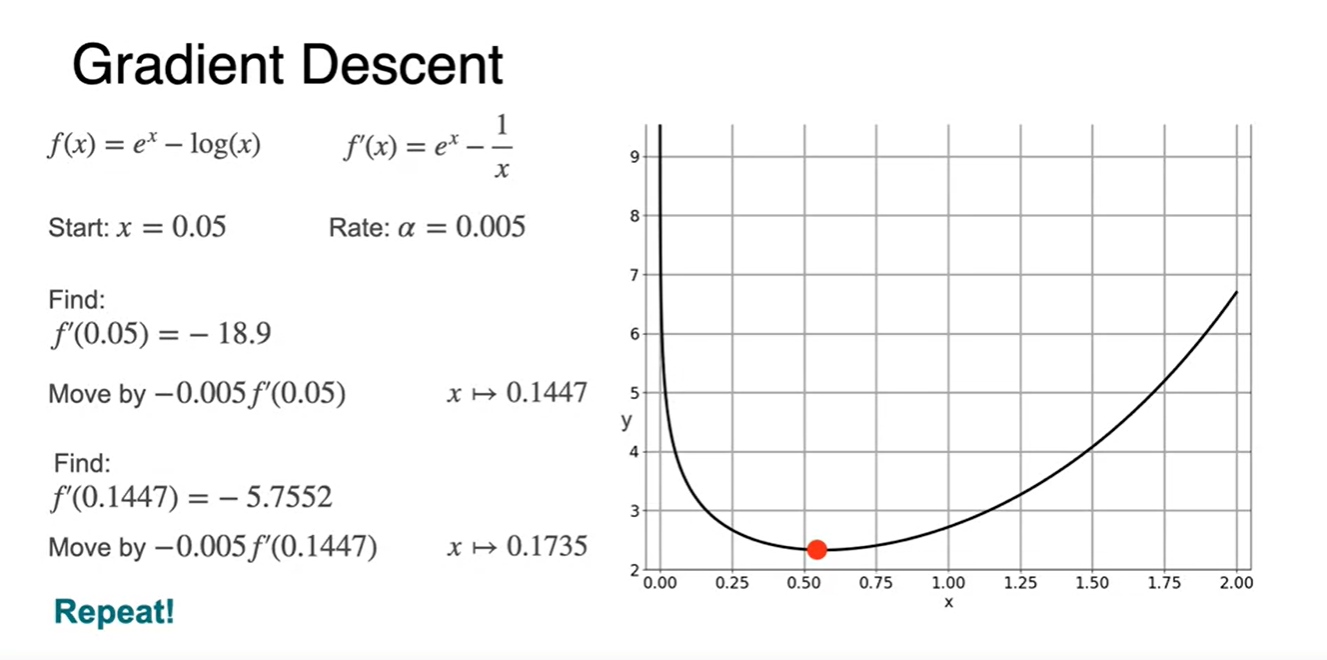
Optimization using Gradient Descent in one variable - Part 3
-
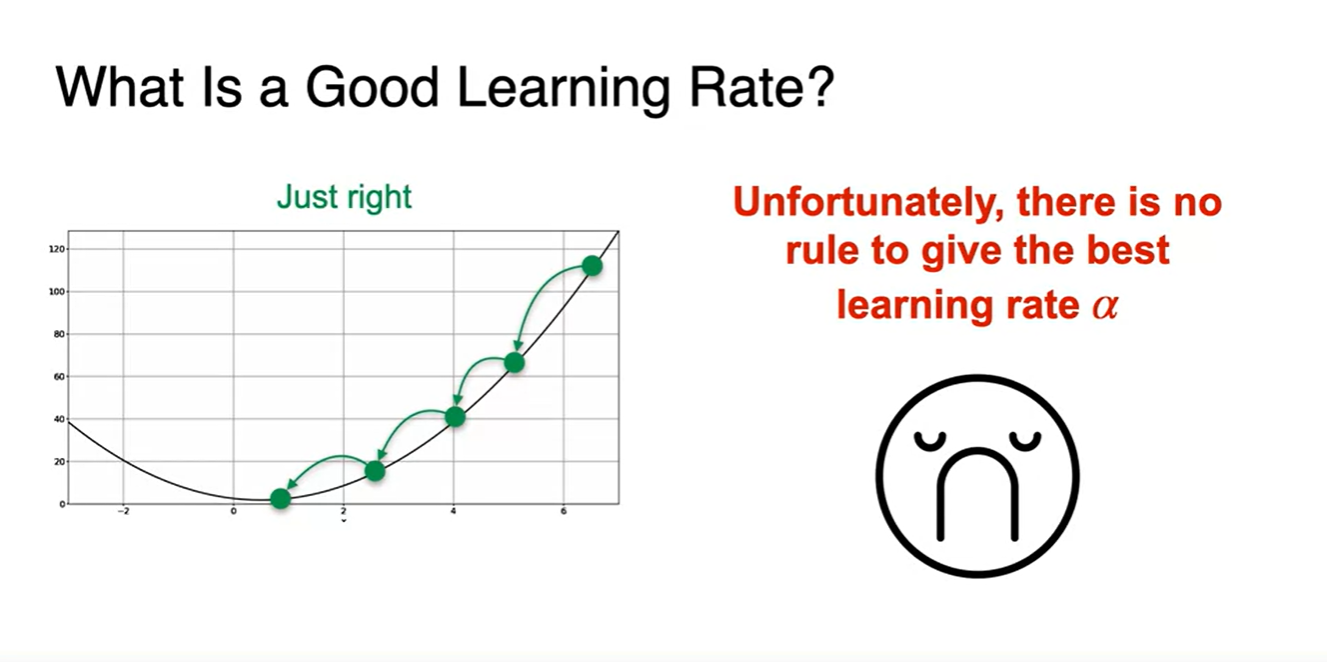
그렇다면 Good learning rate는 얼마인가?
-
learning rate가 얼마일 때가 최적일지에 대한 의문은 Machine learning에서의 중요한 논의 내용 중 하나이다.
- lr이 매우 크거나 매우 작으면 너무 크게 진동하거나 많은 step을 거쳐야만 minumum을 찾을 수 있어 부적절하다.
-
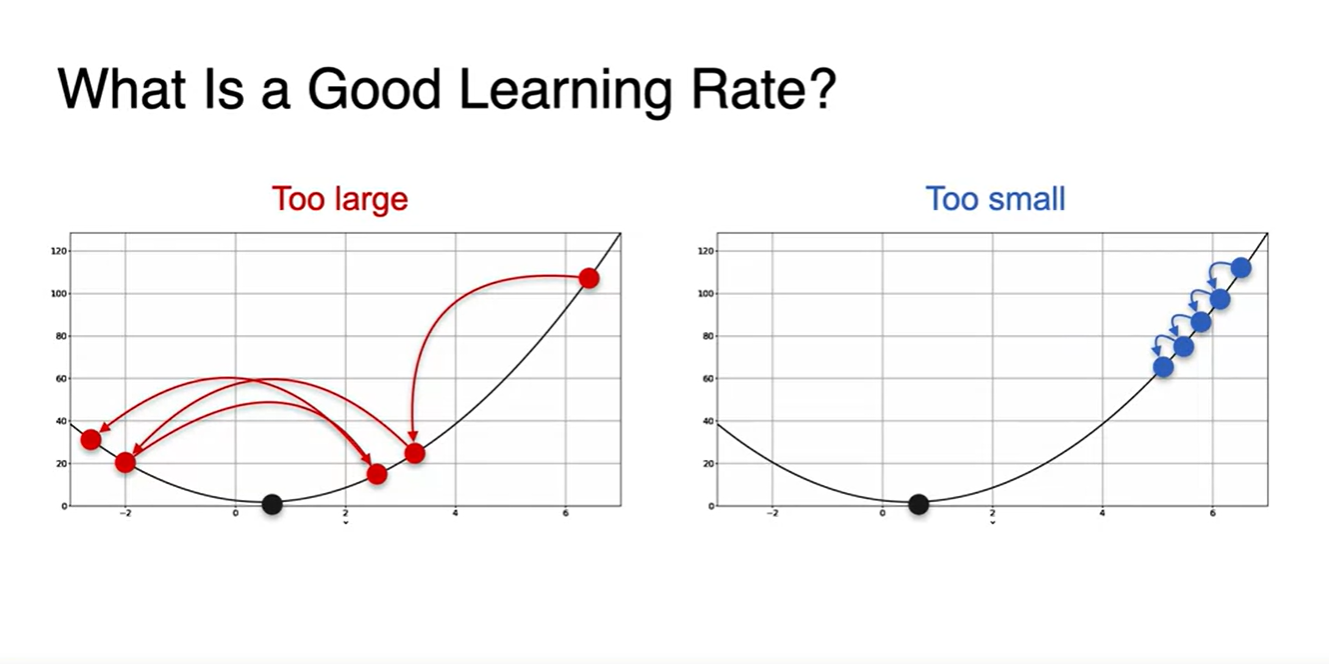
-
딱 알맞는 just right한 learning rate를 찾는 rule은 불행하게도 존재하지 않는다.
- 따라서 다양한 실험과 함께 최적의 Hyper parameter를 찾아가는 것이 중요하다고 할 수 있다.
-
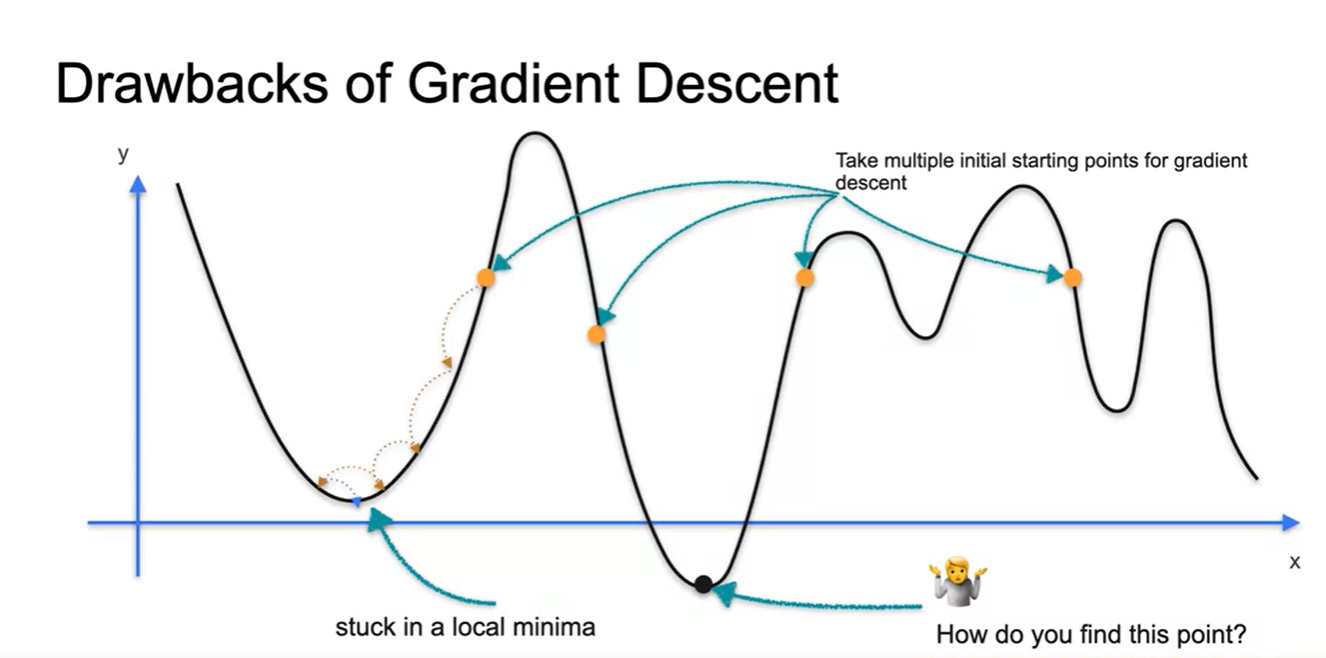
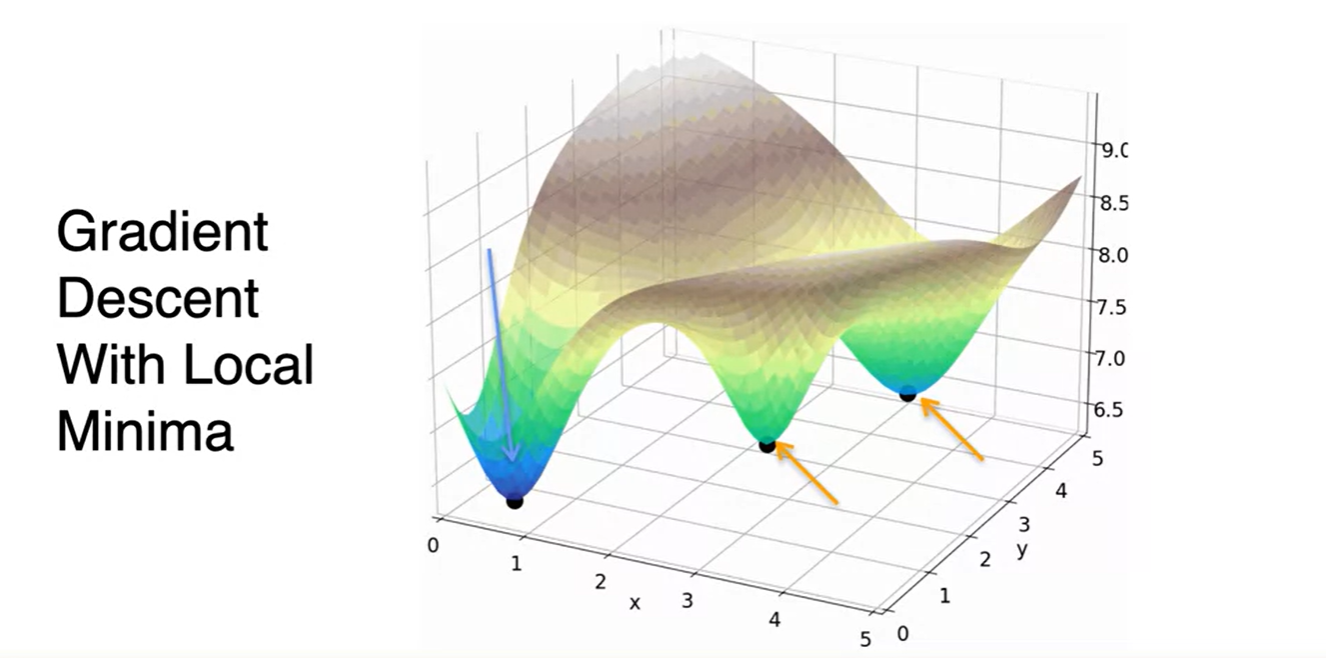
Gradient Descent의 치명적인 약점(Drawback)은 local minima에 빠질 수 있다는 점이다.
- 따라서 starting point가 매우 중요하며 global minima에 도달하기 위해서는 여러 값으로 실험해보는 것이 중요하다!
Optimization using Gradient Descent in two variables - Part 1
-
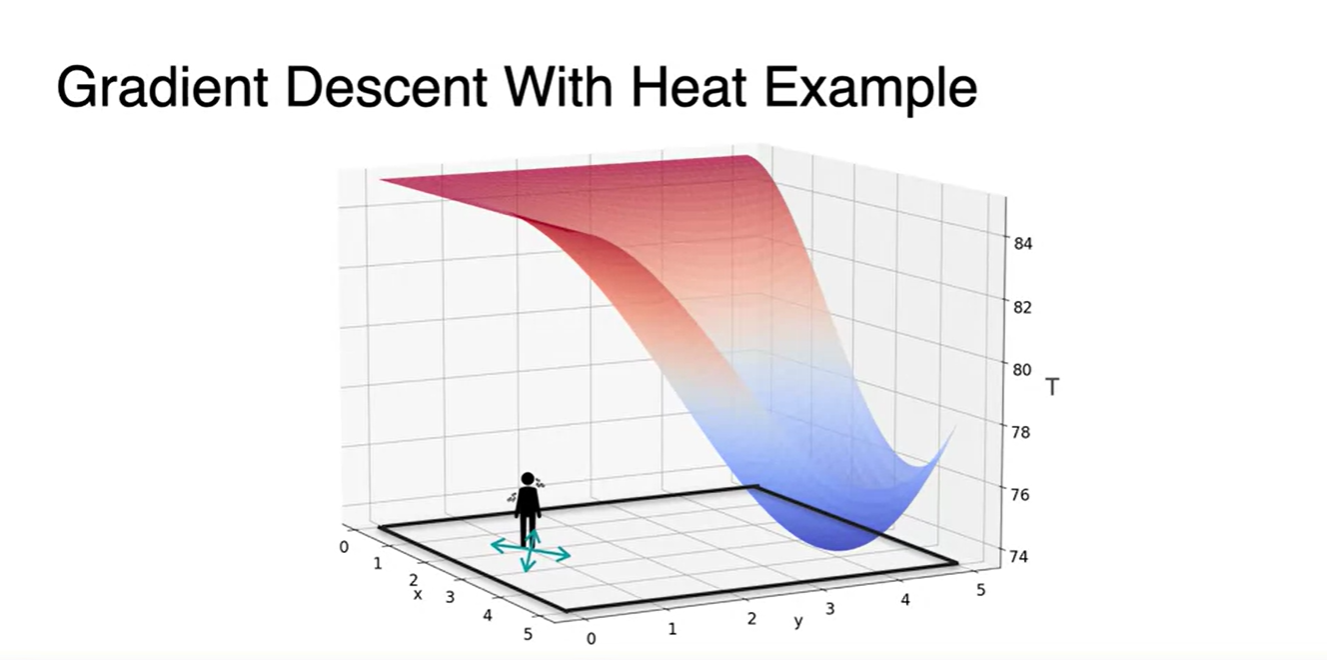
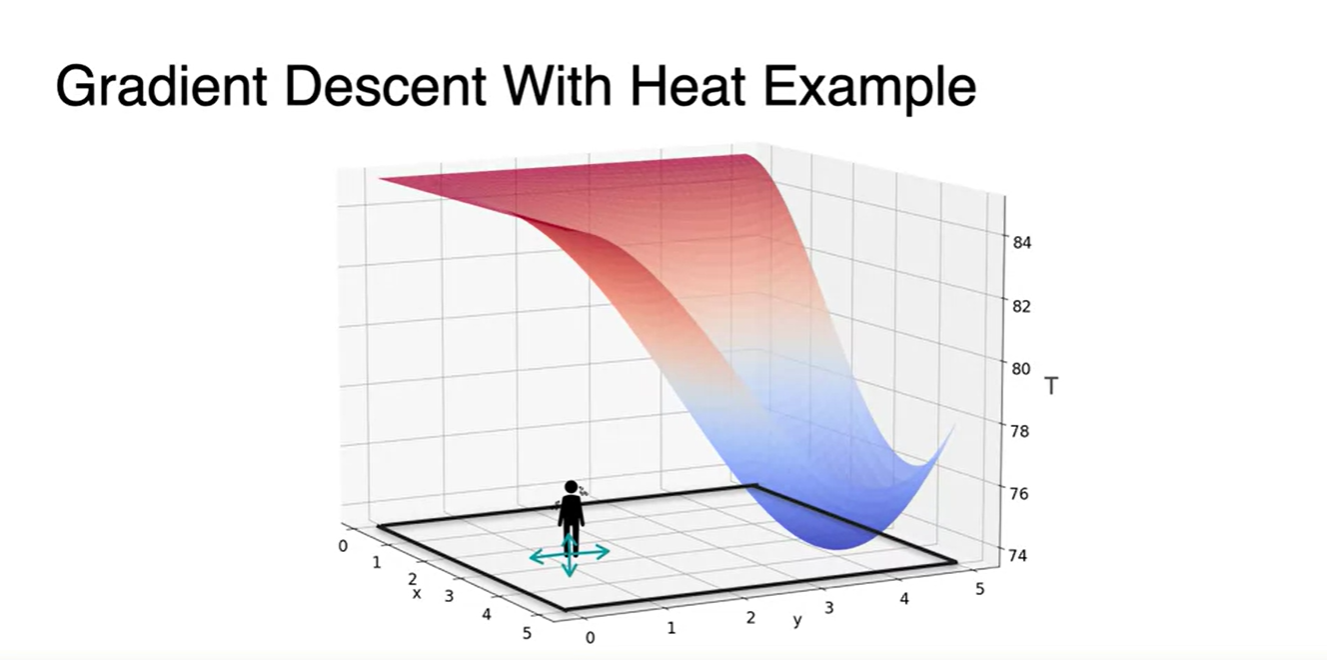
이제 2 variables를 갖는 function의 Gradient Descent를 얘기해보자.
- 이전에 다뤘던 Heat problem에서의 cold point 찾아가기와 같은 맥락이다.
- 한 지점에서의 slope를 찾고 cold point로의 direction만 알면 온도의 minimum을 찾아갈 수 있다.
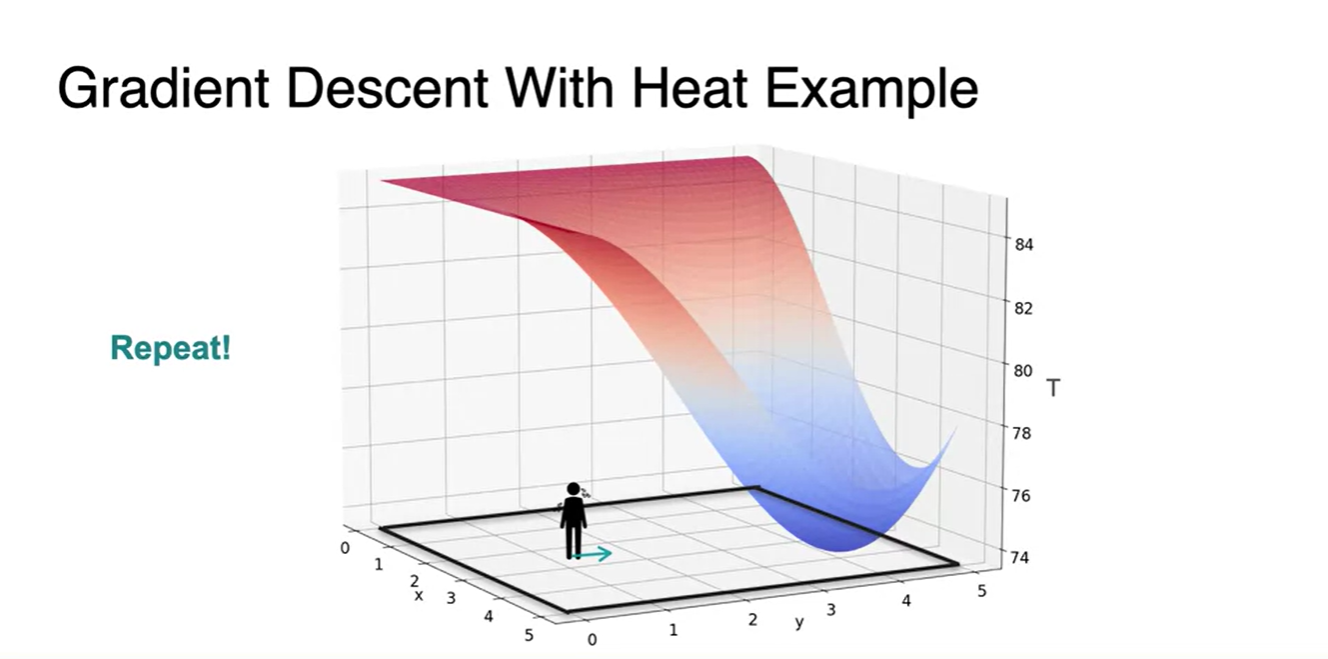
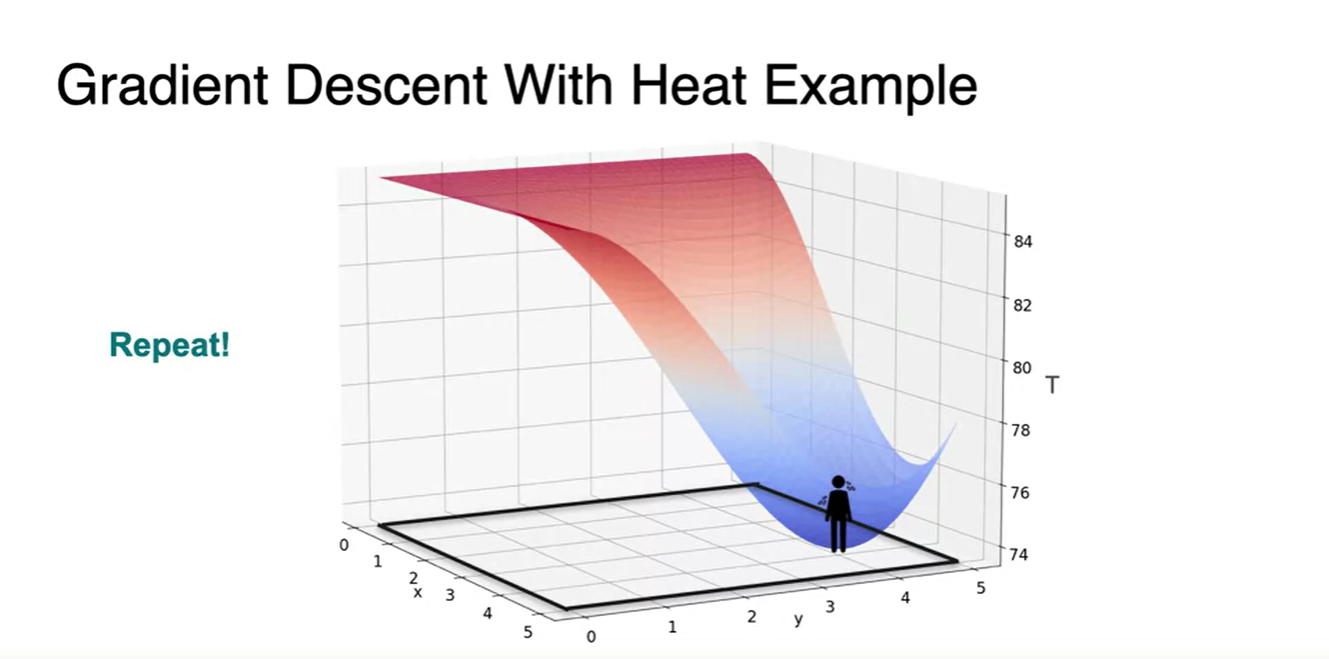
-
그러면 minimum으로 향하는 direction은 어떻게 정의될까?
- 1 variable Gradient Descent와 동일하게 미분(편미분)으로부터 정의될 것이라는 점만 알아두자.
Optimization using Gradient Descent in two variables - Part 2
-
Initial point 에서 각 variable 마다의 미분 함수를 구해보자.
-
를 대입한 각각의 gradient vector를 찾으면 아래 평면에 놓인 검은색 두 방향 벡터로 나타낼 수 있다.
-
전체 벡터는 두 방향 벡터의 합이므로 의 방향은 초록색 벡터(바깥 방향)으로 표현된다.
- 가능한 모든 variable로 미분한 값의 합은 가장 영향력이 큰 방향 벡터로 수렴하게 될 것이다.
-
우리가 움직여야 할 방향은 이러한 방향 벡터(gradient)에 -를 붙인 방향이라는 것도 알아 두자.
-
물리학에서의 퍼텐셜 에너지 미분이 힘의 방향이라는 것과 유사하다.
-
-
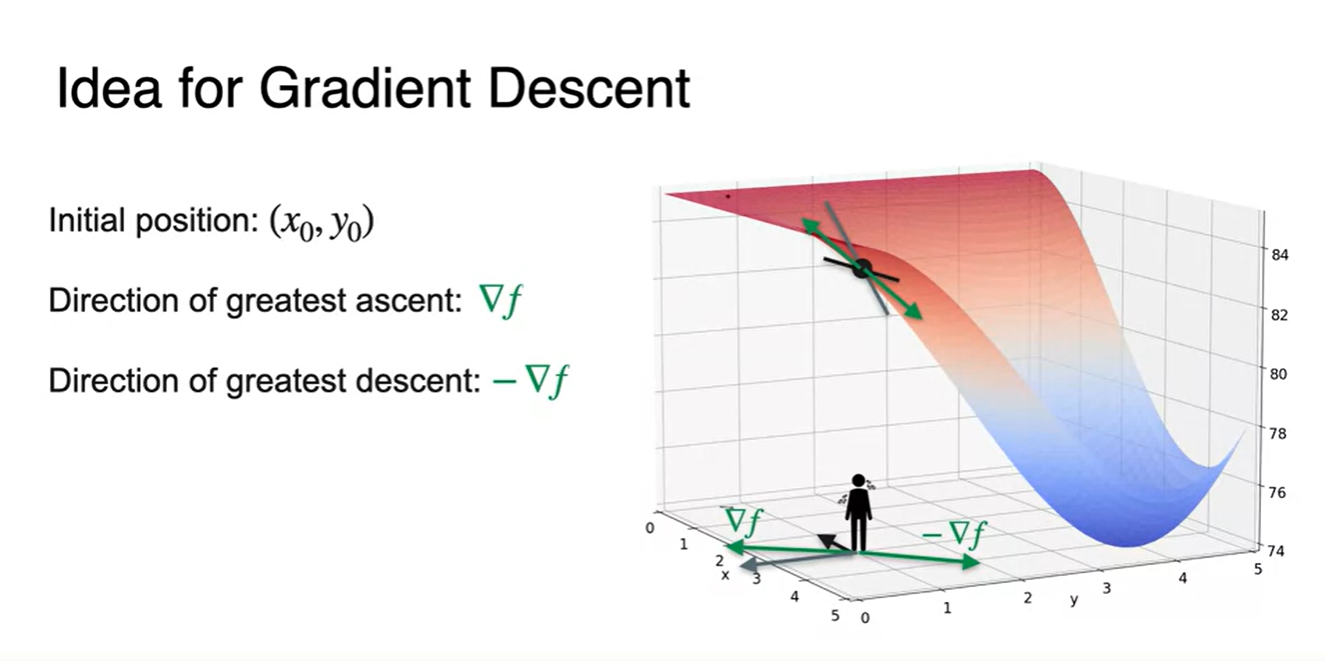
-
Initialize한 position ()로부터 힘의 방향으로 밀어 넣으면
- 우리가 찾는 최소 지점인 minimum으로의 better point를 찾아갈 수 있다.
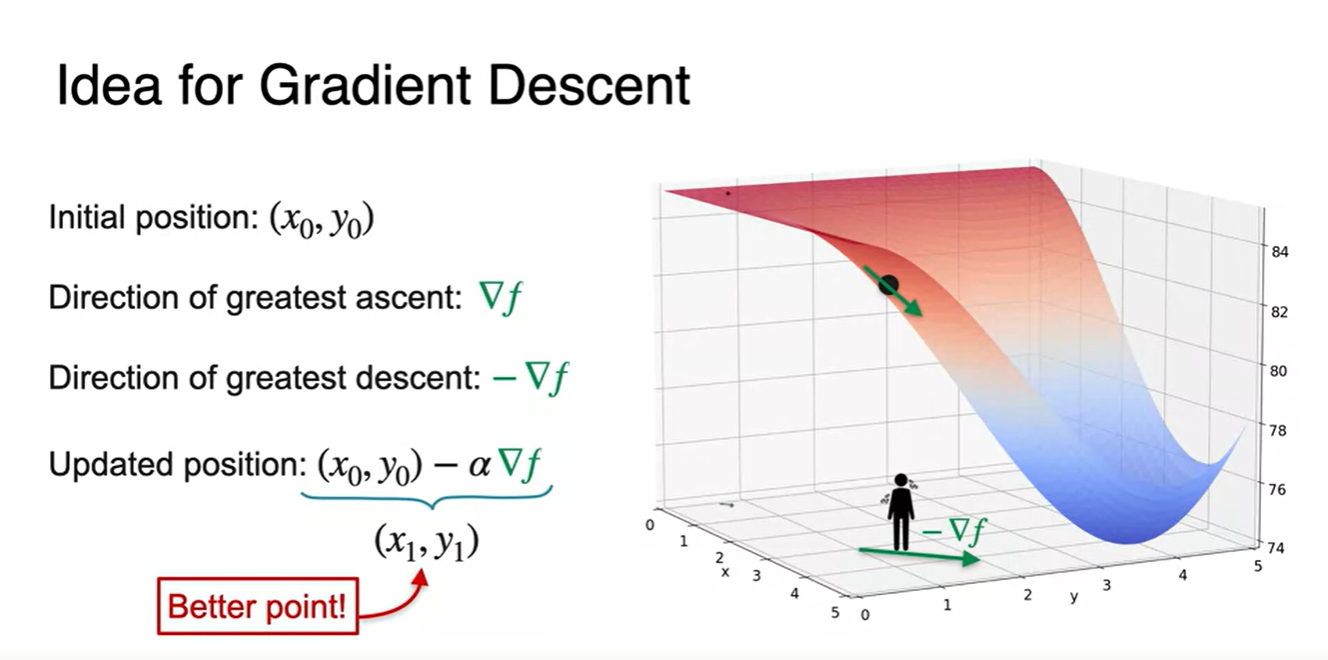
-
이전에 다뤘던 , variables를 갖는 온도 함수 를 다뤄보자.
- Gradient는 편미분으로 미분하고 각각의 값을 행렬로 쌓으면, 특정 방향을 나타내는 벡터 표현이 된다.
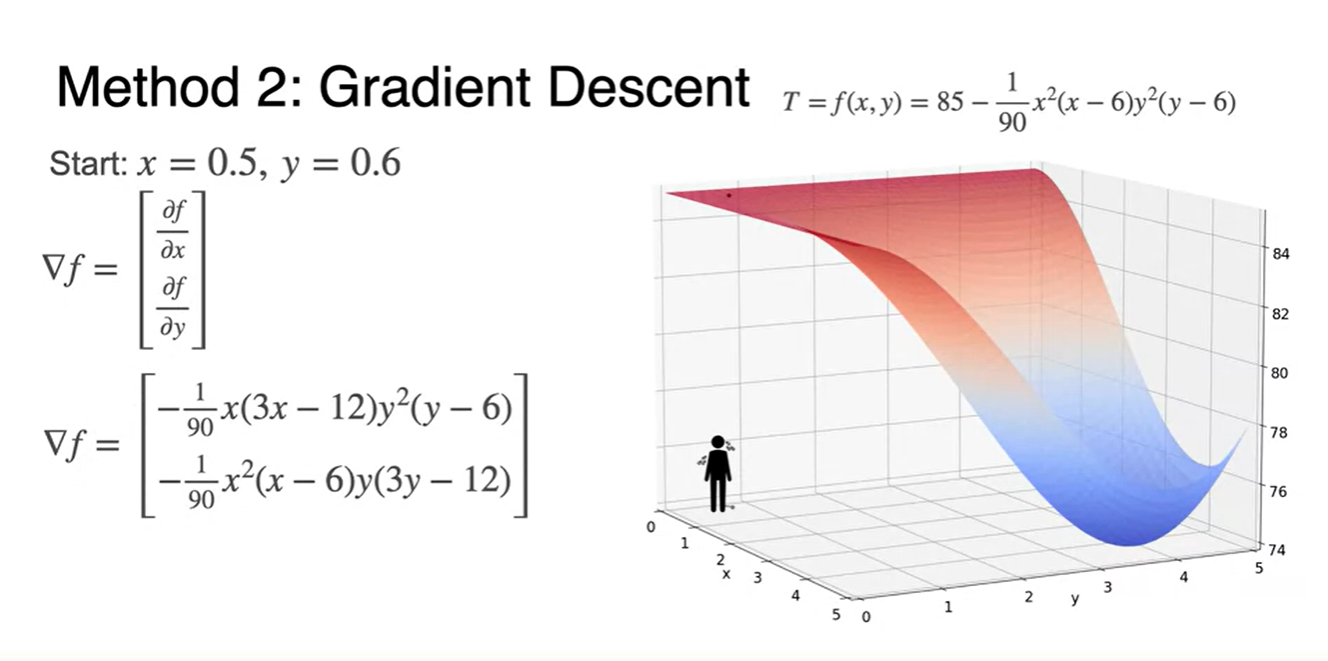
-
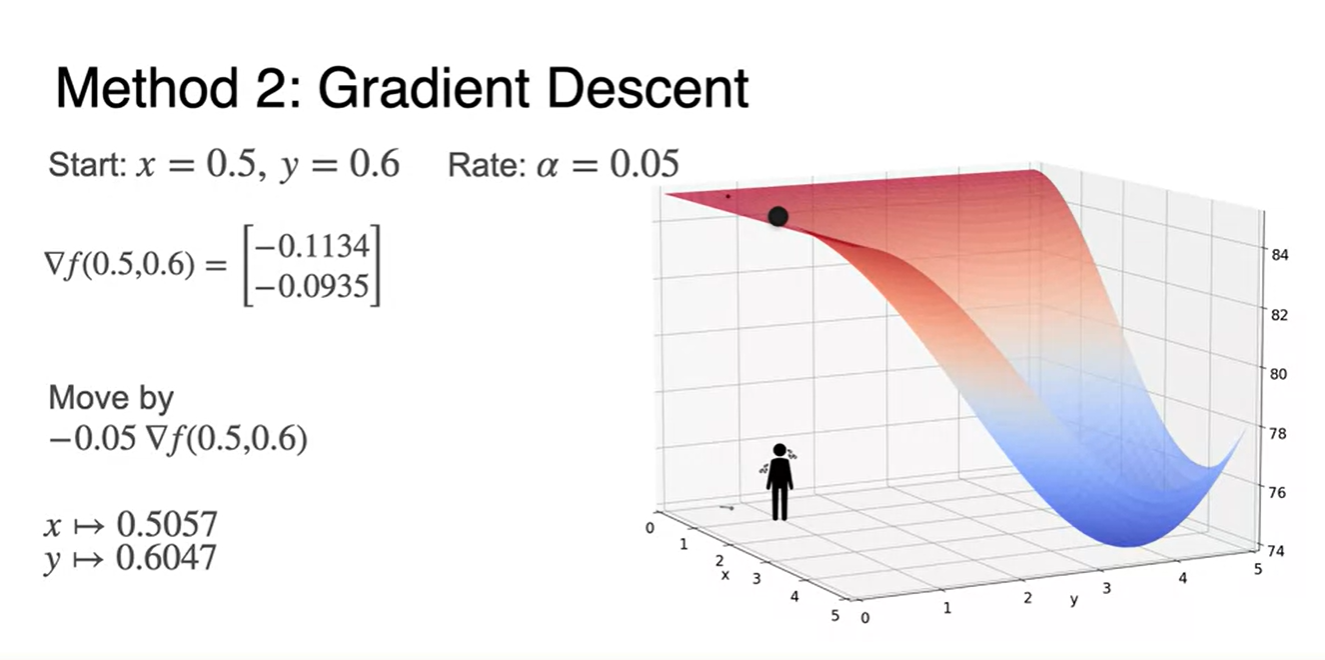
Starting point 에서의 미분으로 gradient를 찾고
-
초기값을 대입한 방향 벡터를 구하여 learning rate와의 곱으로 move하면
- minimum으로 향하는 새로운 point로 안착하게 된다.
-
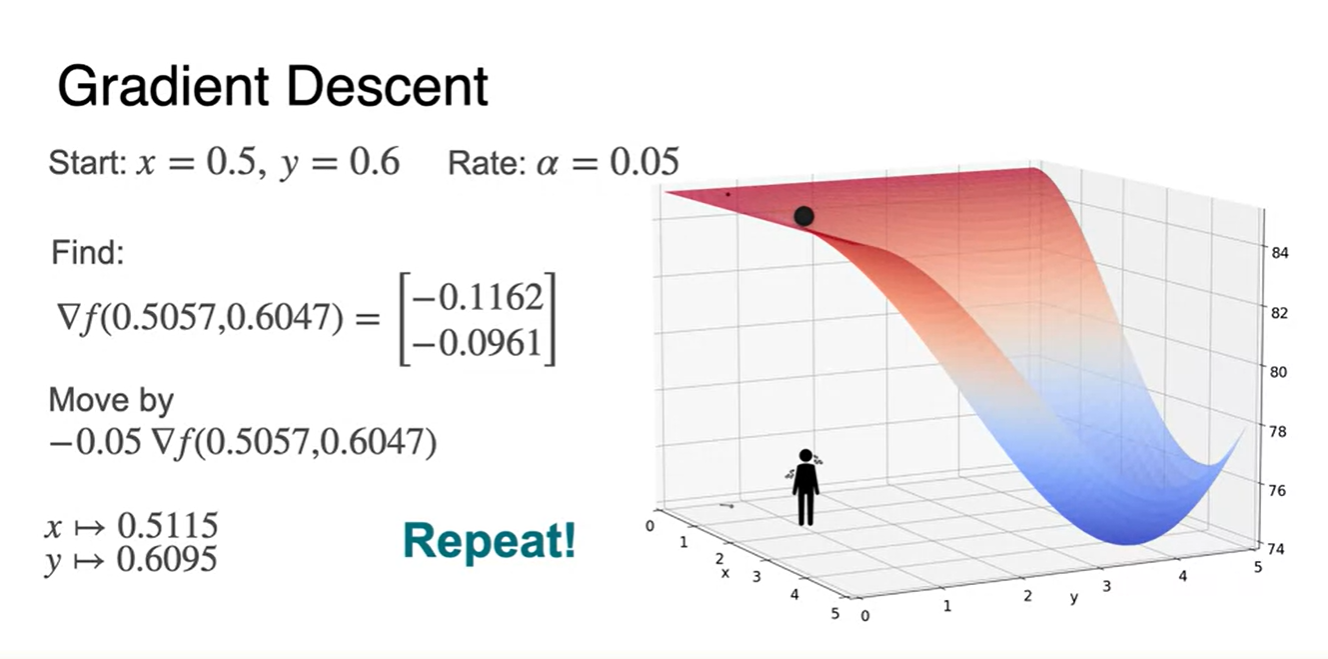
-
다시 움직인 지점에서 gradient를 찾아 lr을 곱한 값으로 해당 지점을 move하면
- minimum으로 향하는 새로운 point로 또 다시 안착하게 된다.
- 이러한 과정을 반복하여 minimum parameter point를 찾아가는 과정이 Gradient Descent다!
-
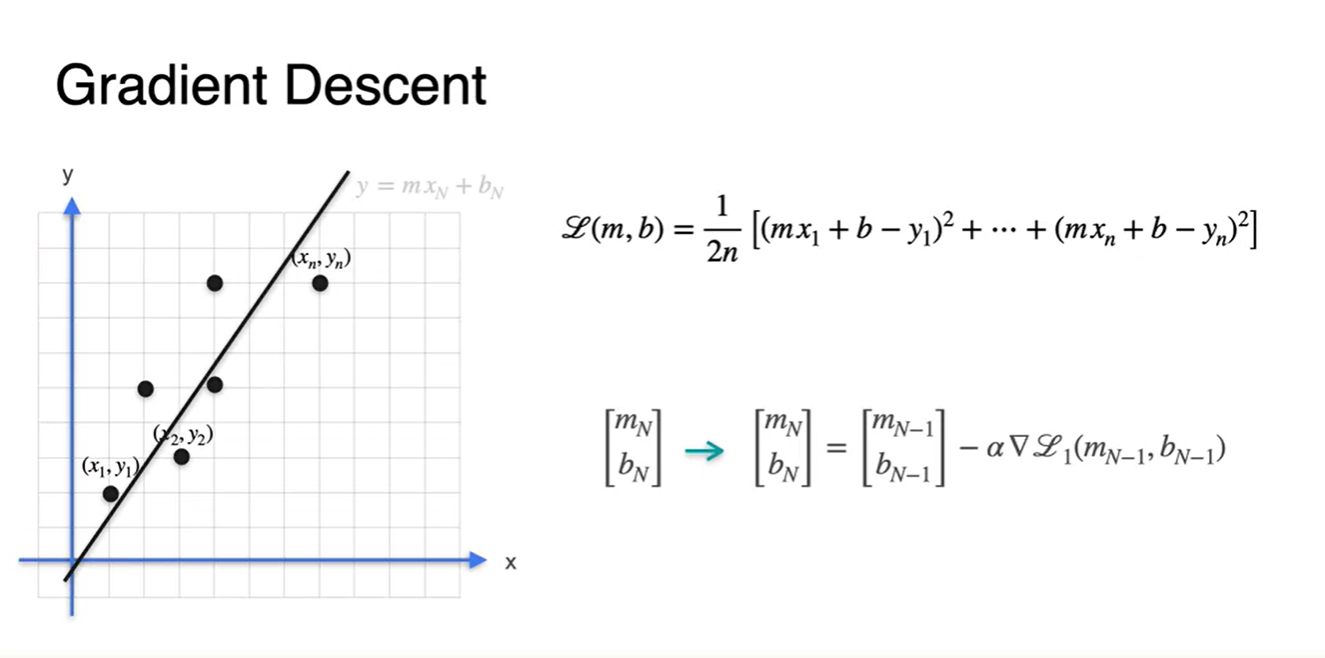
아래의 알고리즘을 머신러닝에서의 parameter 와 로 정리해 보았다.
- lr을 정의하고 starting point()를 잡는다.
→ Parameter Initializing - 각 data point에서의 loss function gradient를 계산하고, 행렬 점화식에 대입하여 새로운 parameter point를 찾는다.
- 2번 step을 반복하며 loss 함수가 minimum이 되는 최적의 parameter(를 찾는다.
- lr을 정의하고 starting point()를 잡는다.

-
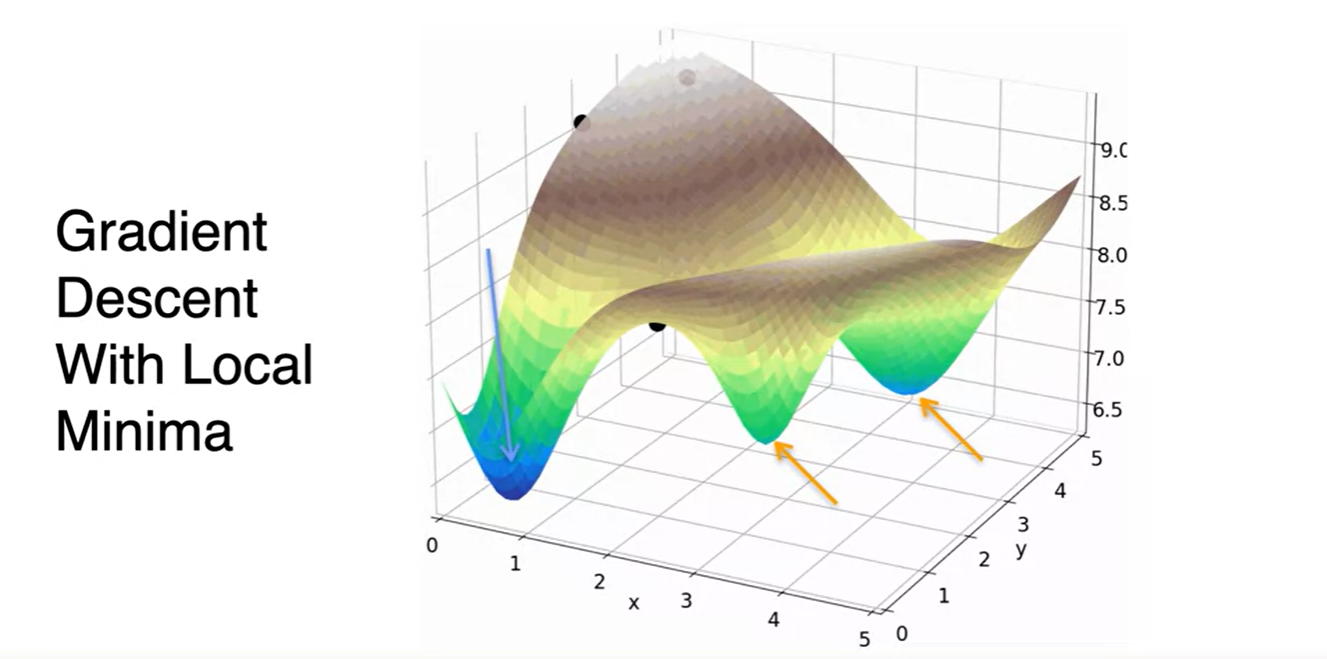
지금까지 소개한 Gradient Descent는 초기 parameter point에 민감하다는 단점이 있다.
- 어디를 시작점으로 하냐에 따라서 local minima에 빠질 수도 있고, Global minima를 향해갈 수도 있기 때문이다.
Optimization using Gradient Descent - Least squares
-
function의 최소점은
- 각 parameter의 편미분으로 gradient가 0인 지점을 찾음으로써 point임을 알 수 있었다.
-
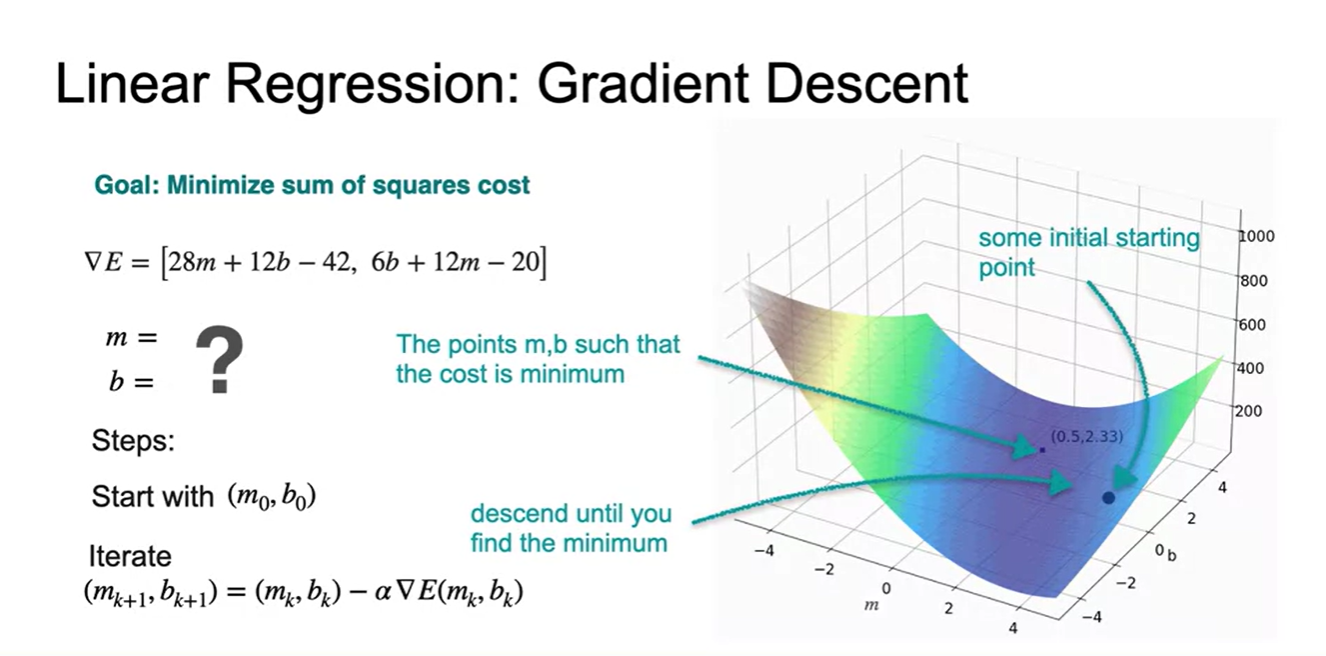
Linear Regression에서의 Loss(Error) function을 미분한 gradient vector를 찾으면
-
로 전개된다.
- 이 때 우리가 하게 될 일은 점을 starting point로 잡아, 점화식을 업데이트 하는 일이다.
-
Optimization using Gradient Descent - Least squares with multiple observations
-
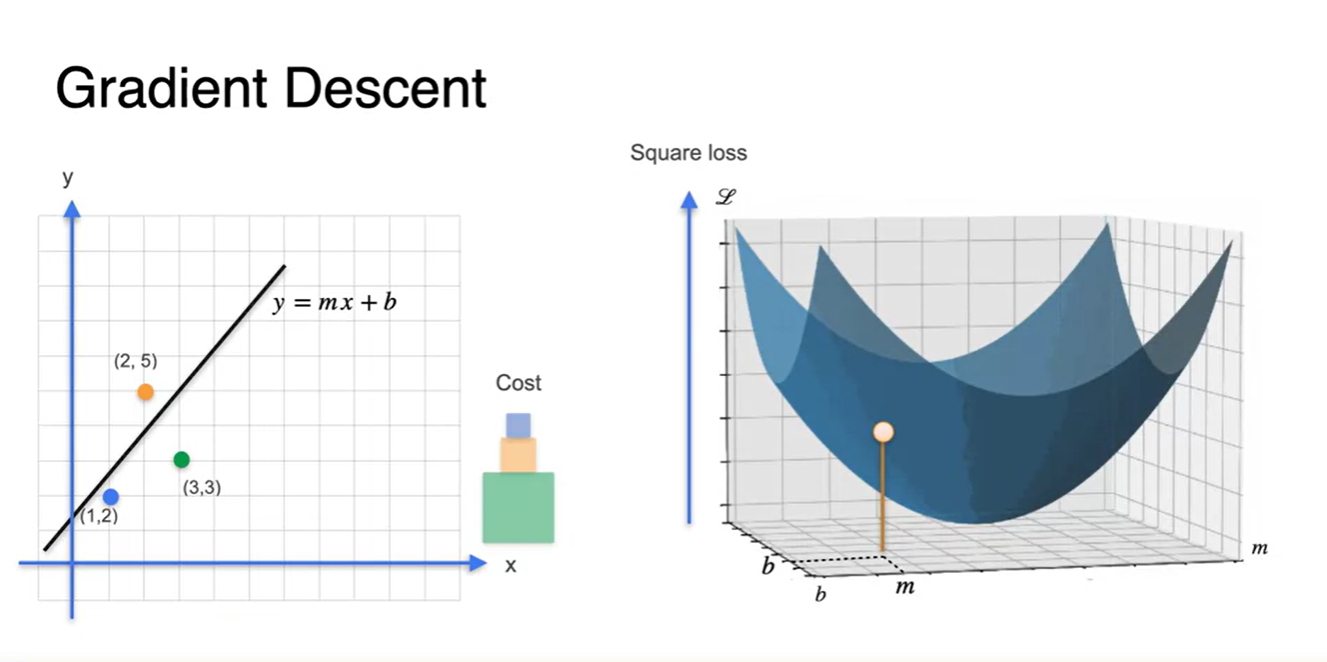
기존에 다뤘던 Linear regression에서의 loss는 (각 데이터 포인트 - 추론값 )의 square(넓이) 합으로 나타낼 수 있었다.
- 이 때 어떠한 parameter 를 초기값으로 설정하면 해당 Loss point의 위치를 그래프로 표현할 수 있다.
-
임의의 선형 방정식을 아래 그림과 같이 오차가 크게 설정한다면 Loss(square 합) 또한 커질 것이다.
- 이 때의 에 따른 Loss point는 당연하게도 큰 값을 가질 수 밖에 없다.
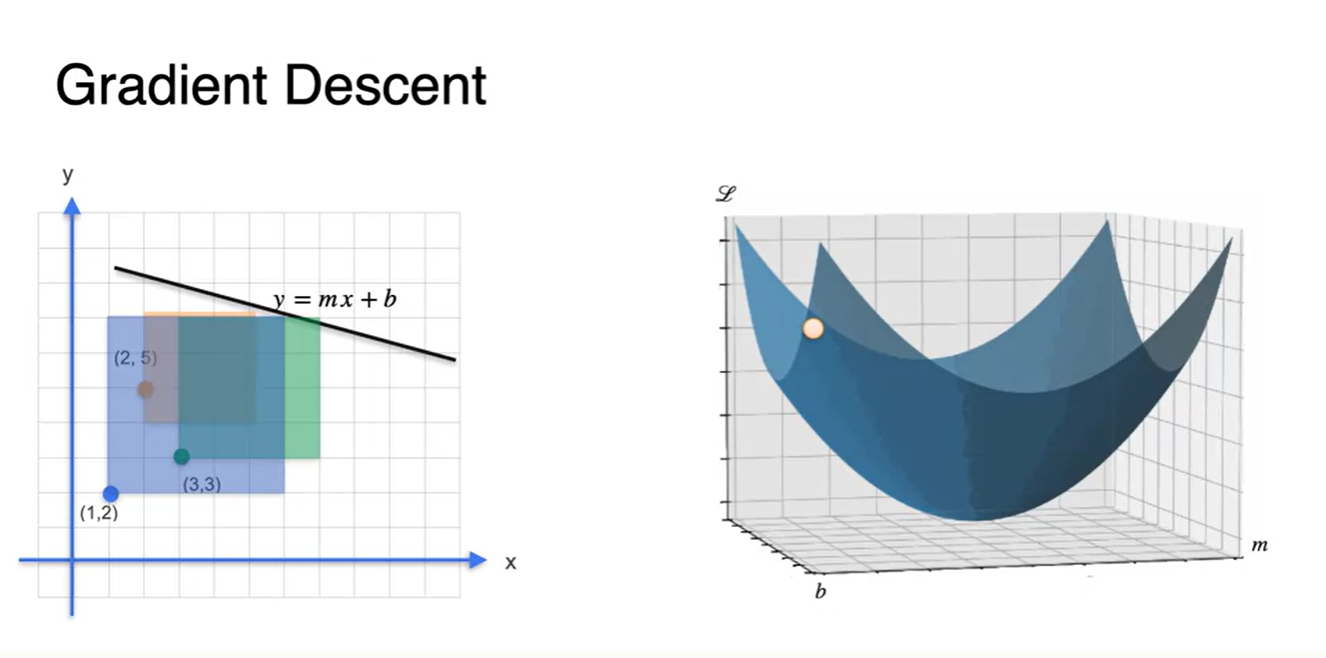
-
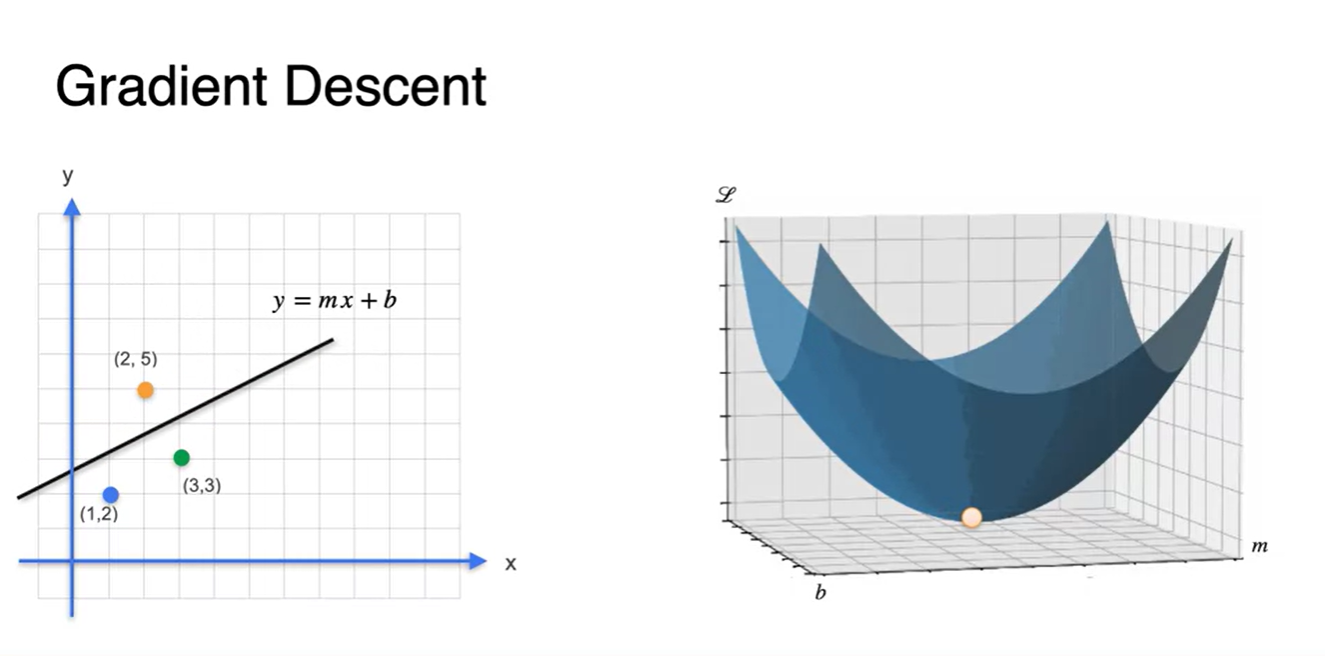
만일 최적의 parameter 한 쌍을 찾게 된다면 해당 지점에서의 Loss point는 0이 될 것이다.
- 이렇듯 Error를 가장 최소화하는 parameter 를 찾아 내는 것이 우리의 궁극적인 목적이다.
- TV 광고에 따른 매출 변화를 예시로 들어보자.
-
육안으로 보기에도 광고에 돈을 많이 들일수록 매출이 높다는 상관관계를 추측할 수 있다.
- 우리는 특정 TV buget을 넣었을 때의 Sales를 추정하고자 싶은 것이 목표이므로 이러한 연관 관계를 설명해줄 선형 방정식을 찾고 싶은 것이다.

-
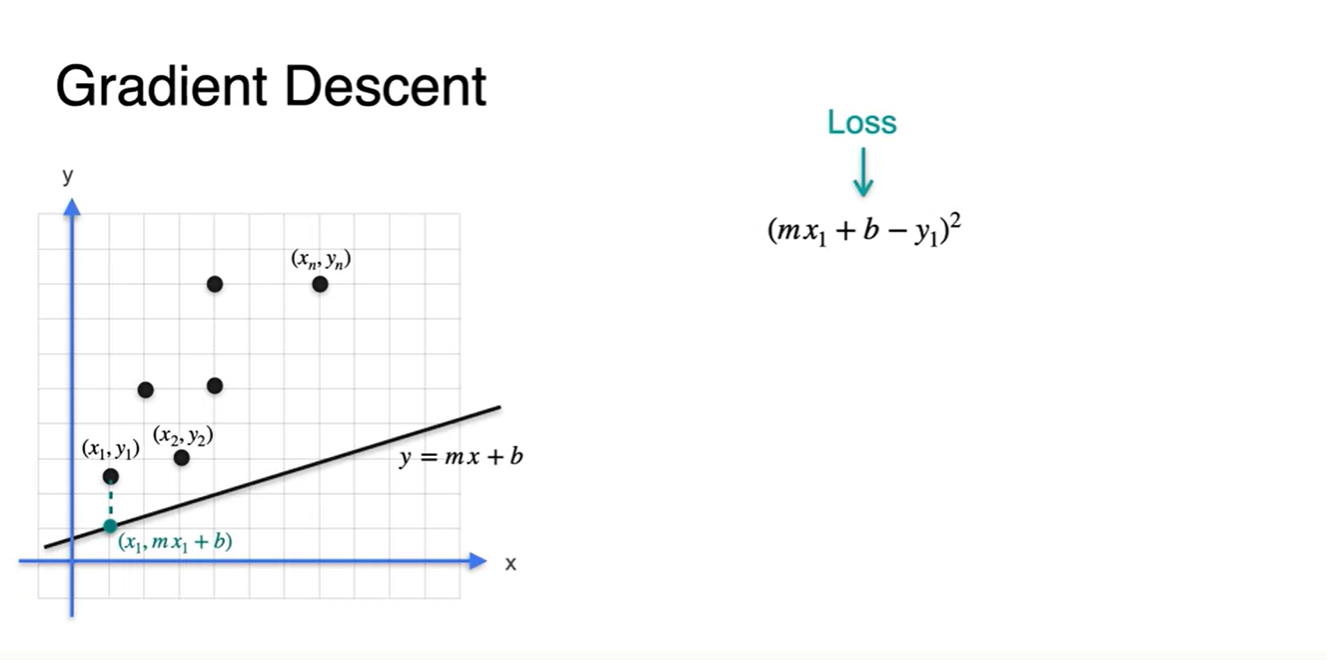
Loss는 정답 와 추론 의 단순 차이로도 나타낼 수 있다.
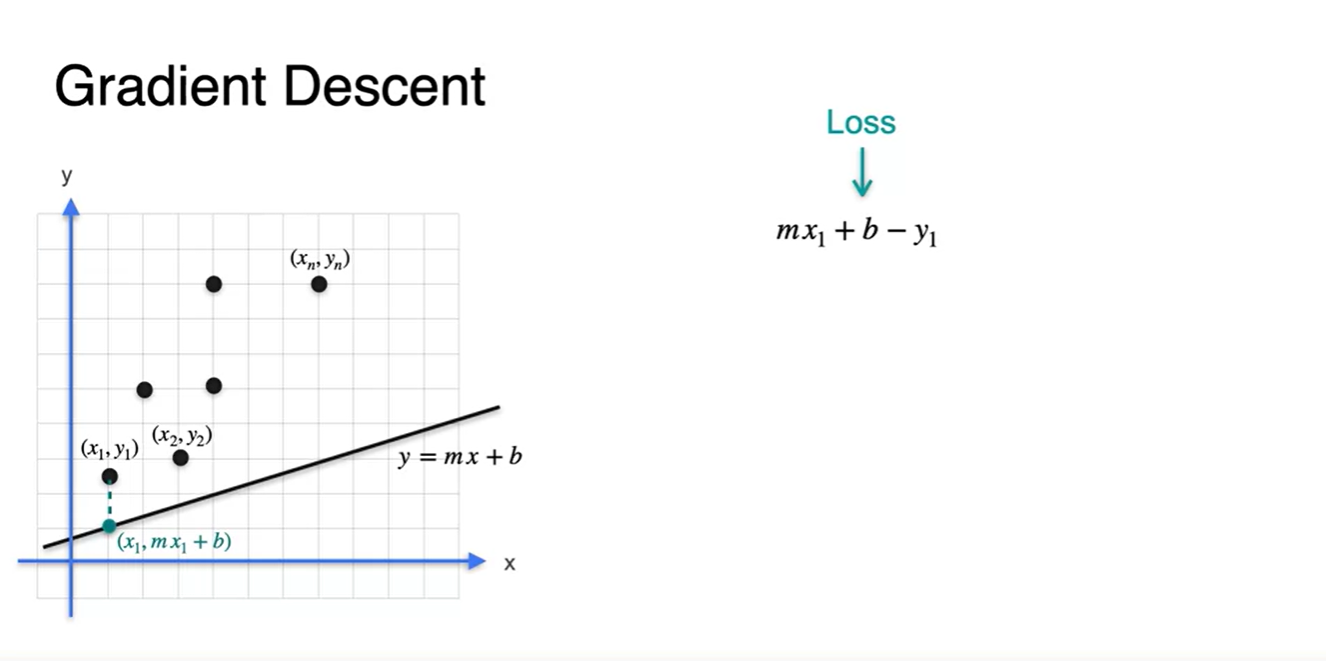
-
편차가 양수(+), 음수(-)를 동시에 가질 때, 이를 합하는 것은 오류를 불러일으킬 수 있기 때문에 제곱을 사용한다.
- Loss는 귀찮겠지만 이렇게 정의되는 것이 좋다.
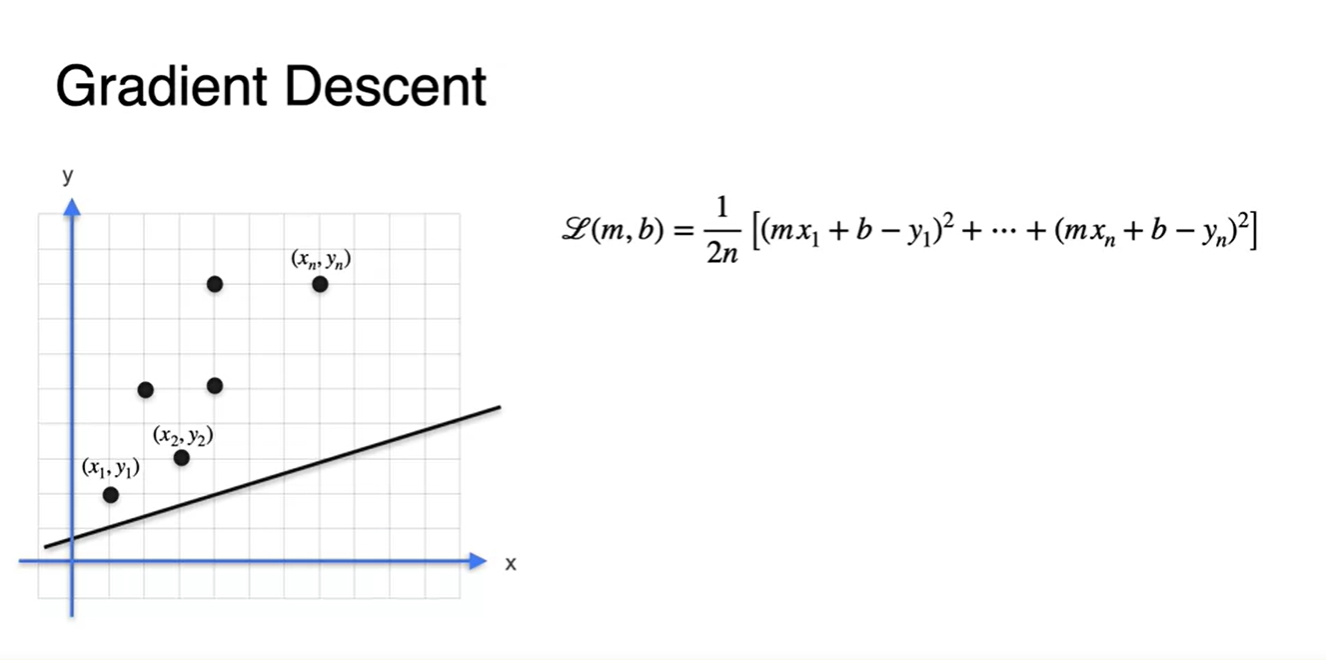
-
각 데이터 point들이 총 개가 있다고 하면 Loss는 각 지점에서의 오차의 평균으로 나타낼 수 있다.
-
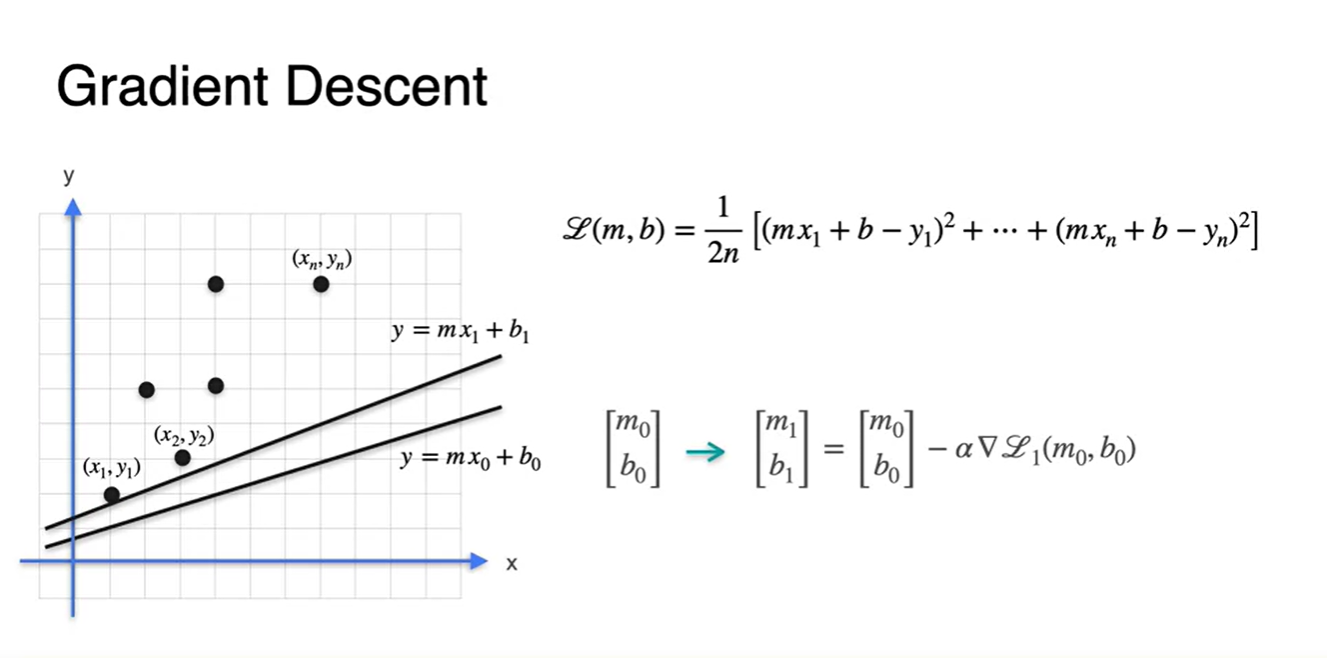
-
Starting point 에서의 gradient descent로
- 을 추론한 next 선형 방정식이다.
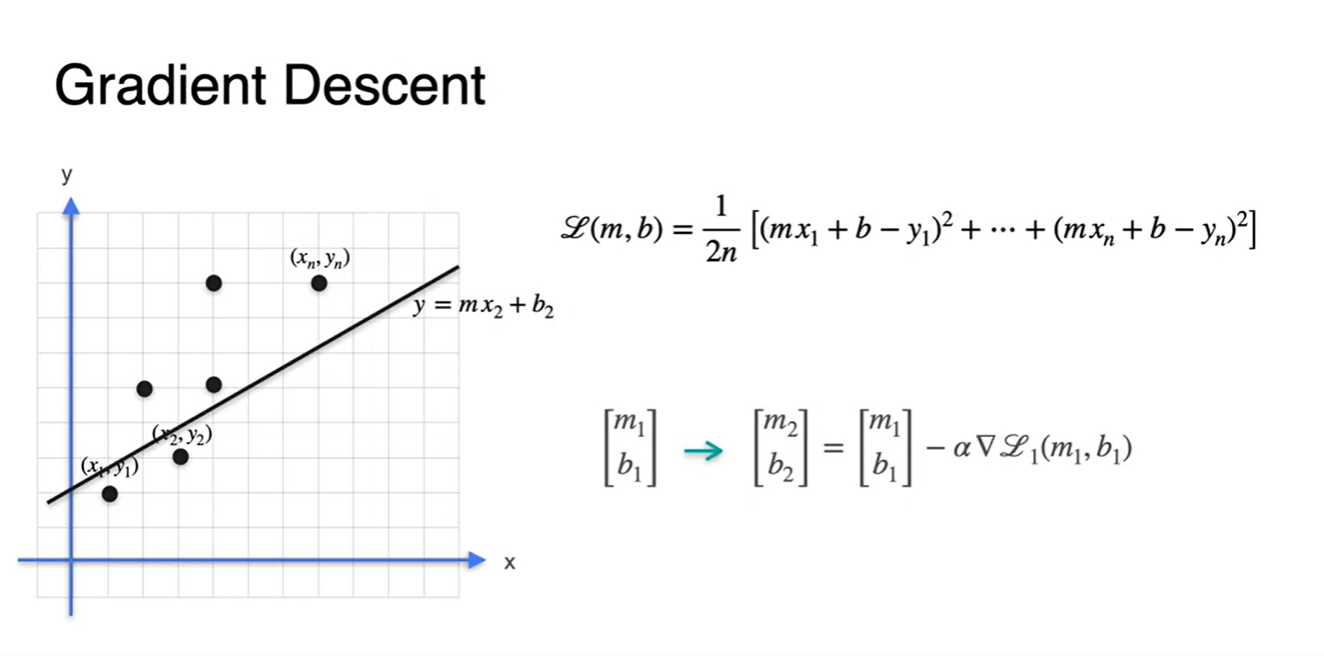
-
에서의 gradient descent로
- 을 추론한 next 선형 방정식이다.
-
에서의 gradient descent로
- 을 추론한 next 선형 방정식이다.
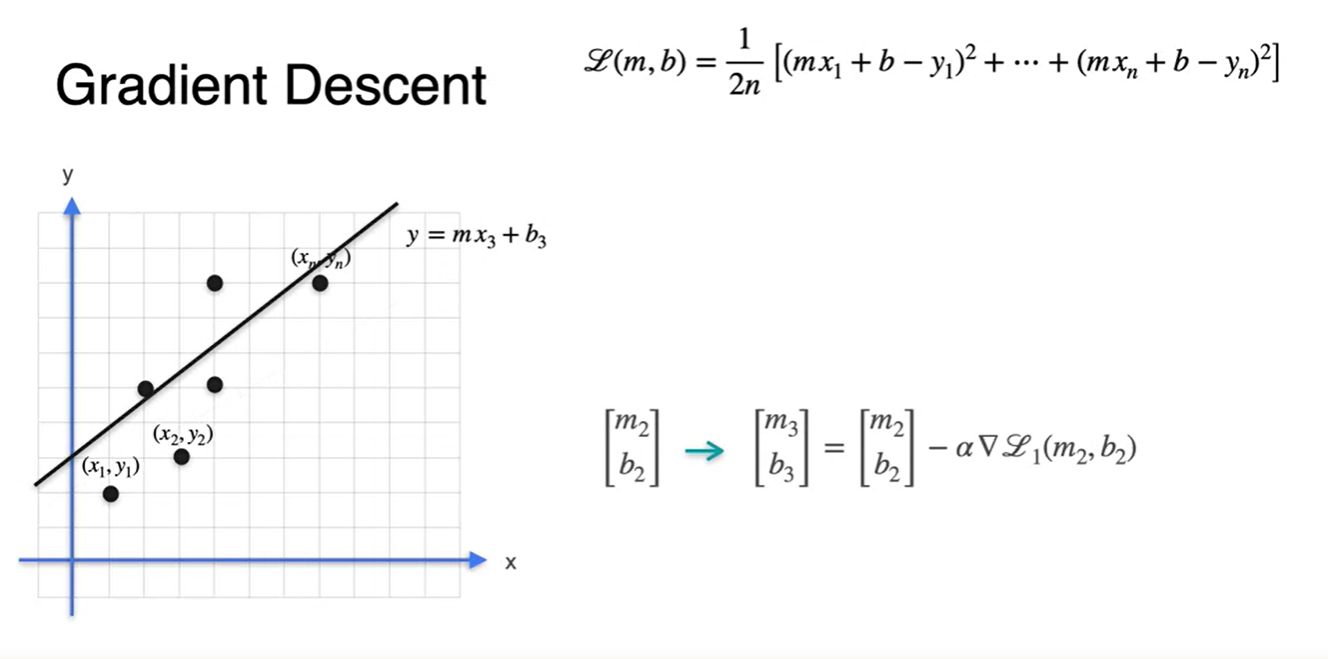
-
이렇게 여러 번(현재 수식 내에서는 번)의 과정을 반복하여 찾아낸
- 최종 parameter 로 선형 방정식을 그려보면 얼추 Loss가 줄어든 지점에 방정식이 표현되었음을 알 수 있다.