System of linear equations

Specialization & Course Introduction

• 이 코스는 총 3개의 챕터로 이루어져있다.

  1. Linear Algebra
  2. Calculus for ML/DS
  3. Probability and Statistics

• 머신러닝은 evidence(data)를 보고 scenario를 예측하는 것이다.

System of linear equations: 2 variables

Machine learning motivation

• Linear Algebra를 master해야만 하는 이유

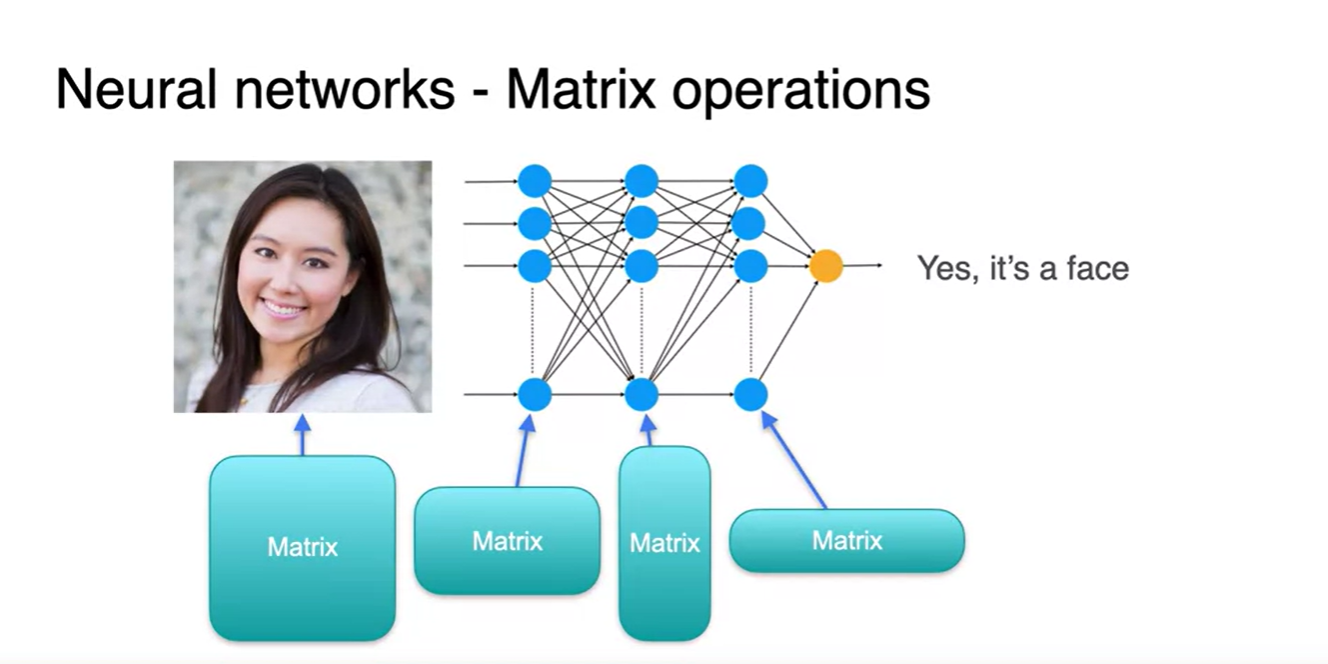
  • Input, Neural network, even Output 모두 matrix form을 하고 있다.
  • Linear Algebra는 Machine Learning의 모든 범주에서 쓰인다.

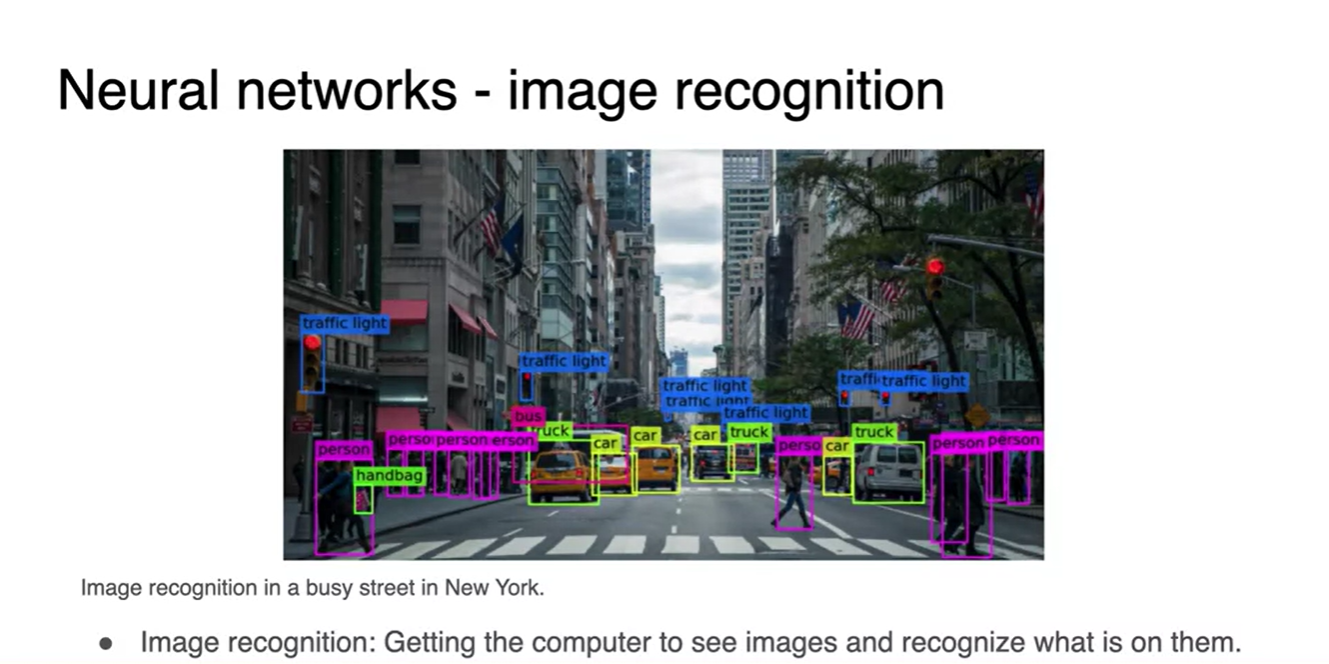
• Image recognition는 그동안 꽤 long term challenge였다.

  • 허나 Image pixels은 결국 쉽게 보면, 한 matrix의 values다!

Systems of sentences

• Sentence 속에는 informations가 존재한다.

  1. 문장들이 중복 없이 여러 정보를 담을 때 : Complete, Non-singular
  2. 문장들이 중복되어 정보를 덜 담고 있을 때 : Redundant, Singular
  3. 문장들이 중복되지는 않지만 서로 모순될 때 : Contraditory, Singular

• 보통 Non-singular한 data는 많은 정보를 담고 있고, Singular한 data는 이보다 적은 정보를 가지고 있다.

  • cf. singular : 특이적, non-singular : 비특이적

• 정보는 우리가 원하는 대로 data에 담을 수 있다.

  • 시스템이 얼마나 중복되는지 측정하는 방법은 rank로 알 수 있다.

• Quiz

  • Dog, Cat, Bird 중 하나는 색깔이 빨간색이다.
  • Dog과 Cat 중 하나는 색깔이 주황색이다.
  • Dog은 색깔이 검정색이다.

  Problem 1. Bird의 색깔은?
  : 빨간색, Dog: 검정, Cat: 주황

  Problem 2. 이 시스템은 singular인가 non-singular인가?
  : Non-singular → 정보가 알차다!

• Singular Value Decomposition(SVD)도 중복된 차원을 분해한다는 점으로 이해하면 되려나?
  • (GPT-4) SVD를 통해 데이터의 중복되거나 불필요한 차원을 제거하고, 가장 중요한 정보만을 남길 수 있습니다.

System of equations

• 문장 안에 숫자들이 포함되면, 적당한 변수와 함께 equation으로 표현할 수 있다.

• Quiz 1

  • Day 1의 정보만으로는 각각의 가격을 찾아내기(clue)가 불가능하다.
  • Day 2의 정보까지 주어진 후, 이 퀴즈의 모든 option이 주어졌다고 하자.
  • Question : 각 과일의 가격은 얼마인가?

• Solution 1을 구하는 과정을 tracking 해보자.

  • Day 1에서 Day2로 넘어가는 과정 중에 바나나 하나가 추가되면서 2달러가 증가했다.
  • 그렇다면 바나나의 가격은 2달러이며, 사과의 가격은 8달러로 결정된다.

• Quiz 2
  • 이번에는 사과 1 + 바나나 1 = 10, 사과 2 + 바나나 2 = 20이라고 해보자.
  • Question : 각 과일의 가격은 얼마인가?

• Solution 2를 구하는 과정을 tracking 해보자.

  • 이 System은 두 개의 같은 방정식이 중복(Redundant)되기 때문에 충분한 정보가 담겨있지 않다.
  • 따라서 무한한 해결책을 가진다. ex. 8+2=10, 5+5 = 10, ...

• Quiz 3
  • 마지막으로 사과 1 + 바나나 1 = 10, 사과 2 + 바나나 2 = 24라고 해보자.
  • Question : 각 과일의 가격은 얼마인가?

• Solution 3를 구하는 과정을 tracking 해보자.

  • 이 System의 문장들에는 서로 모순된 정보가 담겨있다.
  • 따라서 해가 존재하지 않는다.

• Recap

• What is a linear equation?

  • 선형대수는 왼쪽과 같은 선형 방정식을 푸는 것이다. Just add the value.
  • 이 방법은 매우 simple하며 정보를 조작(manipulating)하고 추출(extracting)하기에 유용하다.

System of equations as lines

• 선형 방정식을 공간 안에 표현해보자.

  • 2차원 방정식이라면 line으로 결정되고, 3차원이라면 plane으로 결정된다.
  • 3차원 이상의 방정식이면 시각화 하기 힘든 고차원 내에 mapping 된다.

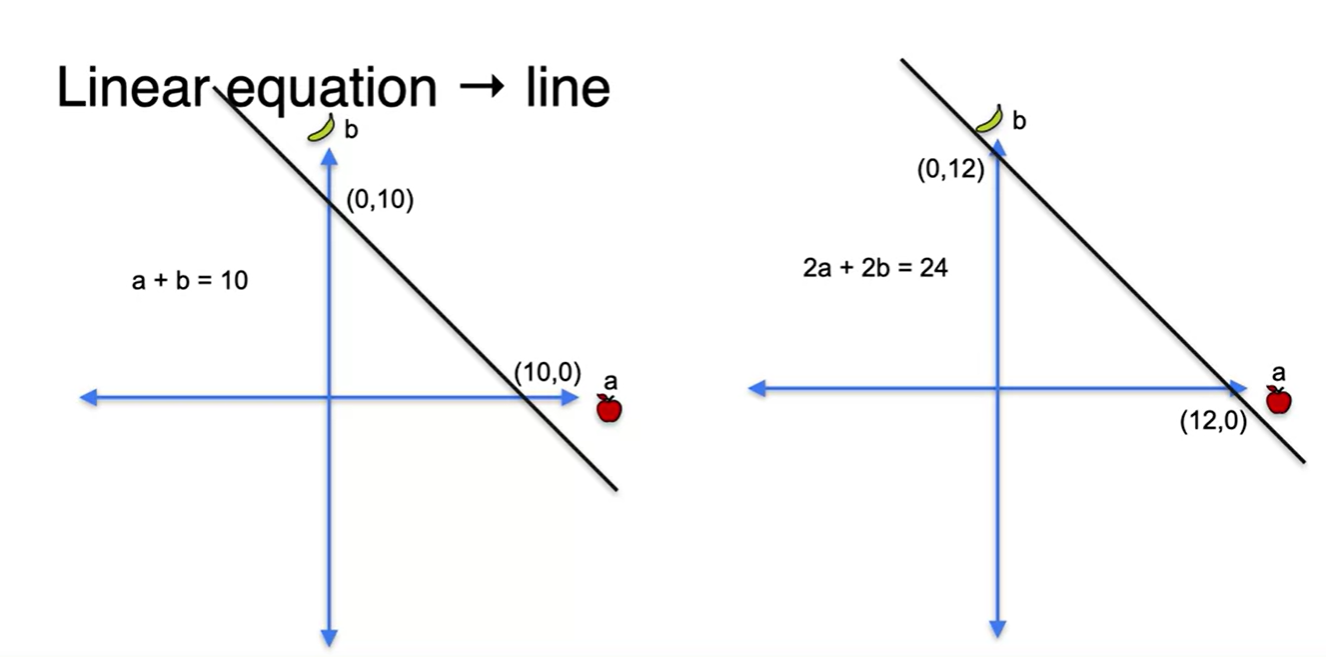
• 해당 방정식을 만족시키는 모든 점을 찍어보면 아래와 같다.

  • y-절편(intercept)과 기울기(slope)로 해당 line의 정보를 표현하는 방법도 존재한다.

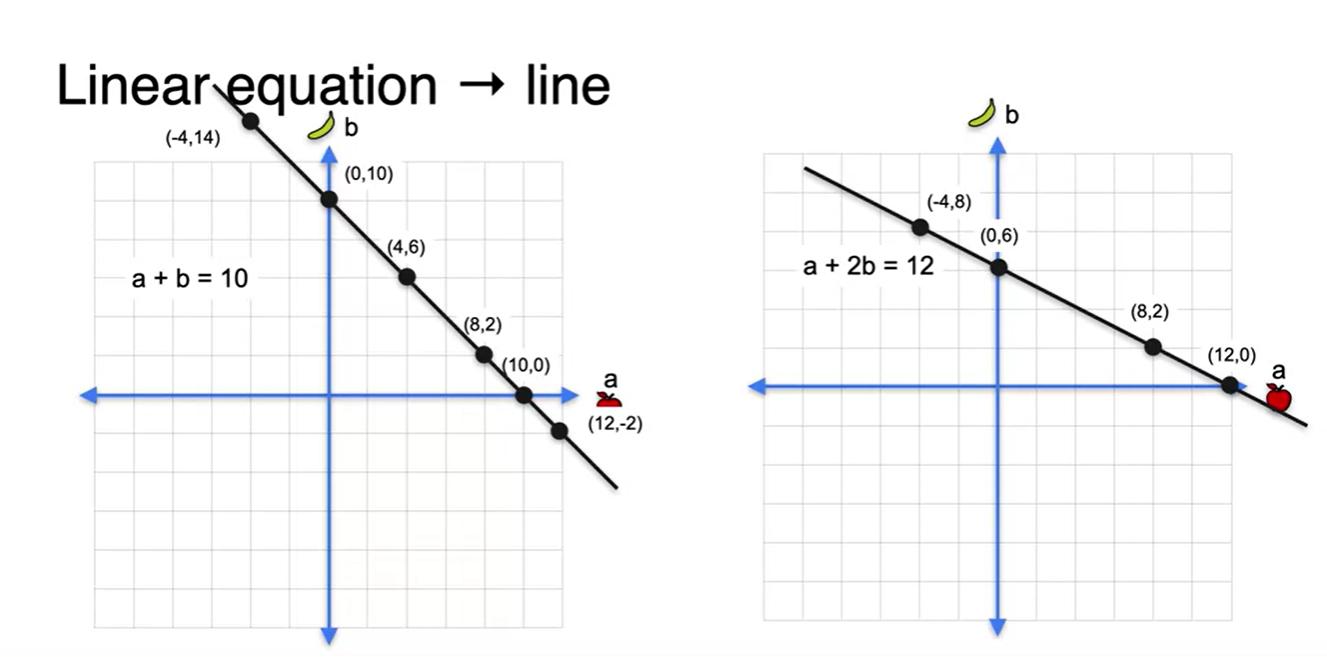
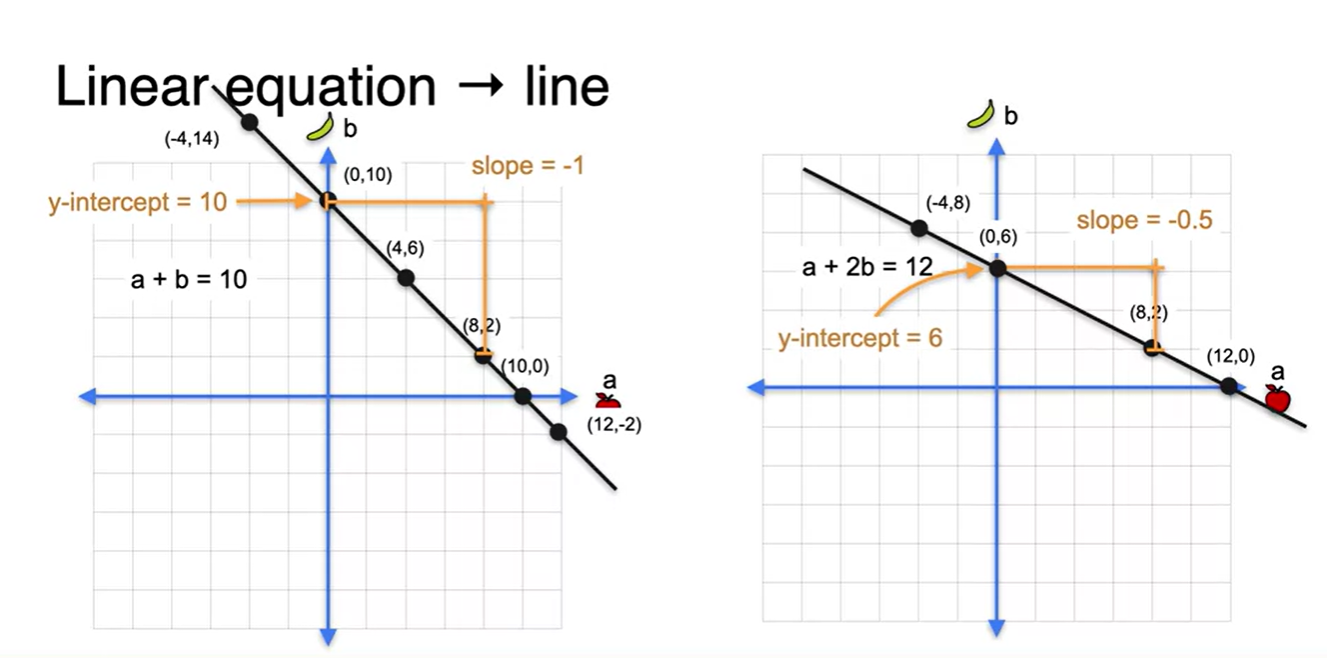
• Algebra로 풀었던 solution을 Geometric하게 겹쳐보면 다음과 같은 해가 결정되는 것을 볼 수 있다. → 해가 있다.

• 만약, 두 번째 케이스라면 어떨까?

  • 마찬가지로 geometric하게 겹쳐보면 수많은 solution을 갖게된다는 점을 알게 된다. → 해가 무한대다.

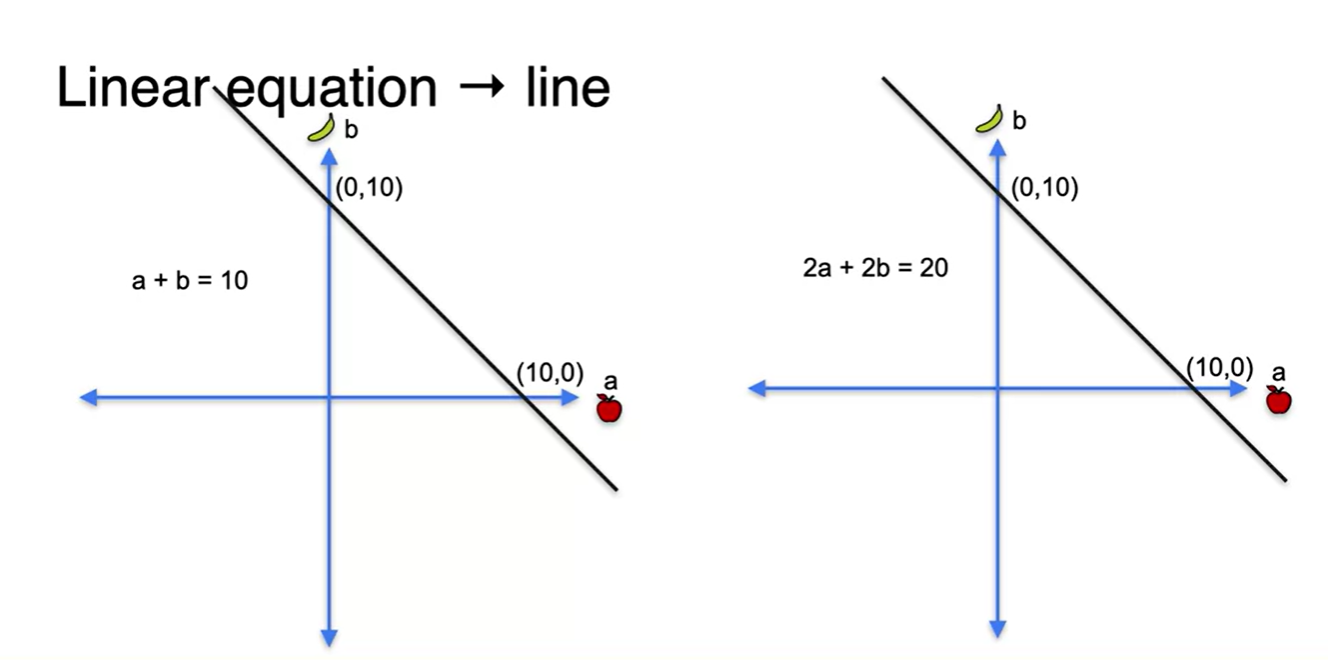
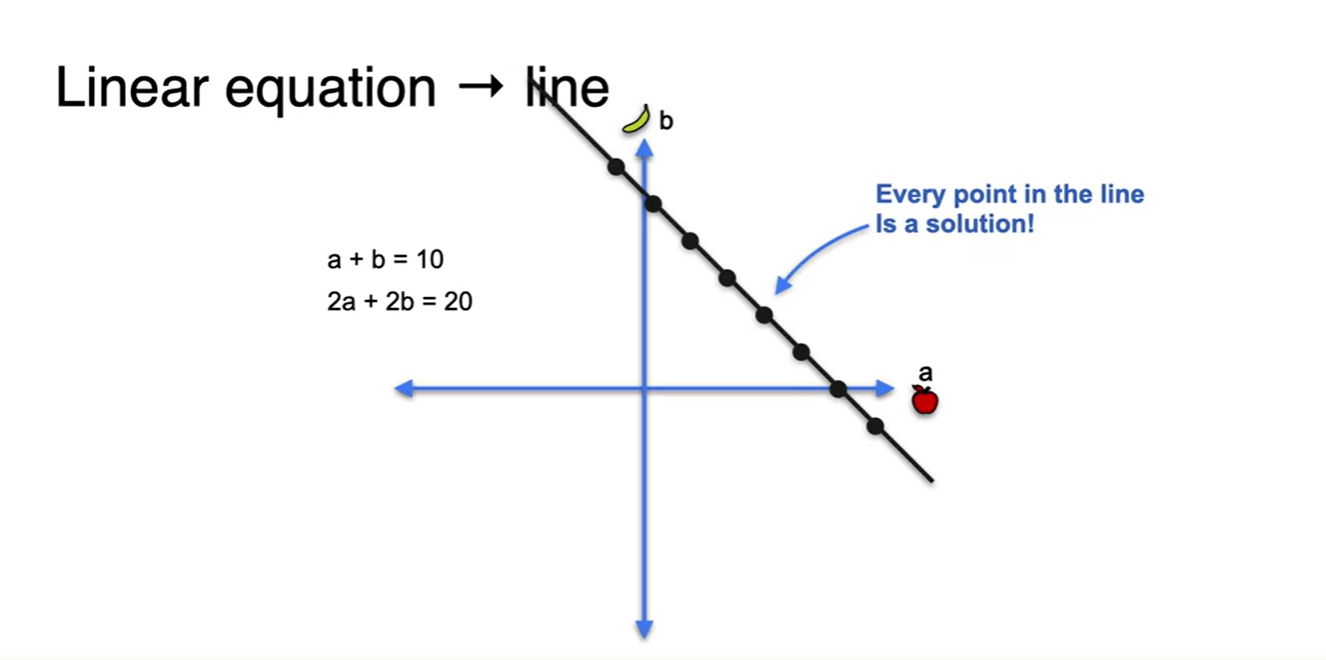
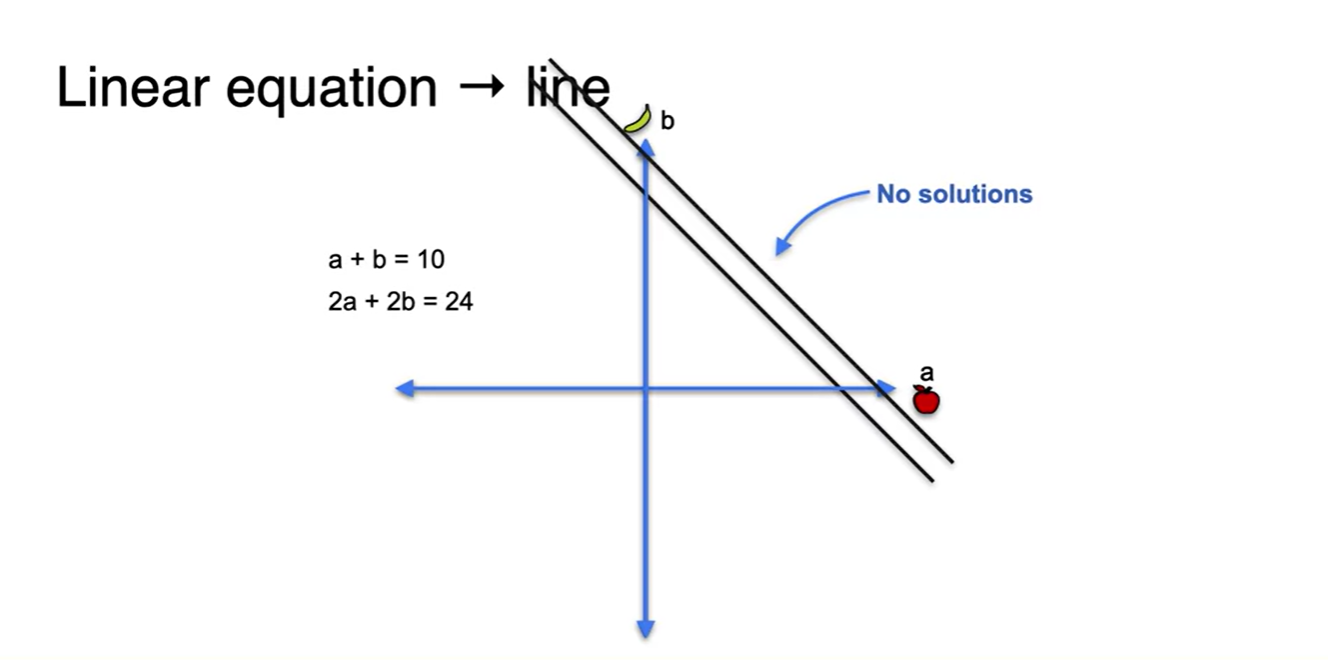
• 세 번째 케이스는 어떨까.

  • Geometric하게 겹쳐보았을 때 parallel하다는 것을 알 수 있다.
  • 두 직선이 평행하면 만나는 점이 영원히 존재하지 않는다. → 해가 없다.

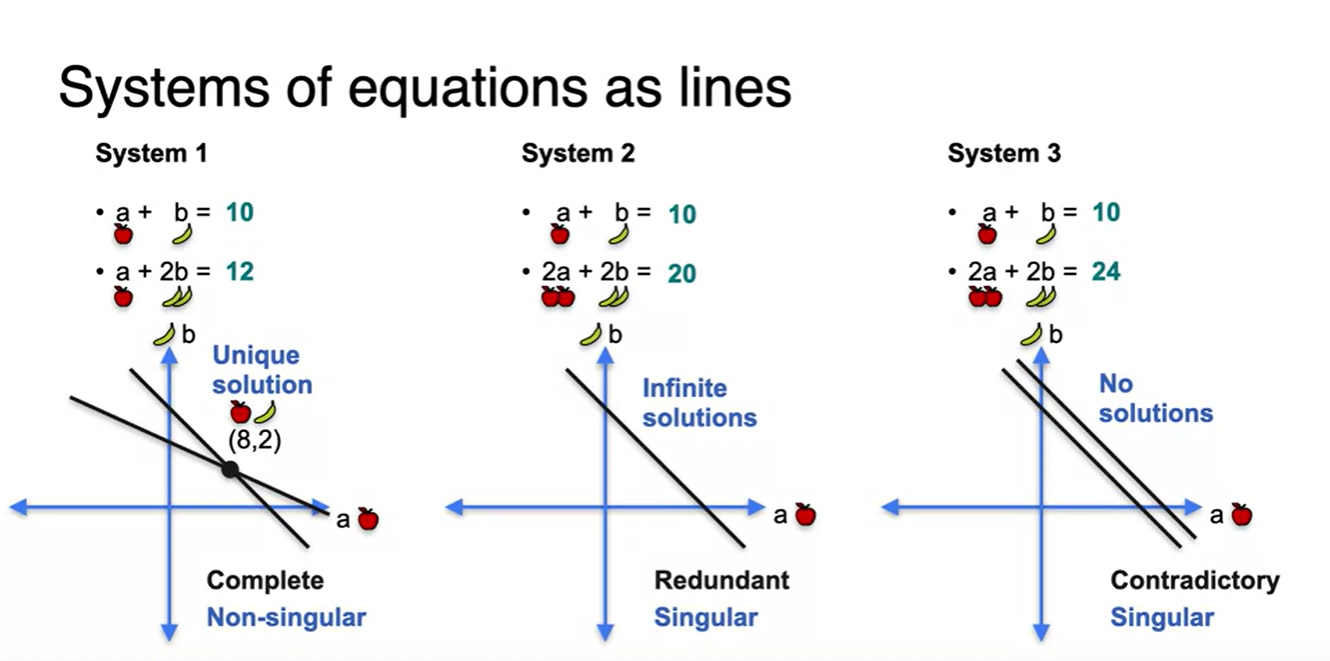
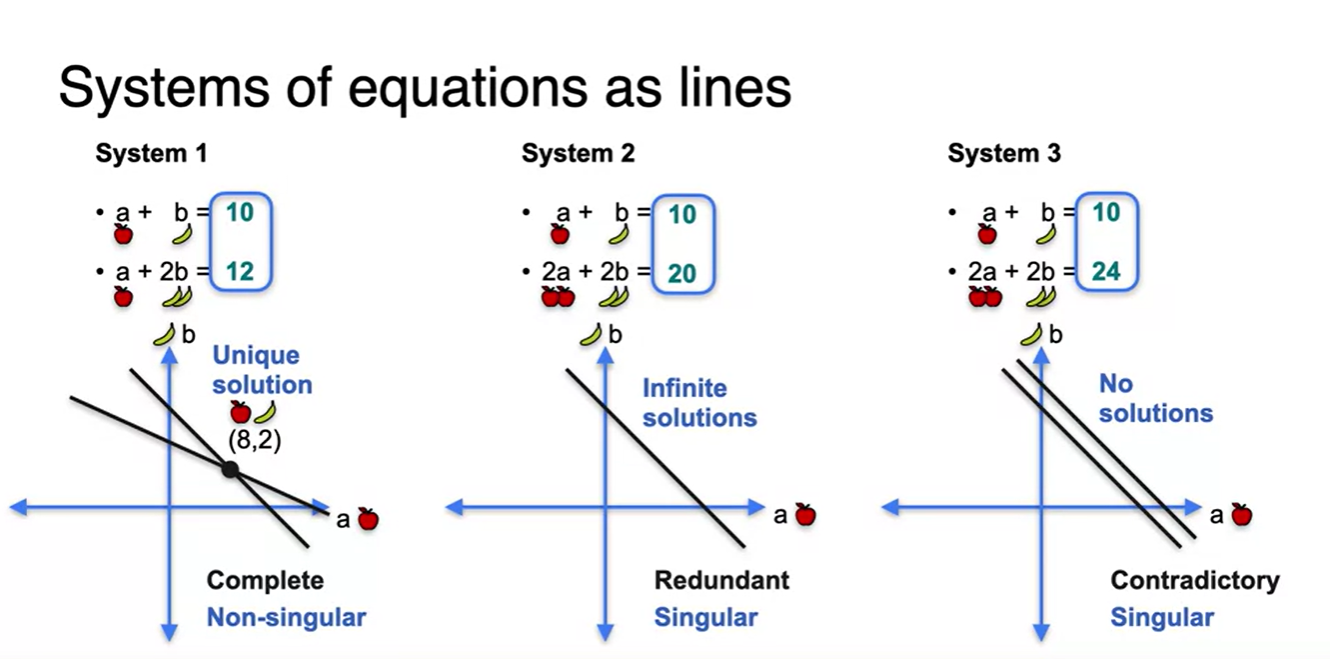
• 세 System을 비교해보자.

  1. 첫 번째 System은 Unique solution을 갖고, Non-singular 값을 가지며 중복되는 방정식 없이 Complete한 상태다.
  2. 두 번째 System은 Infinite solution을 가지며, Singular 값을 갖고, 중복되는 방정식이 존재하는 Redundant한 상태다.
  3. 세 번째 System은 No solution 즉, 해가 존재하지 않고 Singular 값을 가지며 서로 모순된 Contradictory 정보가 담겨있다.

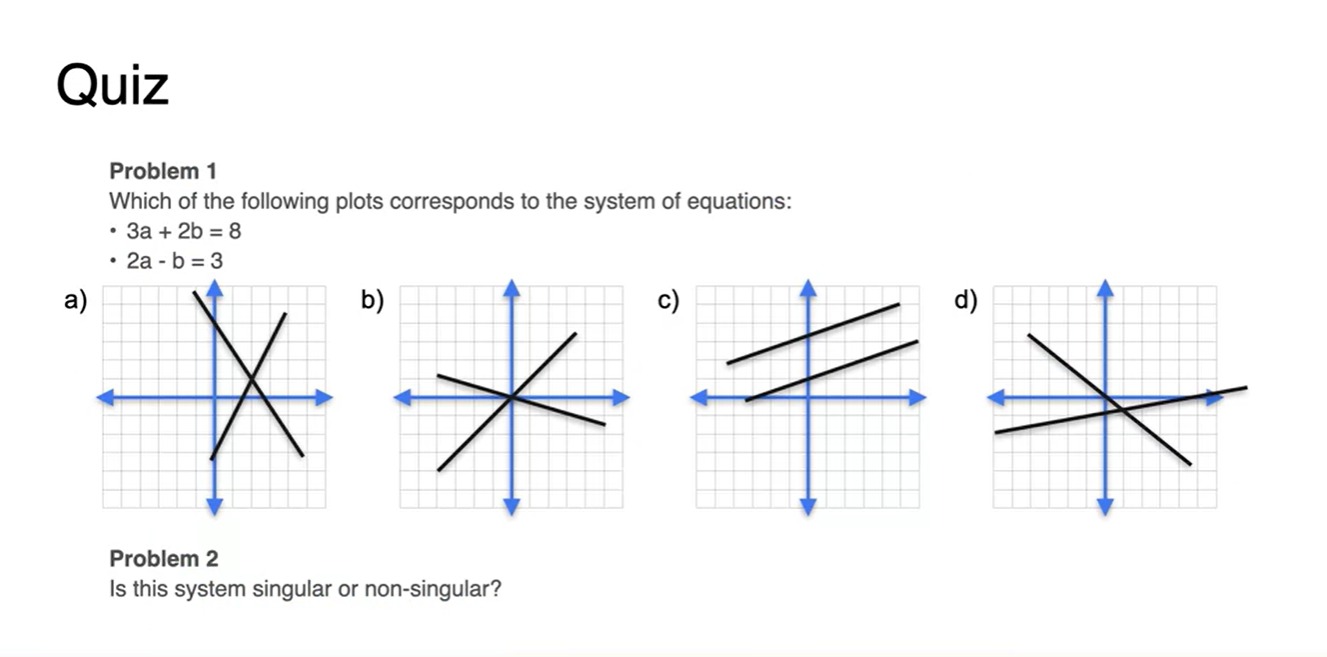
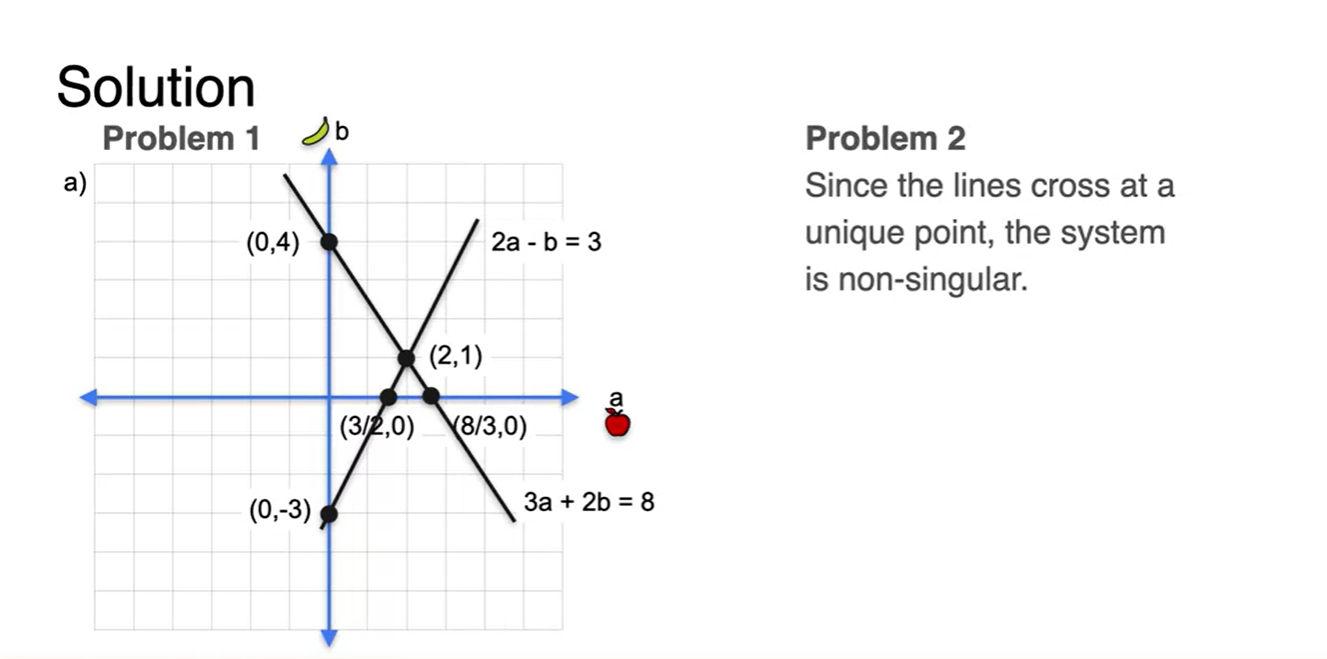
• Quiz

  • Solution : a), Non-singular

A geometric notion of singularity

• Singuarity vs Non-singularity를 geometric하게 표현해보려 한다.

  • 우선, 기존에 3가지 System으로 나누었던 equation의 상수에 주목해 보자.
  • Singularity와 Non-singularity를 두 버킷으로 나누는 기준은 해당 constant들을 0으로 바꾸었을 때 비로소 나타난다.

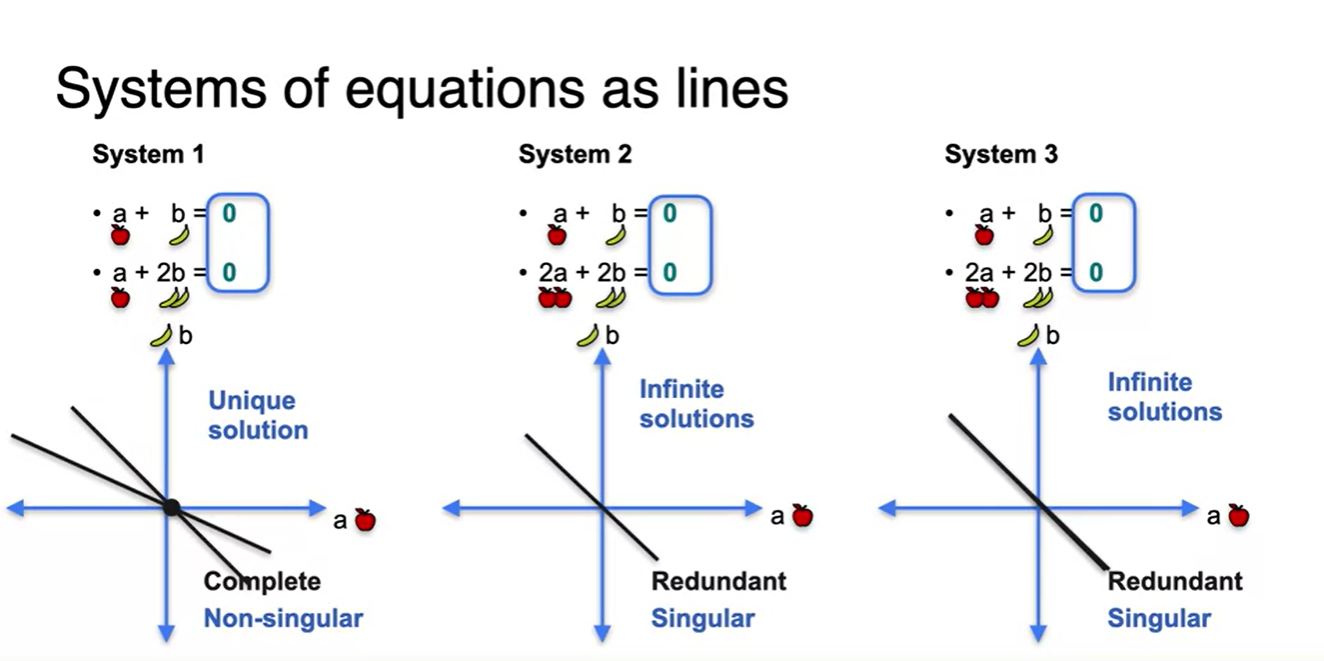
• 여기서 주목할만한 점은 No-solution을 갖던 System 3가 Infinite solutions를 갖는 System으로 바뀌었다는 점이다!

  • 또한, 모든 lines가 항상 원점을 지나는 함수로 변경된다. → 기하학적인 해석
  • 이러한 방식으로 각 equation을 비교하는 것이 앞으로는 더욱 simple하기 때문에 Singular와 Non-singular에 조금 더 주목하면 좋을 것이다.

Singular vs nonsingular matrices

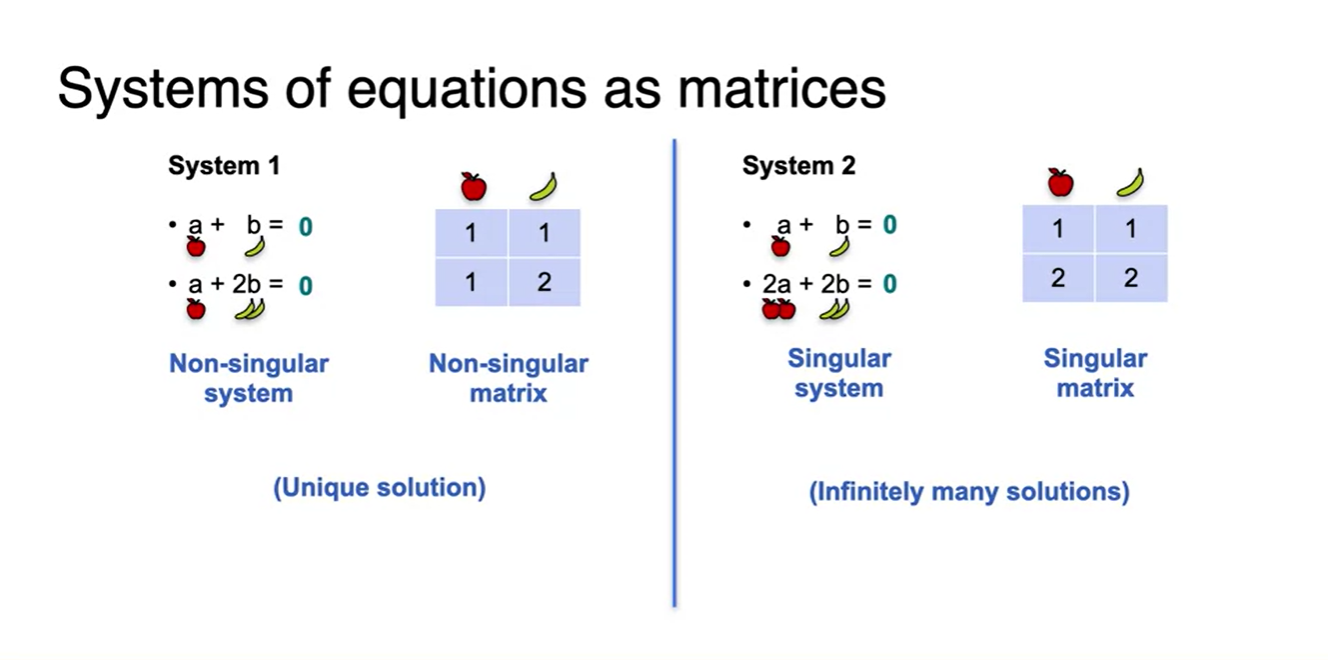
• 위 equations를 matrix로 각각 나타내면 다음과 같다.

  • 2x2 행렬로 나타내었으며, 앞으로는 더 큰 행렬을 보게 될 것이다.
  • 이후 강의에서는 Singular와 Non-singular를 구분하는 더 빠른 방법을 배우게 될 것이다. → 아마도 determinant

Linear dependence and independence

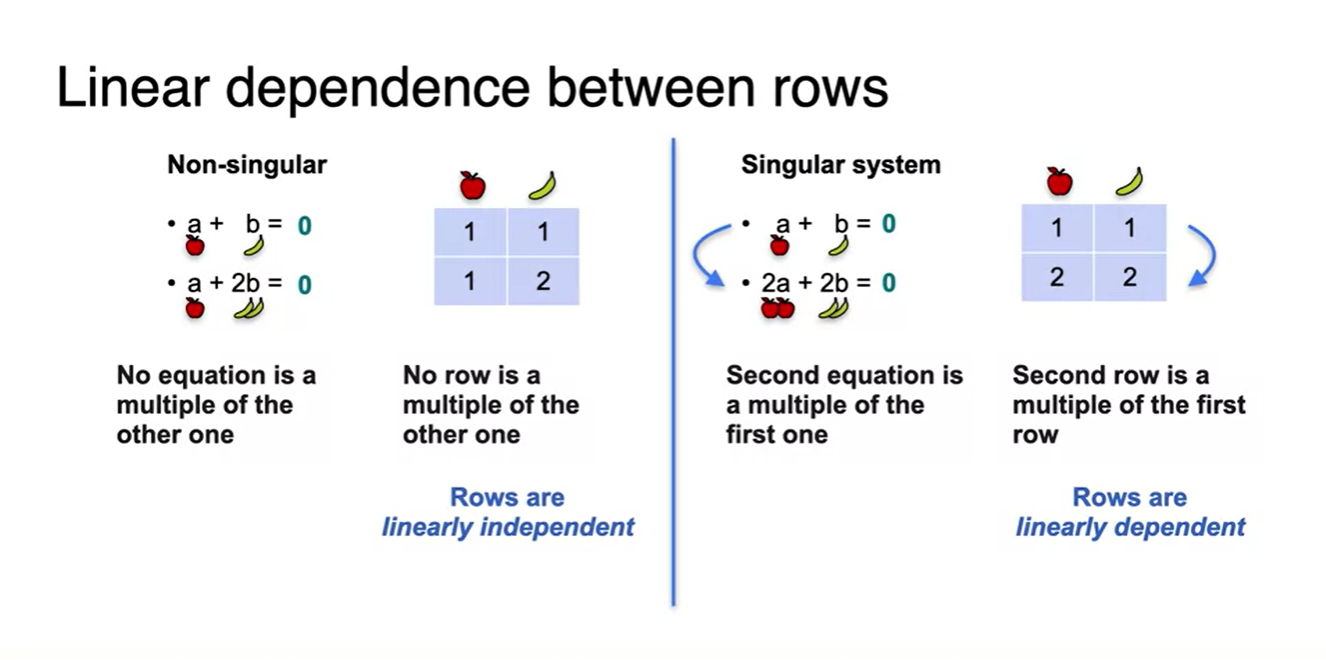
• 아래 그림에서의 두 식을 비교해보자.

  • 오른쪽에 위치한 Singular system은 하나의 식*constant(여기서는 2)를 하면, 다른 하나의 식과 완전히 일치하는 꼴이 된다.
  • 이를 서로 종속 관계에 놓였다고 하여 linearly dependent라 한다.

• 왼쪽 식은 어떠한 constant 값으로도 곱하였을 때 다른 하나의 식을 만들어낼 수 없다.

  • 이를 서로 독립 관계에 놓였다고 하여 linearly independent라 한다.

The determinant

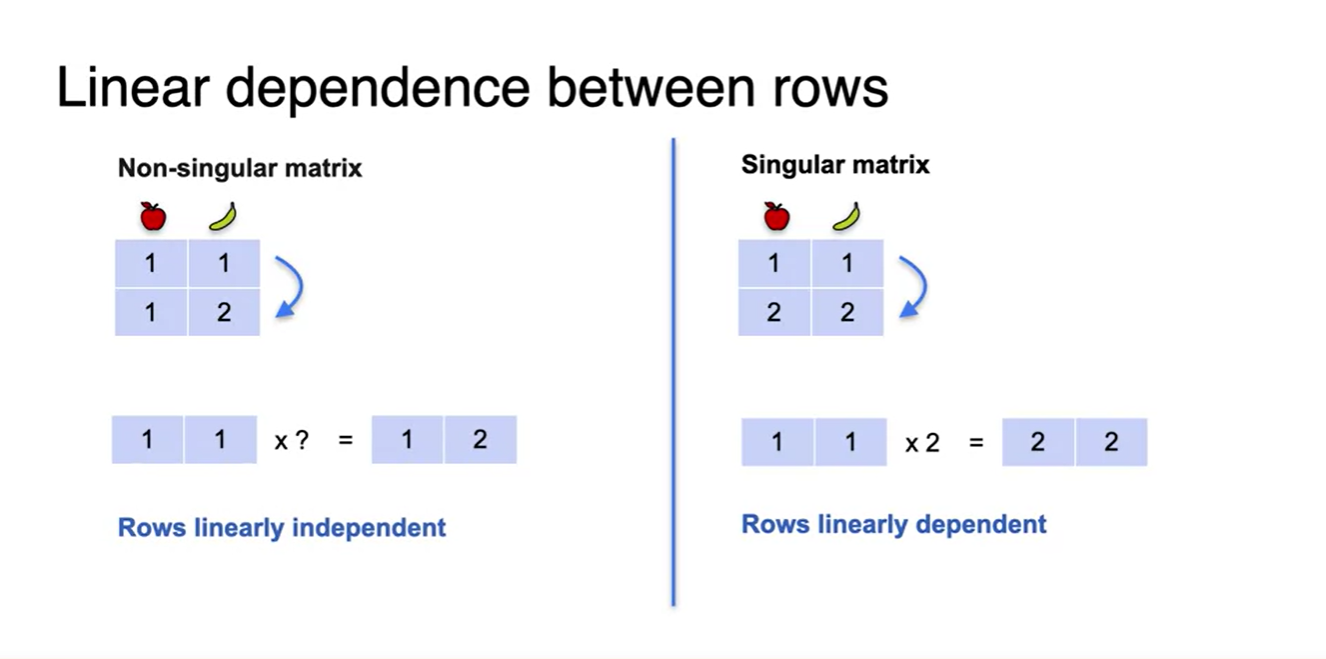
• 앞서 각 행들의 관계가 하나의 constant를 곱하였을 때 같아진다면 Singular matrix이자 linerly dependent 관계에 있다고 본다.
  

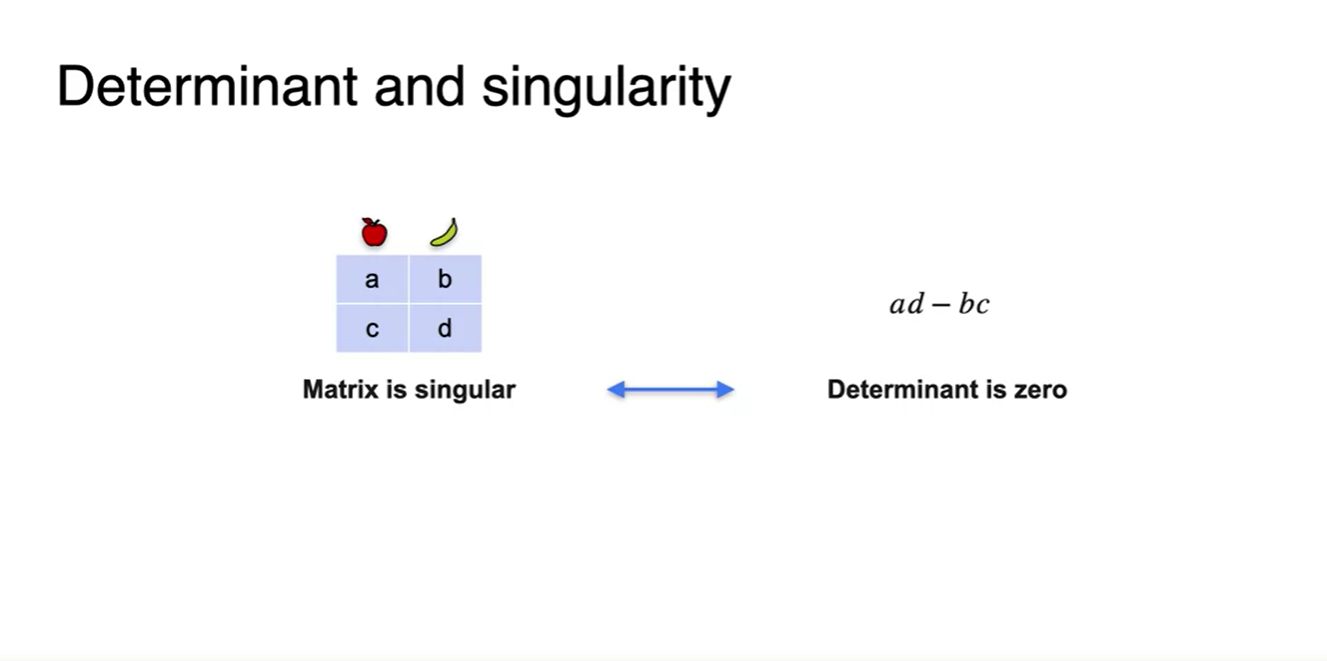
• 해당 matrix가 Singular하다는 것을 확인할 수 있는 방법을 증명해보자.

  • (a, b)의 pair에 k를 곱하면 (c, d)이다.
    • $ak = c$, $bk=d$다.
  • k로 묶어 다시 표현하면 $\displaystyle \frac{c}{a} = \frac{d}{b} = k$로 정리된다.
    • 즉, $ad = bc$이고 $ad-bc=0$일 때 이 matrix는 linearly dep. 하며 Singular matrix다 라는 것을 알아낼 수 있다!

  cf. 그러면 $Av = \lambda I v$로 정리하는 eigenvector 구하기에서도 $det|A−λI|=0$로 해를 찾는데, 이 과정의 의미는?

  • (GPT-4) $A−λI$가 singular, 즉 $det|A−λI|=0$인 경우를 찾는 것은, $A$의 작용이 특정 방향에서는 단순히 스케일링으로 귀결될 수 있음을 의미합니다.
  • 결국, 여러 basis들의 가장 단순한 선형 조합을 이룬 eigenvalues, eigenvectors를 찾아 해당 공간을 simple하게 설명하는 방법의 일환이다!

• Quiz

• Solutions

Ungraded Lab

• Introcuation to numpy arrays

System of linear equations: 3 variables

System of equations (3x3)

• Quiz

  1. a + b + c = $10
  2. a + 2b + c = $15
  3. a + b + 2c = $ 12

• Solutions

• 이번에도 역시 3개의 system이 있다고 생각해보자.

• Solutions

2. c의 정답은 알 수 있지만 a와 b는 a+b=10로 해가 무수히 많다.
3. 2번째 식과 3번째 식으로부터 결정된 c의 값이 다르므로 해가 없다.
4. a+b+c=10을 만족하는 모든 조합이 해가될 수 있으므로 해가 무수히 많다.

• 이제 constant 항을 없앤 다음, 다시 방정식을 정리해보자.

  • 그러면 Non-singular와 Singular로 의미가 간단하게 나뉘게 되며, 해가 존재하는 조건을 구별지을 수 있다.

• 이 방정식을 3x3 행렬로 정리하면 아래와 같다.

System of equations as planes (3x3)

• 이전에 우리가 2x2 행렬로 나타냈던 방정식의 기하학적 의미는 line으로 표현됐다.

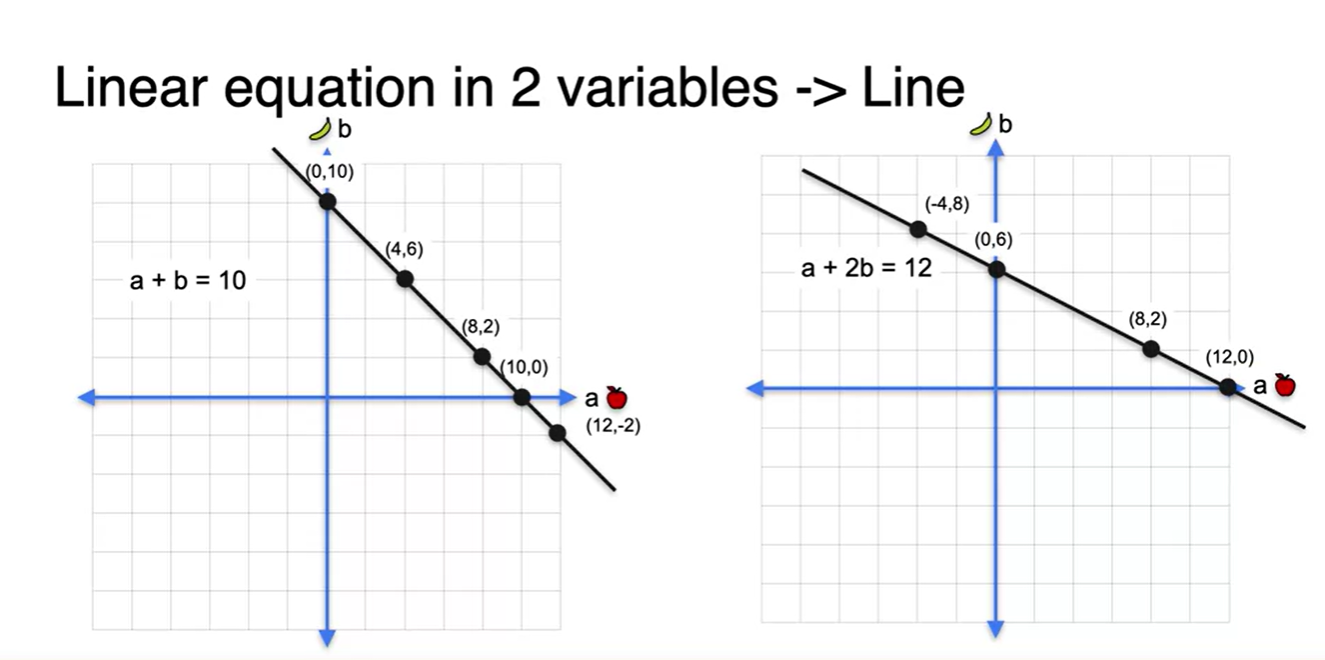
• 3개의 변수로 이루어진 방정식을 고려해보자.

  • 해당 방정식을 만족하는 임의의 점들을 찍으면 그림에 찍힌 점들과 같다.
  • 세 점들을을 비롯한 모든 점을 연결하는 공간은 3차원의 공간 상에서 plane으로 형성되며, 이러한 공간이 해당 방정식의 해가 존재하는 공간이다.

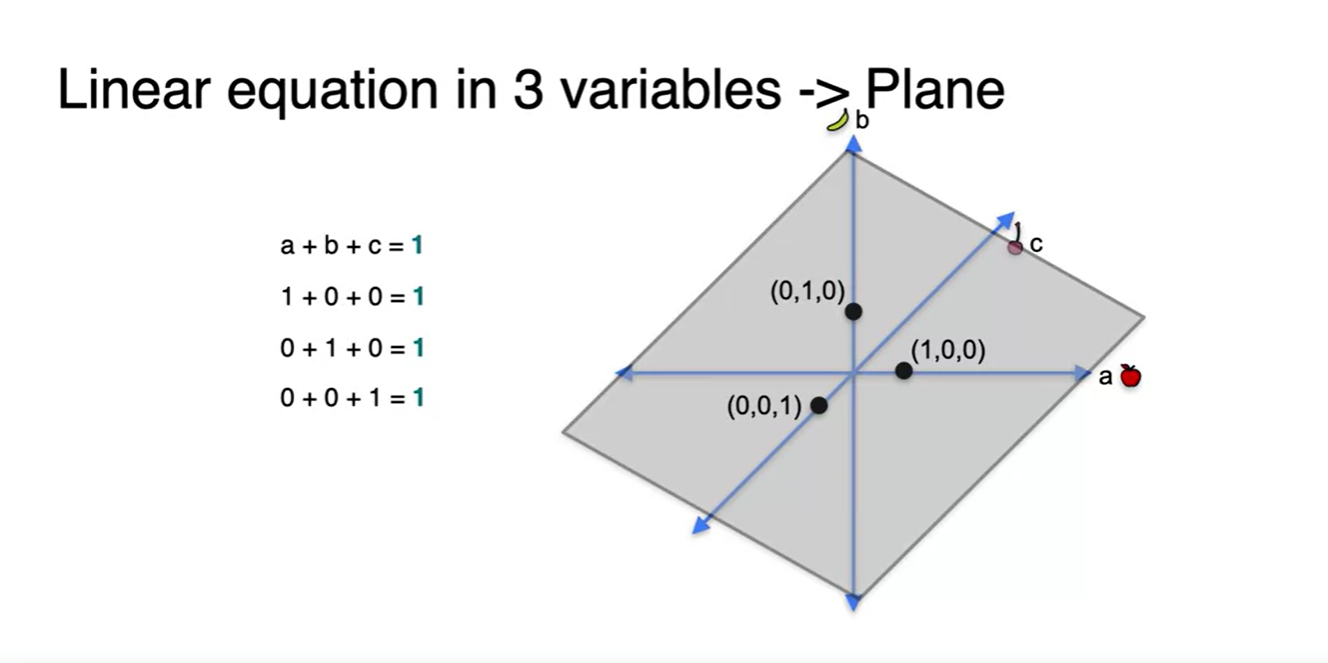
• 방정식의 constant가 0일 때는 항상 원점을 지난다.

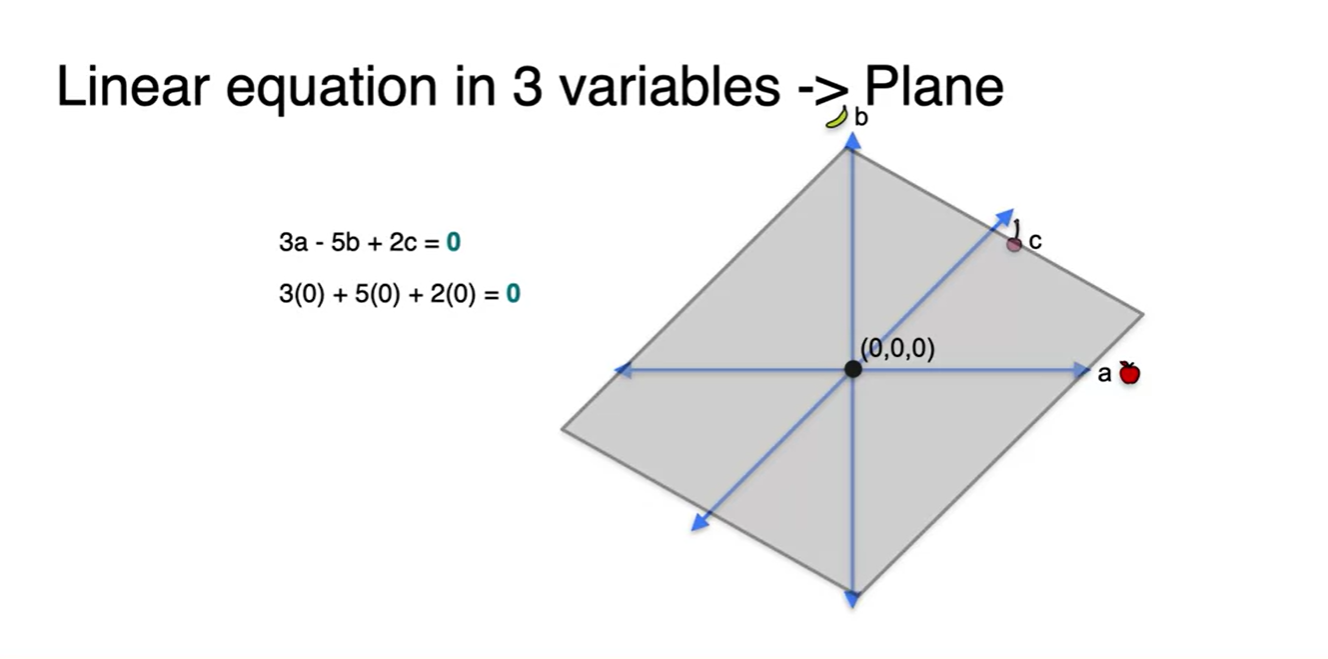
• System 1의 모든 방정식을 3차원 공간 상에 나타내면 아래 그림과 같다.

  • 세 평면이 만나는 unique(유일한) 교점은 바로 (0, 0, 0)이다.
  • Non-singualr하며, unique solution을 갖는다.

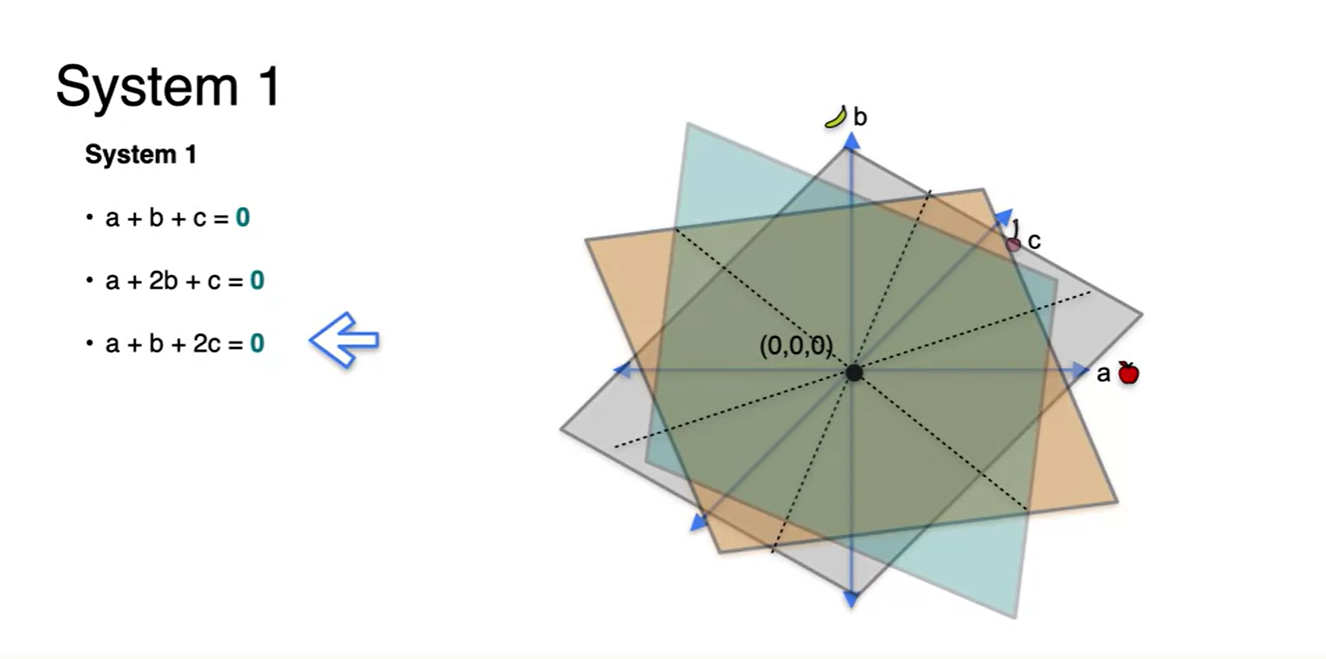
• System 2의 모든 방정식을 3차원 공간 상에 나타내면 아래 그림과 같다.

  • 세 평면의 교점 집합은 하나의 line(교선)이 된다.
  • Singular하며, multiple solutions를 갖는다.

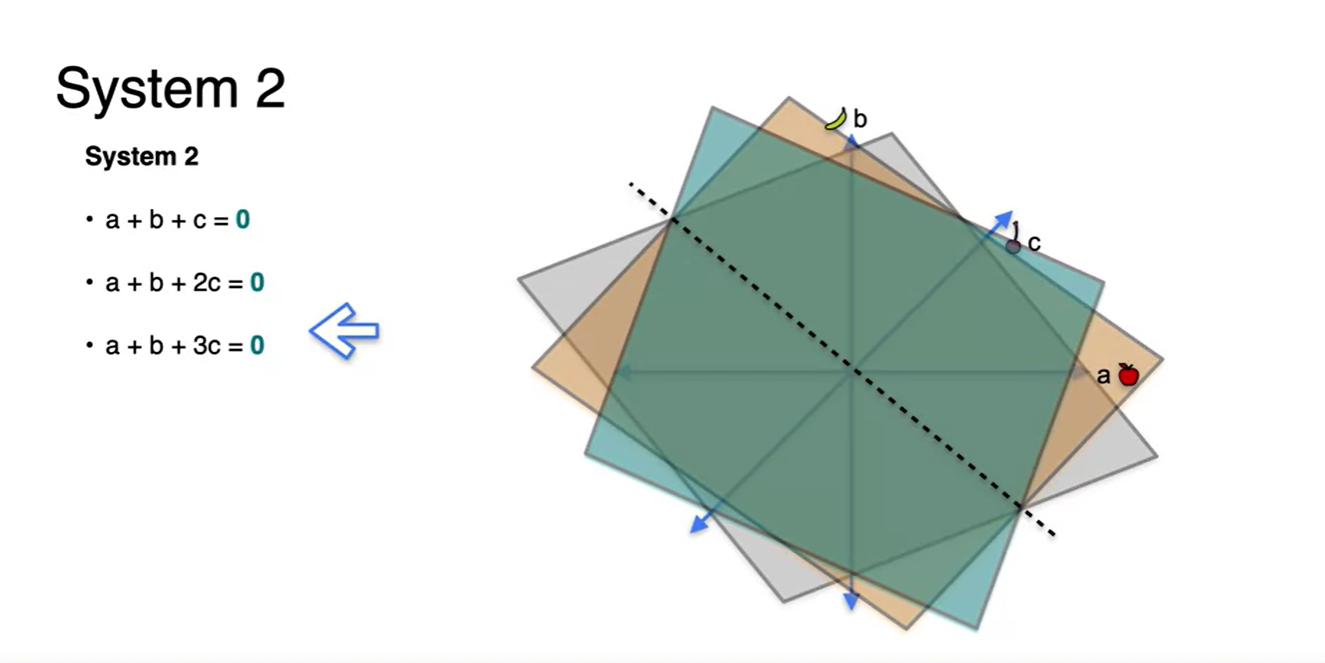
• System 3의 모든 방정식을 3차원 공간 상에 나타내면 아래 그림과 같다.

  • 세 평면의 교점 집합은 하나의 평면 plane이다.
  • Singular하며 해가 무수히 많다.

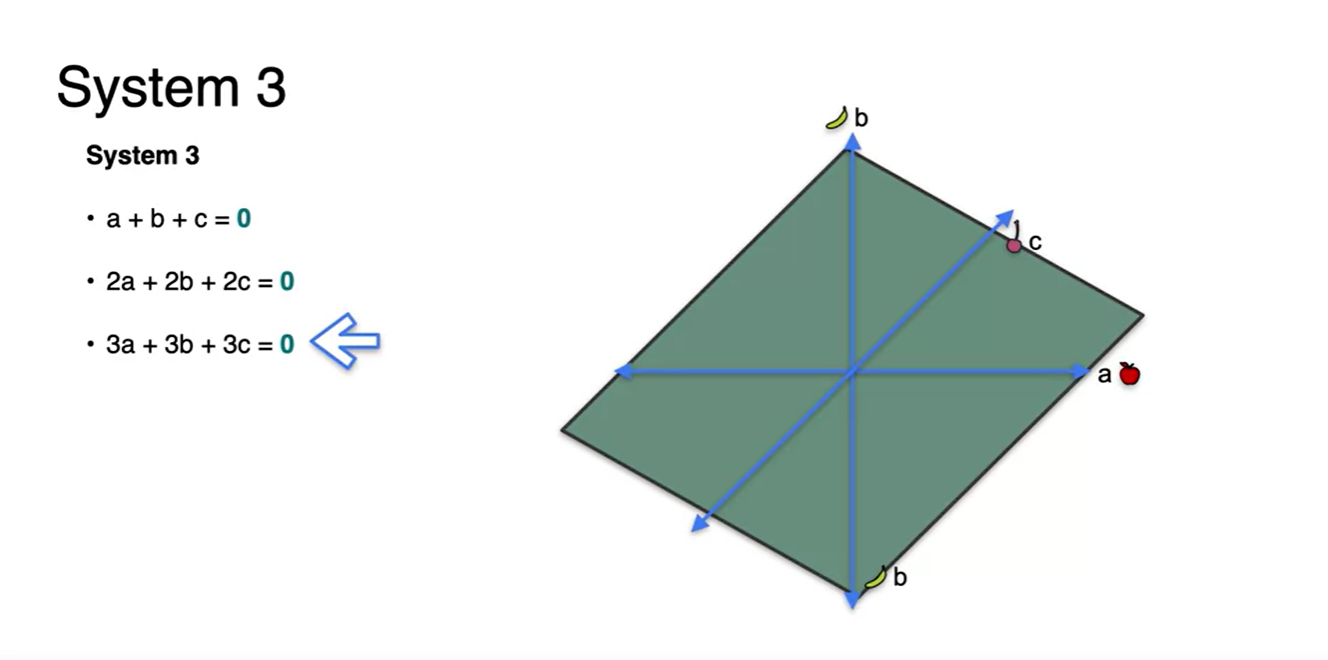
Linear dependence and independence (3x3)

• 아래 방정식은 row1과 row2의 합으로 row3를 만들어 낼 수 있기 때문에 linearly dependent하다.

  • 마찬가지로 singular하다고 볼 수 있다.

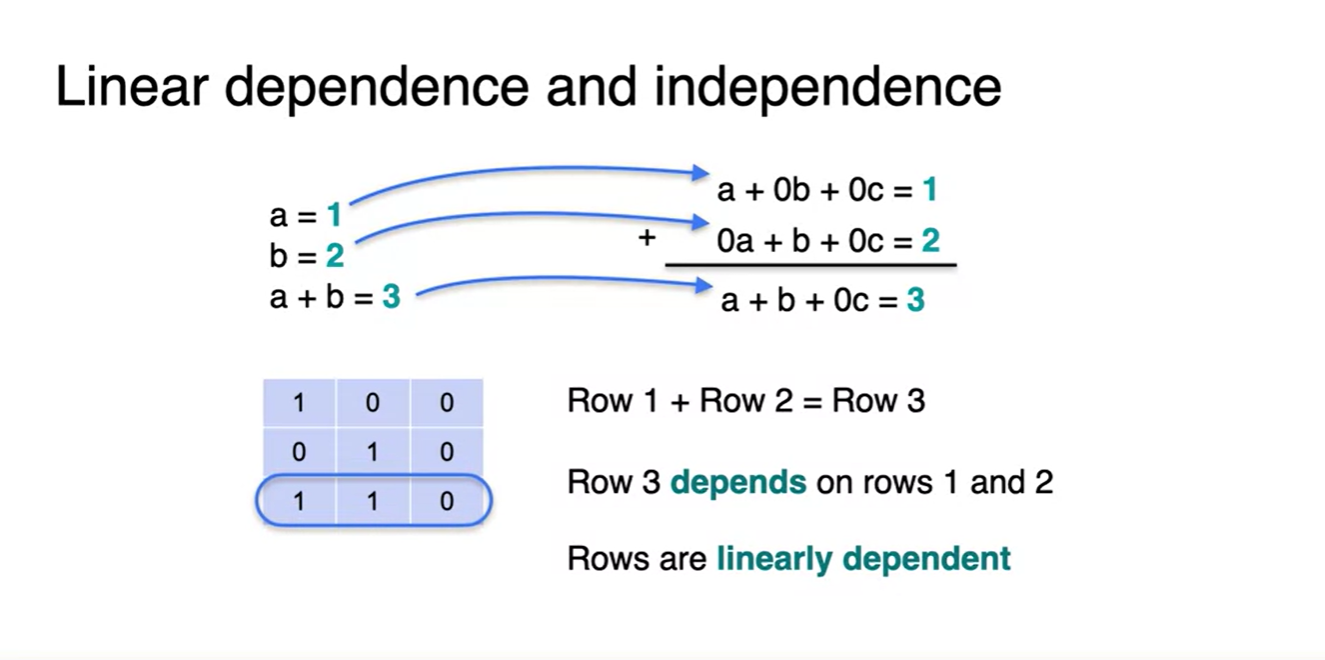
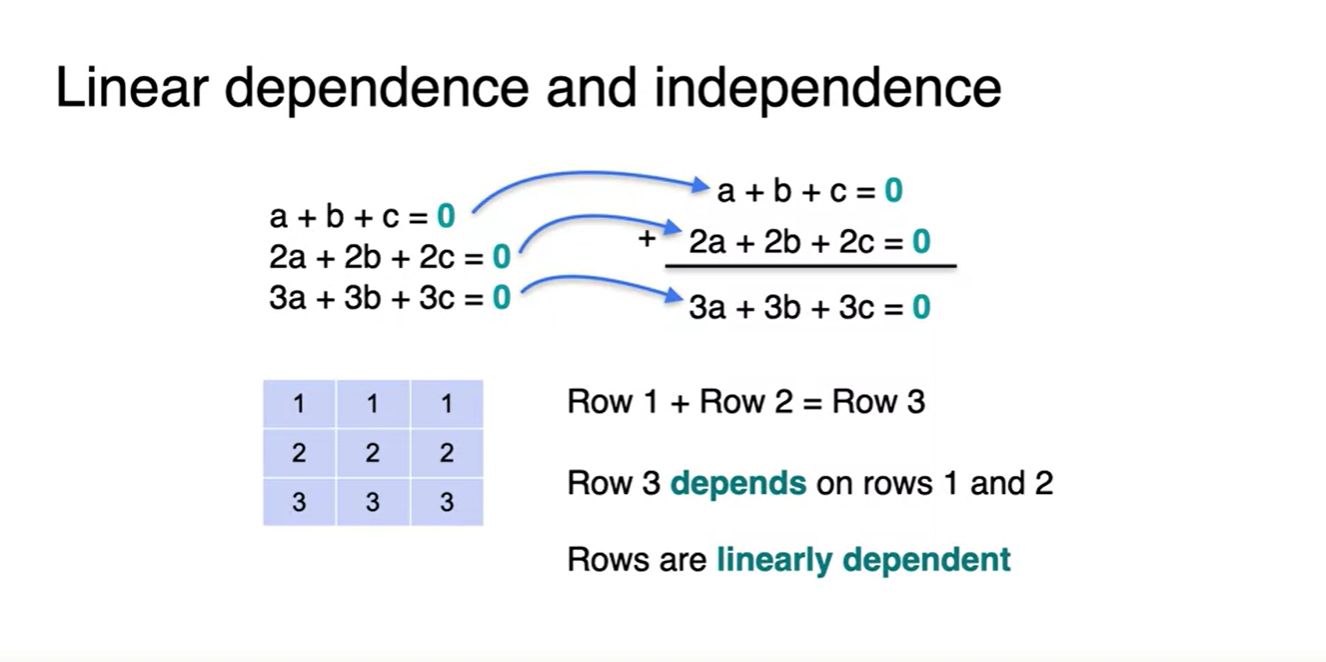
• 우리가 이전에 보았던 System 역시 row끼리의 합으로 또 다른 row를 표현할 수 있기 때문에, linearly dependent하다고 본다.

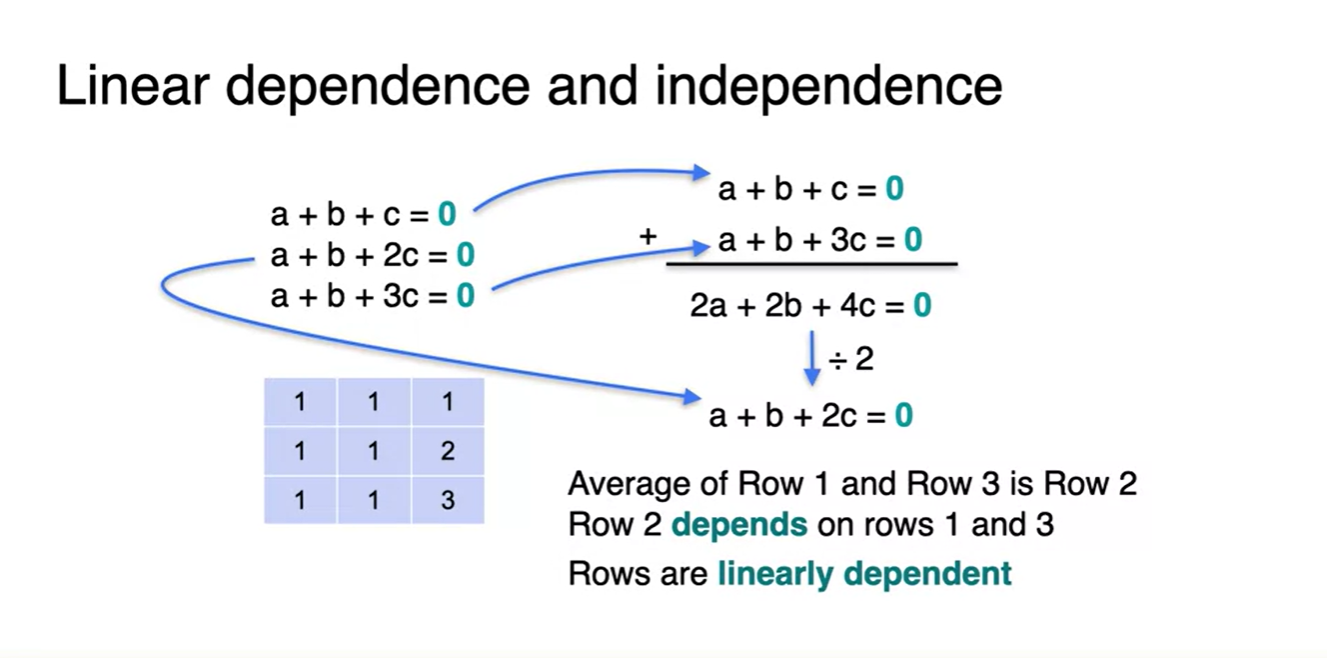
• 아래와 같은 상황에서는 조금은 복잡할지라도, 2개 row들의 선형 결합으로 다른 하나의 row를 표현할 수 있기 때문에 역시 linearly dependent하다.

• 각 row들 간의 관계가 없다면 linearly independent하다.

• Quiz

• Solutions

  • 각 row들간의 관계로 linearly dependent/independent를 결정할 수 있다.
  • 더불어 Singular/Non-singular도 결정할 수 있다.

The determinant (3x3)

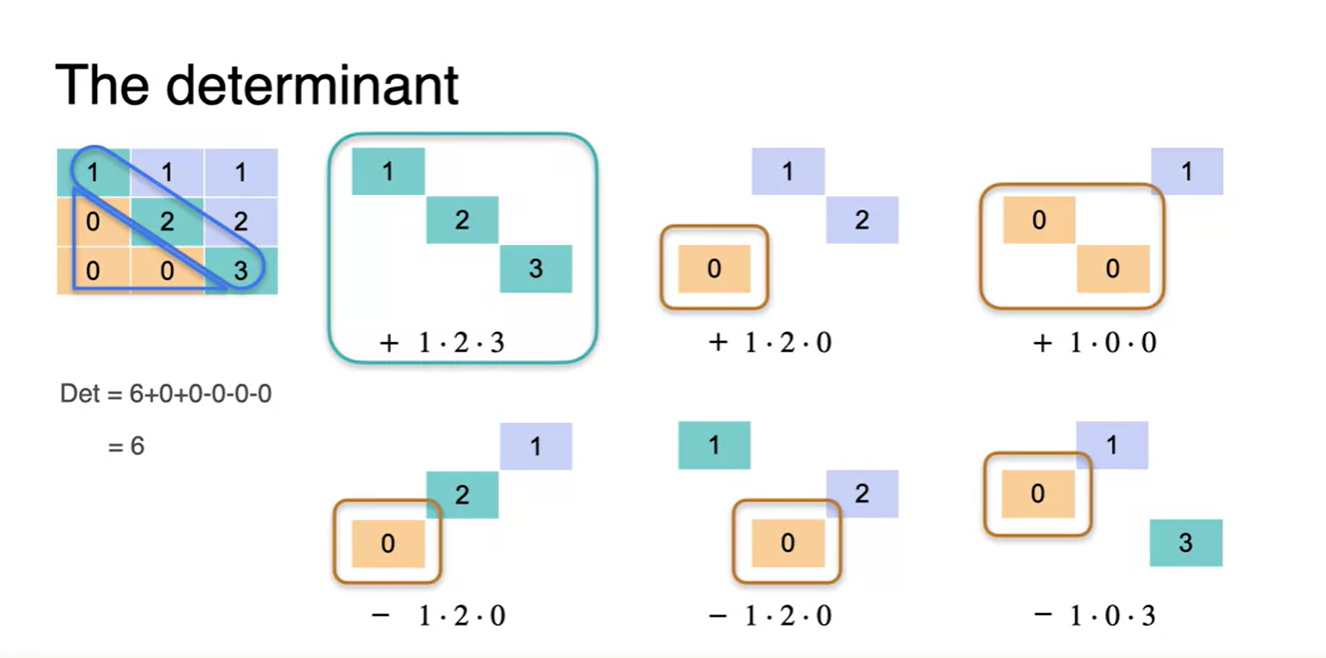
• 2x2 행렬에서 determinant를 계산했던 방법을 비슷하게 3x3에 적용해보자.

  • 이 방법은 내가 학부 때 교수님께 전수 받은 아주 굉장한 방법이었다.

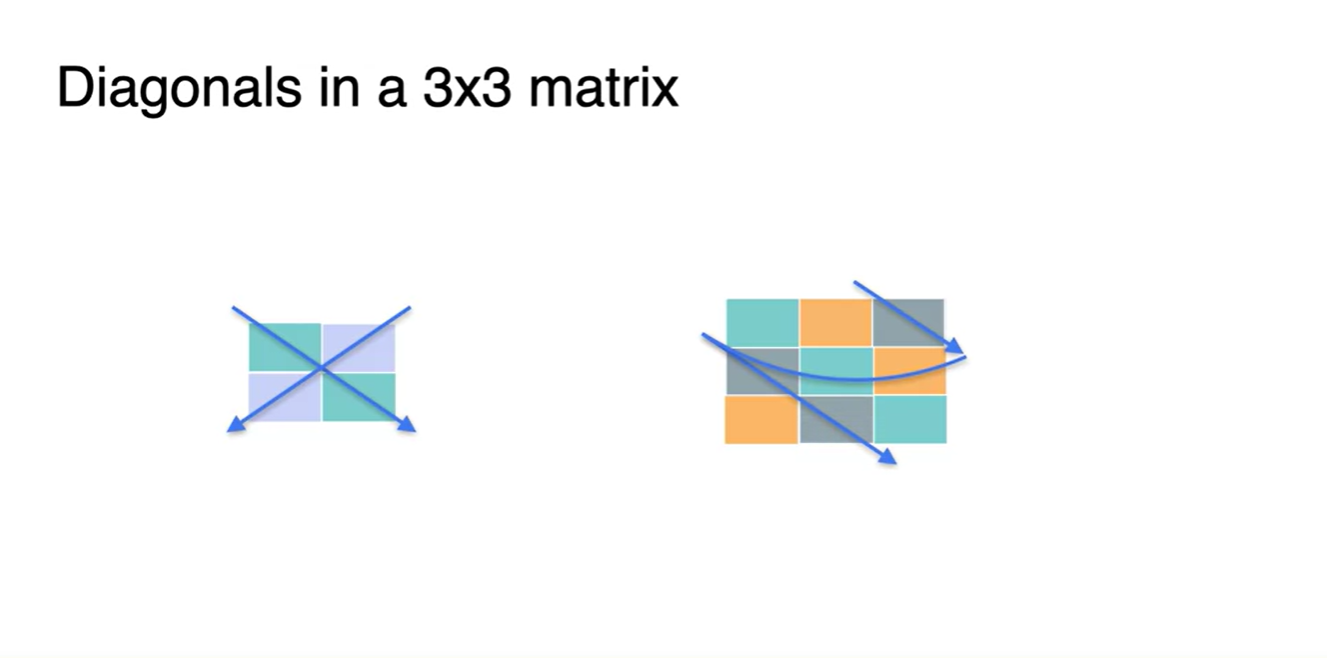
• 오른편 대각선은 add, 왼편 대각선은 subtract하여 determinant를 구한다.

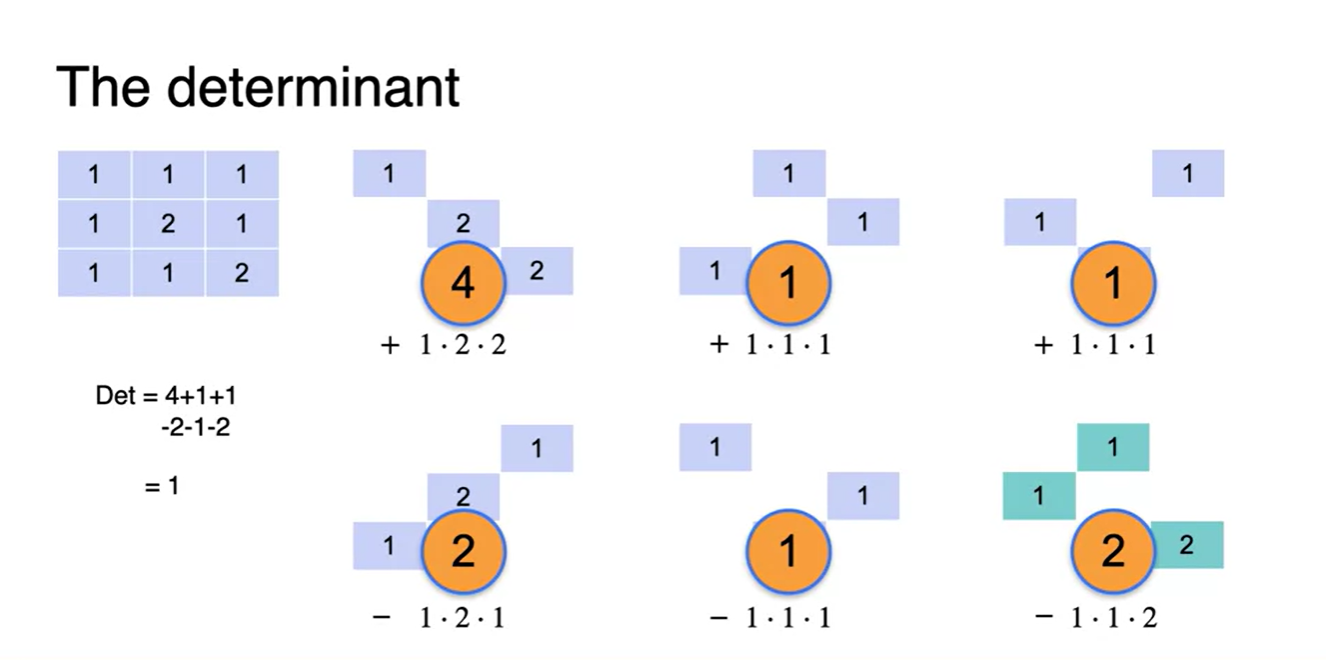
• Quiz와 각각의 solutions들을 구하기 위해 determinant를 계산하여 나타내었다.

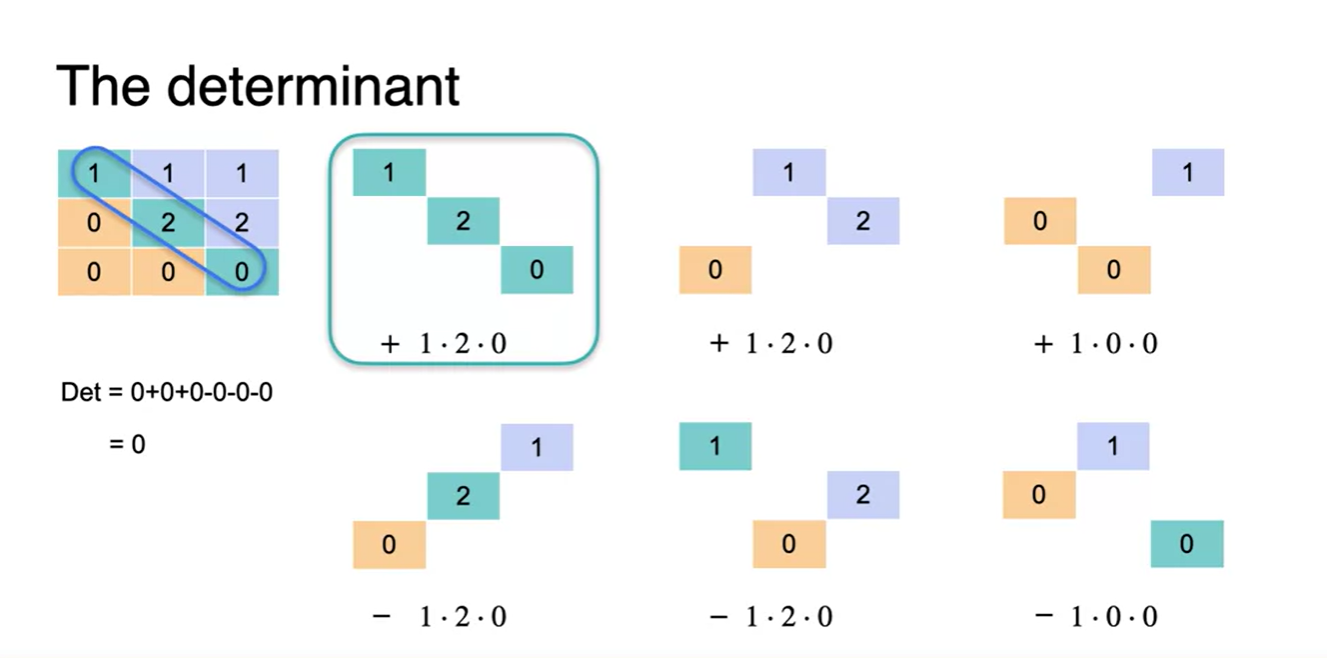
• 아래와 같은 상부 삼각 행렬은 determinant가 diagonal한 원소들의 곱으로 표현된다.

  • 따라서 이러한 꼴로 matrix를 만들면 diagonal determinat만 계산해도 해당 행렬의 특징을 파악하기 쉬워진다.
  • 첫 그림은 full rank로 이루어진 Non-singular한 matrix라는 것을 알 수 있고, 두 번째 그림은 full rank가 아닌 Singular한 matrix임을 알 수 있다.

---

• 출처 : [Coursera] Mathmatics for Machine Learning and Data Science