[MMD] Linear Algebra for Machine Learning and Data Science Week 2
Solving system of linear equations
Solving system of linear equations: Elimination
Machine learning motivation
-
몇 가지 machine learning applications에 대해 소개하려 한다.
- 소리 데이터도 matrix 형태로 표현할 수 있기 때문에 Speech recognition과 같은 task에 적용 가능하다.
- 물고기들의 음파 신호를 수집하여 bio-habitats를 정의하는 데에도 쓰일 수 있다.
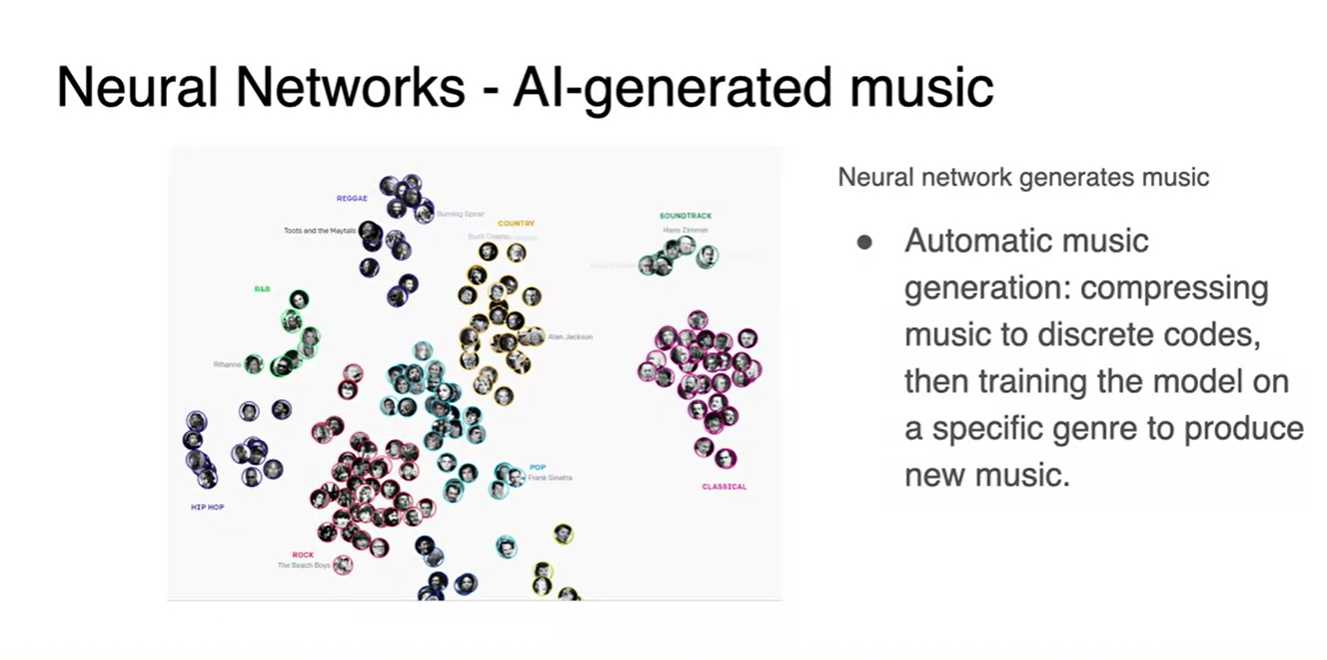
- 장르별 music에 대해서도 generating이 가능하며 이미지나 비디오와 같은 데이터들도 처리할 수 있다.

Solving non-singular system of linear equations
-
선형 방정식의 해를 찾는 데에 도움이 되는 방법에 대해 알아보자.
- 부가적으로 해당 방정식이 Singular인지 Non-singular인지에 대해서도 알 수 있다.
-
우선, 우리가 기존에 풀어왔던 문제를 다시 보자.
- 이 문제는 바나나 하나가 더 추가되면서 얼마가 변했는지를 보고, 바나나의 가격과 사과의 가격까지 결정할 수 있는 system이다.
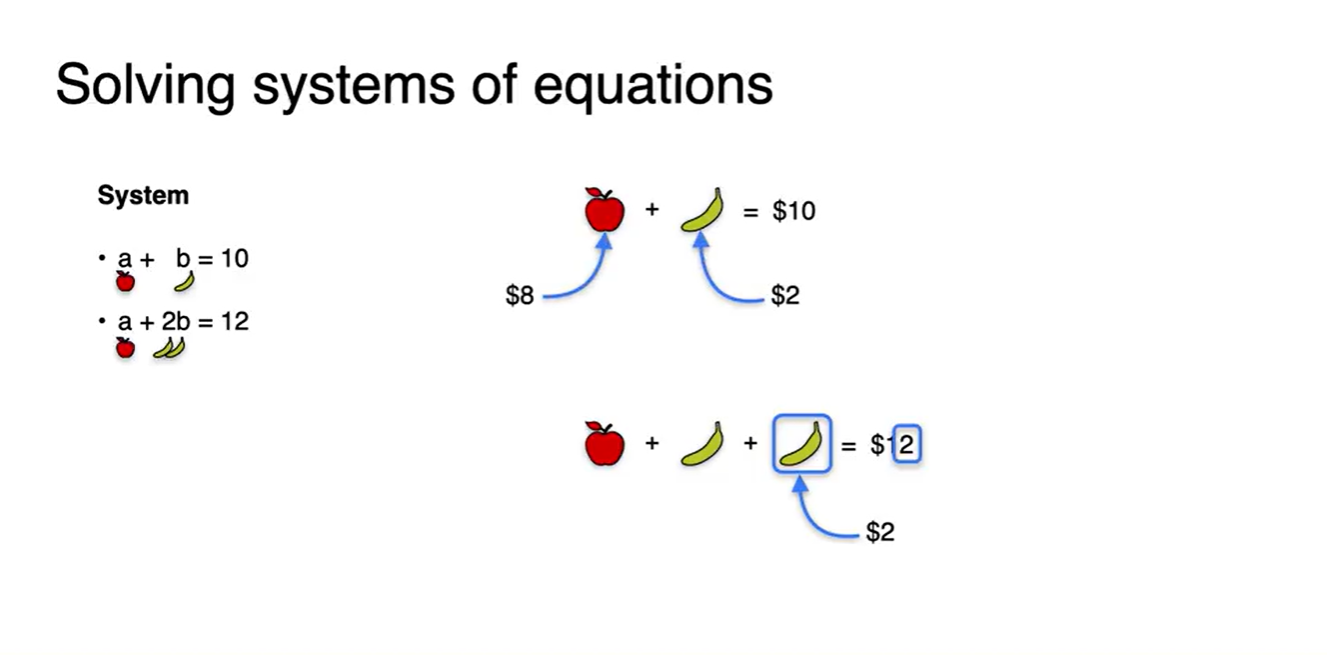
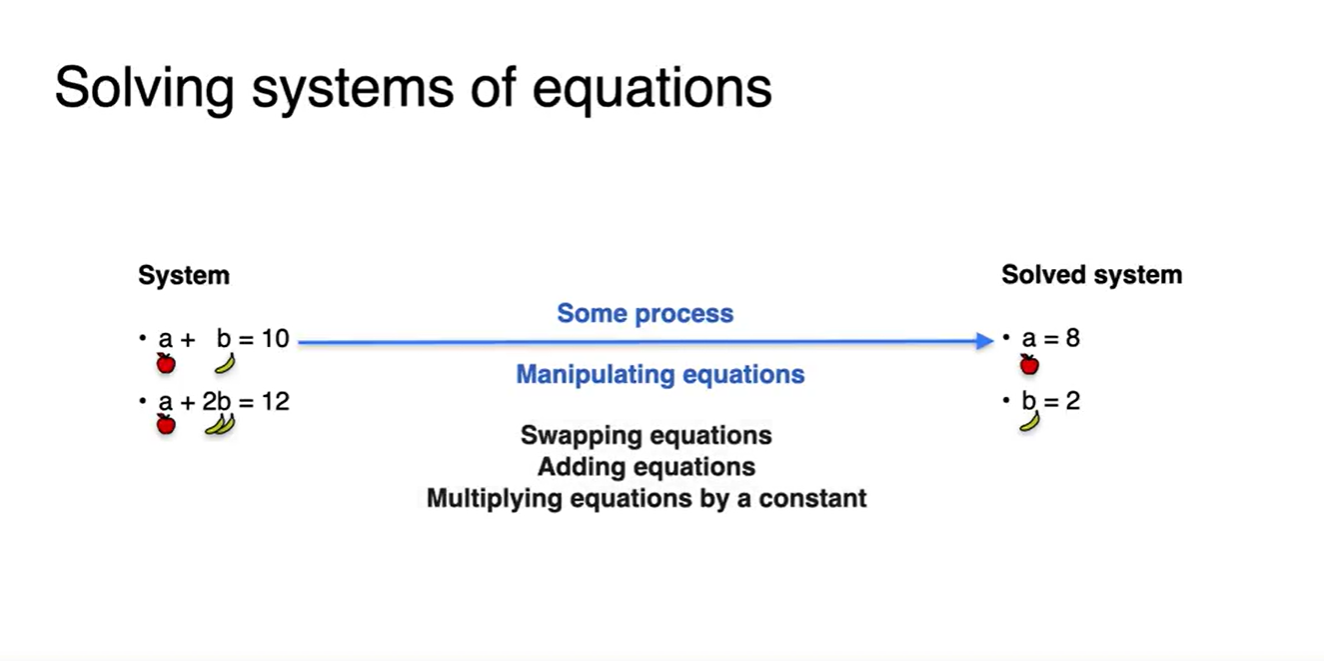
- 사실 이 과정은 우리의 뇌에서 숨은 manipulating을 거쳐 빠르게 풀 수 있는 문제였다.
- 우리는 이 과정을 'a'라는 변수를 지우는 것에서부터 시작했음을 알 수 있다.

- Manipulating equations의 기법은 크게 Multiplying과 Adding이 있다.

-
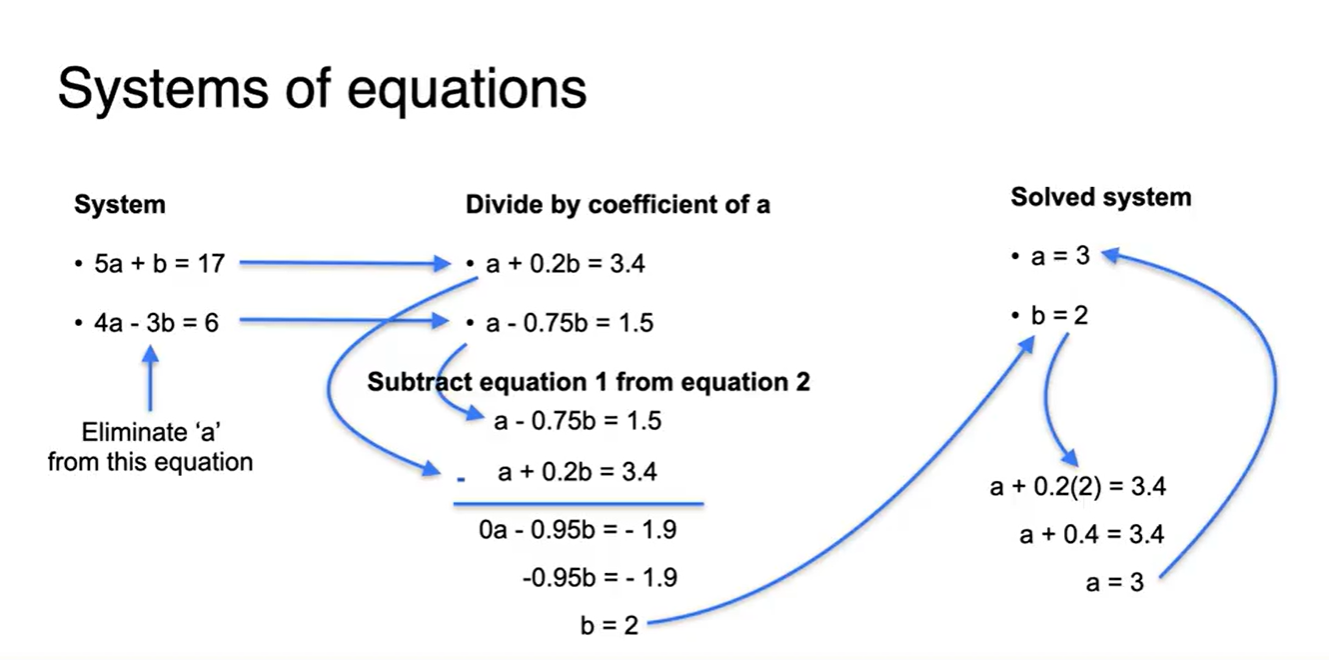
더 어려운 examples을 풀어보자.
- 두 방정식 속 하나의 변수를 지우기 위해 Eliminating 작업을 진행한다.
- Adding, Dividing, Subtracting, Multiplying ...
- 적절한 연산을 활용하여 하나의 변수를 지우는 것이 첫 번째 목표다.
-
만약 두 변수중 하나의 곱해진 상수가 0이라면 어떨까?
- 여기서는 두 번째 방정식의 a변수의 coefficient가 0이다.
- 그러면 b의 값이 결정되는 것이며 첫 번째 방정식에 대입하여 a를 구한다.

-
아래 문제를 풀어보라.
- (두 번째 방정식 - 첫 번째 방정식*4)으로 a를 eliminating하고, 이를 방정식에 대입하여 b를 구한다.

Solving singular systems of linear equations
-
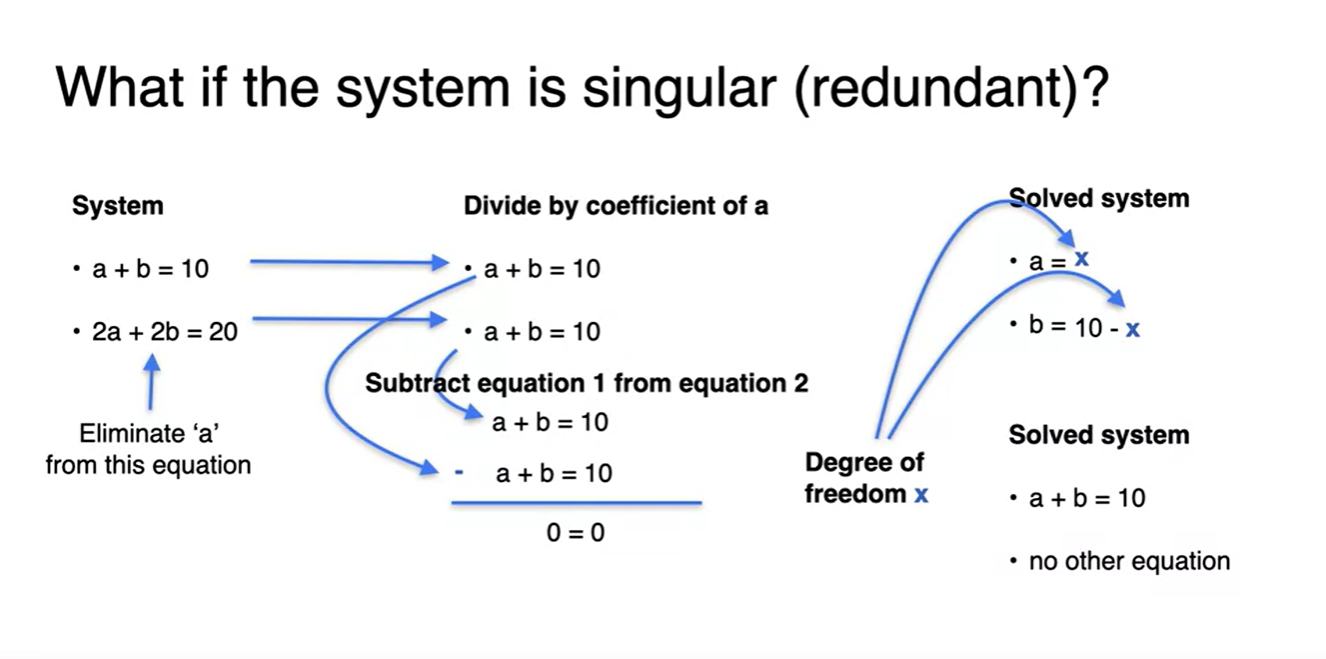
System이 Singular하다면 어떨까? (Redundant)
- 아래 식을 아까와 똑같은 방법으로 하나의 변수를 Eliminating하면 의 수식이 만들어진다.
- 따라서 이 system의 해는 을 만족하는 모든 values가 해가 될 수 있고, unique한 solution이 정해지지 못한다. → Singular의 특징!
-
Contradictory한 Singular System이라면 어떨까?
- 'a' 변수를 eliminating해보면 이번에는 라는 모순된 수식이 만들어진다.
- 즉, 해가 존재하지 않는다(no solution)는 것을 의미하며, 이 또한 Singular의 특징이 된다.

-
아래 문제를 풀어보라.
- (첫 번째 식*2 - 두 번째 식)으로 eliminating을 진행하면 수식이 만들어진다.
- 해가 무수히 많음(Infinite many solutions)을 의미하며 해당 system이 Singular하다고 볼 수 있다.

Solving systems of equations with more variables
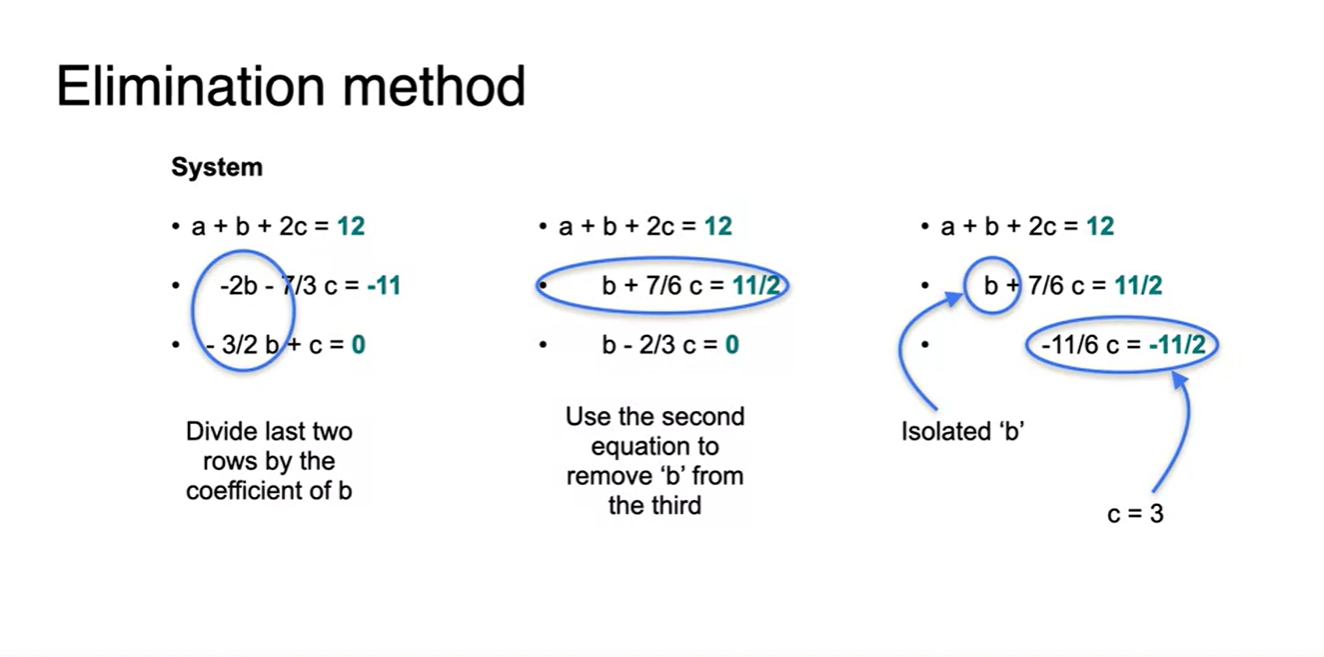
- 3개의 변수를 가진 equations라면 어떨까
- 이번에도 역시 하나의 변수를 지우기 위해 manipulating한다.

-
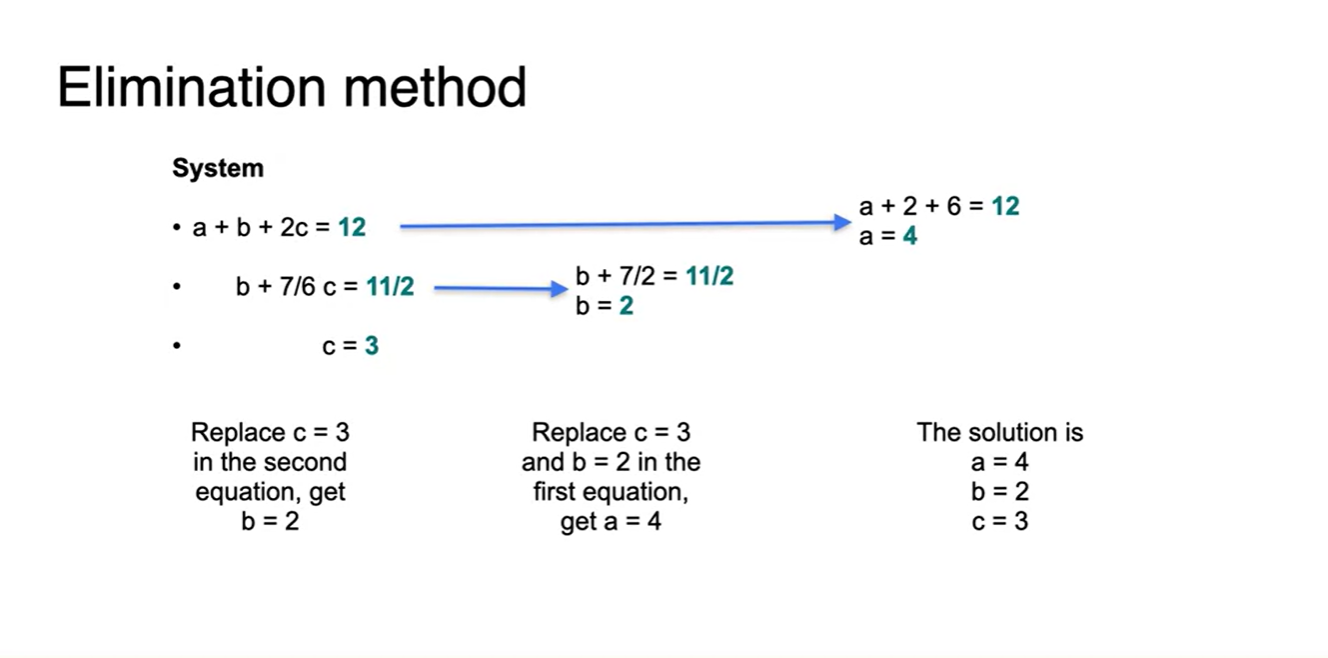
위의 예제에서 'a'라는 변수를 지우고 나면 첫 번째 식은 'a' 변수를 포함한 유일한 수식이 되고, 'b', 'c'가 함께 포함된 방정식이 2개 생긴다.
- 마찬가지의 방법으로 'b' 변수가 담긴 유일한 수식과 'c'에 관한 수식으로 정리한다.
- 이를 바탕으로 해를 구하면 'a', 'b', 'c'의 unique solution이 결정된다.
Matrix row-reduction
-
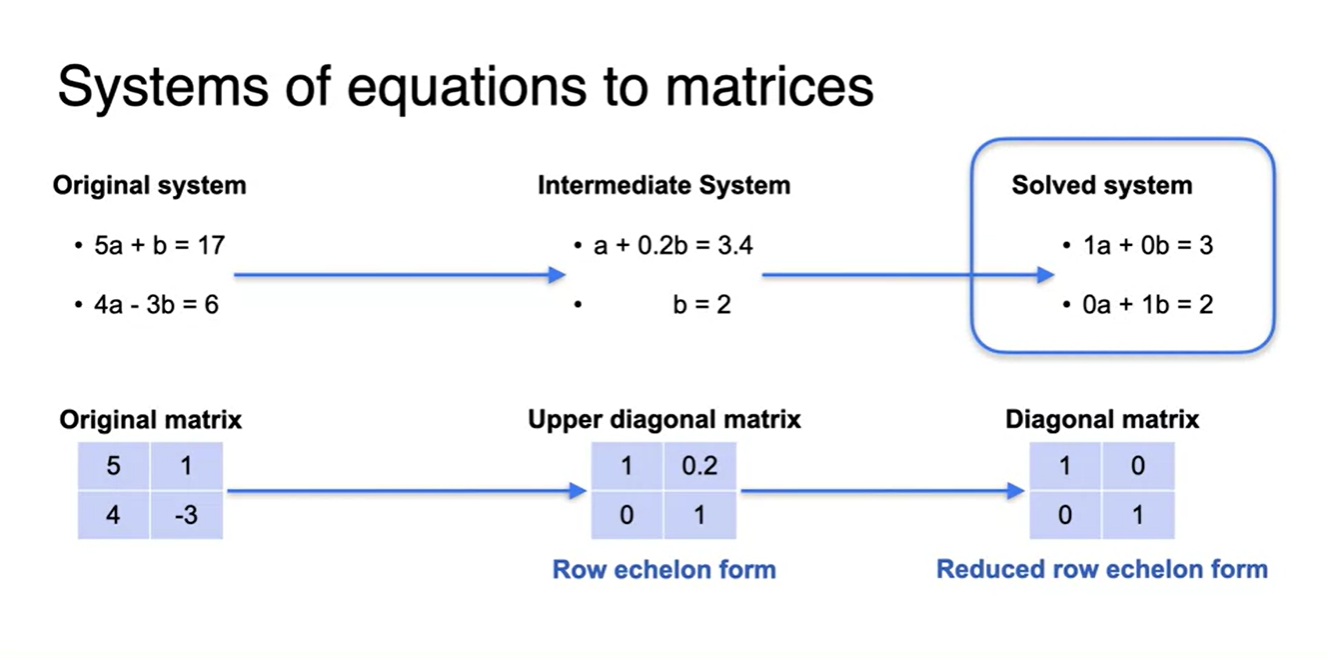
기존에 방정식으로 풀어왔던 eliminating 작업을 matrix 형태로 푸는 방법은 아래와 같다.
- constant를 제외한 matrix만 가져와서 Original matrix를 Upper diagonal matrix로 만드는 작업을 거쳐, Diagonal matrix로 만드는 것이 최종 목표다.
- 이 때 Upper diagonal matrix 형태가 Row echelon form이다.
- Diagonal matrix 즉, 각 변수의 해만 담을 수 있는 행렬의 형태가 Reduced row echelon form이라 한다.
- constant를 제외한 matrix만 가져와서 Original matrix를 Upper diagonal matrix로 만드는 작업을 거쳐, Diagonal matrix로 만드는 것이 최종 목표다.

-
Singular System들의 Row echelon form은 다음 그림과 같다.
- Redundant한 System
- Contradictory한 System (여기서는 다루지 않는다. → constant 항 부재)
- 위 두 System은 fully Diagonal matrix가 형성되지 않는다.



-
결과적으로 Row echelon form의 형태는 아래 세 가지 경우에 국한된다.
- Diagonal 원소가 0인 방정식의 오른쪽 항들은 전부 0이기 때문에,
- Diagonal 원소가 모두 1인 form
- 위쪽에 위치한 식의 일부는 diagonal 원소가 1, 아레쪽은 0인 form
- Diagonal 원소가 모두 0인 form
- Diagonal 원소가 0인 방정식의 오른쪽 항들은 전부 0이기 때문에,

Row operations that preserve singularity
-
이번에는 행을 Switch해 보자.
- Switching 이후, matrix가 Singularity가 보존되는지 확인하는 것이 목적이다.
-
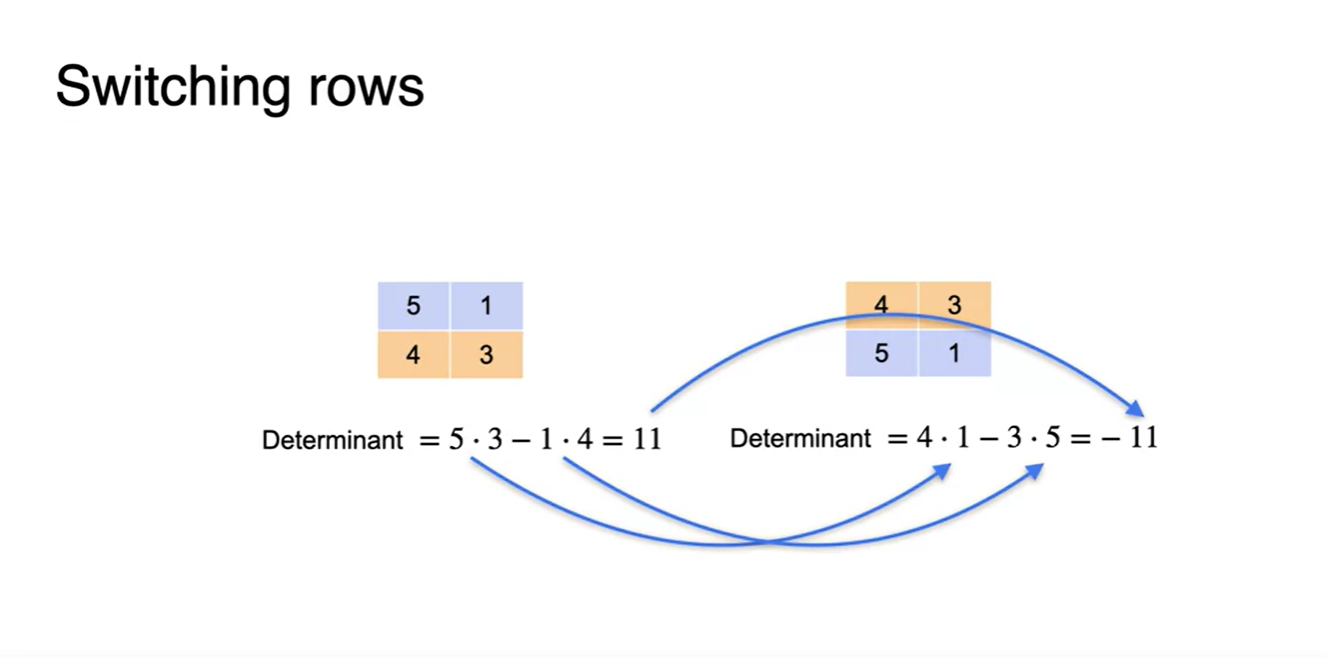
위의 그림을 보면 행을 서로 switching 했을 때의 determinant가 양수 ↔ 음수로 전환된다는 점을 알 수 있다.
- 이는 diagonal 항이 앞 뒤로 뒤바뀌었기 때문이며, determinant가 0일 때도 성립한다.
- determinant가 0일 경우 Singular한 matrix라고 보기 때문에, 행을 바꿔도 해당 System의 Singularity가 보존되는 것이라고 봐도 무방하다.
-
이번에는 행을 Multiplying한 것과 Adding한 것의 determinant를 구해보자.
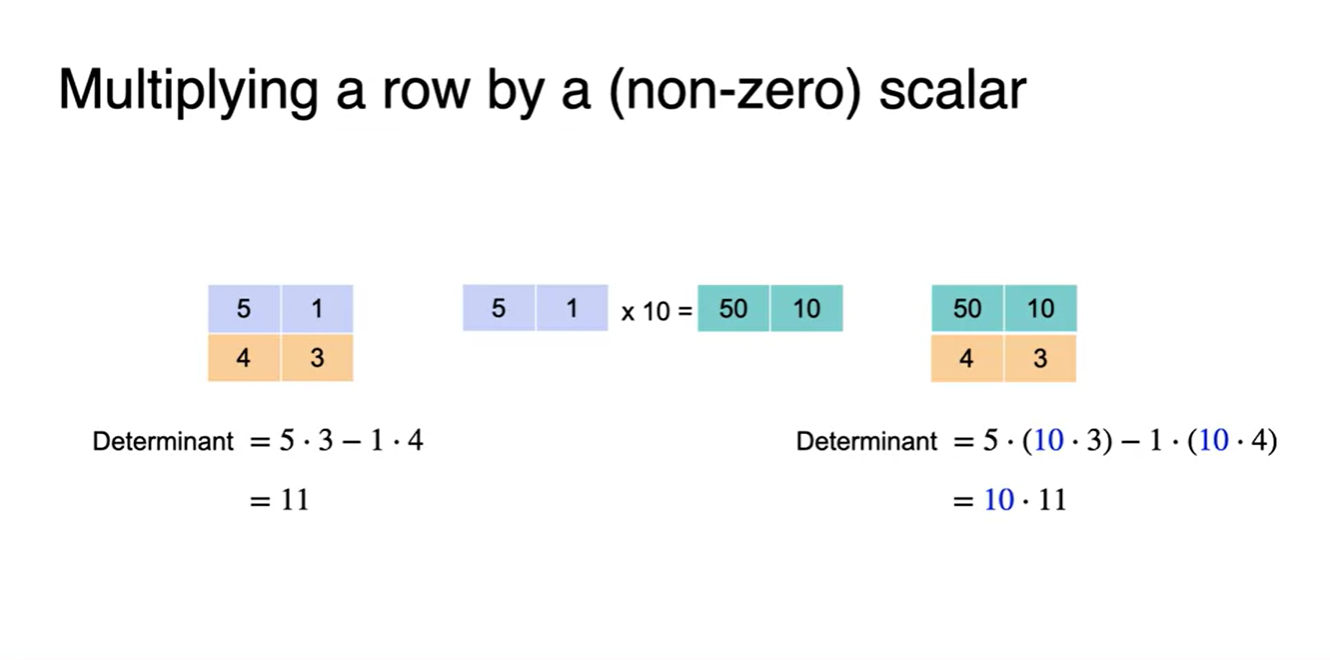
- Multiplying 작업 이후, determinant는 원래 determinant에 해당 scalar를 곱한 값으로 전개된다.
- 이는 아마도 행렬의 결합 법칙 특성 때문이라고 보면 될 것이다.
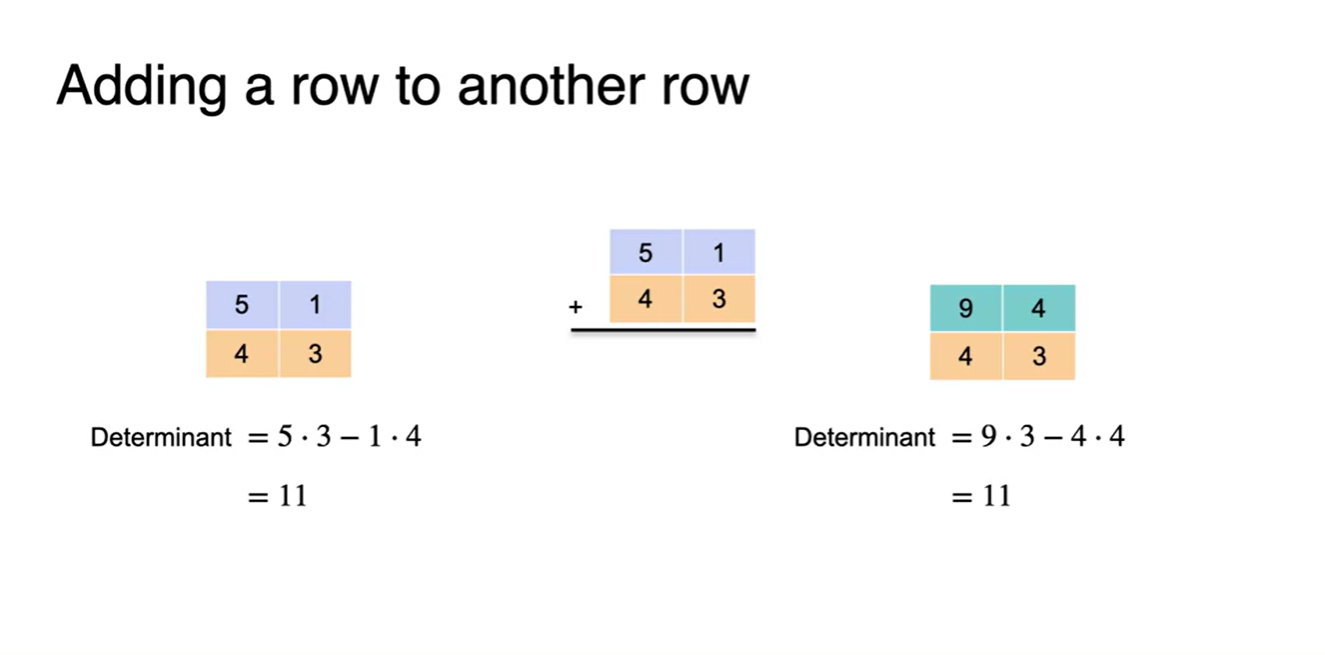
- Adding 작업은 아무리 봐도 조금 신기한데, 풀어서 해결해보면 결국 맥락은 비슷하다.
- (9*3 - 4*4)로 계산된 저 식은 사실 ((5+4)*3 - (1+3)*4) 이렇게 전개되며, 각 항을 교차로 곱한 값이 서로 삭제되기 때문이라 볼 수 있다.
- Multiplying 작업 이후, determinant는 원래 determinant에 해당 scalar를 곱한 값으로 전개된다.
The rank of a matrix
-
선형 방정식이 전달하는 정보의 양을 측정하는 방법은 rank에 달렸다.
- rank를 계산하고 응용하는 방법에 대해서 알아보자.
-
머신러닝에서 rank 응용 분야 중 하나는 '이미지 압축'이다.
- 훨씬 적은 공간을 사용하여 이미지 픽셀을 저장하는 방법으로 주로 쓰인다.
- 아래 그림과 같이 Rank가 15-50 부터는 original한 이미지의 특징을 잘 표현하고 있음을 알 수 있다.
- 즉, 해당 공간을 가장 잘 설명하는 몇 가지 basis만 가지고도 이미지의 특징은 잘 보존되며 저장 공간은 줄어들 수 있다는 장점이 생긴다.

- Systems of information의 양을 살펴보자.
- 각 동물의 색깔을 결정하는 정보의 양은 왼쪽에 있는 System 1일 때 가장 예측 가능하다.
- 정보가 담긴 독립적인 내용을 나타내는 방정식의 개수를 Rank라 한다면 다음과 같은 방식으로 계산된다.


-
Rank와 Solutions의 관계는 다음과 같다.
- Rank가 가득 차 있다면, 각 변수의 solution을 결정할 수 있는 정보가 많으므로 solution space의 공간은 확 줄어들 수밖에 없다.
- 다르게 말하면, Rank가 작을수록 추론에 쓰이는 정보가 줄어들기 때문에 solution space가 넓어진다.
- 따라서 Rank는 (full rank의 값 - dimension of solutions space)로 계산된다.
- Rank가 가득 차 있다면, 각 변수의 solution을 결정할 수 있는 정보가 많으므로 solution space의 공간은 확 줄어들 수밖에 없다.
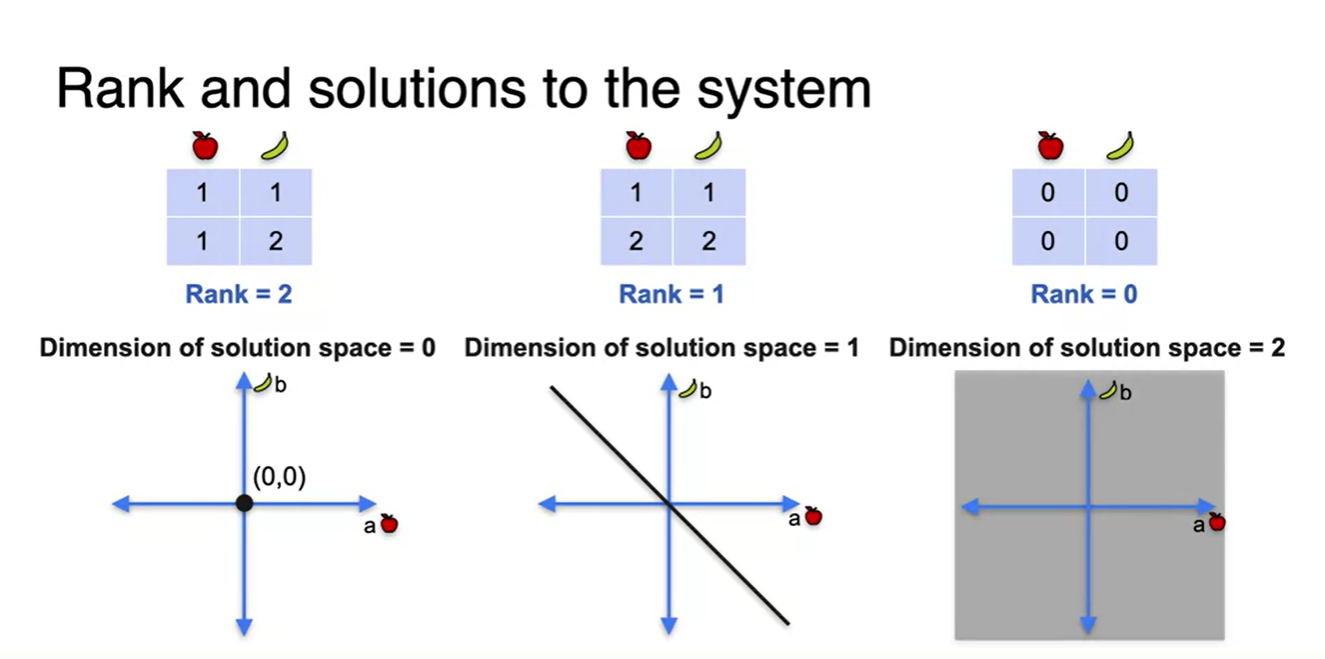

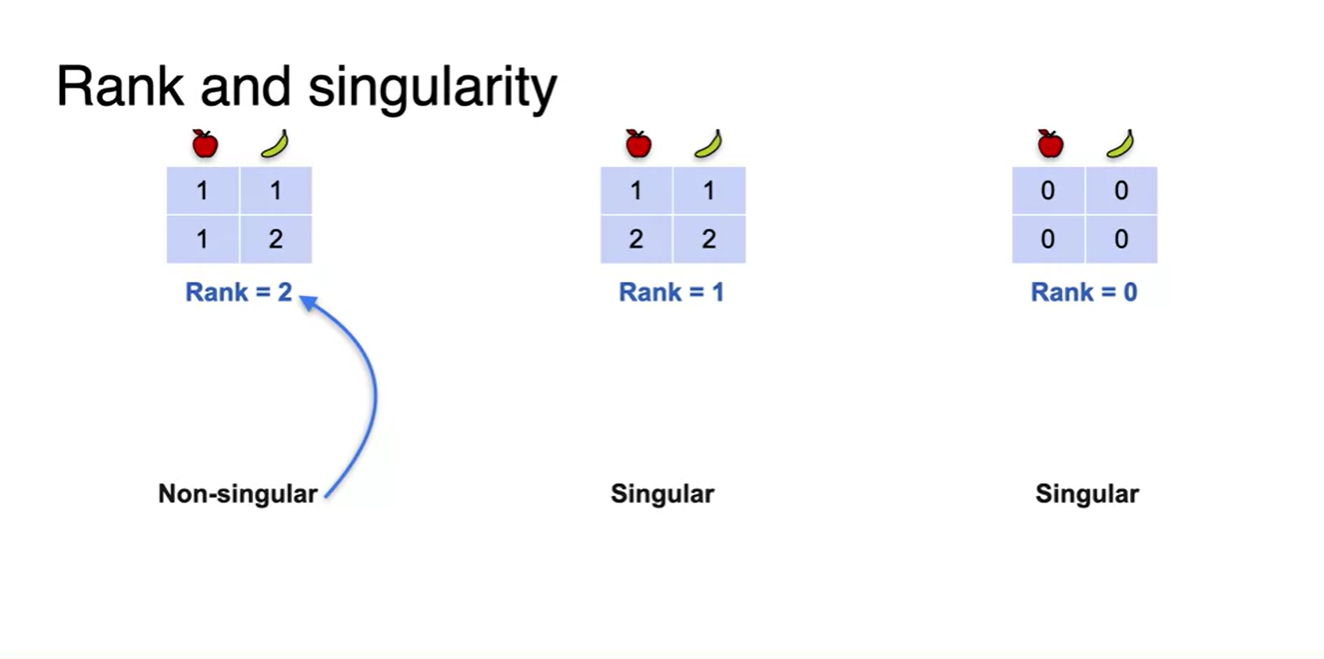
- Rank가 높을수록 정보가 충분하다고 보기 때문에, full rank 상태일 때 Non-singular matrix를 형성할 수 있다.
- Redundancy도 존재하지 않는 상태를 말한다.
-
아래 문제를 풀어보자.
- 나는 determinant를 계산해서 Singular인지 Non-singular인지 찾았다.
- Non-singular한 System일 때, rank는 full rank라는 명제를 기억하자.

The rank of a matrix in general
-
아래 System 4개를 비교해보고 Equations의 개수와 Rank의 관계를 밝혀보자.
- 단순히 Equations 개수가 아닌 각 방정식의 Pieces of Informations로 Rank가 결정된다는 것을 알 수 있다.

-
Rank를 계산할 수 있는 쉬운 방법은?
- Matrix의 Row echelon form을 만들어 해결할 수 있다.
- 일단 REF를 형성하고 나면, Rank의 개수는 물론 Singularity와 Non-singularity한 성질까지도 결정지을 수 있을 것이다.
- Matrix의 Row echelon form을 만들어 해결할 수 있다.

- Row echelon form의 형태는 다음과 같다.
- 이를 쉽게 구할 수 있는 방법은 아래에서 설명하겠다.
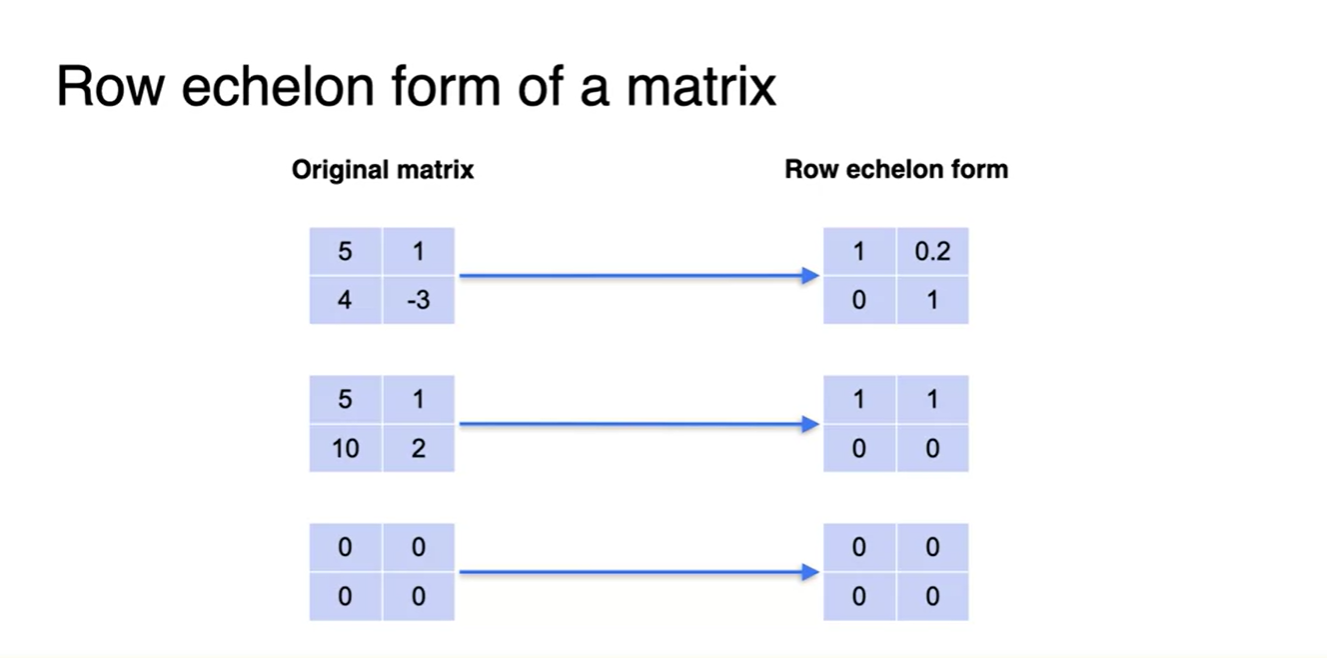
-
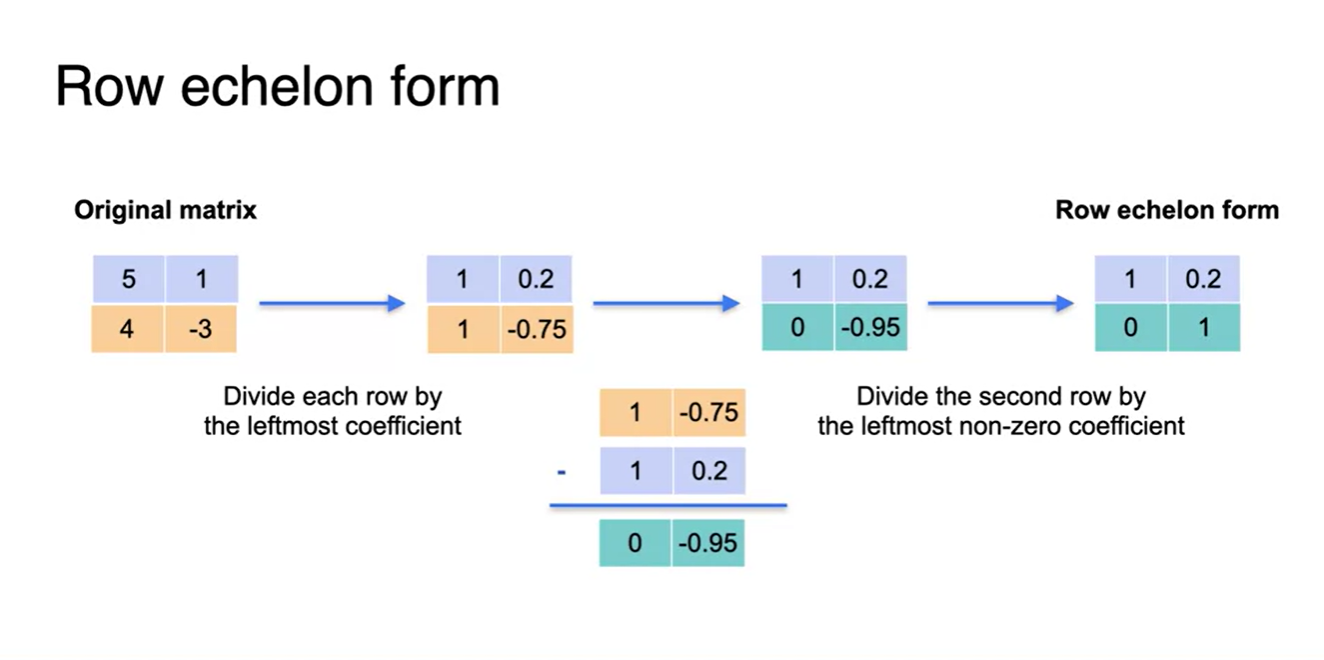
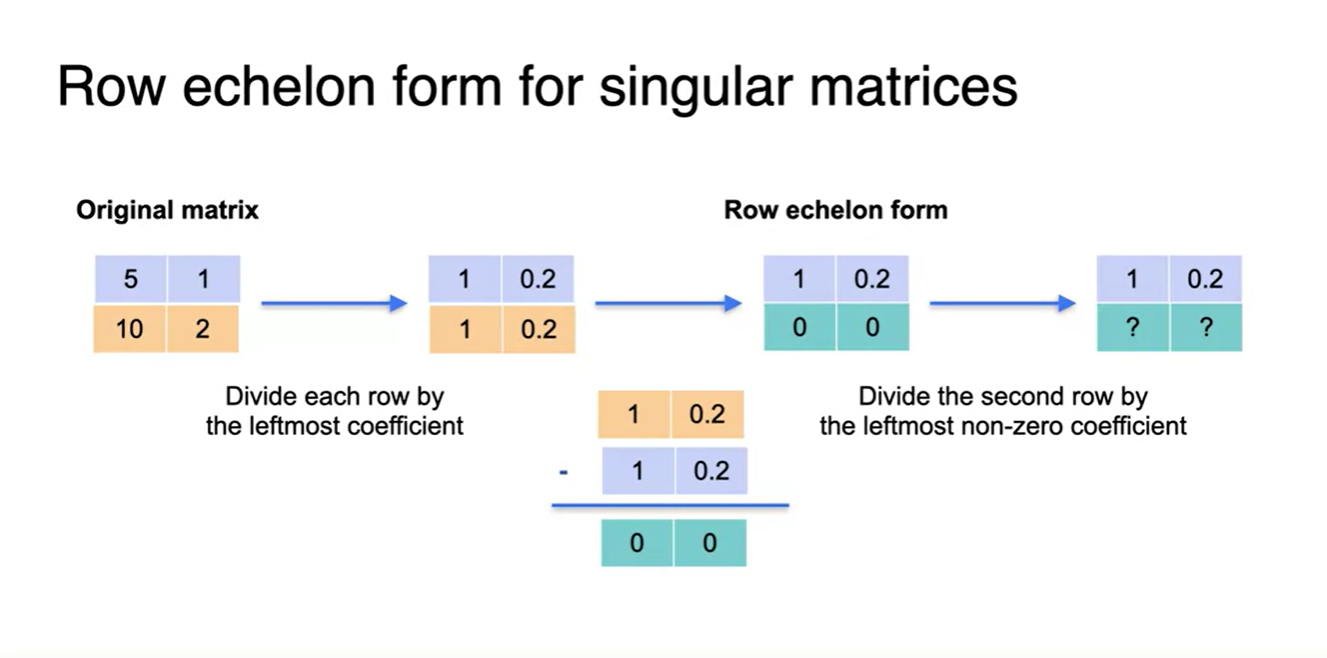
가장 쉬운 방법은 아래의 과정을 따르는 것이다.
- 각 row의 가장 왼쪽 값으로 식 전체를 나눈다.
- 하나의 row를 다른 하나의 row로 빼주어 한 벙정식의 첫 번째 원소를 0으로 만든다.
- 해당 방정식의 두 번째 원소가 non-zero라면 이를 한 번 더 나누어 1로 만든다.
- 만약, 나눠줄 값이 non-zero가 아니라면(zero 라면) 해당 matrix가 그대로 REF가 되는 것이다.

-
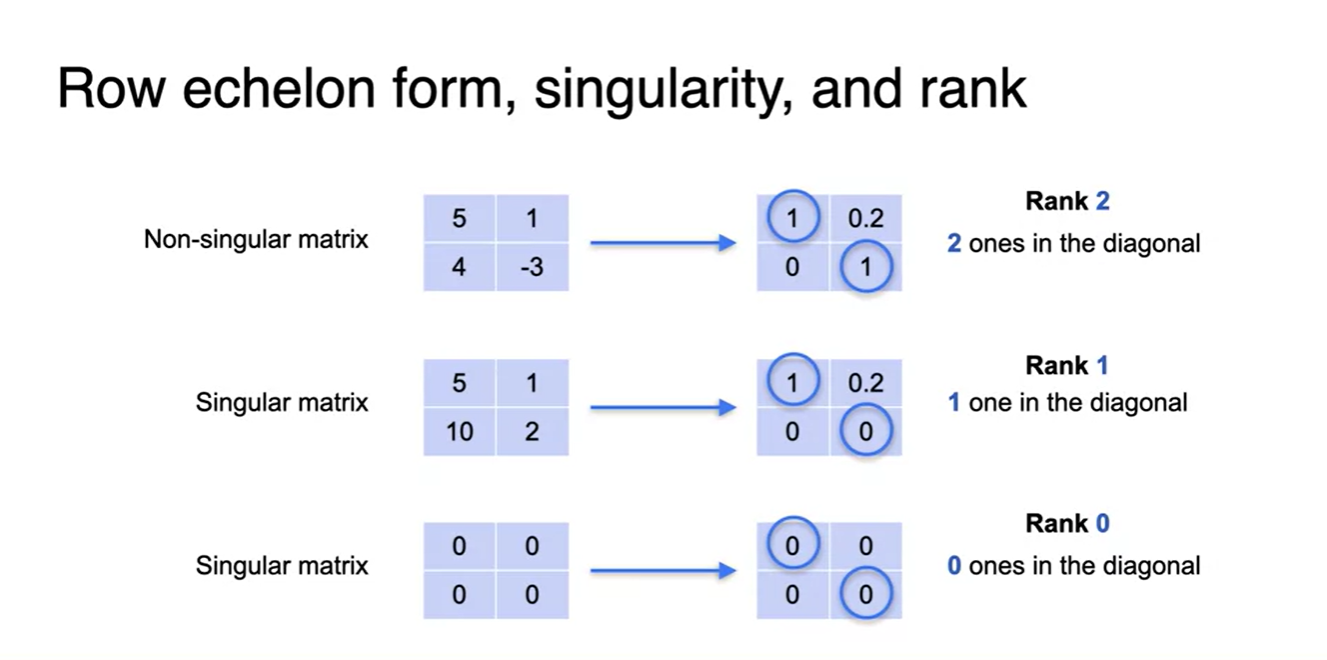
이제 Row echelon form과 Singularity, 그리고 Rank의 관계를 밝혀보자.
- Row echelon form의 형태가 꽉찬 diagonal을 형성하고 있으면 full rank이자 Non-singularity matrix임을 나타낸다.
- Row echelon form의 diagonal한 원소 중 0이 포함되어 있으면 Rank가 full rank보다는 적고, Singularity한 matrix 상태임을 나타낸다.
Row echelon form in general
-
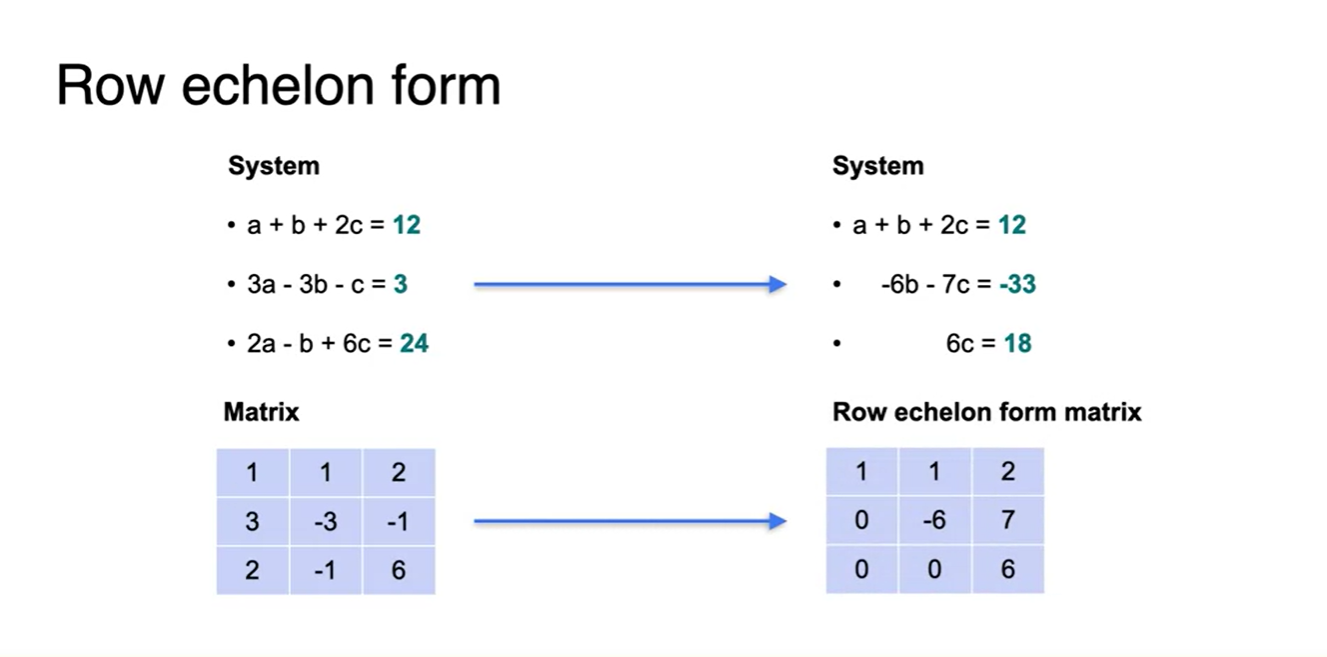
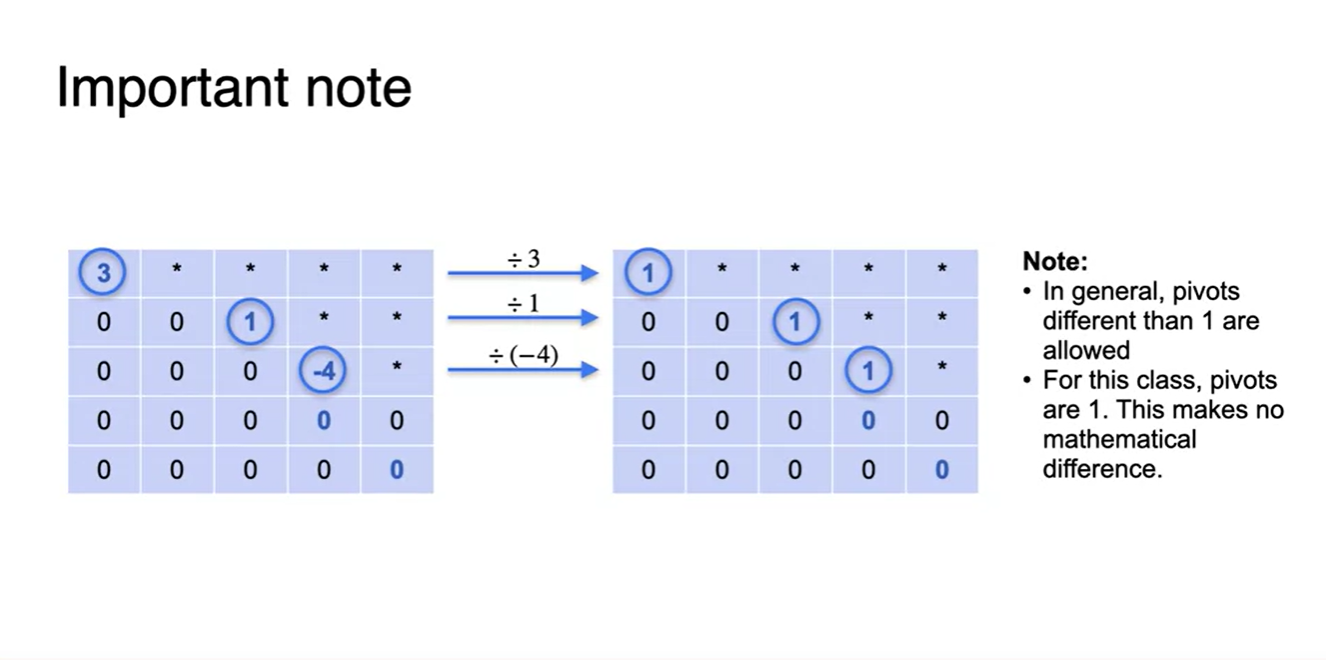
Row echelon form의 diagonal 원소를 꼭 1로 만들 필요는 없다.
- 아래 수식과 같이 상삼각행렬의 꼴을 만들면 된다.
-
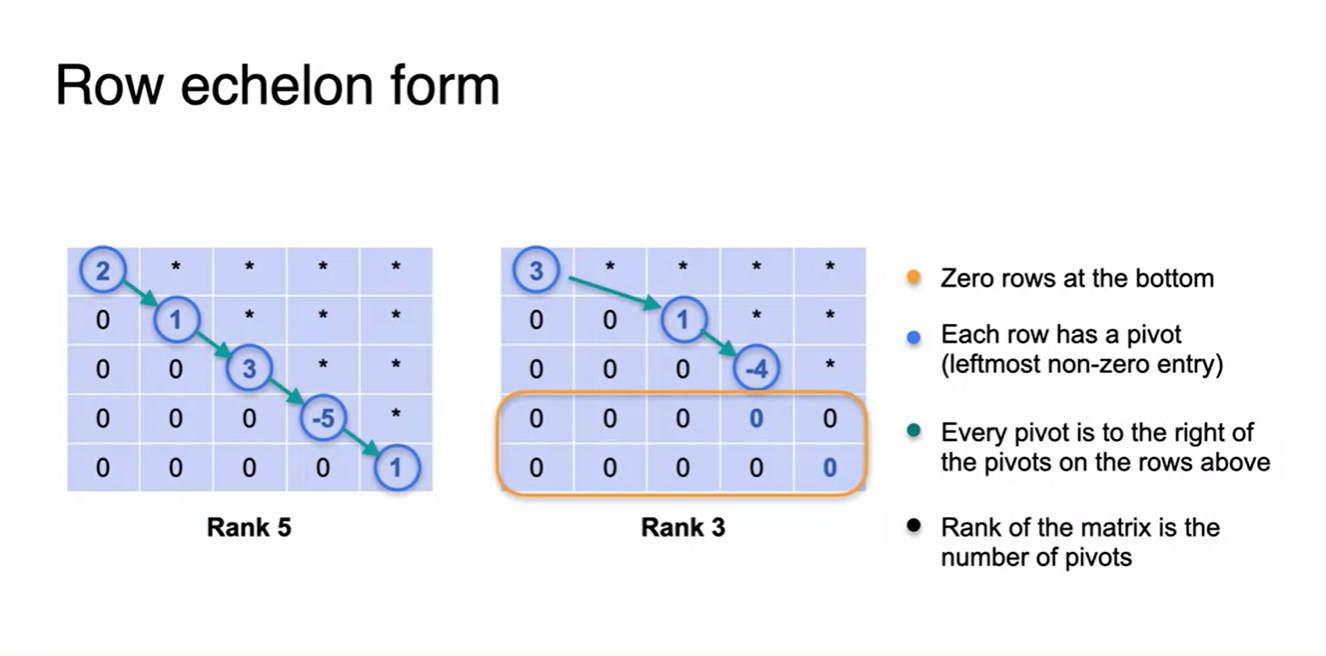
아래의 general한 특징을 살펴보자.
- Rank가 5로 full한 matrix는 zero rows가 존재하지 않는다.
- Rank가 fully하지 않은 matrix는 가장 아래애 zero rows가 존재한다.
- 각 row의 가장 왼쪽에는 non-zero한 pivot 원소를 가지고 있다.
- 이 때, pivot 원소는 위쪽에 위치한 pivot column의 오른쪽에 위치한다.
- 결론적으로, Rank는 pivots의 개수를 나타낸다..
- Rank가 5로 full한 matrix는 zero rows가 존재하지 않는다.
- 이후, 각 원소의 값으로 나눠주는 작업까지 진행하는 것이 general form을 만드는 방법이다.
- 우리는 앞으로 오른쪽과 같은 matrix를 작업까지 진행할 것이다.
- Pivots를 1로 만드는 과정은 matrix의 rank를 변경하지도, singularity를 변경하지도 않으므로 보존성을 보장한다.
-
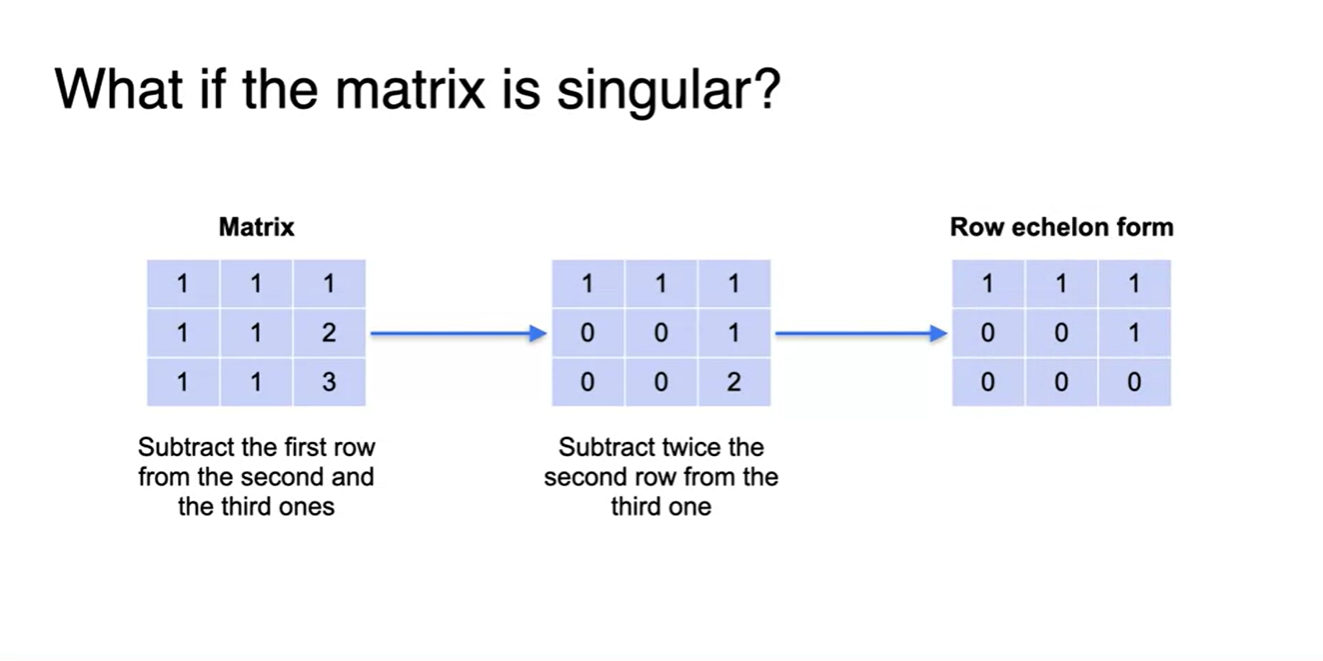
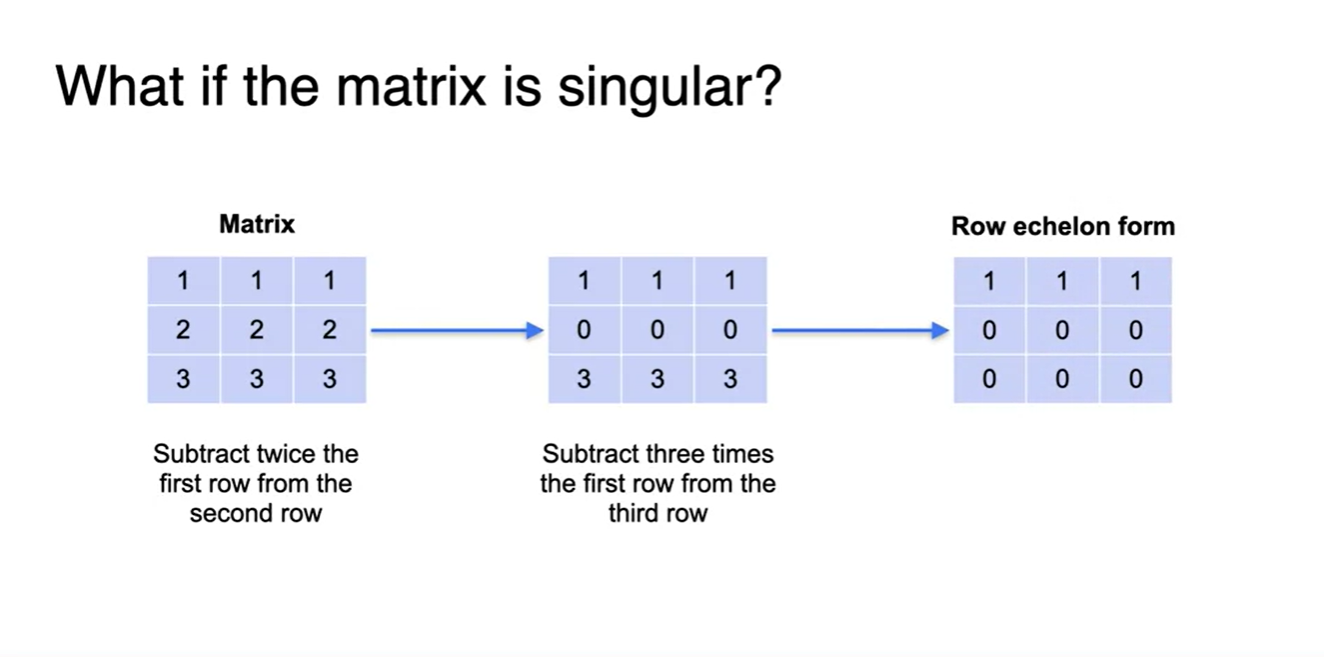
Matrix가 Singular하다면 Row echelon form의 형태는 어떨까?
- Rank의 개수는 fully하지 않으며 pivot의 개수 또한 전체 행의 개수에 비해 부족하다.
- 이 때 diagonal 원소도 0이 껴있는 형태가 될 수 밖에 없다.
-
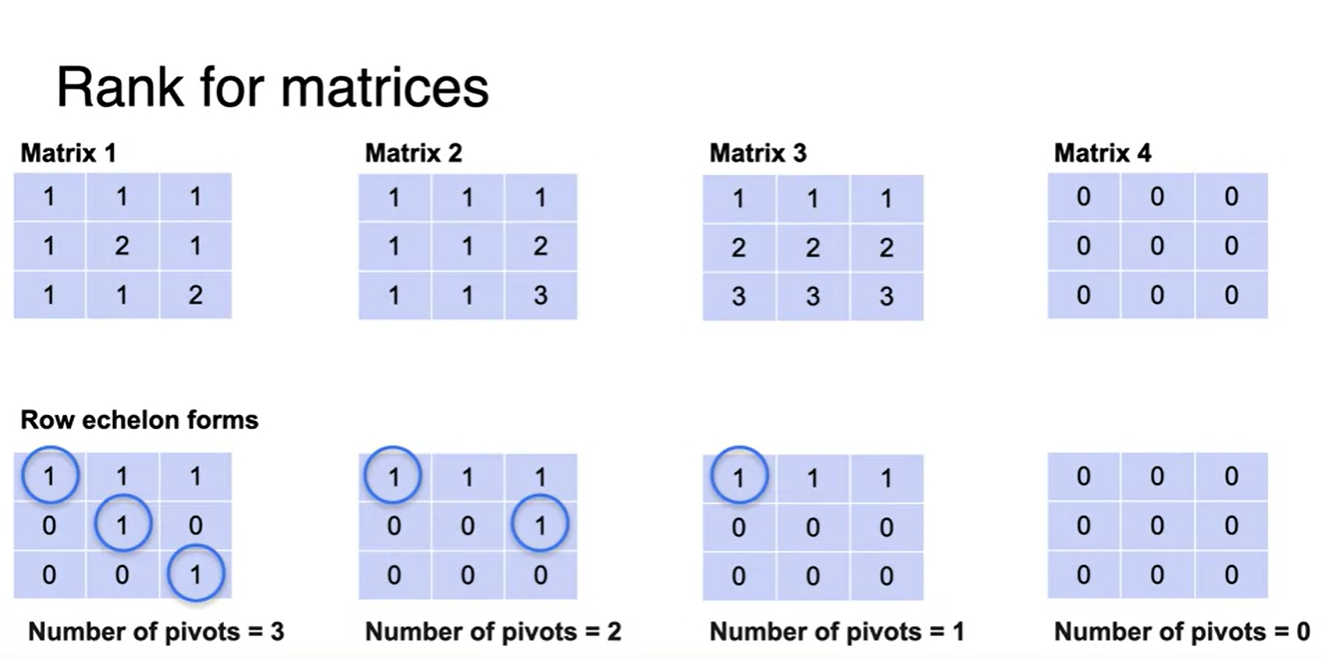
다양한 System의 Row echelon form을 구해보자.
- 이렇게 하면 matrix의 rank도 알 수 있고, pivots의 원소가 무엇인지까지 확인할 수 있다.
- rank의 개수는 곧 pivot의 개수다!
- 이렇게 하면 matrix의 rank도 알 수 있고, pivots의 원소가 무엇인지까지 확인할 수 있다.
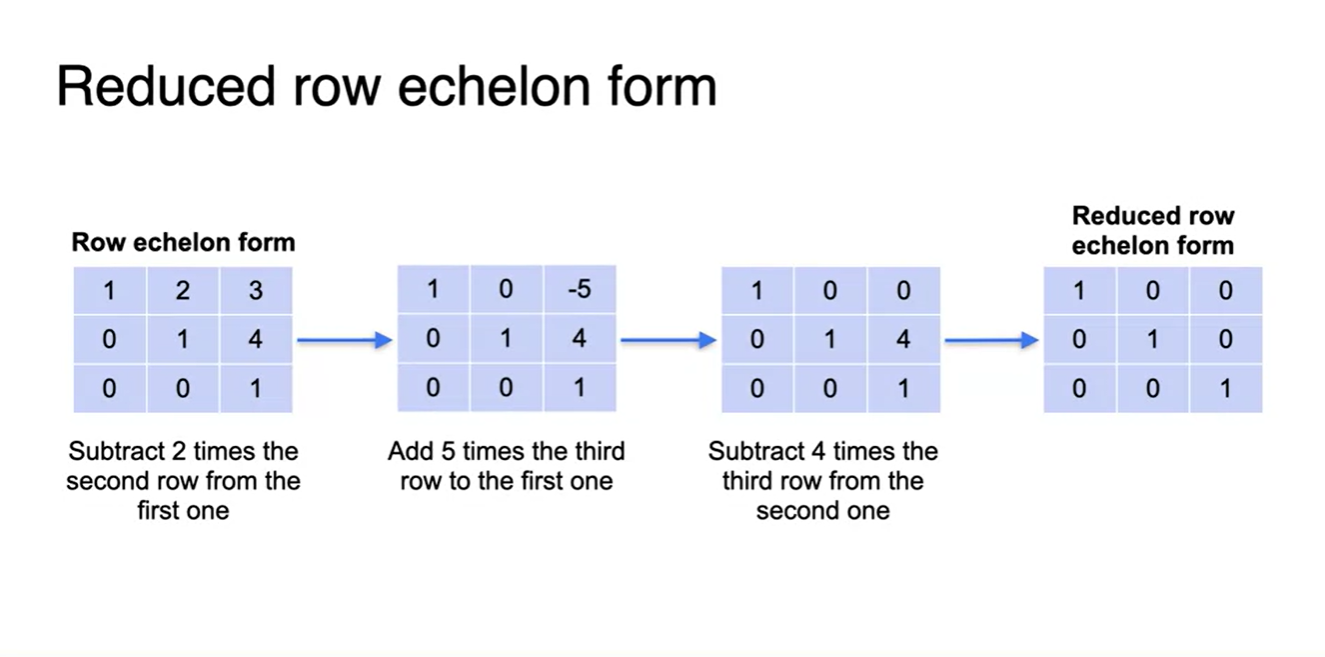
Reduced row echelon form
-
Reduced row echelon form은 기존에 Row echelon form으로 전개했던 matrix를 한 번 더 계산하여 Diagonal matrix로 나타내는 것을 말한다.
- 그러면 diagonal 변수의 solution을 결정할 수 있는 형태로 전개되는 것이다.
- 아래와 같이 (0, 1)의 row에 0.2를 곱한 값을 이용하여
- (1, 0.2) row의 0.2를 삭제해주는 과정으로 최종 정리할 수 있다.
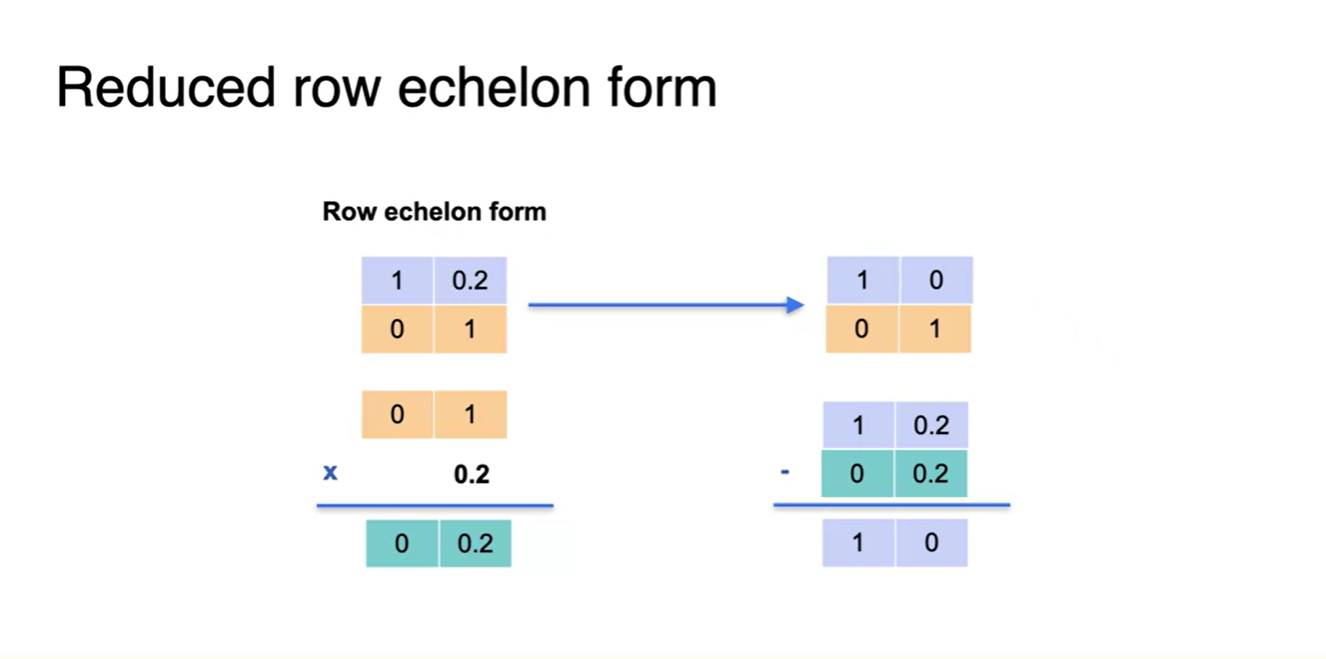
- Reduced row echelon form의 특징은 pivot 원소의 above한 자리까지도 0이 된다는 사실이다.
- Reduced가 붙은 이유가 바로 여기에 있다!

-
기존 Row echelon form → Reduced row echelon form을 만들어주기 위해서는 pivot 원소의 above 항들이 모두 0이어야 한다.
- pivot 원소를 1로 만드는 방법은 앞서 설명했듯 가장 왼쪽 원소로 나눠주면 된다.

- 예제를 통해 확인해보자.
- 여러 연산을 거쳐 diagonal 형태의 pivots만을 남기는 것이 RREF 과정의 핵심이다.