[MMD] Linear Algebra for Machine Learning and Data Science Week 3
Vectors and Linear Transformations
Vector algebra
Machine Learning Motivation
-
머신러닝에서 가장 활발하게 행렬이 사용되는 분야는 바로 GAN(생성적 적대 신경망)이다.
- GAN이 생성하는 이미지는 매우 사실적이어서 실제와 구별이 불가능할 정도다.

-
Text를 Input으로 받아 들여 Image를 생성하는 분야에서도 활발히 적용 가능하다.
- Text-to-Image나 Image-to-Text generation task도 수행할 수 있다.
- 이를 수행하기 위해서는 행렬이나 벡터의 연산을 잘 조작하여 이용하는 것이 핵심이다!

Vectors and their properties
-
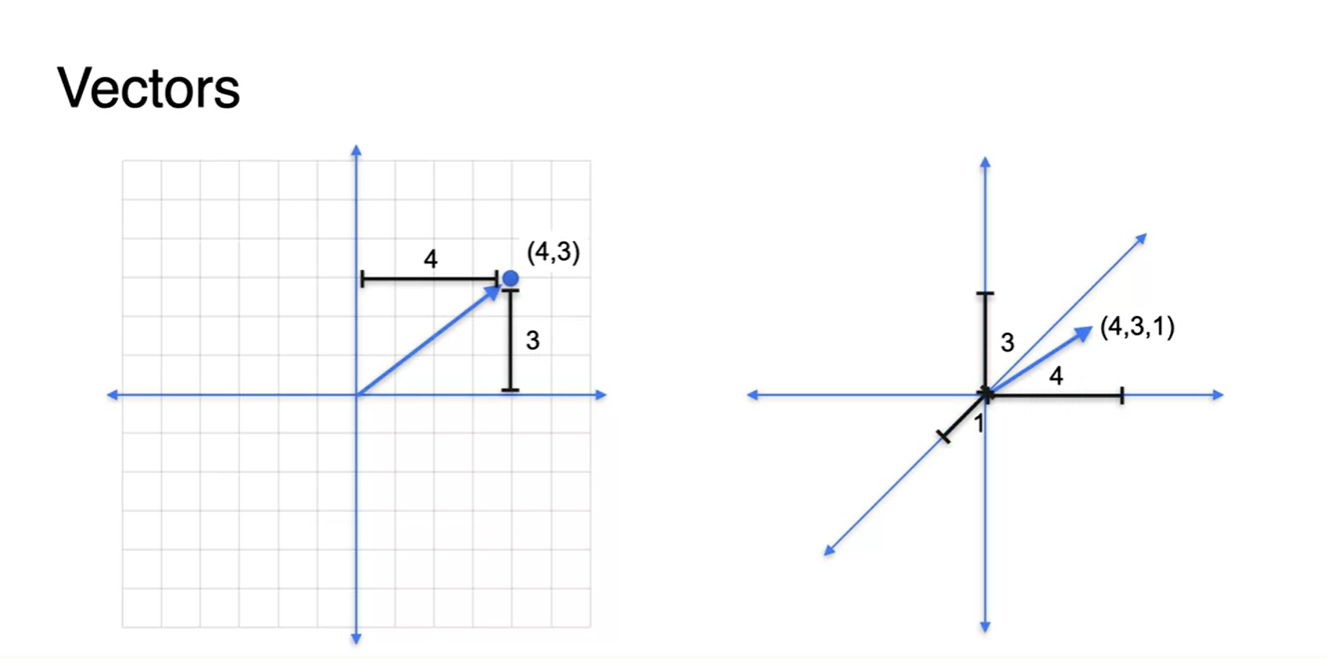
Vector는 성분 원소가 튜플 형태로 묶인 꼴을 하고 있다.
- 2차원 벡터라면 (3, 4)와 같은 형태로, 3차원 벡터라면 (4, 3, 1)과 같은 형태로 표현 가능하다.
- 벡터가 지닌 2가지 핵심 성질은 magnitude(size)와 direction이 존재한다는 것이다.
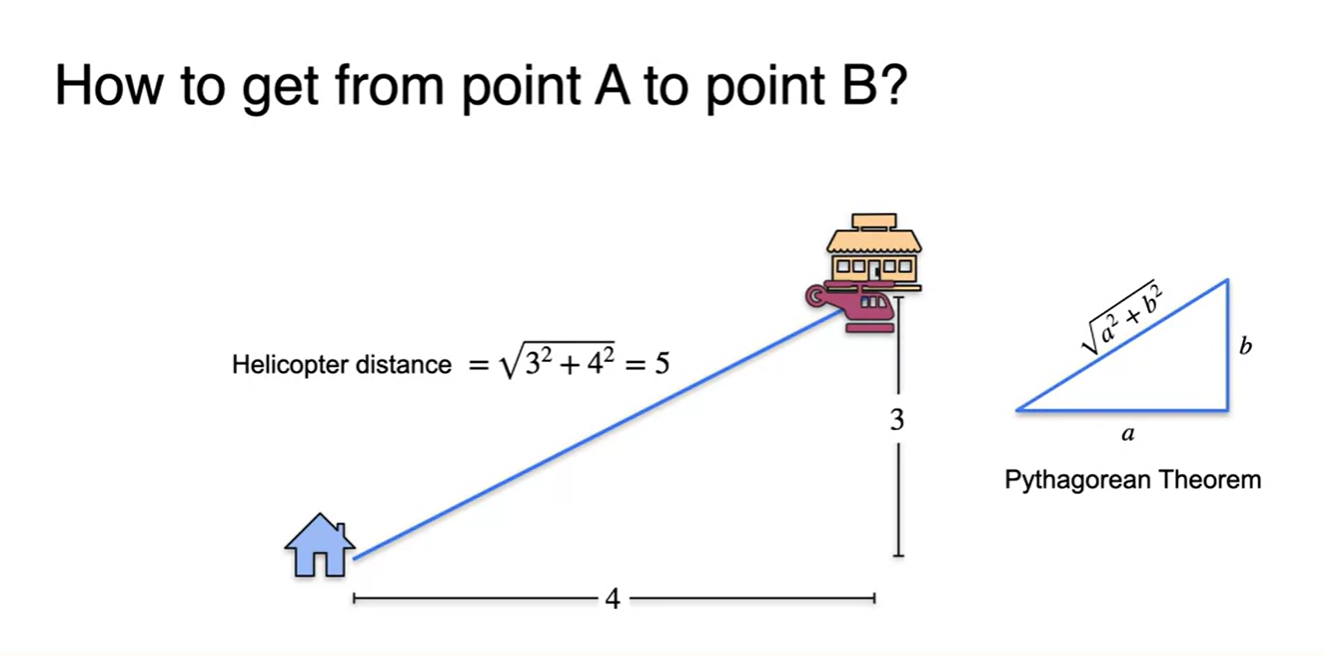
- 인접한 두 위치의 거리를 재는 방법에 대해 알아보자.
- 먼저, 큰 도로만 지나갈 수 있다고 한다면 의 거리를 가야만 한다.
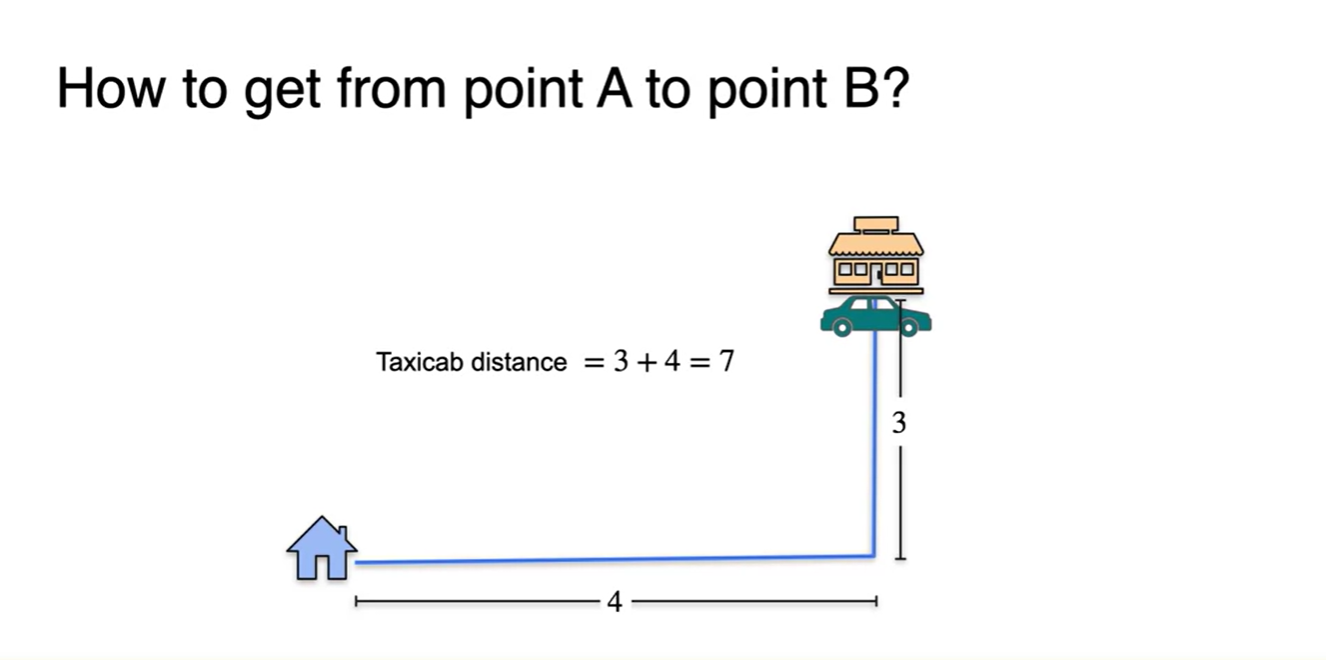
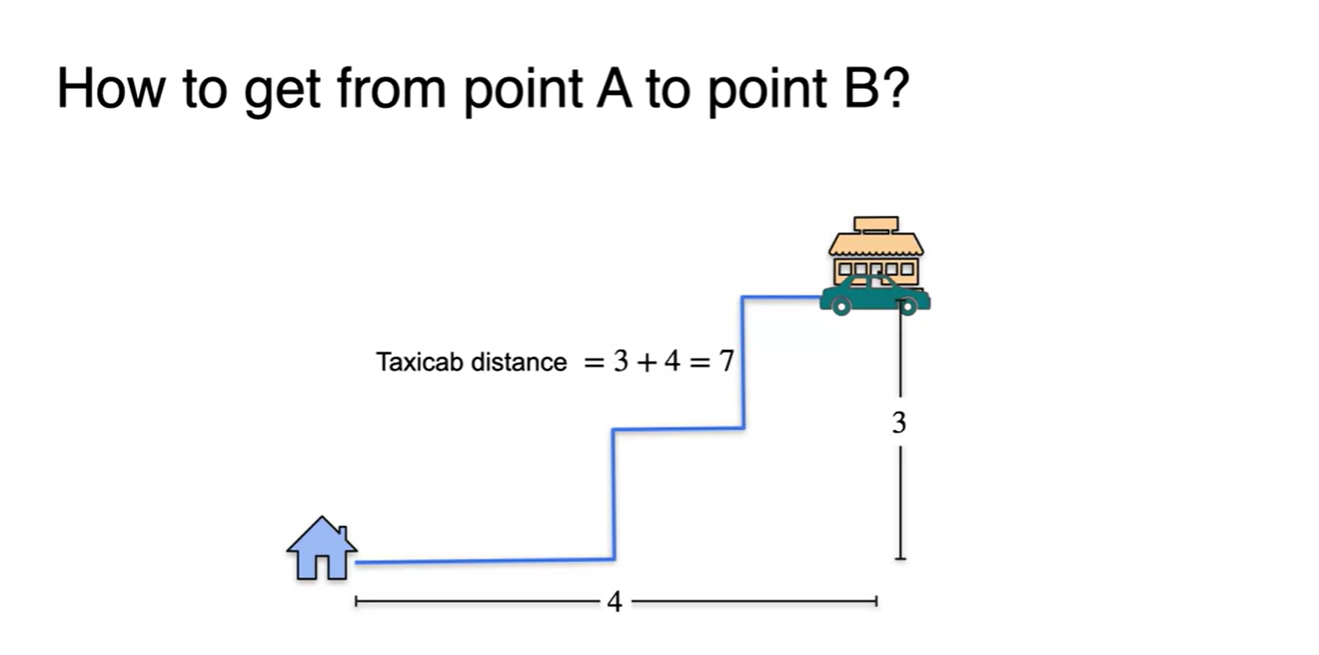
-
경로를 약간 틀어서 지그재그로 가더라도 해당 경로의 길이 합은 언제나 이다.
- 이를 택시거리 즉, taxicab distance라 하겠다.
-
만약 헬리콥터라면 일직선으로 갈 수 있으므로 피타고라스 정리에 의해 의 거리로 갈 수 있다.
- 이 경로가 두 지점을 잇는 가장 최단거리다.
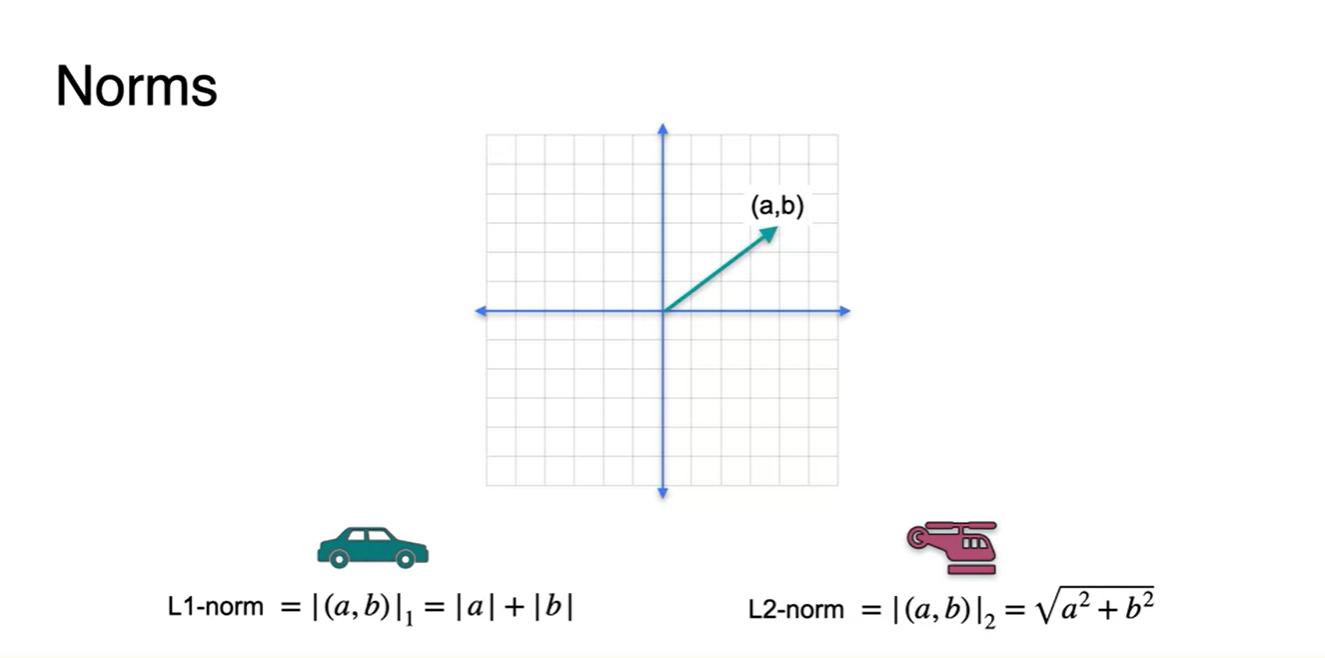
- Norm에 대해 알아보자.
- L1 norm은 택시가 가는 경로이며, L2 norm은 헬리콥터가 가는 경로로 정의한다.
- 원점에서 (a, b)의 지점으로 가는 길은 L1 norm일 때 각각의 양수 크기만큼을 더한 것이며, L2 norm은 피타고라스 정리에 의한 거리임을 알 수 있다.
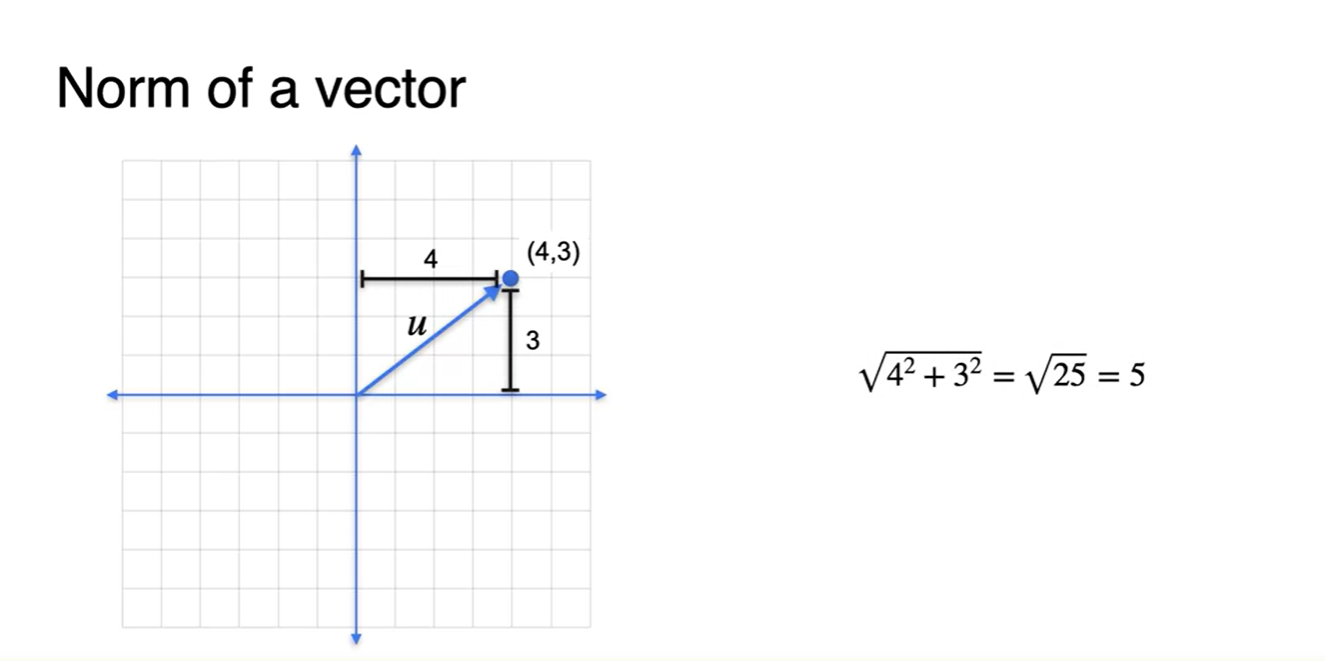
-
Norm의 default 값은 L2 norm이고, 벡터의 크기를 나타내기도 한다.
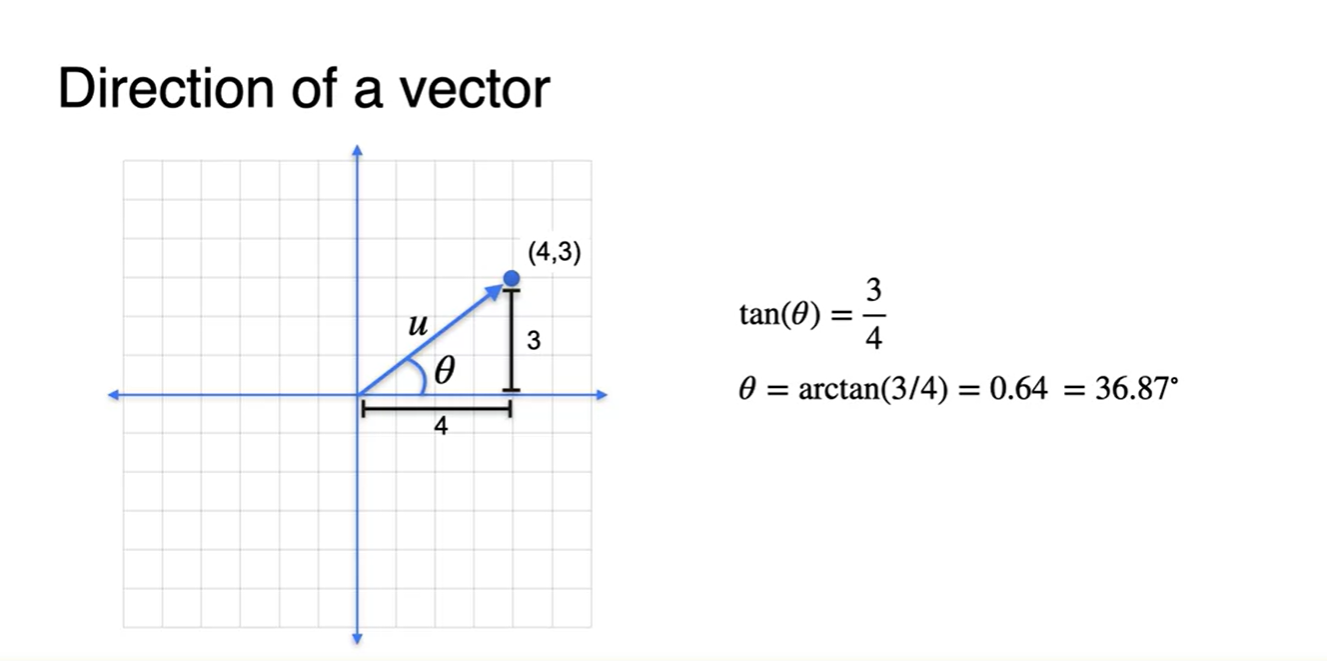
- Direction은 angle(각도)로 표현하며 로 값을 표기한다.
- 각도를 알고 싶다면 와 같은 연산으로 구하면 된다.
Sum and difference of vectors
-
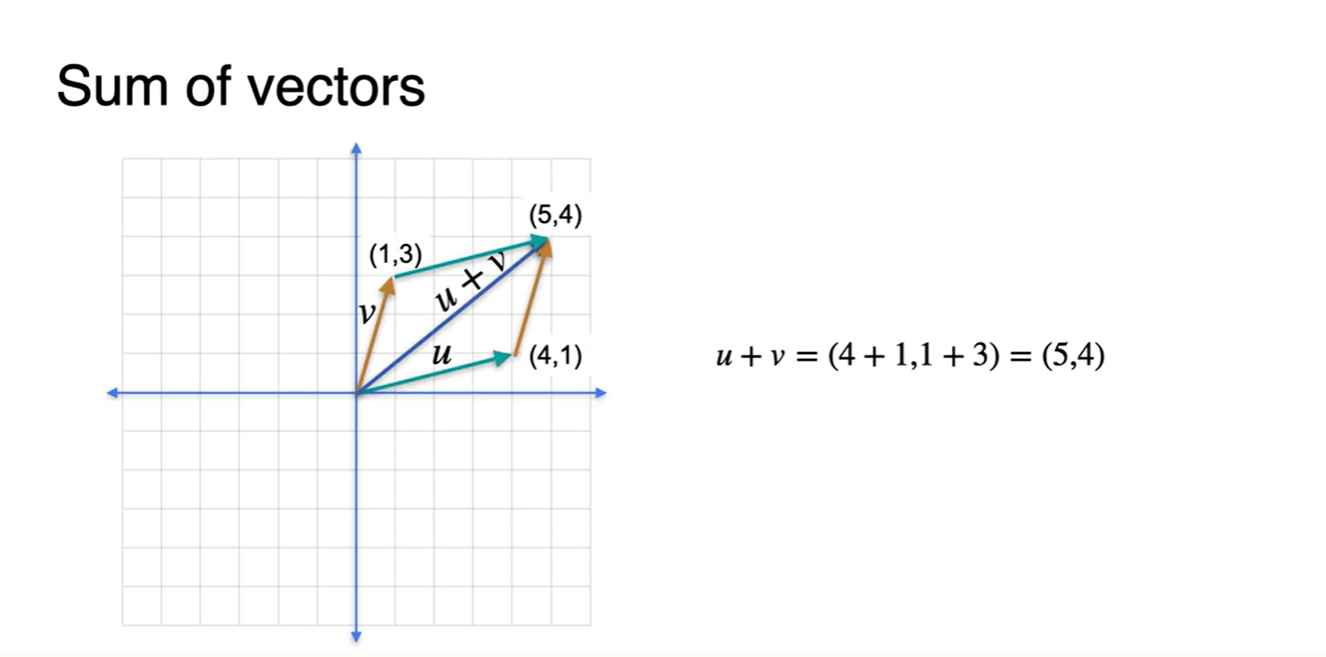
Vector는 Sum과 Subtract 연산이 모두 가능하다.
- Sum은 각 성분의 합으로 나타낼 수 있고, 이는 기하학적으로 두 벡터를 통해 만들 수 있는 평행사변형의 대각선 벡터와 정확히 일치한다.
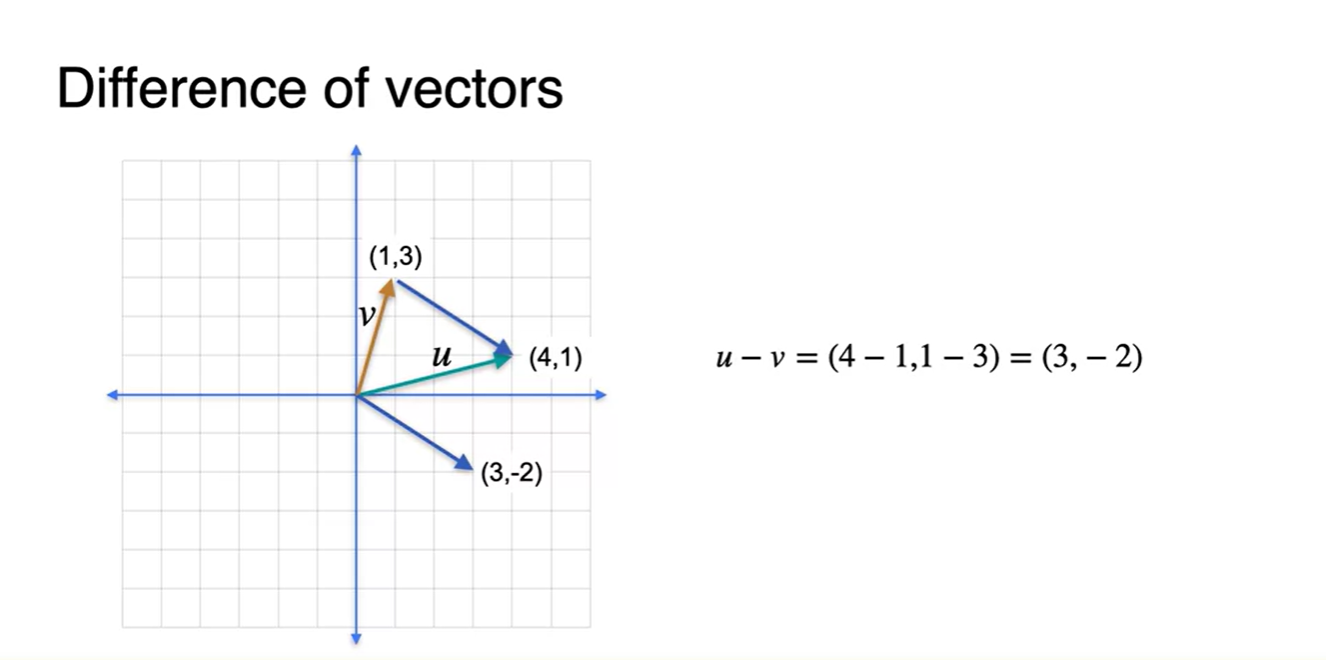
- Subtract 즉, Difference는 각 성분의 차이로 나타낼 수 있으며, 이는 기하학적으로 한 벡터의 시작점과 다른 벡터의 끝점을 이어서 표현할 수 있는 방향을 가리킨다.
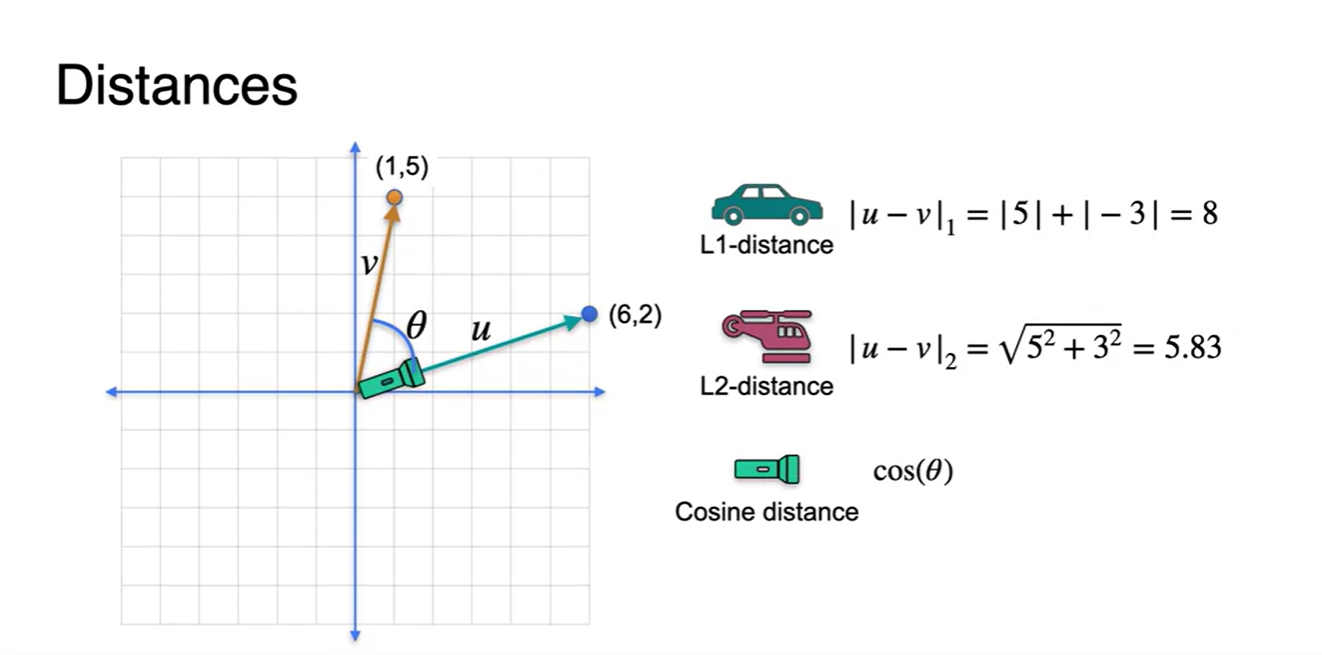
Distance between vectors
-
Vecters 간의 Distance를 재는 방법은 총 세 가지가 있다.
- L1 norm(distance)
- L2 norm(distance)
-
그 중에서도 머신러닝에서는 를 많이 사용한다고 한다.
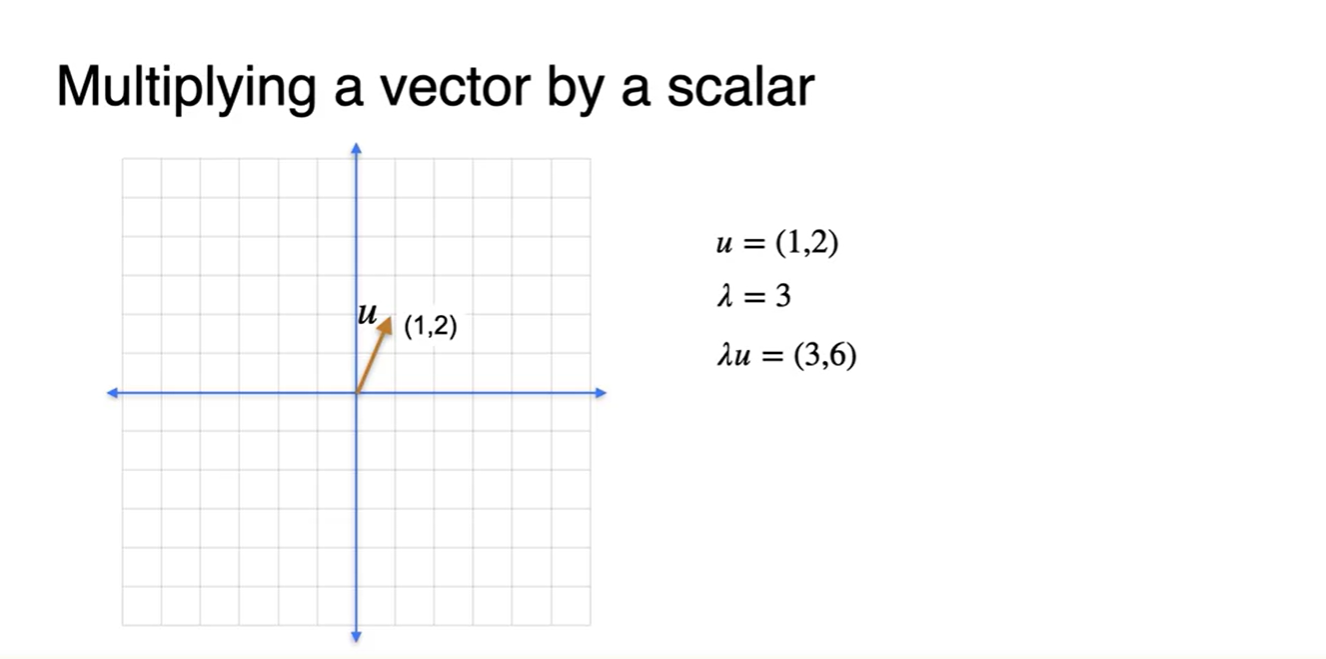
Multiplying a vector by a scalar
-
Vector에 scalar 값을 곱하는 것 또한 가능하다.
- 양수 scalar 값을 곱하면 벡터의 방향은 변화시키지 않고 scale만 키워준다.
- 음수 scalar 값을 곱하면 벡터의 방향은 반대 방향이 되며 scale에 따라 벡터의 크기 또한 변화한다.
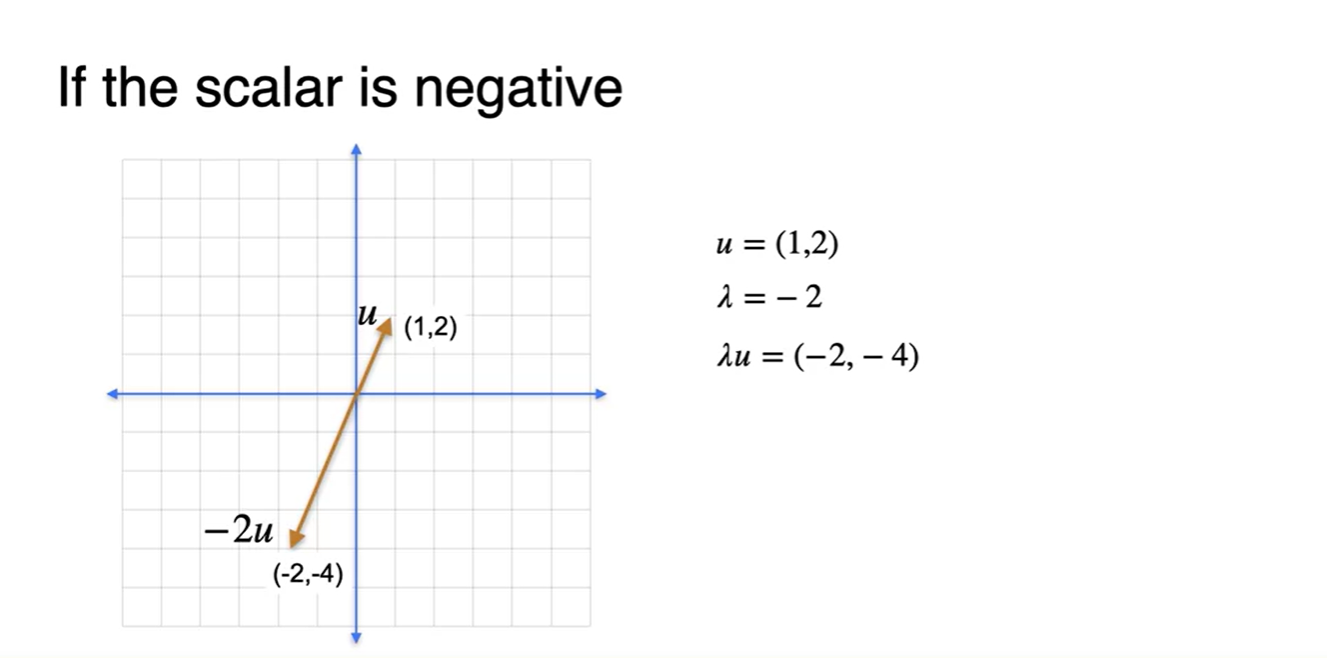
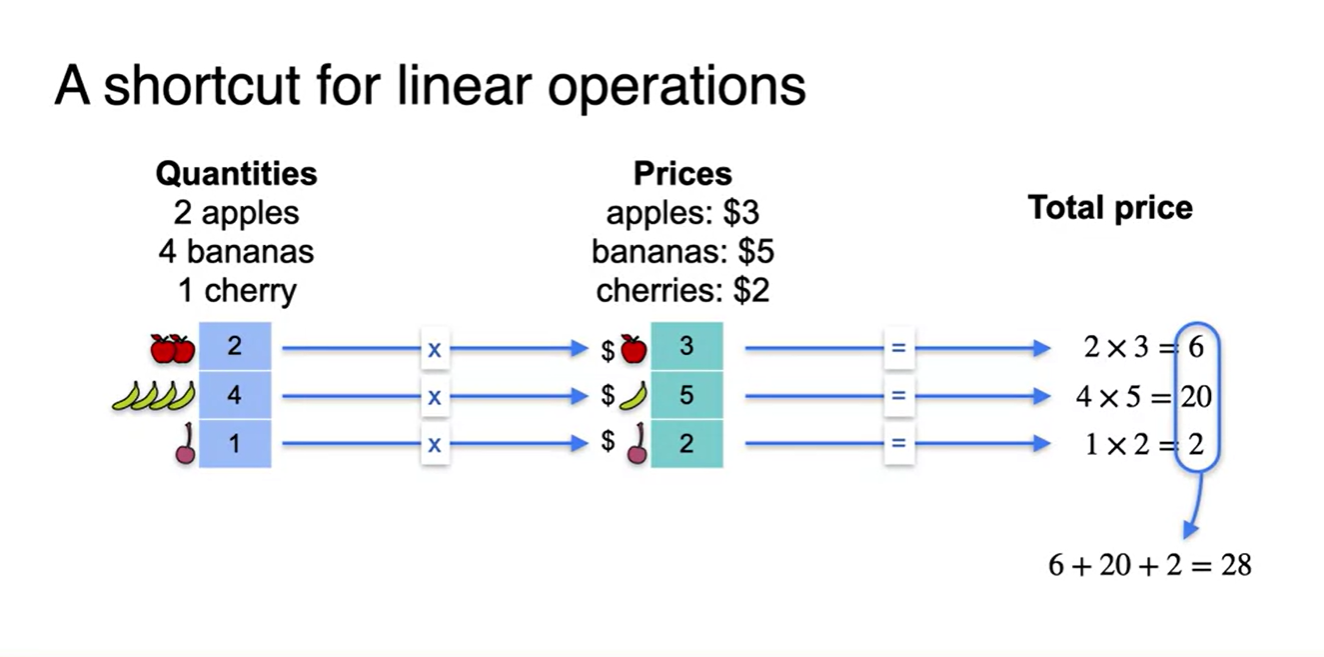
The dot product
-
Dot product는 선형대수에서 가장 중요한 개념이다.
- 아래 예제는 dot product를 계산하는 방법에 대해 소개한다.
- 사과, 바나나, 체리의 양과 가격을 각각 독립적으로 곱하여 전체 price를 구하는 문제다.
- 이는 두 벡터를 아래와 같은 형태로 바꾸어 계산한 것이다.
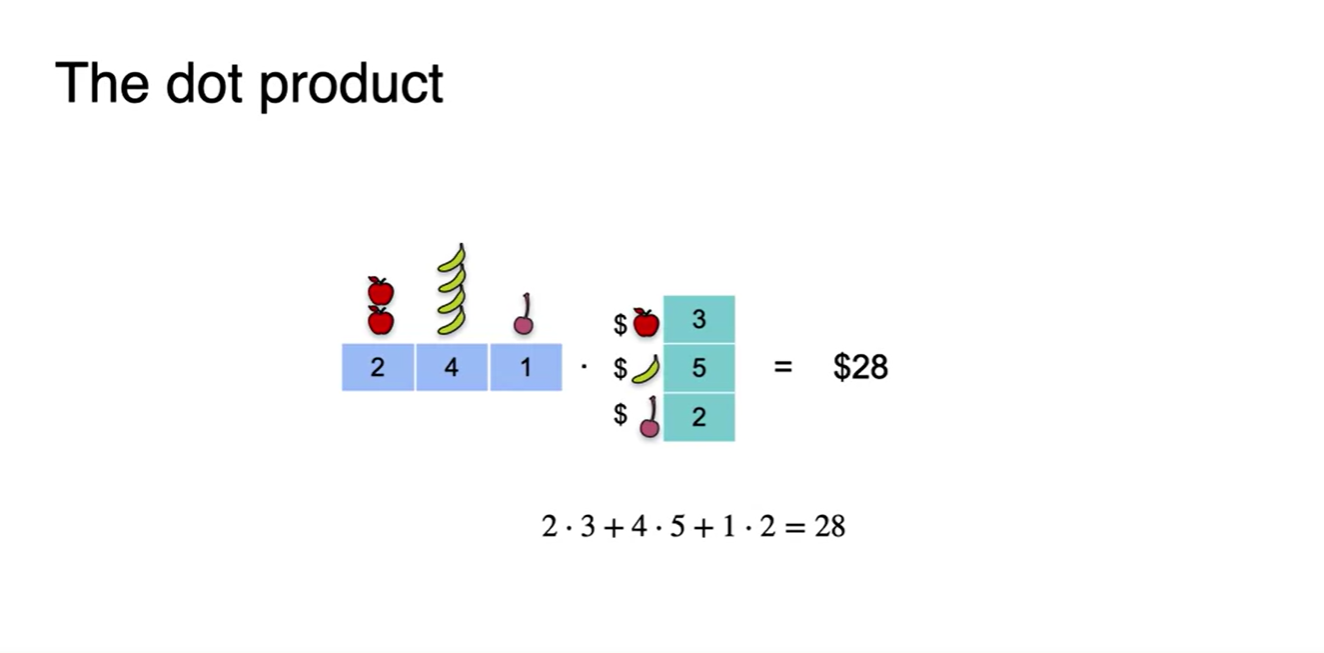
-
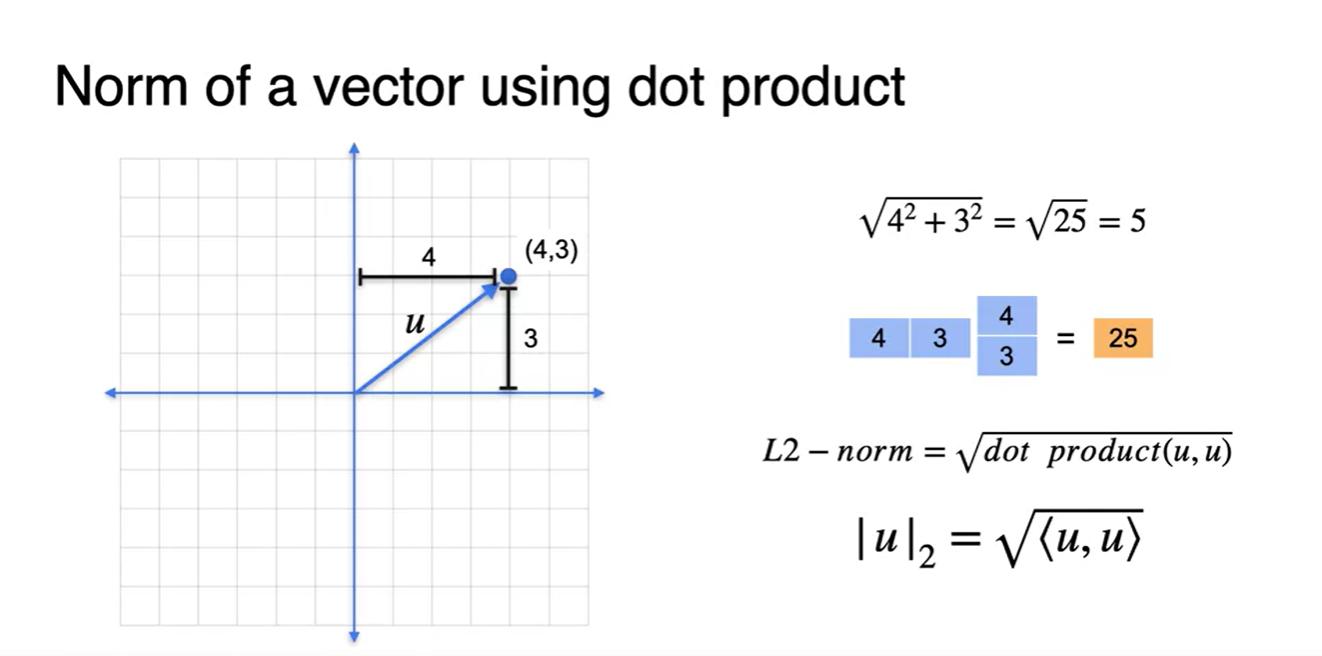
한 가지 추가적인 특징은 L2 norm이 한 벡터를 self-dot product한 결과의 square root 값이라는 것이다.
-
즉, 같은 방향의 벡터 성분을 각각 제곱하여 모두 더한 식과 동일하다.
- 이러한 수식으로 전개될 수 있다.
-
Geometric Dot Product
-
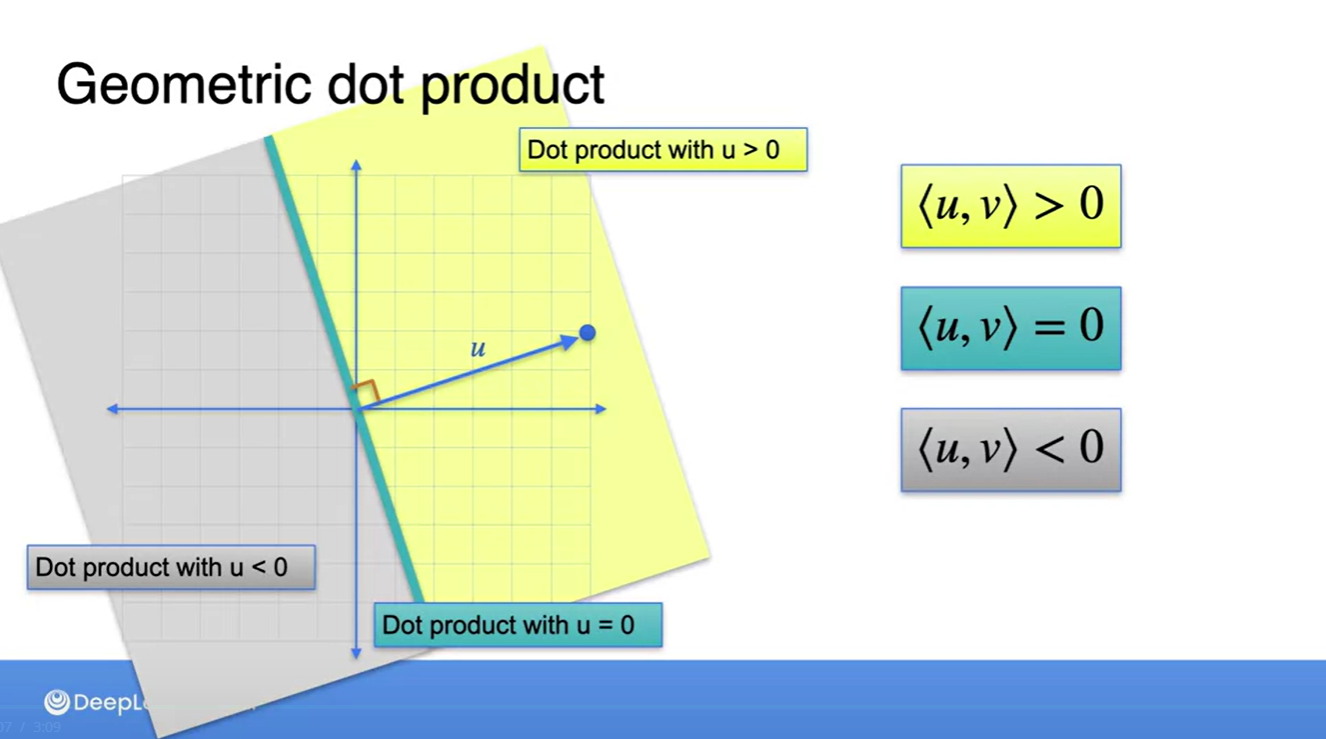
기하학적으로 angle과 dot product의 관계는 매우 중요하다.
- 우선 orthogonal(perpendicular)한 벡터들의 dot product는 항상 0이다.
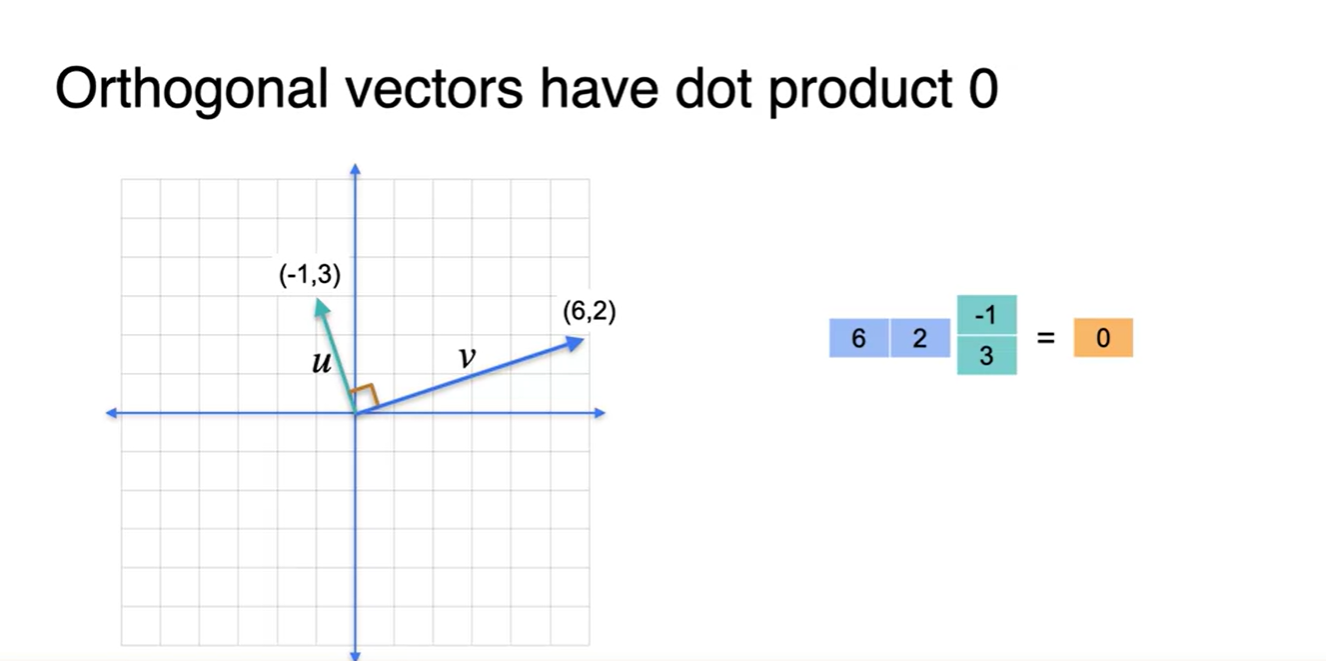
-
같은 방향인 두 벡터의 dot product는 해당 벡터 크기의 제곱이고, 수직한 방향인 두 벡터의 dot product는 0이다.
- 그렇다면 그저 그런 angle을 가진 두 벡터의 dot product는 어떻게 구할까?
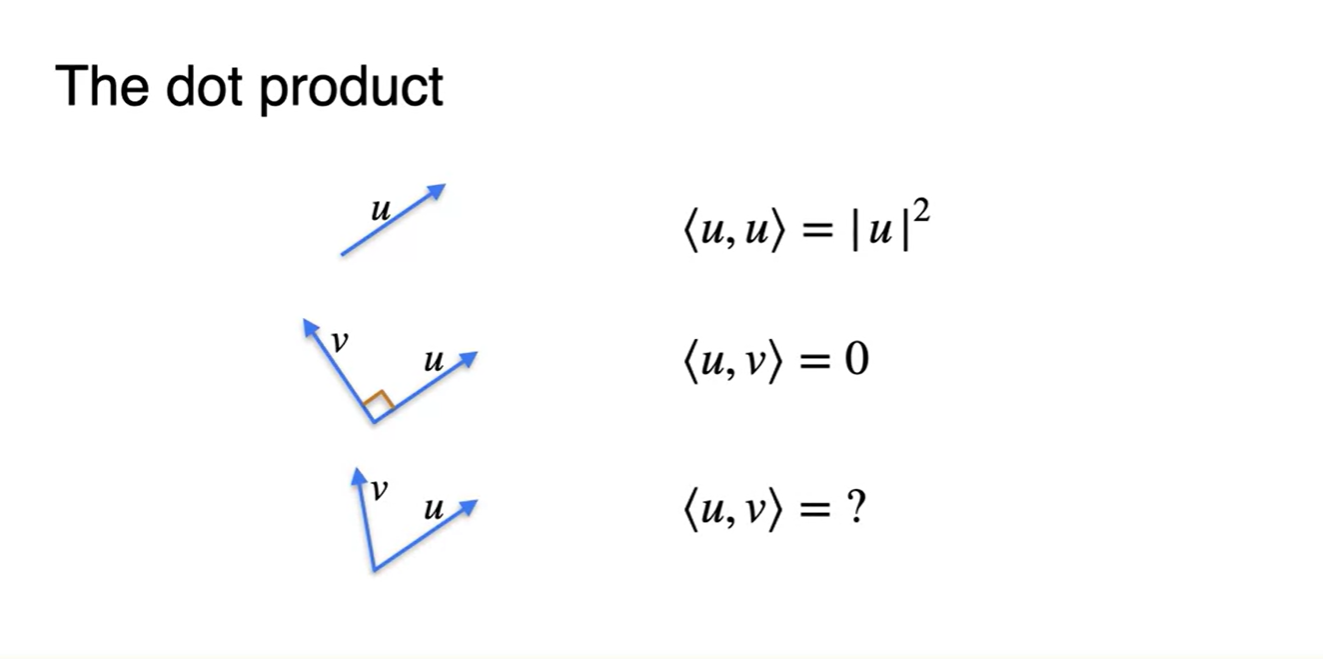
-
일반적으로 dot product란 하나의 벡터()를 다른 하나의 벡터()에 projection(정사영) 내려 형성한 새로운 벡터()와의 성분곱이다.
- 이는 원래 벡터()에 를 곱한 값을 다른 벡터와의 성분곱으로 연산한다.
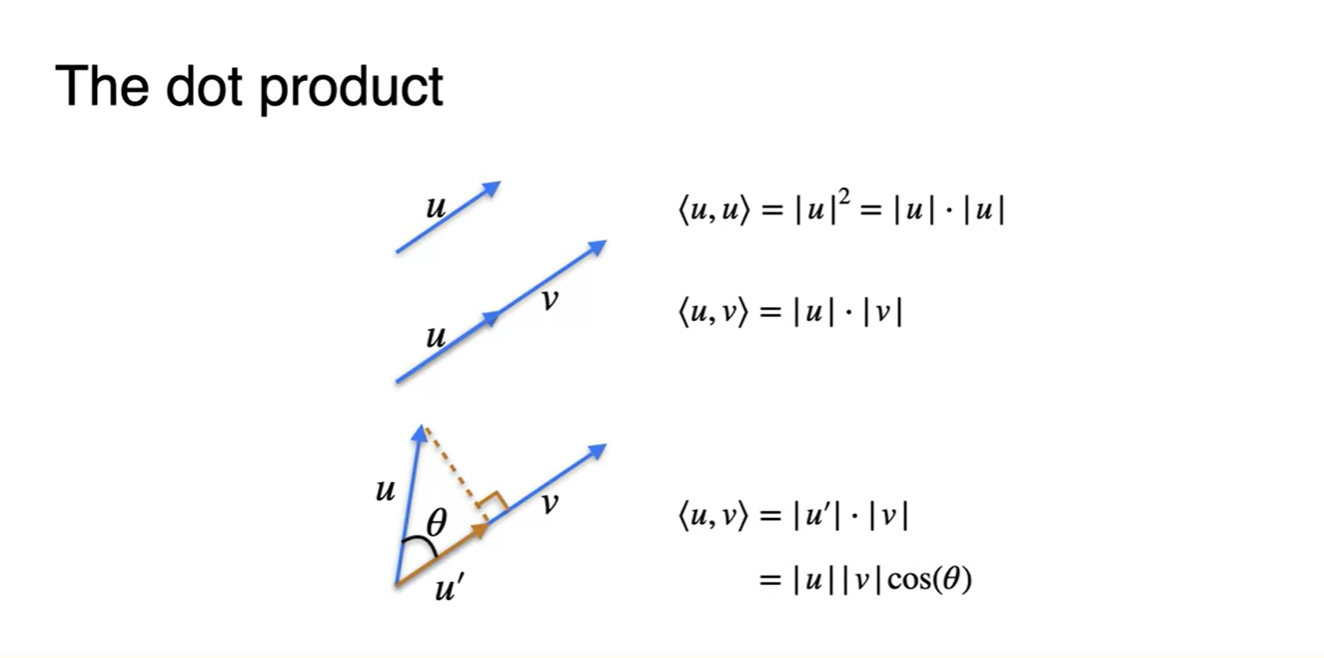
-
Dot product가 positive라면 (6, 2) 벡터와 예각을 이루는 벡터와의 성분곱이며, negative라면 (6, 2) 벡터와 둔각을 이루는 벡터와의 성분곱이다.
- (6, 2) 벡터와 수직하다면 dot product는 어김없이 0임을 알 수 있다.
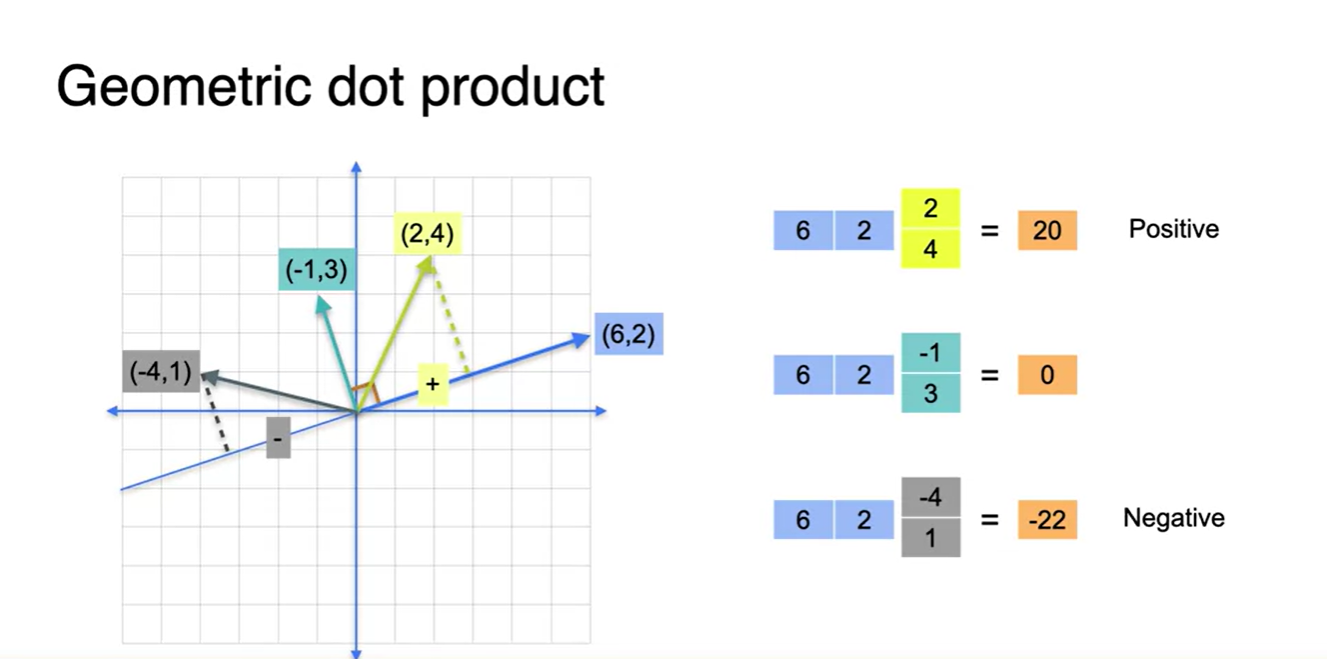
- 따라서 기하학적인 공간 상에 그림으로 표현하면 아래와 같은 범위에서 dot product의 부호가 결정된다고 할 수 있다.
Multiplying a matrix by a vector
-
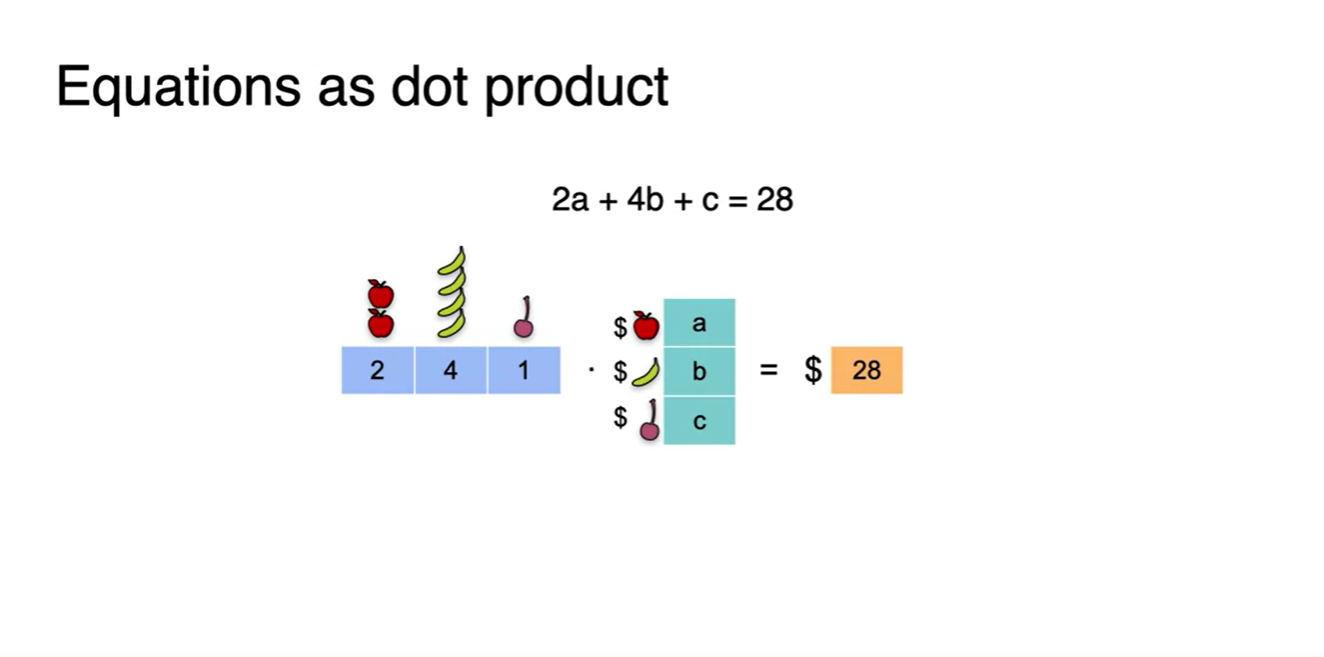
Dot product에 변수가 포함되어 있는 경우를 비교해보자.
- 사과, 바나나, 그리고 체리의 가격을 a, b, c 변수로 두어 몇 개를 샀는지에 대한 정보를 dot product 해 보자.
- 이 과정을 세 개의 System으로 나눠서 풀어 쓰면 아래 그림과 같다.
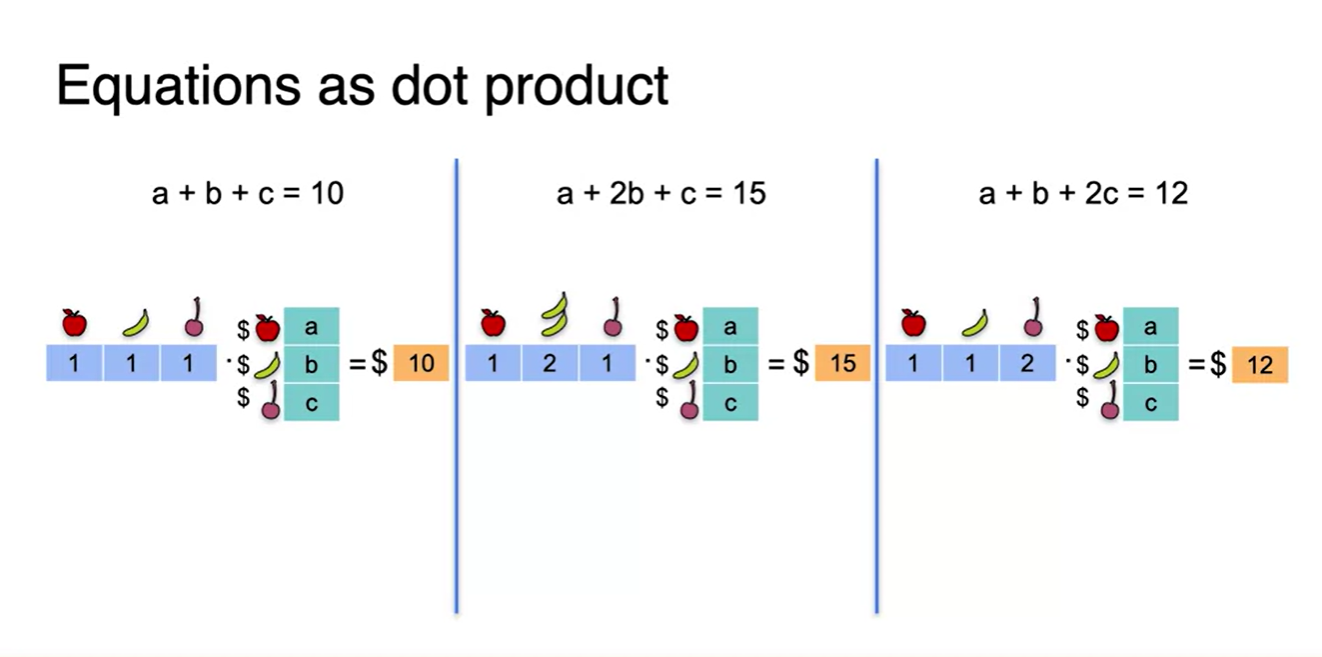
-
이제 이 equations를 하나로 합치는 작업을 진행할 것이다.
-
아래 그림의 오른쪽 형태를 보면 각 열의 정보가 사과, 바나나, 체리에 해당하는 정보를 담고 있다는 것을 알 수 있다.
- 열벡터는 한 변수의 상태를 여러 차원에서 나타내는 역할을 한다.
-
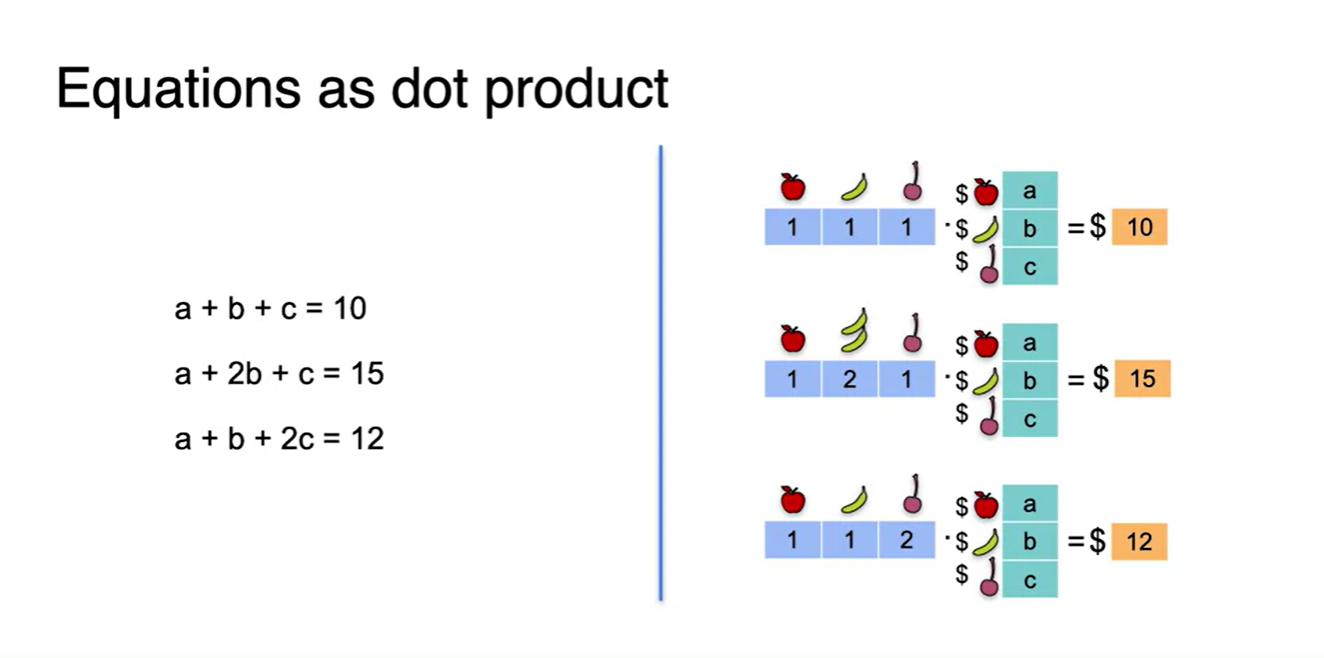
- 위 equantions를 하나의 행렬로 합치면 아래와 같은 꼴이 형성된다.
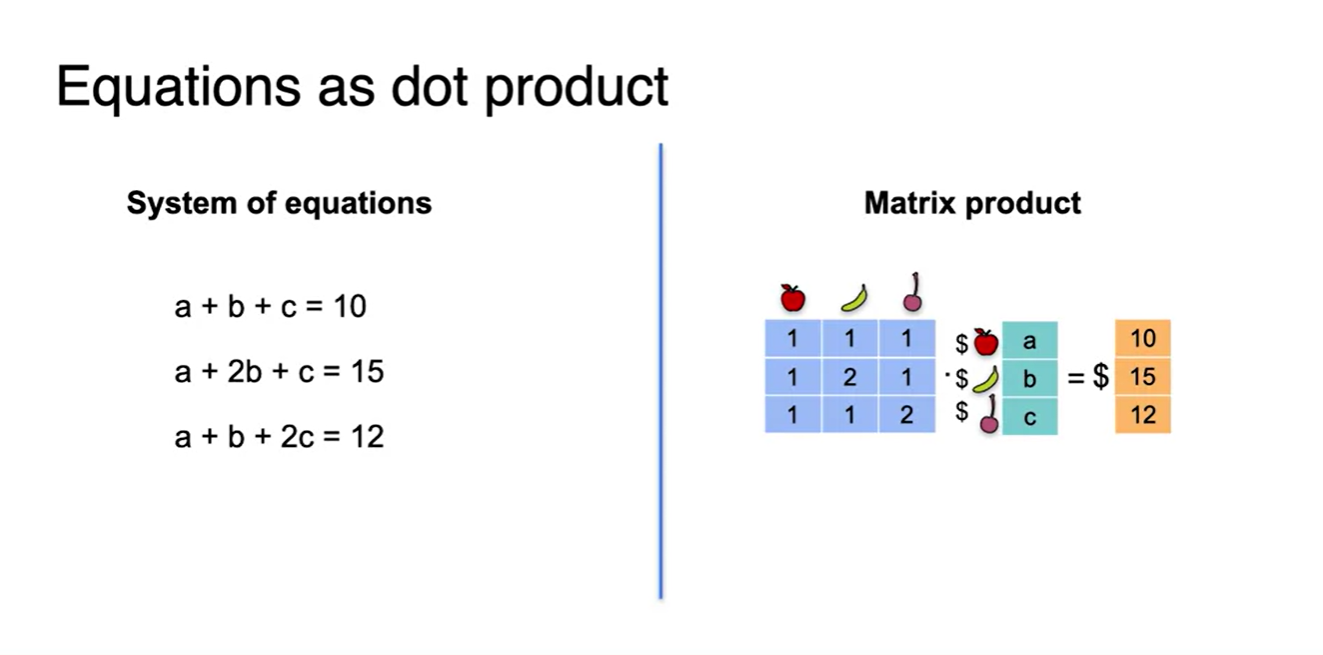
- 앞으로는 아래와 같은 형태로 matrix를 전개할 예정이다.

Linear transformations
Matrices as linear transformations
-
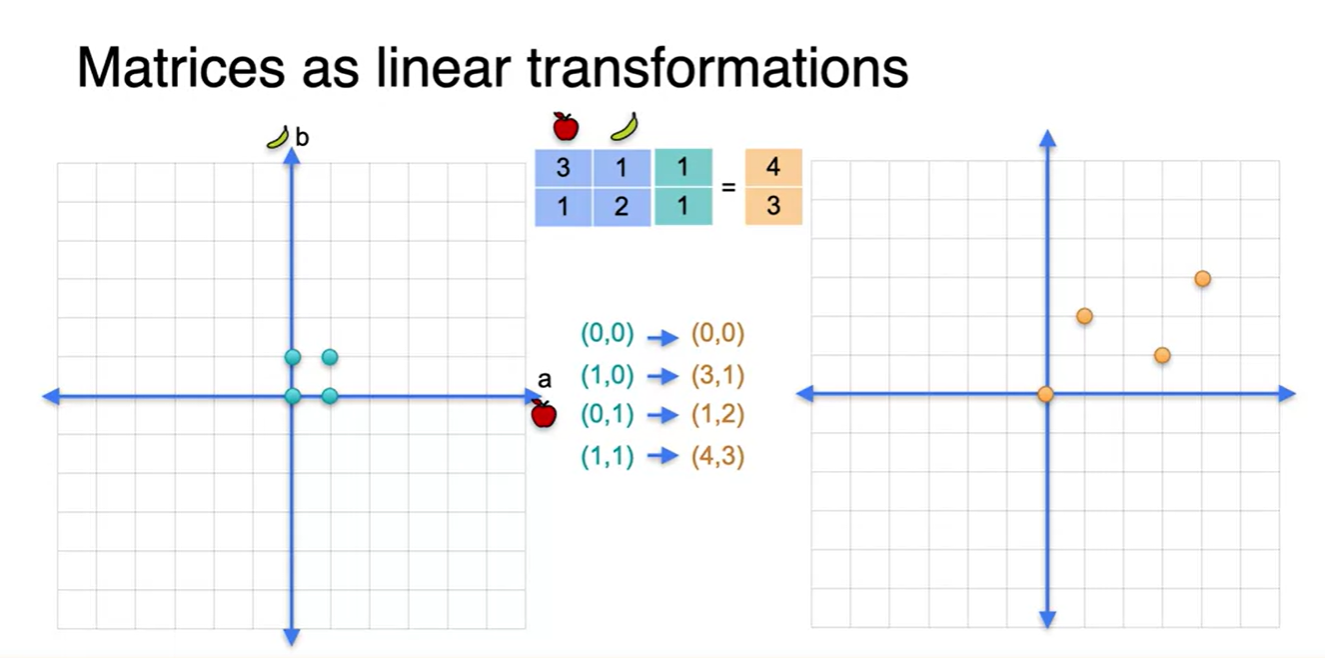
행렬을 표현하는 또 다른 방법인 linear transformations에 대해 알아보자.
- 우선, 사과와 바나나의 양을 나타내는 2x2 행렬이 있다.
- 왼쪽의 공간에 존재하는 벡터를 초록색으로, 오른쪽 공간에 존재하는 벡터를 주황색으로 표시한다.
- 그런 다음, 왼쪽 점을 2x2 matrix로 linear transform하여 오른쪽 점으로 mapping한다.
- 그러면 사갹형을 이루고 있는 네 개의 점이 평행 사변형을 이루며 새로운 점으로 변형되어 찍히게 된다는 것을 알 수 있다.
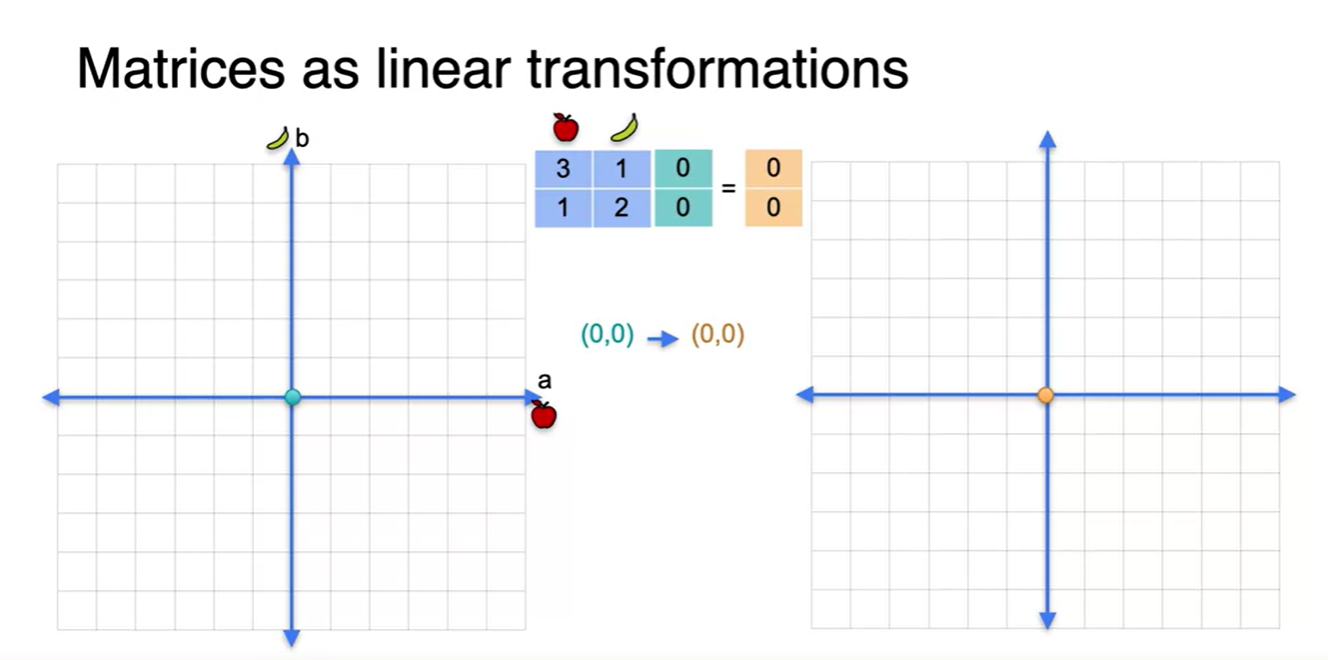
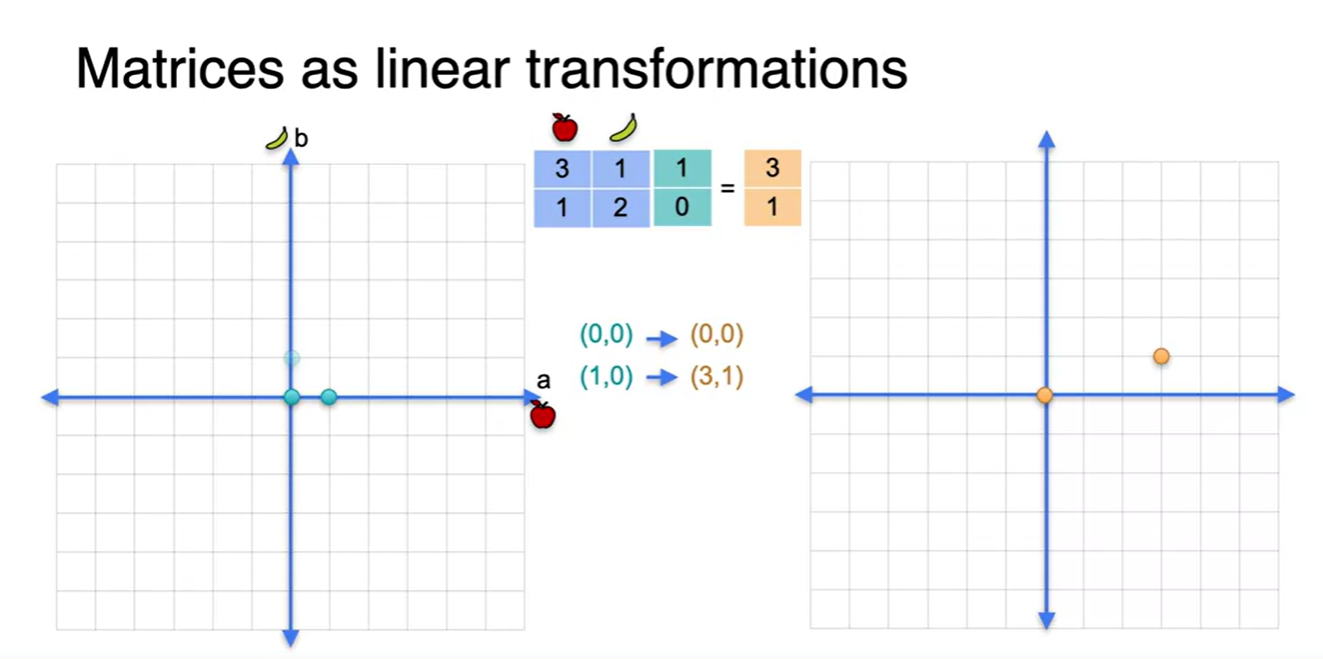
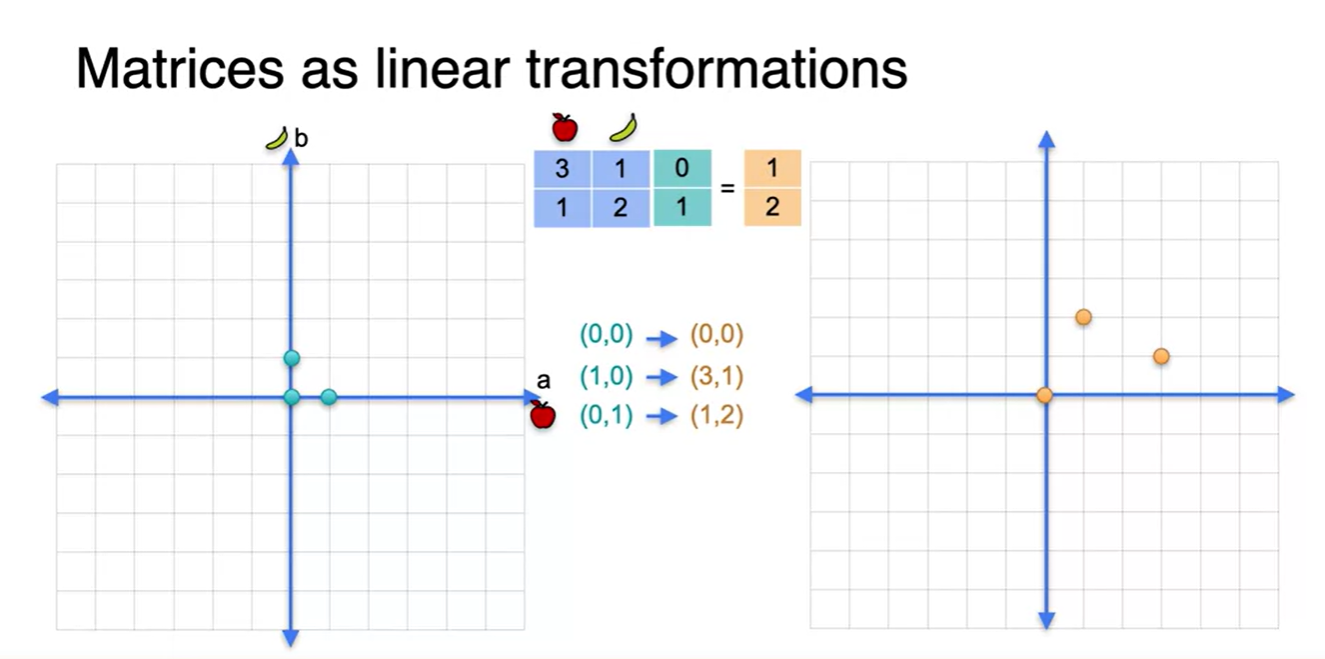
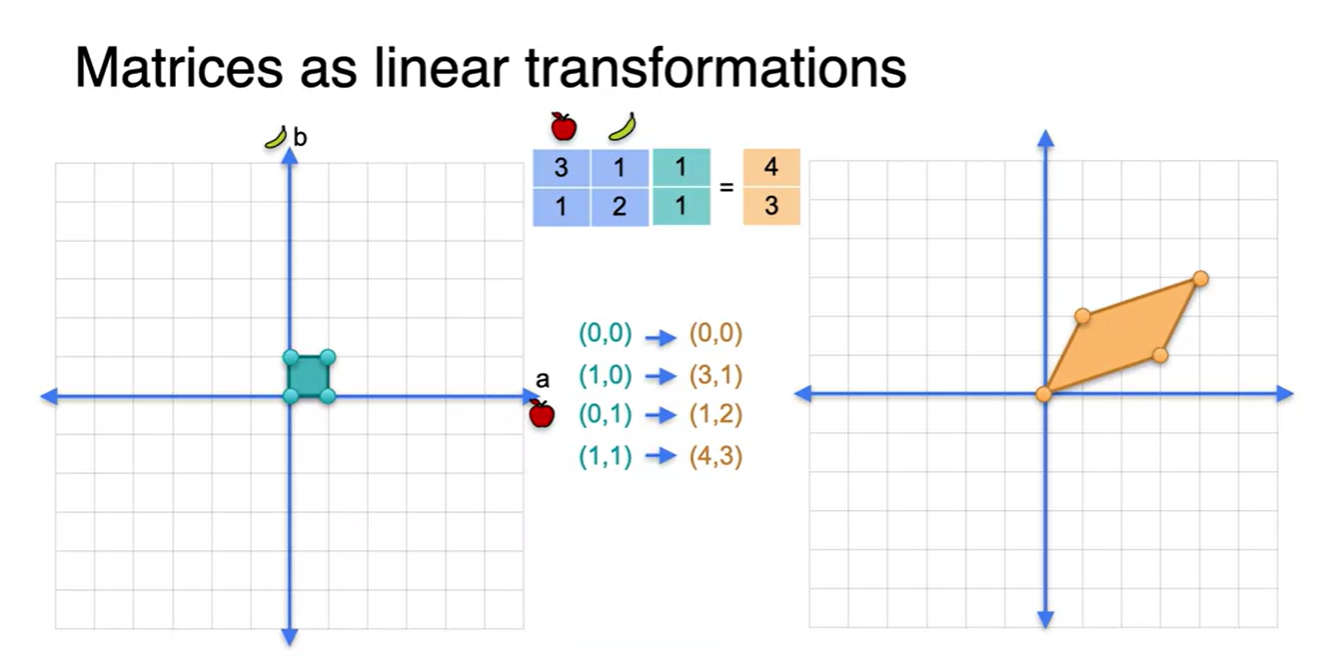
-
네 개의 점을 이으면 사각형의 한 평면과 평행 사변형의 한 면이 만들어진다.
- 왼쪽의 네 점이 바로 basis라 불리는 점들인데, 이 개념은 굉장히 중요하니 기억해두자.
- 네 점을 잇는 작은 평면을 확장하면, 결국 해당 공간 전체를 표현할 수 있는 평면으로 이루어졌음을 알 수 있다.
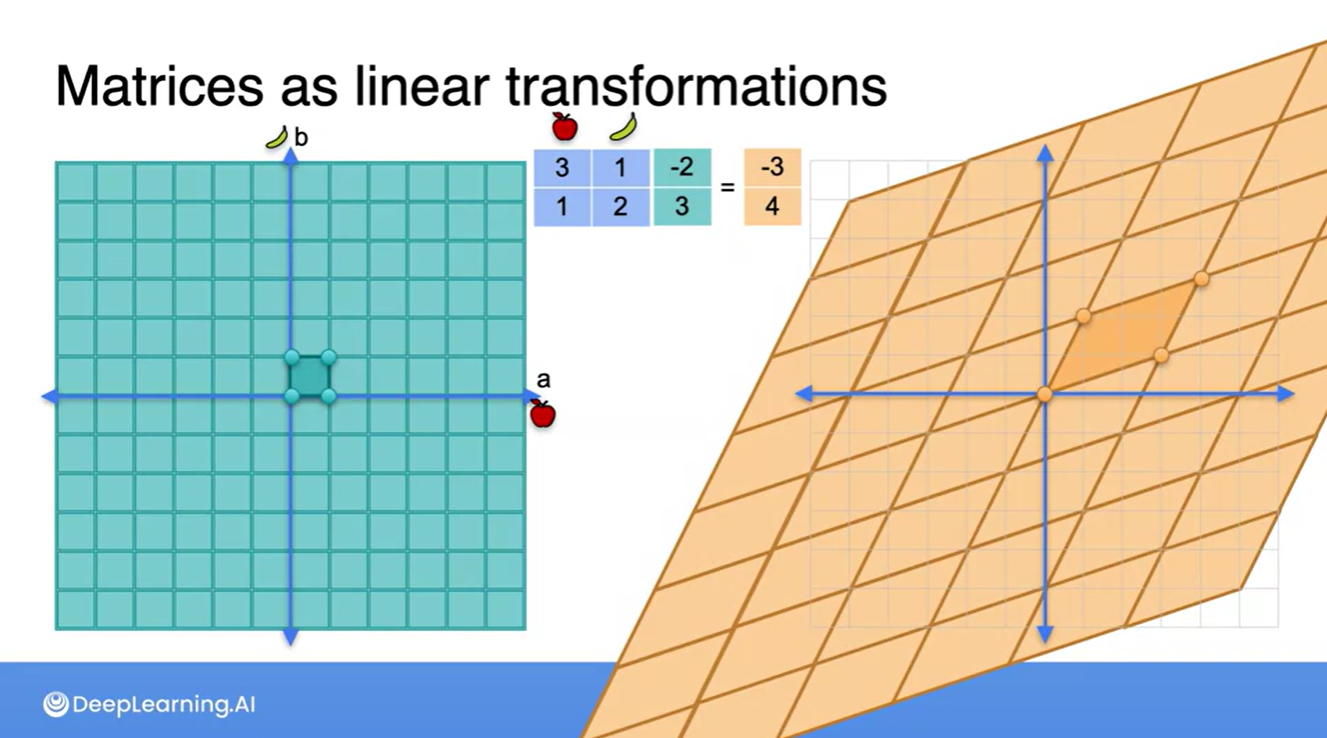
-
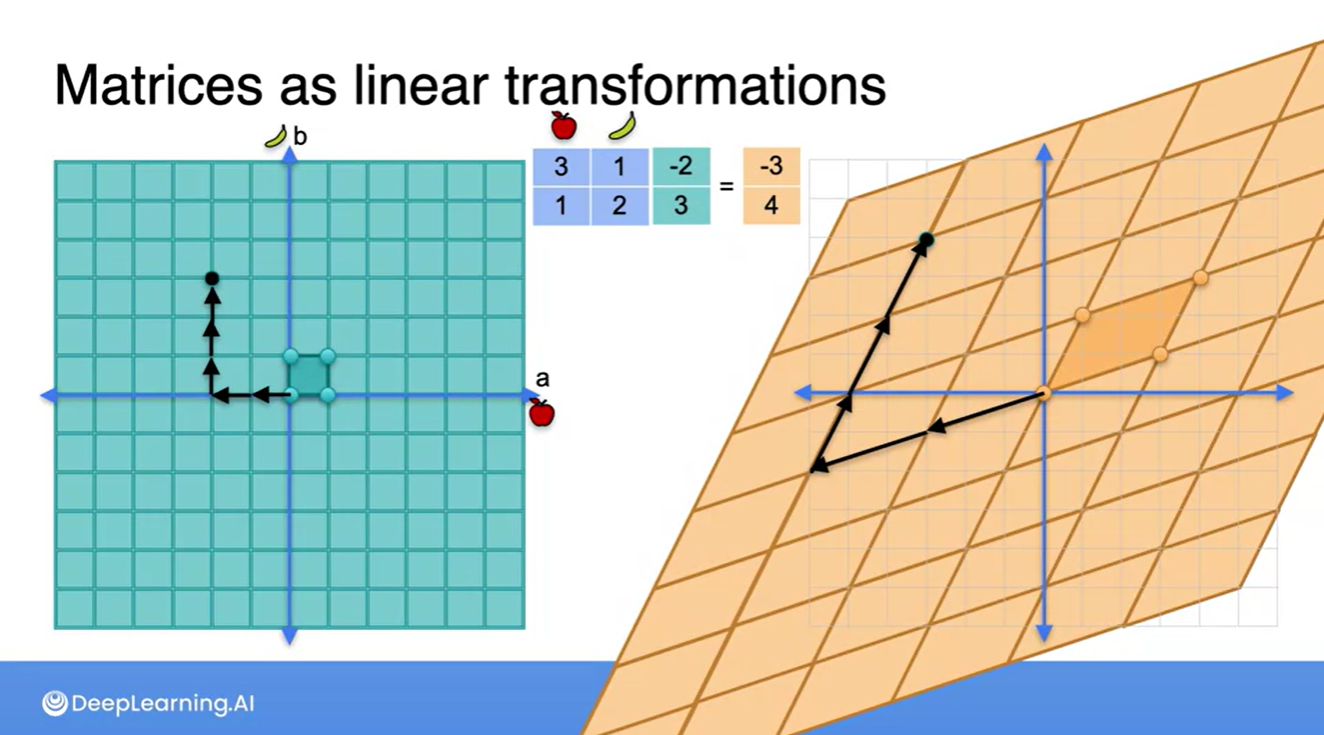
여기서 조금 더 나아가 (-2, 3)의 벡터를 왼쪽과 오른쪽의 평면에서 표현해보자.
-
기존 basis가 담긴 평면 상에서는 (-2, 3)의 벡터를 (왼쪽으로 2칸, 위쪽으로 3칸) 움직여서 표현할 수 있다.
-
오른쪽의 변형된 공간에서 또한 마찬가지로, 비틀어진 공간 상의 basis로 (왼쪽으로 2칸, 위쪽으로 3칸) 움직이는 것은 동일하다.
- 그러나, 최종 도착 지점은 변화한다.
- 원래의 basis를 갖는 공간 상에서는 (-2, 3)이었던 지점이 linear transform 이후 (-3, 4) 지점을 갖게 되는 것을 알 수 있다!
-
-
이번에는 2x2 matrix가 과일 개수를 나타낸 행렬, 초록색 벡터가 각 과일의 가격이라고 하자.
- 첫 번째 방정식은 첫째날 지불한 금액, 두 번째 방정식은 둘째날 지불한 금액이라고 한다면,
- 변형된 공간 상의 basis는 First day(첫째날)과 Second day(둘째날)로 형성되며 기존의 a, b basis 상에서의 점으로 표현하면 (4, 3)의 벡터로 나타내진다.

Linear transformations as matrices
- 아까와 비슷하게 네 지점을 선형 변환시켜 공간에 표현하면 아래 그림과 같다.
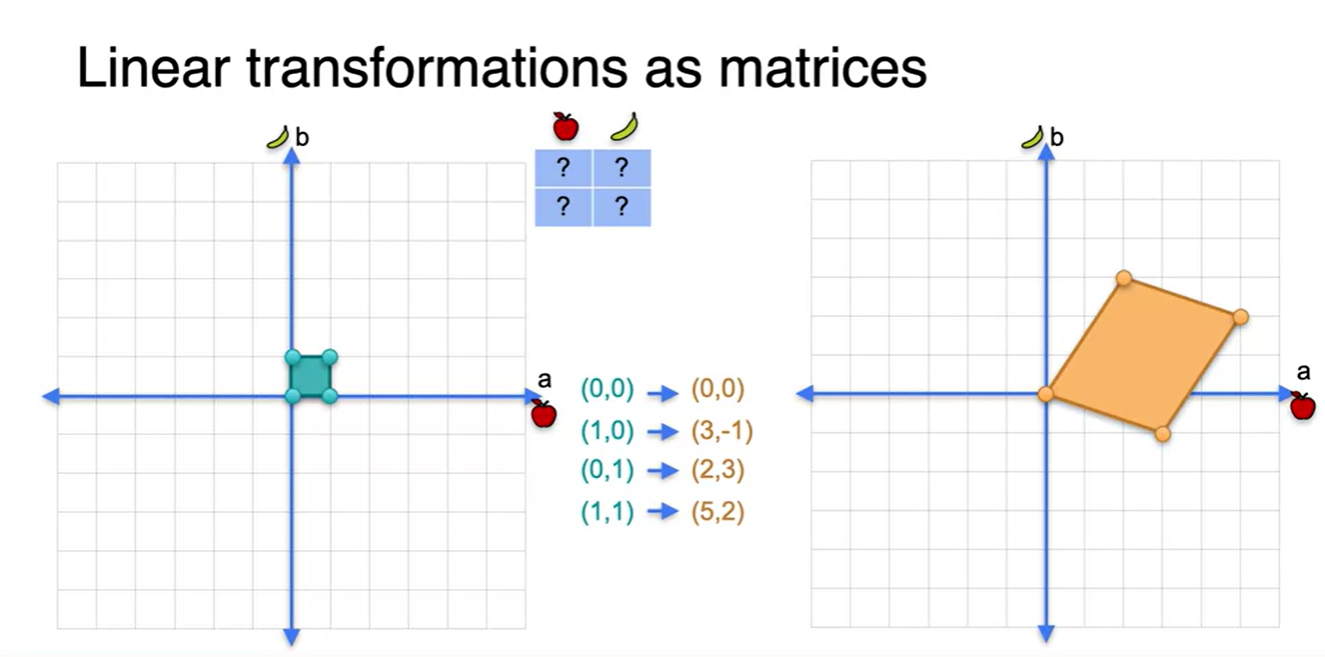
-
여기서 우리는 네 개의 점을 굳이 모두 표현할 필요 없이, (1, 0)과 (0, 1) 벡터만 있어도 2차원 평면 전체를 표현할 수 있다.
-
바로 이 점을 basis라 부를 것이며, 구체적인 정의는 해당 공간을 전체적으로 표현할 수 있는 가장 최소한의 벡터 집합이라 생각하면 된다.
-
아래와 같이 왼쪽 공간 상에 존재하는 초록색 벡터에 2x2 matrix를 씌워 주황색 벡터가 존재하는 공간으로 표현했다면 그림과 같이 벡터가 변형된다.
- 벡터는 열로 표현하므로, column에 주목하여 보라.
-
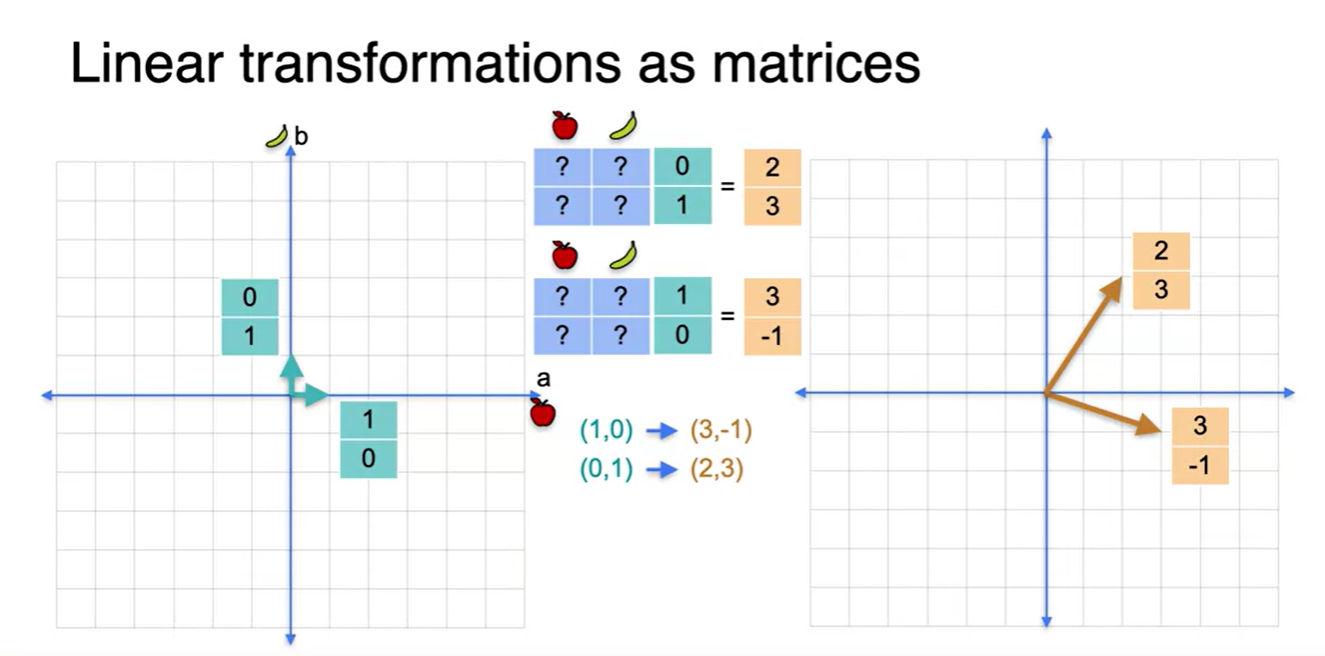
Matrix multiplication
-
Linear transformation 2개를 결합해보자.
- 2x2 matrix 2개를 (0, 1), (1, 0)의 기저에서부터 시작하여 linear transforms 할 것이다.
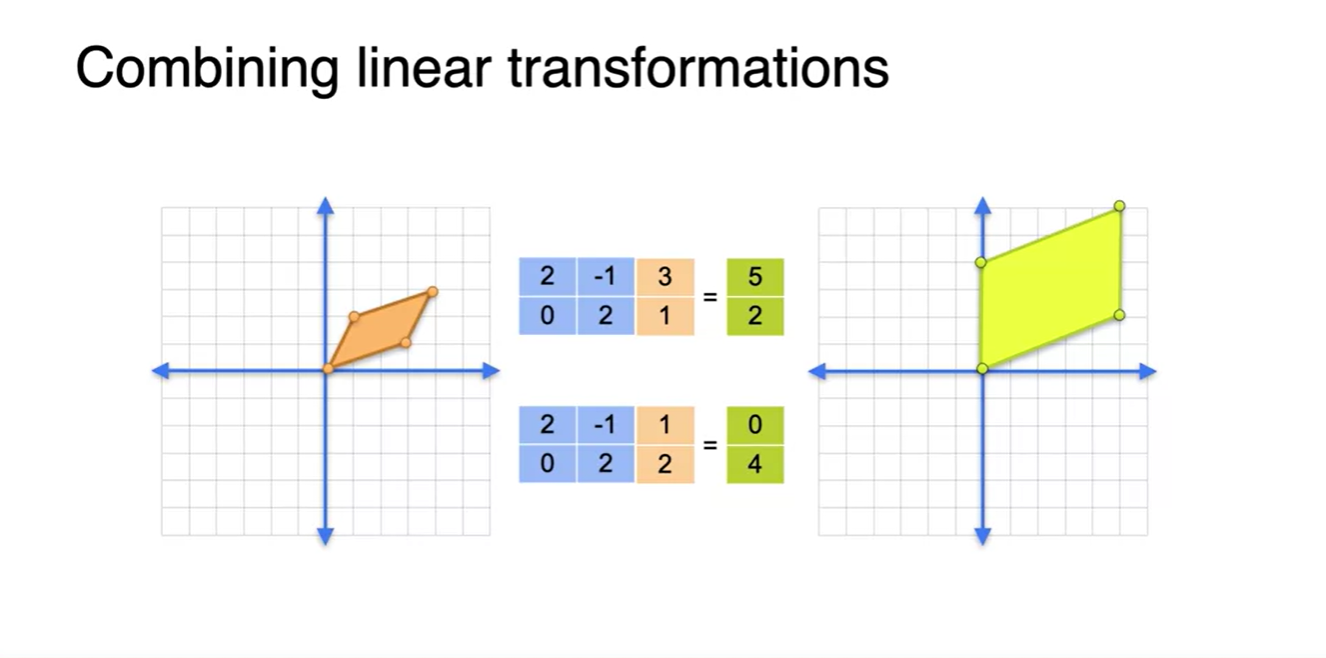
- 아래 그림은 (0, 1), (1, 0)의 초록색 벡터들을 파란색의 matrix로 선형 변환하여 (3, 1), (1, 2)의 주황색 벡터들을 얻은 결과를 나타낸다.
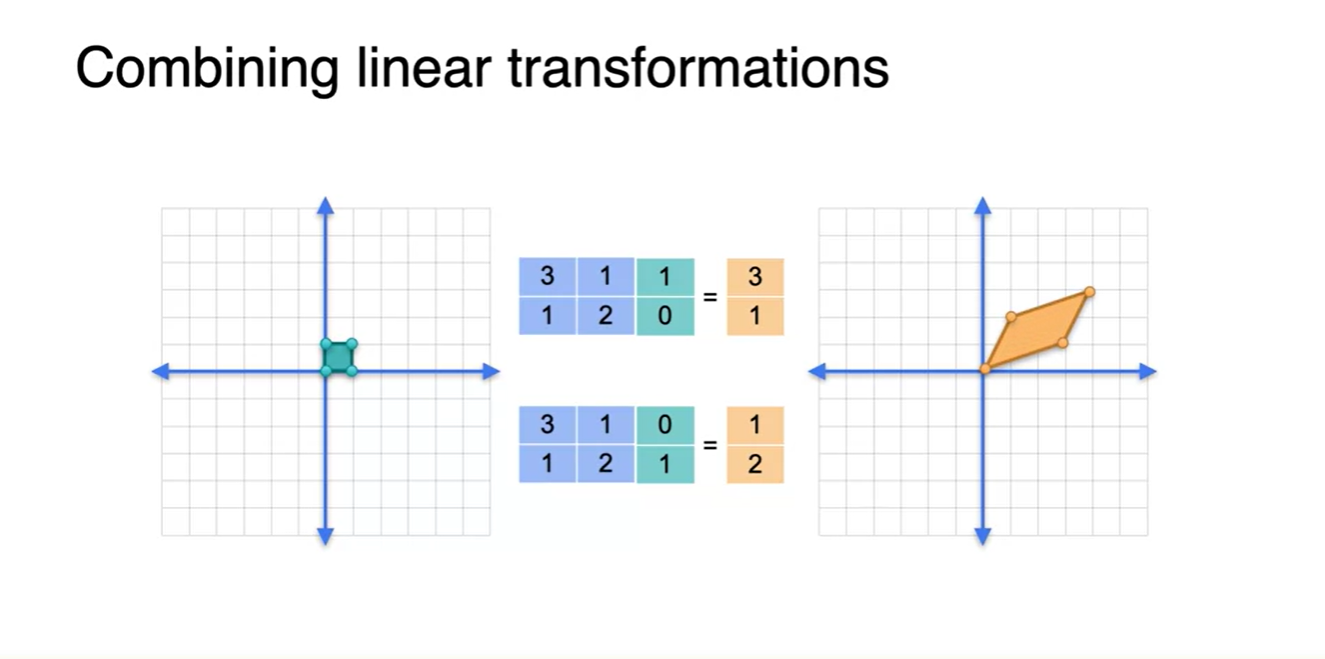
-
다음 결과는 (3, 1), (2, 1)의 주황색 벡터들을 또 다른 파란색 matrix로 선형 변환하여 (5, 2), (0, 4)의 연두색 벡터들로 표현한 것을 나타낸다.
- 즉, 두 번의 linear transforms으로 벡터가 존재하는 형태를 변형시켜 주었다.
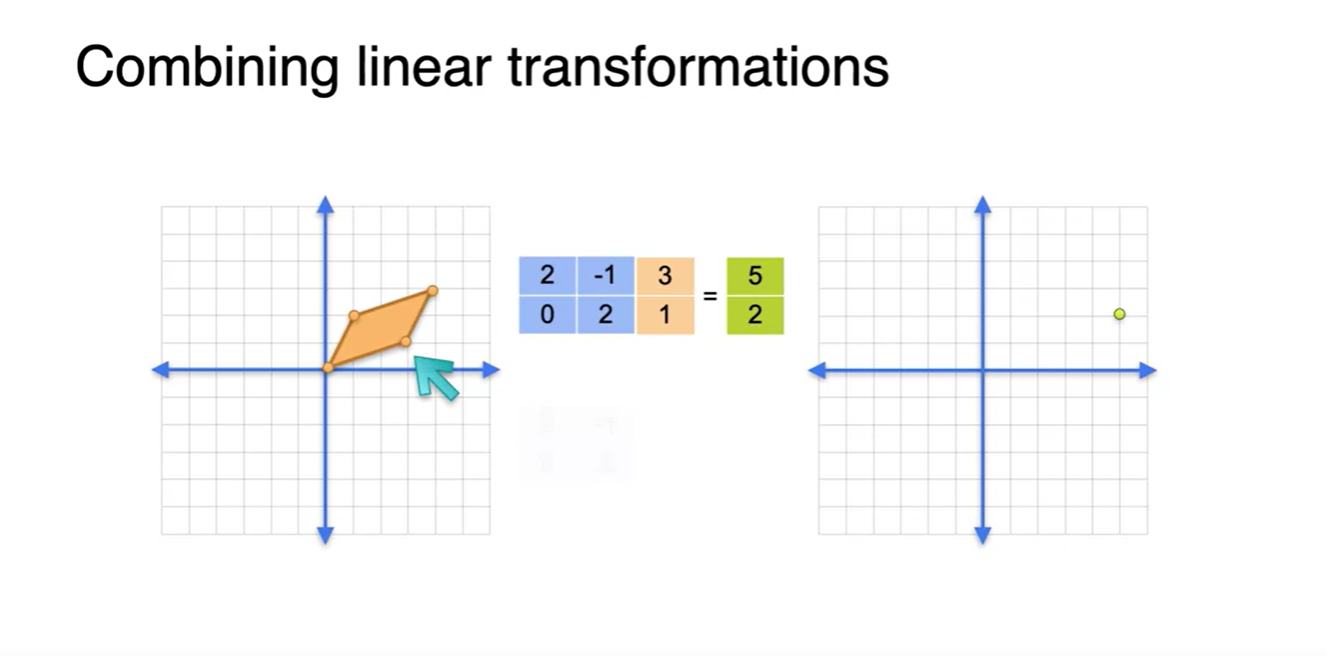
-
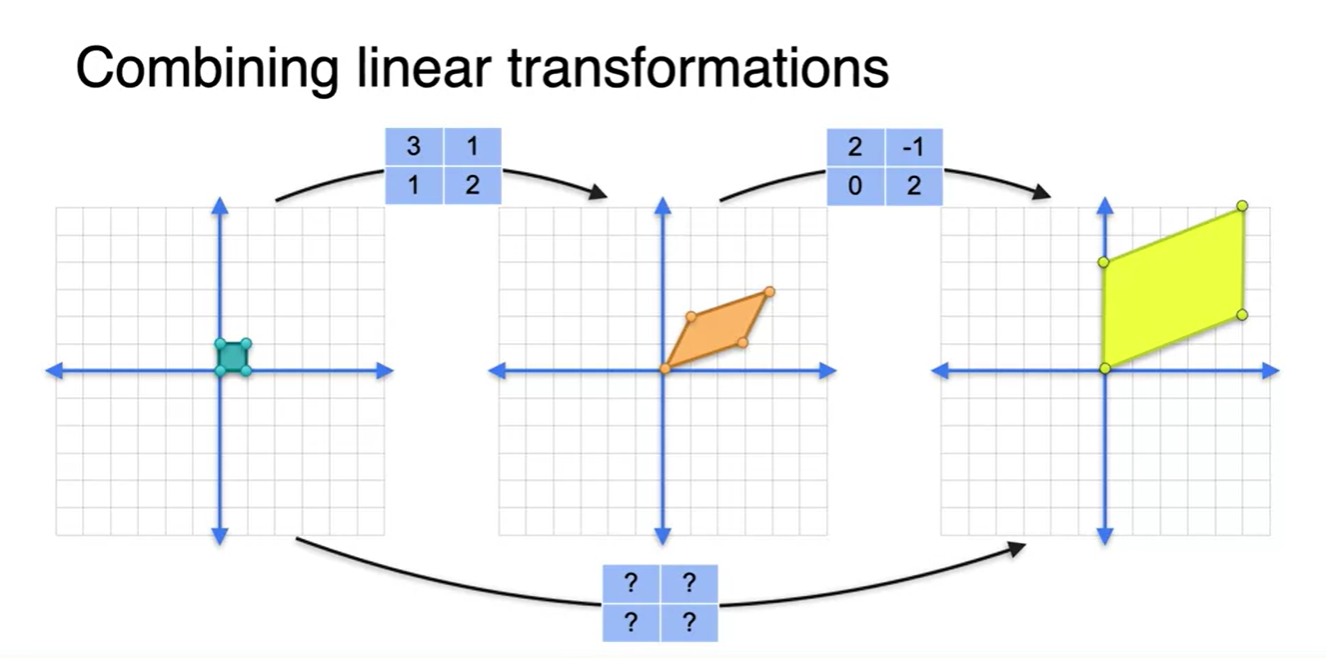
이러한 과정은 사실상 두 번의 linear transform을 한 번의 transform으로 치환하여 나타낼 수 있다.
- 이것이 바로 선형 공간의 특징이며, 한 번의 transform으로 표현할 수 있는 파란색 matrix가 얼마인지 그 값을 유추해보자.
-
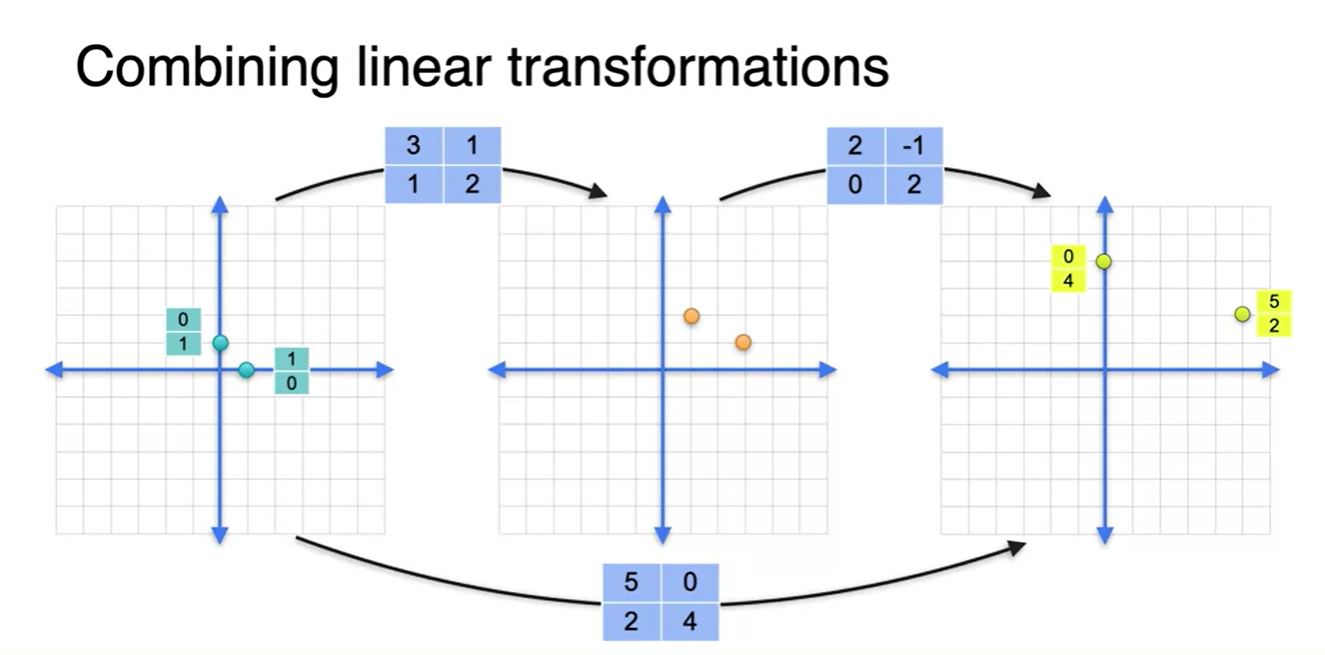
가장 왼쪽에 존재하는 basis 벡터들이 어떤 벡터들로 변환되었는지를 살펴보자.
- (1, 0) → (5, 2) 벡터가 되었고, (0, 1) → (0, 4) 벡터로 변환되었다.
- 중간 과정에서의 2x2 행렬을 살펴보면, basis에 곱해지는 행렬의 열벡터는 바로 transform된 이후의 벡터를 가리킨다. → (3, 1), (1, 2)
- 따라서 두 층을 결합한 matrix의 열벡터는 (5, 0), (2, 4)가 되어야 한다는 것을 알 수 있다.
-
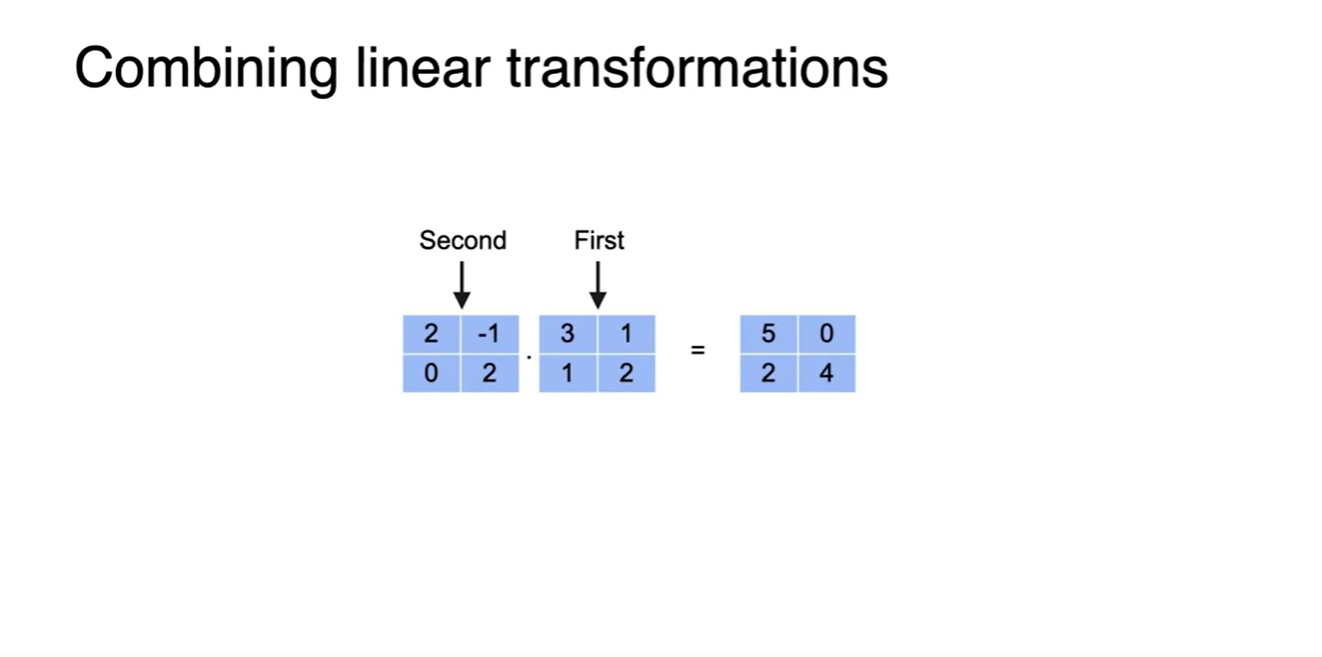
두 층으로 나뉘어있던 matrix의 곱은 최종 벡터를 선형 변환시키는 하나의 matrix가 된다.
- 이 때, 먼저 곱해줘야 하는 행렬이 앞선 층이므로 연산 순서는 First → Second 즉, 안쪽에서부터 벡터와 곱해줘야 한다.
-
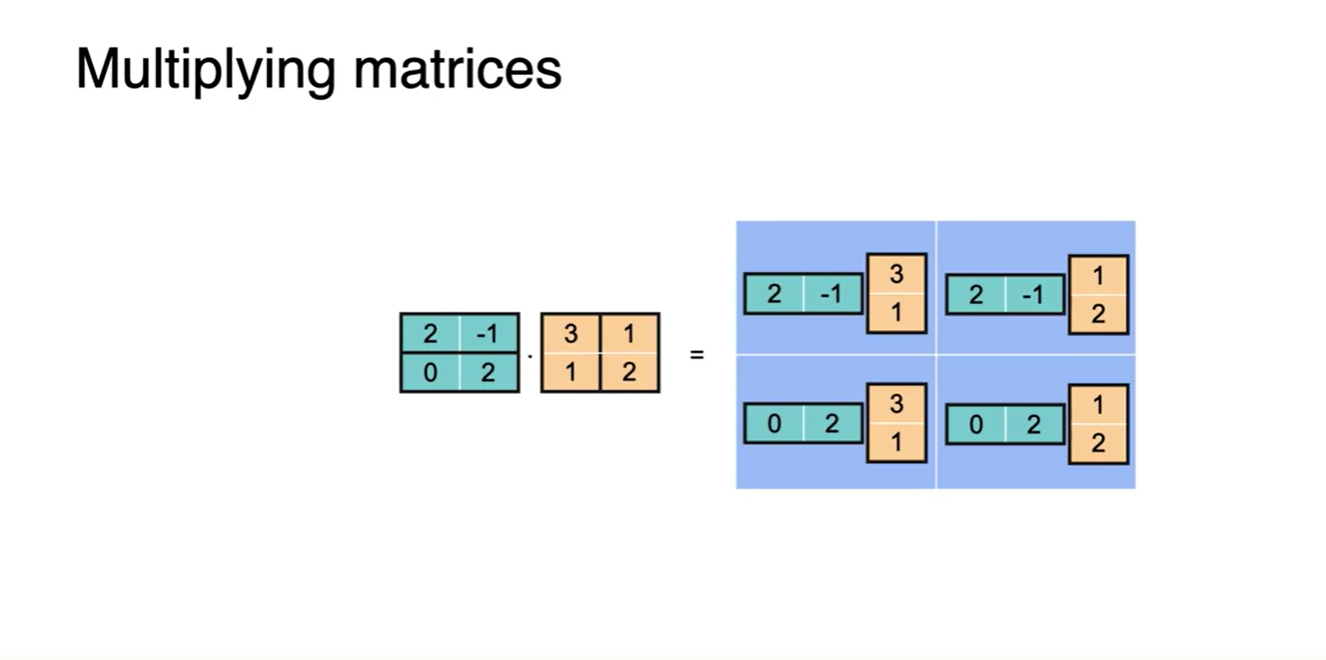
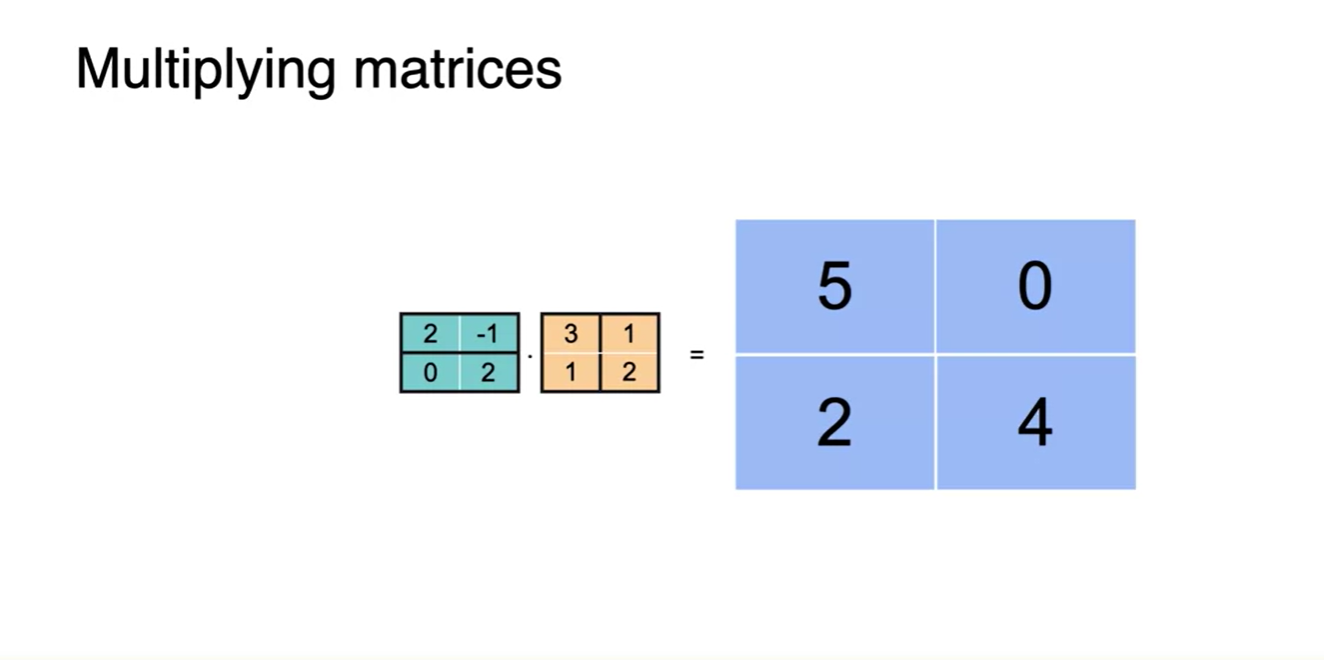
Matrix Multiplying은 각 항들의 dot product로 구해낼 수 있다.
- 위치 정보를 담은 또 하나의 linear transform matrix로 나타낸다.
The identity
-
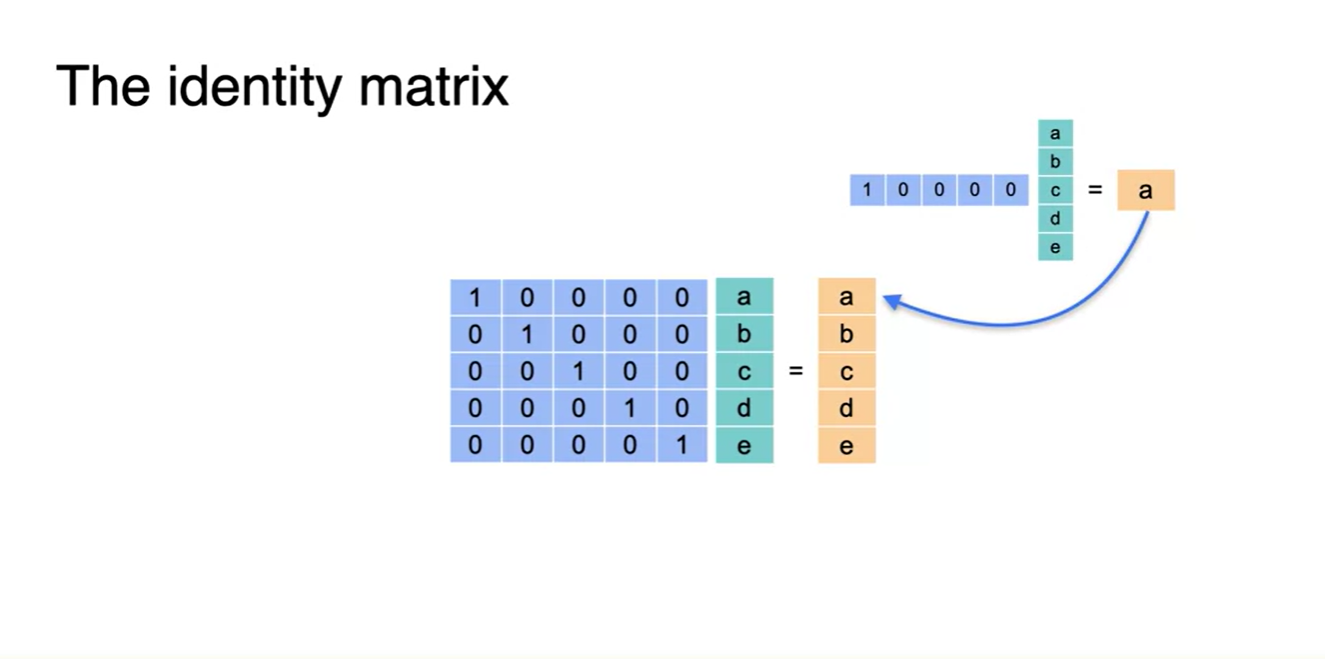
Identity matrix란 행렬 곱으로 선형 변환하여도 원래와 같은 값이 나오도록 만드는 matrix의 형태다.
- 아래 그림과 같이 1을 원소로 갖는 diagonal한 matrix라면 어떤 벡터에 통과시켜도 같은 항의 원소가 나온다.
-
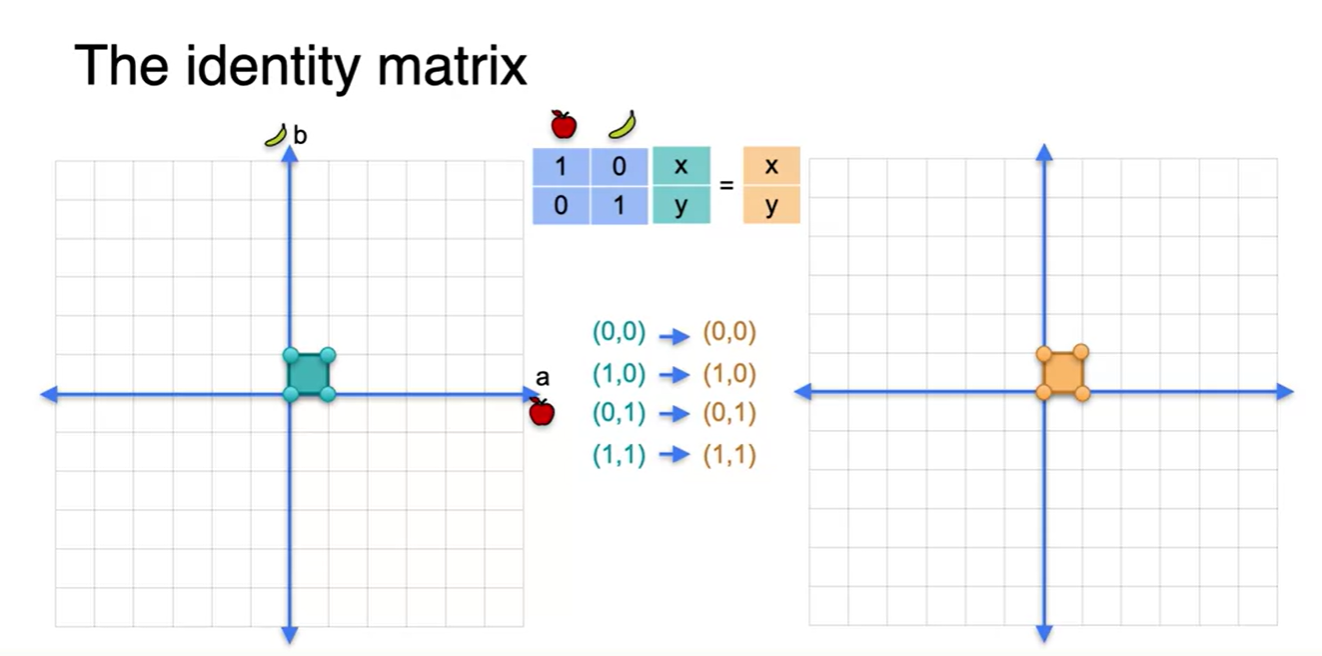
네 점을 꼭짓점으로 하는 평면을 결정지어도 원래의 벡터와 변환된 벡터 모두 같은 점을 가리키며, 평면의 모양 또한 동일하다.
- 이러한 변환에 쓰이는 matrix를 Identity matrix라 한다.
Matrix inverse
-
그렇다면 이번엔 linear transform을 두 번 진행 시켜서 다시 원래의 공간으로 되돌리고 싶다면 어떻게 할까?
- 앞서 살펴봤듯이 원래의 공간을 한 번에 똑같은 공간으로 매핑시키는 matrix는 Identity matrix였다.
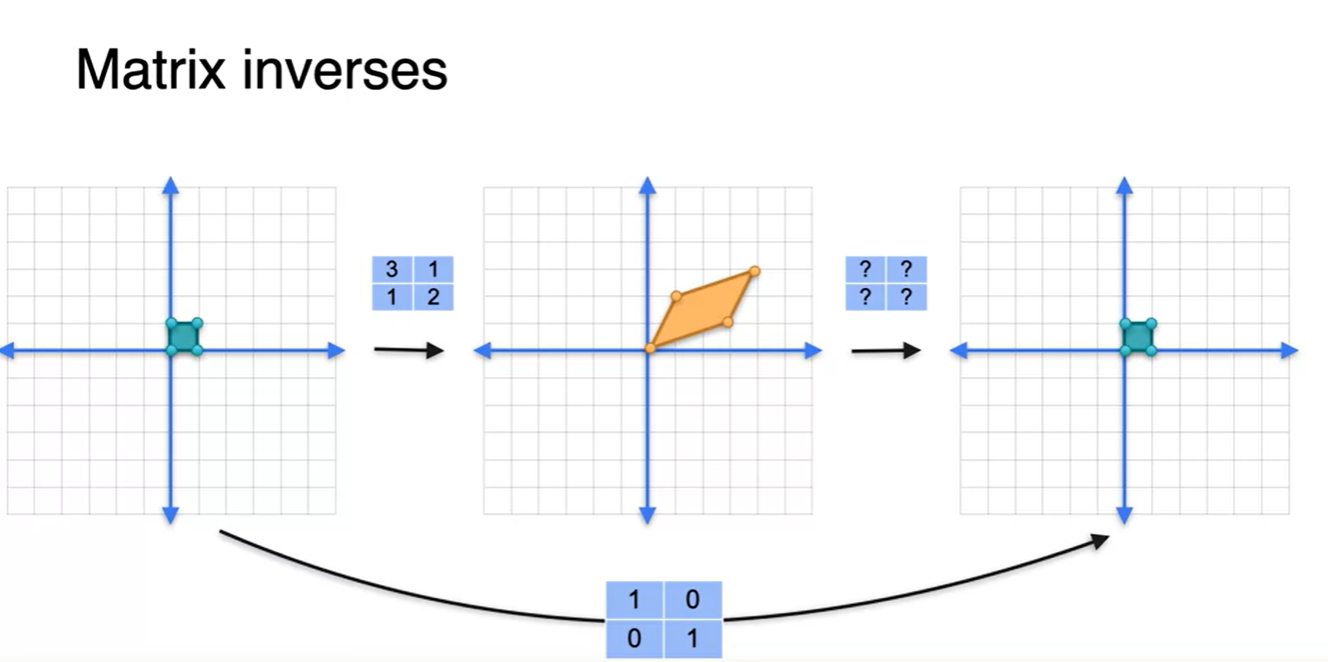
-
즉, 두 matrix의 multiplying으로 Identity matrix를 만드는 방법을 사용하면 된다.
-
Dot product를 진행하여 해당 방정식을 풀면 (a, b, c, d)의 한 쌍이 나올 것이다.
-
다시 말해, first(뒤쪽) matrix가 second(앞쪽) matrix의 inverse matrix가 되면 곱해서 I(1)을 만들 수 있는 원리다.
- 지금은 아래 그림에 정답을 기록해놓았다.
-
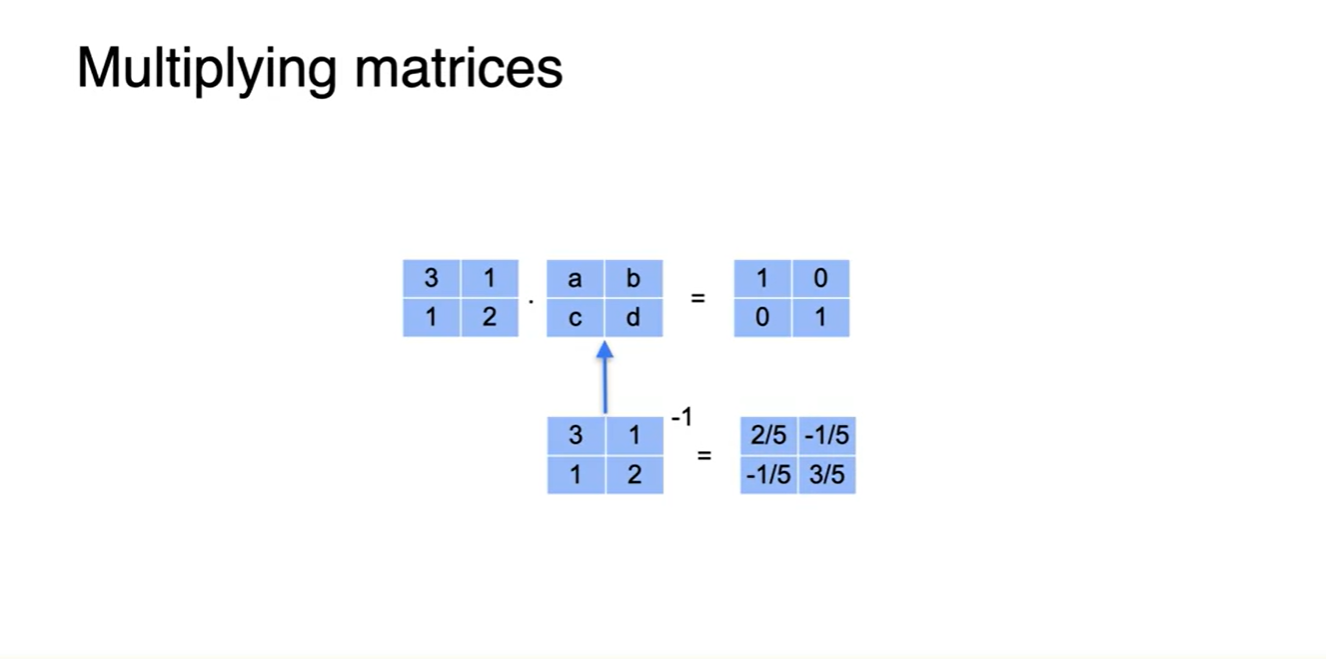
-
정석대로 풀면 아래와 같은 결과로 (a, b, c, d) 항을 얻을 수 있다.
- 이 (a, b, c, d) 행렬은 앞서 존재하는 (3, 1, 1, 2) 행렬의 inverse matrix다!

-
영상에서는 나오지 않았지만 공식은 다음과 같다.
-
또 다른 예제를 풀어보자.
-
아래의 첫 번째 문제는 inverse가 존재하는 matrix고, 두 번째 문제는 inverse를 찾을 수 없는 matrix다.
-
이는 deteminant를 0으로 만드는지에 대한 여부로 판단이 가능하다.
-


Whitch matrices have an inverse?
-
한 matrix의 Inverse matrix가 존재하는지에 대한 여부는 Singularity와도 연관성이 있다.
- Non-singular matrix는 항상 inverse가 존재한다.
- 그에 반해 Singular matrix는 inverse가 존재하지 않는다.
- 우리는 Singularity를 determinant로 구분해 왔으므로, determinant가 0인지 아닌지에 따라 inverse가 존재 여부를 판단할 수 있다.

Neural networks and matrices
-
Neural networks에서 쓰이는 linear transform에 대해 정리해보자.
- Natrural language processing(자연어 처리)에서 쓰이는 Spam of Not-spam 문제를 보자.
- "Lottery"라는 단어와 "Win"이라는 단어가 해당 메일이 등장하는 횟수를 기록하고, 이 메일이 Spam인지 아닌지를 라벨링하여 규칙을 예상해보라.
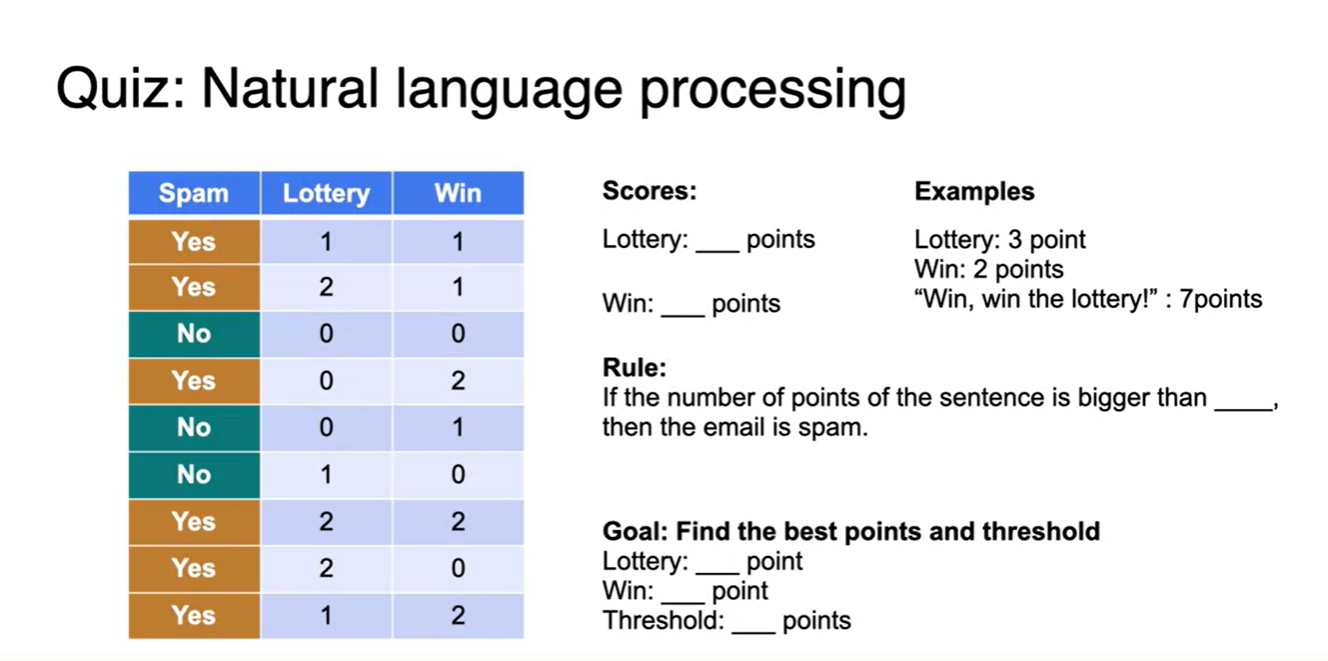
-
"Lottery"의 등장 횟수와 "Win" 등장 횟수에 곱해지는 가중치를 얼마로 두어야 최소 제한 조건을 가지며, 이 두 값의 합이 얼마의 threshold를 일때 최종적으로 Spam임을 반환하는가?
-
표를 보고 조금만 생각해보면 둘 중 하나의 값이 최소 1이상이고, 평균 내었을 때 threshold가 1.5임을 알 수 있다.
-
각 단어의 횟수 * "Lottery"와 "Win"의 가중치 points를 1로 두면 각 단어의 등장 횟수 * 1(weight) = 계산값(linear transformed)을 이용할 수 있다.
- "Lottery"나 "Win" 중 둘 중 하나가 1을 넘지 않더라도 평균값이 1.5 이상일 때 Spam 여부를 결정지을 수 있기 때문이다.
-
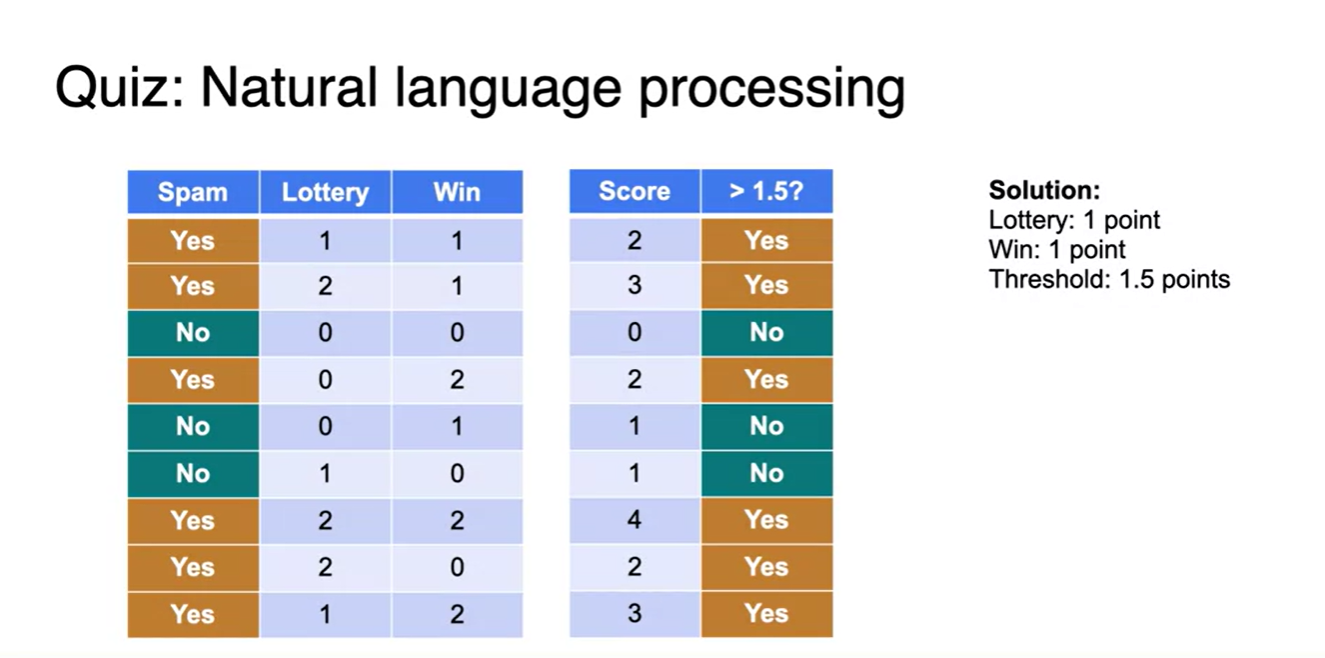
-
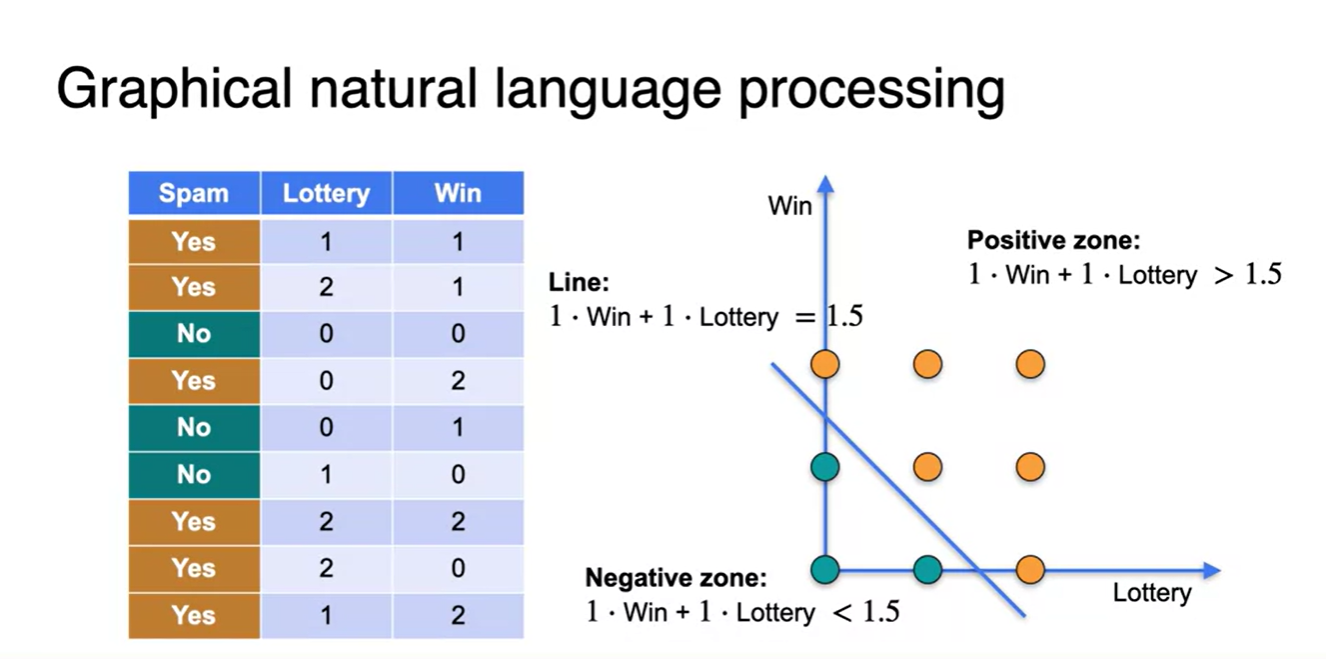
Graphical하게 각 점들을 찍어보면, 아래와 같은 하나의 직선으로 Spam or Not-spam이 결정된다는 것을 알 수 있다.
- 이 때 basis는 "Lottery", "Win"의 등장 횟수, 가중치는 1, threshold는 1.5인 직선으로 선형 분류 문제를 풀 수 있다는 것을 나타낸다.
- 1.5 기준 더 큰 값을 가지면 Spam, 1.5보다 더 작은 값을 가지면 Not-spam
-
모델의 가중치 벡터가 (1, 1)이고 input이 (2, 1)일 때와 (0, 1)일 때를 각각 dot product 해보면, 1.5보다 더 큰지 작은지를 판단할 수 있다.
-
이게 지도학습 머신러닝에서 하는 linear transform 과정이다.
-
Input에 맞는 Label을 제시하여, 데이터 분포를 잘 구별할 수 있는 가중치 행렬(여기서는 1차원 벡터)를 찾고, 얼마의 threshold로 정하는게 좋을지까지 완성하는 과정인 것!
- 여기서 말하는 threshold는 후에 bias라 표현되는 항으로 왼편에 넘겨질 것이다.
-


- 이제 모든 데이터를 mapping 시켜보면 1.5 기준 Spam인지 아닌지를 확실히 구별지을 수 있다.
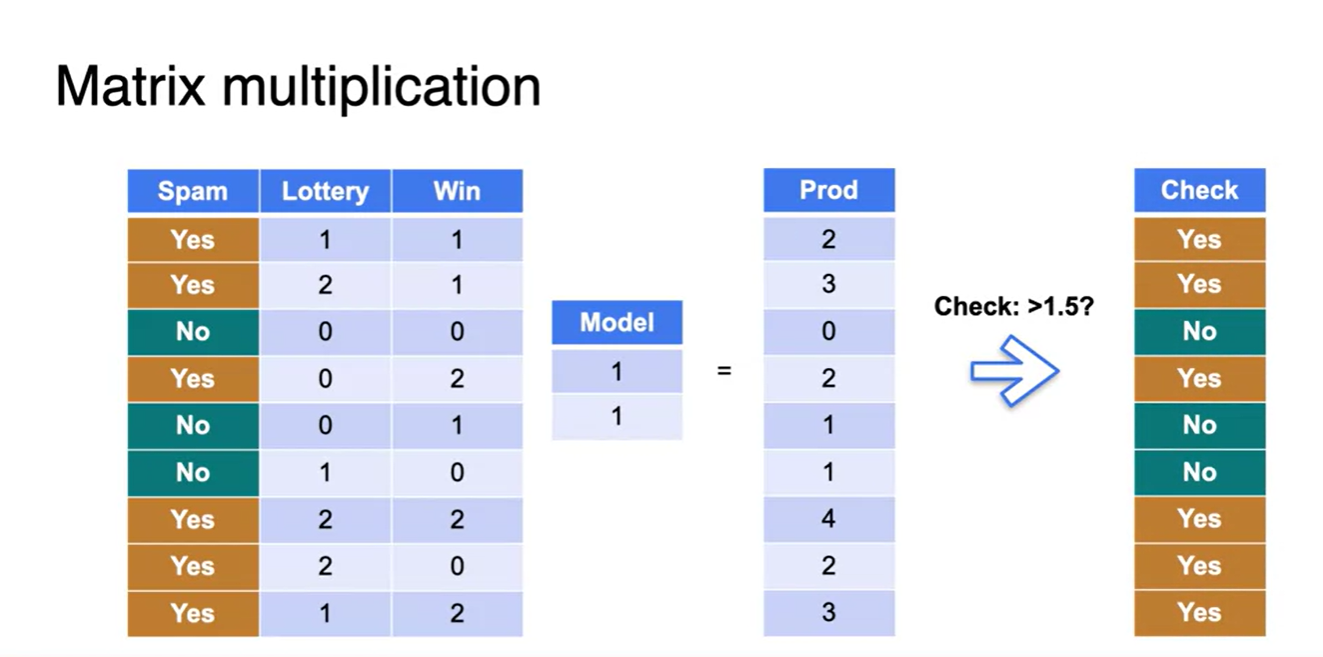
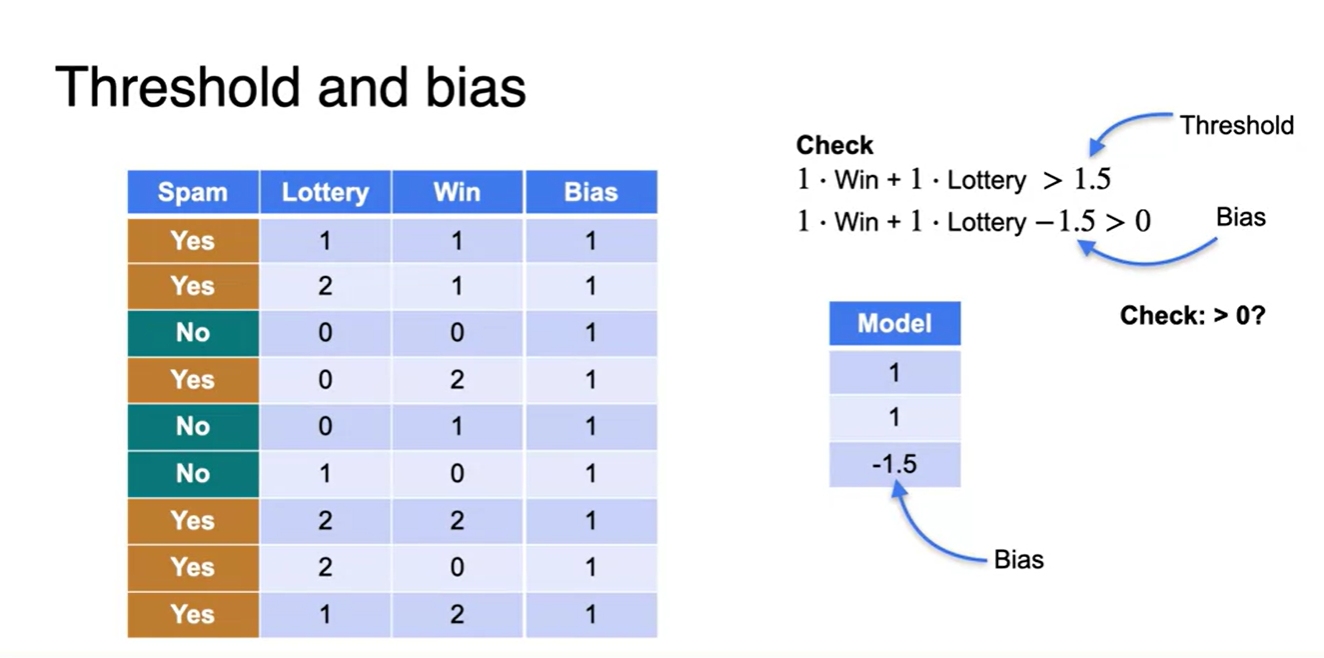
- 1.5보다 큰지 작은지로 체크했던 threshold를 bias 항을 추가시켜 왼편에 넘겨보자.

- 그러면 이렇게 데이터 행렬에도 bias 열이 추가되고, 가중치 행렬에도 해당 항이 추가된다.
-
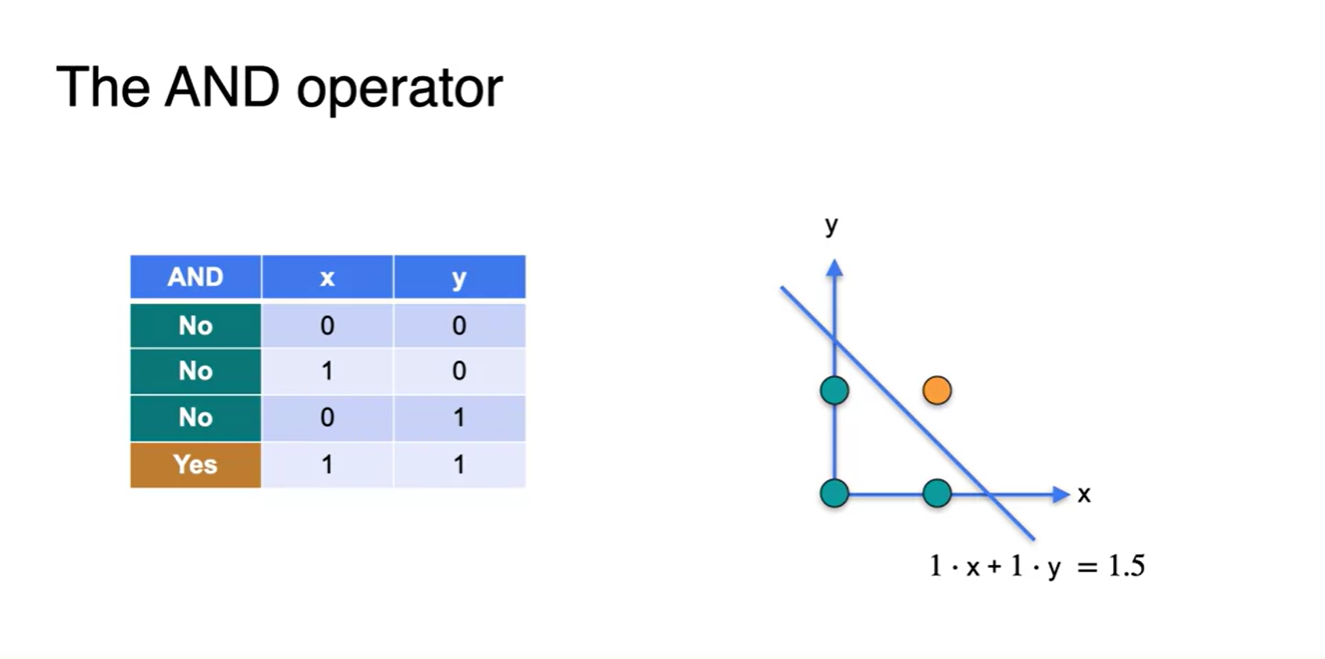
이러한 선형 분류기 모델은 AND 연산자를 판단하는 데에도 적용된다.
- 데이터와 가중치 행렬의 Dot product, 그리고 Graphical한 공간에서의 해석까지 완전히 들어맞는다.

-
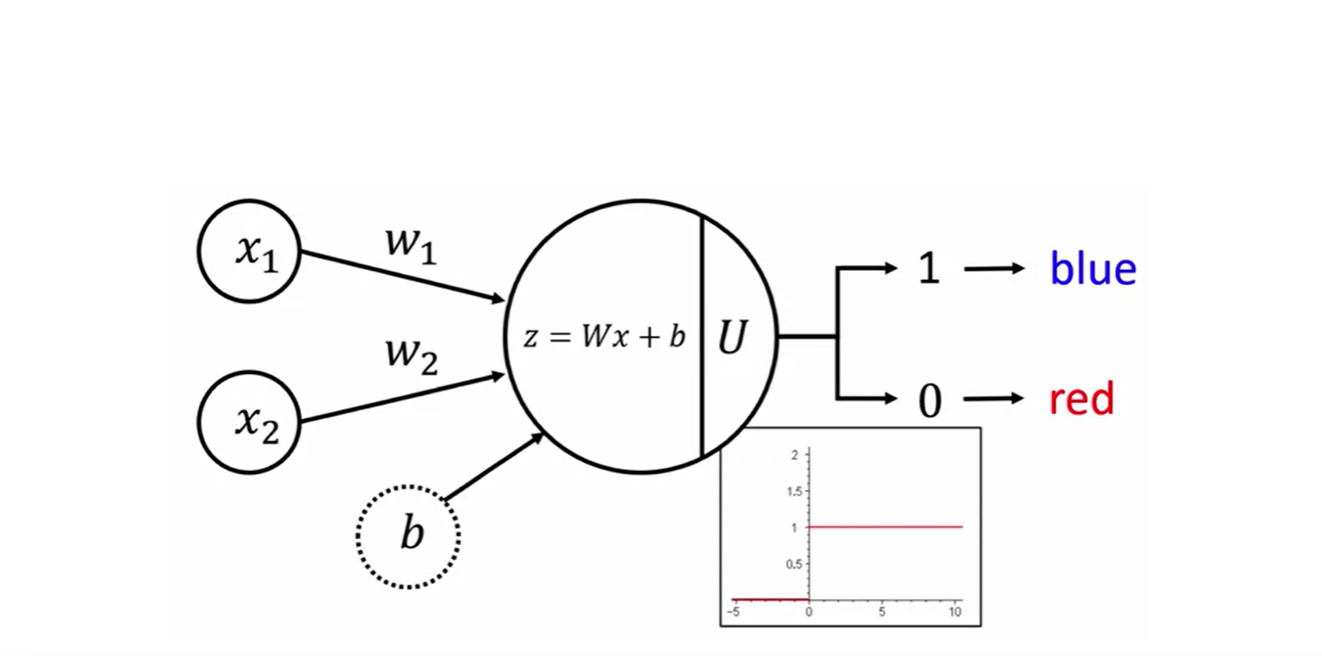
이러한 모델을 perceptron이라 부른다.
- 데이터와 가중치 행렬의 dot product로 계산한 linear transform을 적절한 threshold로 판단하는 모델을 말한다.
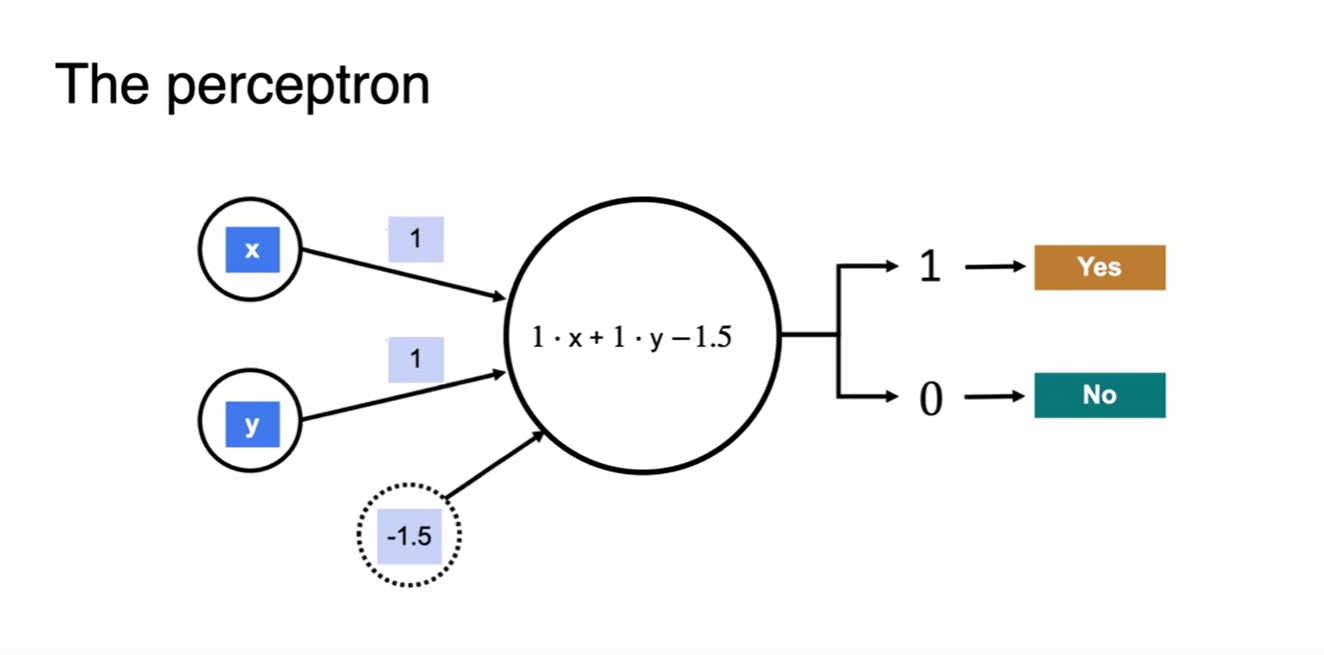
- 앞으로 우리가 살펴볼 Neural network 모델은 바로 이러한 계산 과정으로 특정 task를 수행하는 모델을 만드는 것이라 할 수 있다.