[MMD] Probability & Statistics for Machine Learning & Data Science Week 4
Week 4 - Confidence Intervals and Hypothesis testing
Lesson 1 - Confidence Intervals
Confidence Intervals - Overview
-
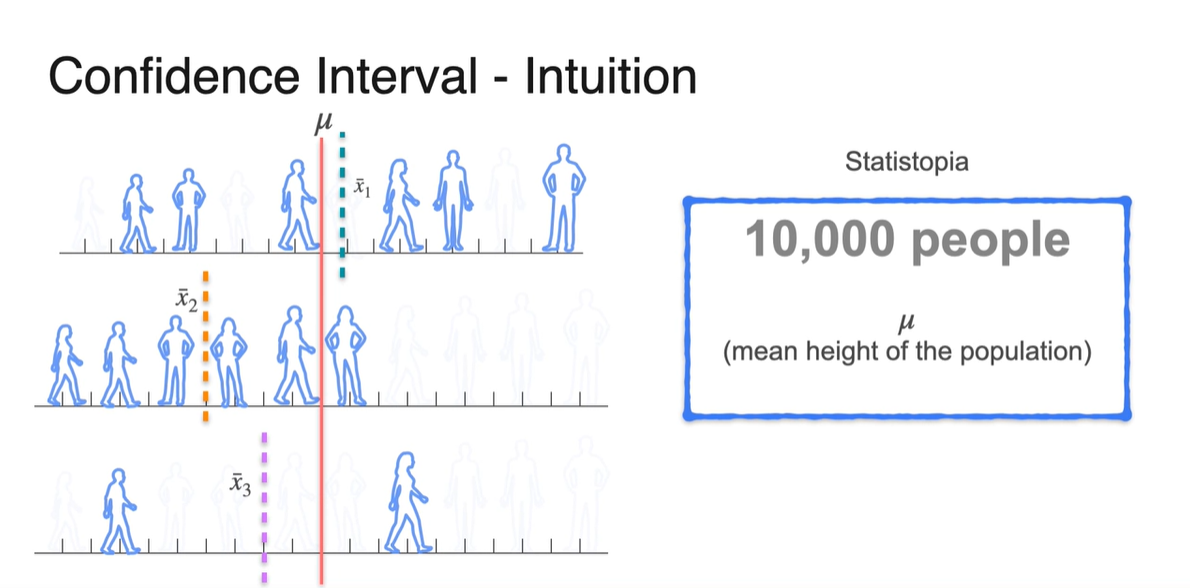
Statistopia 예제에서 다룬 10,000명의 사람들의 키 분포를 떠올려보자.
- 사실상 우리는 population mean인 는 알 수 없기 때문에, 표본(sample) mean인 , , 를 측정해서 모집단을 추정하는 방법을 택한다.
-
그러나 특정 샘플이 완벽하게 정확할 것이라고 기대할 수는 없으며, 매번 다른 표본 평균을 얻게될 것이기 때문에 모집단의 평균을 구하는 일은 매우 어려운 일이다.
- 즉, 실제로 얼마나 정확한지에 대해서는 항상 불확실(uncertainty)할 수 있다!
-
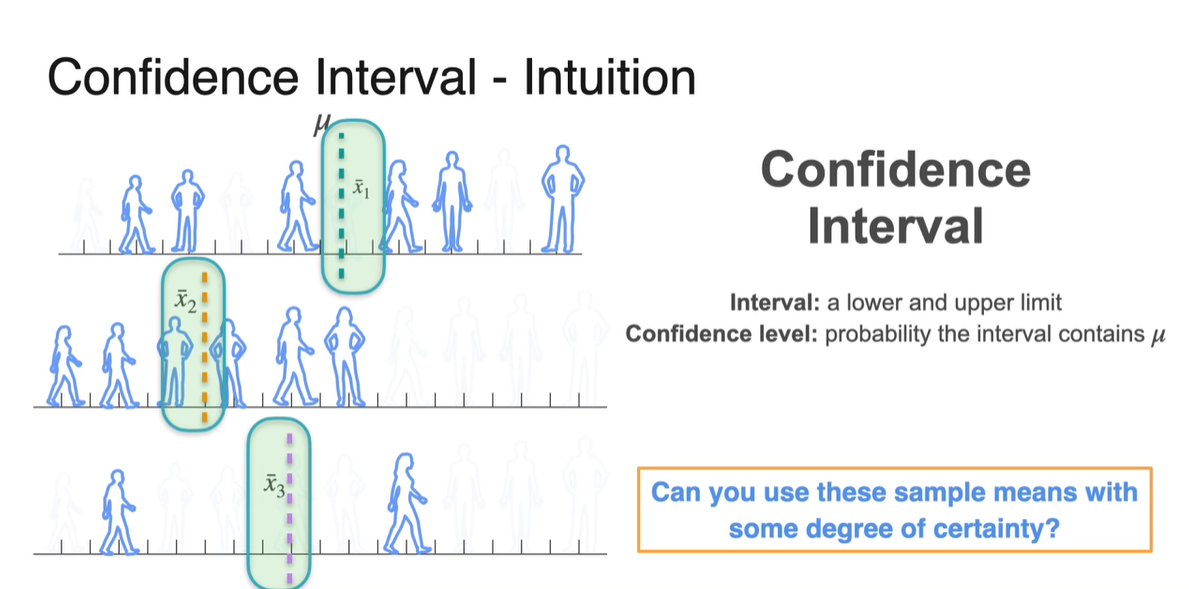
Confidence Interval은 뽑힌 sample mean들을 가지고 어느 정도(degree)의 certainty를 만족하면서 population mean()을 추정하고 싶을 때 사용한다.
- Interval은 lower limit과 upper limit을 뜻하며 Confidence level은 해당 구간에 가 포함될 확률을 의미한다.
-
아래 예시를 통해 Confidence Interval(신뢰 구간)에 대해 알아보자.
- 만약 당신이 길을 걷다가 열쇠를 떨어뜨렸는데 어디에서 잃어버렸는지를 모른다.

-
이제 당신은 친구를 만나, 열쇠를 찾기 위해 "열쇠가 있을 법한(guess)" 곳에 차를 정박하고 "적당한 구간(search distance)"을 탐색하기 시작한다.
- 차를 정차할 곳은 어디든 가능하며 열쇠를 떨어뜨렸을 가능성이 가장 높은 곳에 정차하면 된다.
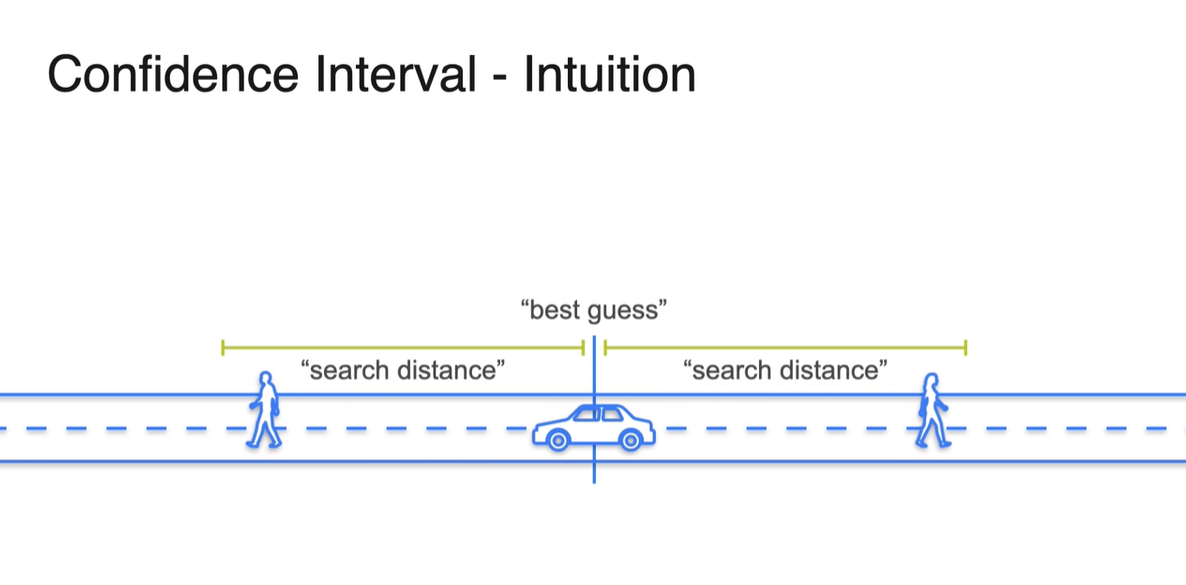
-
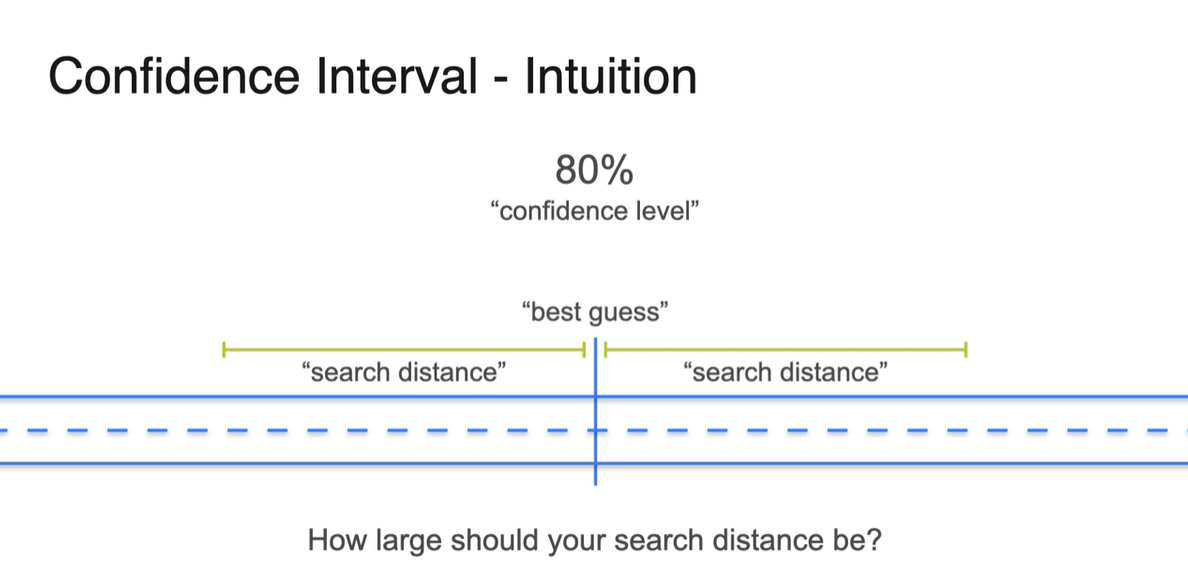
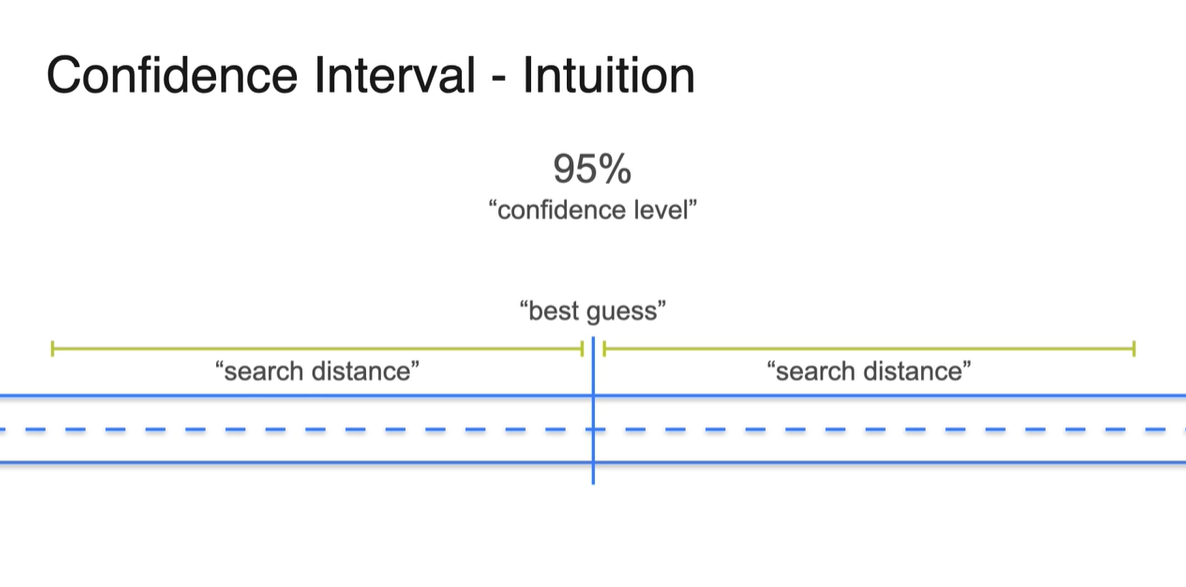
만약 80% 확률을 신뢰 구간으로 설정했다면, 해당 interval 안에는 80%의 확률로 열쇠가 있을 것이라는 믿음을 바탕으로 한다.
-
허나 95% 확률로 confidence level이 높아진다면 열쇠를 찾을 확률은 높아지지만 search distance가 넓어지기 때문에 더 많은 탐색을 해야한다.
-
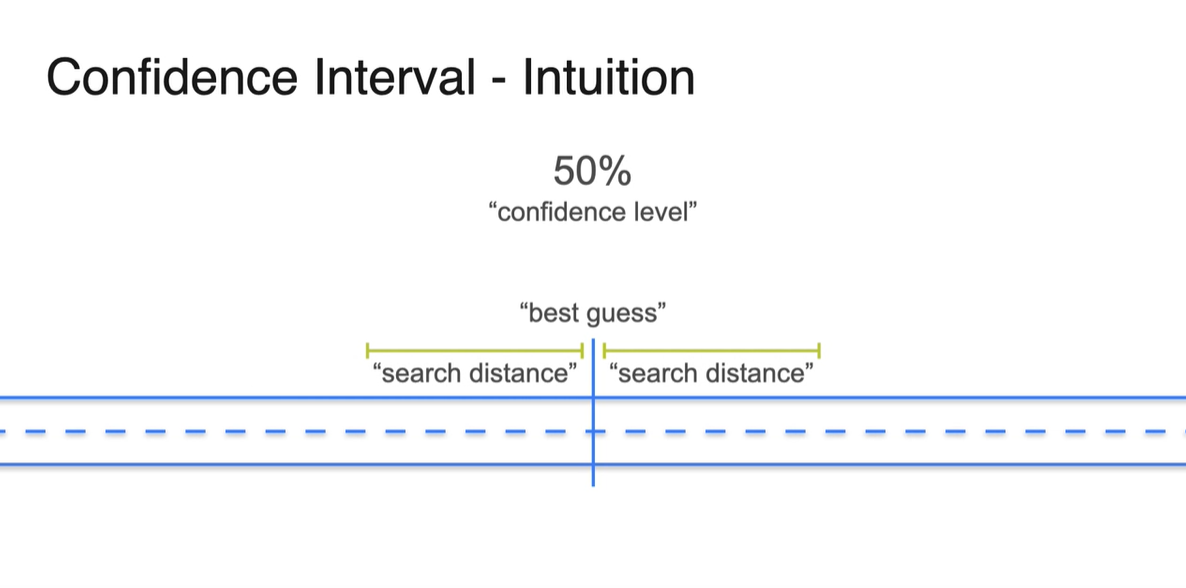
50% 확률을 설정한다면 탐색할 영역이 좁아져서 공수가 덜 들어가나, 해당 interval 내에서 열쇠를 찾을 확률이 확 떨어지기 때문에 trade off라 볼 수 있다.
-
-
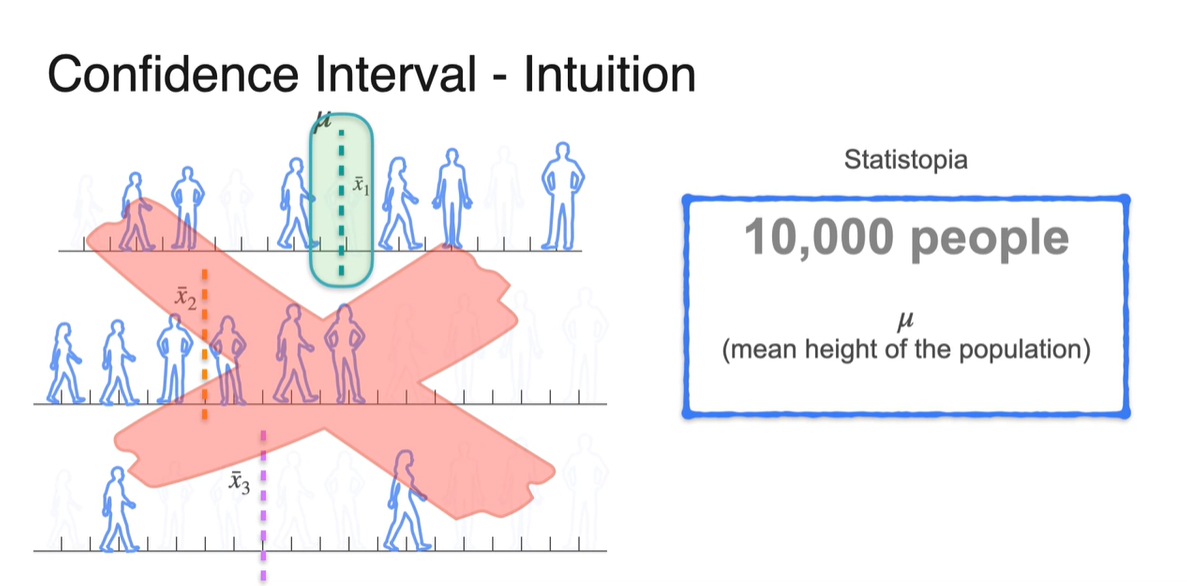
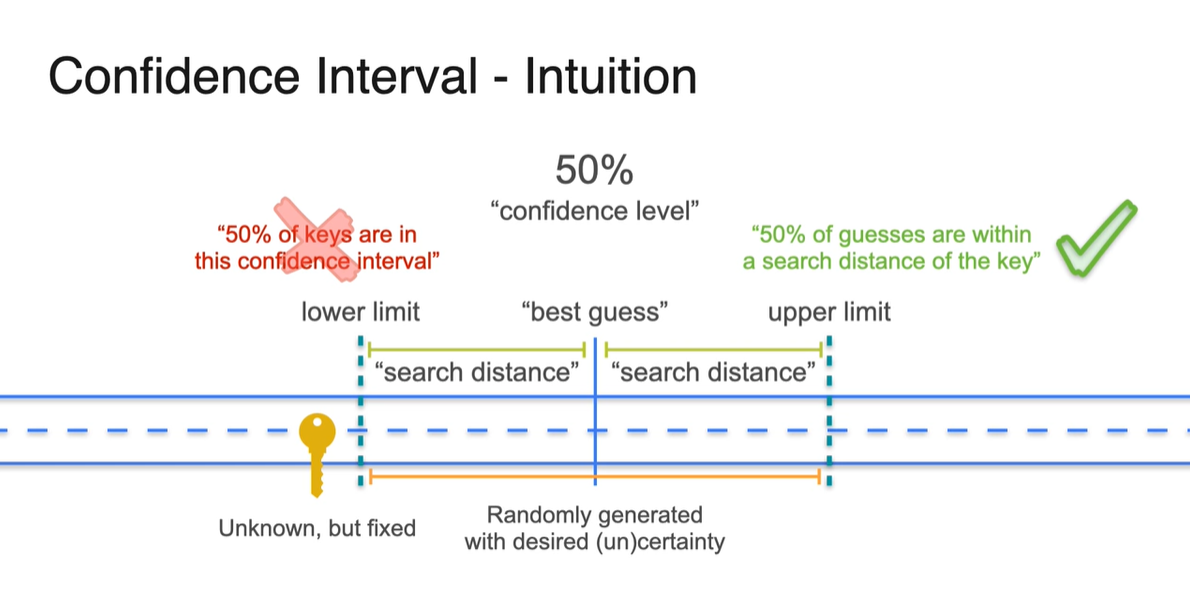
Confidence Interval(신뢰 구간)의 정의는 사실, "50%의 열쇠"를 찾는 것을 뜻하는 것이 아니다.
-
열쇠가 있는 위치는 "하나"이며 고정이기 때문에, 우리는 열쇠가 있는 위치를 "guess"할 수밖에 없다는 점을 명확히 해야한다.
- 이러한 guesses 중에서 각 guess의 interval 내에 실제 열쇠의 위치()가 있을 것이라고 certainly하게 말할 수 있는 정도가 confidence level이다.
-
-
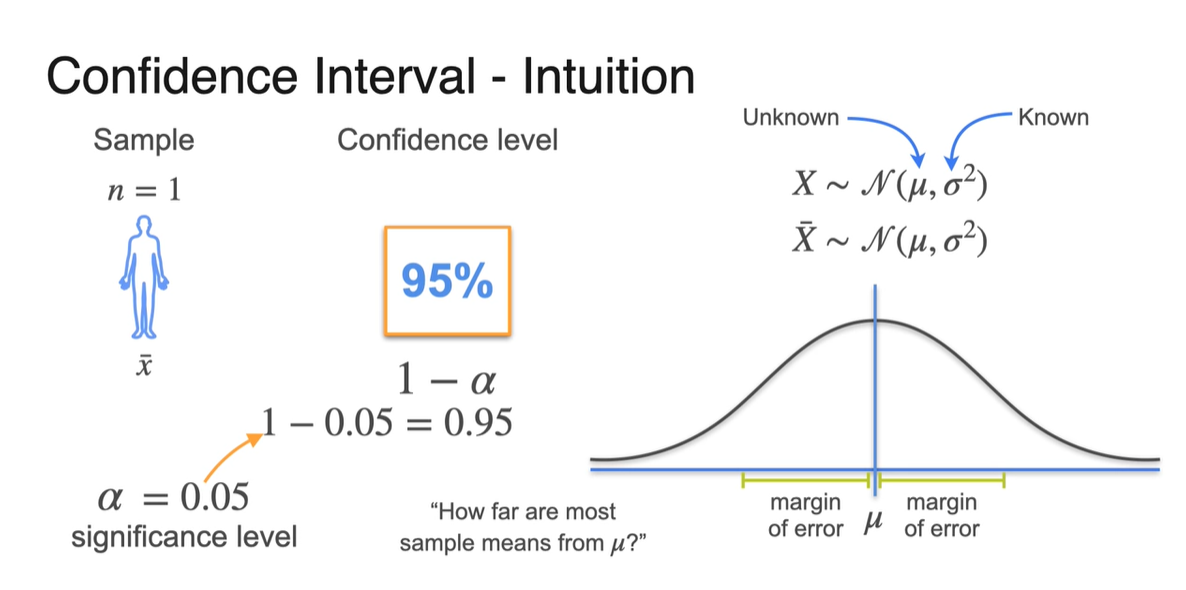
Population random variable 는 을 따른다.
-
이 때, 는 Unknown value이고, 는 Known value로 설정한다.
- 일반적으로는 두 가지 모두에 대해 불확실하지만, 지금은 평균만 알 수 없는 가장 간단한 방법으로 문제를 설정하였다.
-
Sample의 수를 로 하여 표본 평균 을 계산하면, 표본 평균의 random variable 또한 을 따른다.
- 하지만 사실은 와 가 완전히 같지 않을 것이 분명하다.
-
따라서 표본 평균이 오차 한계를 벗어날 확률을 뜻하는 significance level 를 설정한다.
- 는 보통 매우 작은 숫자이므로 표본 평균의 confidence level인 는 1에 가깝게 설정된다.
-
-
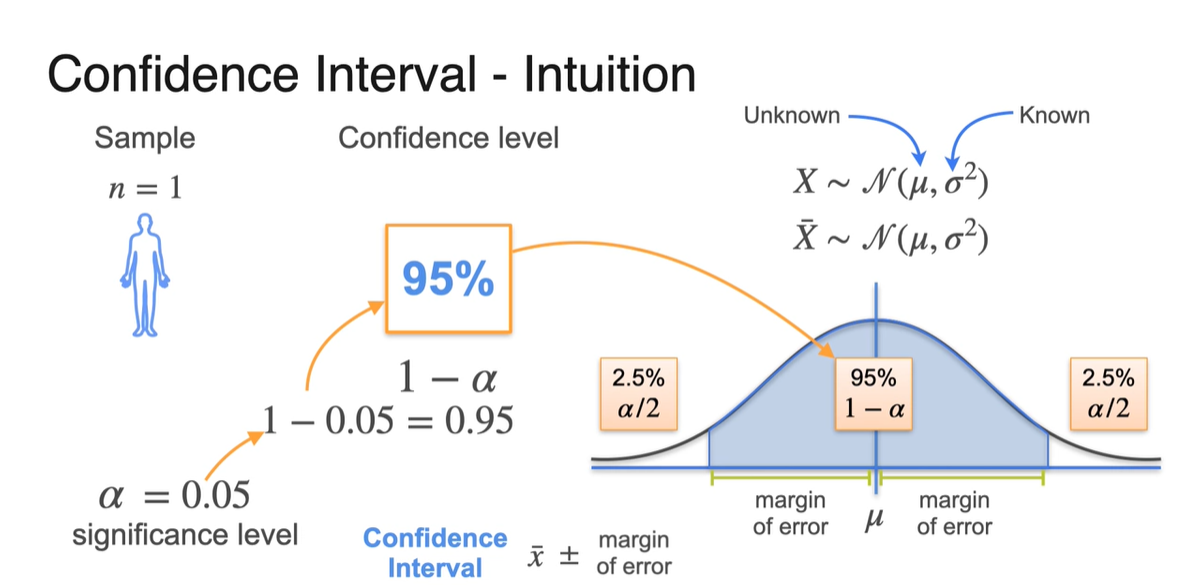
이제 confidence level을 확률로 생각하여 기존 population 분포의 95%에 해당하는 구간을 색칠해보자.
-
나머지 5%는 정규 분포의 대칭성에 의해 양쪽에 2.5%씩 나눠가진다.
- 따라서 Confidence Interval은 sample mean 로부터 margin of error(2.5%)한 값으로 구간 limit을 구할 수 있다.
-
-
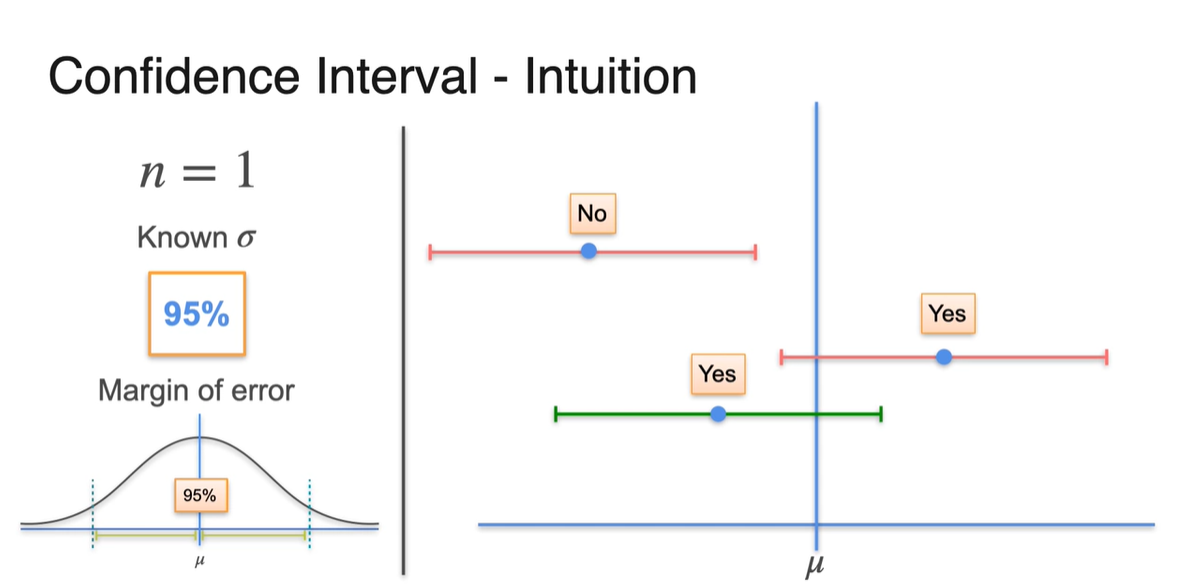
이제 Known 에 대해, 의 sample 수와 confidence level 95%로 margin of error를 설정하여 sample을 뽑아 보자.
- 각 sample mean을 중심으로 하는 분포로부터 95%의 confidence level로 margin이 설정된 구간 내에 가 포함되었는지를 확인하면 3개 중 2개는 이를 만족한다.
-
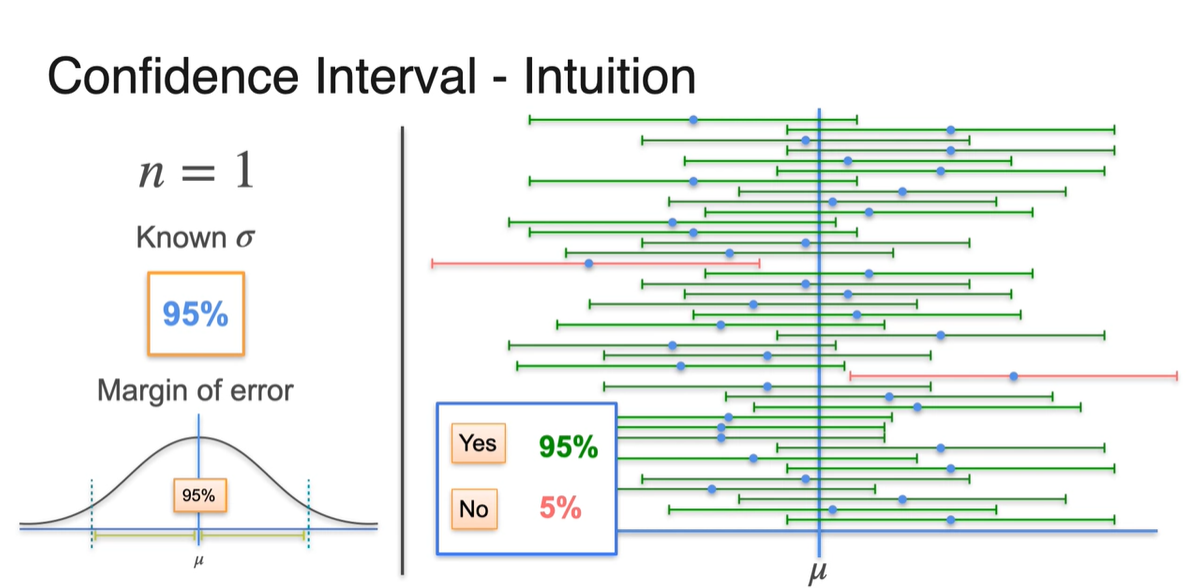
이제 여러 개의 sample을 선정하여 margin 내에 가 포함되었는지를 확인하면 95%는 맞고 5%는 아닐 수 있다.
- 이러한 범위 내에서 sample을 generating하도록 설정해주는 것이 confidence level의 진정한 정의다.
-
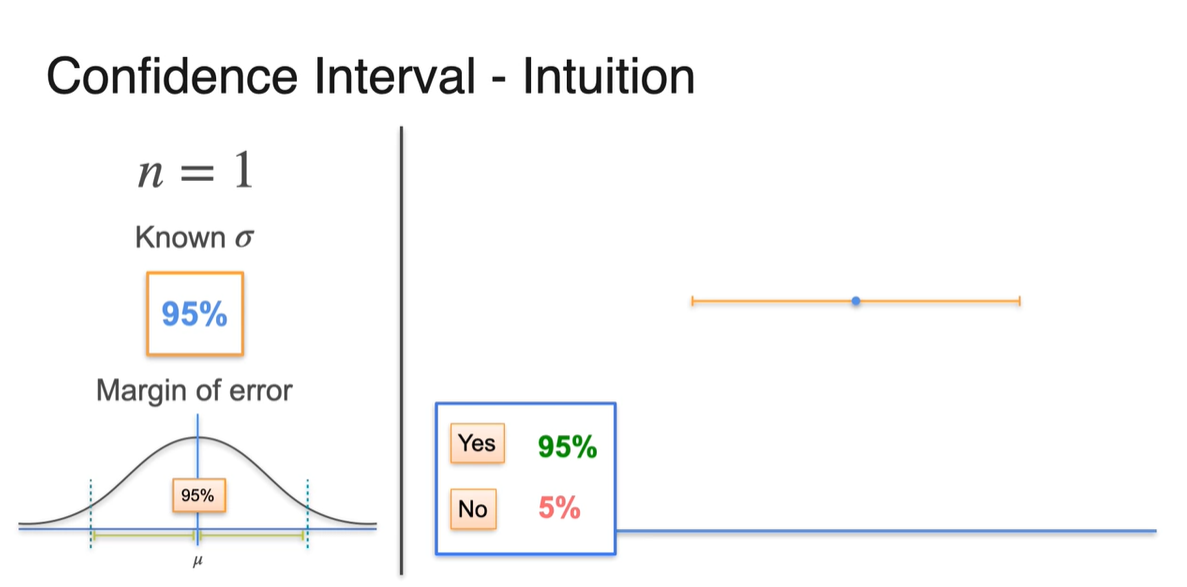
지금은 일 때의 상황이기 때문에 sample이 하나다.
- 완벽하게 확신할 수는 없지만, 이렇게 생성된 신뢰 구간의 95% 내에는 가 포함되어 있음을 믿으며 추정하는 것이다.
Confidence Intervals - Changing the Interval
-
우리는 Sample과 Population의 관계를 다음과 같이 나타낸 적이 있다.
- 현재는 sample의 개수를 로 표현했기 때문에 와 기 같다.
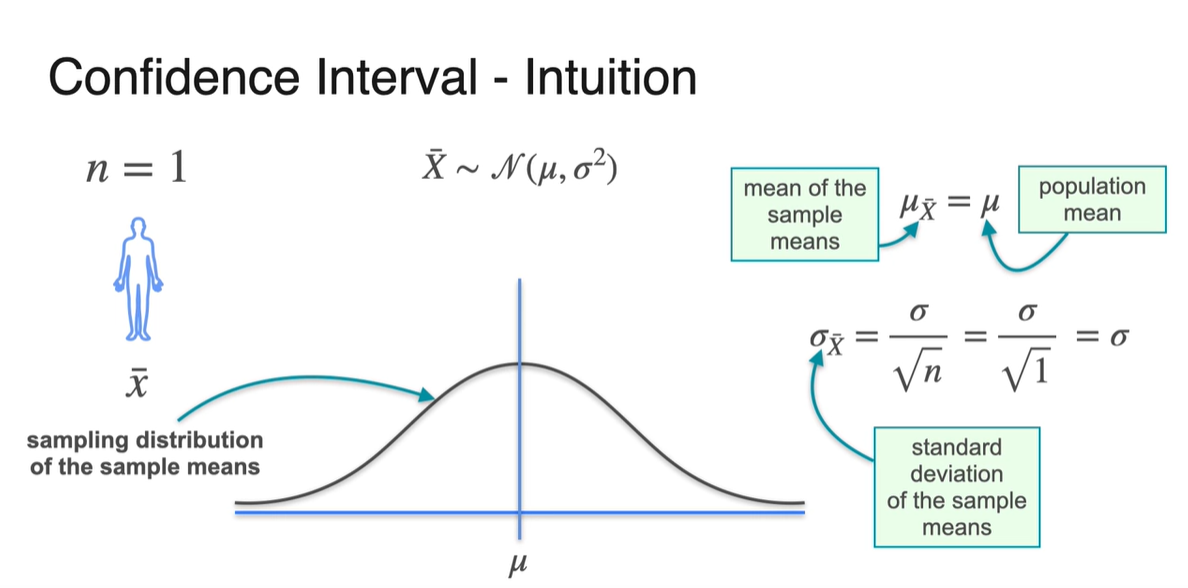
-
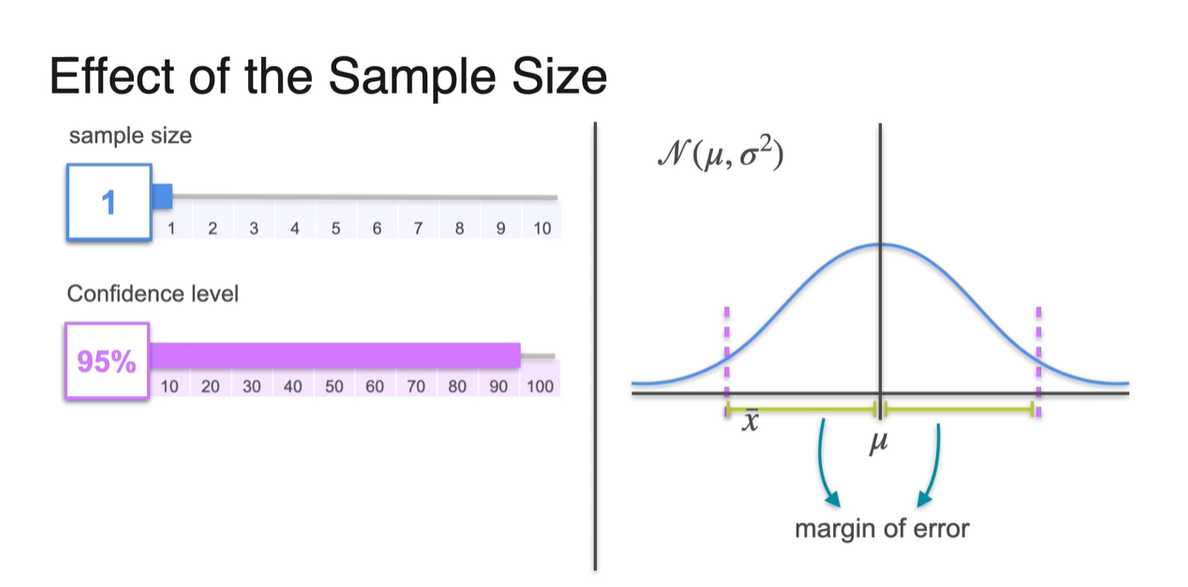
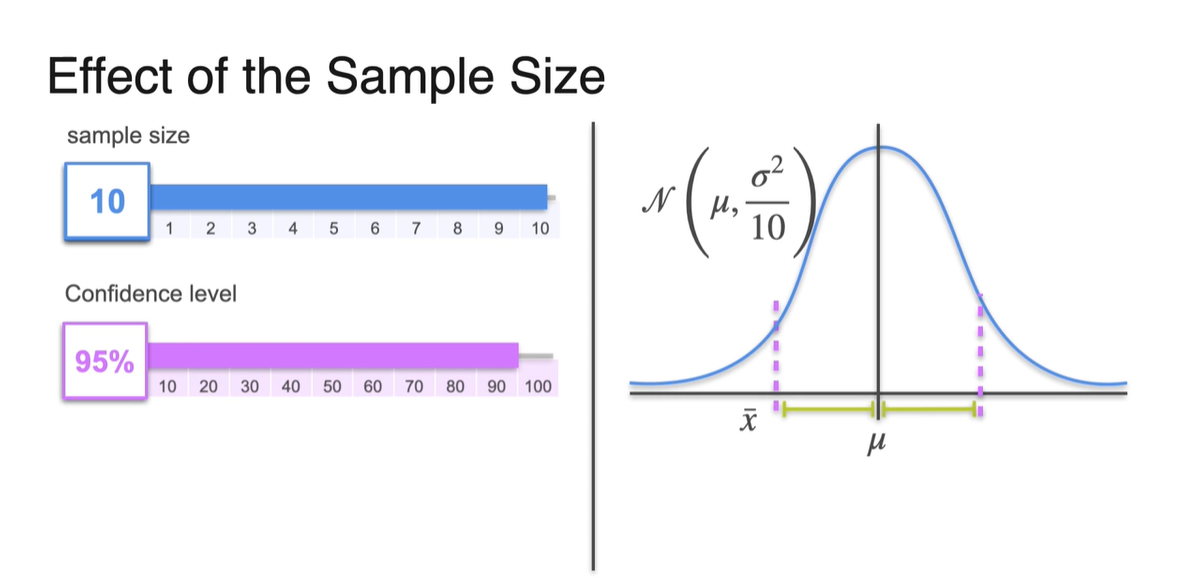
Sample size가 2로 커진다면 아래와 같이 가 로 원래 크기보다 감소한다.
- 분산은 narrow 정도를 나태내는 것이기 때문에 분포가 다소 뾰족하게 변하는 것을 알 수 있다.
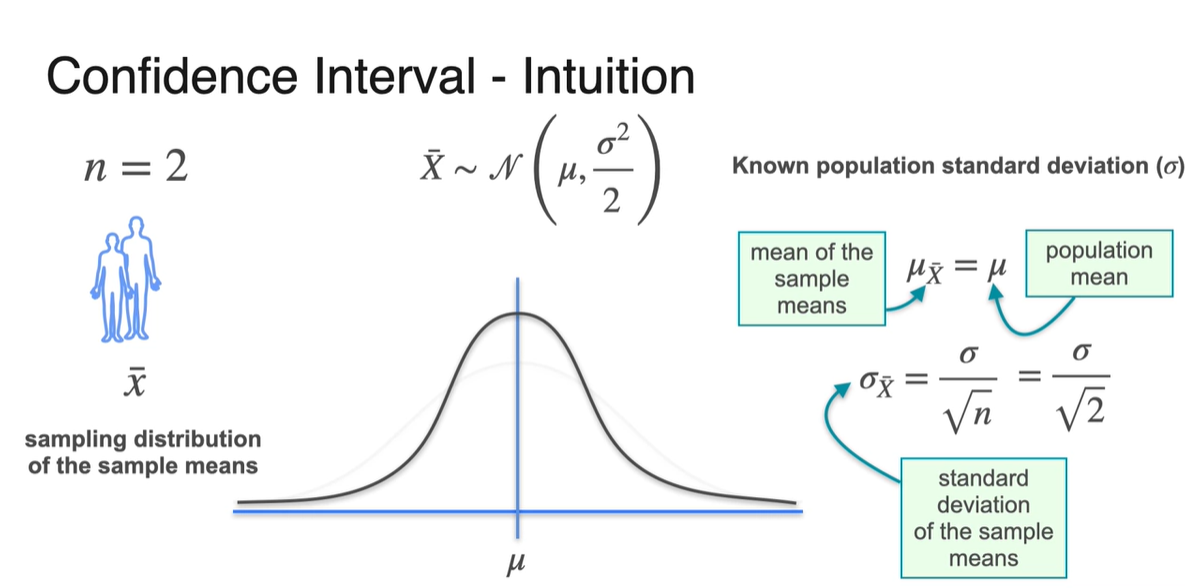
-
일 때와 일 때의 95% 신뢰 구간을 비교해보자.
- 같은 95%의 확률이더라도 sample size가 크다면 margin of error 범위가 더 줄어드는 것을 알 수 있다.
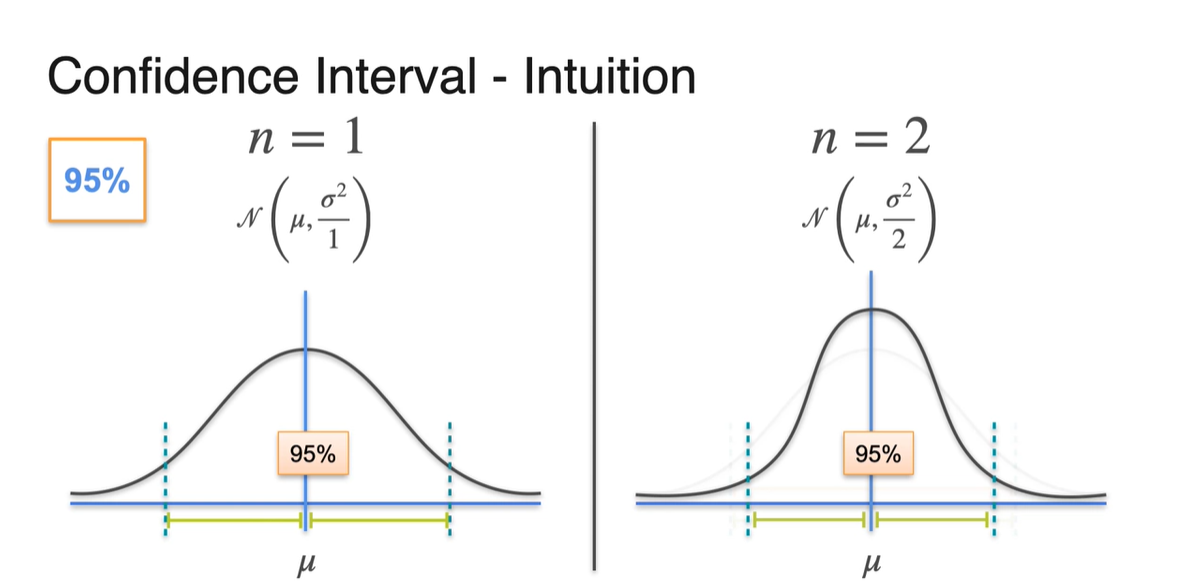
- 일 때와 일 때를 비교해보아도 마찬가지다.
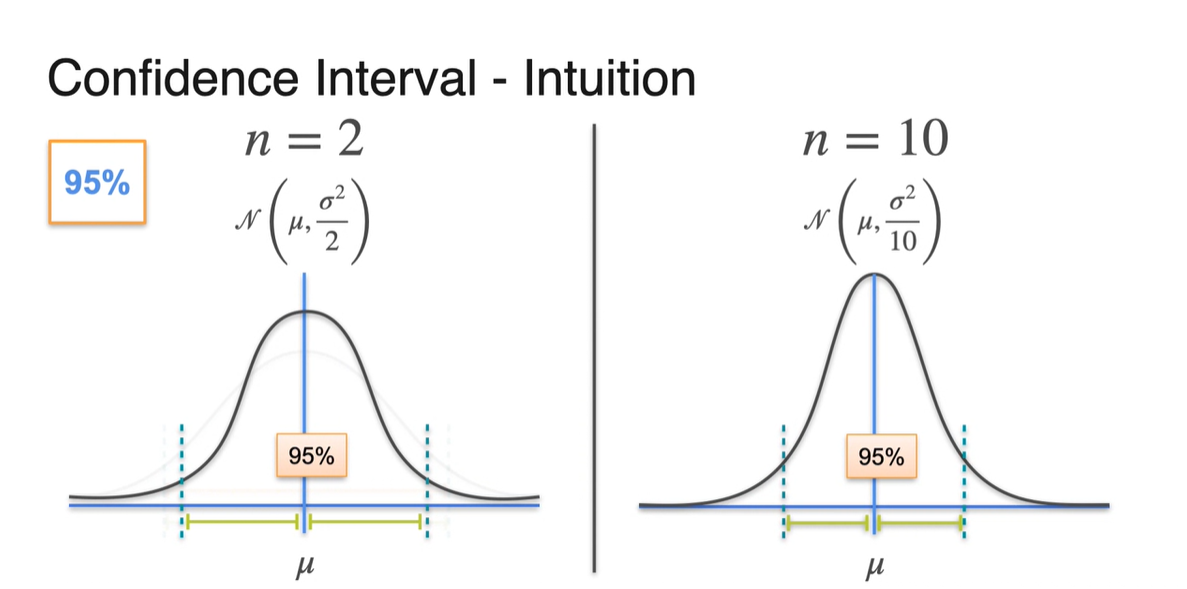
-
이제 sample size에 맞게 sample mean들을 구해, 95%의 신뢰 구간 내에 기존 분포 를 포함하는지에 대한 여부를 조사해보자.
- Sample size가 클수록 error 범위가 줄어든다고 했으므로, 이 크다면 sample mean 가 와 더 가깝게 추정 가능하다는 사실을 알 수 있다.
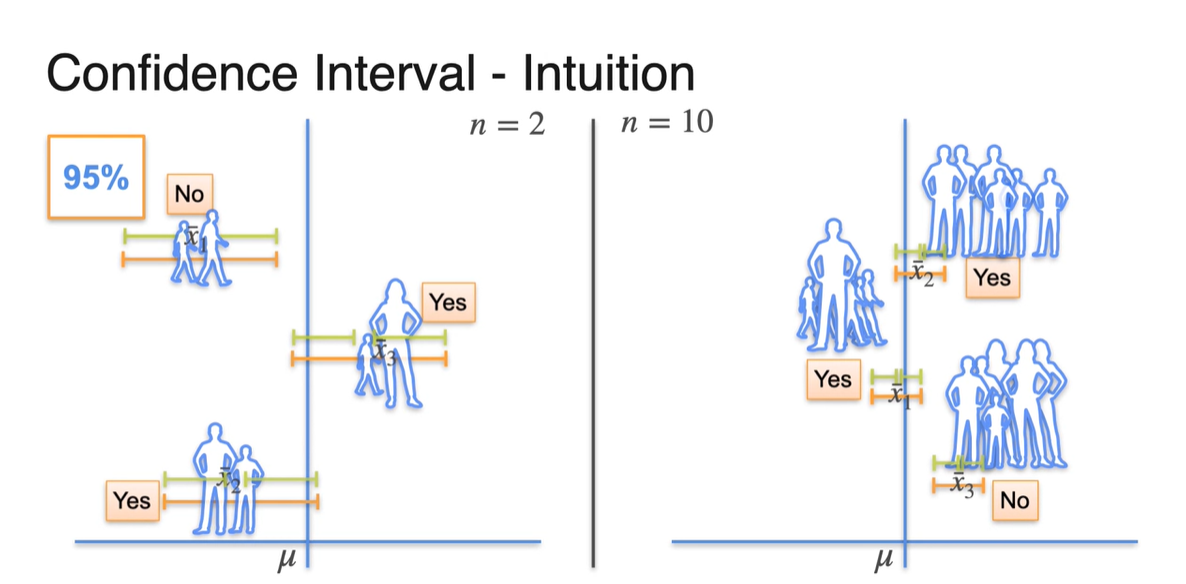
-
같은 95%를 만족하는 확률로 confidence level을 설정하였다고 하더라도 의 크기에 따라 보여지는 sample mean의 분포 양상은 다소 다를 수 있다.
- 즉, sample size를 크게 설정할수록 sample mean의 값 자체가 와 거의 동일하게 계산된다는 점이 key point다.
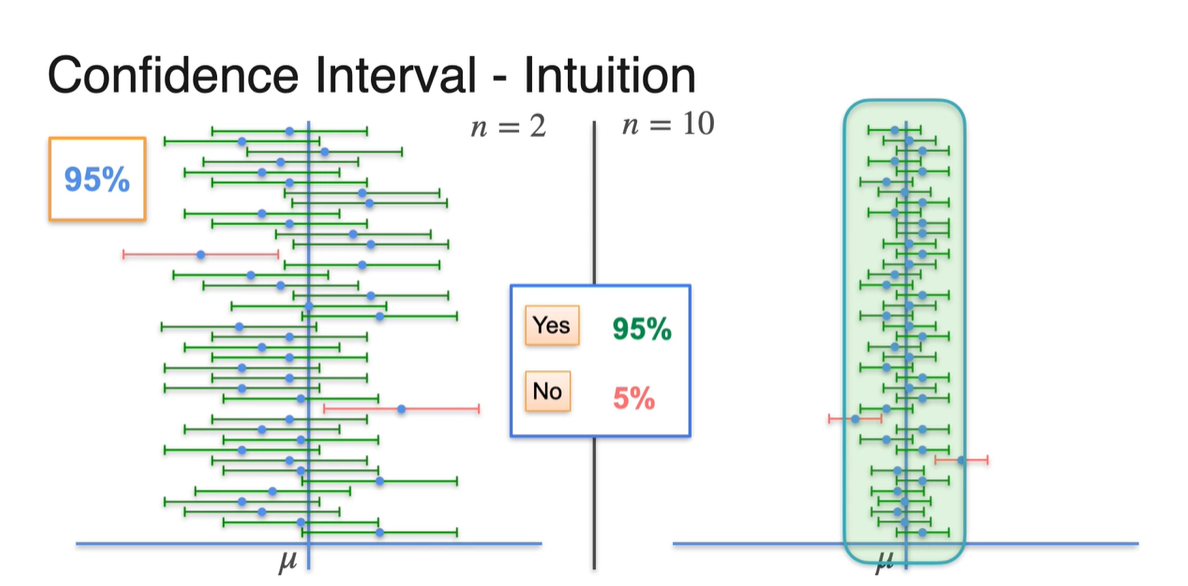
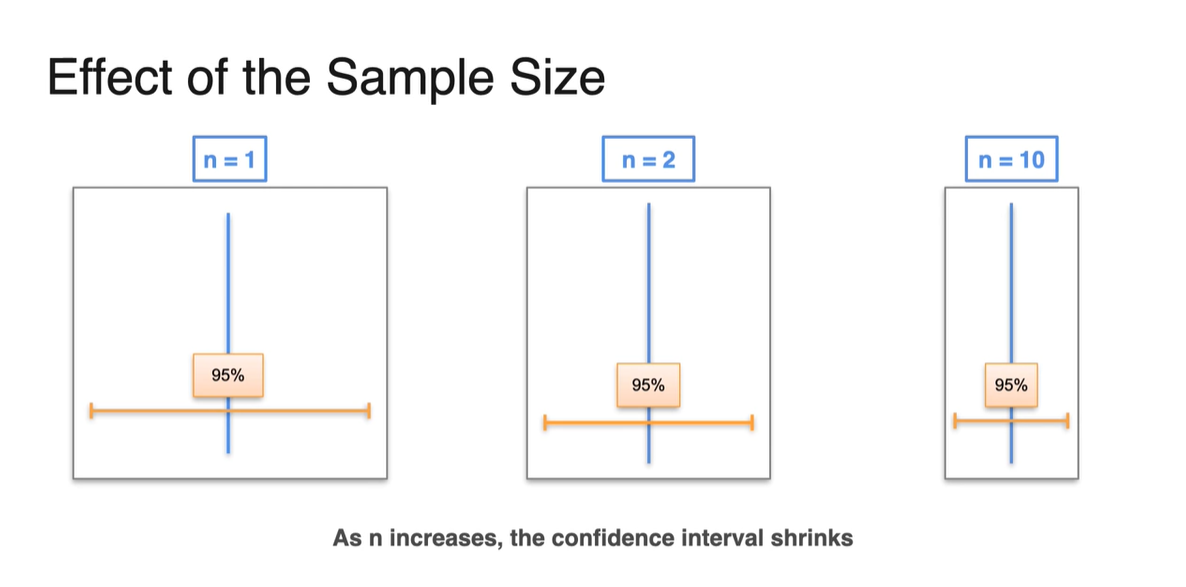
- 아래는 sample size에 따른 margin of error의 범위 차이를 나타낸다.
-
같은 confidence level이더라도 이 클수록 sample mean이 로부터 멀리 떨어지지 않은, 더 narrow한 구간 내에 존재한다.
- 다시 말해, 이 커지면 confidence interval은 줄어든다.
-
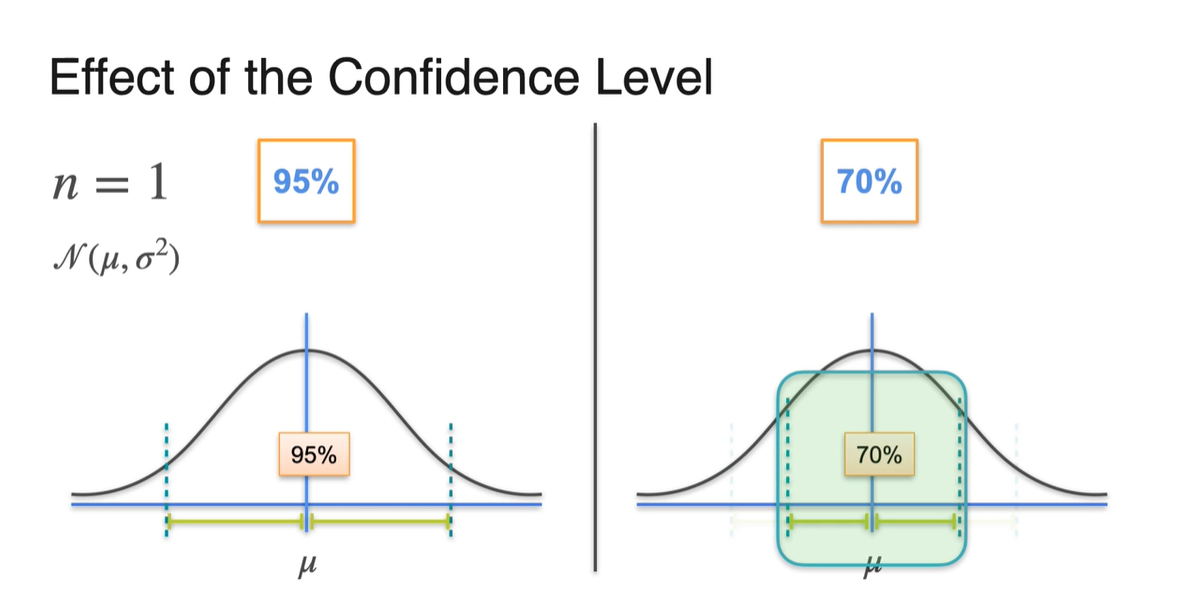
이번에는 sample size 을 고정시켜, confidence level을 70%으로 변화시켜 보자.
- 그러면 margin of error는 더 줄어들 것이다.
-
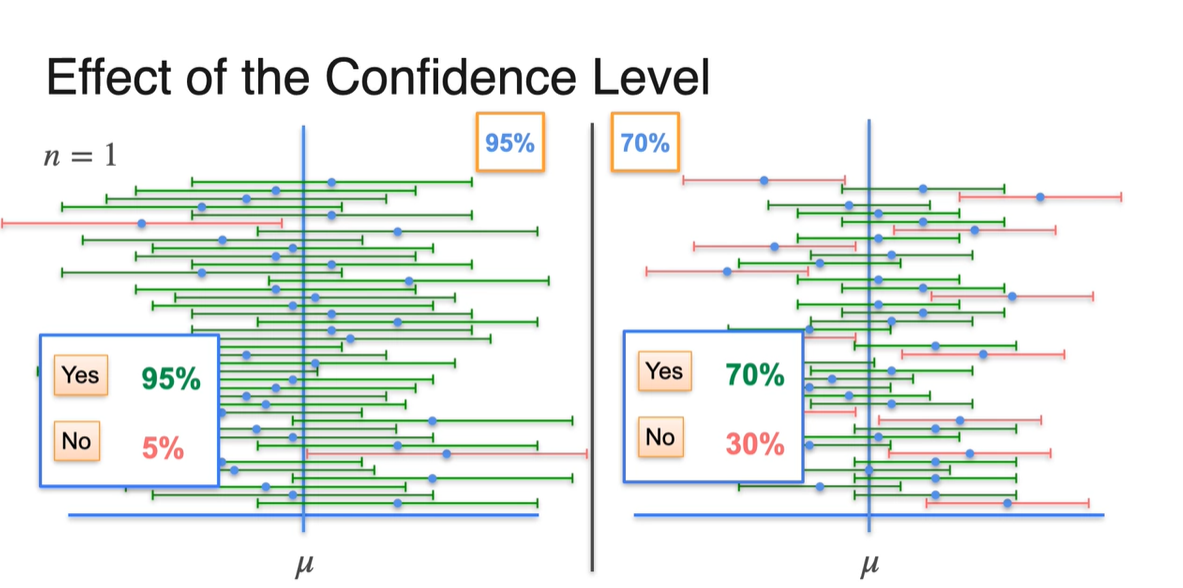
Sample size를 로 고정하고, 95%와 70%의 확률로 confidence level을 다르게 설정한 결과를 비교한 것이다.
- Confidence level이 감소하면 Margin of error가 줄어들기 때문에 sample mean의 구간이 를 포함하게 될 가능성이 줄어든다.
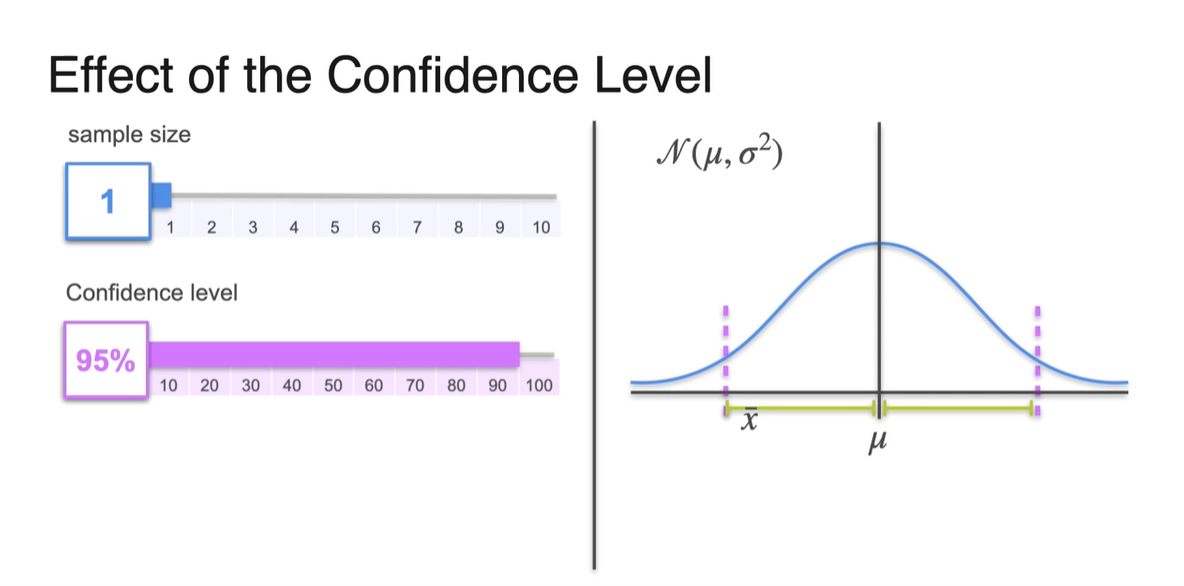
- 아래는 confidence level에 따른 margin of error의 범위 차이를 나타낸다.
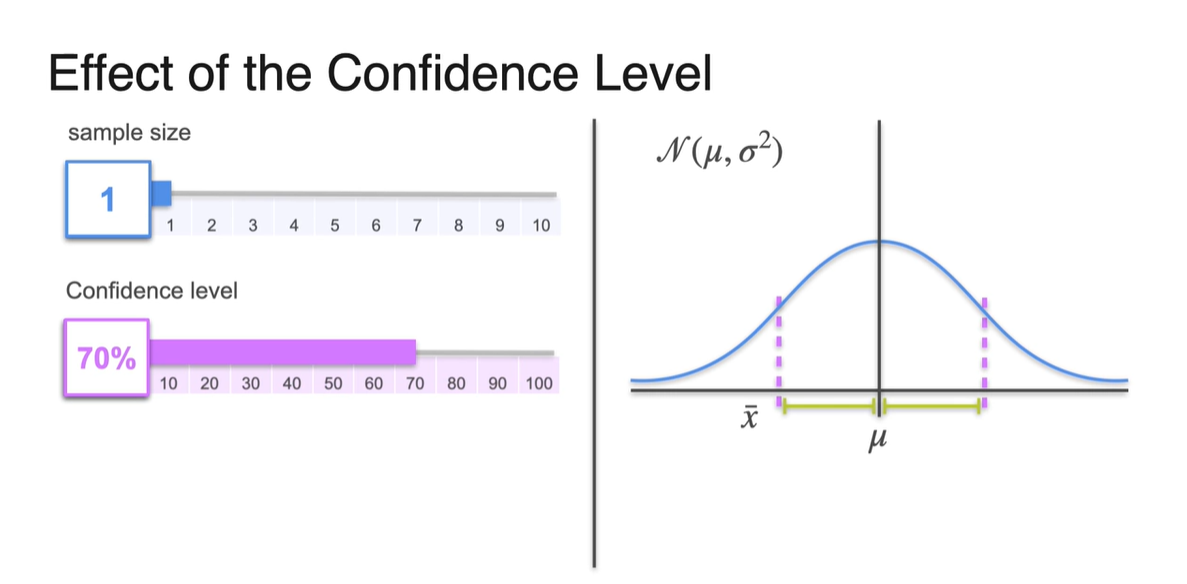
-
요약하자면 다음과 같다.
- 신뢰 구간은 sample mean의 양쪽 side에 margin of error를 붙여 넓힌 구간이다.
- 신뢰 수준은 신뢰 구간이 를 포함하게 될 확률을 의미한다.
- 신뢰 수준을 높인다면 신뢰 구간은 좁아진다.
- 표본의 개수가 크다면(데이터가 많다면) 신뢰 구간의 범위는 좁아진다.
- 신뢰 수준을 낮춘다면 신뢰 구간의 범위는 줄어든다.

Confidence Intervals - Margin of Error
-
Sample mean의 confidence interval로부터 margin of error를 정의해보자.
- Confidence Interval의 lower limit과 upper limit이 나타내는 범위까지가 margin of error다.
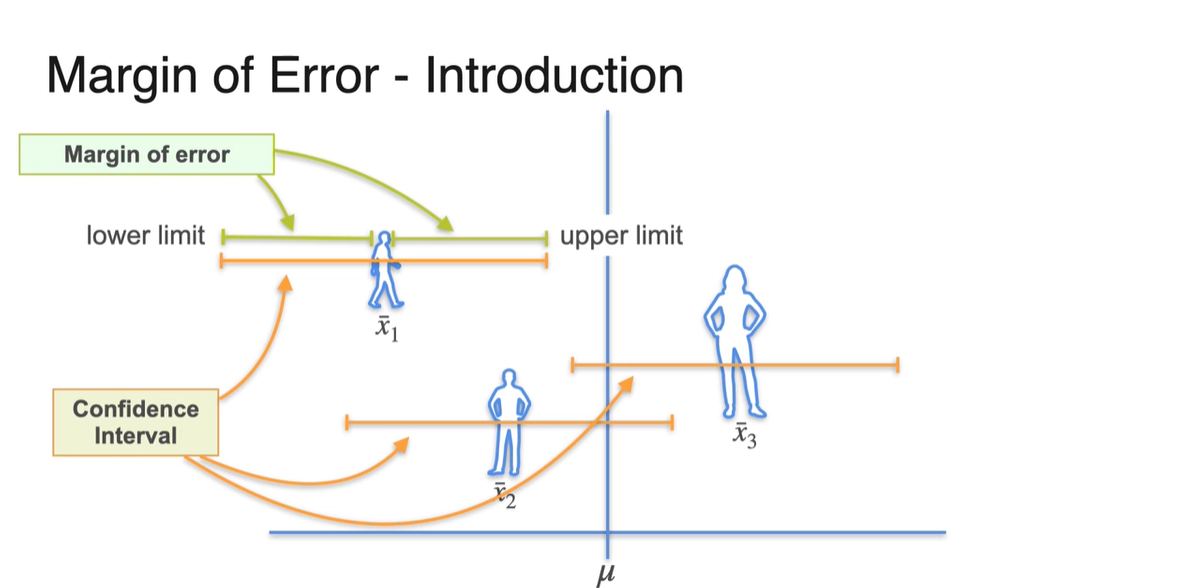
-
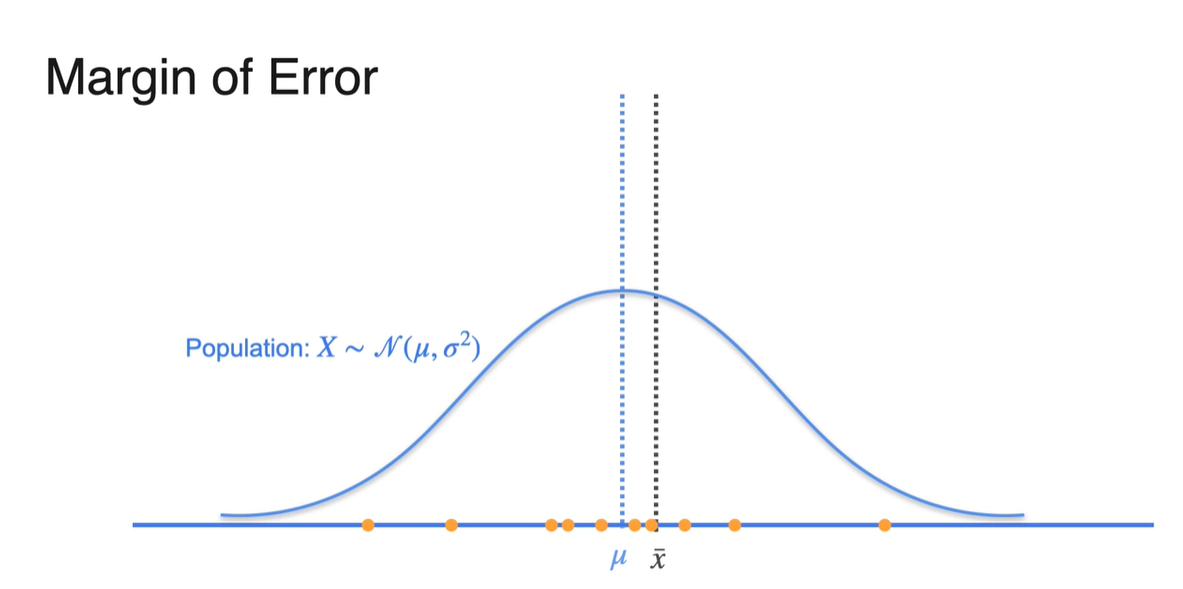
Population의 분포가 파란색과 같다면 뽑힌 sample들은 아래 주황색으로, sample mean 는 검은색으로 표기하였다.
- 만약 키가 더 작은 사람들로 sample을 형성하였다면 는 왼쪽으로 치우칠 것이며, 키가 더 큰 사람들로 sample을 형성했다면 는 오른쪽으로 치우친다.
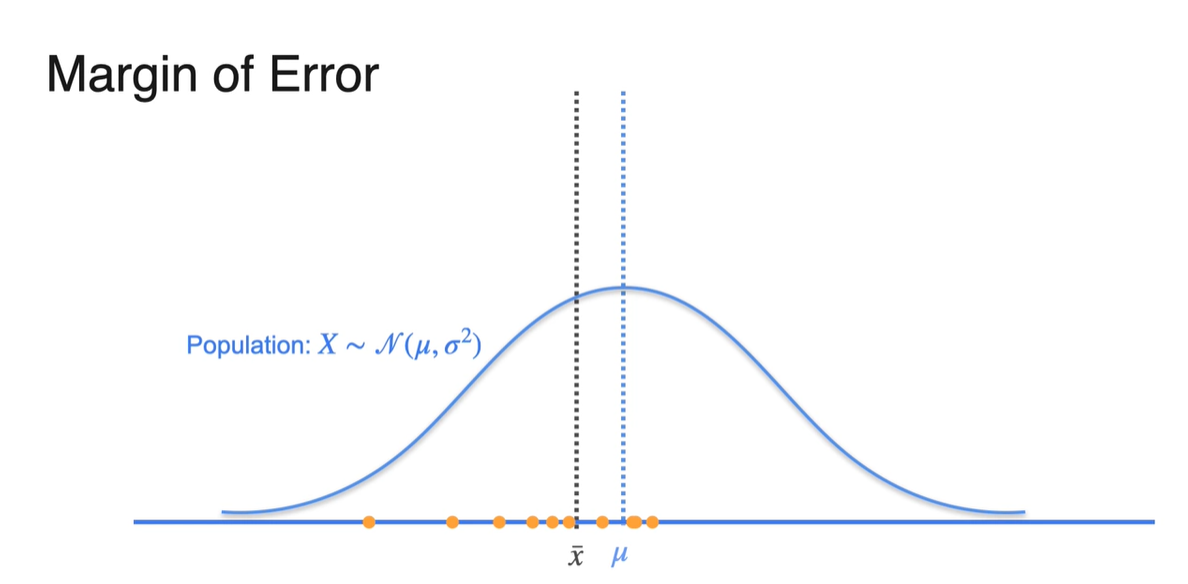
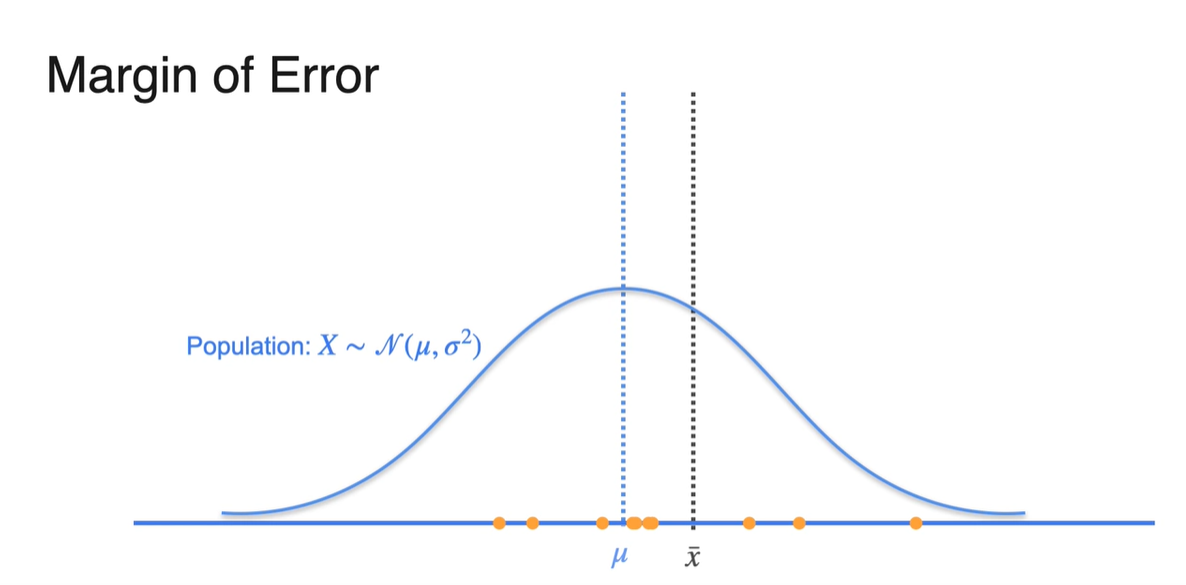
- Sample size 이 매우 크다면 분포의 형태가 population mean 에 매우 가깝게 형성된다.
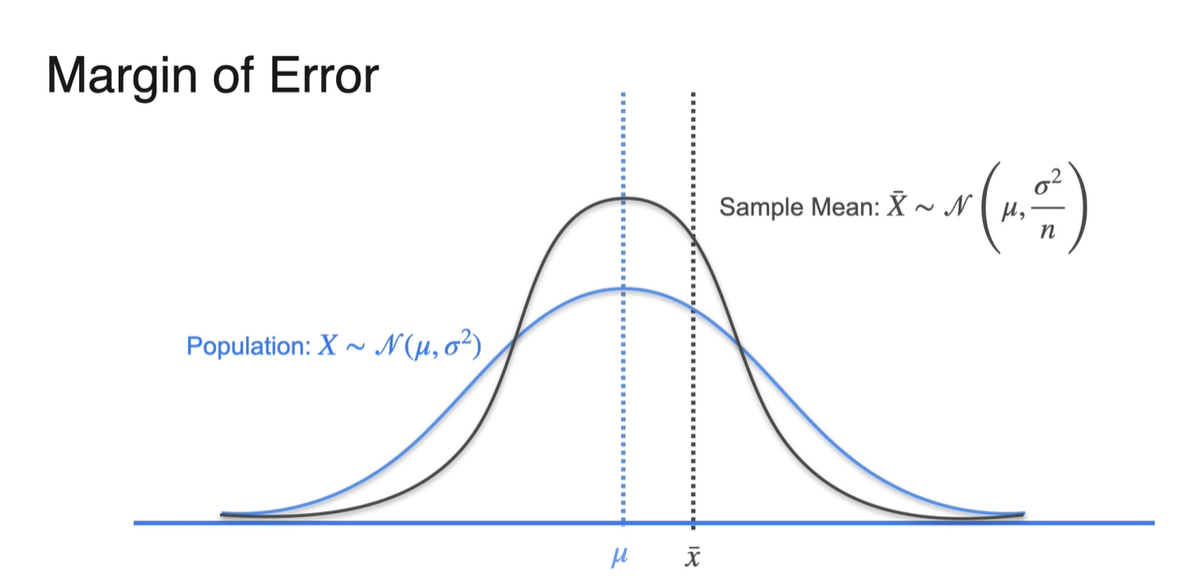
-
그런데 우리가 알 수 있는 건 sample mean과 sigma 뿐이다.
- 그렇다면 어떻게 Confidence Interval을 설정할 수 있을까?
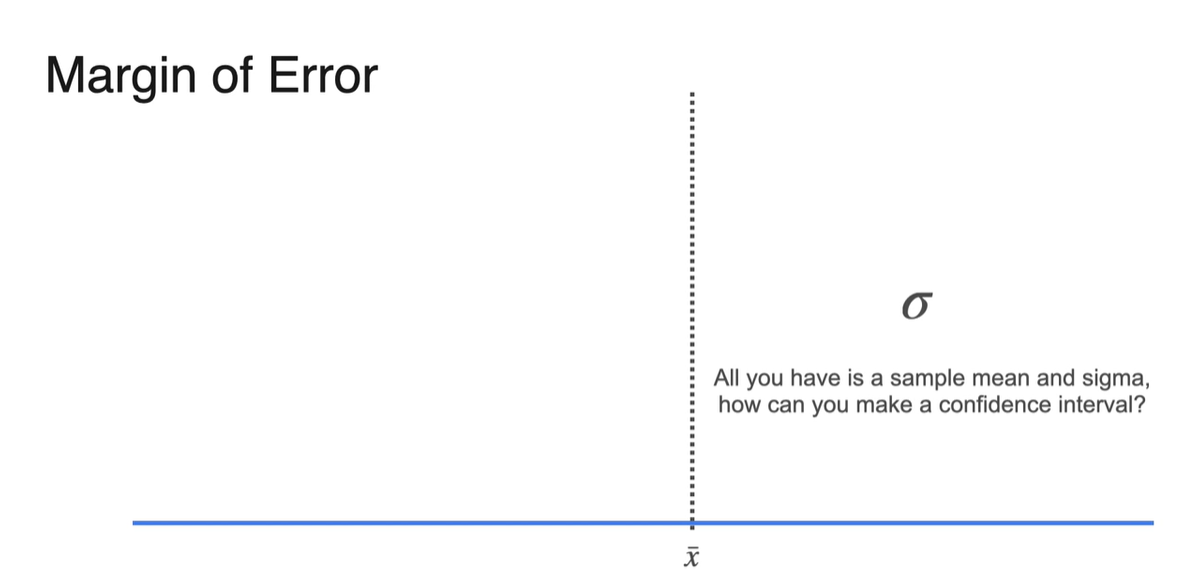
-
Normal distribution의 특징부터 살펴보자.
-
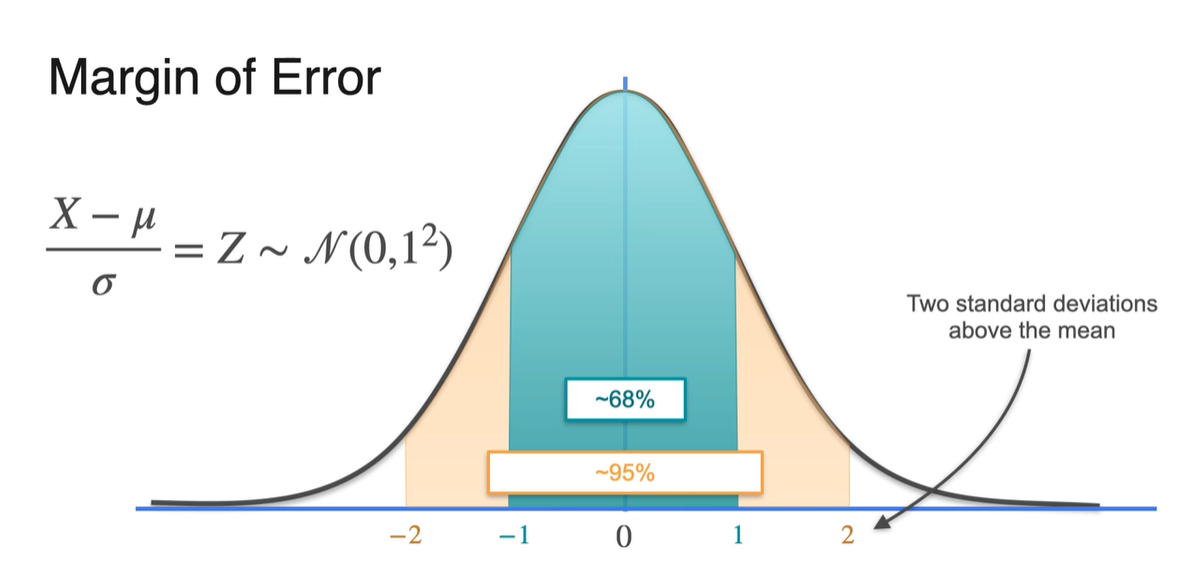
평균인 로부터 , 한 구간의 넓이를 계산하면 68%, 95%의 면적을 얻을 수 있다.
- 1 또는 2를 나타내는 값은 -scores로 표현 가능하기 때문에 random variable 를 로 바꿔서 표현해보자.
-
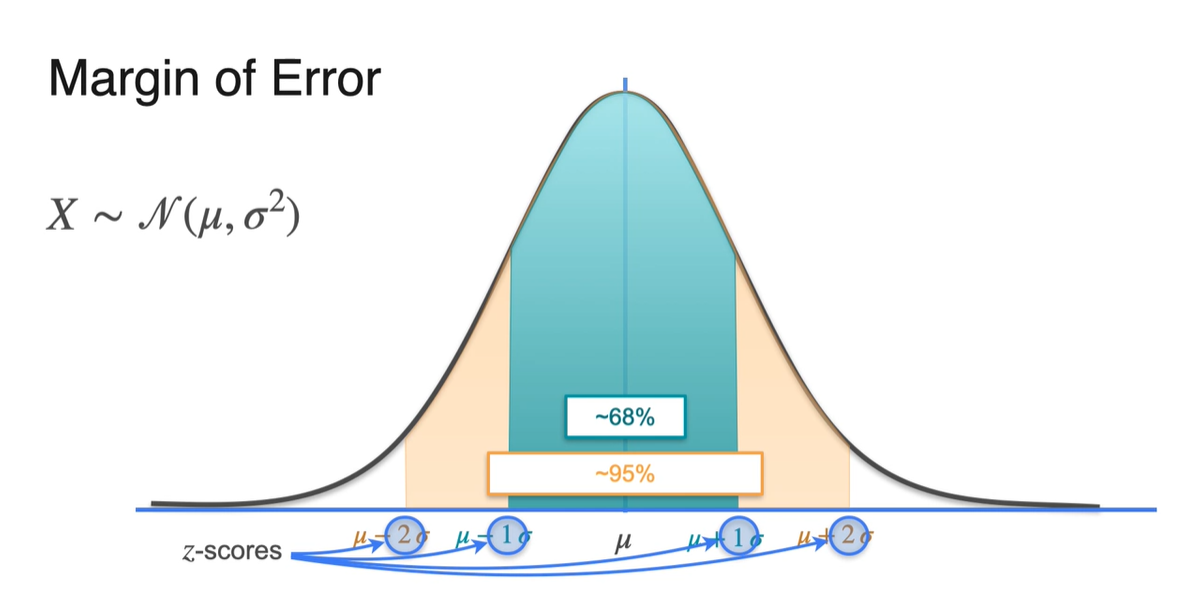
-
로 모든 random variable을 계산하면 변수가 모두 숫자로만 표현 가능해진다.
- 이 때 평균은 0이며, 2라고 표현된 값은 사실 평균 로부터 2배의 standard deviation()가 더해진 값이라고 볼 수 있다.
-
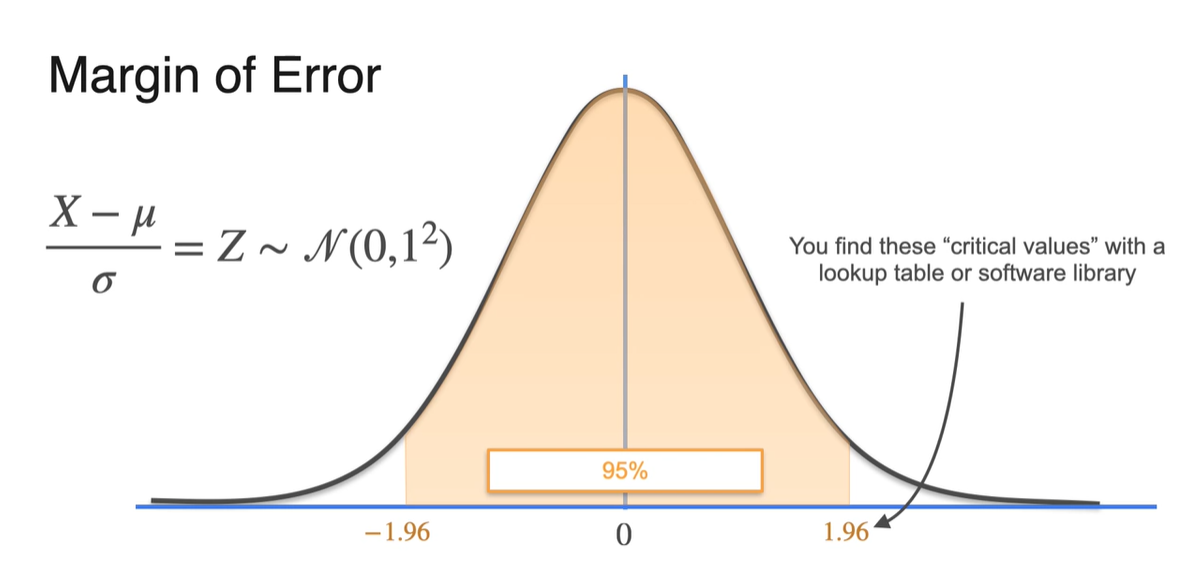
명확하게는 1.96일 때 아래 면적이 95%임을 만족한다.
- 그리고 해당 값은 software library의 "critical values"로 표현된 값을 찾아 알아낼 수 있다.
-
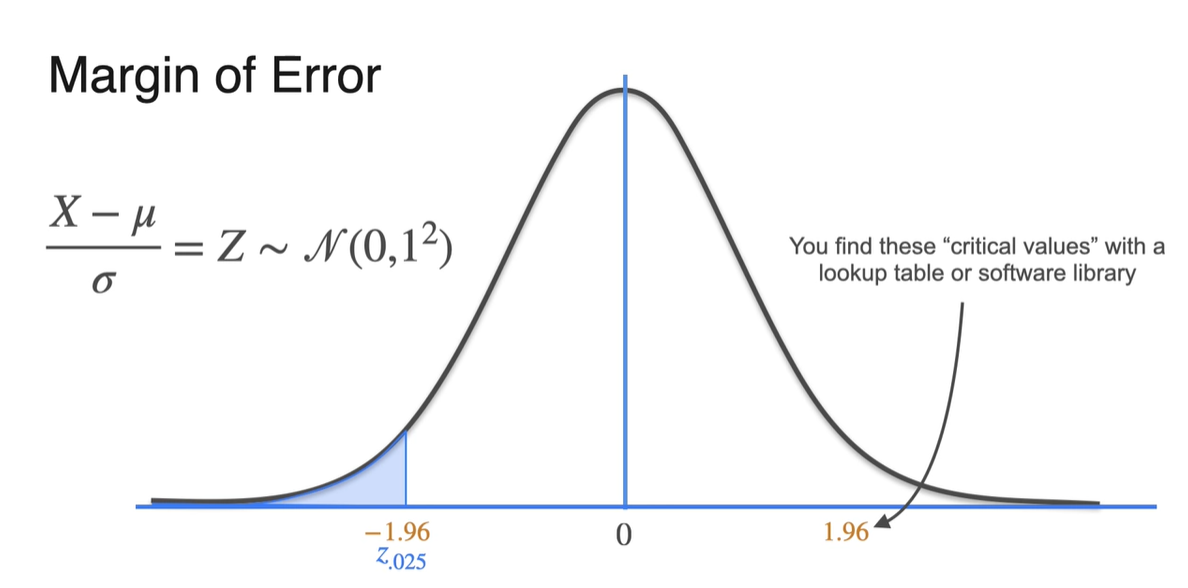
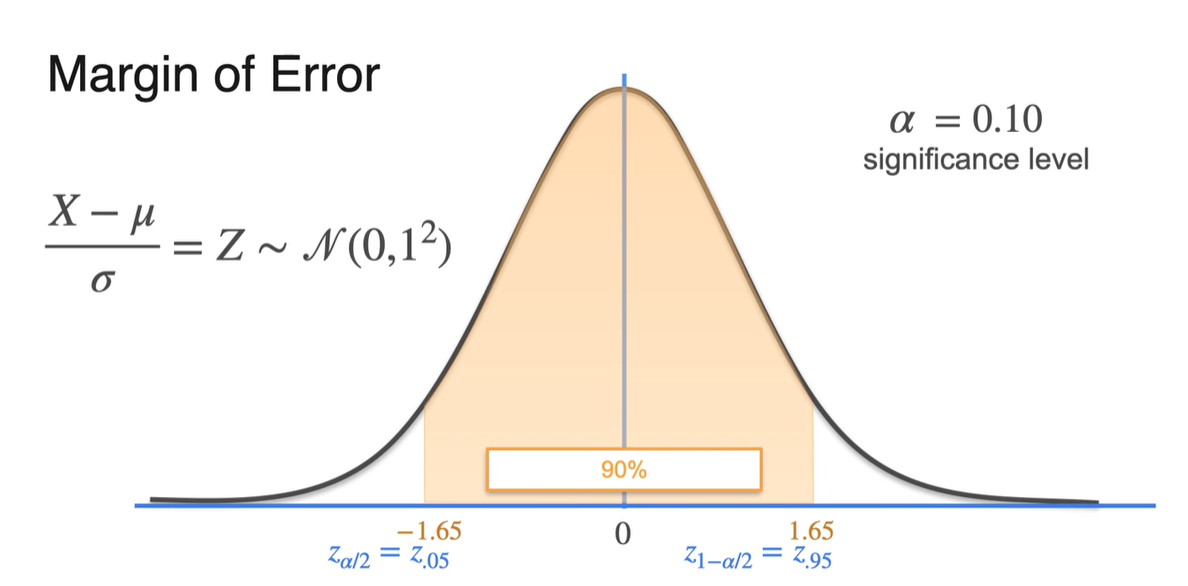
를 0.05(5%)로 설정했을 때에는 경계선에서의 lower limit을 0.05의 1/2인 로 표현할 수 있다.
- Upper limit은 로 표현된 값을 찾아주면 된다.
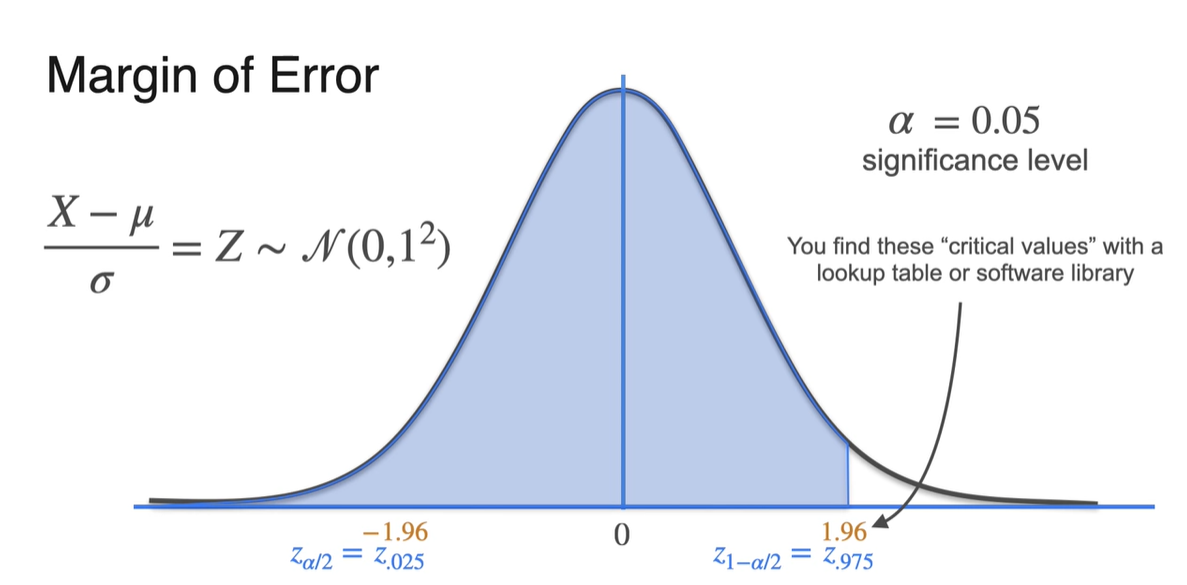
- 가 0.10이라면 양 끝 부분의 면적이 10%라는 뜻이므로 와 가 경계를 나타낸다.
-
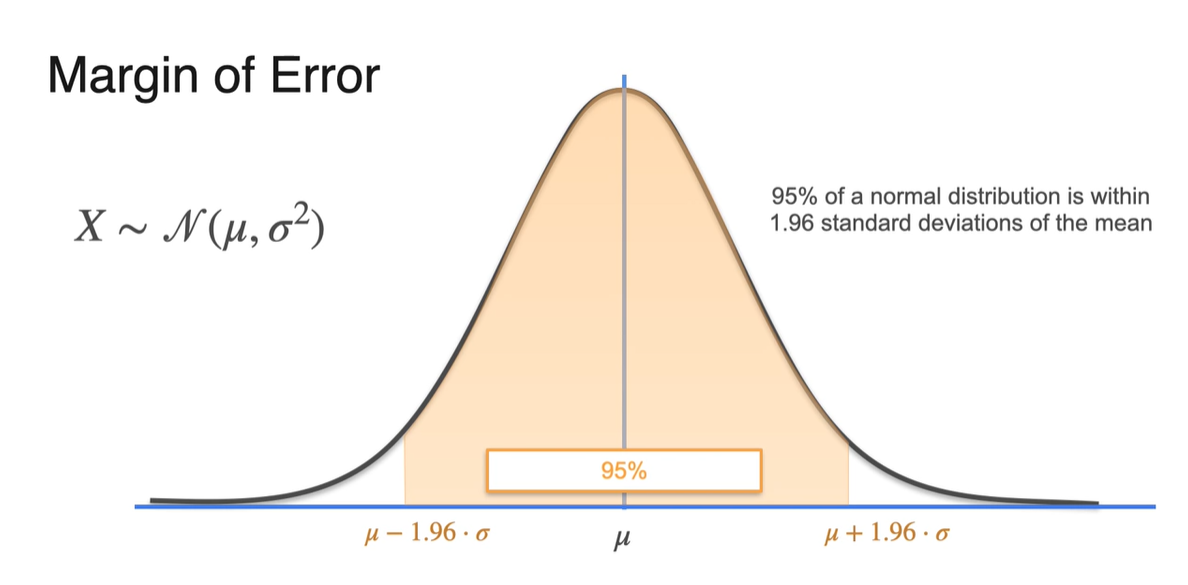
정규화를 진행하지 않은 random variable 로, 95%의 confidence level을 다시 표현해보자.
- Lower limit과 upper limit의 값은 로 표현할 수 있다.
-
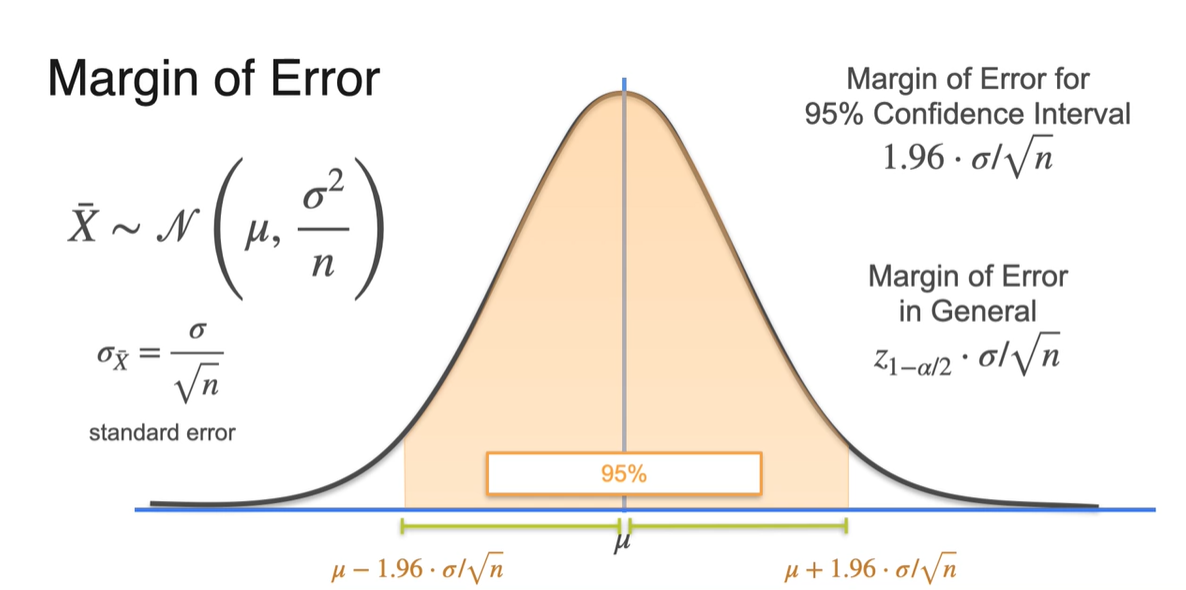
만약 sample size까지 고려한 분포로 설명한다면 을 따르기 때문에
표준 편차 가 로 표현된다.-
그러면 margin of error의 값이 이 된다.
- 1.96이 기존 random variable 의 값이었으므로 에 을 곱한 값이 sample 분포의 margin of error다.
-
-
Confidence Interval은 아래와 같은 수식으로 정리 가능하다.
-
Sample mean 의 confidence level 95%인 구간 →
-
이를 통해 population mean 의 구간을 추정하면 다음과 같다.
-
-
결론적으로 Confidence Interval은 로 표현 가능하다.
-




- CLT에 따라 충분히 많은 sample size를 유지하는 한, 위와 같은 정리는 유효하다.
Confidence Intervals - Calculation Steps
-
Confidence Interval을 구하는 방법에 대해 step by step으로 알아보자.
-
Sample mean 를 찾는다.
-
Confidence level인 (1-)를 설정한다.
-
Critical value 를 계산한다.
-
Standard error 을 계산한다.
-
Margin of error(구간의 절반) 를 계산한다.
-
Sample mean 에서 margin of error를 하여 population mean이 있을 범위를 구한다. → confidence interval
-
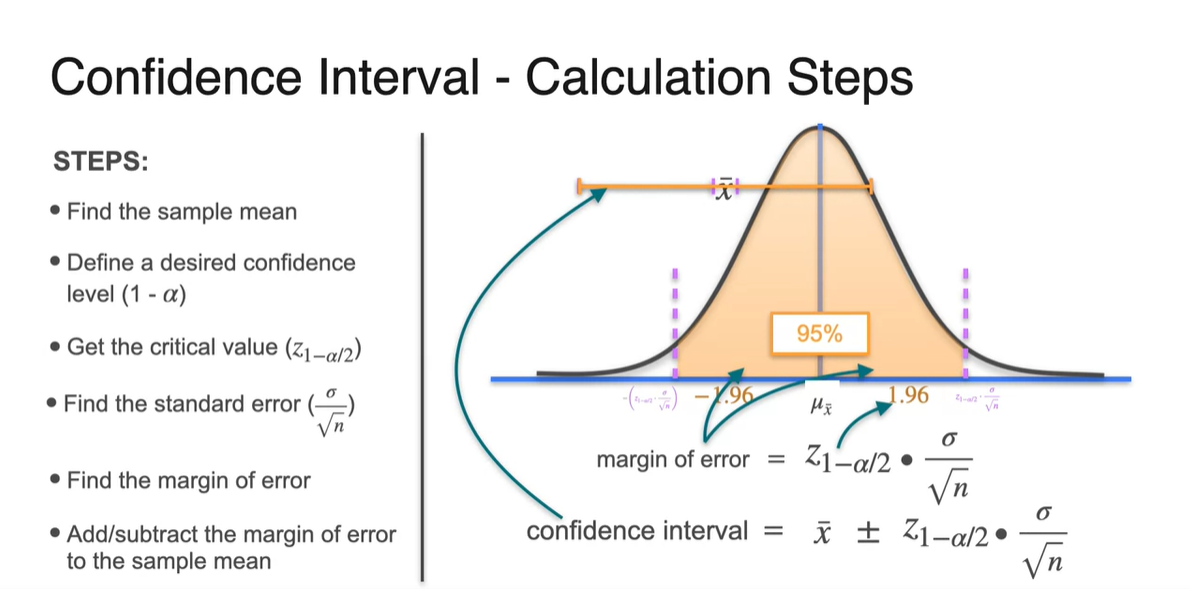
-
신뢰 구간을 계산할 때 가정해야 할 몇 가지 조건이 있다.
- Sample은 random 추출된다.
- Sample size가 30 초과일 때, normal distribution임을 가정할 수 있다.

Confidence Intervals - Example
-
6,000명의 성인이 존재하는 Statistopia 사람들 중에서 49명을 random select하여 와 를 구해보자.
- 95%의 신뢰 구간을 설정한다면 는 1.96이며, 이를 가지고 condidence interval을 계산해보자.

- 먼저 margin of error 를 계산하면 7의 결과값이 나온다.

-
Confidence interval은 sample mean 의 margin of error 한 값이므로, 170에서 7을 더하거나 빼줌으로써 계산할 수 있다.
- 신뢰 구간은 sample mean으로부터 margin of error를 계산한 구간 내에, population mean이 있다고 95%의 신뢰도로 확신한다는 내용을 의미한다.
We are 95% confident that the true average height in Statistopic is between 163cm and 177cm.

Calculating Sample Size
- 우리는 방금 49명의 sample size로 95%의 confidence level을 만족시킨 결과, margin of error가 7cm임을 얻었다.
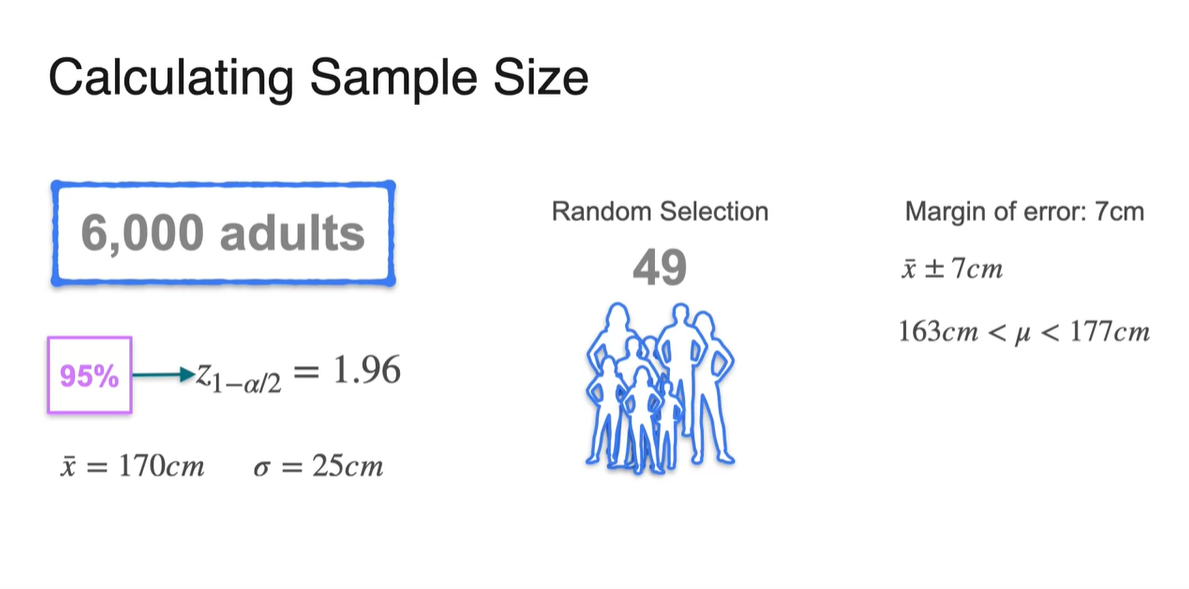
-
만약 이 오차 범위를 더 줄이고 싶어서 3cm의 margin of error를 원한다면 최소 몇 명의 사람들을 sampling하면 될까?
- 이제 관점을 바꿔 sample size의 최소 개수를 계산해보도록 하자.

-
Margin of error의 식은 이다.
-
가 170cm이고 가 25cm일 때, margin of error가 3보다 작거나 같음을 만족하기 위하여 의 값을 계산하면 아래와 같이 수식을 얻을 수 있다.
-




-
원하는 margin of error를 얻기 위한 최소 sample size를 계산하는 대한 공식은 다음과 같다.

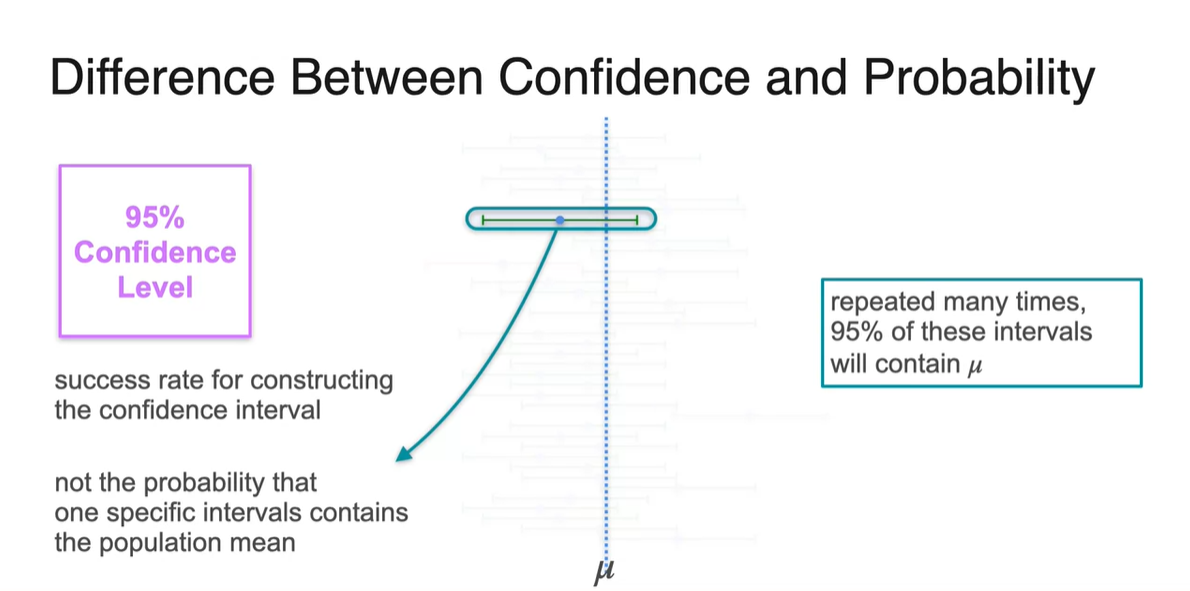
Difference Between Confidence and Probability
-
사실 confidence와 probability는 엄밀한 차이가 있다.
- Confidence interval은 해당 구간 내에 population parameter가 있을 "확률"이라기 보단 95%의 time 정도로 "성공"한다는 개념이다.

-
Population mean은 fixed 되어 있고 unknown하다는 점이 큰 특징이다.
- 또한, 특정 probability distribution을 가지지 않는다.
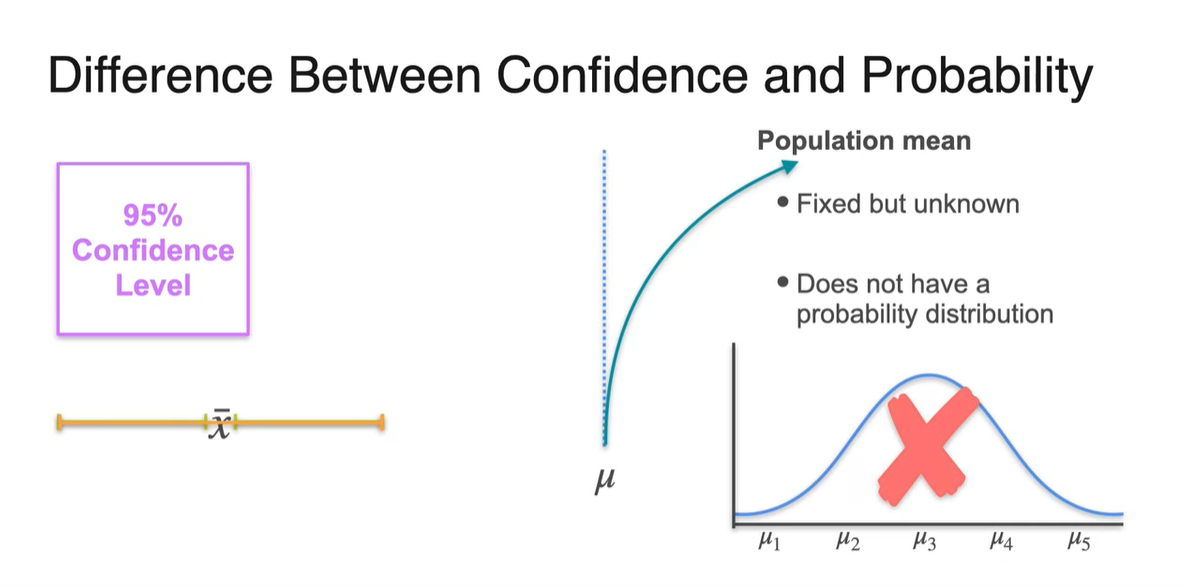
- 우리가 알 수 있는 사실은 오로지 계산된 interval 내에 population mean이 있을지 없을지에 대한 정보 뿐이다.

- 그리고 95%의 "확률"로 population mean 가 해당 간격에 속하지 않을 수도 있다.

-
그러나 sample의 분포는 표본 평균 와 approximated된 평균 가 존재하기 때문에, 몇 번의 times로 confidence interval이 평균 를 포함하는지를 count할 수 있다.
- 즉, Confidence level은 sampling된 표본의 confidence interval 내에 가 포함될 "성공" rate라고 보아야 한다.
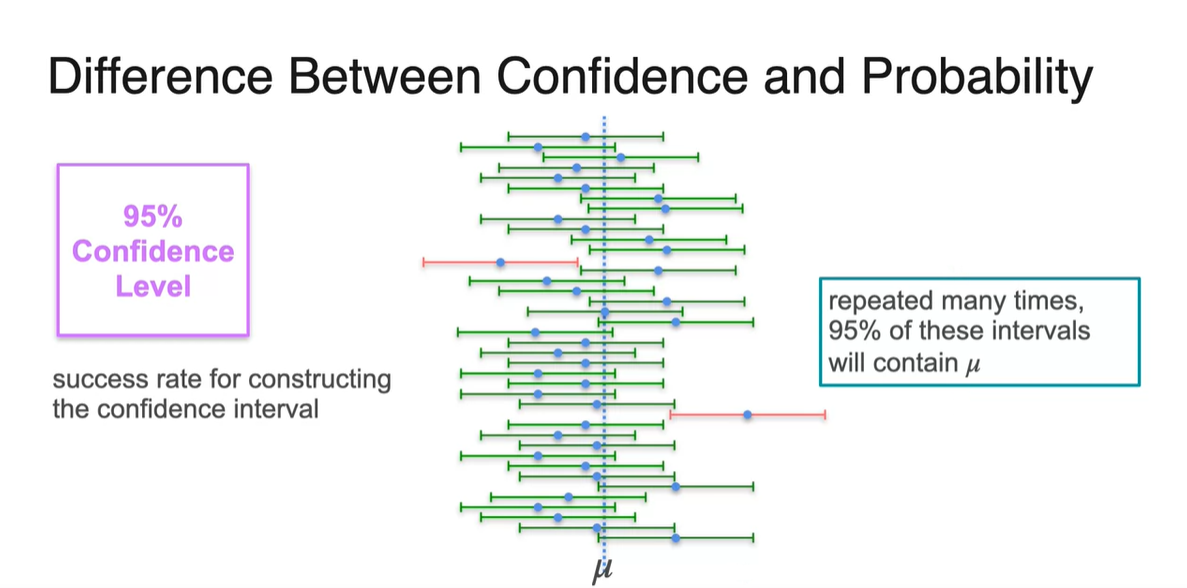
-
다시 말해, 특정 interval 내에 population mean이 포함될 "확률"이 아니란 뜻이다.
- Generating된 sample 중에서 population mean을 포함하게 될 success rate로 보아야 한다.
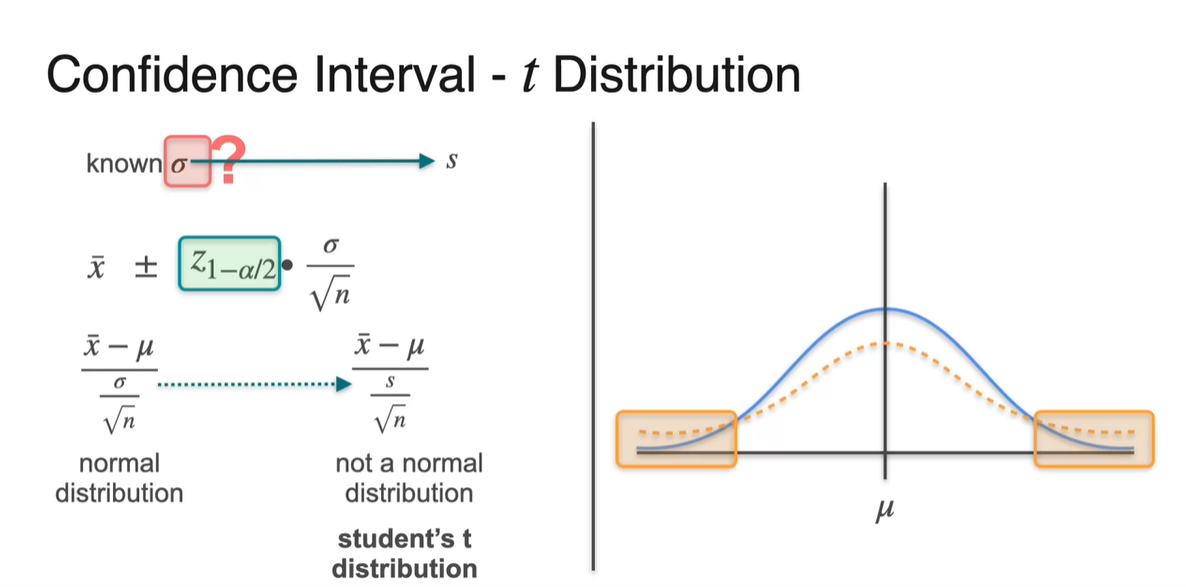
Unknown Standard Deviation
-
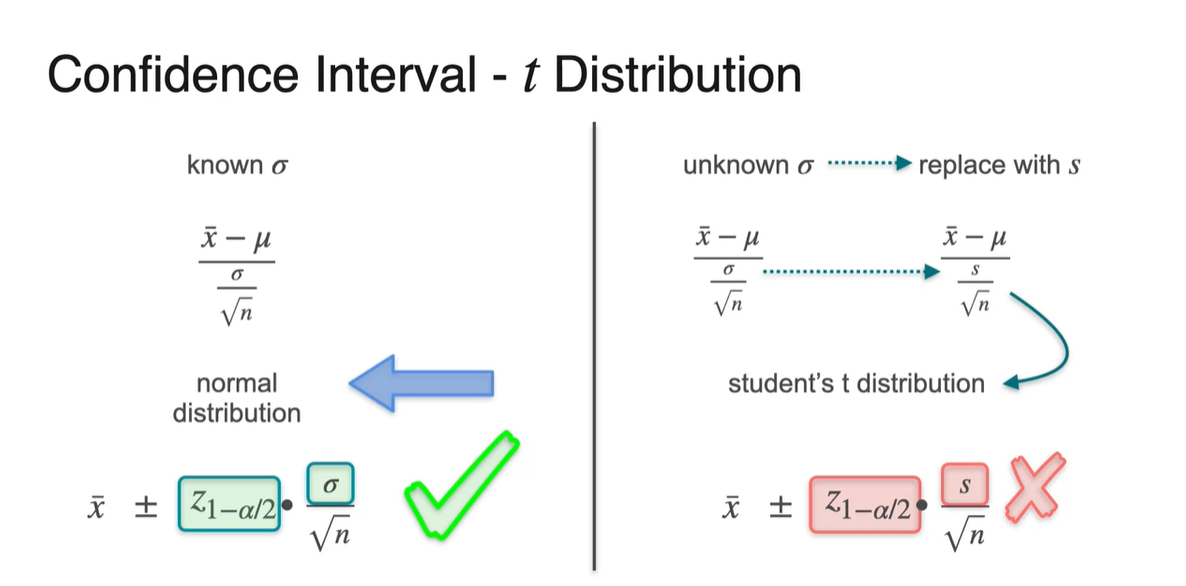
지금까지 우리는 population deviation 를 알고 있다는 가정 하에 문제를 풀었었다.
-
그러나 대부분의 상황에서는 population에 대한 분포를 전혀 모르므로, sample deviation으로 수식을 약간 고치는 작업이 필요하다.
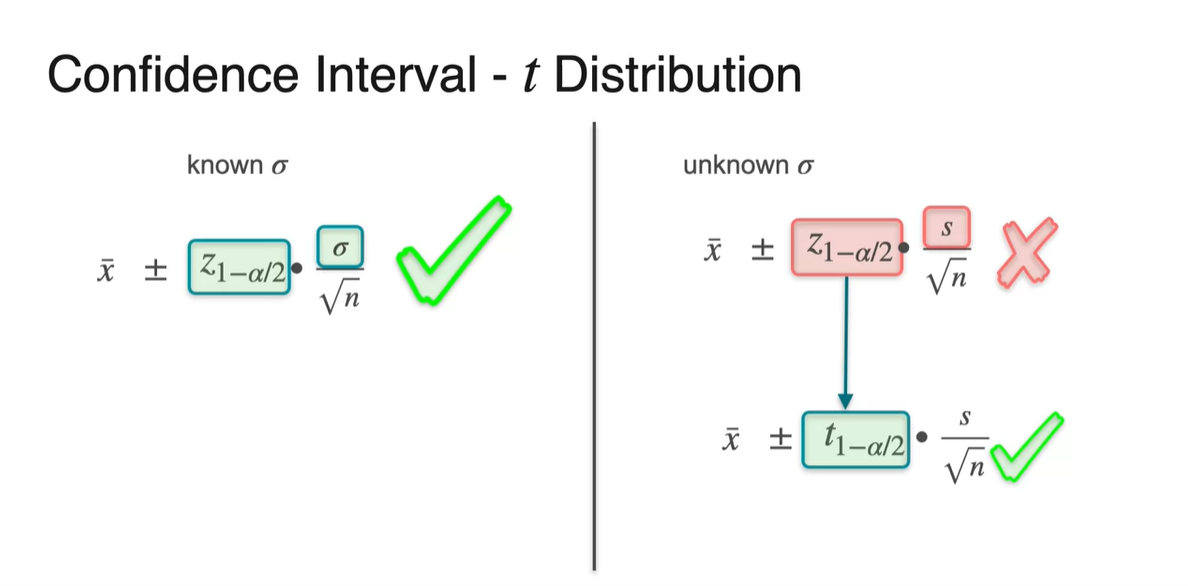
- 이를 student's t distribution이라 하며 수식적으로는 으로 정리한다.
-
그리고 이러한 분포는 실제 분포에 비해 꼬리가 훨씬 더 두껍다는 특징이 있다.
-
-
그러나 sample deviation 를 사용한다 하더라도 여전히 문제점은 존재한다.
- 바로 가 population 정규 분포에 의존하기 때문에 sample에 대한 정규화 값으로 고쳐주어야 한다.
- 우리는 이제부터 score를 student score로 고쳐서 계산할 것이다.
-
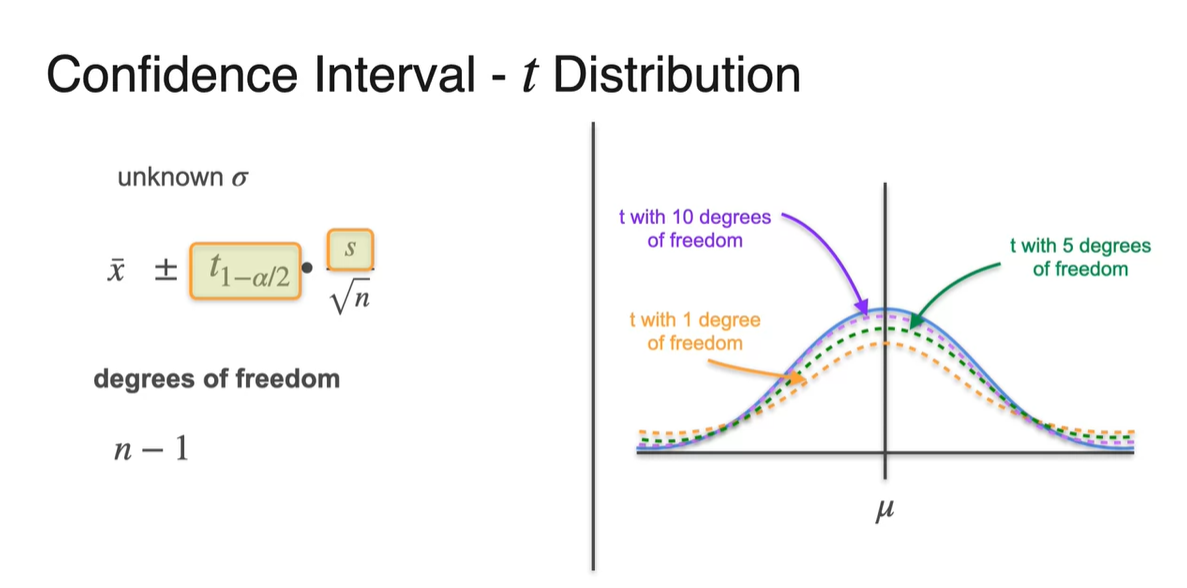
distibution은 degree of freedom이 이라는 점을 유의해야 한다.
- 이 클수록 population 분포와 거의 유사해진다는 점 또한 유념하자.
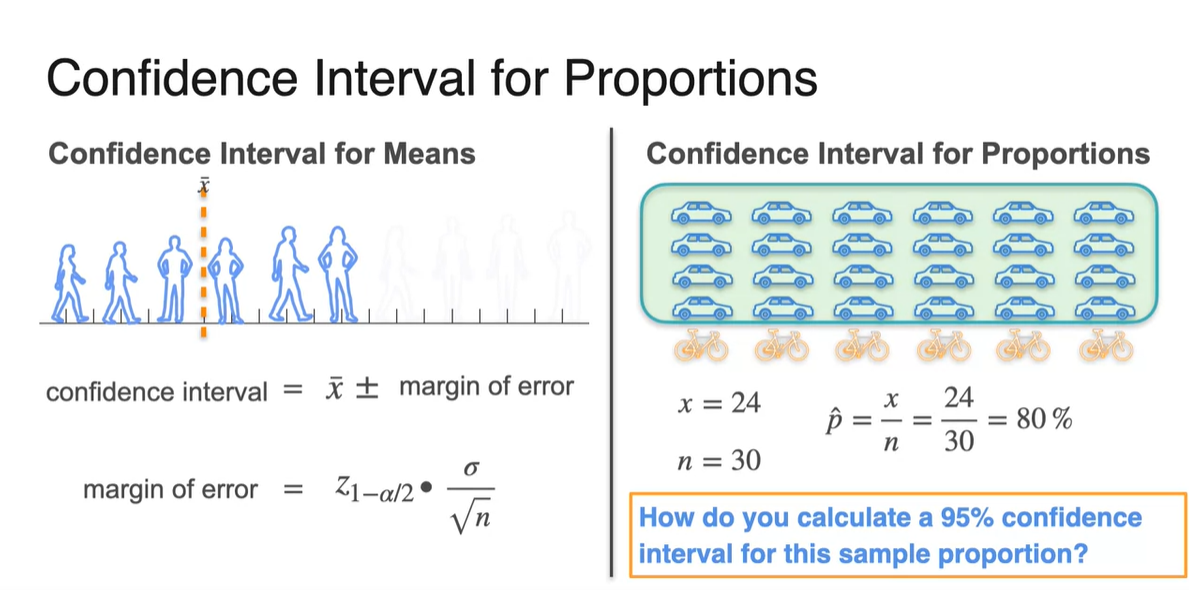
Confidence Intervals for Proportion
-
특정 사건이 일어난 proportion(비율)을 알고 있을 때의 Confidence Interval은 어떻게 계산할까?
- 로 구할 수 있는 margin of error와 을 알고 있을 때의 상황에서 95%의 신뢰 구간을 구해보자.
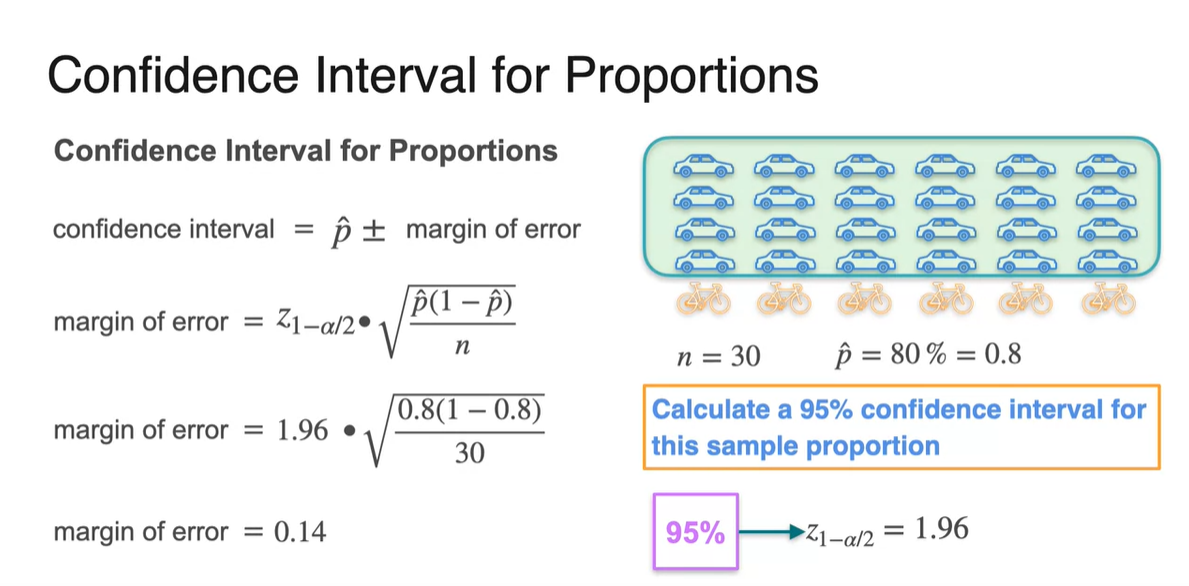
-
이 때의 Confidence Interval은 margin of error로 계산한다.
- Standard error 는 로 대체된다.

- 만약 이 0.8일 때를 가정하여 계산해보면 margin of error는 0.14의 값을 갖게 된다.
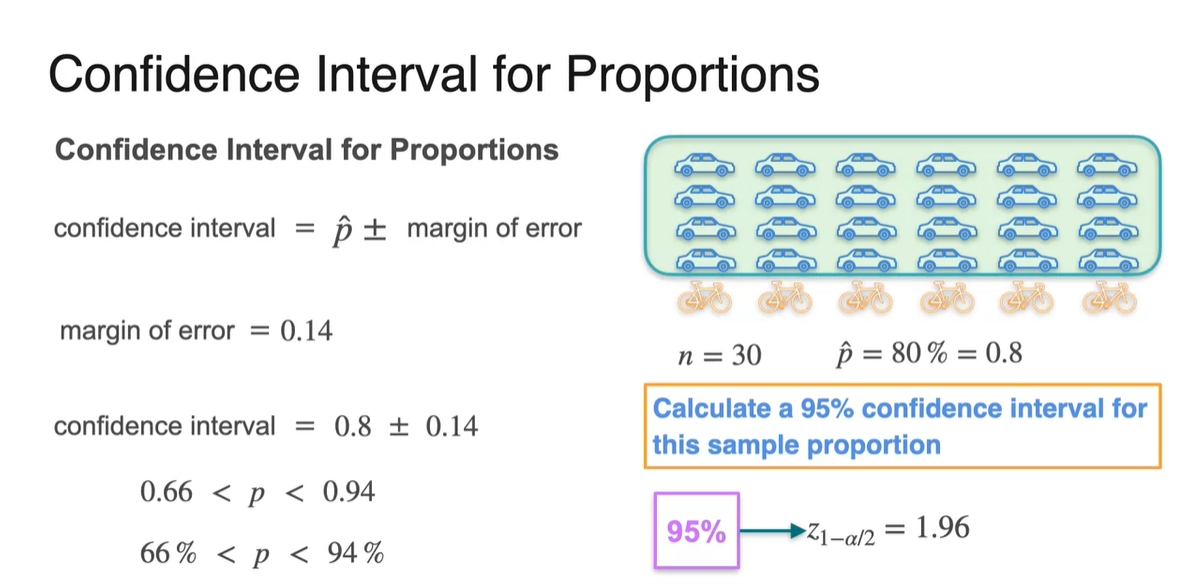
-
이를 이용하여 population proportion 를 추정하면 다음과 같다.
- Confidence Interval:
Lesson 2 - Hypothesis Testing
Defining Hypotheses
-
가설을 세우는 방법에 대해 알아보자.
-
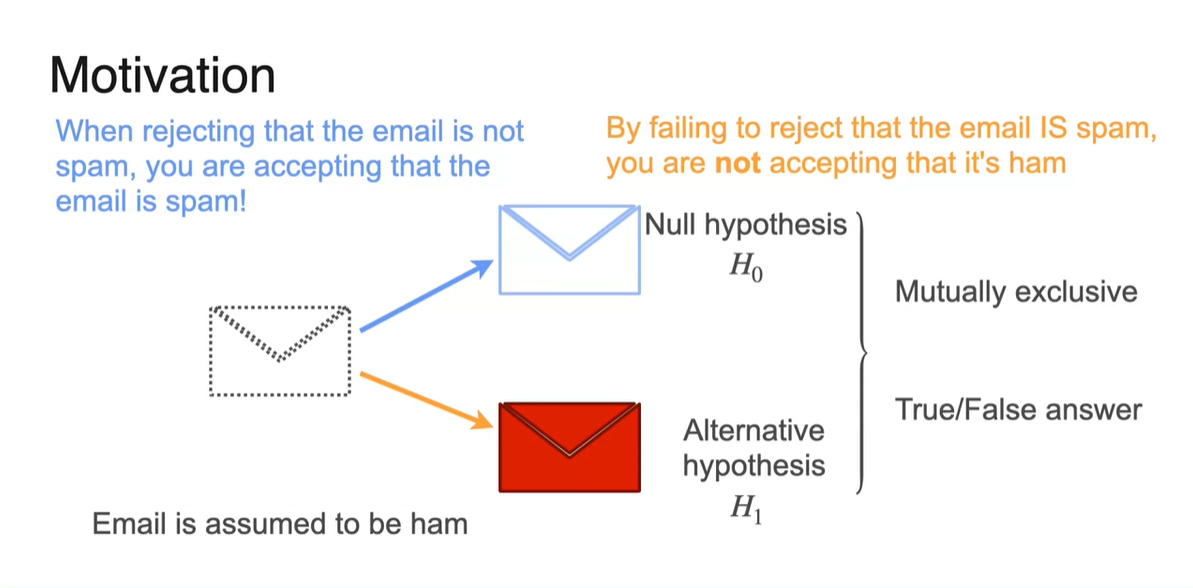
Email이 Spam인지 Ham인지 판단하는 방법은 Null hypothesis(귀무 가설) 와 Alternative hypothesis(대립 가설) 을 설정하는 것이 우선이다.
- 이러한 문제는 좋은 이메일을 Spam 이메일로 착각하는 경우가 훨씬 더 나쁜 경우이므로, 모든 이메일을 Ham 메일로 가정하는 것부터 출발한다.
-
Ham 메일과 Spam 메일은 동시에 일어날 수 없기 때문에 T/F 문제로 치환되며, 아무런 일도 일어나지 않고 안전한 상태를 귀무 가설로 가정한다.
- 그리고 다양한 evidence를 보았을 때, 귀무 가설이 기각된다면 대립 가설이 참으로 받아들여진다.
즉, 오답을 알아차리는 것이 가장 중요한 task다!
-
-
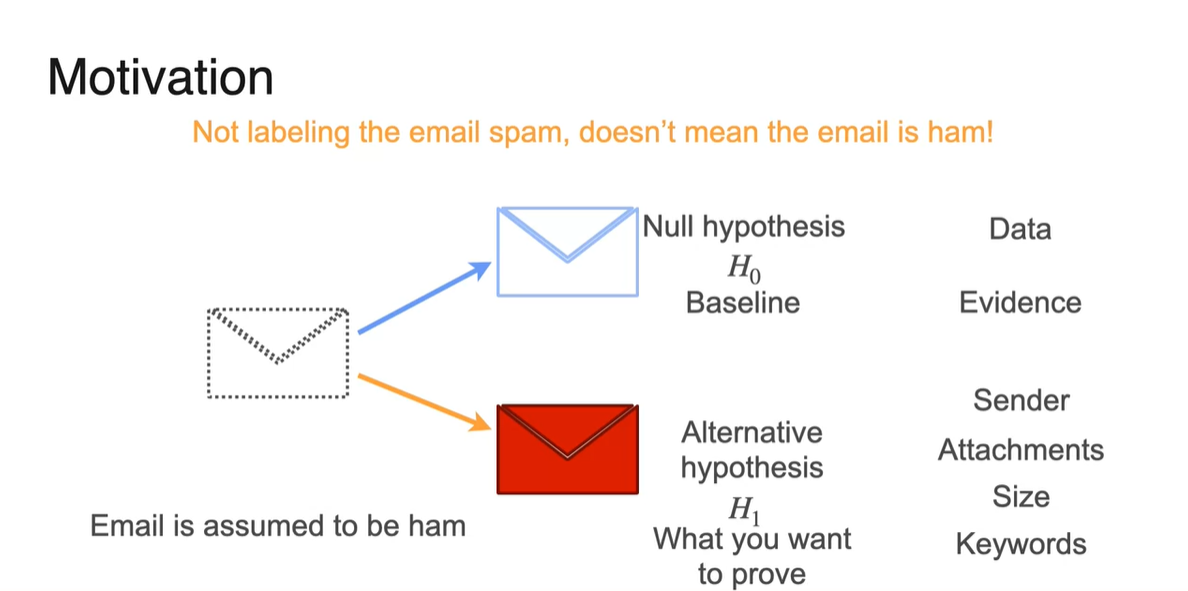
이 때 귀무 가설은 기준선(Baseline), 대립 가설은 경쟁 진술(opposite to prove)을 나타낸다.
-
가설 검정의 목적은 Data와 증거를 보고 Spam인지 Ham인지에 대한 두 가설 중 하나를 결정하는 것이라 볼 수 있다.
-
수집된 증거가 해당 메일이 Spam임(대립 가설)을 충분히 입증하지 못할 경우, 귀무 가설을 기각하는 것이다.
-
-
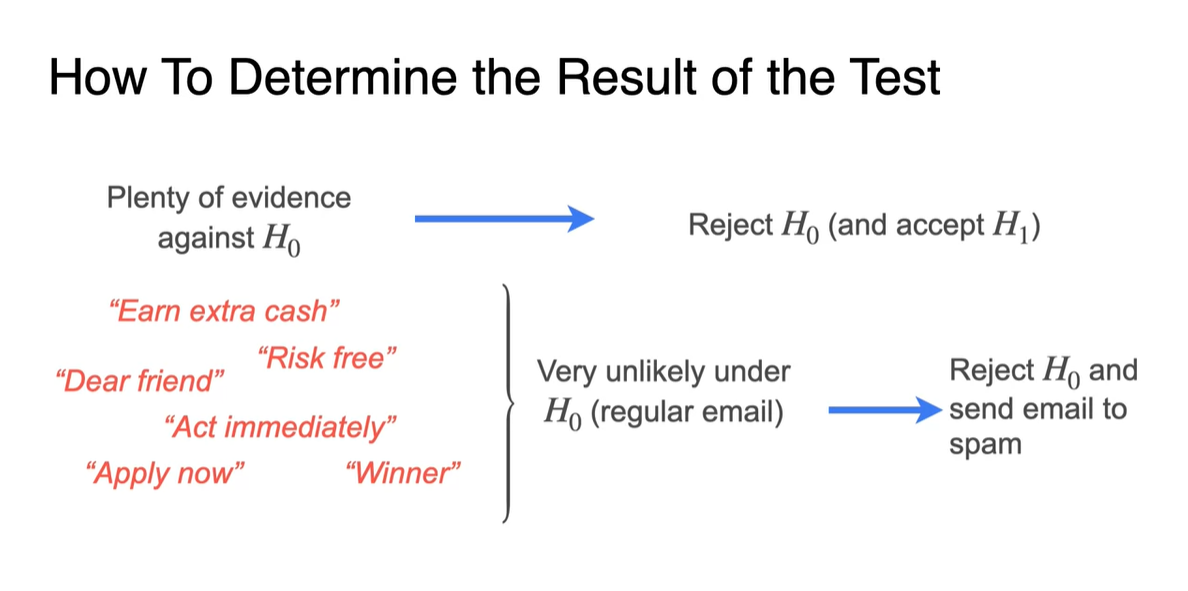
어떠한 표본이 귀무 가설 를 반대하는 증거를 충분히 입증했다면, 귀무 가설을 기각하고 대립 가설 을 받아들이게 된다.
-
예를 들면 "Dear Friend", "Risk Free"와 같은 trigger phrase가 나타날 때, Spam이 아닐 것이라는 귀무 가설을 기각할 만한 충분한 증거가 있다고 볼 수 있다.
- 다시 말해 Spam일 확률이 높다는 뜻이고, 그 즉시 귀무 가설을 기각하여 대립 가설인 spam 처리 항목으로 보내는 과정을 말하는 것이다.
-
Type I and Type II errors
-
Type I error와 Type II error에 대해 알아보자.
-
Type I error는 Ham 메일을 Spam 메일로 잘못 보낸 경우로, Positive를 False라 예측한 error를 말한다.
-
Type II error는 Spam 메일을 Ham 메일로 잘못 보낸 경우로, Negative를 False라 예측한 error를 말한다.
- 어느 경우가 더 wrong decision이라 받아들여 지는가?
-

-
Type I과 Type II error를 표로 나타내면 다음과 같다.
-
Not spam이라 가정한 positive 귀무 가설 을 기각했다면 Type I error, Spam이라 가정한 negative 귀무 가설 을 기각했다면 Type II error라고 한다.
- 그 외의 경우는 올바르게 예측했으므로 Correct 값이다.
-

-
Regular email을 spam으로 보내버릴 경우, 그 반대의 경우보다 더 worse하다.
-
어느 정도의 한계까지는 Type I error를 납득해줄 수 있을까?
→ 이에 대한 내용이 Significance level이다.
-

-
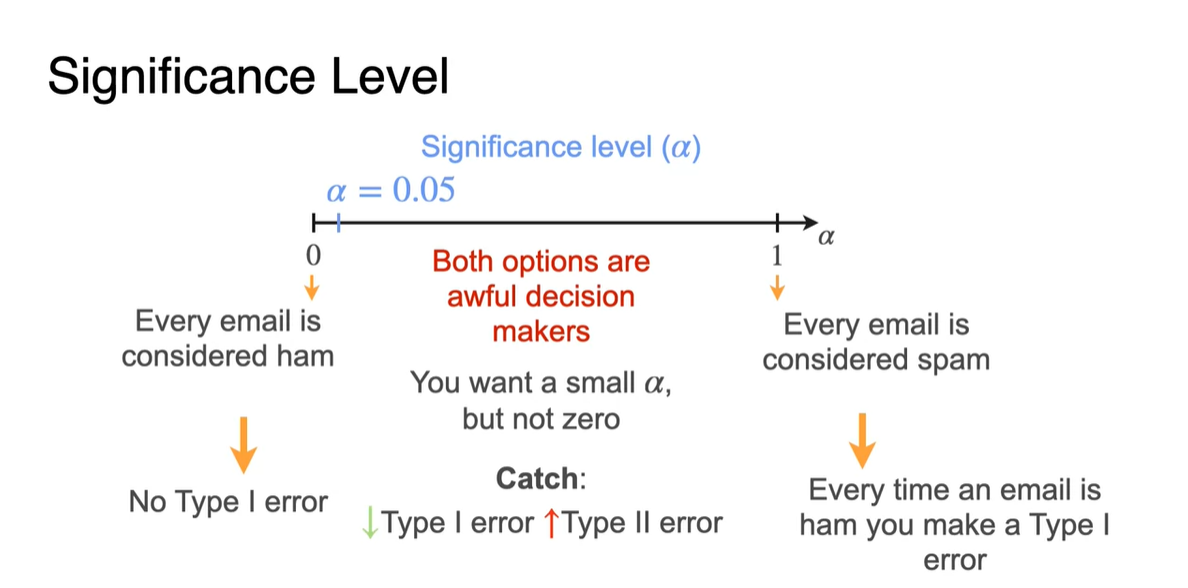
Significance level 가 0이라고 한다면 Email을 모두 ham으로 가정하였을 때, 한 개도 기각된 게 없다는 뜻이므로 관대하게 받아들일 수 있다. (No Type I error)
- 반면 Significance level 가 1이라면 Email을 모두 ham으로 가정하였는데, 모두 기각되었다는 뜻이므로 매우 화가 나는 상황일 것이다. (Every time Type I error)


-
일반적으로 우리는 정도의 수준까지는 용남할 수 있다고 판단한다.
-
즉, 귀무 가설을 5% 정도까지는 기각할 수 있을 때 좋은 귀무 가설과 대립 가설을 세웠다고 보며 가 small일수록 가정과 가까운 정답을 얻는다.
- 그런데 가 0에 가까우면 Type I error는 줄어드는 대신, Type II error이 커지기 때문에(Not ham, but spam) 이를 balance 있게 잘 잡아주는 것이 필요하다.
-
-
Significance level은 Type I error를 범할 최대 확률이며, 이는 귀무 가설 를 가정했을 때 이 가설이 기각될 최대 확률과 같다.
- 따라서 주어진 data을 기반으로, 를 거부할지 말지에 대한 여부를 결정하는 임계값이라 볼 수 있다.
A type I error occurs when we incorrectly reject the null hypothesis when it is actually true, while a type II error occurs when we fail to reject the null hypothesis when it is actually false.

Right-Tailed, Left-Tailed, and Two-Tailed Tests
-
아래와 같은 Heights Example을 보자.
- 18세 이하 10명의 Heights를 평균 내었더니, inches의 결과를 얻어내었다고 하자.
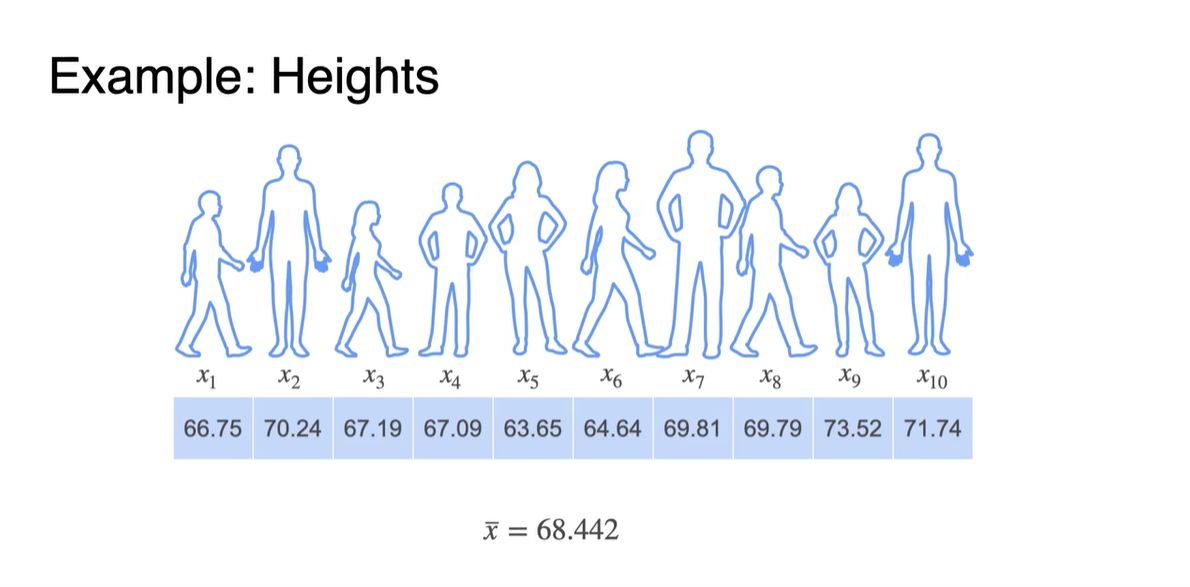
-
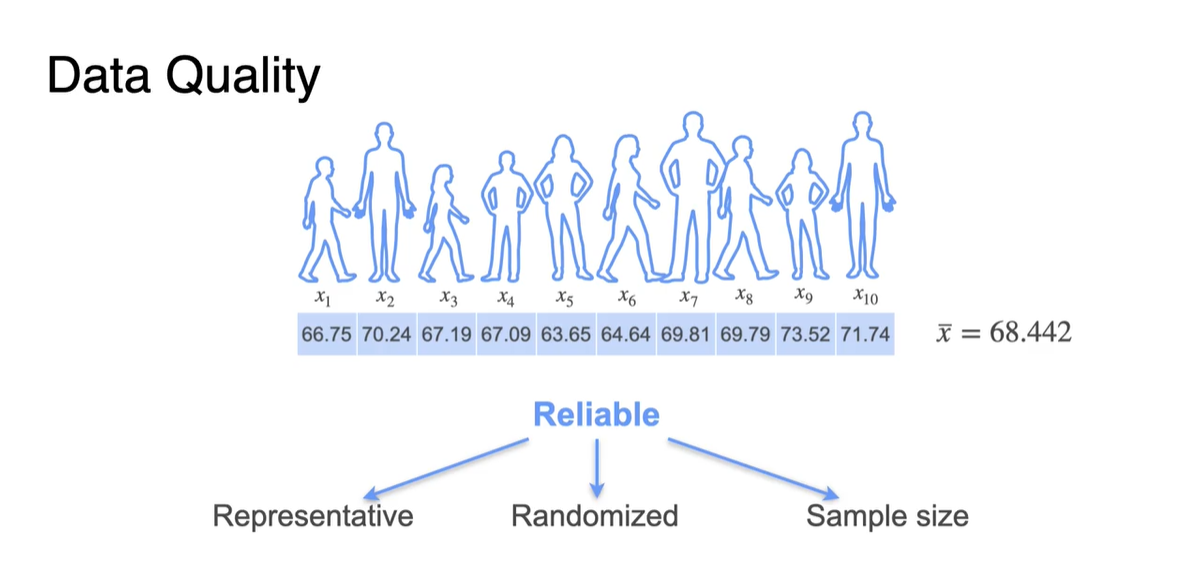
이 때 Data quality를 최대한 높게 유지하면서 Sample을 뽑으려면 다음 세 가지 조건을 만족시키며 추출하면 된다.
- Representative(표현력 있고), Randomized(랜덤 추출이며) Sample size가 충분히 커야 한다.
-
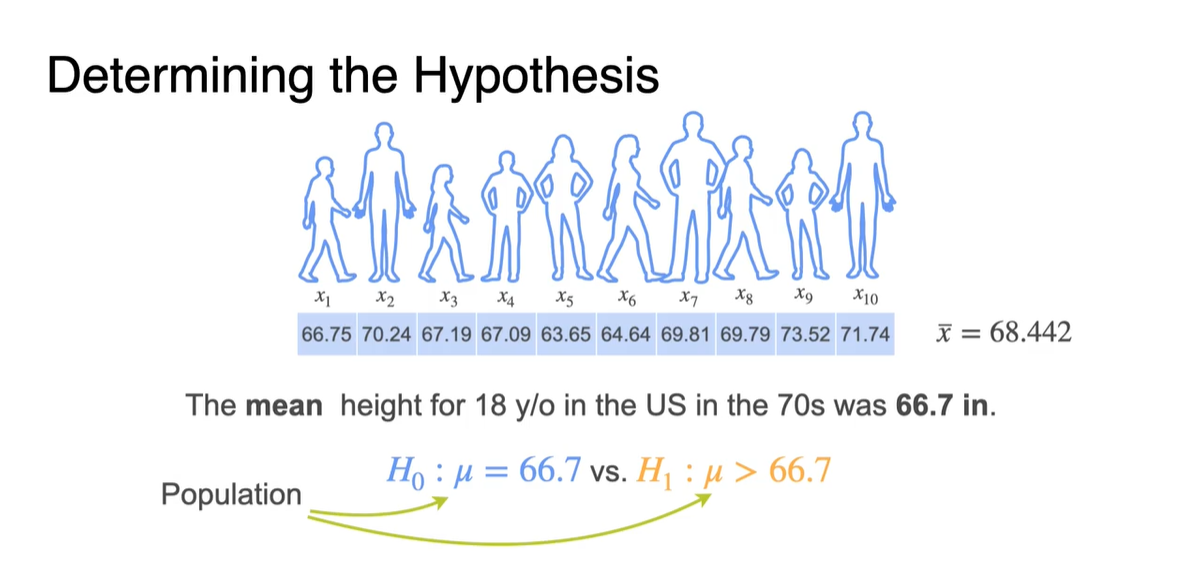
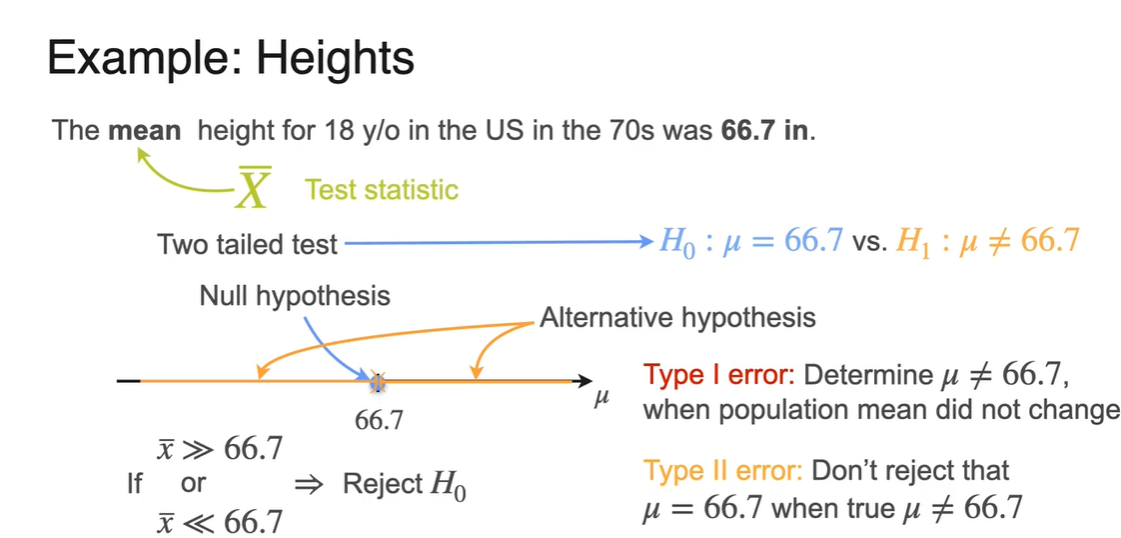
이제 70년대 US 사람들의 키 평균(66.7)에 관한 정보를 바탕으로 가정을 세워보자.
-
현재 아이들의 키가 70년대 아이들의 키 평균보다 커졌다는 주장을 하기 위해서는 다음과 같은 가정을 세워 검증해보아야 한다.
- Population의 mean이 변하지 않았을 것(66.7)이라는 귀무 가설 와 일 것이라는 대립 가설 를 세운다.
-
-
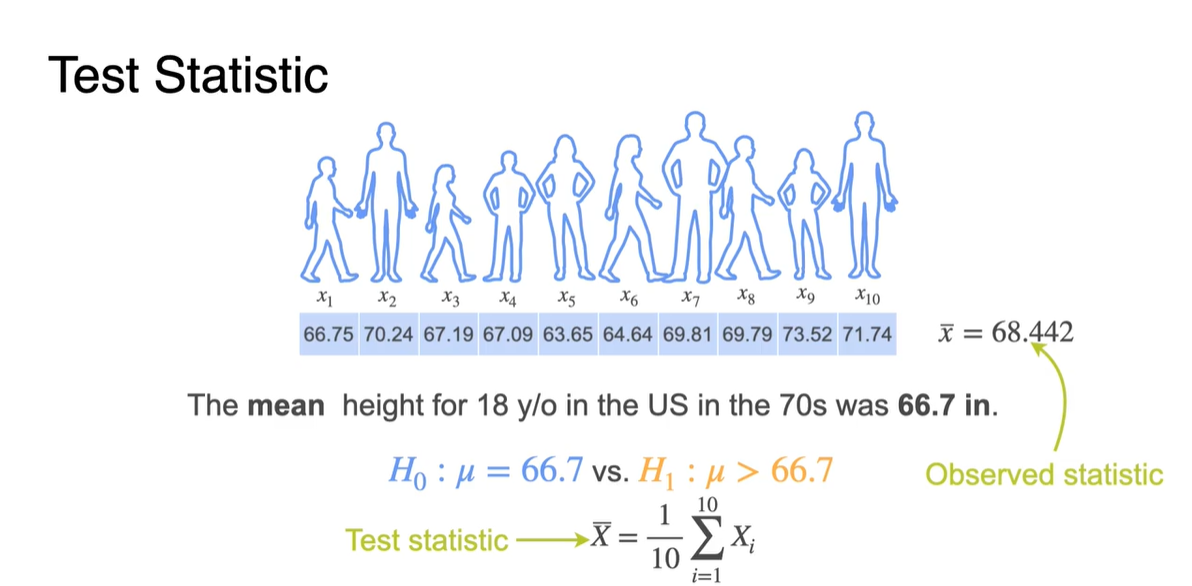
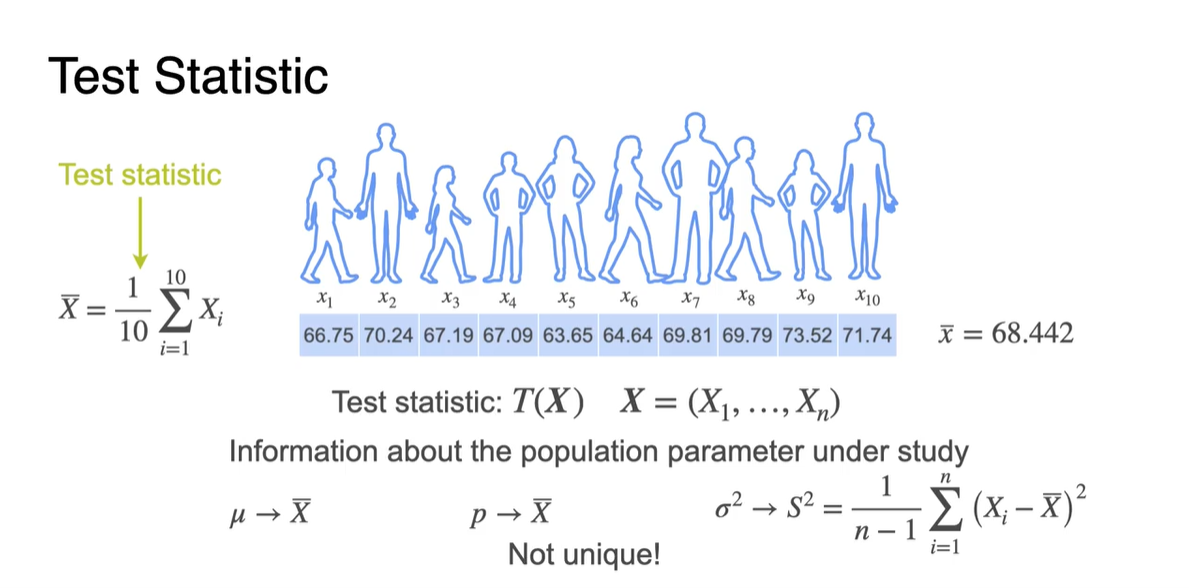
그런 다음 10명의 sample size를 가진 표본을 뽑아 이에 대한 평균 로 test해보자.
- 기존에 뽑았던 sample의 는 Observed statistic이며, 현재 뽑은 sample은 우리의 가정을 검증하기 위해 뽑아진 set이다.
-
Test를 위해 sample을 개만큼 더 뽑아 보자.
-
이러한 test set은 다음과 같은 세 가지 다양한(Not unique) 방법으로 population parameter를 추정할 수 있게 만들어준다.
-
따라서 검증하고 싶은 데이터의 특징에 따라 방법을 달리하여 test하면 된다.
-
-
일반적으로 다음의 3가지 questions를 통해 가설을 검증한다.
-
Right-Tailed Test → vs
-
Left Tailed Test → vs
-
Two-Tailed Test → vs
- 세 가정 모두 70년대와 비교하였을 때 키의 평균이 변하지 않았다는 우호적인 가정을 귀무 가설로 세운다.
-

-
Right-Tailed test는 다음과 같은 과정으로 이루어진다.
일단 sample이 population에 매우 근사하다는 가정 하에 를 얻어 test를 진행한다.
-
Null hypothesis(귀무 가설) 66.7을 기준으로 이보다 큰 키를 가진 sample mean이 나타날 경우 를 Reject한다.
-
Type I error는 population이 변하지 않았다는 가정 하에 sample mean이 을 얻을 때의 상황을 가리킨다.
-
Type II error는 sample mean이 을 가리킴에도 불구하고 귀무 가설 을 유지하는 것을 가리킨다.
-
-

-
Left-Tailed test는 위와 반대되는 과정으로 이루어진다.
-
Null hypothesis(귀무 가설) 66.7을 기준으로 이보다 작은 키를 가진 sample mean이 나타날 경우 를 Reject한다.
-
Type I error는 population이 변하지 않았다는 가정 하에 sample mean이 을 얻을 때의 상황을 가리킨다.
-
Type II error는 sample mean이 을 가리킴에도 불구하고 귀무 가설 을 유지하는 것을 가리킨다.
-
-

-
Two-Tailed test는 위의 두 가지 상황을 종합한 과정으로 이루어진다.
-
Null hypothesis(귀무 가설) 66.7을 기준으로 이보다 크거나 작은 키를 가진 sample mean이 나타날 경우 를 Reject한다.
-
Type I error는 population이 변하지 않았다는 가정 하에 sample mean이 일 경우를 가리킨다.
-
Type II error는 sample mean이 을 가리킴에도 불구하고 귀무 가설 을 유지하는 것을 가리킨다.
-
-
p-Value
-
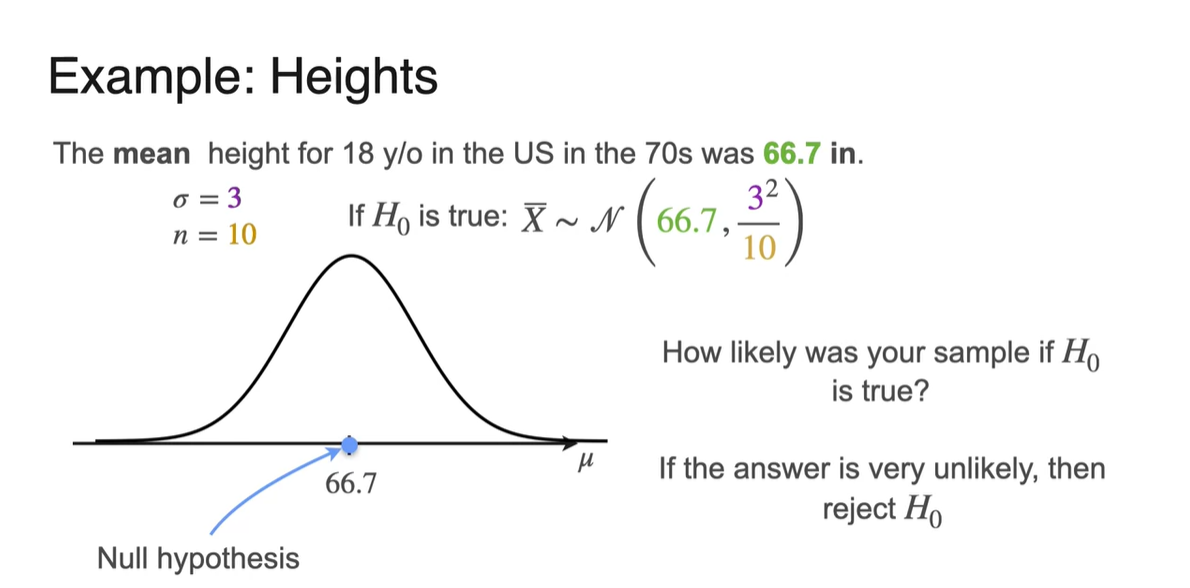
우리는 70년대 18세 이하의 키 평균인 66.7 inches라는 "정보"로부터 모집단의 평균이 여전히 변하지 않았다는 가정()을 세웠다.
-
모집단의 sample size가 이고 표준 편차가 (unknown, but known)이라면, 가 True일 때 해당 분포는 를 형성한다.
-
이 때 "가 참일 때 표본이 참일 것이냐?"에 대한 질문에 대답이 거의 불가능(unlikely)하다면 를 reject하는 근거가 된다.
- 그렇다면 를 reject하기 위한 증거의 기준을 어느 정도로 세워야 할까?
-
-
모집단의 분포를 Gaussian으로 가정하여 observation을 처리해보자.
-
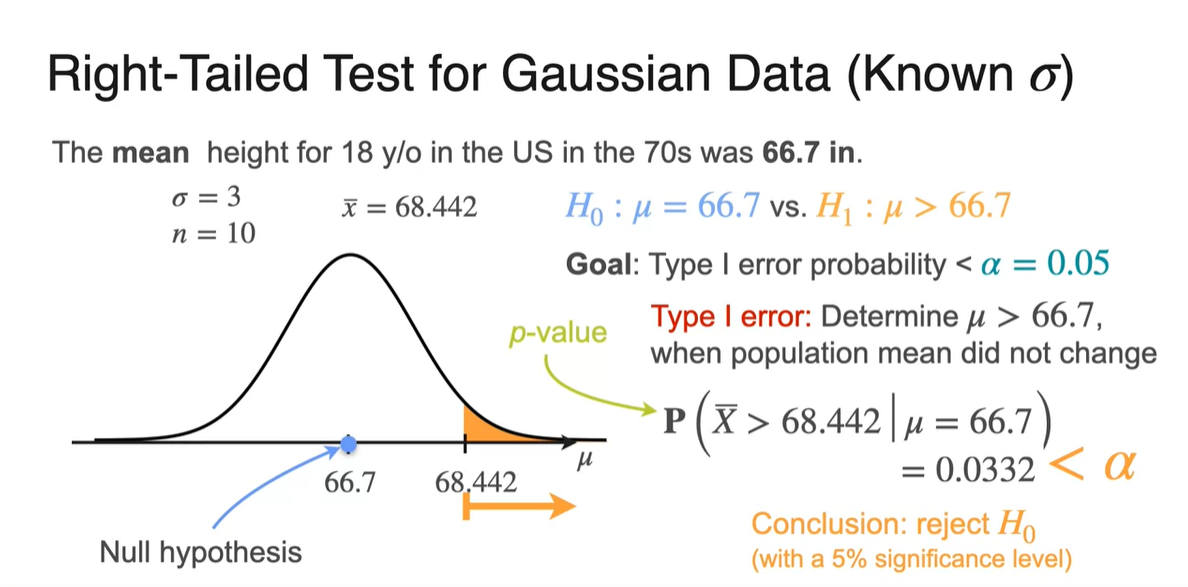
Significance level(유의 수준) 를 0.05로 설정하였다는 말은 어떠한 사건에 대한 확률이 0.05 미만이라면 Type I error로 보겠다는 말이다.
-
이를 목표로 하여 를 관측하였다면, 68.442보다 단순히 큰 값을 관측하였을 때의 모든 확률은 로 계산한다.
- 이는 모집단의 분포로부터 구해진 것이며 이 값을 -value라고 부른다.
-
현재 관측값의 -value가 0.0332로 계산되었으므로, 0.05보다 작은 값을 가지기 때문에 Type I error로 보아 을 기각하는 것이 합리적이라 판단한다.
-
-
-value란 가 True임을 가정하였을 때 test statistic이 가질 수 있는 값이 매우 극단적으로 벗어났을 때를 의미하는 확률값(probability)이다.
-
다시 말해, 관측값으로부터 으로 향하는 direction으로 모두 더한 확률값이다.
-
Decision rule은 다음과 같다.
- If -value < → reject , accept
- If -value > → don't reject
-

-
Right-tailed, Two-tailed, Left-tailed test는 다음과 그림과 같이 검정한다.
-
가 가정한 모집단의 분포이며 가 관측값의 통계치, 는 귀무 가설()로 세운 와 동일한 평균이다.
- 방향이 으로의 방향 즉, 를 reject하게 되는 방향이다. (Two-tailed)
-

-
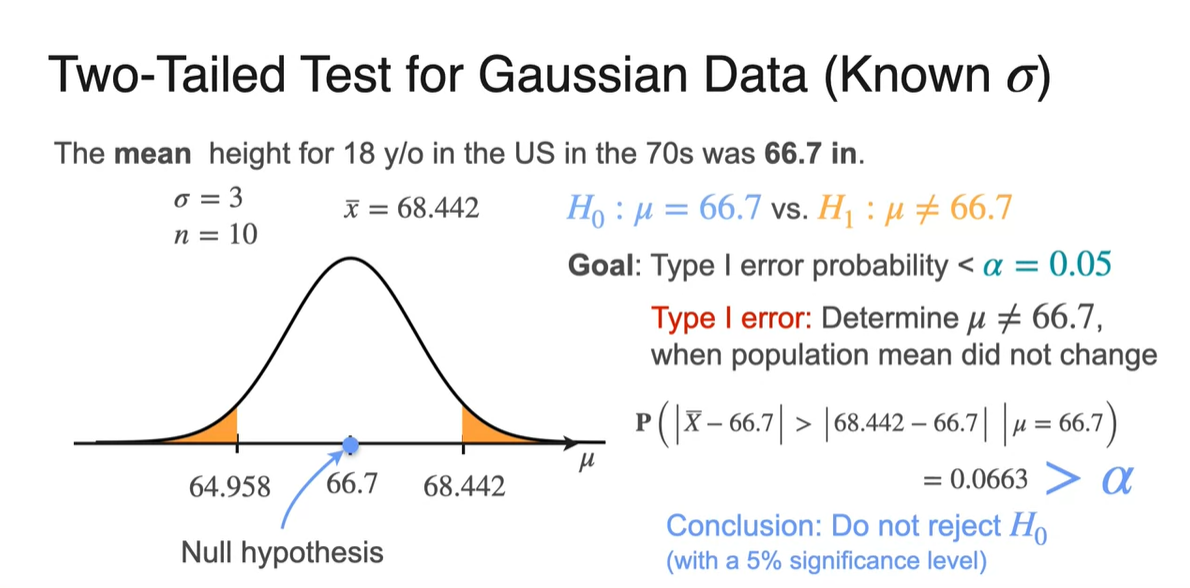
Two-tailed test에서의 -value 계산은 observed value인 68.442와 인 66.7의 차이만큼의 값을 양쪽에서 고려해야 한다.
- Significance level을 0.05로 똑같이 세워 검정하면 0.0663의 -value를 얻을 수 있고, 이는 보다 큰 값을 가지므로 를 reject하지 않는다.
-
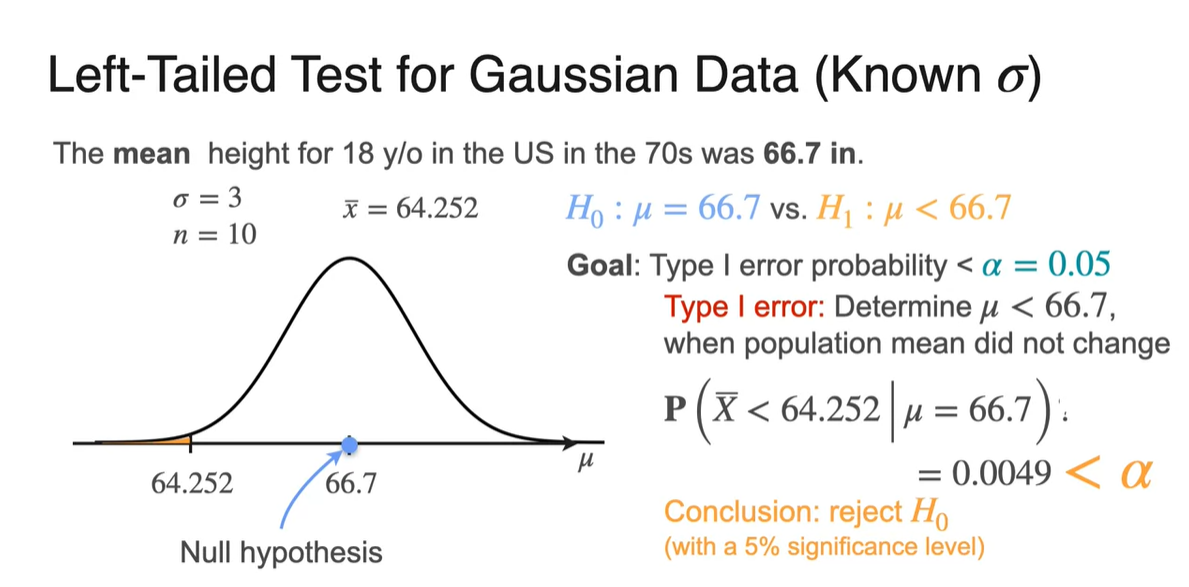
마지막으로 Left-tailed test는 Right-tailed test와 비슷하게 검정한다.
- 마찬가지로 -value가 0.05보다 작기 때문에 를 reject한다.
-
이제 -statistic으로 검정하는 방법에 대해 소개한다.
-
를 이용해 모집단을 gaussian으로 가정하고, 가 True임을 가정한다면 을 따른다.
- 로 standardization(정규화)하면 을 따른다.
-

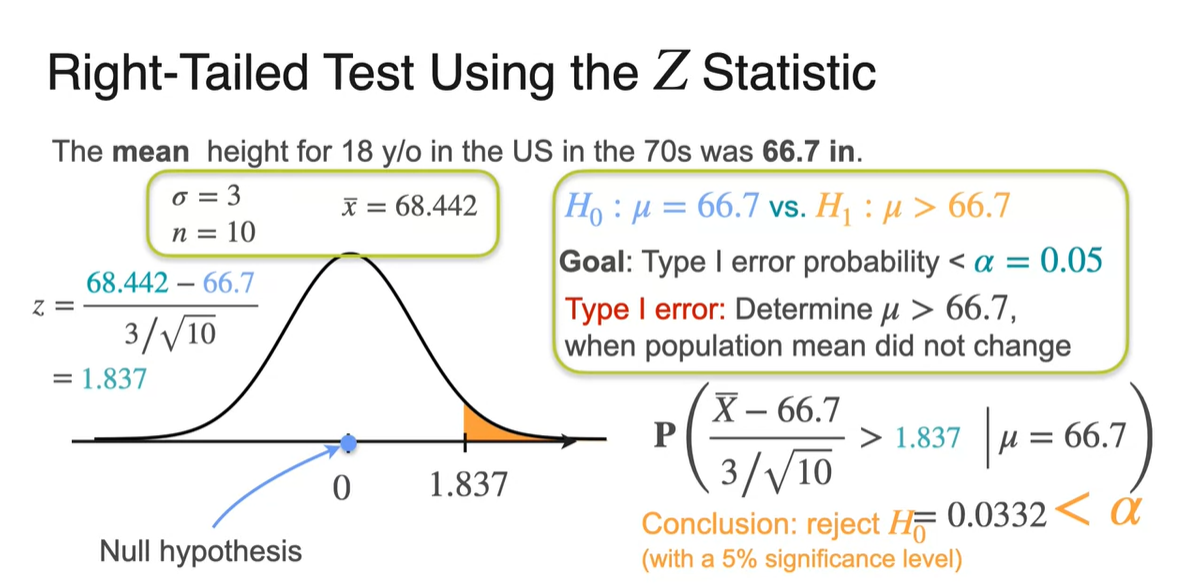
- Right-tailed test에서 를 계산해보자.

-
이는 기존 모집단 분포를 Standardizing한 분포에서, 초과의 확률을 -value로 구하는 것과 같다.
- 값을 활용하는 이유는 분포의 확률 테이블을 이용할 수 있기 때문에 더 쉽게 확률값을 계산할 수 있기 때문이다.
Critical Values
-
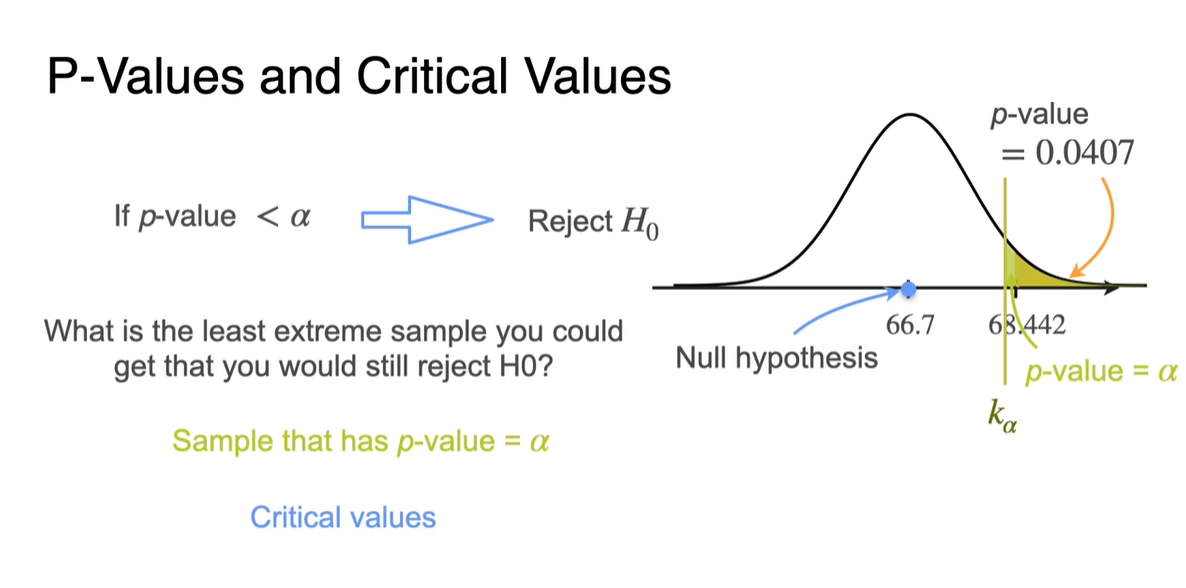
Critical Value란 Sample이 의 -value를 "딱" 가질 때의 variable을 말한다.
-
방금까지는 observation인 이상의 확률이 0.05를 넘네, 안 넘네의 검증으로 접근했다면, 이번에는 -value일 때의 observation을 계산해보는 것이다.
- 이를 의 notation으로 표현하겠다.
-
-
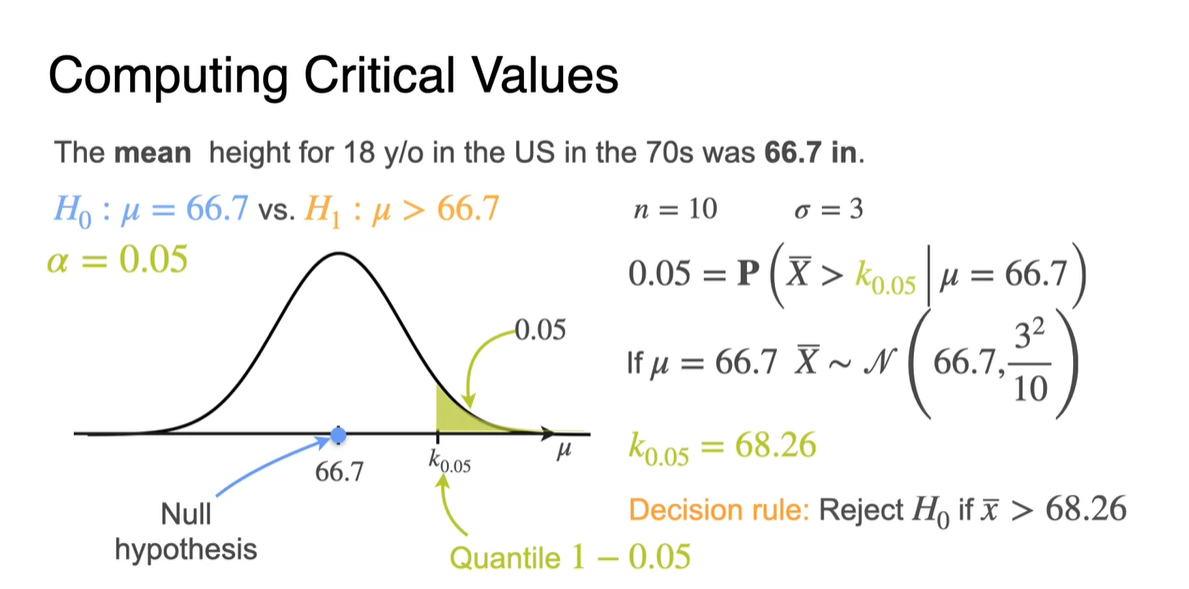
가 0.05라면 1-0.05의 quantile 값을 critical value 로 명칭한다.
-
로 수식 전개하면 임을 얻어낼 수 있다.
- 따라서 어떠한 observation 가 68.26을 벗어난다면, 는 즉시 기각된다.
-
-
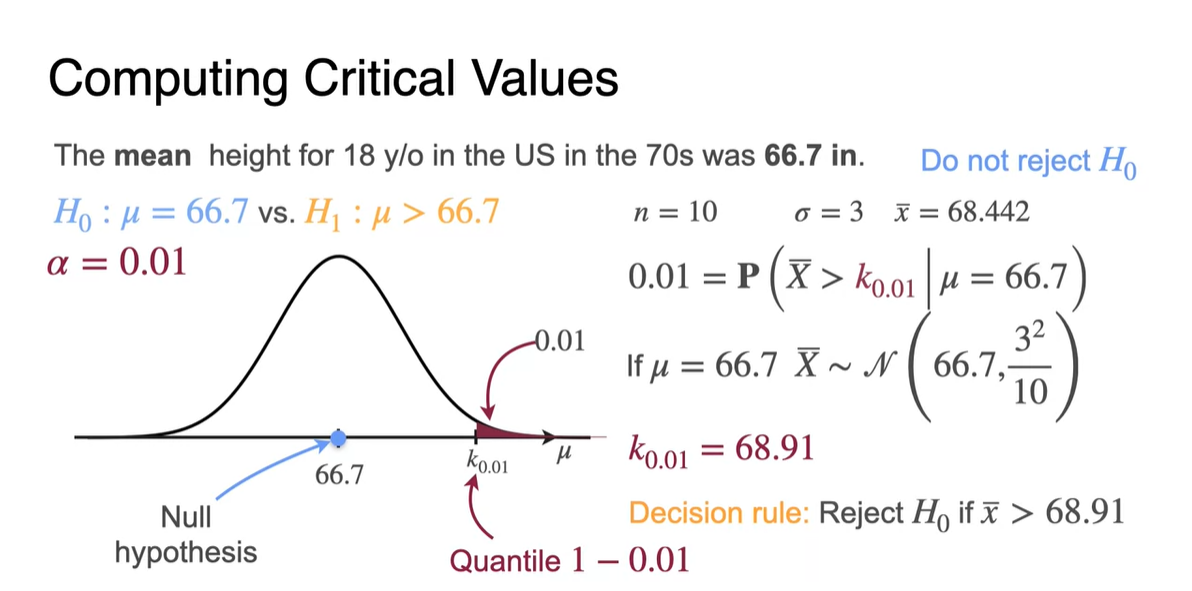
가 0.01이라면 1-0.01의 quantile 면적은 이전보다 확 줄어든다.
이는 가 0.05일 때보다는 관측값을 더 관대하게 바라보겠다는 의미로 받아들이자.
- Critical value인 -value 은 68.9로 계산되며, 이보다 큰 키의 평균이 나온다면 는 즉시 기각될 수 있다.
-
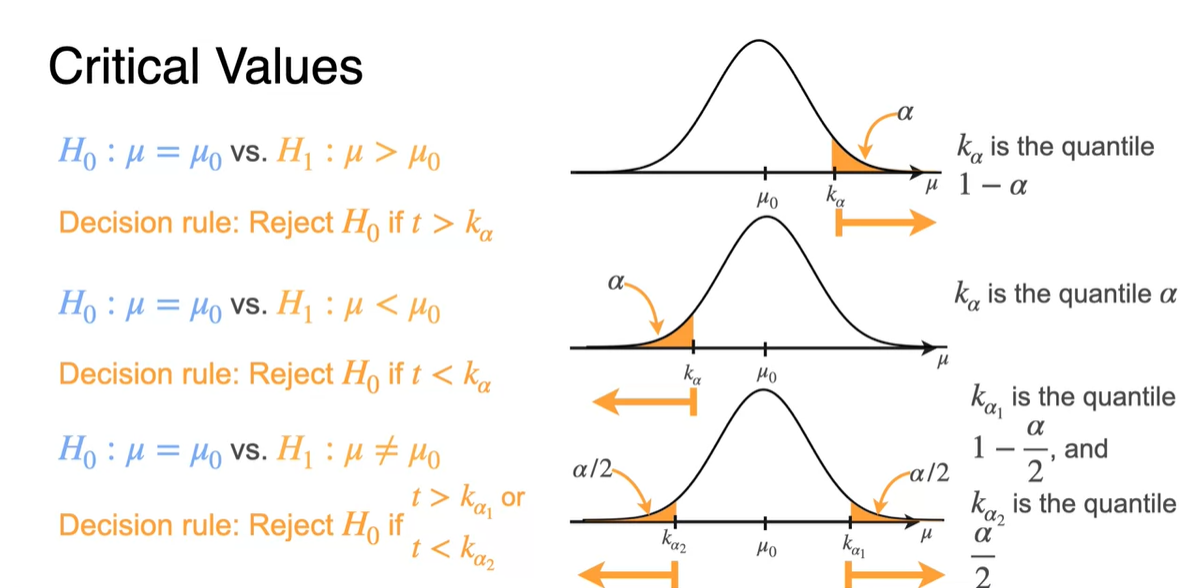
Right-tailed, Left-tailed, Two-tailed의 test는 아래와 같은 각각의 notation으로 critical values를 찾아낼 수 있다.
- Two-tailed test는 를 절반 나눠서() 계산한다.
-
-value와 cricical values 접근법은 모두 Hypothesis를 검정하는 동일한 방법론이다.
- 특히 cricical values 접근법은 데이터를 모두 모은 뒤 검정하기 쉬운 방법론이기 때문에 Type II error를 찾아내기에도 유용하다.

Power of a Test
-
지금까지는 라는 귀무 가설을 기반으로 Type I error만 중점적으로 다뤘었다.
- Type II error는 이 False일 때 귀무 가설 가 기각되지 않는 경우를 의미하는 또 다른 유형의 오류이므로 이에 대해 좀 더 자세히 알아보자.

-
방금까지는 가 0.05일 때의 -value로 critical value를 산정하여, Decision rule을 계산하면 "관측값 가 68.26 이상일 때 를 기각"하는 것으로 판단했었다.
-
Type II error는 일 때 을 기각하지 않는 상황으로 예를 들 수 있다.
-
가 66.7이 아니라 70이라는 자체가 의 가정이 틀렸다는 것을 의미하기 때문이다.
-
따라서 우리는 값을 구해 Type II error의 확률을 결정한다.
-
-

-
임을 가정했으므로 Type II error는 분포로부터 계산되어야 한다.
-
즉, observed value(sample)에 영향을 받지 않고 오로지 Hypothesis의 분포에 따라 확률값이 산정된다는 것이다!
- 은 0.0333으로 계산되며 이 값을 우리는 라는 notation으로 설정한다.
-

-
Power of the Test는 가능한 인(가 아닌) 모든 에 대하여 를 reject할 모든 확률을 말한다.
- 아래 table 값 중에서도 가 False임을 가정할 때 가 reject되는 경우의 evidence(correct)가 매우 유용하게 쓰인다.

-
Type II error는 이며 라는 값으로 산정했었다.
-
Power of the Test는 라서 Type II error와 상호보완적 관계이며 와 같다.
- 다시 말해 Power of the Test와 Type II error는 와 의 관계를 가진다.
-

-
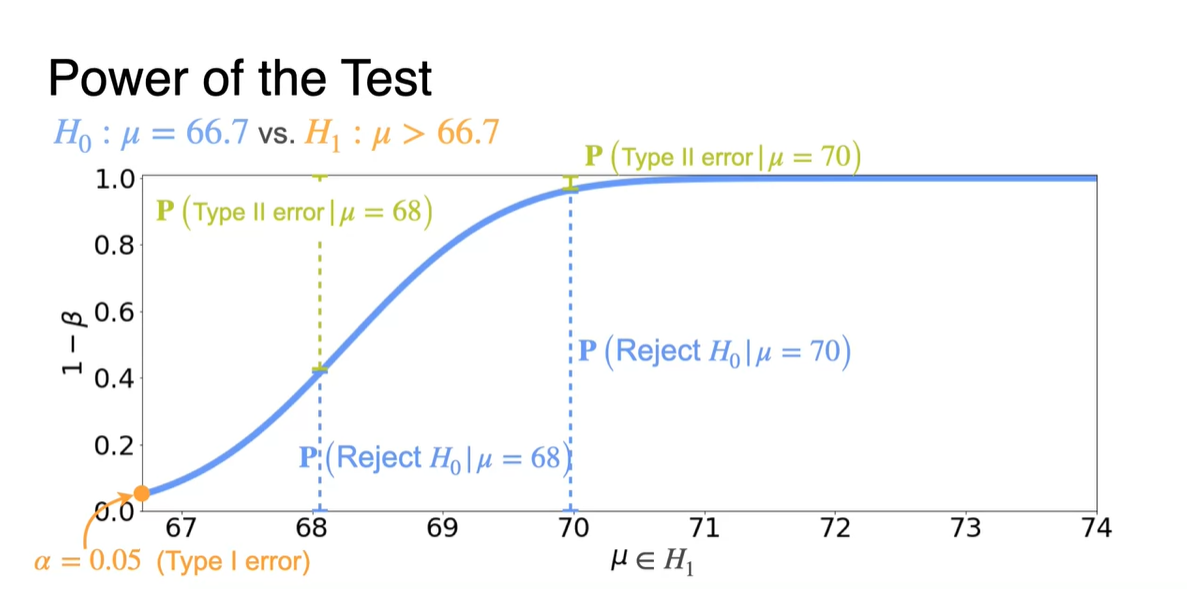
아래 그림은 에 따른 Power of the Test() 그래프를 나타낸다.
-
가 68일 때와 70일 때를 가정하였을 때, 이 reject될 확률은 Power of the Test 값이다.
- Type II error는 와 같으므로 y축의 위에서부터 내려오는 간격에 해당한다.
-
또 한 가지 재밌는 사실은 가 극단적일수록 값이 1에 가까워진다는 것이다.
- 이는 가 표본 평균 분포의 평균을 결정하기 위한 모집단의 평균이므로 의미있는 관측이라 볼 수 있다.
다시 말해, 가 초반 모평균으로부터 극단적으로 멀어질수록 Type II error 즉, 기존 가설 를 reject하지 않을 확률이 적다는 얘기다. → Reject할 확률 ↑
-
-
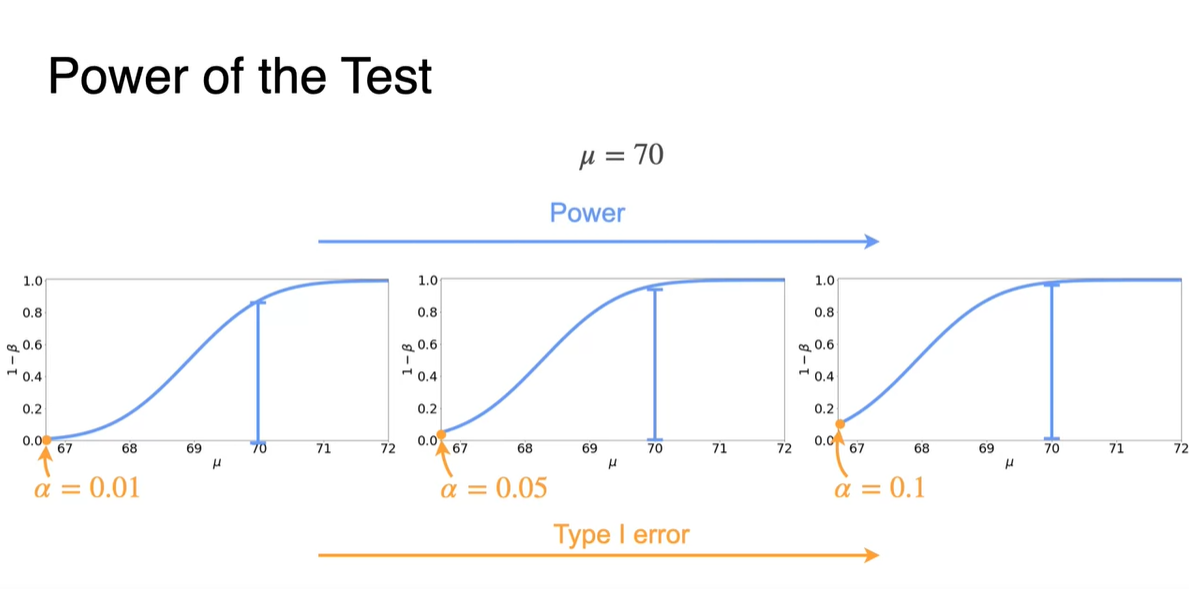
이번에는 값에 따른 Power of the Test 분포의 차이를 보여준다.
-
가장 왼쪽 값의 값이 가 증가함에 따라 커지며, 이 지점의 Power of the Test 값은 바로 Type I error다.
- 이는 관측값을 Hard하게 바라볼수록 값은 커진다는 뜻이며, 이에 따라 Type I error일 확률이 커진다는 것을 의미한다.
-
-
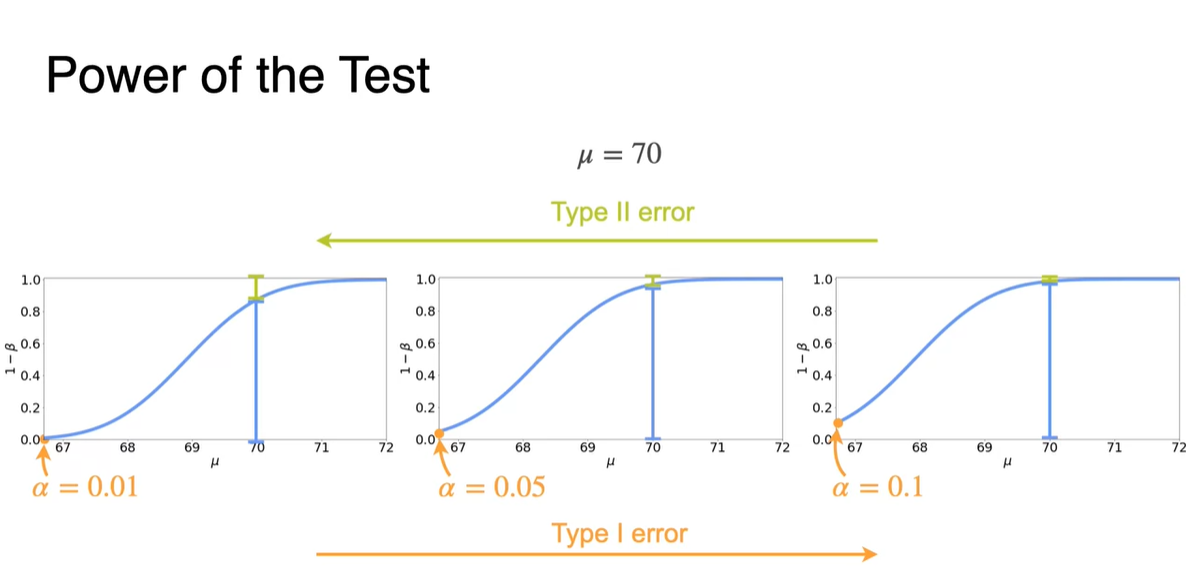
Type II error의 경우 위와 반대로 해석한다.
- 관측값을 관대하게 바라볼수록 값은 작아지며, 초기 Hypothesis 설정에 문제가 생길 확률이 커져 Type II error 확률이 커진다는 것을 의미한다.
Interpreting Results
-
Hypothesis Testing의 절차(step)에 대해 정리해보자.
-
Hypothesis를 설정한다.
- Null hypothesis가 baseline이다. →
- Alternative hypothesis는 우리가 증명하고자 하는 진술이다. →
-
Test를 design한다.
- Test statistic을 설정한다. →
- Significance level을 설정한다. →
-
Sample로부터 observed된 표본 평균을 활용하여 검정한다. →
-
데이터를 기반으로 결정을 내린다.
- 만약 -value가 significance level보다 작다면 를 reject한다.
- 그러나 이는 생각만큼 간단하지 않고, 종종 실수를 할 수 있기 때문에 어려운 일이다.
-

-
지금까지 배운 내용을 정리해보자.
- Type I error(): Null hypothesis가 참일 때 가 reject된 경우
- Type II error(): Null hypothesis가 거짓일 때 가 reject되지 않은 경우
- Significance level(): Type I error가 최대인 확률
- Error: ↓ ↑ (반비례)

-
몇 가지 misconception에 대해 정리해보자.
-
우리는 -value를 바탕으로 의 기각 유무를 결정하기 때문에, -value가 곧 가 참임을 보증하는 것이라 오해할 수 있다.
- 그러나 이는 올바른 명제가 아니다.
-

-
또한, 를 기각하지 않는다고 해서 가 무조건 참이라는 뜻도 아니다.
- 이는 아직 enough evidence가 쌓이지 않았기 때문이라 해석하는게 좋다.

t-Distribution
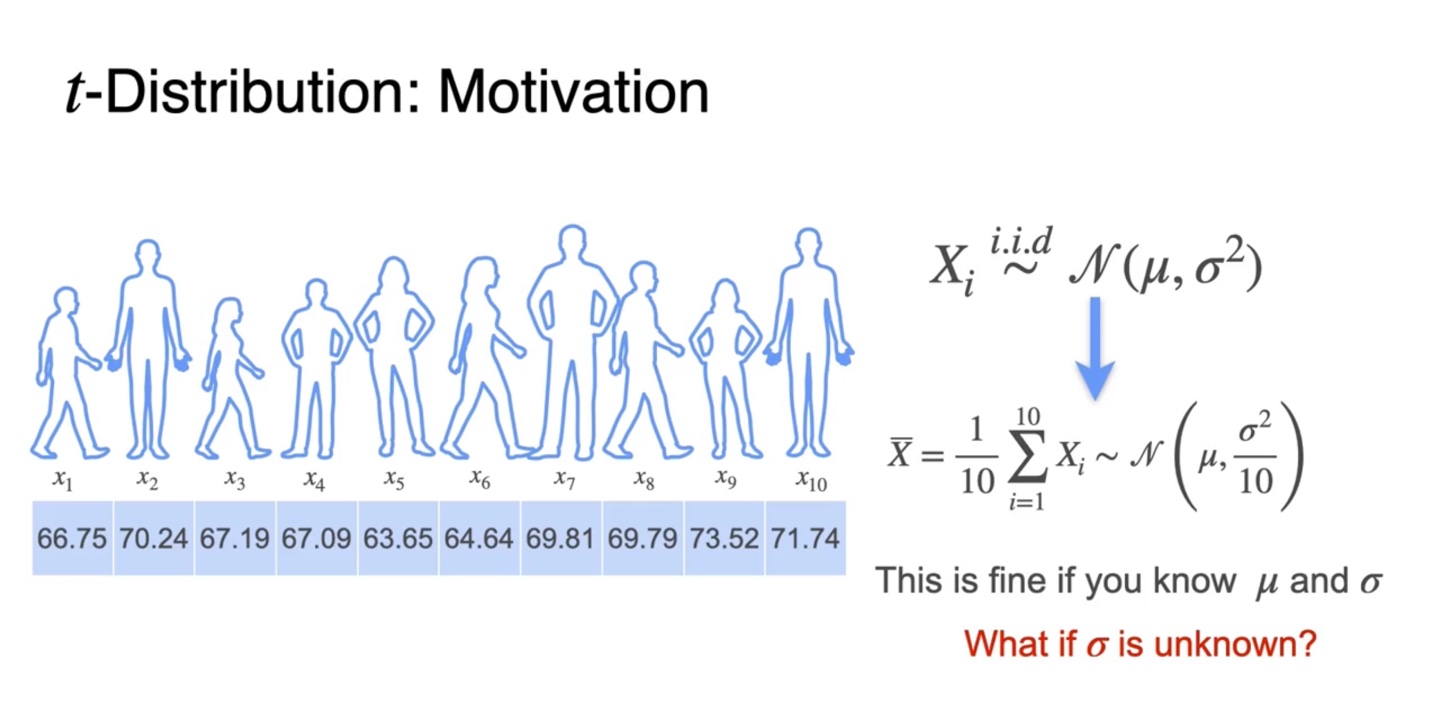
-
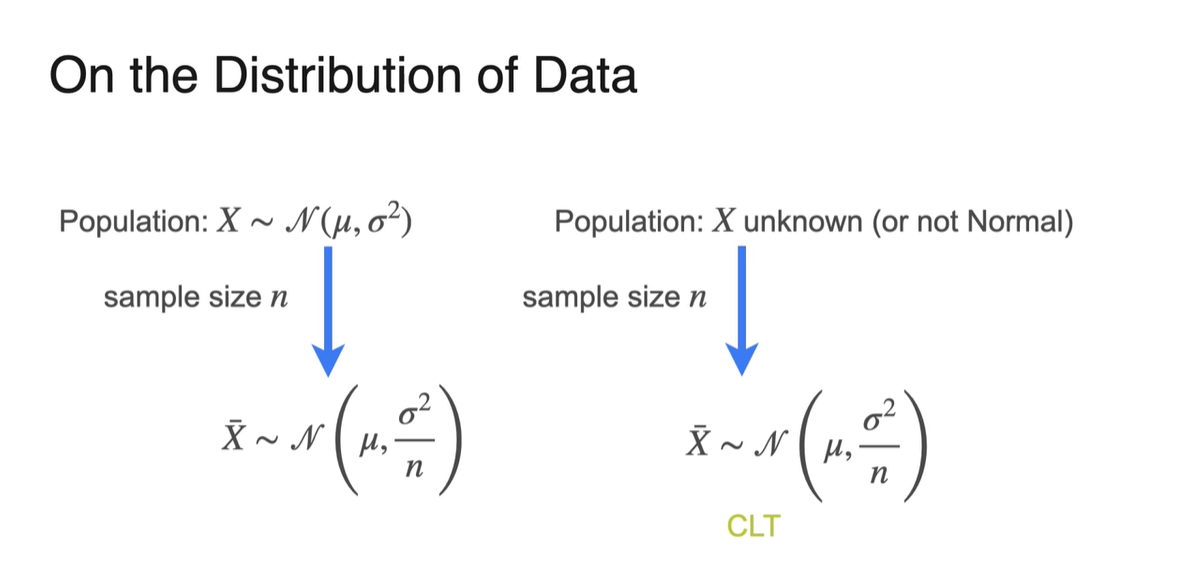
지금까지 우리는 모집단의 가 i.i.d하게 뽑혔을 때 를 따른다면, sample mean이 를 따른다고 말할 수 있었다.
- 그러나 이는 어디까지나 를 알 때의 경우이며 가 unknown 상황일 때에는 student 분포인 t-distribution을 이용해야 한다.
-
Student t-distribution은 대신 의 notation을 갖는 값을 이용한다.
-
모집단의 알려진 표준 편차 를 이용하면 (standardization)를 따랐다.
-
그러나 student t-distribution을 이용하면 가 현재 상황에서는 를 따른다고 보장할 수 없다.
-

-
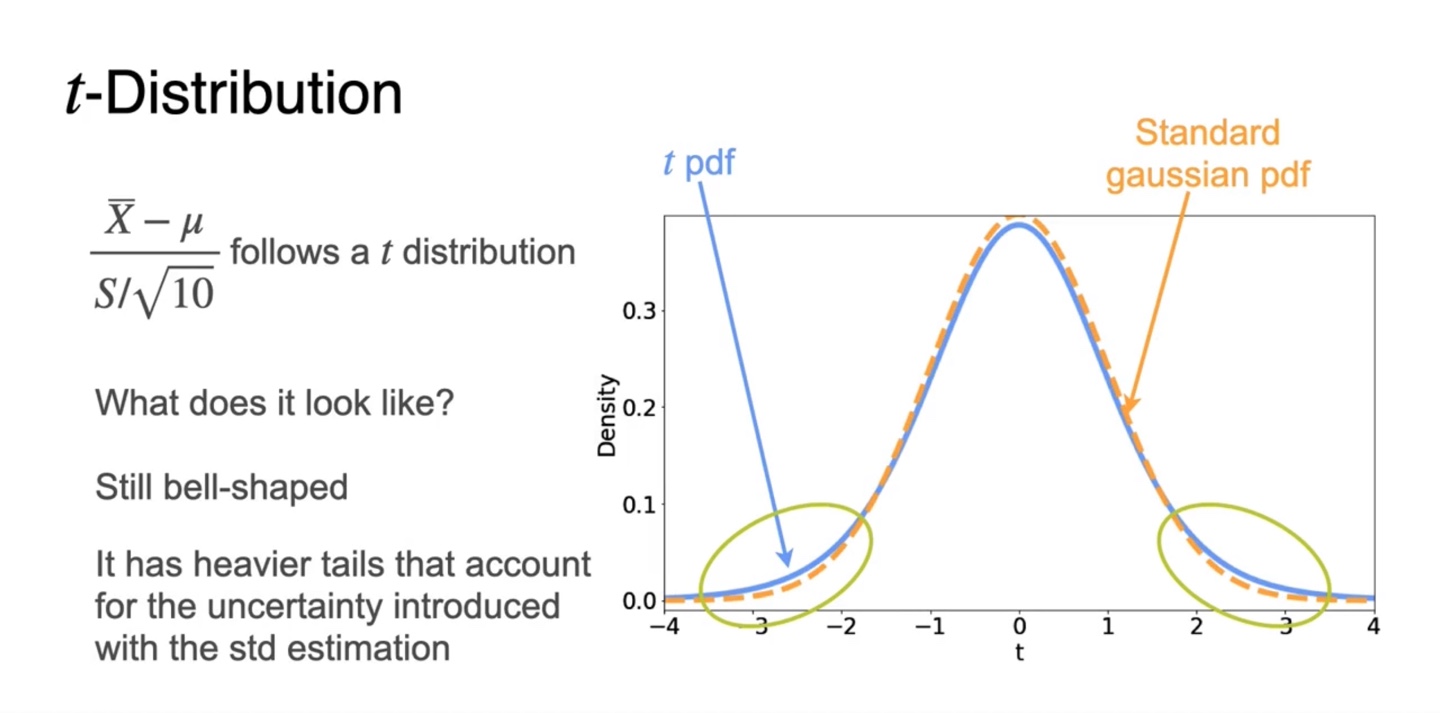
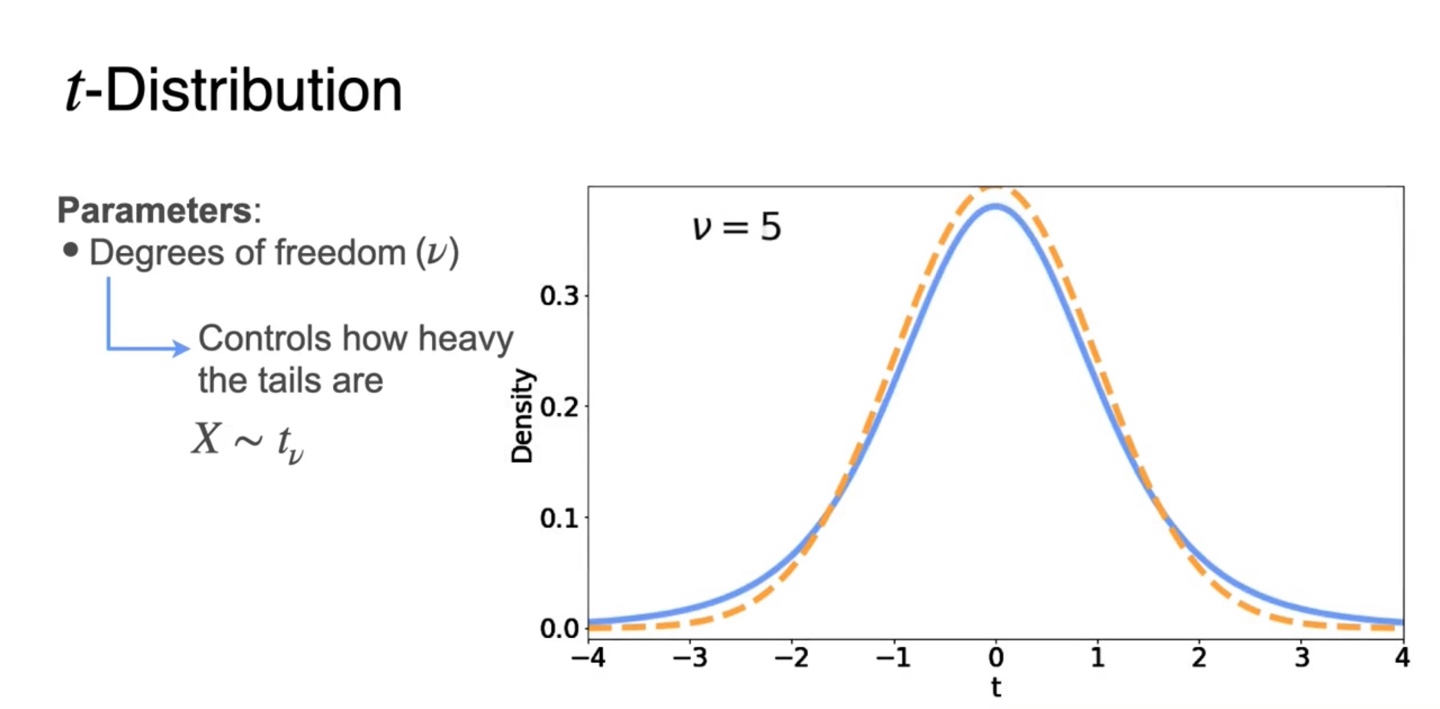
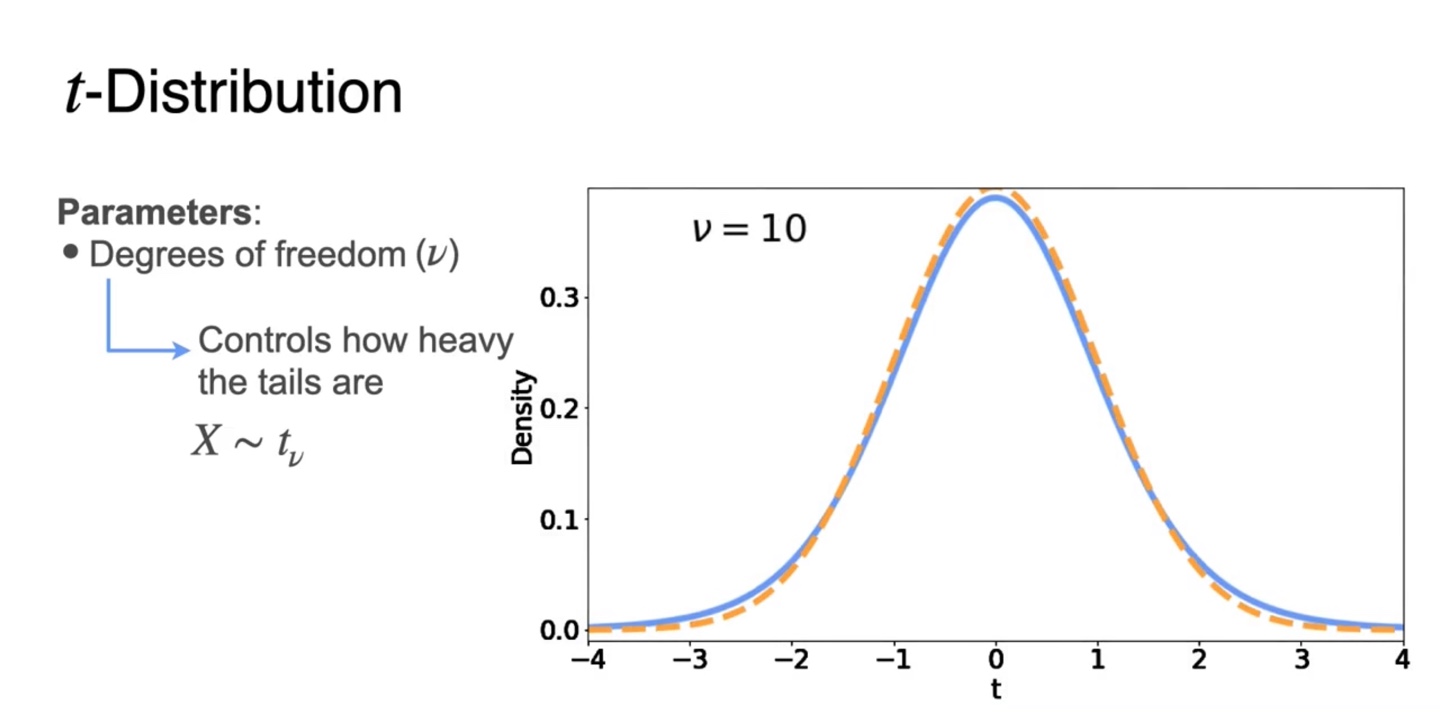
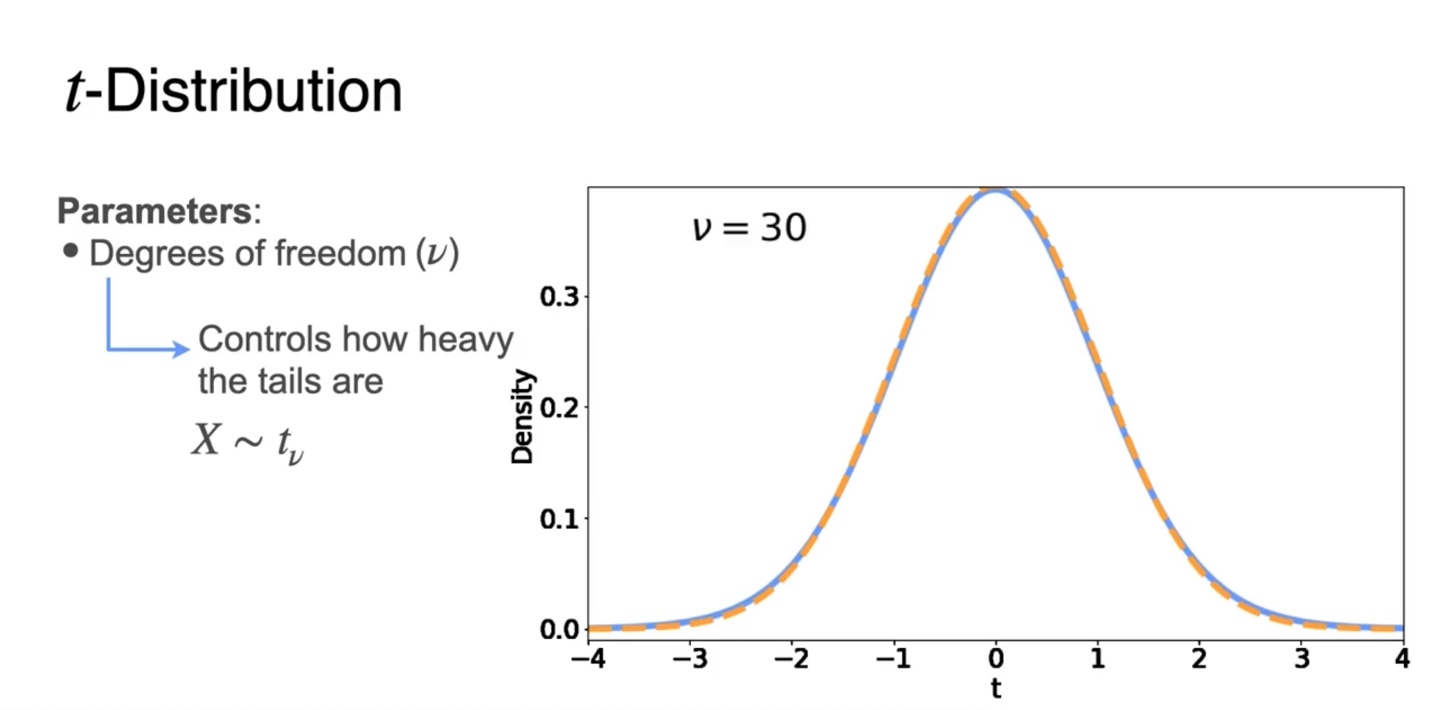
Standard gaussiang pdf와 t pdf를 비교한 그래프를 보자.
- 두 분포 모두 bell-shaped를 띄지만 t 분포가 조금 더 tails가 heavy하다.
-
이 때 우리는 Degrees of freedom()를 설정하여 분포를 설명한다.
-
를 따른다면 에 따라 tail의 heavy 정도를 조절하는 것이다.
- 가 커질수록 분포는 gaussian에 가까워지며 으로 커질때쯤 거의 gaussian이라 가정해도 충분할 정도다.
-
-
Degrees of freedom()은 sample size에만 영향을 받는 값이다.
- 로 설명할 수 있으며, 이 클수록 T-statistic을 gaussian 분포로 가정할 수 있다.

t-Tests
-
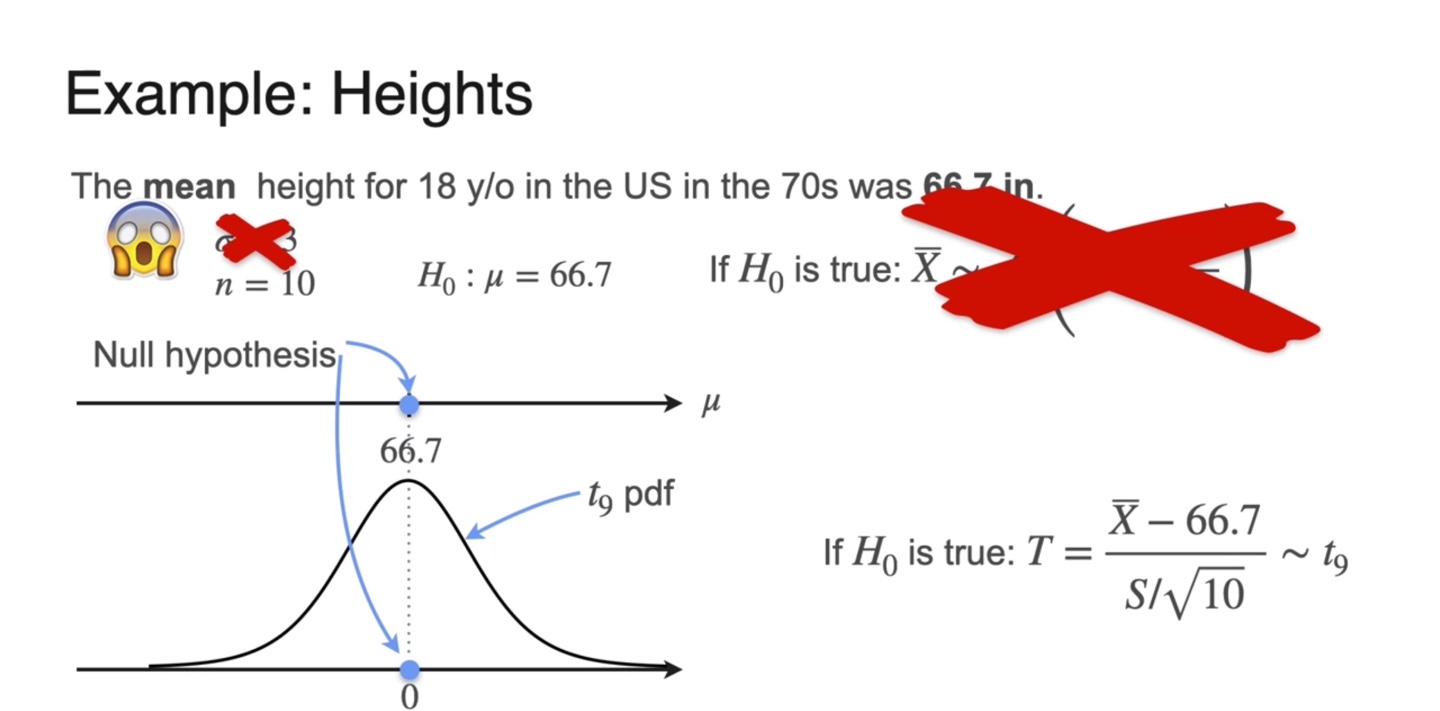
앞서 다뤘던 Heights 예제에서는 가 를 따른다고 이야기할 수 있었지만 를 알 수 없는 상황에서는 T-statistic을 활용해야 한다.
- 이제 를 구해 pdf로 Null hypothesis를 검정할 것이다.
-
Right-tailed test (unkonwn )는 아래와 같이 해결한다.
-
먼저 observed mean 로부터 의 를 이용해 를 구한다.
-
-value는 로 계산되었으며, 보다 큰 값을 가지기 때문에 를 reject하지 않는다.
-
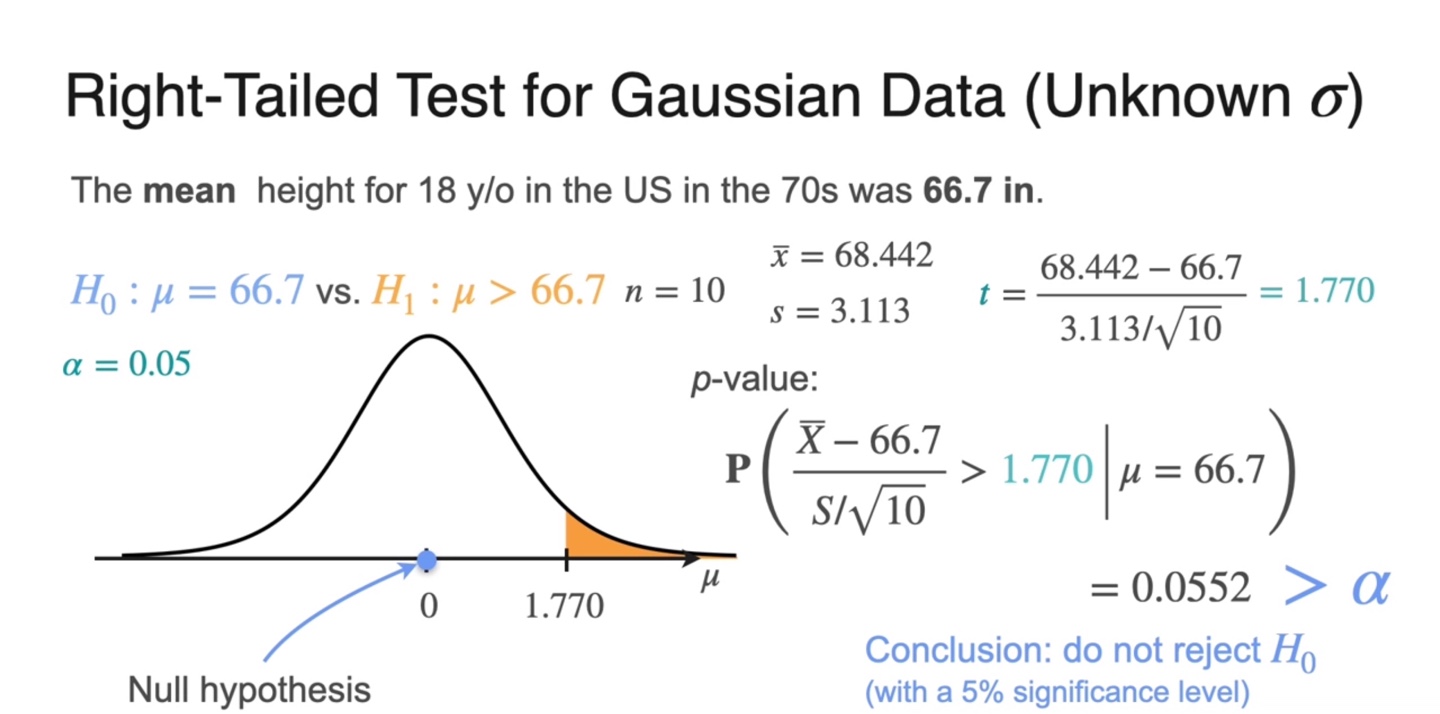
-
Two-tailed test (unkonwn )는 아래와 같이 -value를 계산한다.
-
로 계산되었으며, 보다 큰 값을 가지기 때문에 를 reject하지 않는다.
- Two-tailed test에서는 -value가 한 쪽만 고려할 때보다 2배만큼 커진다.
-
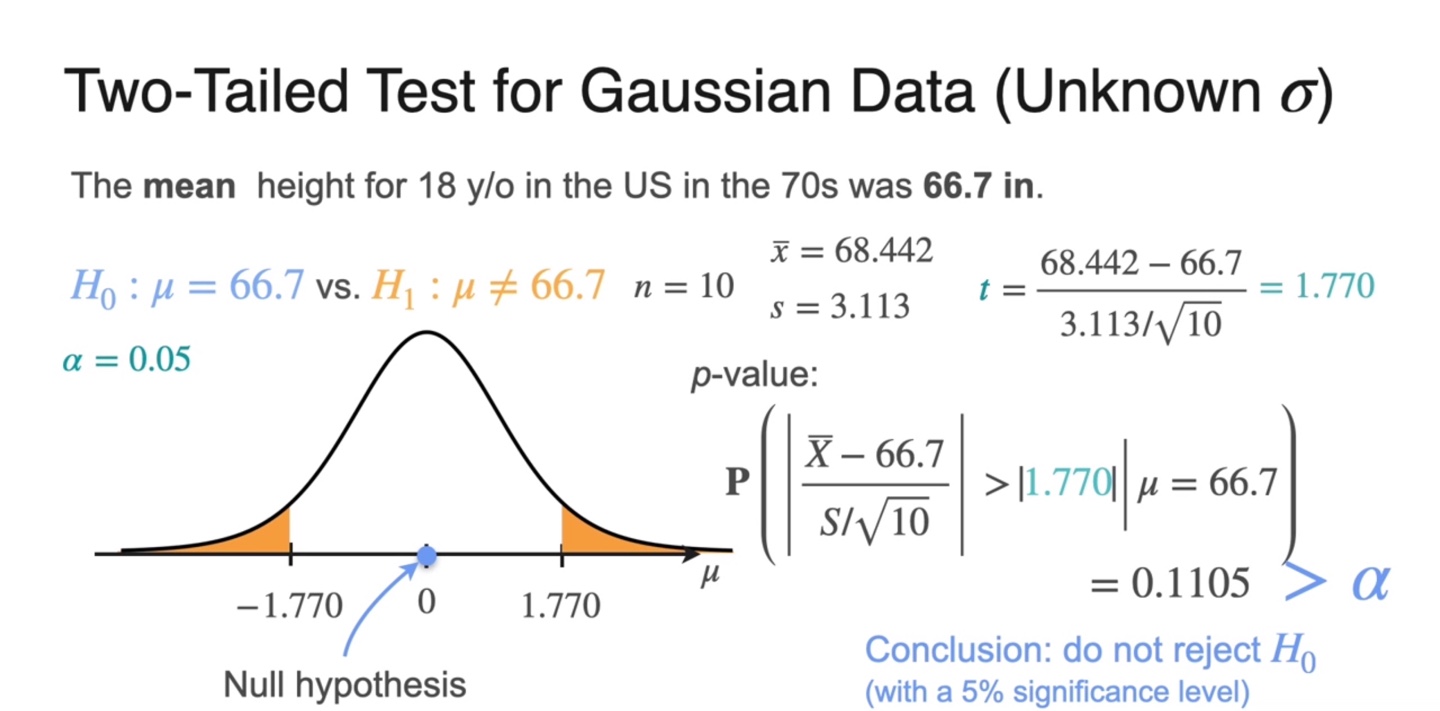
-
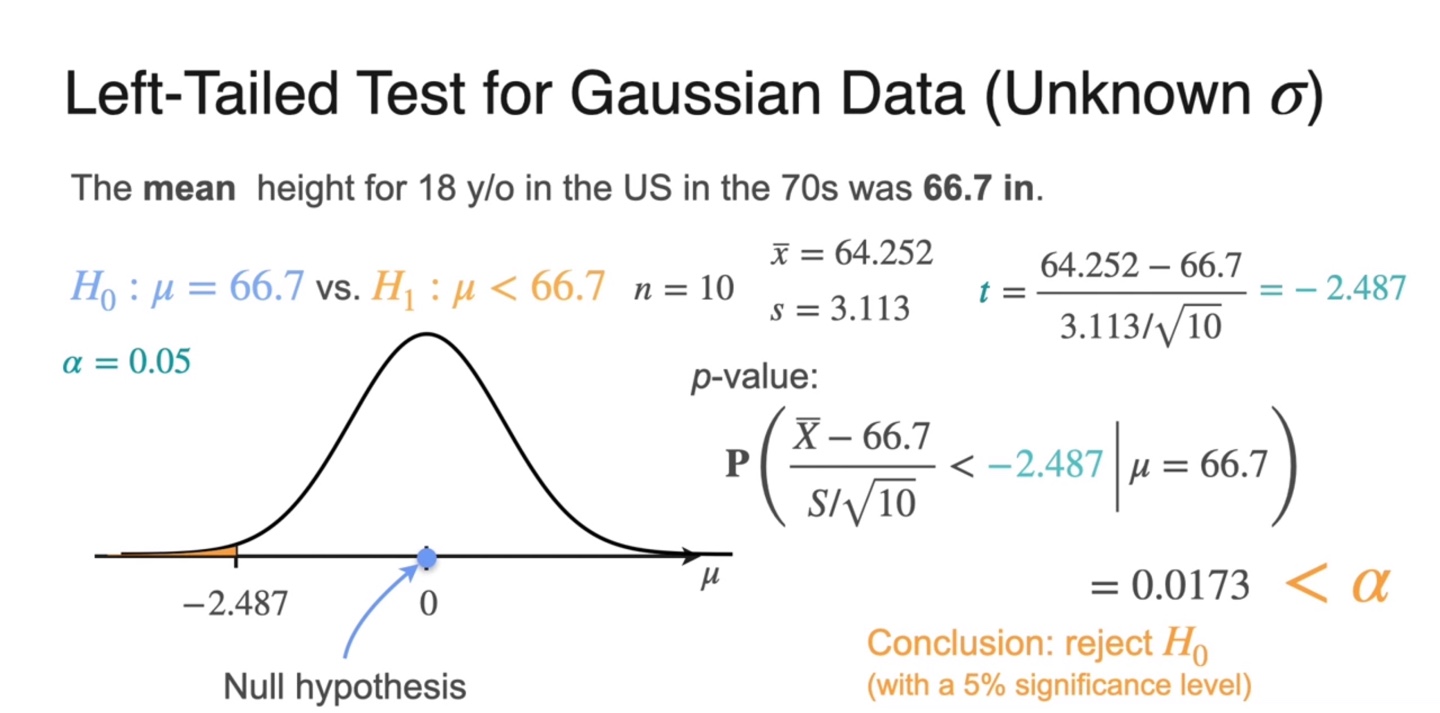
Left-tailed test (unkonwn )는 아래와 같이 -value를 계산한다.
- 으로 계산되었으며, 보다 작은 값을 가지기 때문에 를 reject한다.
Two Sample t-Test
-
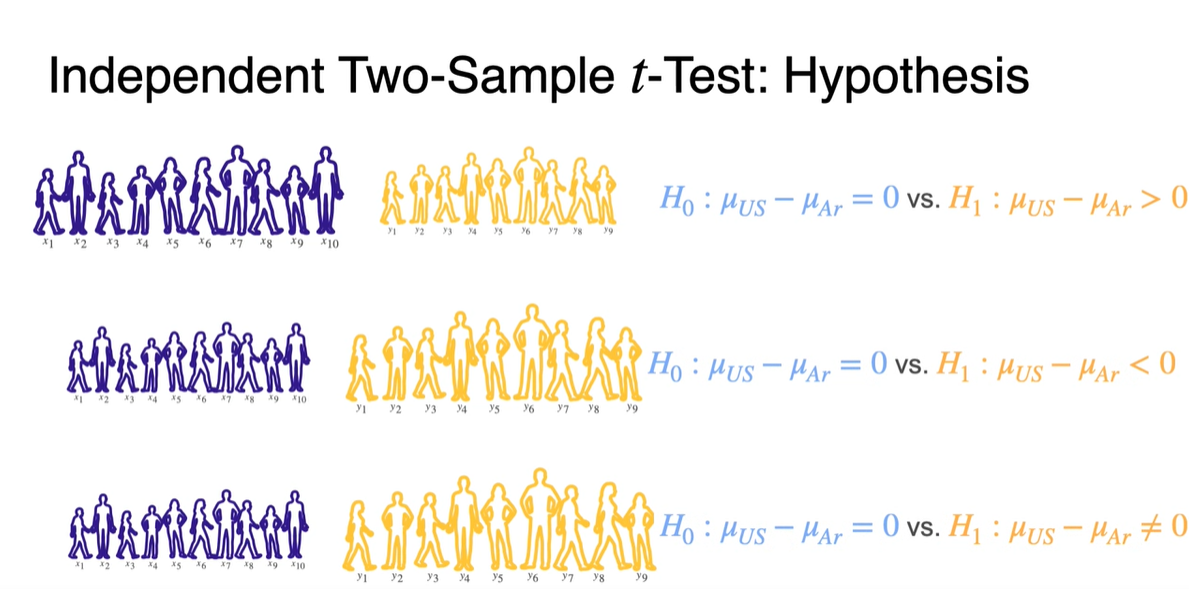
이번에는 독립된 두 Sample에서의 -Test를 진행해보자.
-
US의 18세 이하 Height와 Argentina의 18세 이하 Height를 각각 , 개 뽑아 통계 내보자.
- 두 sample mean 와 는 아마도 같지 않을 것이다.
-

-
이제 Hypothesis를 설정하자.
- 귀무 가설 는 두 sample mean이 같다는 가정()을 바탕으로 하며, Right-tailed, Left-tailed, Two-tailed 총 3가지 경우의 test가 가능하다.
-
이러한 -test는 다음과 같은 상황에서 이루어져야 한다.
-
두 그룹의 sample을 이루는 사람들은 모두 달라야 하고 normally distribution으로부터 independent하게 뽑혀야 함을 가정한다.
- 이 때 와 가 각각 , 를 따른다면, 도 인 normal distribution을 따른다.
-

-
우리는 와 를 모르기 때문에 와 로 표본 평균을 교체해야 한다.
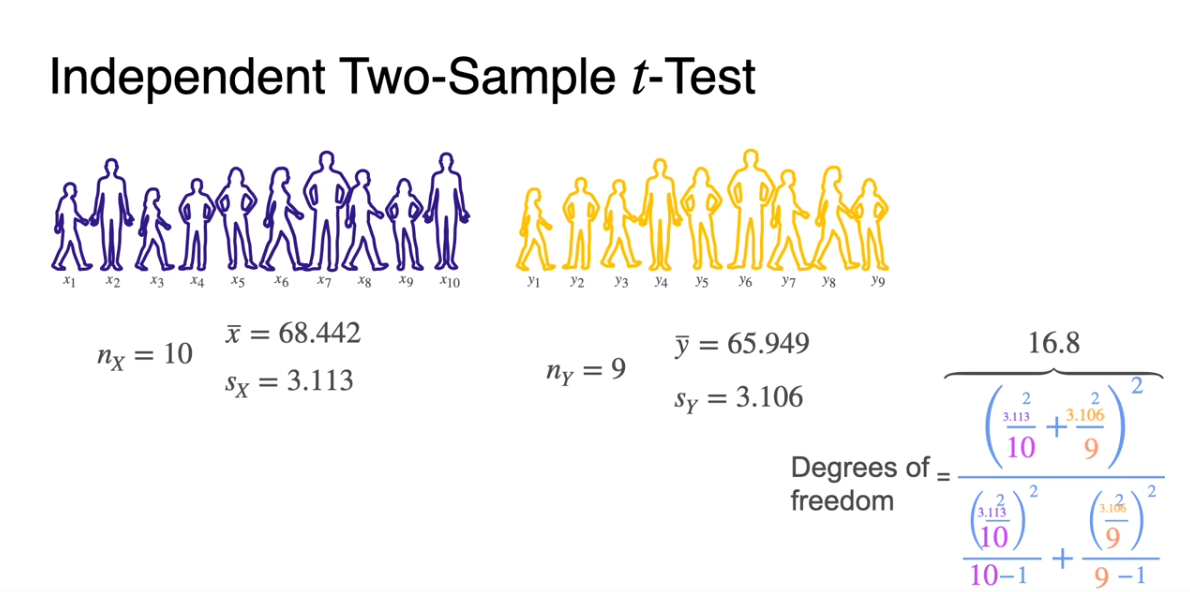
- Degrees of freedom은 와 같이 계산한다.

-
우리가 구했던 값들을 바탕으로 두 sample의 Degrees of feedom을 계산한 결과는 16.8과 같다.
- 따라서 를 따른다.

-
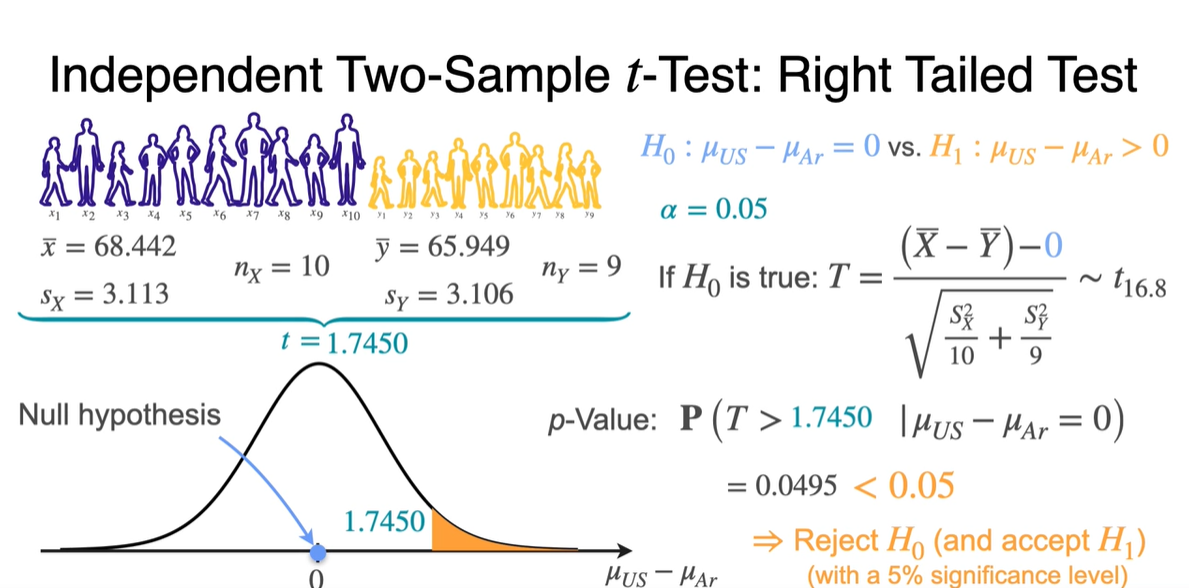
이를 바탕으로 Right-tailed test를 진행할 때에는 Null hypothesis에 의해 으로 설정한다.
- 계산 결과, 는 1.7450과 같고 -value는 0.05 미만이므로 를 reject한다. ( accept)
-
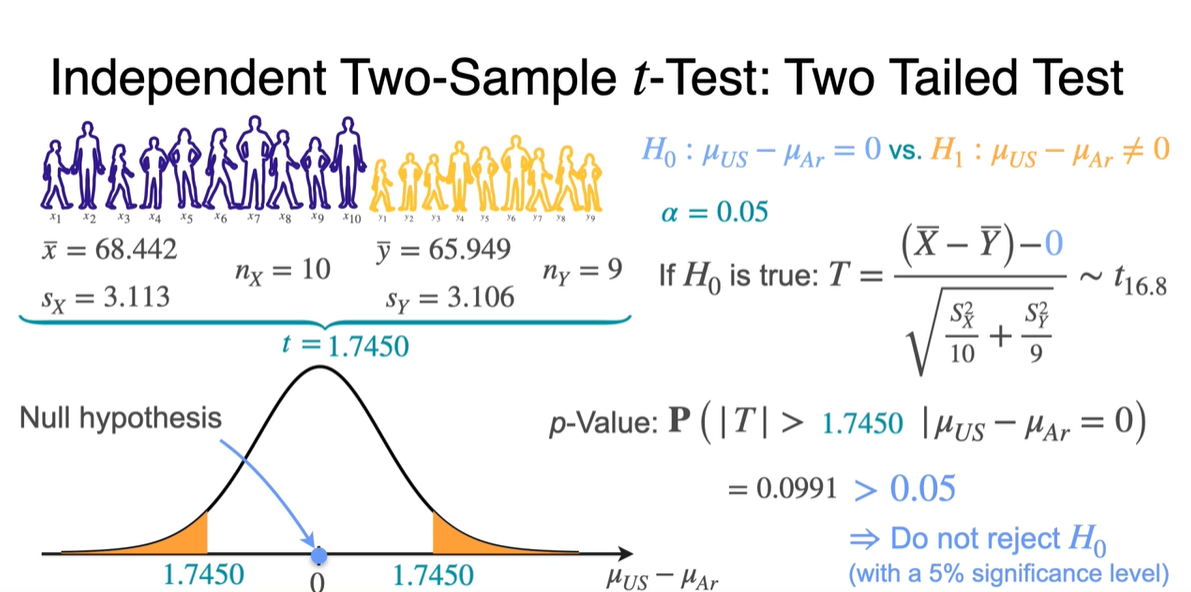
Two-tailed test는 를 구해야 한다.
- -value의 합산이 2배이므로 0.05보다 큰 값을 가져 를 reject하지 않는다.
Paired t-Test
-
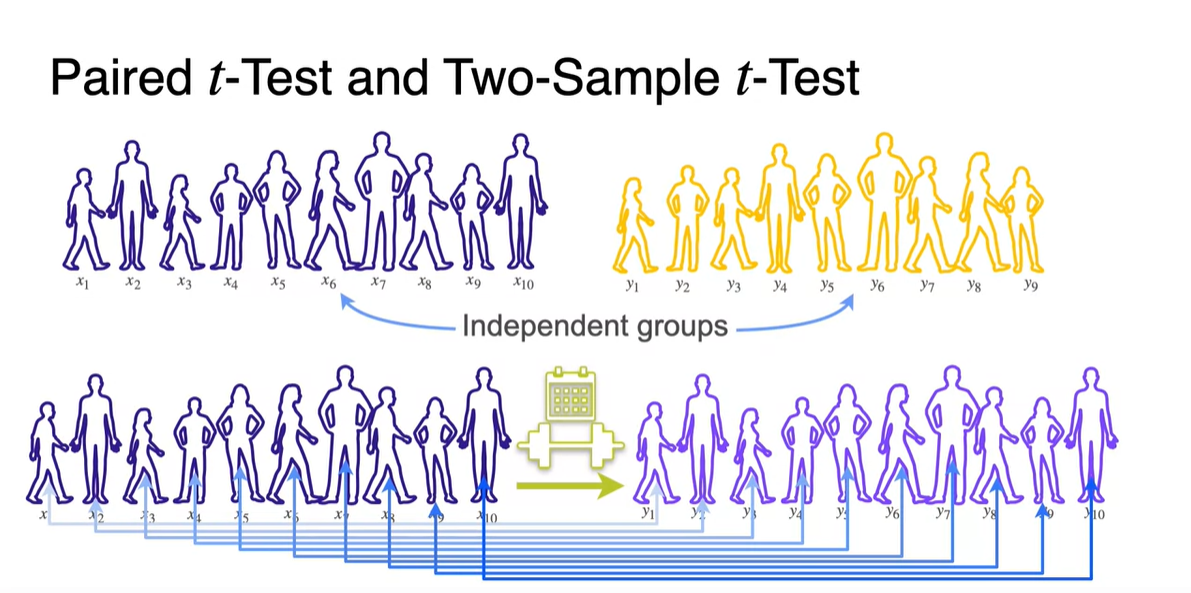
Paired t-Test는 한 sample 내에서의 사람들이 "체중 감량을 얼마나 했는지"와 같은 표본의 차이를 test하기 위한 목적을 지닌다.
- 따라서 비교군인 두 sample의 통계량이 dependent하다.
-
이제 우리가 궁금한건 pair한 두 sample 원소의 variable 차이의 평균이다.
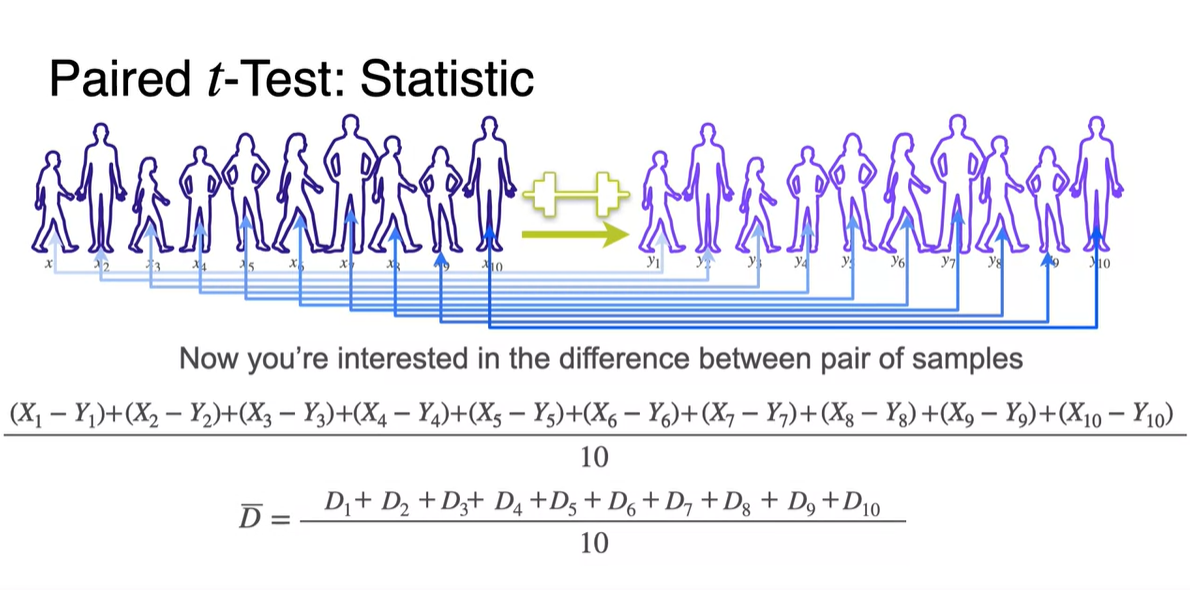
-
만약 와 가 gaussian이라면 두 variables의 차이 도 gaussian이다.
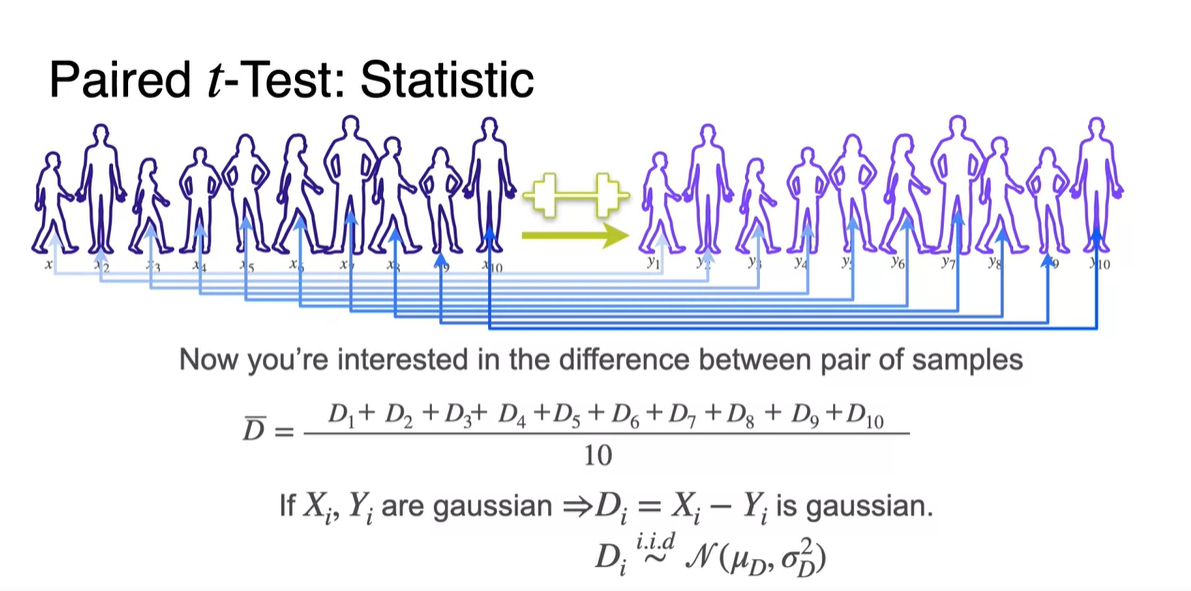
-
를 구하려 했으나 를 알지 못해 를 구해야 한다.
- 를 구해 test statistic을 진행한다.
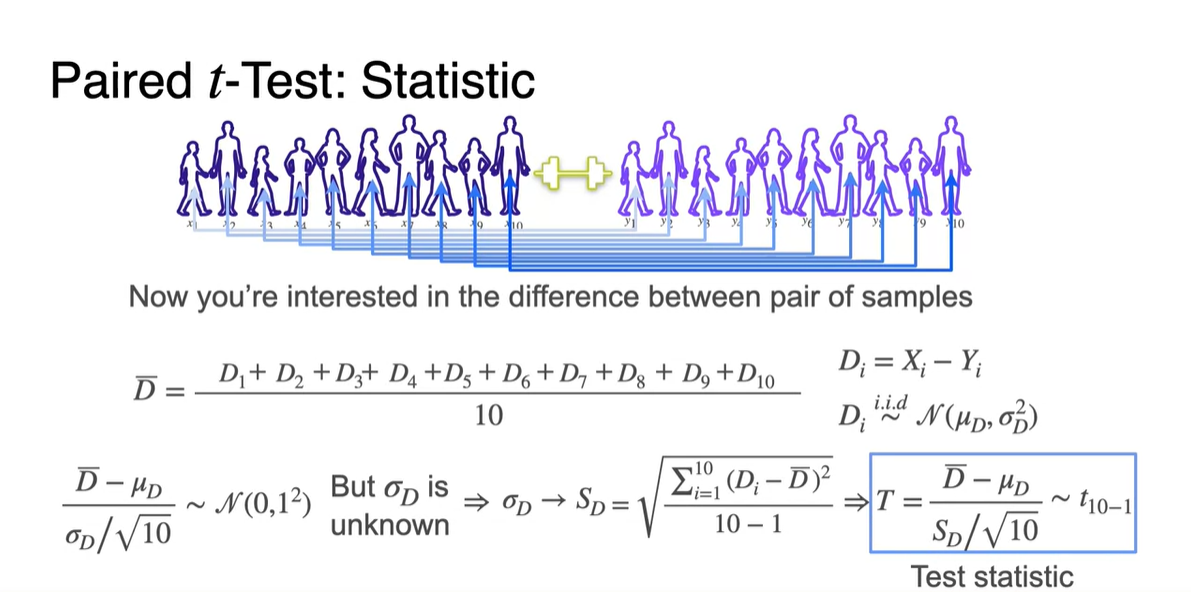
-
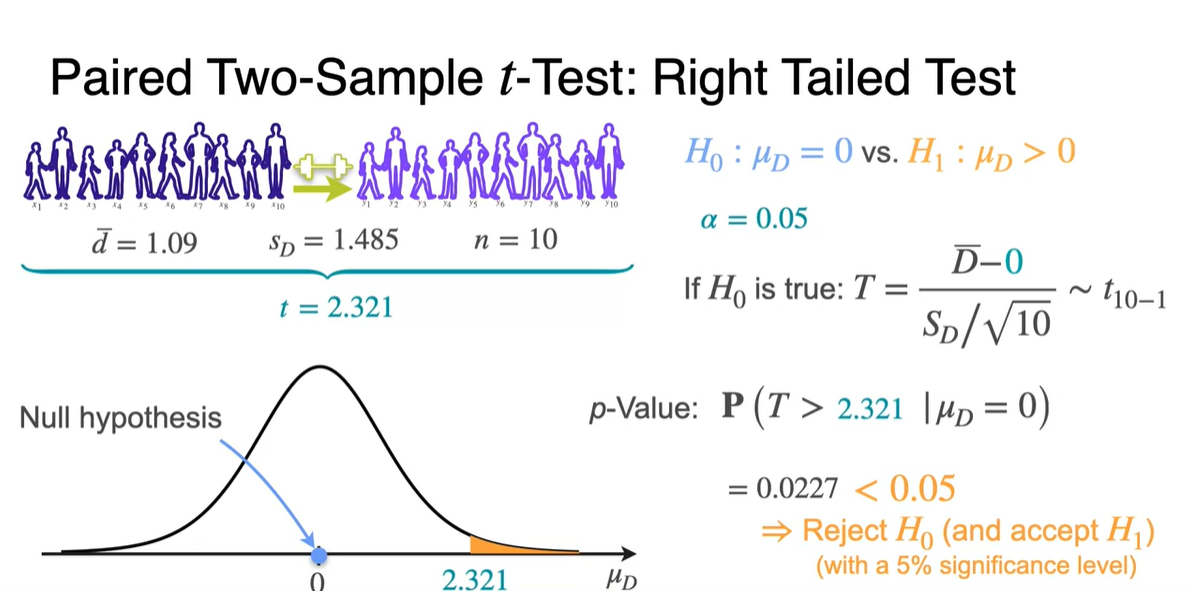
두 sample의 관측값을 대입하여 를 통해 와 를 계산하자.
- 이를 바탕으로 값을 구하면 2.321를 얻을 수 있다.
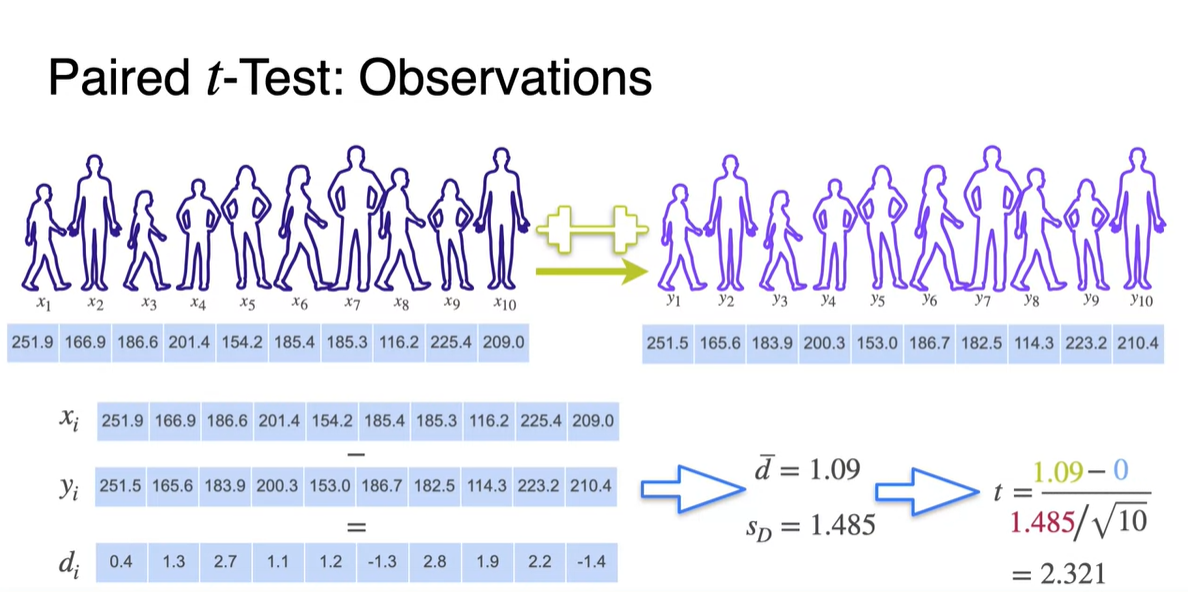
-
Right-tailed test는 (차이가 없음)을 가정한다.
- 이를 바탕으로 값을 계산하고, -value를 찾으면 0.05보다 작아 를 reject하게 된다.
ML Application: A/B Testing
-
A/B testing은 다음과 같은 상황에서 test할 수 있는 방법론이다.
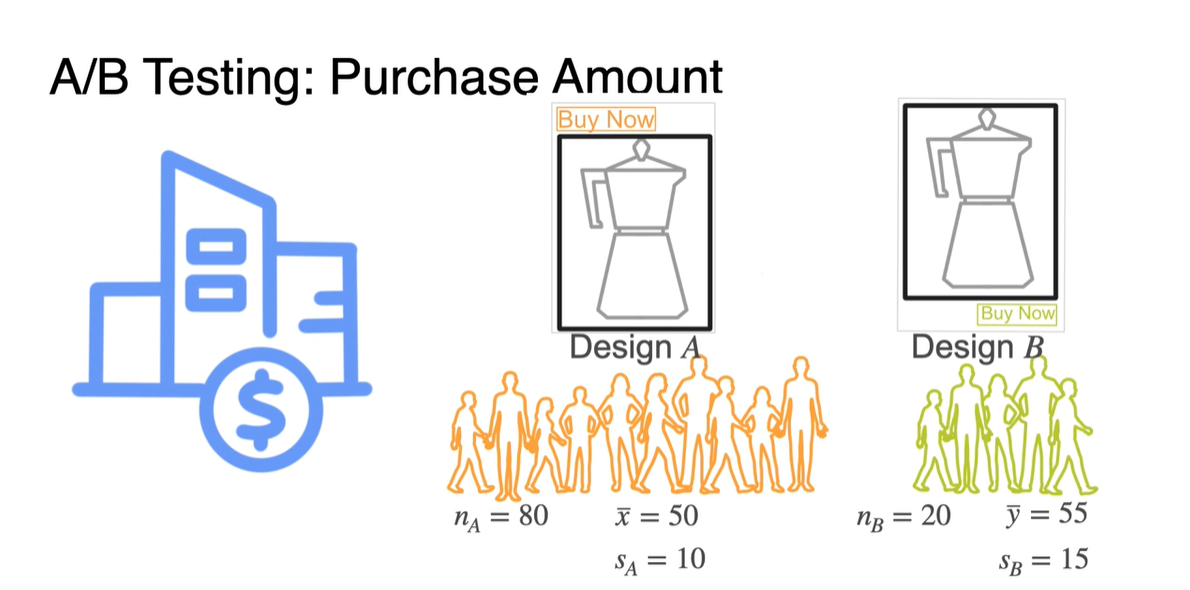
- Design A와 Design B의 선호도를 비교하고자 각 sample에 모인 집단의 통계량을 계산하고, 두 집단의 차이가 어느 정도인지를 비교하기 위해 쓴다.
-
귀무 가설 을 바탕으로 값을 계산해보자.
-
와 는 normal distribution을 따르므로 를 따른다.
- 를 계산하면 -1.414고 이를 바탕으로 -value를 계산하면 0.05보다 큰 결과를 얻어 를 reject하지 않는 결론에 이른다.
-

-
A/B testing과 -test의 절차는 다음과 같다.
-
2개의 variations(A/B)를 선정하여 두 sample을 randomly하게 분리시켜 outcome을 측정한다.
- 이 때 statistical하게 analysis하기 위해 -Test를 진행하는 것이다.
-
-
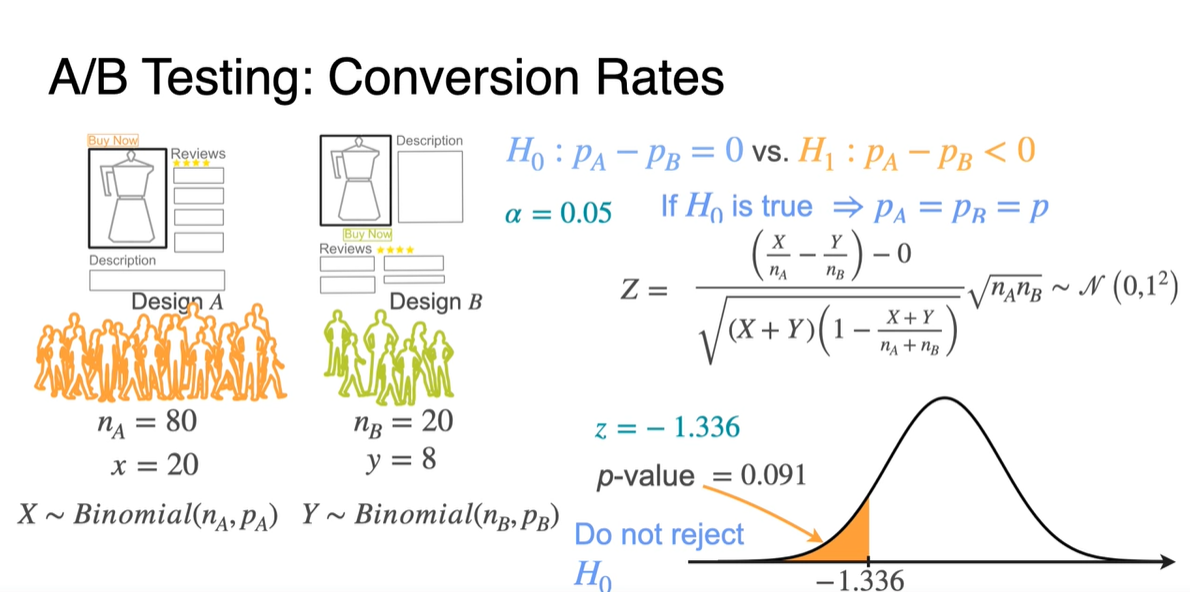
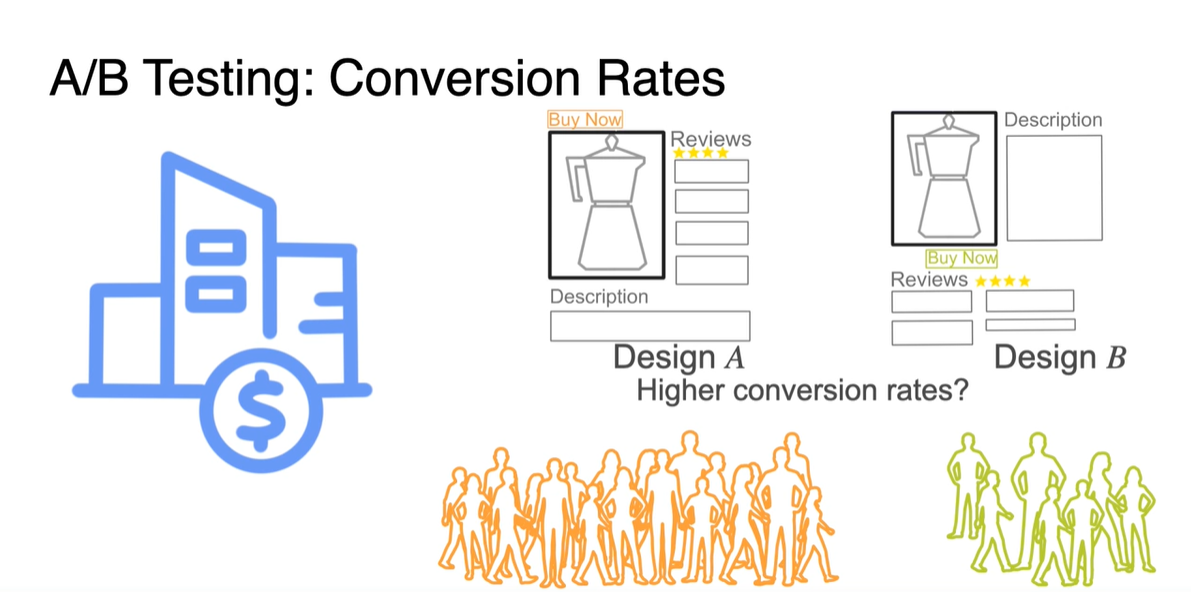
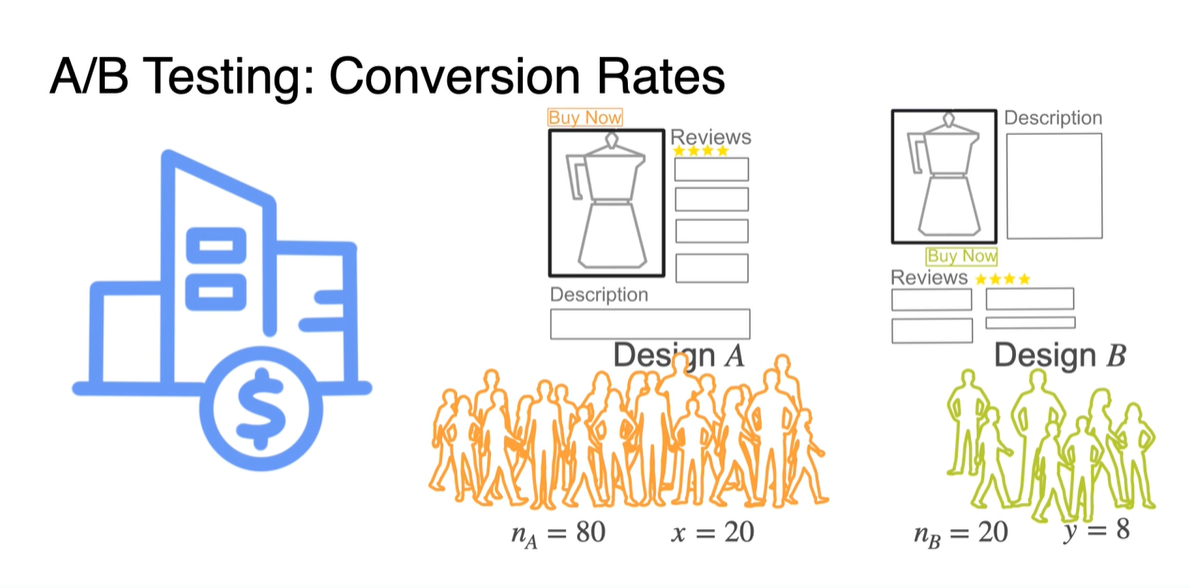
Conversion Rate(전환률)을 알아보기 위해 두 Design A/B를 선택한 사람들의 비율을 측정한다고 해보자.
-
Design A를 선택한 사람들은 총 80명으로 만족도를 1/0으로 측정한 결과 20명이 만족했다는 결과를 얻었다.
-
Design B를 선택한 사람들은 총 20명으로 8명이 만족했다는 결과를 얻었다.
-
-
A/B testing의 귀무 가설 는 만족도의 비율 , 이 차이가 없다는 가정을 전제로 한다.
-
이고 를 따른다면 두 variable을 뺀 변수 또한 Normal distribution을 따를 것이다.
- 전환률 조사는 일반적으로 Left-tailed test를 진행하며(B로의 전환이 목적이니까) significance level 는 0.05로 설정하였다.
-

-
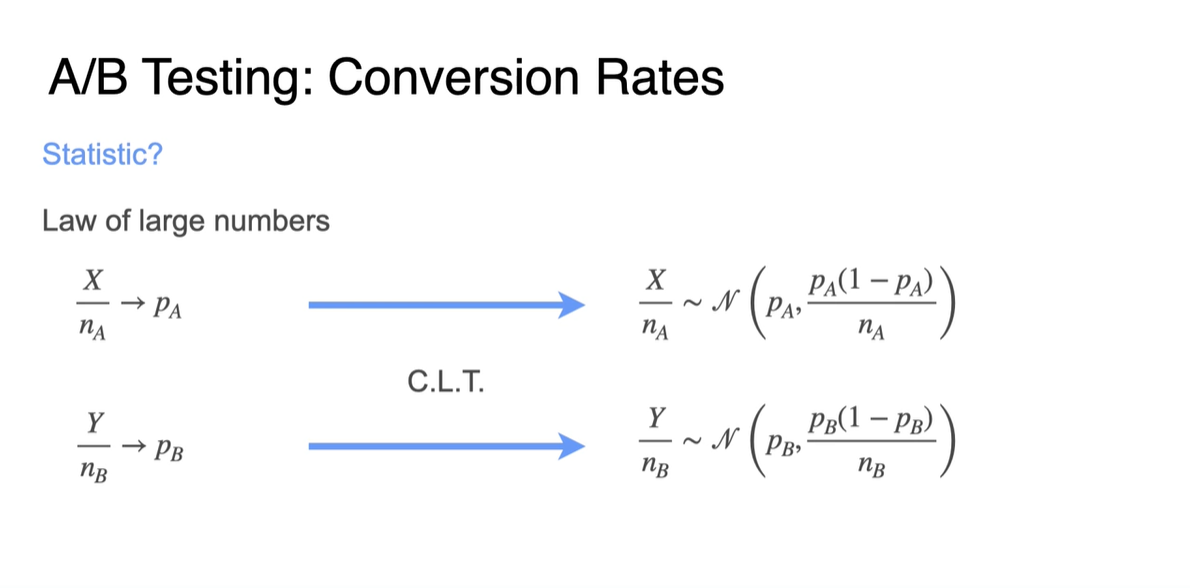
Law of large numbers(큰 수의 법칙)에 의해 proportion만으로 Bin 확률을 표현하는 것이 가능하다.
&
-
Centeral Limit Thorem(CLT, 중심 극한 정리)에 의해 각 proportion은 Normal distribution을 따른다.
&
-
-
이제 두 집단의 proportion 차이를 변수로 하여 새로운 Normal distribution의 notation을 표현해보자.
-

-
만약 가 참임을 가정한다면 다.
- 이를 이용하여 분산을 재정의하면 로 정리할 수 있다.

-
그러나 사실 우리는 명확한 값을 알지 못하기 때문에 두 sample 이용하여 추정한 전체 proportion 로 교체해야 한다.
-
이를 바탕으로 test statistic을 진행한다면 다음과 같은 값이 정규 분포를 따른다고 가정한 뒤 수행한다.
-

- 관측 결과를 대입하여 를 계산한 결과 -1.336을 얻었다.

-
이제 -value를 계산하여 0.091의 값을 얻었고, 인 0.05 이상의 값이 계산되었으므로 를 reject하지 않는다는 결론을 얻었다.
- 다시 말해, 전환률의 차이가 (더 추정해 보아야 알겠지만) 거의 없음을 의미한다.