Week 3 - Sampling and Point estimation

Lesson 1 - Population and Sample

Population and Sample

• Statistopia라는 섬에 사는 사람들의 평균 신장(average height)를 알고 싶다.

  • 해당 섬 속에 사는 모든 사람의 신장을 조사하여 전체 사람 수로 나눠주면 평균을 아주 쉽게 구할수 있다.

    • Easy Peasy Lemon Squeezy !

• 그러나 만약, 전체 10,000명의 사람들이 섬에 모여 산다면 이들의 모든 신장을 조사하여야 하가 때문에 더이상 쉬운 문제가 아니게 된다.

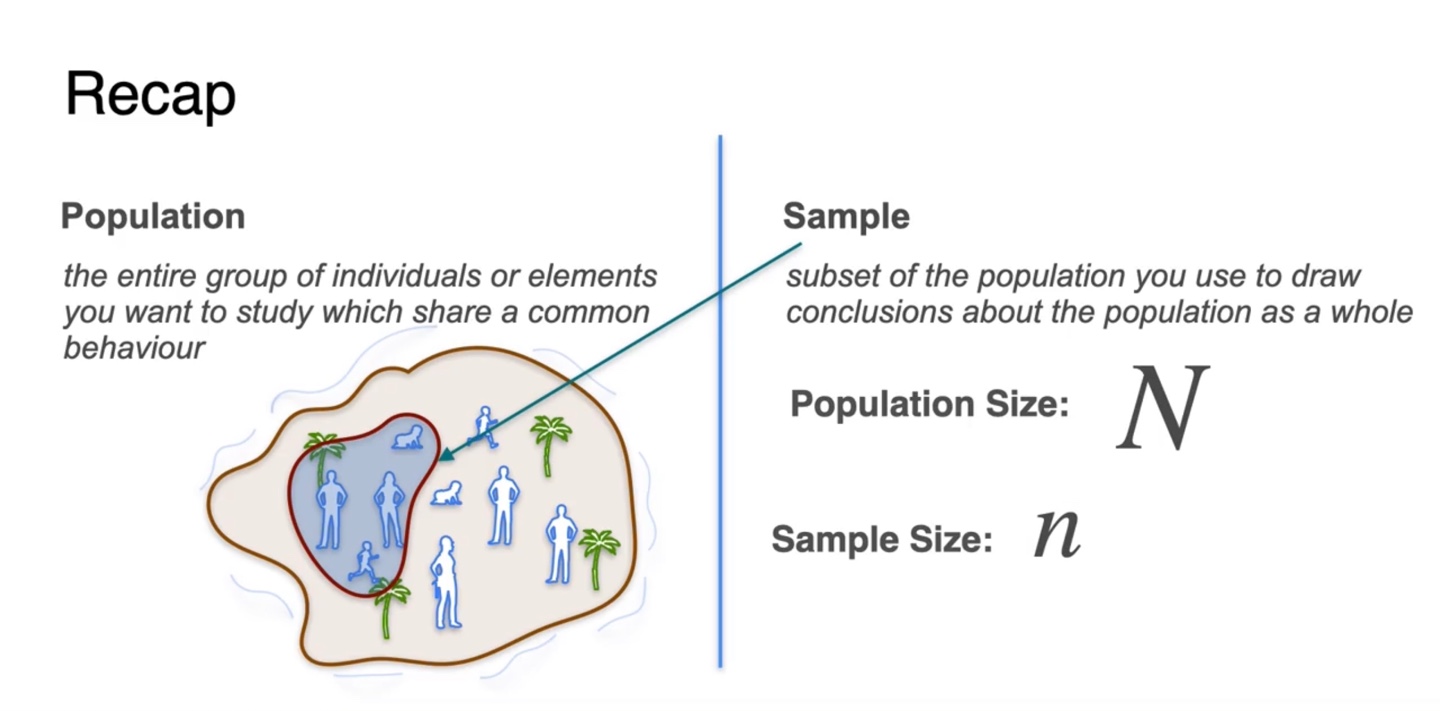
• Population이란 어떠한 통계를 내고자 할 때 알아야 하는, 그룹 내 개개인의 entire한 개수를 말한다.

  • 현재 모든 사람의 신장을 구하고자 하므로 Statistopia에 사는 10,000명의 사람들이 population이다.

• Sample은 선택한 사람들의 숫자로(일부) 통계적 수치를 내고자 할 때 정의된다.

  • 전체 population의 subset으로 결과를 알아내고자 할 때 사용된다.

• 만일 population의 숫자가 10,000이라면 이는 기호로 $N$이라 정의한다.

  • Sample size의 기호는 $n$으로 표기하며 1부터 9,999까지의 값을 갖게될 것이다.

• Random Sampling이란 전체 population의 일부 sample을 random으로 선정하는 것을 말한다.

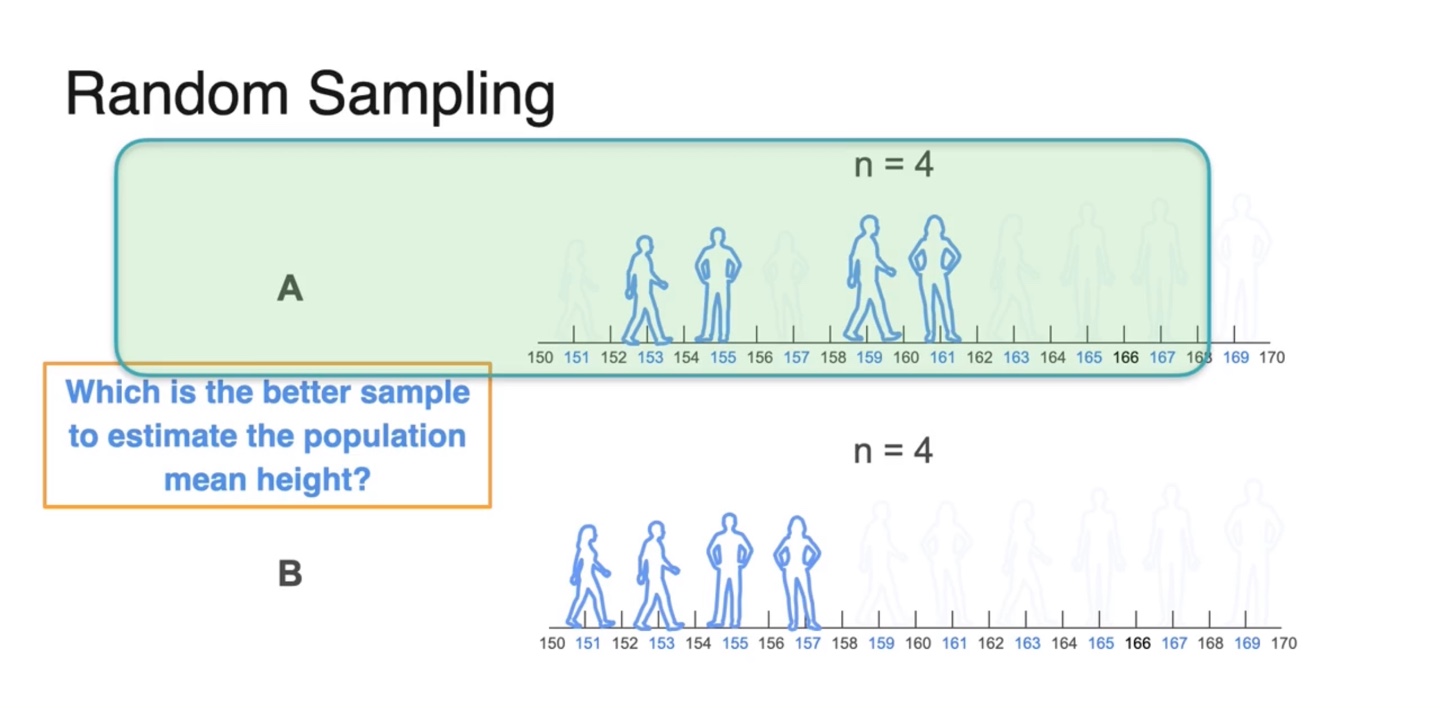
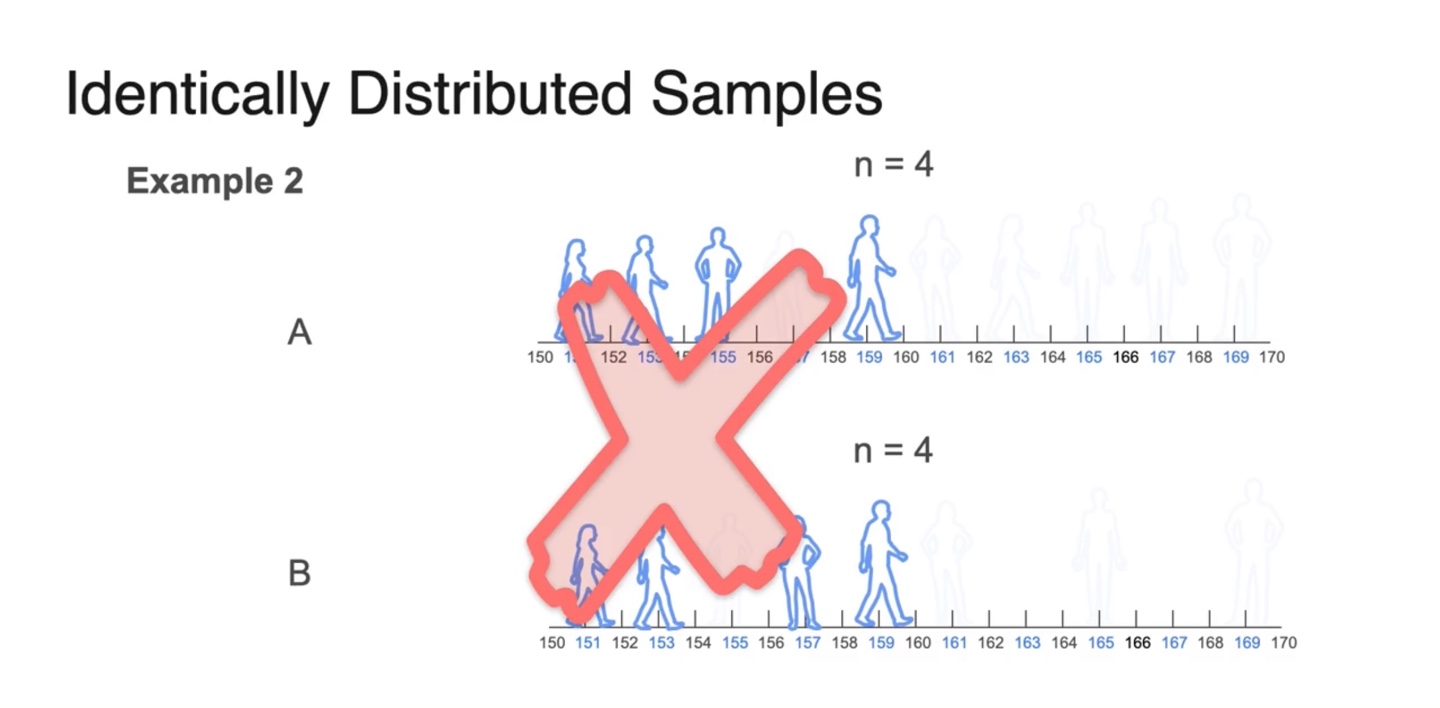
  • 만약 $n=4$라면, $A$ 집단이나 $B$ 집단으로 random하게 4명을 선택한 subset이 하나의 sample이 된다.

  • 이 중 어떤 집단이 population의 mean height를 더 잘 표현하고 있을까?

    • $B$ sample은 키가 작은 사람들이 대부분의 sample을 대표하고 있기 때문에 평균값이 낮게 나올 수 있으므로, $A$ 집단의 sample이 population에 가깝다.

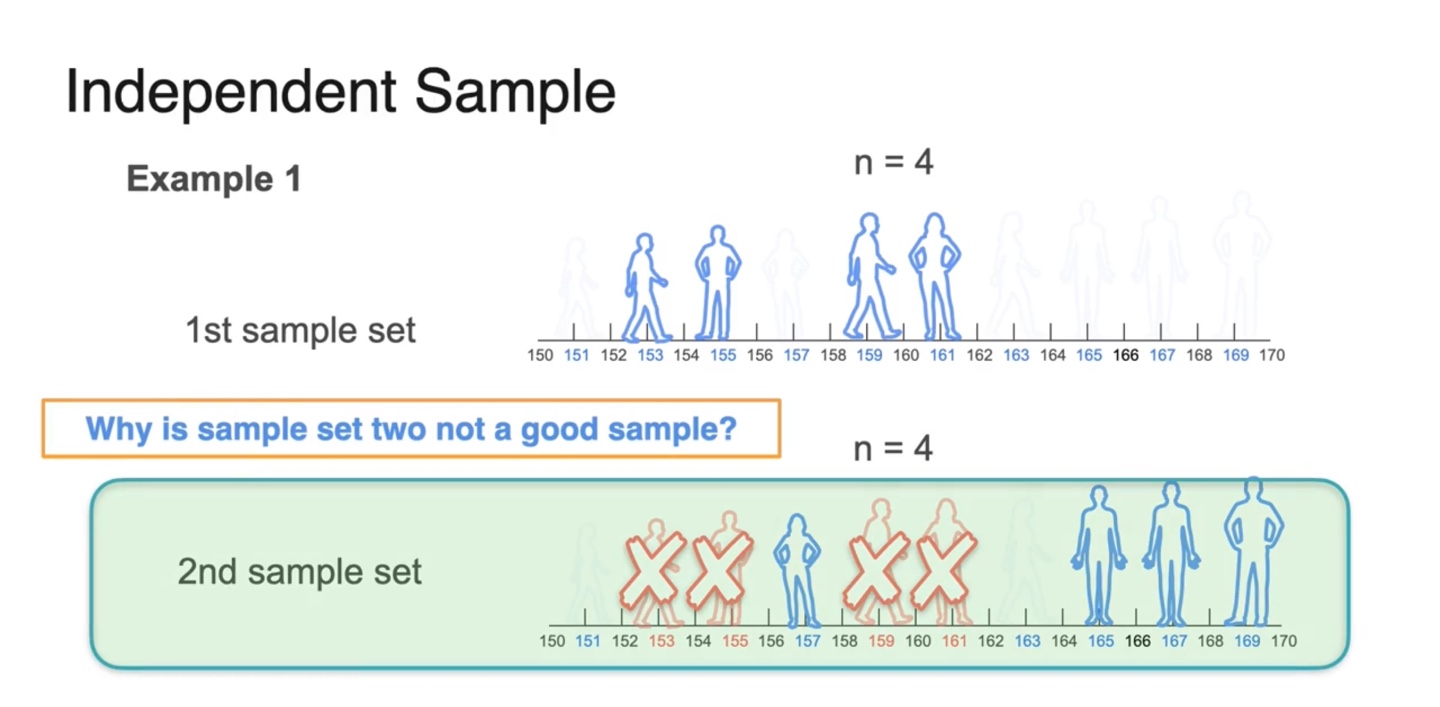
• 만약 첫 번째 sample을 뽑고 두 번째 sample을 뽑을 때, 첫 번째 sample의 원소들을 뽑지 못한다면 어떨까?

  • 이렇게 되면 두 번째 sample이 첫 번째 sample의 추정에 큰 영향을 받게 될 것이므로 좋지 않은 sampling이라고 한다.

    • 즉, independent하지 않고 두 사건이 dependent해 진다.

• 따라서 중복을 허용하며 sampling하는 것이 중요하다.

  • 이전 sample set에 의존하지 않도록 random sampling해야 하는 것이다.

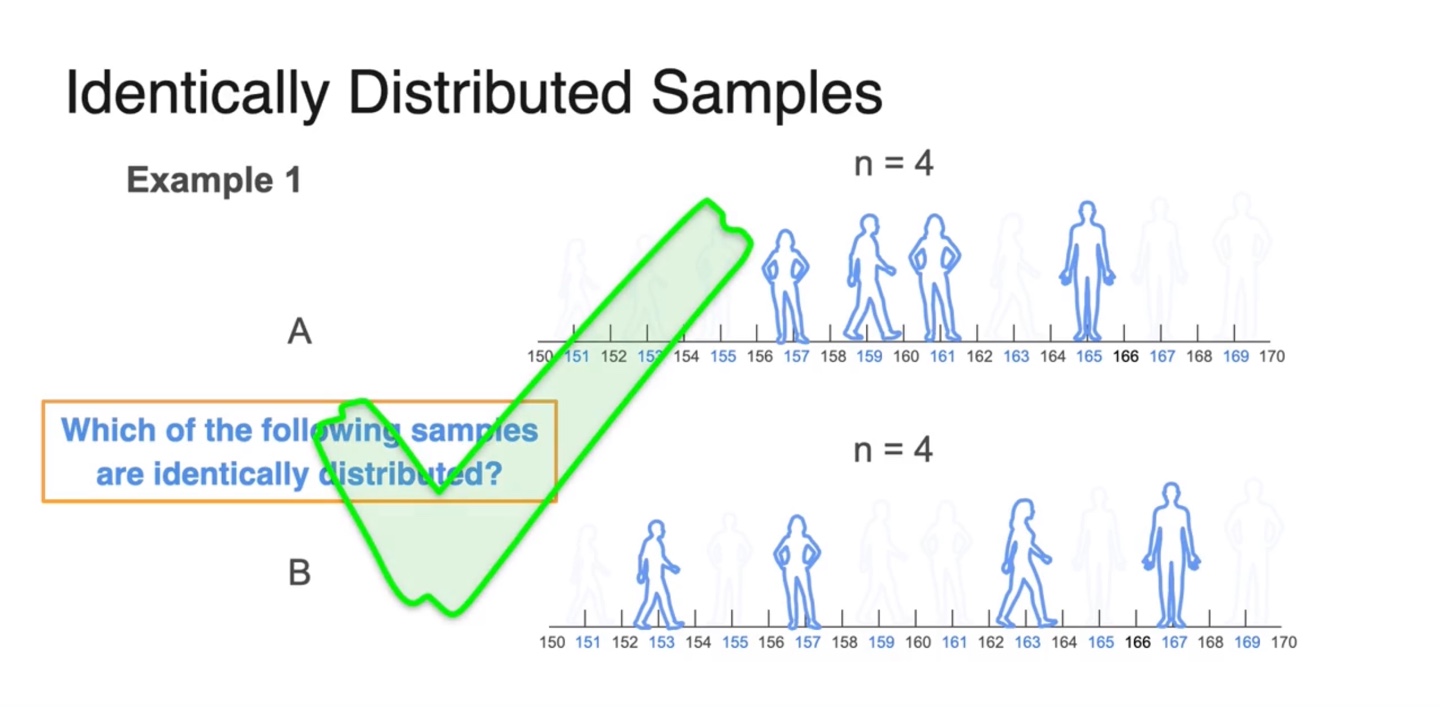
• Sampling시 가장 중요한 점은 independent identically distributed(i.i.d)한 규칙을 적용해야 한다는 점이다.

  • 두 sample의 sampling 규칙이 동일하고 표본 분포가 다양할 때 더욱 의미를 가진다.

• 아래와 같이 특정 지역에 사람들만 국소적으로 sampling된다면 좋은 sampling이라고 볼 수 없다.

  • 따라서 sample이 independent하고 identically distributed되어 있는지 확인해야만 한다.

• 예를 들어, Avocado Toast의 trend를 알고자 US 내의 avocado 가격의 통계를 알아보고 싶다고 가정해 보자.

• Population은 무엇이라고 말할 수 있을까?

  • 바로, 미국에서 판매되는 모든 아보카도가 연구 대상이 된다.

• 해당 예제에서의 sample은 무엇을 가리킬까?

  • 4개의 store를 선정하여 그 곳에서 팔린 아보카도의 가격이 sample이다.

    • 즉, population의 subset이다.

• Population과 Sample은 머신 러닝에서 어떻게 쓰일까?

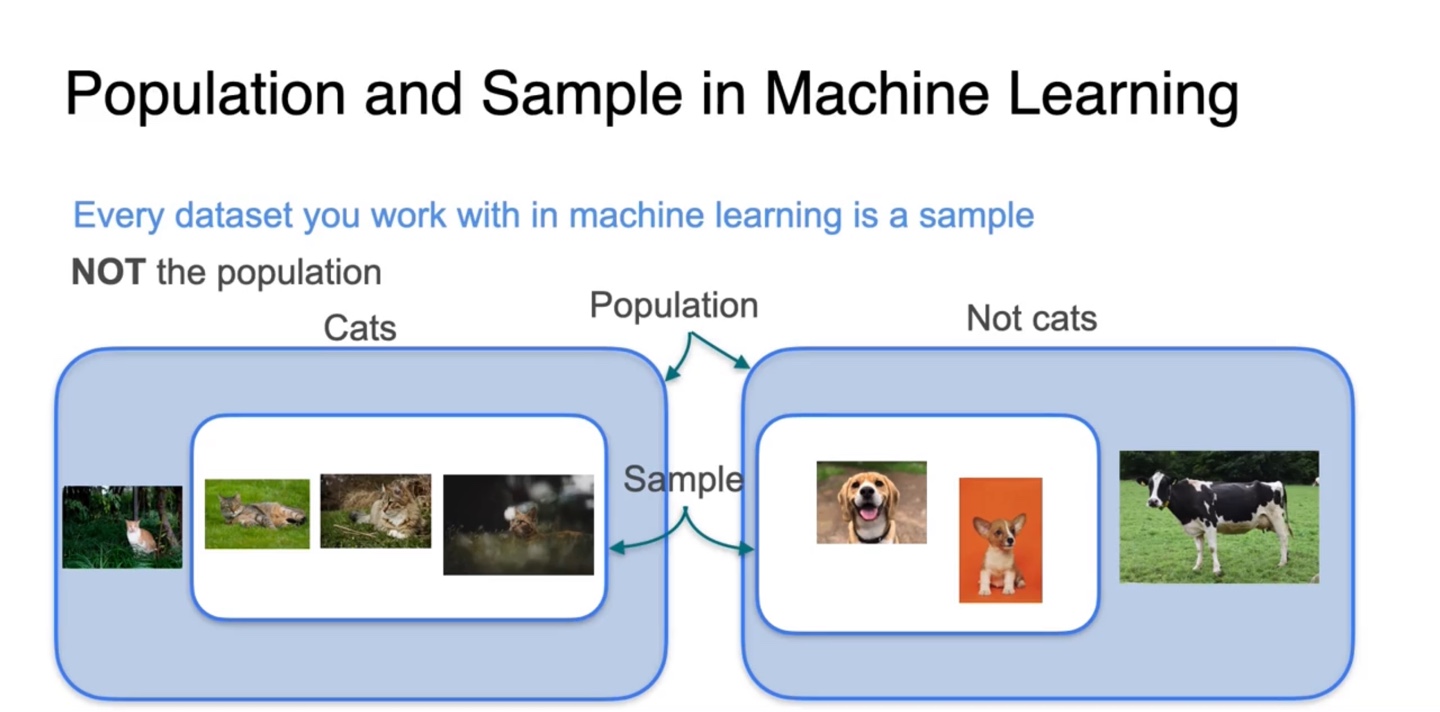
  • 우리는 지구 상에 존재하는 모든 Cats와 Not cats의 수를 셀 수 없기 때문에, sample을 이용한 분류 및 추정만 가능하다.

  • 이후에 다루는 "큰 수의 법칙"에 의해 population에 가장 가까운 근사치의 평균 혹은 분산과 같은 통계치들을 추정하는 과정이 머신 러닝인 것이다.

• 우리는 population의 수를 $N$, sample 내 개수를 $n$으로 표기할 것이다.

  • Sample $\subset$ Population의 관계를 가진다.

Sample Mean

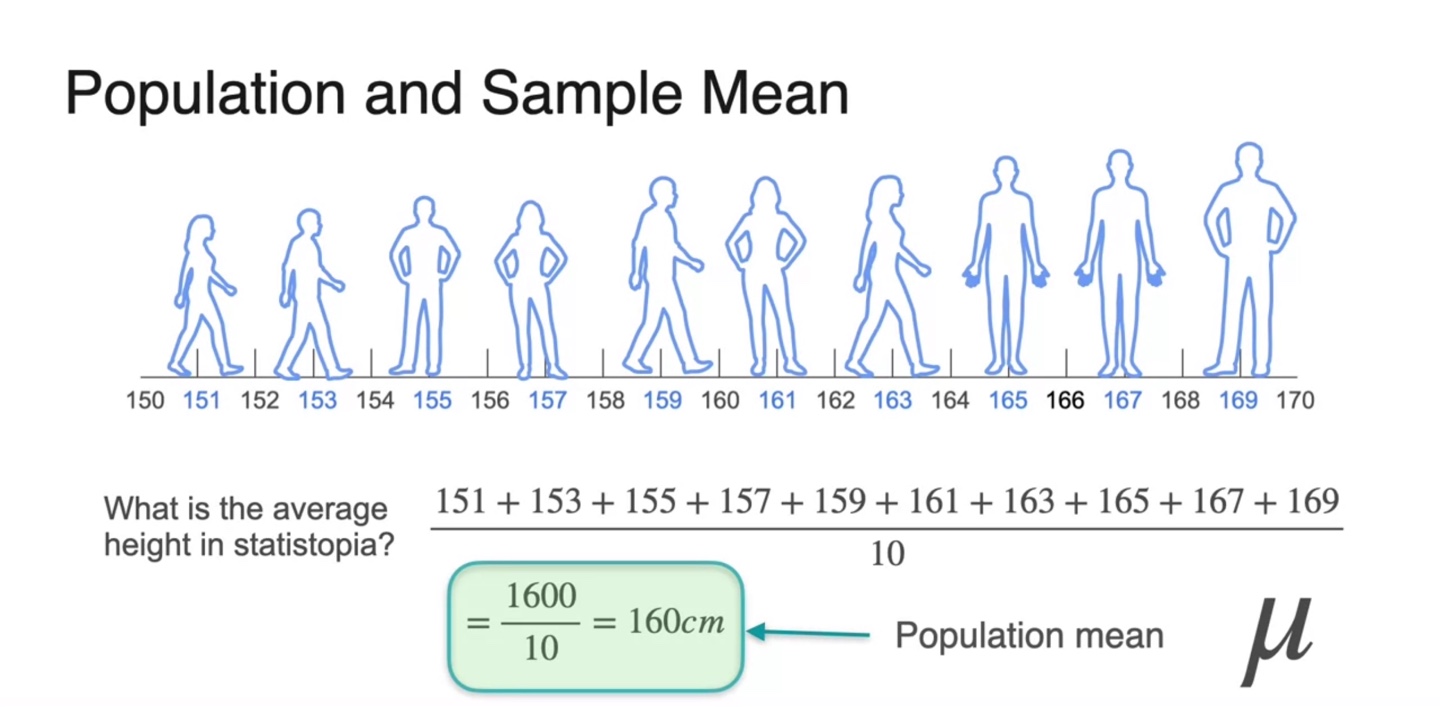
• Statistopia의 사람들 키가 아래와 같이 조사되었다고 하자.

  • 이들의 평균은 160cm로 계산되었고 우리는 이를 $\mu$라는 mean값으로 표기한다.

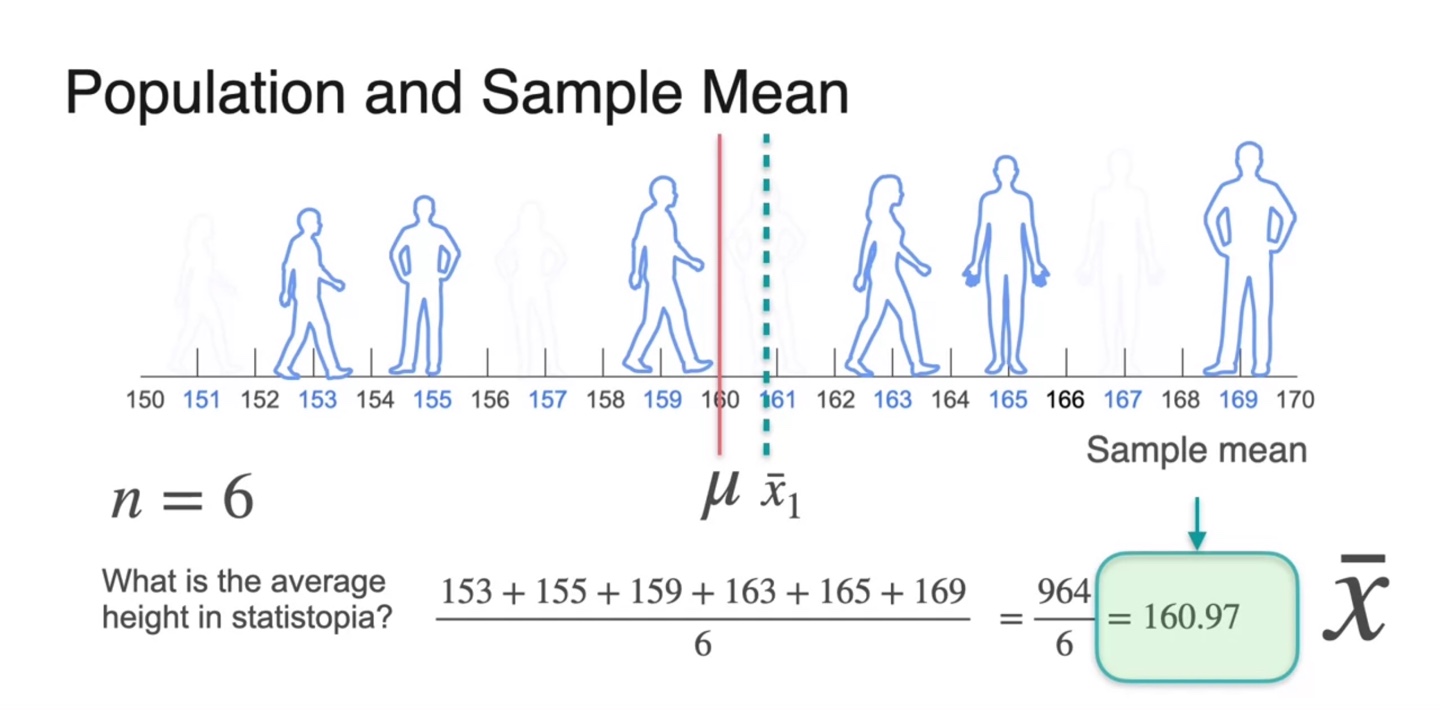
• 이 중 6명을 sample로 선정하여 평균치를 계산한 결과 160.97cm가 얻어졌다.

  • 전체 population 평균 값 $\mu$를 빨간 선으로 표기하였고, 첫 번째 sample을 통해 얻어진 표본 평균을 $\bar{x}_1$로 표기하여 수직선에 나타낸 결과가 아래와 같다.

• 또 6명으로 두 번째 sample을 골라 표본 평균을 계산한 결과 156cm가 얻어졌다.

  • 이를 $\bar{x}_2$로 표기하여 노란 점선으로 나타낸 결과는 아래와 같다.

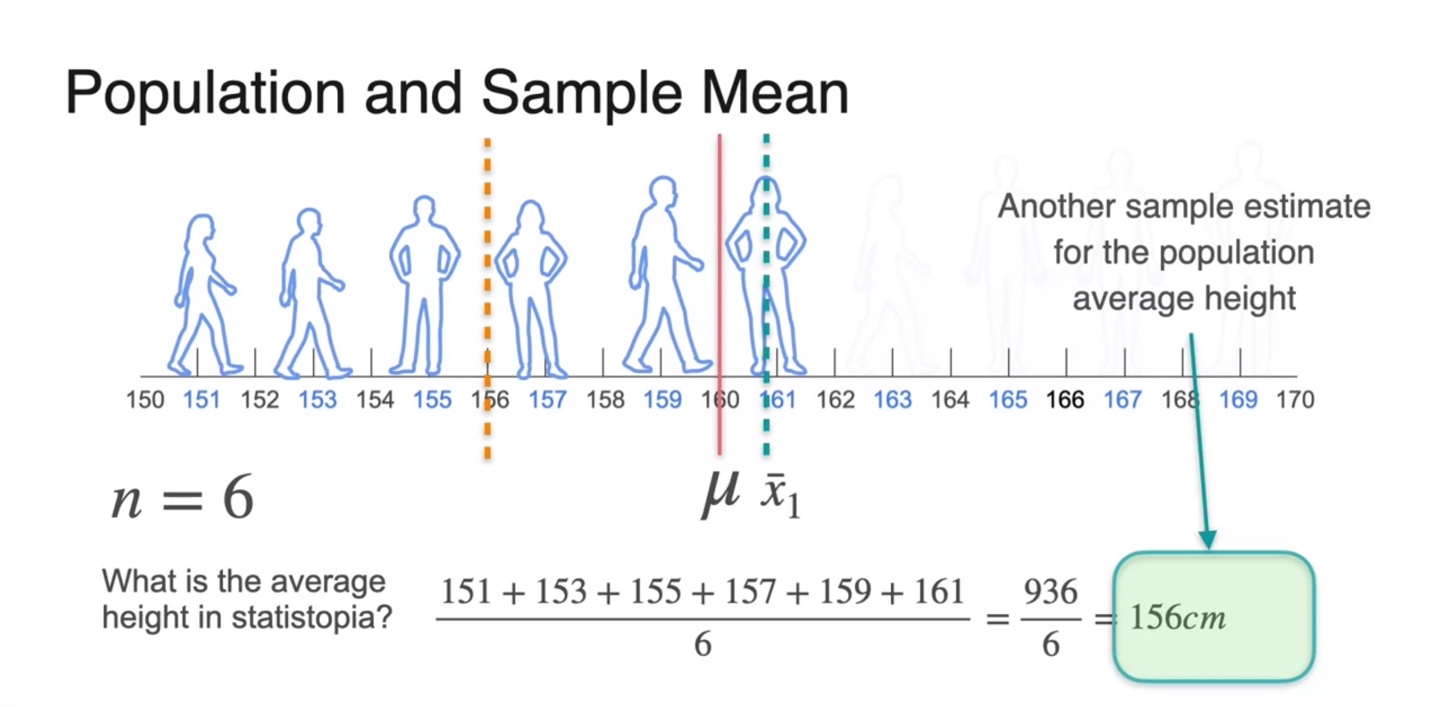
• 첫 번째 sample과 두 번째 sample 중 population mean height를 더 잘 표현한 set은 무엇인가?

  • 첫 번째 sample의 평균 $\bar{x}_1$이 $\mu$에 더욱 가까우므로 첫 번째 sample이 population을 더 잘 표현한다고 볼 수 있다.

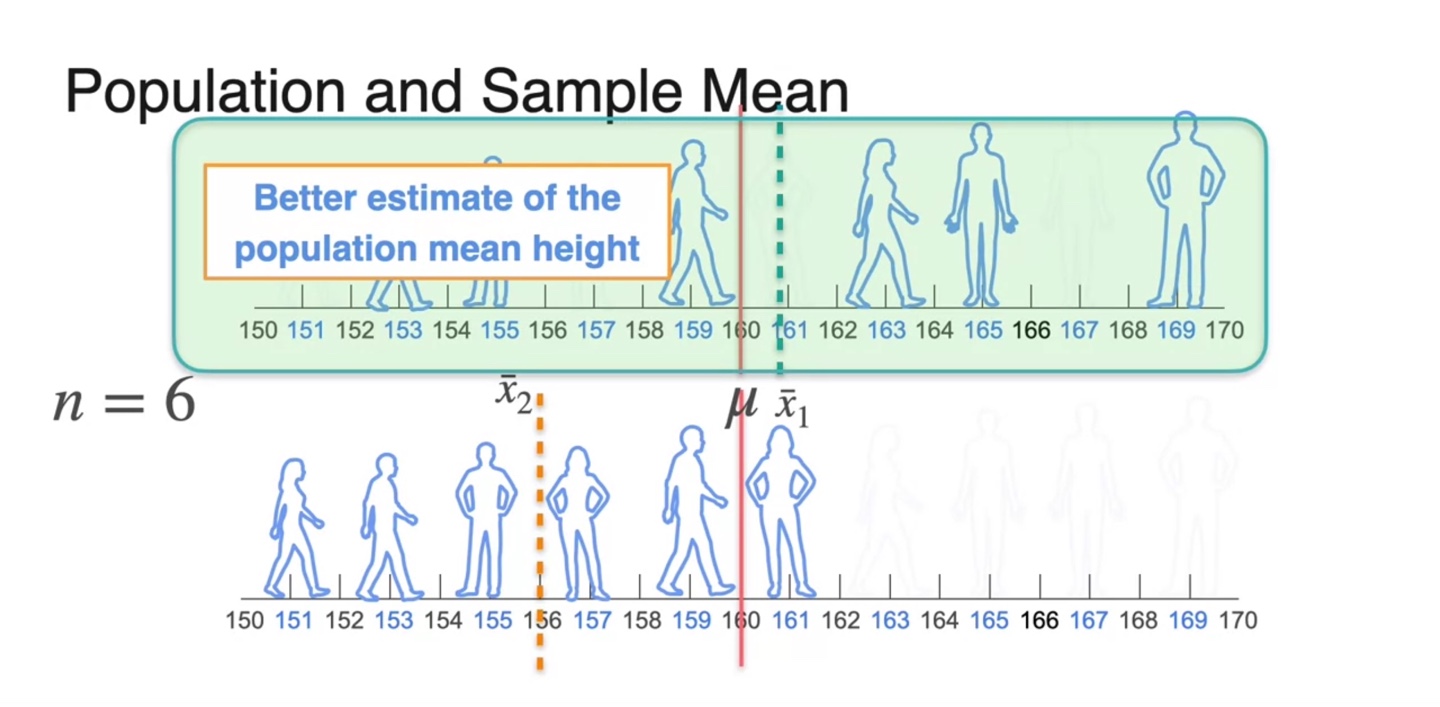
• 이번에는 2명으로 구성된 세 번째 sample을 골라, 평균치를 계산한 결과 158cm가 얻어졌다.

  • $\bar{x}_3$보다 $\bar{x}_1$이 population mean $\mu$에 가까우므로, 첫 번째 sample이 여전히 전체를 더 잘 표현하고 있다고 볼 수 있다.

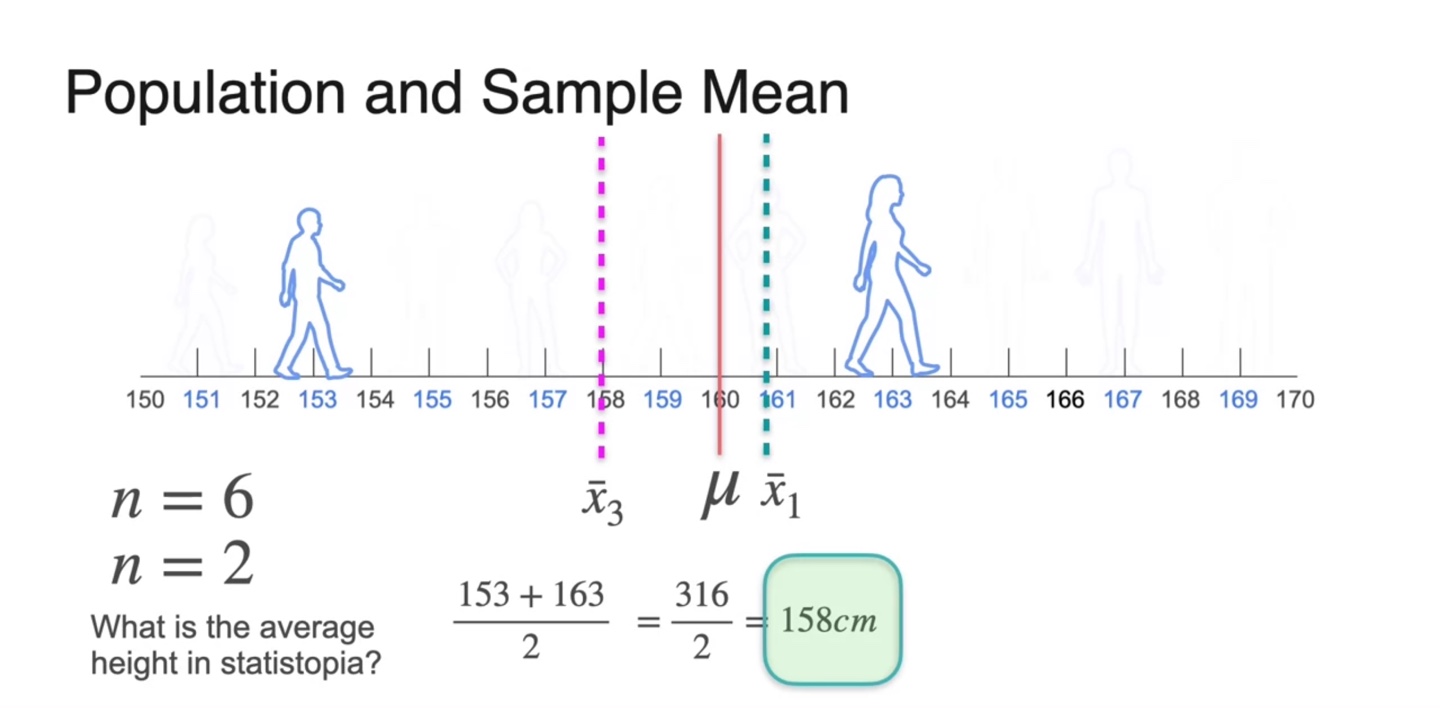
Sample Proportion

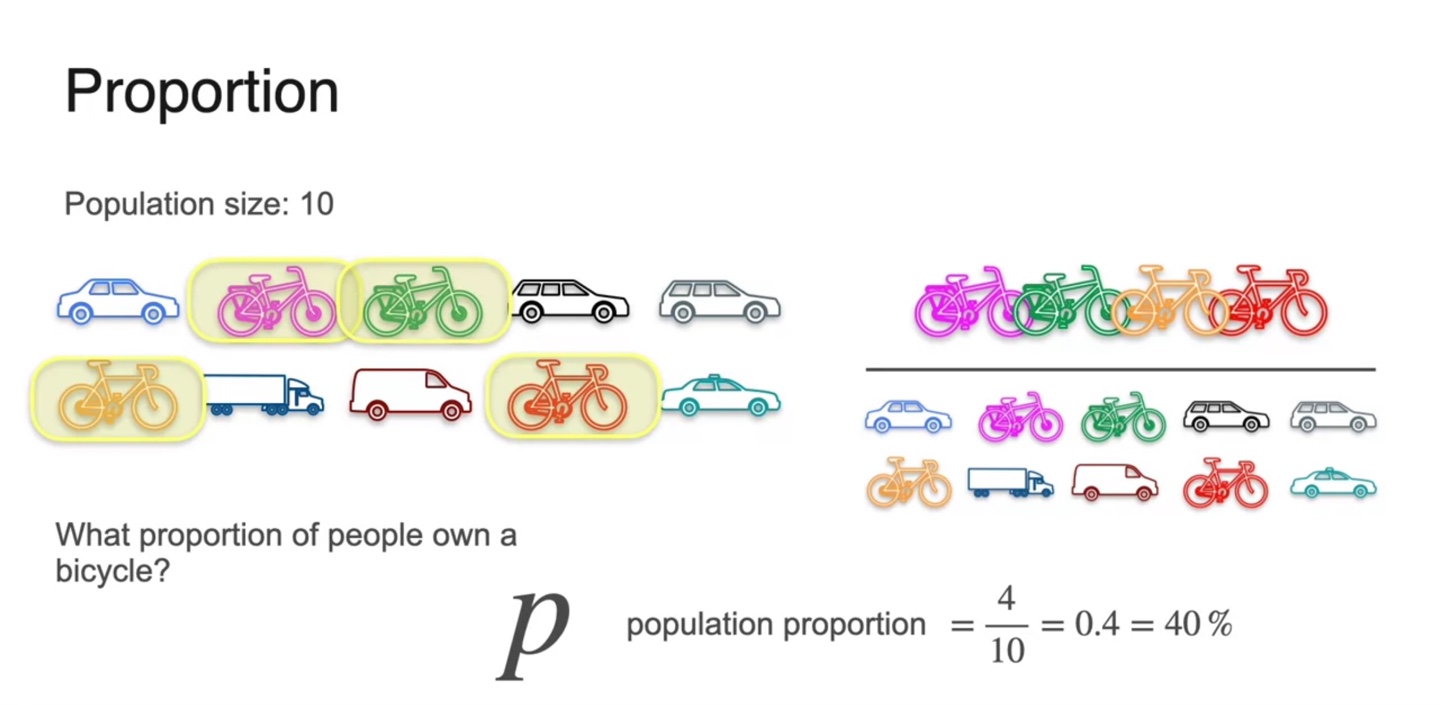
• 아래와 같이 전체 10명의 사람들이 어떤 대중교통을 이용하는지에 대한 통계를 내보자.

  • 이 중 자전거를 타는 사람들의 비율은 전체 10명 중 4명이므로 다음과 같이 계산된다.

    • Population proportion : $p = \displaystyle \frac{4}{10} = 40\%$

• Proportion은 전체 population($N$)개 중에 알고자 하는 item의 개수(number of $x$)의 비중을 나타내는 값이다.

  • 따라서 기호로는 $p$라고 표기하며 두 값을 나누어 계산한다.

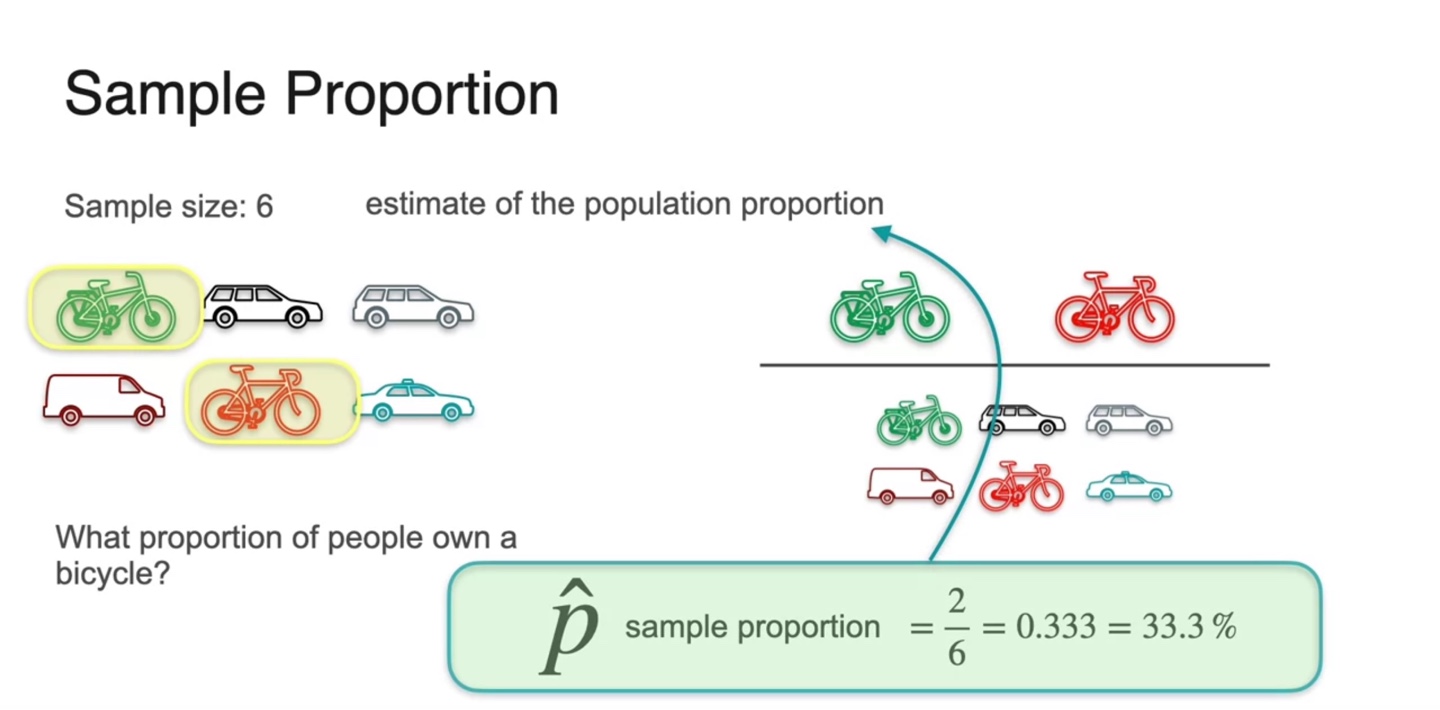
• Sample의 proportion은 $\hat{p}$으로 표기한다.

  • Sample size가 6일 때 자전거를 타는 사람의 수가 2라면, $\displaystyle \frac{2}{6}$의 값으로 계산되는 것이다.

Sample Variance

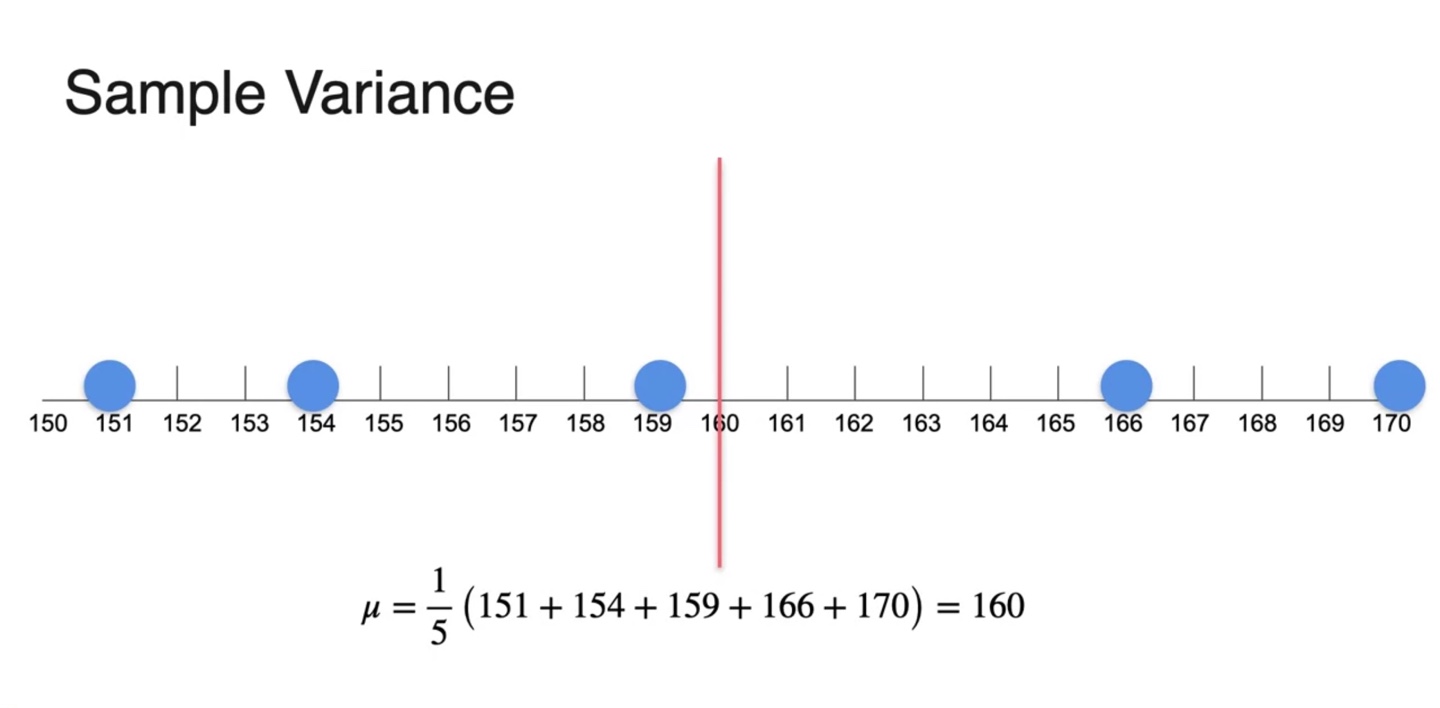
• 아래와 같은 5개의 samples의 평균을 구해보자.

  • 평균 $\mu$는 160으로 계산되었다.

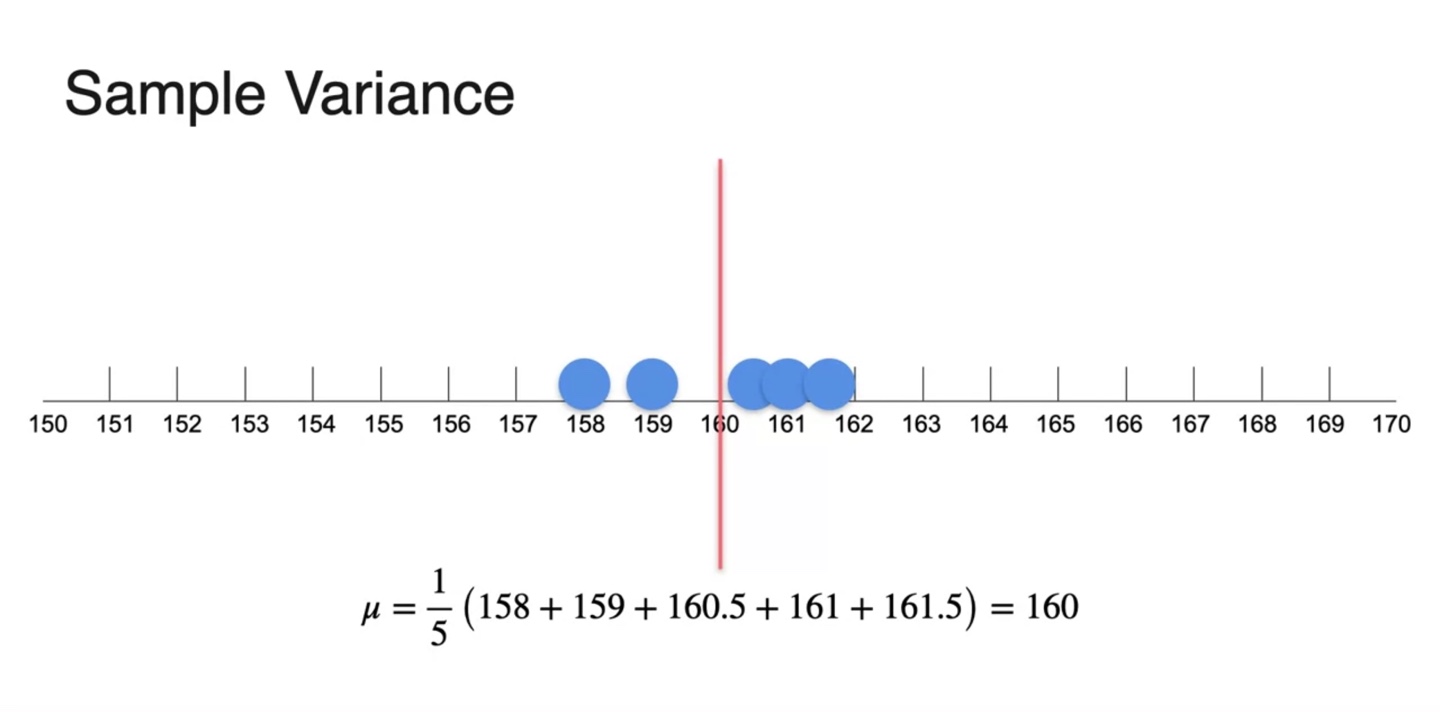
• 또 다른 sample의 평균을 구해보자.

  • 두 번째 sample의 평균 $\mu$ 또한 160으로 계산되었다.

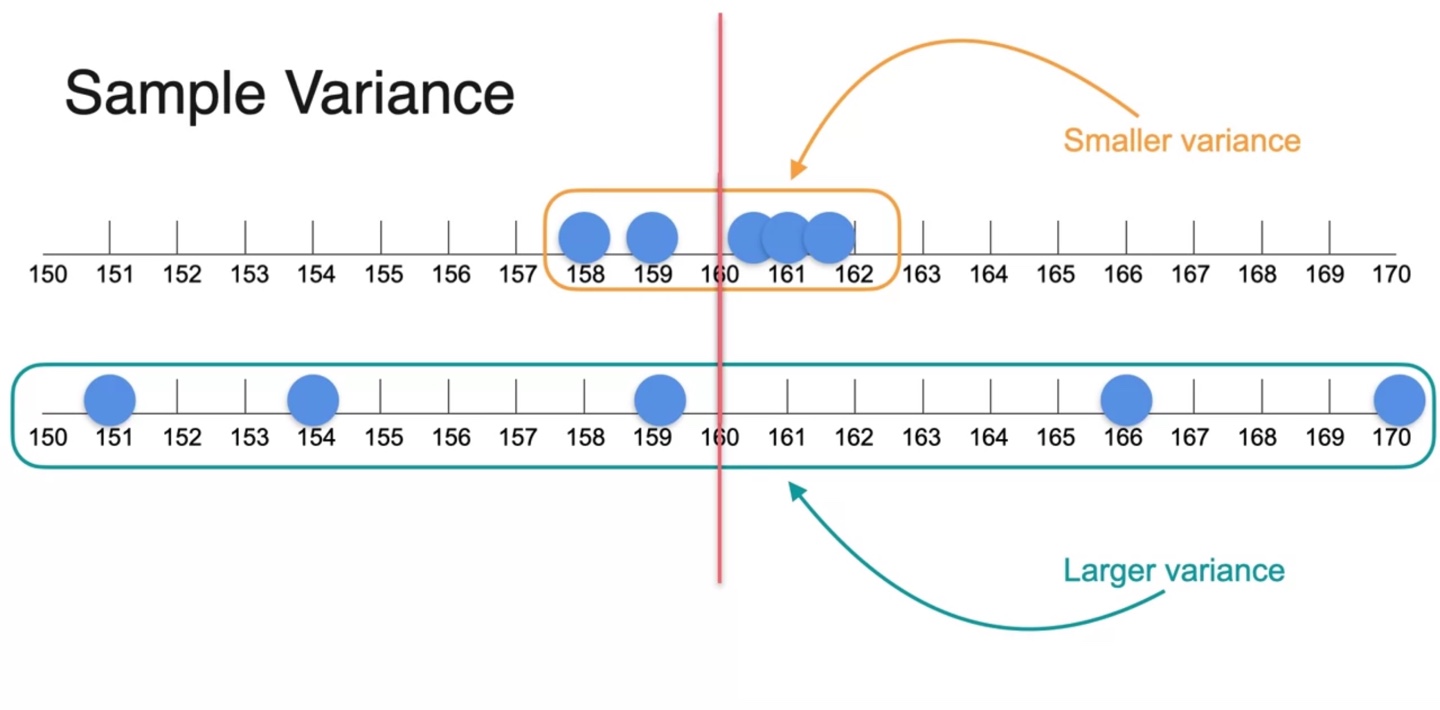
• 분포의 분산을 나타내는 variance는 평균으로부터 떨어진 거리에 영향을 받는다.

  • 따라서 첫 번째 sample의 분산이 두 번째 sample의 분산보다 smaller variance를 가진다.

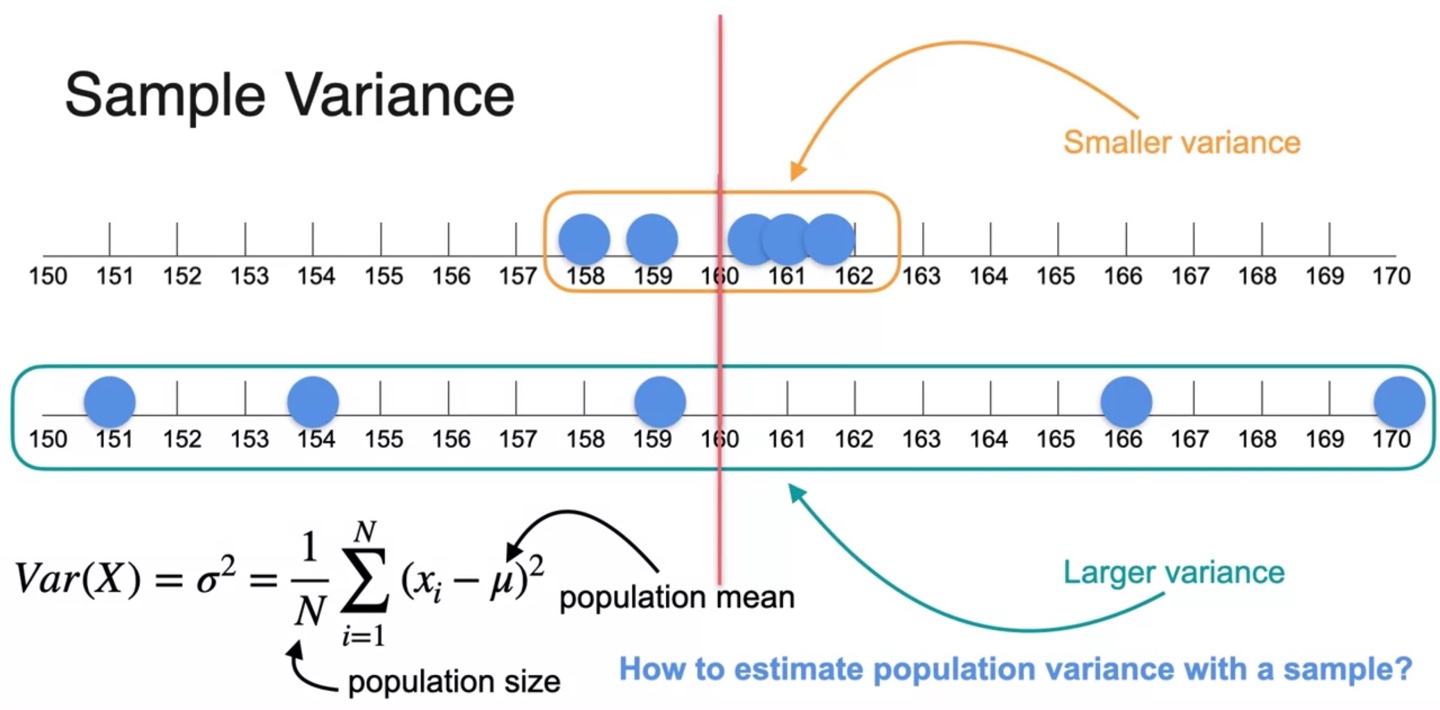
• 이를 수식으로 표현하면 $Var(X) = \sigma^2 = \displaystyle \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2$로 정의된다.

  • Population size $N$과 population mean $\mu$로 표현한 population variance는 위와 같이 구하였으나, sample의 분산은 어떻게 구해야 할까?

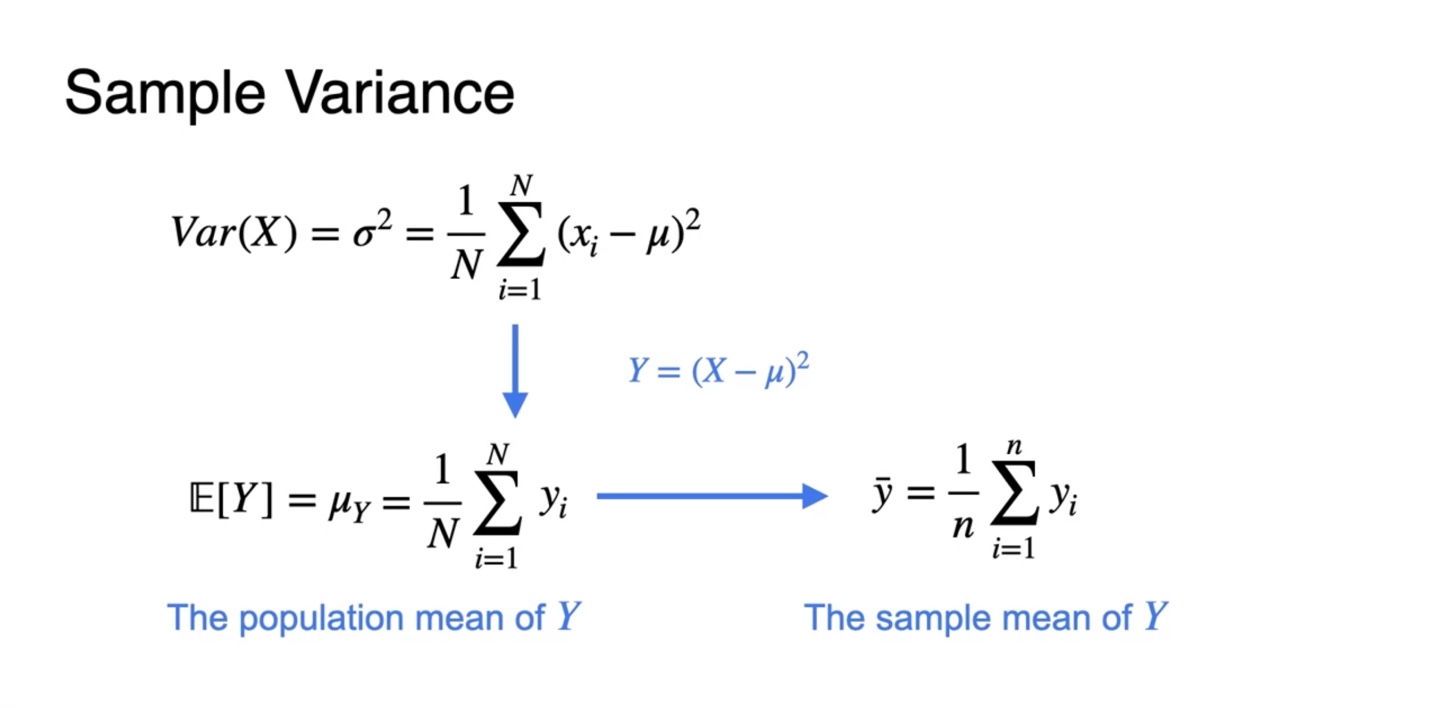
• 만약 확률 변수 $Y$가 $(X-\mu)^2$과 같다고 한다면, population의 mean은 $\mathbb E[Y]$와 같다.

  • $Var(X) = \sigma^2 = \displaystyle \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2$

    $\Rightarrow \mathbb E[Y] = \mu_Y = \displaystyle \frac{1}{N} \sum_{i=1}^{N} y_i$

• 예를 들어, $n$개의 sample을 추출한 확률 변수 $Y$의 표본 평균을 구하고자 한다면 아래와 같은 수식을 구함으로써 해결할 수 있다.

  • $\bar{y} = \displaystyle \frac{1}{n} \sum_{i=1}^{n} y_i$

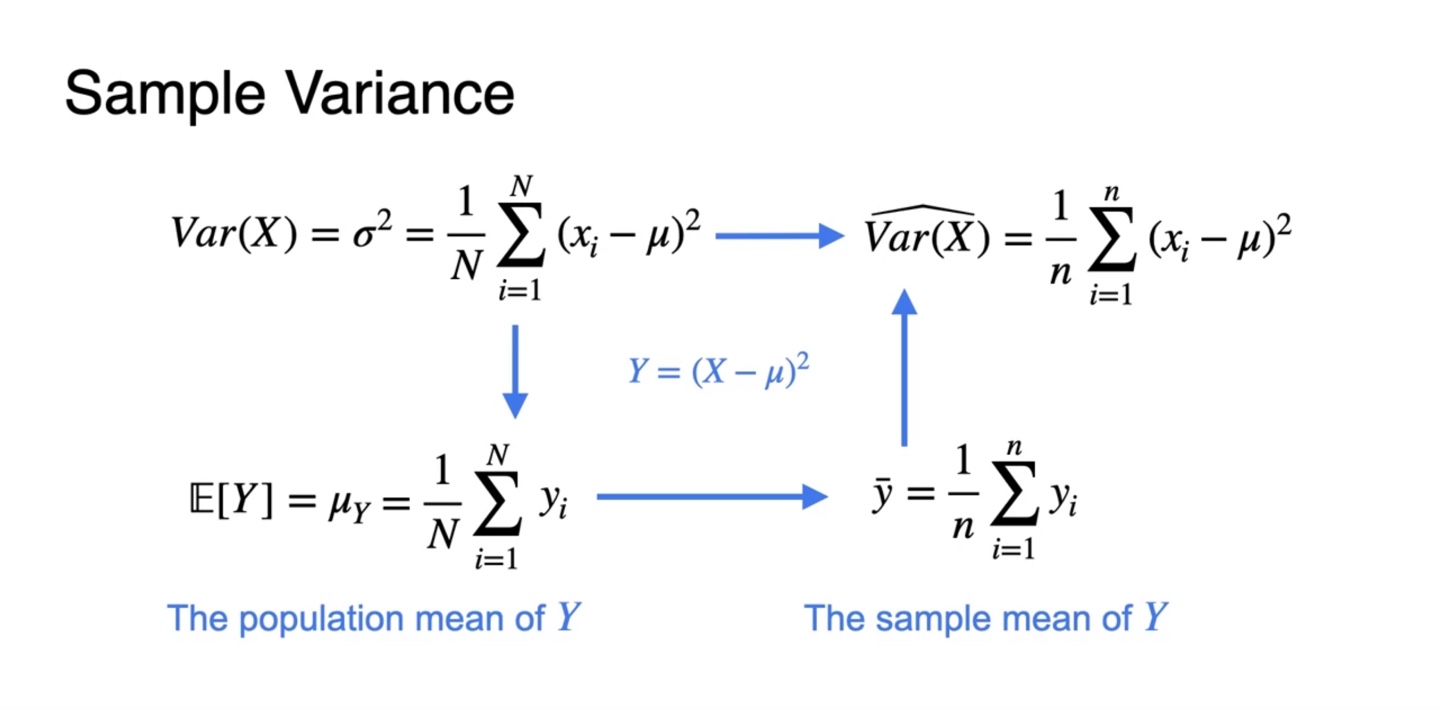
• 이를 다시 확률 변수 $X$로 표현하면 $\widehat{Var(X)}$ 기호로 표기하며 수식은 아래와 같다.

  • $\widehat{Var(X)} = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2$

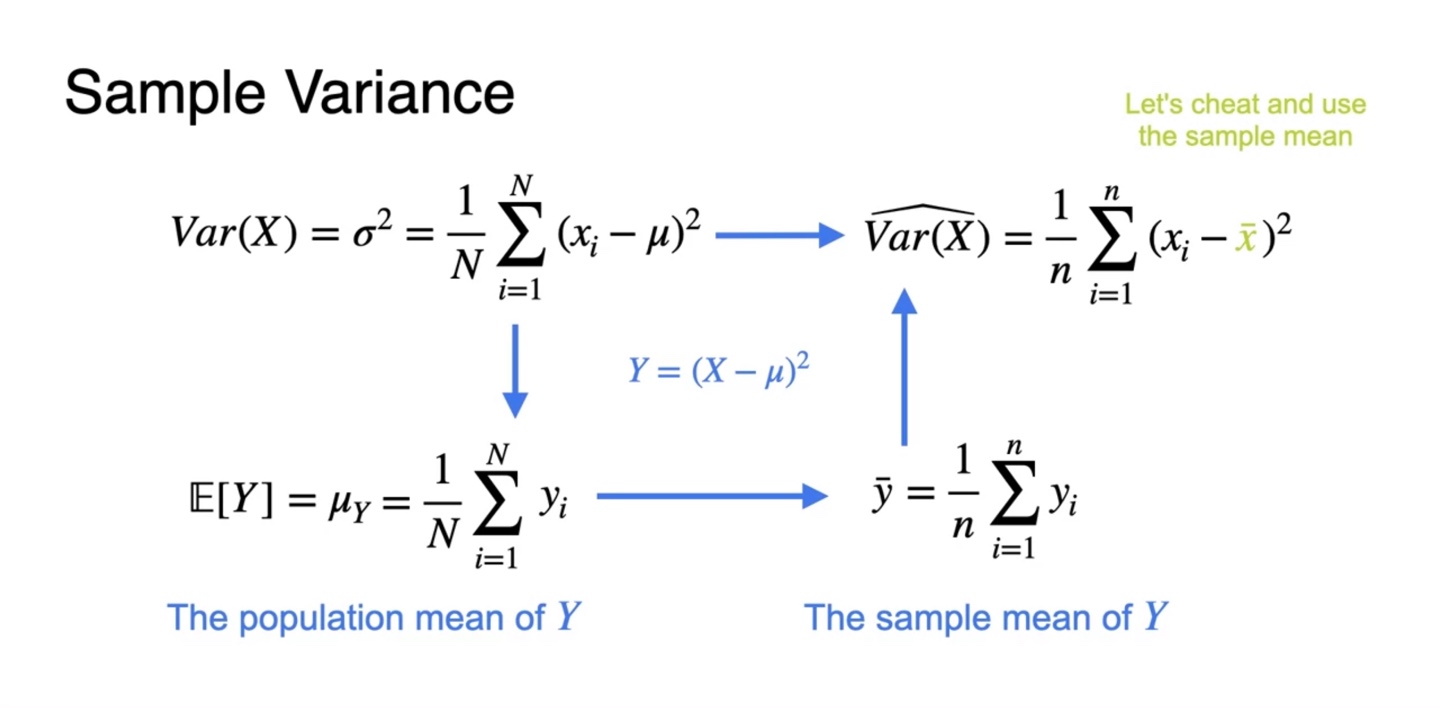
• 이 때 사용된 mean $\mu$는 popular mean이므로, sample mean인 $\bar{x}$를 이용할 필요가 있다.

  • 따라서 $\widehat{Var(X)} = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2$와 같이 수식을 바꿔 variance를 다시 구해보도록 하자.

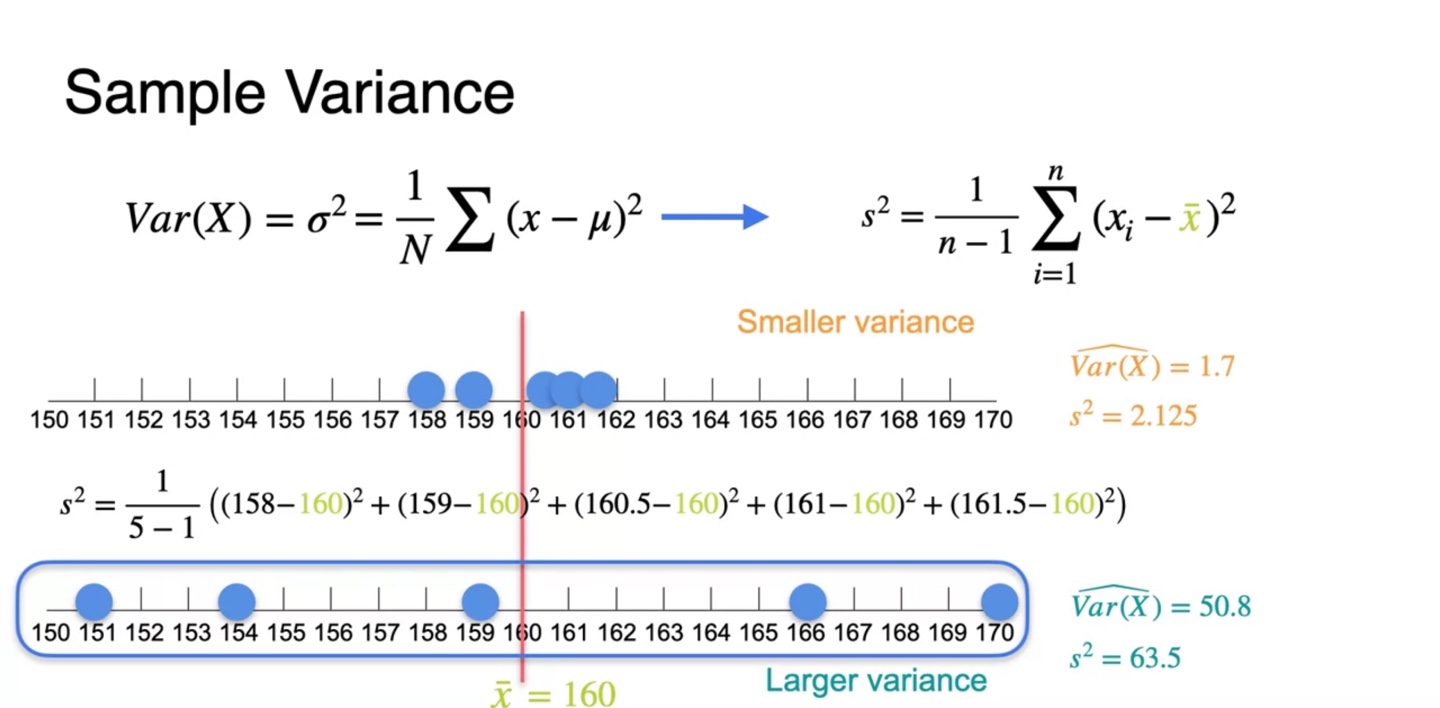
• 첫 번째 sample의 $\widehat{Var(X)}$을 구하면 1.7로 계산된다.

  • 이 때 사용된 평균값은 $\mu$를 대체한 sample mean $\bar{x}$다.

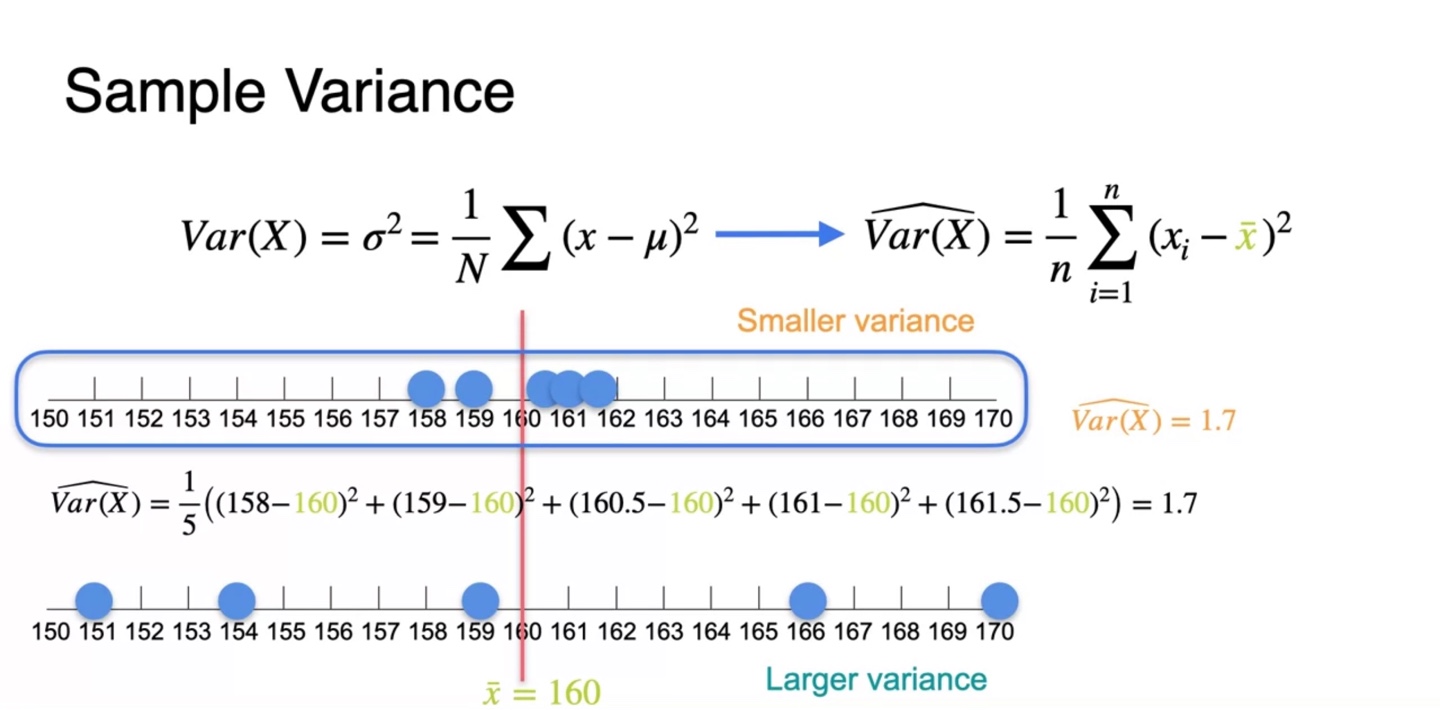
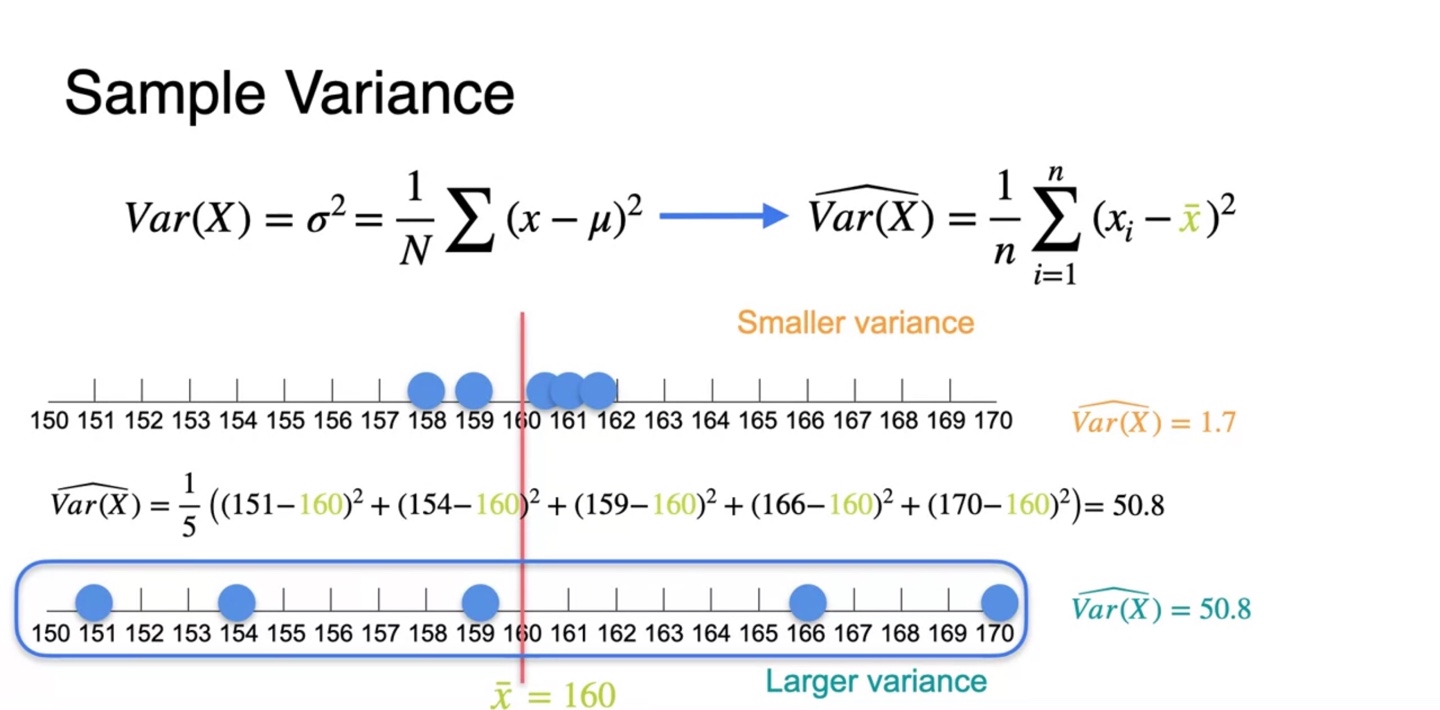
• 두 번째 sample의 $\widehat{Var(X)}$는 50.8로 계산된다.

  • 마찬가지로 sample 평균값 $\bar{x}$은 160이며 위 예시에 비해 각 변수들 사이의 관계가 약 7배만큼 차이가 나는 것을 알 수 있다.

    • 이를 통해 variance는 $7^2$배의 값으로 추정된다는 점도 계산 없이 알아낼 수 있다.

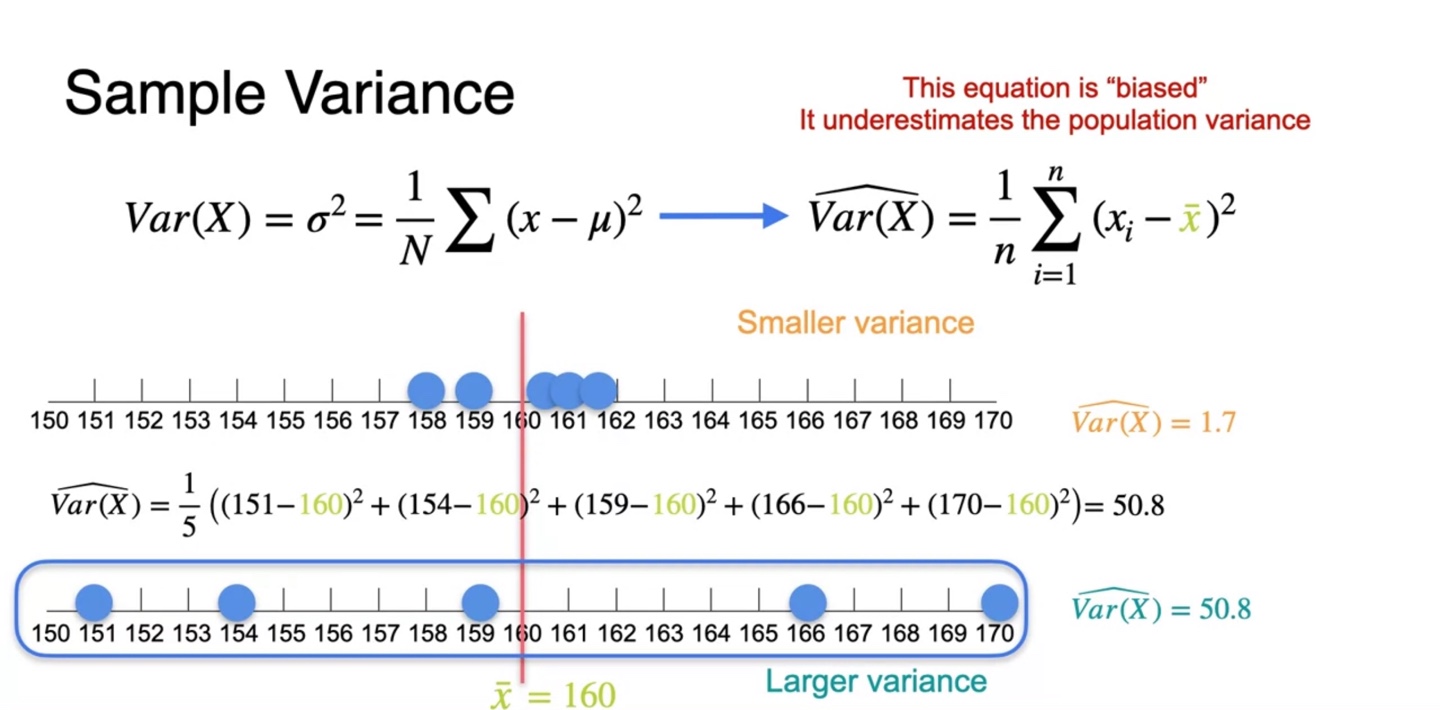
• 그러나 현재 sample variance를 구하는 공식은 다소 "biased"되어 있다고 표현한다.

  • 현재의 $\widehat{Var(X)}$ 공식으로는 population variance를 정확하게 계산할 수 없다!

• 아래와 같은 예를 들어보자.

  • 모자에 1, 2, 3 카드를 넣고 하나씩 뽑는 상황이다.

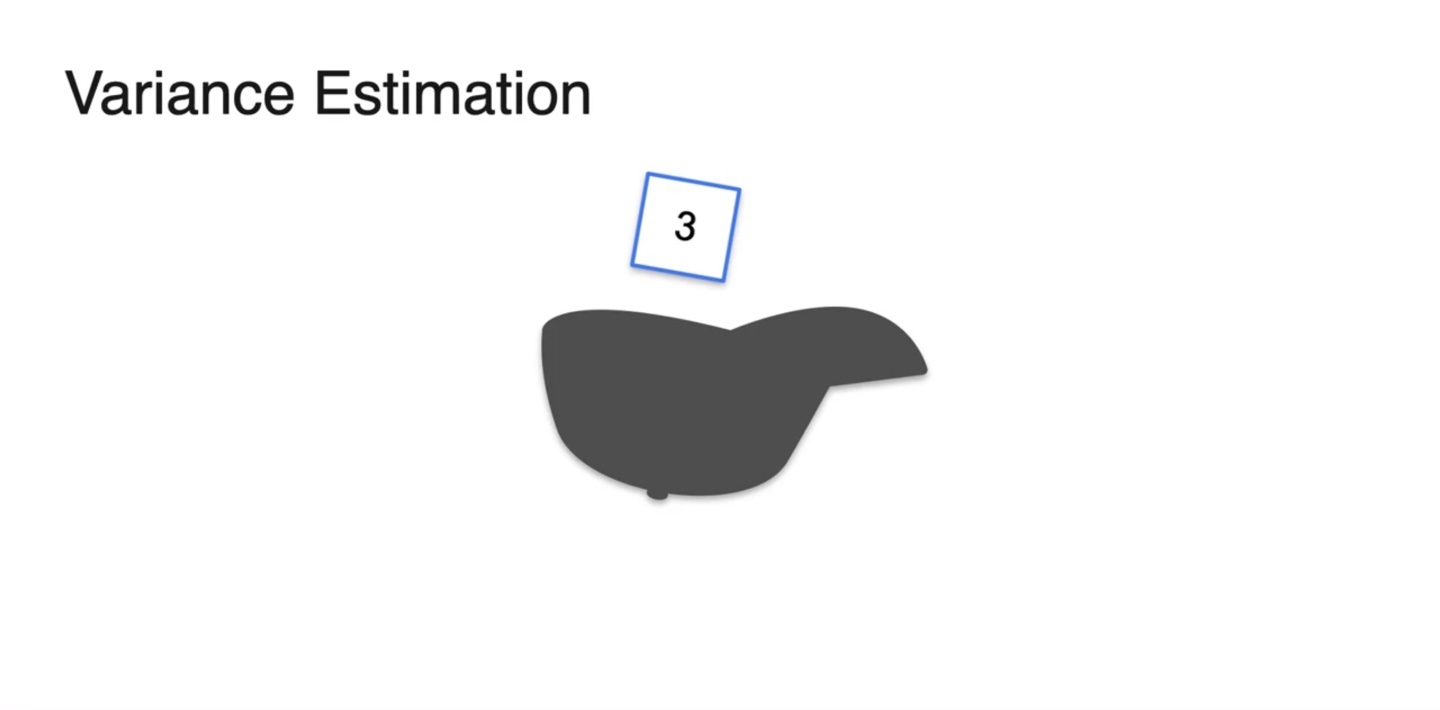
• 한 번의 시행에서 얻을 수 있는 평균값 $\mu$는 $\mu = \displaystyle \frac{1+2+3}{3} = \frac{6}{3} = 2$로 계산된다.

• Variance는 각 확률 변수와 평균 $\mu$의 차이를 제곱한 평균으로 계산한다.

  • 이를 통해 population variance($\sigma^2$)를 계산한 결과 $\displaystyle \frac{2}{3}$으로 계산되었다.

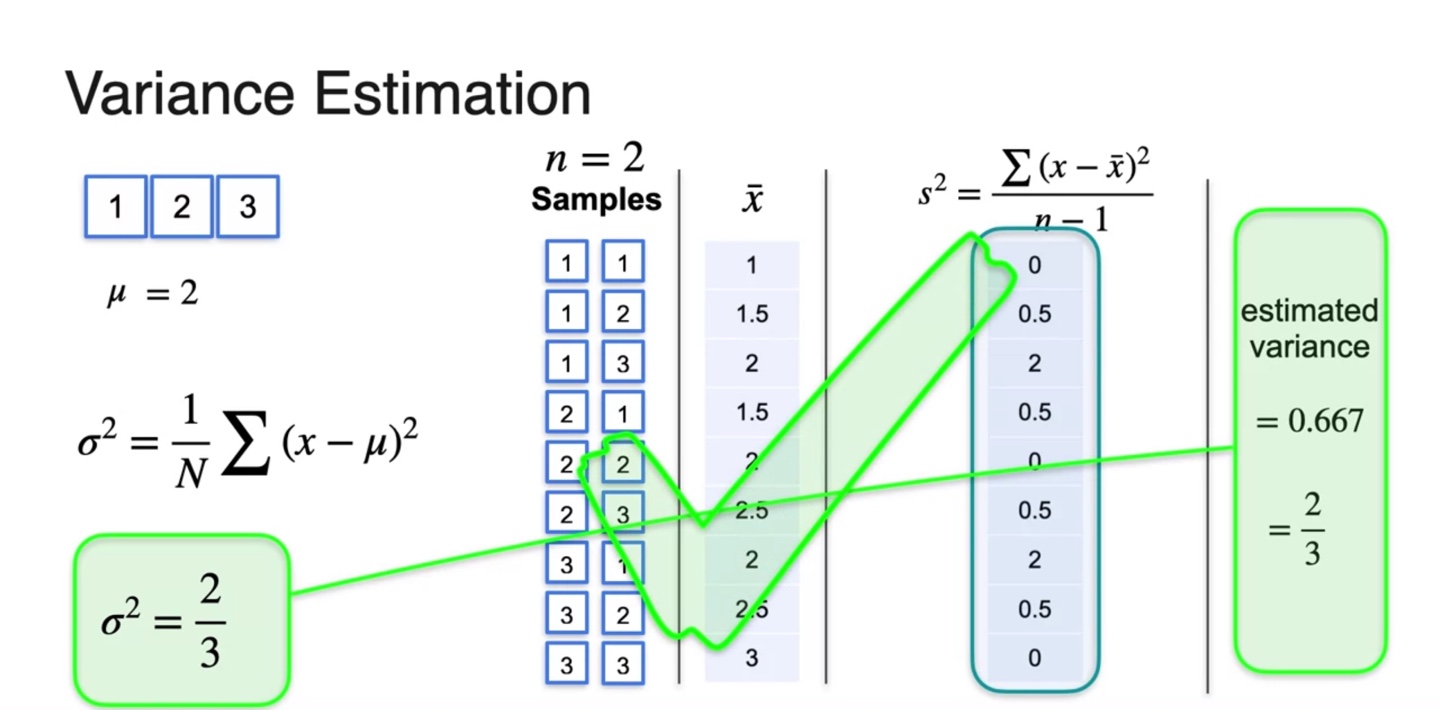
• 이제 $n=2$의 크기로 sample을 뽑아 각 sample의 평균을 계산하여 sample mean $\bar{x}$과의 차이로 variance를 구해보자.

  • 계산 결과 $\displaystyle \frac{1}{3}$로 계산되었으나 실제 population variance $\displaystyle \frac{2}{3}$와 다소 차이를 보인다.

• 여기서 중요한 개념인 sample variance에 대한 수식이 나온다.

  • $s^2 = \displaystyle \frac{\sum (x-\bar{x})^2}{n-1}$ 즉, $n$이 아닌 $n-1$로 나누는 조정 작업이 필요하다!

    • 이렇게 되면 실제 population variance인 $\displaystyle \frac{2}{3}$의 값을 얻어낼 수 있음을 알 수 있다.

• $n-1$의 역할은 bias를 fix하는 의미를 갖는다.

  • 매우 적은 data라면 $n$과 $n-1$의 차이가 크게 나타날 것이므로, statistical technique인 $n-1$을 나눠주는 과정이 필요하다.

• 위와 같은 수식으로 기존 예제의 sample variance를 다시 계산한 결과 1.7에서 2.125로, 50.8에서 63.5로 증가했음을 알 수 있다.

  • $n$이 아니라 $n-1$로 나누었기 때문에 분모가 더 작아져 값이 커진 것이라 이해하면 된다.

• Population variance와 Sample variance의 formula는 아래와 같은 차이를 가진다.

  • Population variance : $Var(X) = \sigma^2 = \displaystyle \frac{1}{N} \sum (x-\mu)^2$

  • Sample variance : $s^2 = \displaystyle \frac{\sum (x-\bar{x})^2}{n-1}$ or $\widehat{\sigma^2} = \widehat{Var(X)} = \displaystyle \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n}$

    • 데이터가 충분히 크다면 $n$으로도 sample variance를 나타내는 데에 문제가 없을 수 있으나 $n-1$을 활용하는 것이 common sample variance라고 한다.

Law of Large Numbers

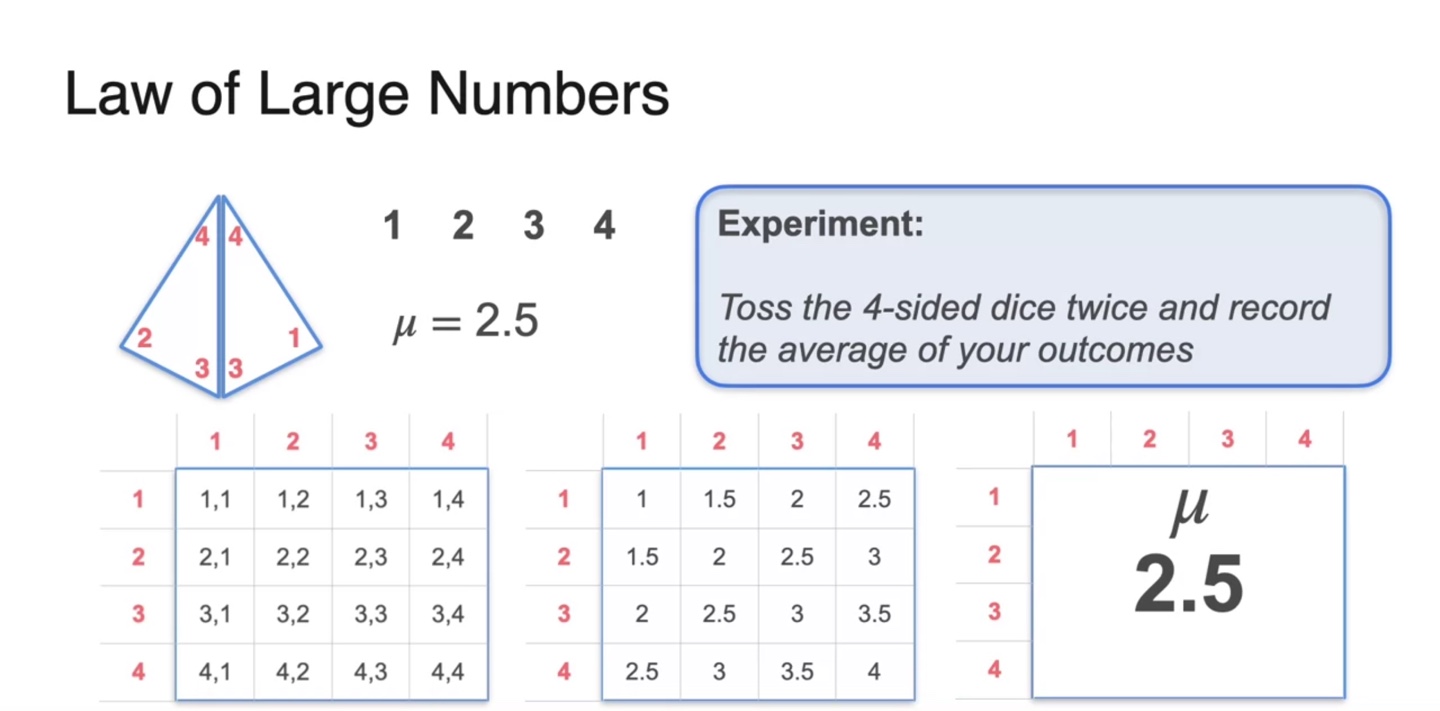
• Law of Large Numbers, 큰 수의 법칙에 대해 알아보자.

  • 4개의 variables를 갖는 dice를 굴리는 상황에서, 다음과 같은 $n=2$의 sample 평균치를 얻어 전체 population mean $\mu$를 계산한 결과 2.5가 얻어졌다.

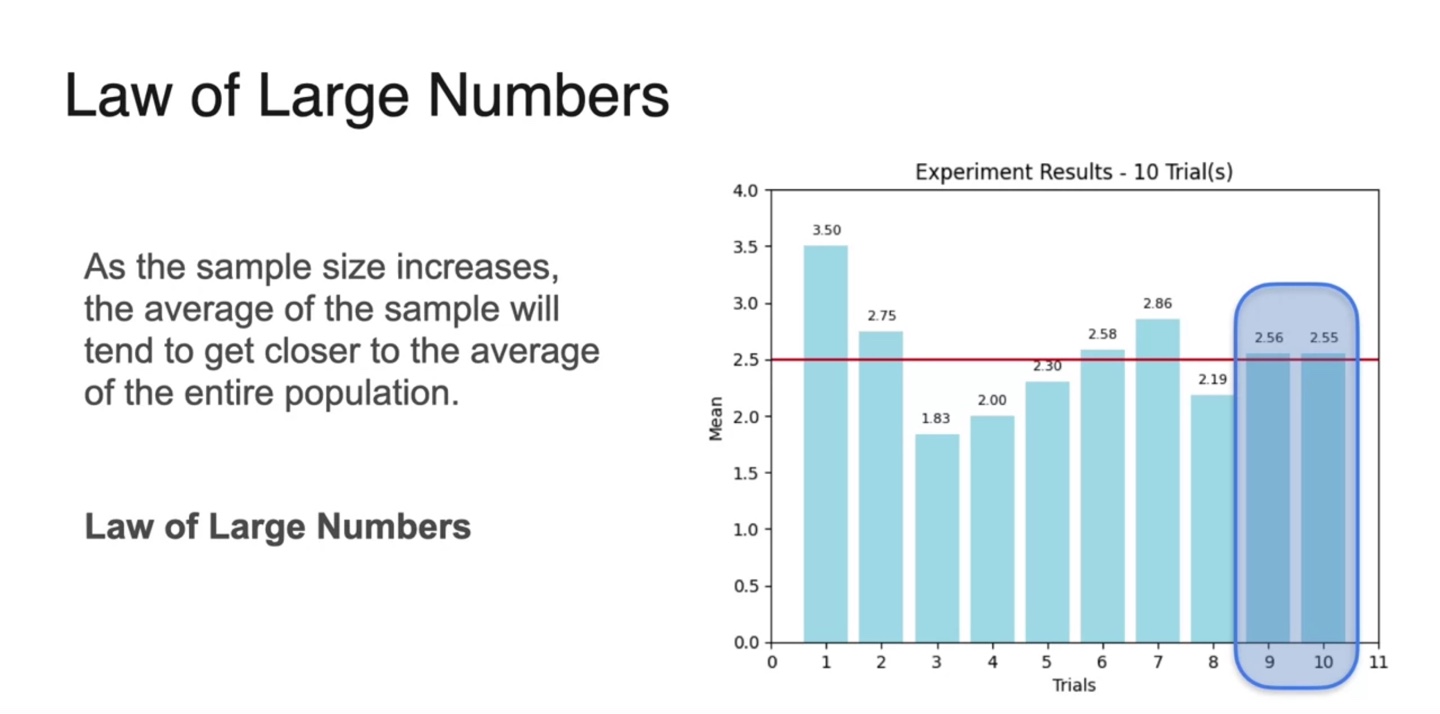
• Population mean인 $\mu=2.5$를 빨간색 선으로 표현하여 여러 sample 값들의 평균을 기록해보자.

  • 1번의 trial로 (4, 3)의 sample이 얻어졌고, 평균낸 결과($\bar{x}_1$)를 오른쪽에 나타내었다.

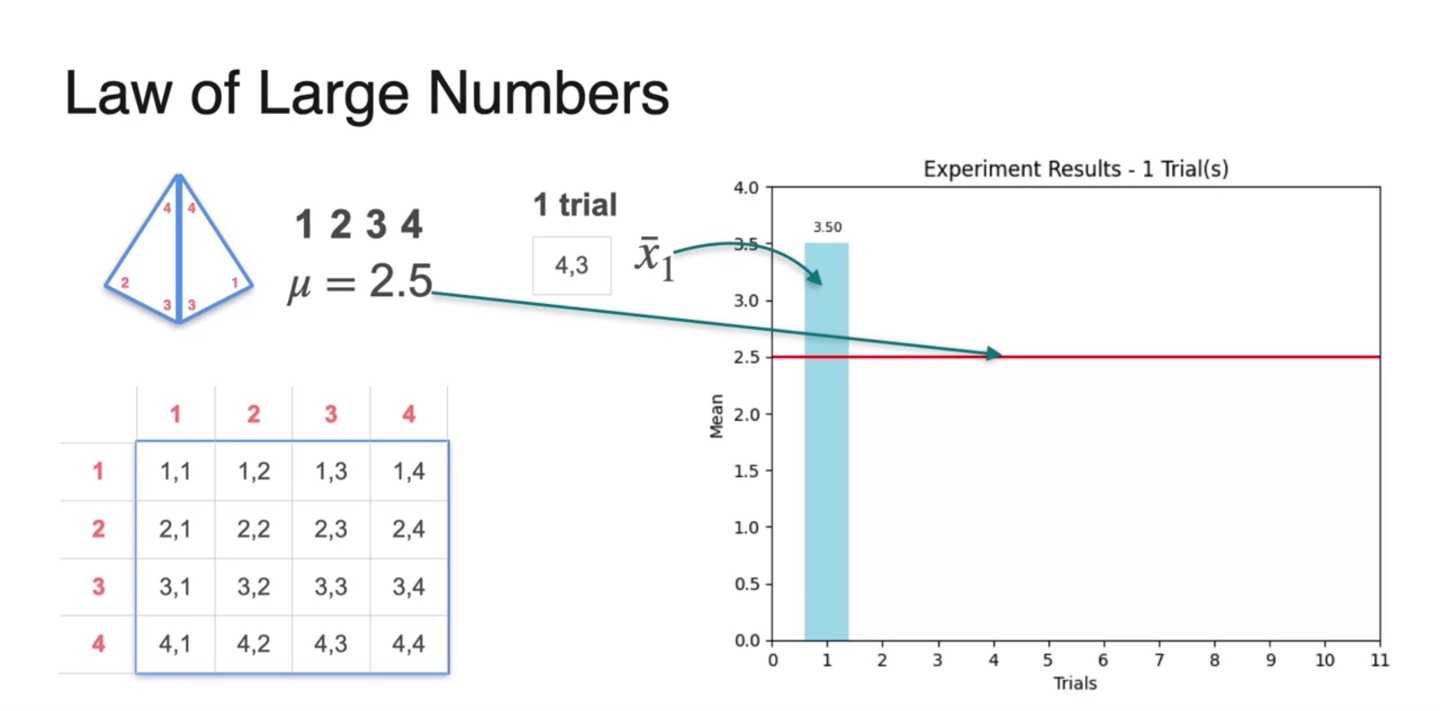
• 그런 다음 2번의 trial을 가중 평균으로 구한 값, 2.75를 오른쪽에 표현하였다.

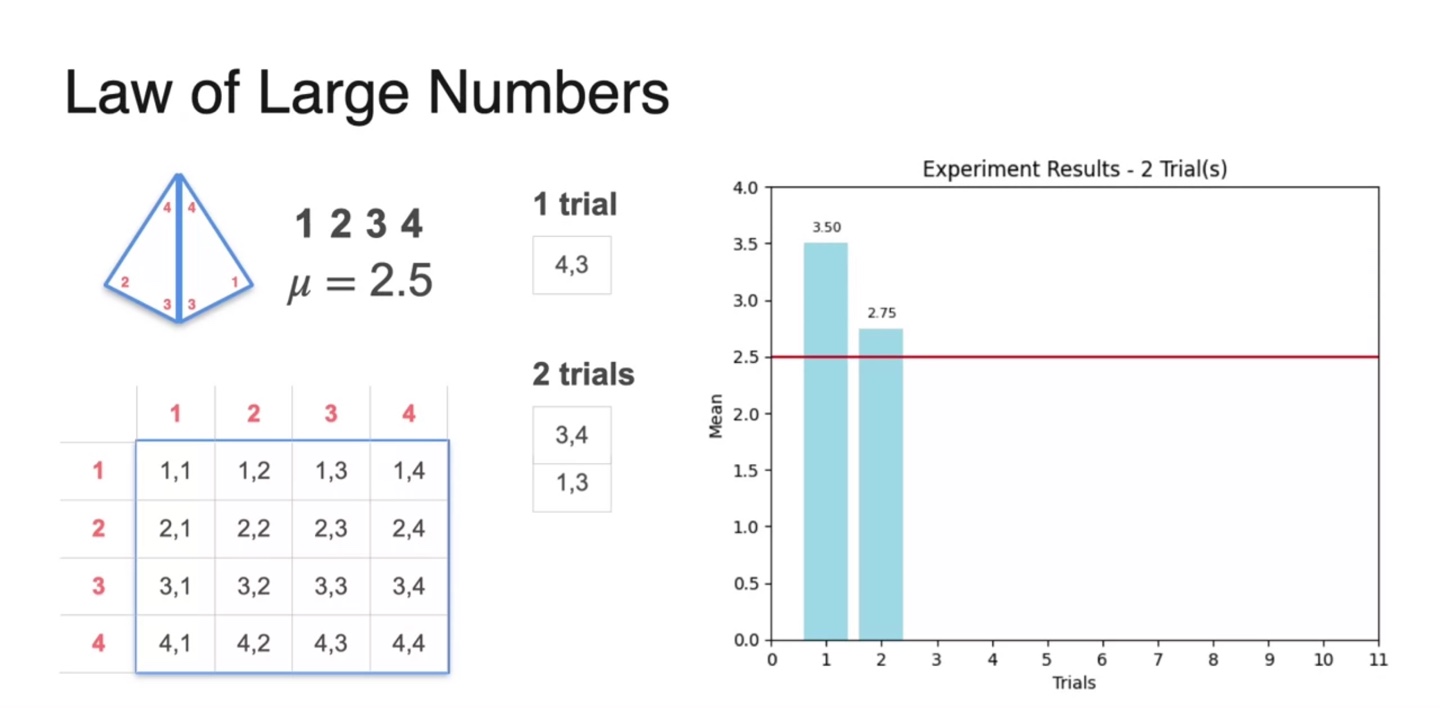
• 3번, 4번의 trial을 통해 얻어낸 평균치들을 계속해서 기록했다.

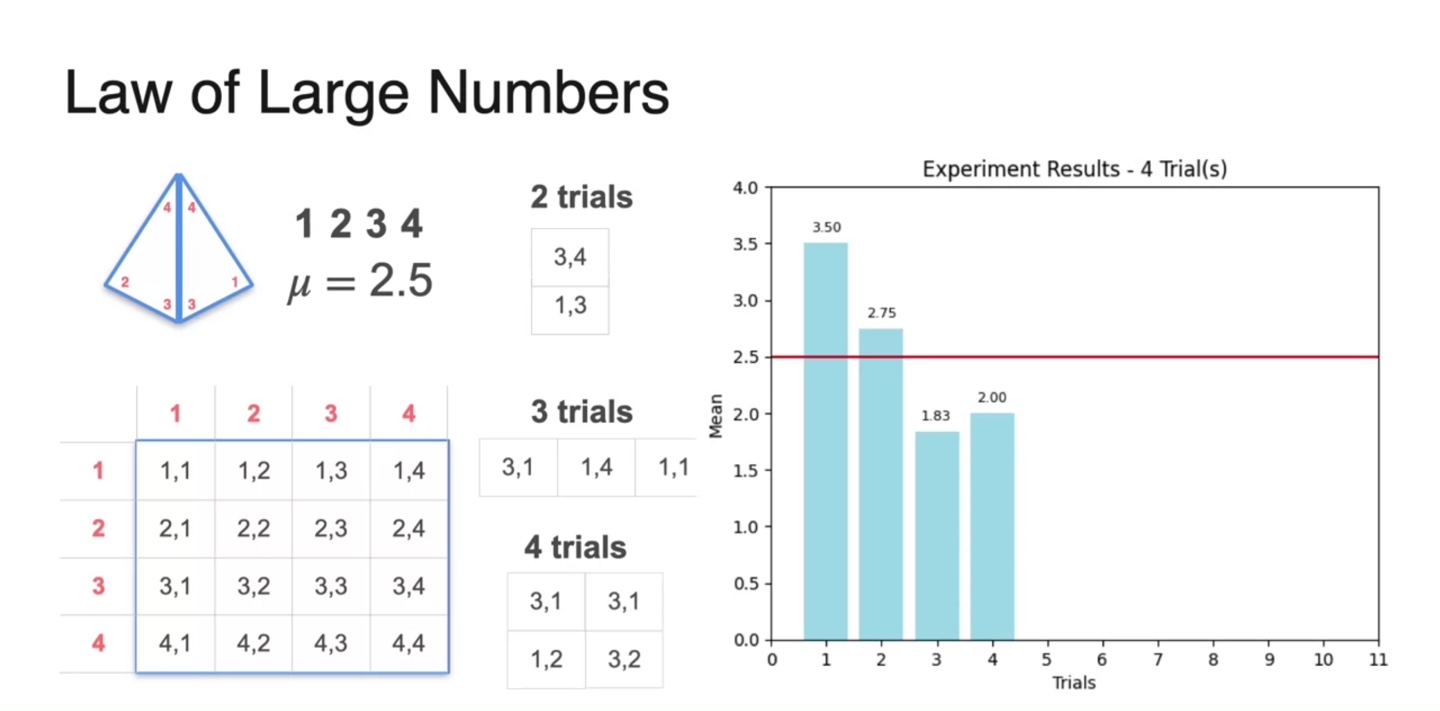
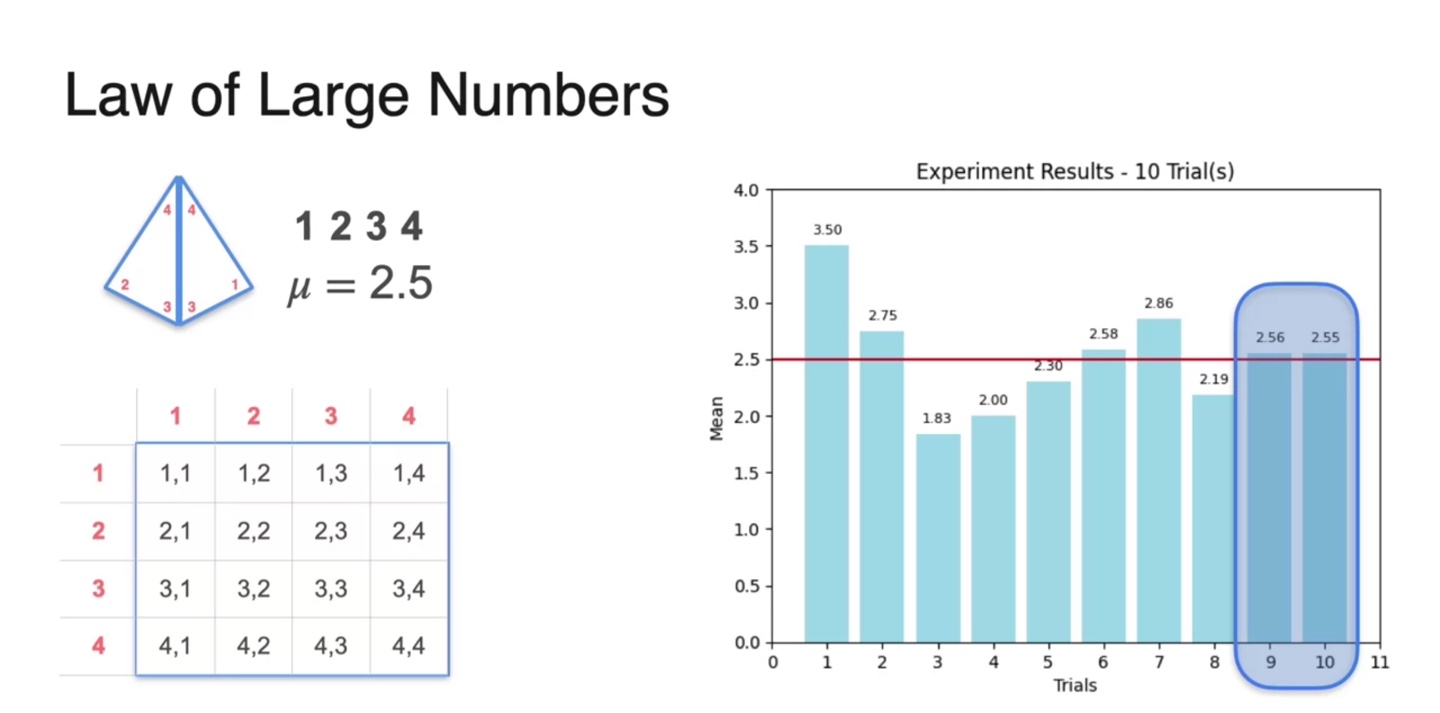
• 그러자 9번에서 10번의 trial로 얻은 평균치가 $\mu$인 2.5에 다소 가깝게 얻어졌다.

  • 이를 통해 적당히 큰 $n$으로 sample을 얻어내면 population mean에 근접할 수 있다는 점을 우리는 추측할 수 있다.

• 이러한 법칙을 Law of Large Numbers, "큰 수의 법칙"이라 한다.

  • 확률 변수 $X$가 i.i.d를 따르고 무한대에 가깝도록 매우 큰 숫자라면 sample의 expected value가 전체 $\mathbb E[X] = \mu_{X}$를 대신할 수 있을 정도가 된다.

    • 즉, 매우 큰 수로 변수를 sampling하면 전체 모집단의 평균과 같은 값이 된다고 봐도 무방하다.

• 아래와 같은 조건일 때 말이다.

  1. Sample이 random하게 뽑혀야 한다.
  2. Sample size가 충분히 커야 한다.
  3. 관측의 결과가 independent해야 한다.

Central Limit Theorem - Discrete Random Variable

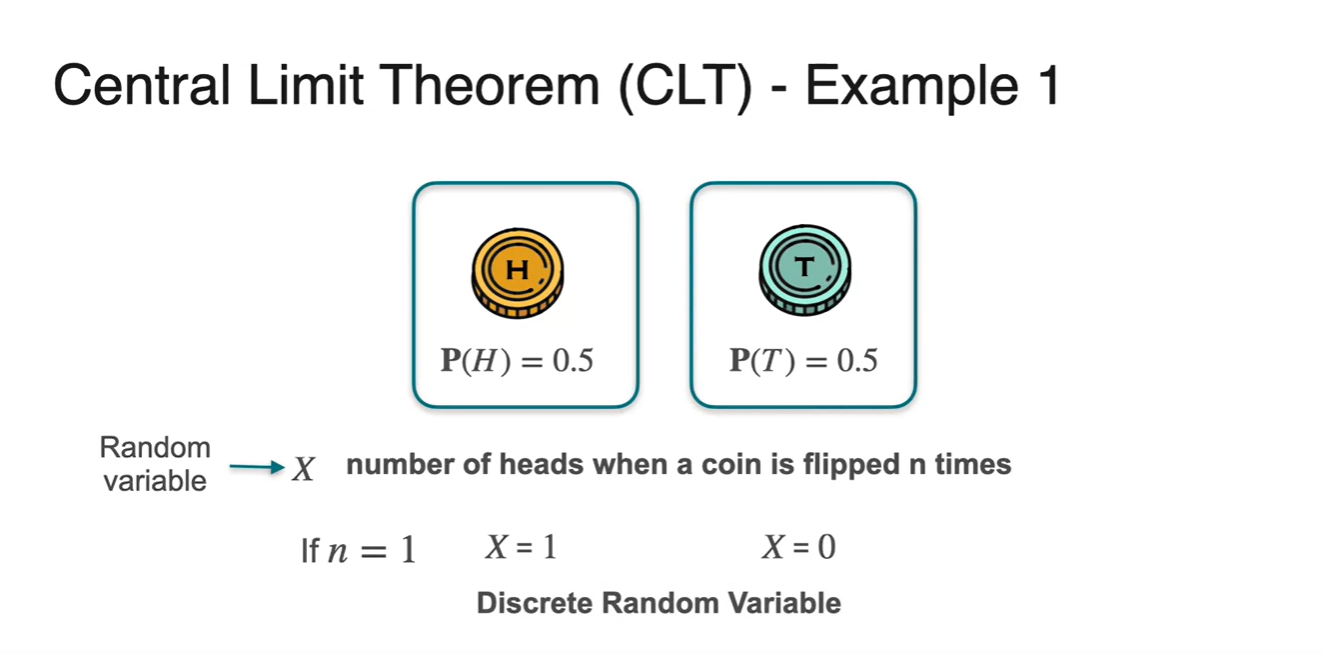
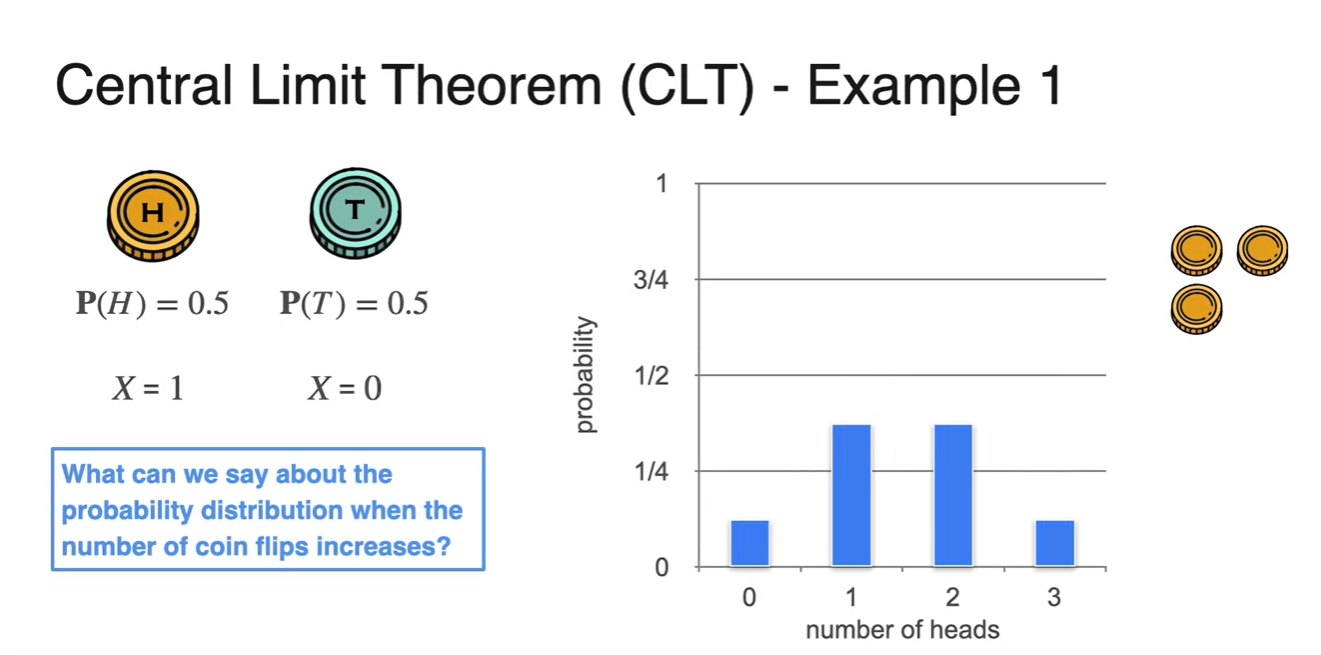
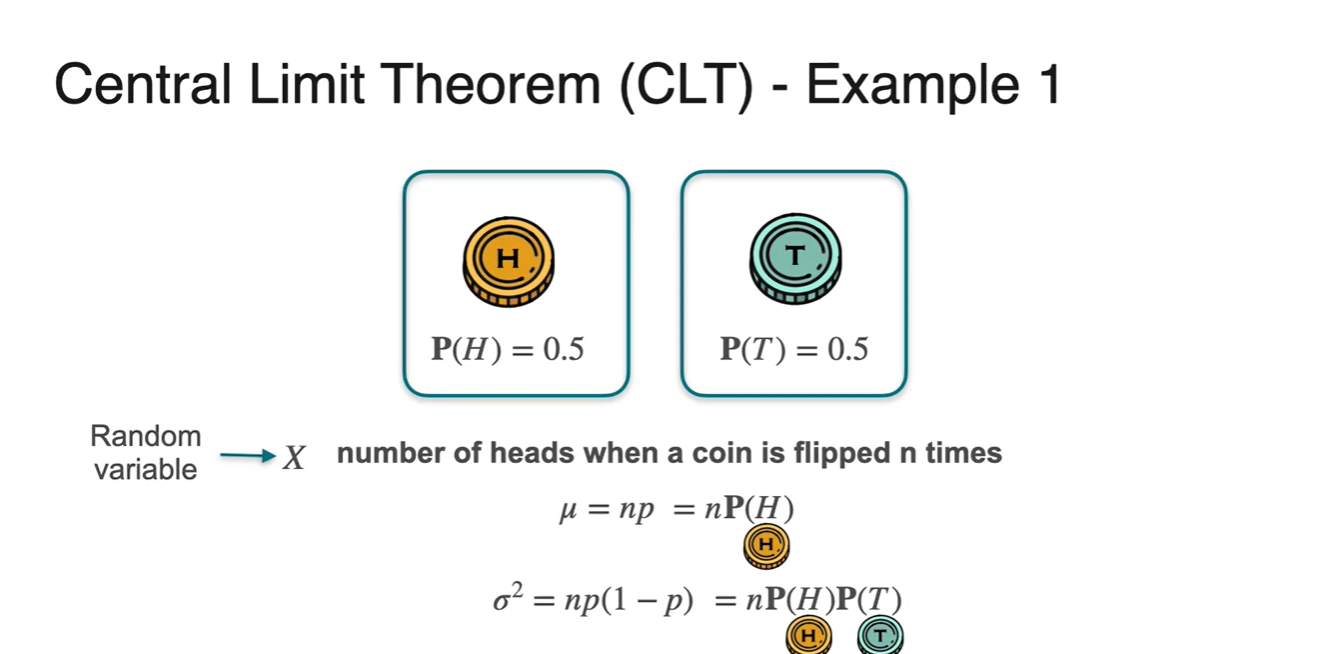
• 아래와 같은 동전 던지기 예시를 들어 중심 극한 정리, CLT에 대해 알아보자.

  • 만약 시행 횟수가 1번이라면 Head의 확률 변수를 1, Tail의 확률 변수를 0로 discrete하게 나타낼 수 있다.

• 한 번의 시행으로 얻을 수 있는 확률은 아래와 같이 둘 다 1/2이다.

  • 이를 Bernoulli(베르누이) distribution으로 나타내면 다음과 같은 그래프를 얻게 된다.

    • 만일 여러 번의 시행을 반복하면 어떤 분포를 갖게 될까?

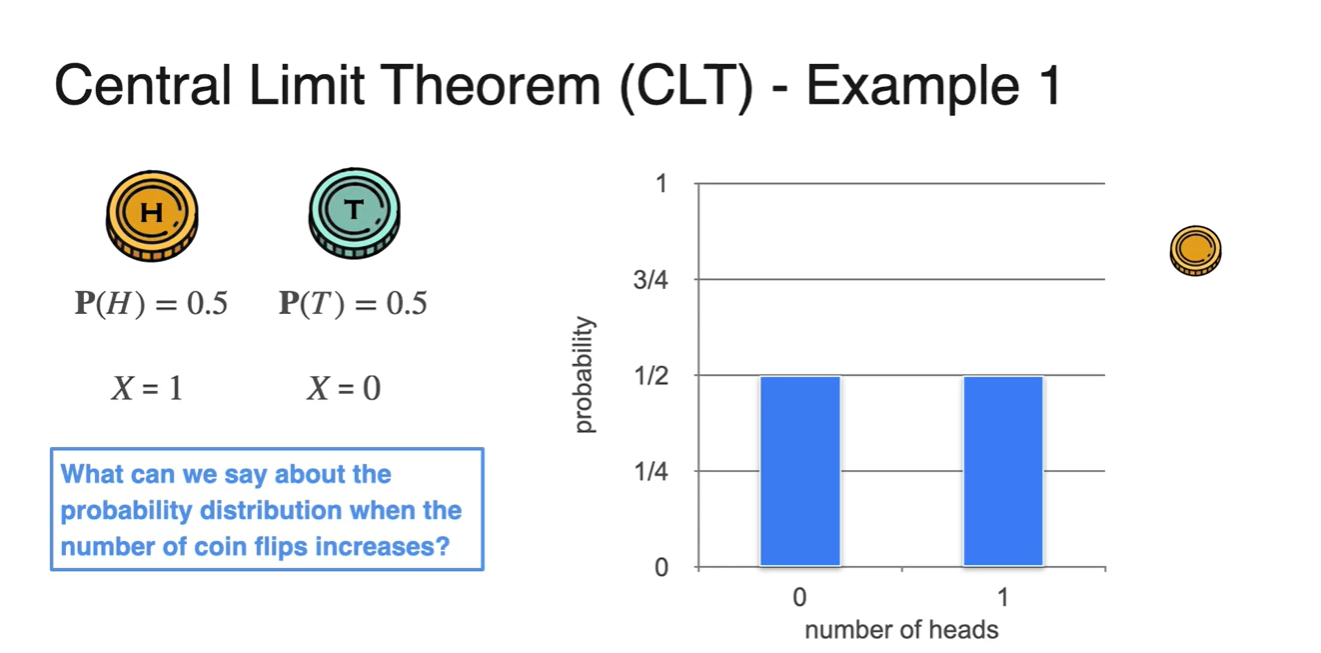
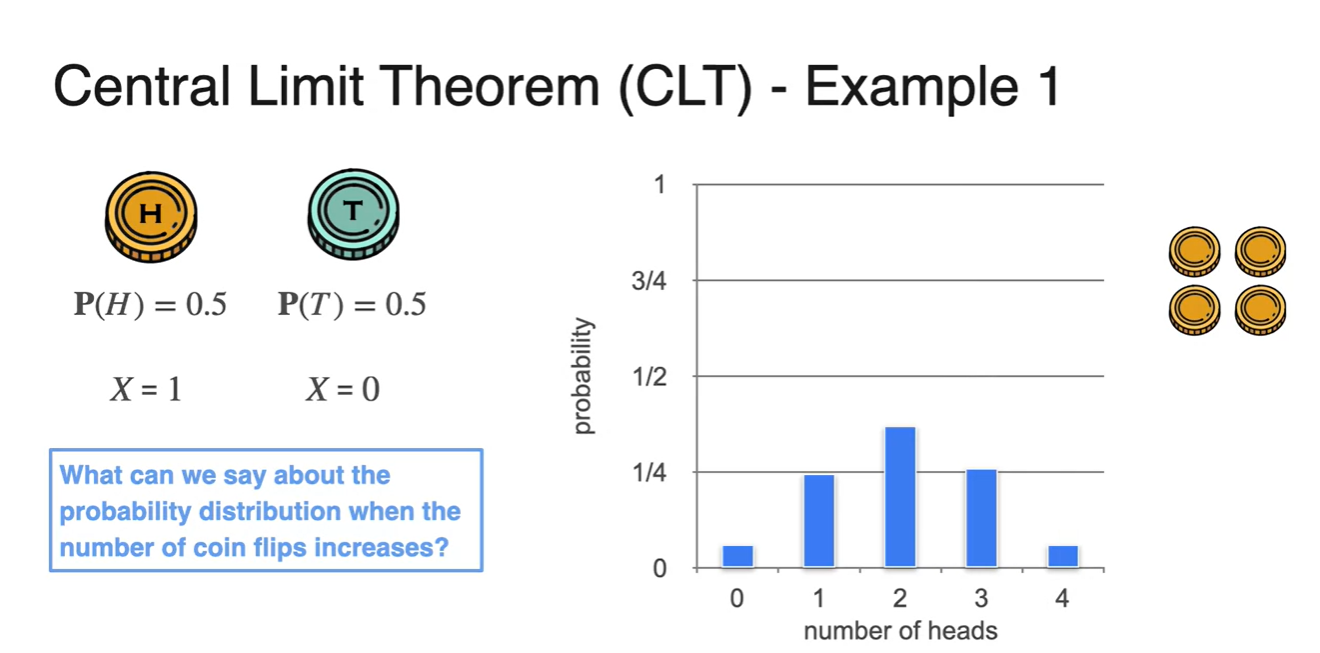
• 아래 펼쳐질 그래프들은 Bernoulli 분포를 갖는 동일한 동전을 2개, 3개, 10개 반복하여 얻어낸 ditribution이다.

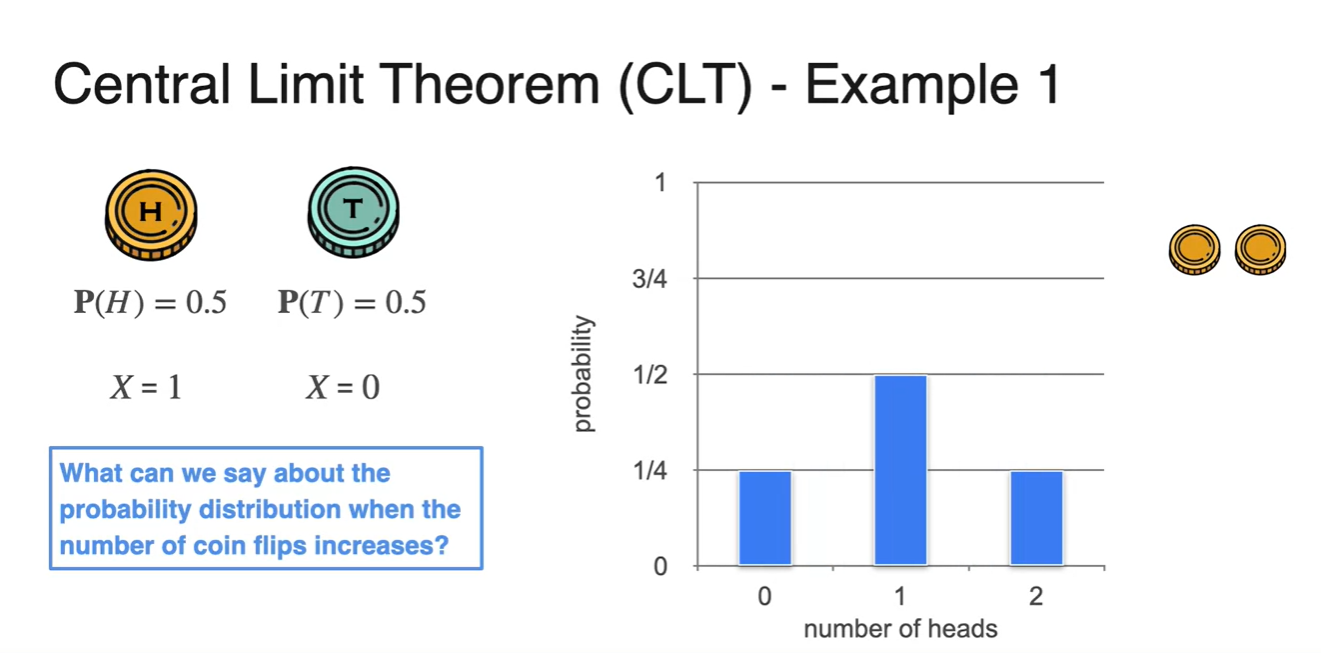
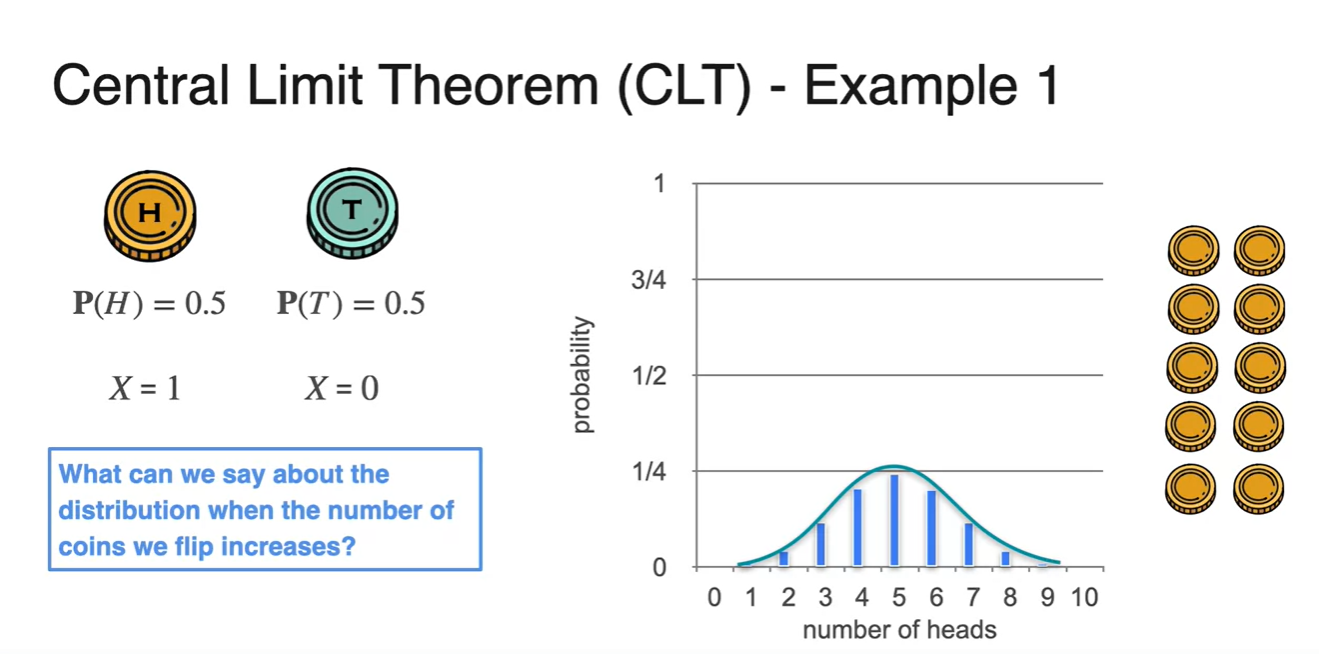
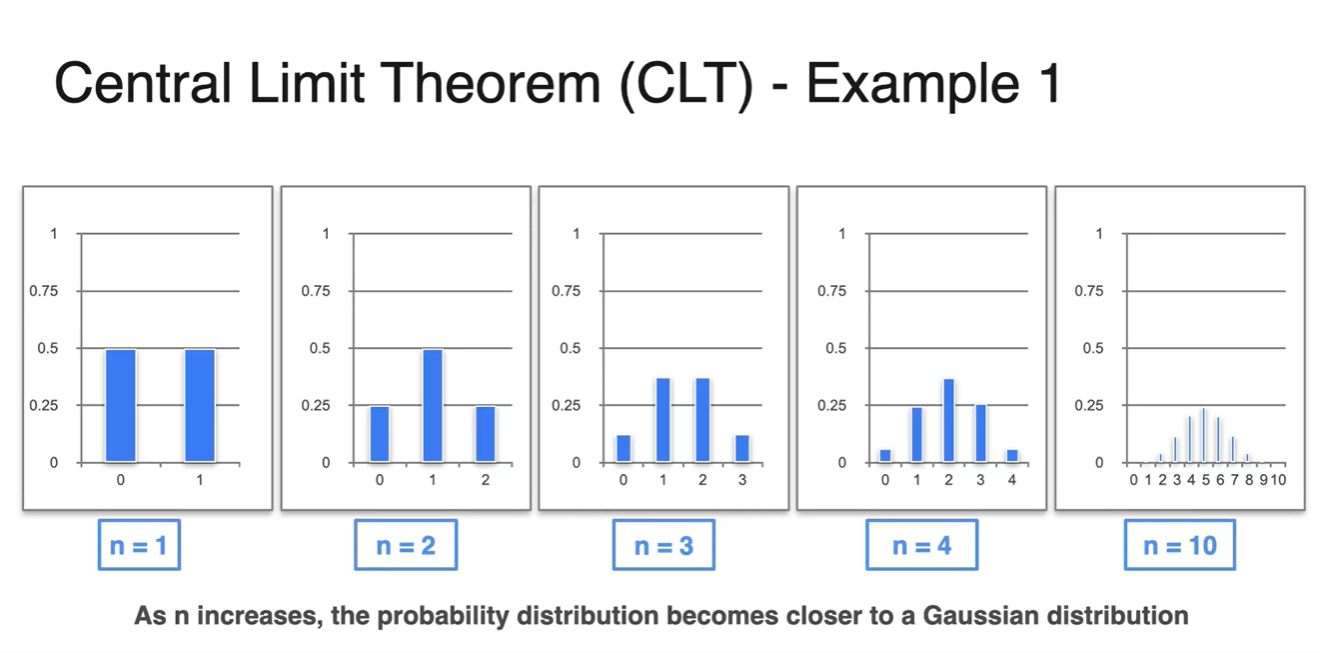
• 실험 결과 분포의 모양이 점점 bell shape 즉, 종 모양을 갖는 Normal ditribution과 비슷해진다는 것을 알 수 있었다.

• Binomial distribution(Bernoulli distribution을 따르는 사건을 n번 시행)의 평균과 분산을 구하는 공식은 아래와 같다.

  • Mean : $\mu = np = nP(H)$
  • Variance : $\sigma^2 = np(1-p) = nP(H)P(T)$

• 만약 시행 횟수 $n=1$이라면 평균 $\mu$와 분산 $\sigma^2$는 아래와 같이 계산된다.

  • Mean : $\mu = np = 1 \times 0.5 = 0.5$
  • Variance : $\sigma^2 = np(1-p) = (1 \times 0.5)(0.5) = 0.25$

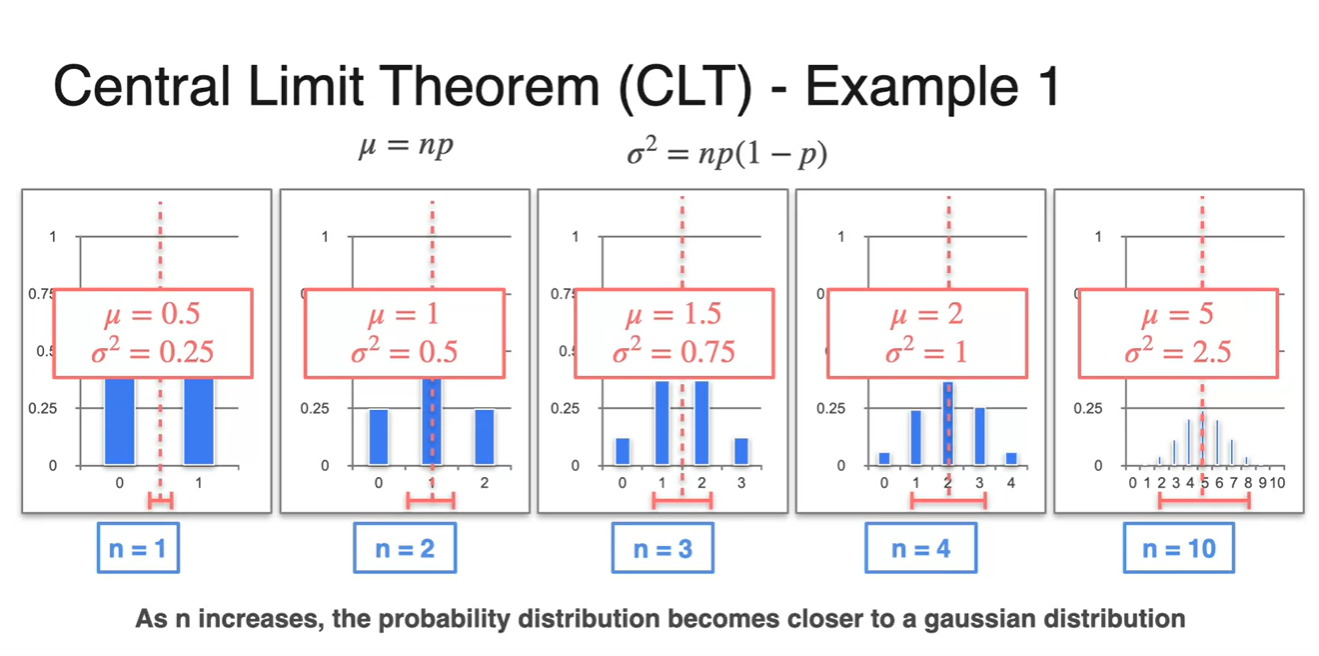
• 여러 번 시행한 결과에 따라 평균과 분산을 구해보면 다음과 같은 결과를 얻을 수 있다.

  • 공통점은 평균이 Random variables의 중간 지점을 따른다는 점과 분산이 중심으로부터 symmetric하다는 점이다.

• 따라서 시행 횟수 $n$(samples 개수)이 늘어날수록 Normal distribution에 가까워진다.

  • 이러한 정리가 바로 Central Limit Theorem, CLT이다.

Central Limit Theorem - Continuous Random Variable

• 이번에는 변수가 Continuous한 경우에서의 CLT를 정의해보자.

  • 상담을 받기 위해 기다린 시간을 확률 변수 $X$로 설정하고, 0부터 15까지의 값으로 쪼개어 각 범위에 놓인 확률을 uniform distribution으로 가정한다.

    • $X \sim u(0, 15)$

• $n$번의 실험으로 얻은 확률 변수 $X$들의 평균을 새로운 변수 $Y_n$으로 표기해보자.

  • 기존 확률 변수 $X$의 samples 평균인 새로운 변수 $Y$의 distribution은 어떻게 생겼을까?

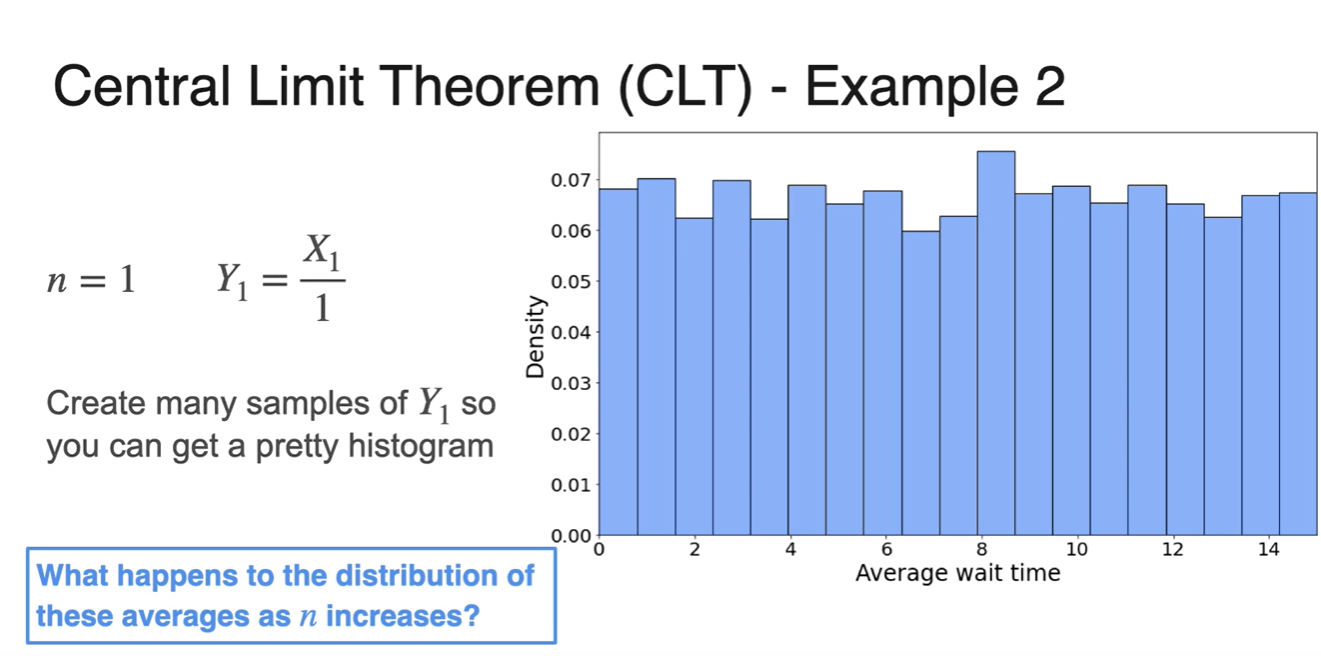
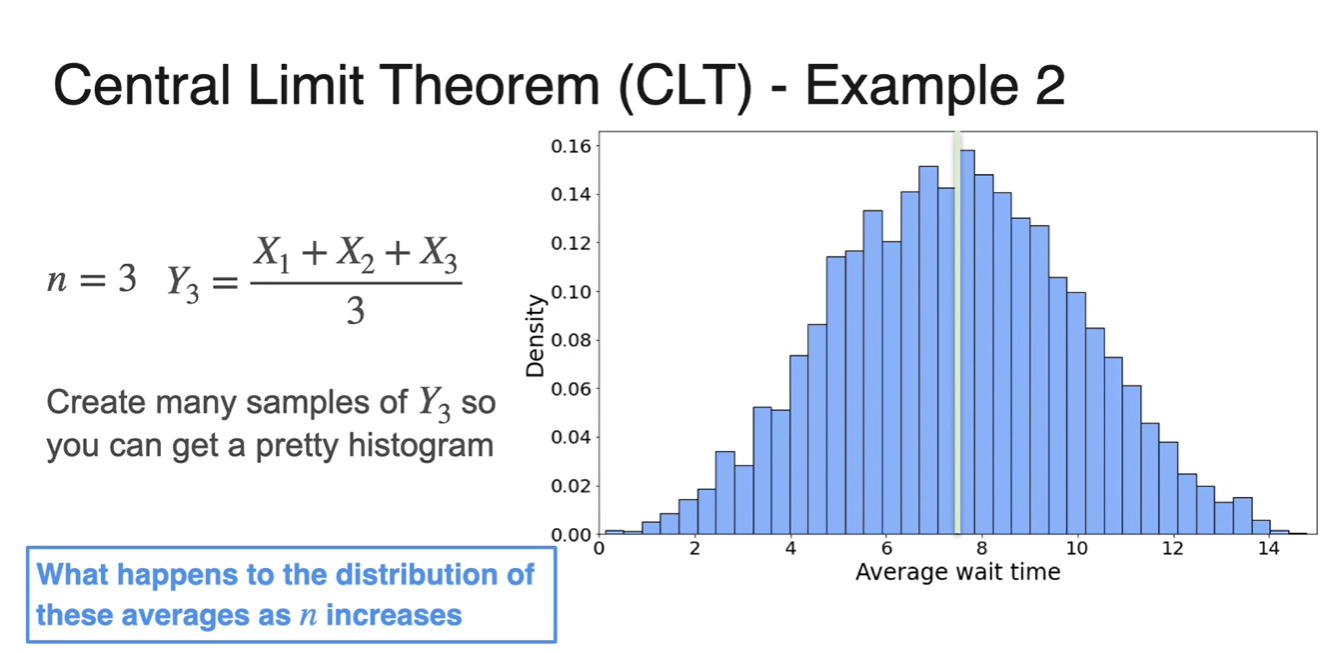
• $n=1$이라면 확률 변수 하나만 뽑아서 나타내었을 때의 분포를 말한다.

  • 시행 횟수가 1이므로 변수의 합($X_1$ only)에 나눠지는 값이 1이다.

    • 이는 기존 분포인 uniform ditribution과 거의 동일함을 알 수 있다.

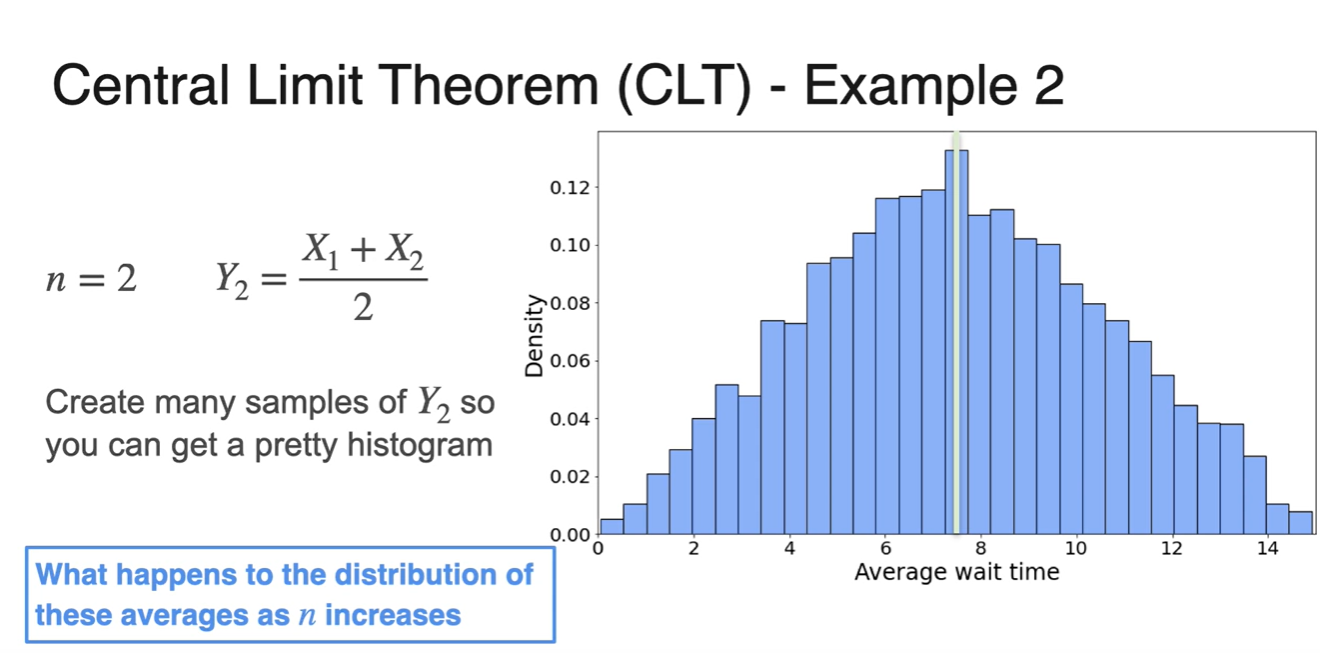
• $n=2$라면 확률 변수 두 개를 뽑아 평균내었을 때의 분포를 말한다.

  • 시행 횟수가 2이므로 $X_1$과 $X_2$ 변수의 합에 나눠지는 값이 2이다.

    • 기존 분포보다 종모양에 가깝고 평균이 중앙값에 위치한다는 점을 알 수 있다.

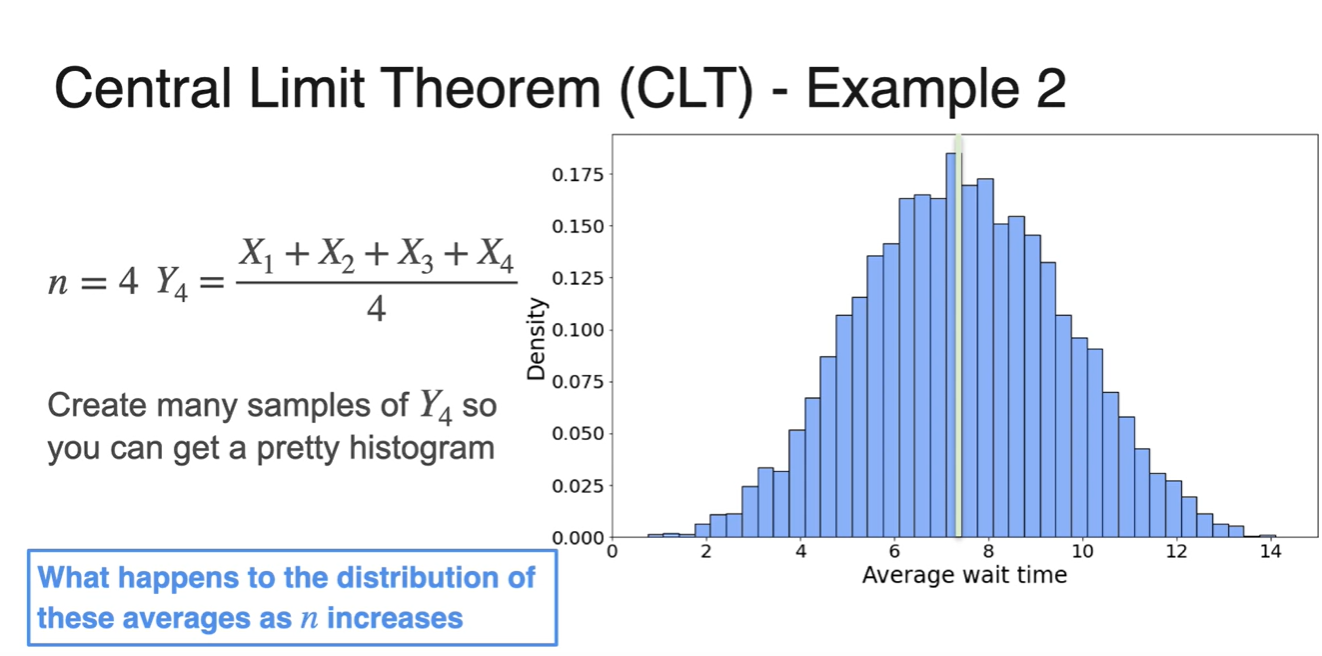
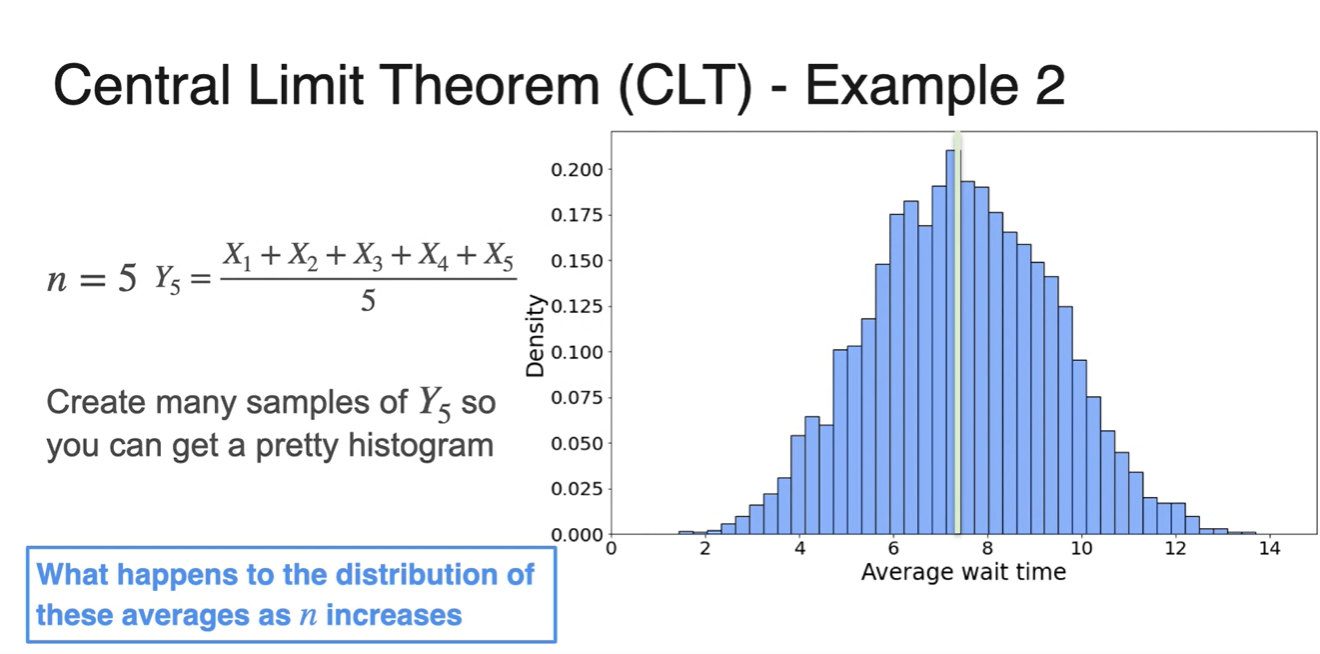
• $n=3$일 때와 $n=4$, $n=5$일 때 모두 종 모양에 가까운 그래프 분포가 그려진다.

  • 그리고 $n$이 클수록 중심에 가까운 narrow 그래프 모양을 띄게 된다.

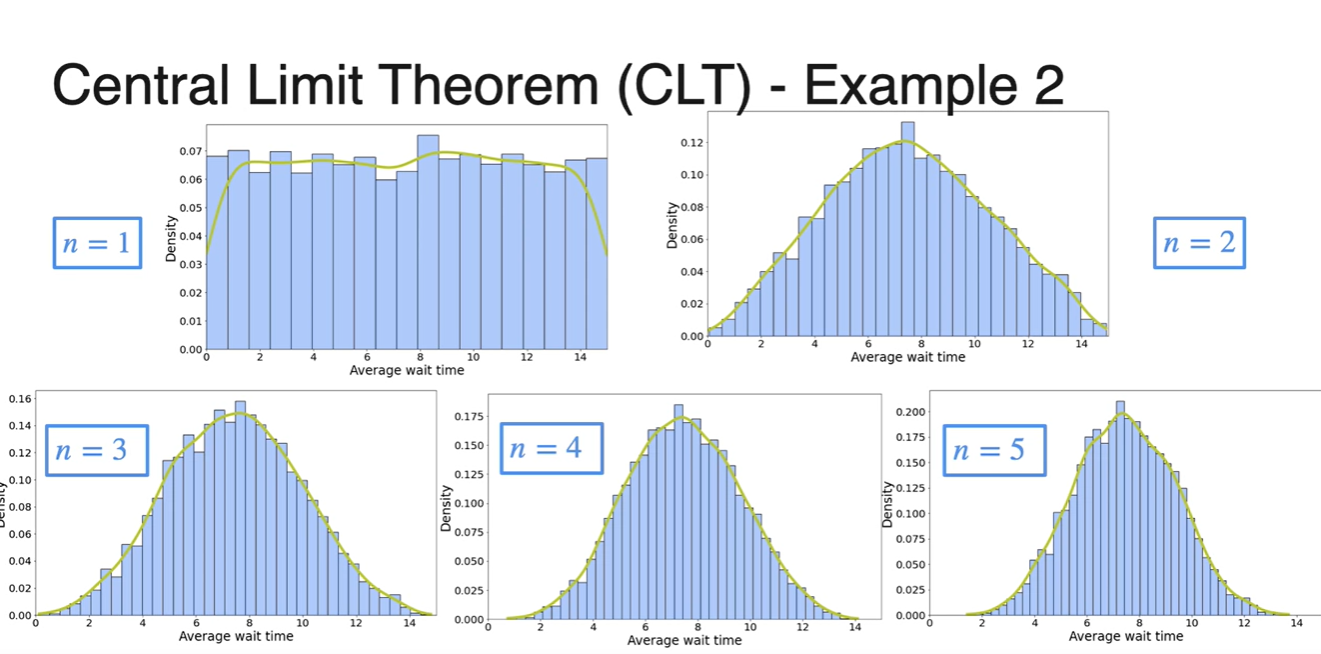
• 위 그래프들을 한 곳에 모아 보자.

  • 초록색 선그래프는 Kernel Density Estimation(KDE)에 의해 그려진 추정 그래프다.

• $Y_n$은 i.i.d한 확률 변수 $X$의 sample을 모아 평균낸 분포의 확률 변수다.

  • 기댓값과 분산을 수식적으로 정리하면 아래와 같은 결과를 얻을 수 있다.

    $\mathbb E[Y_n] = \mathbb E[\displaystyle \frac{1}{n} \sum_{i=1}^{n} X_i] = \frac{1}{n} \sum_{i=1}{n} \mathbb E[X_i] = \frac{1}{n} n \mathbb E[X] = \mathbb E[X] = \mu$
    $Var[Y_n] = \displaystyle Var(\frac{1}{n} \sum_{i=1}^{n} X_i) = \frac{1}{n^2} \sum_{i=1}^{n} Var(X_i) = \frac{1}{n^2} nVar(X) = \frac{Var(X)}{n} = \frac{\sigma}{n}$

• 아래 주황색 그래프는 normal distribution의 그래프를 나타낸 것이다.

  • Large enough한 변수들의 평균값은 normal distribution이라 가정할 수 있을 정도로 분포가 거의 비슷하다는 점을 알 수 있다.

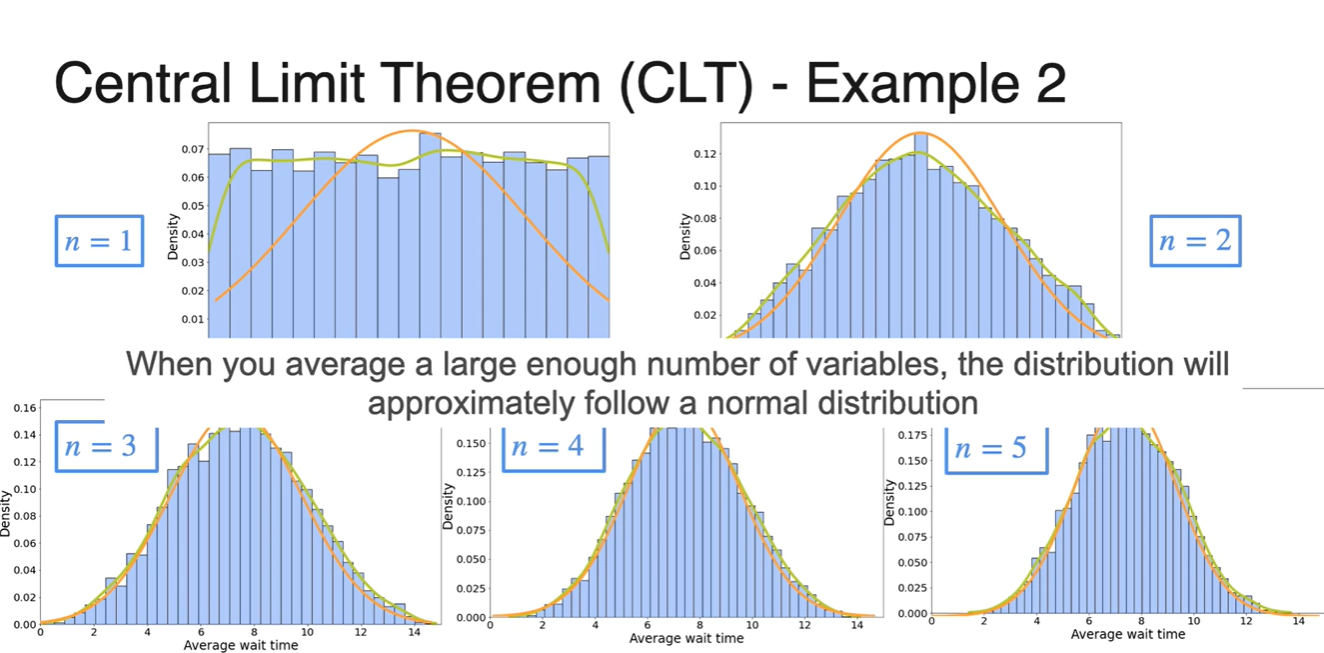
• 공식적으로 $\displaystyle \frac{Y_n - \mu}{\sqrt{\sigma / n}}$ 변수는 $n$이 매우 클수록 Normal distribution $N(0, 1)$을 따른다.

  • cf. 임의의 확률 변수 $X$에 대하여 $Z = \displaystyle \frac{X-\mu}{\sigma}$라면, $Z \sim N(0, 1)$을 따랐었다.

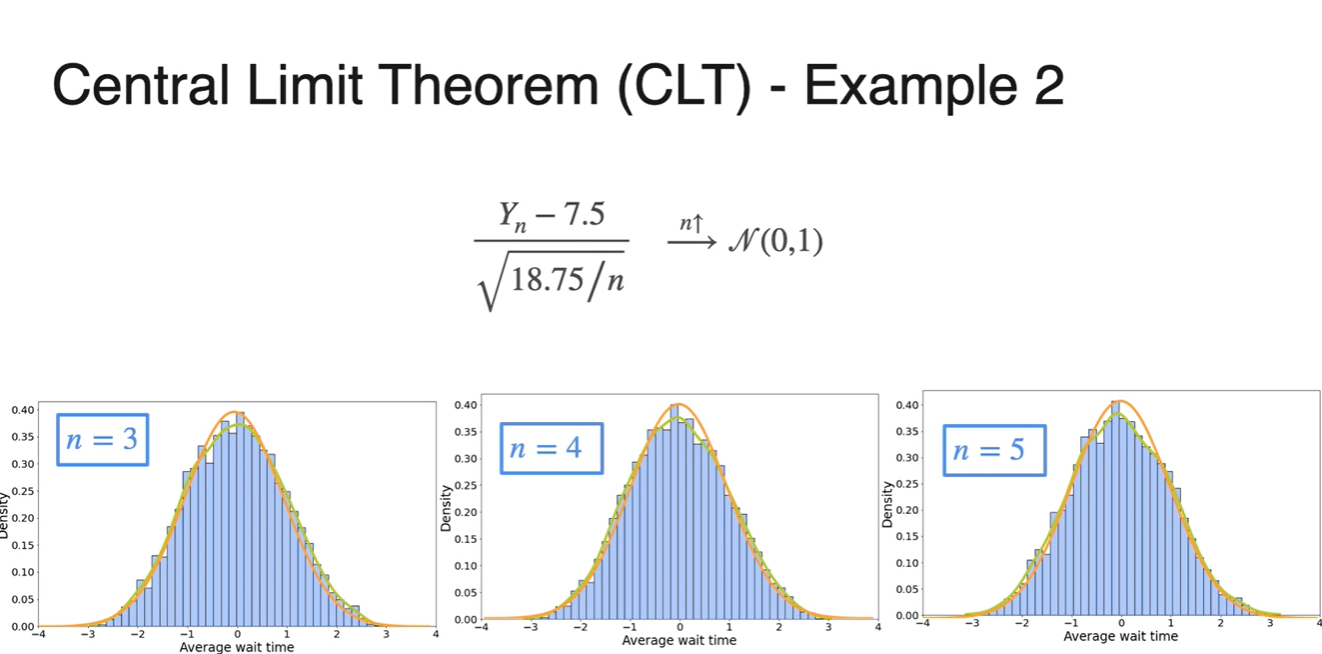
• 해당 분포를 population 평균 및 분산과 비교하면 다음과 같은 차이를 보인다.

  • Mean : $\mu_{Y_n} = \mu$
  • Variance : $\sigma^2_{Y_n} = \displaystyle \frac{\sigma^2}{n}$

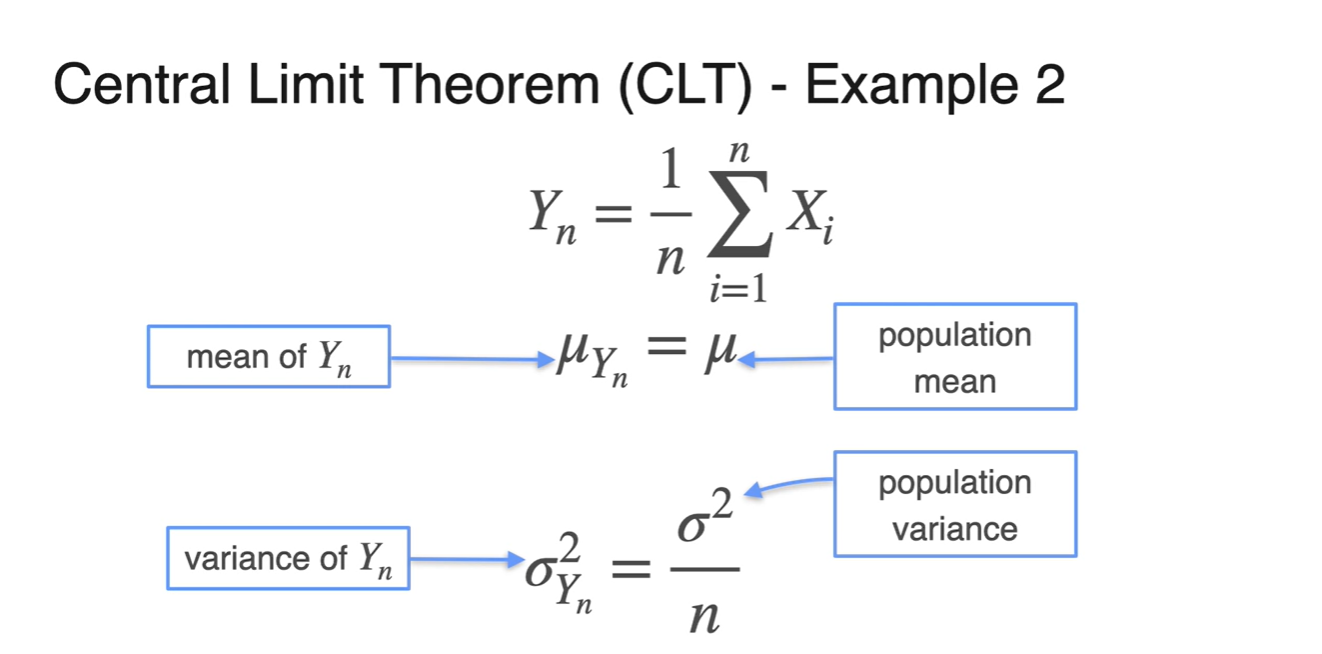
• $n \rightarrow \infin$로 갈 때, 확률 변수 $Y_n$의 값이 아래와 같은 수식으로 정리될 때, 정규 분포를 따르게 된다.

  • $Y_n = \displaystyle \frac{1}{n} \sum_{i=1}^{n} X_i$이면, $\displaystyle \frac{\displaystyle \frac{1}{n} \sum_{i=1}^{n} X_i - \mathbb E[X]}{\sigma_X} \sqrt{n}$은 $\sim N(0, 1^2)$을 따른다.

    • $\displaystyle \frac{\displaystyle \frac{1}{n} \sum_{i=1}^{n} X_i - \mathbb E[X]}{\sigma_X/\sqrt{n}} = \displaystyle \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \sim N(0, 1^2)$로도 나타낼 수 있다.

    • 참고 : https://m.blog.naver.com/clstat/222105062195

• $\displaystyle \frac{1}{n}$으로 묶어 정리하면 아래와 같이 정리된다.

  • $\displaystyle \frac{\displaystyle \sum_{i=1}^{n} X_i - n \mathbb E[X]}{\sqrt{n} \sigma_X} \sim N(0, 1^2)$

Lesson 2 - Point Estimation

Maximum Likelihood Estimation: Motivation

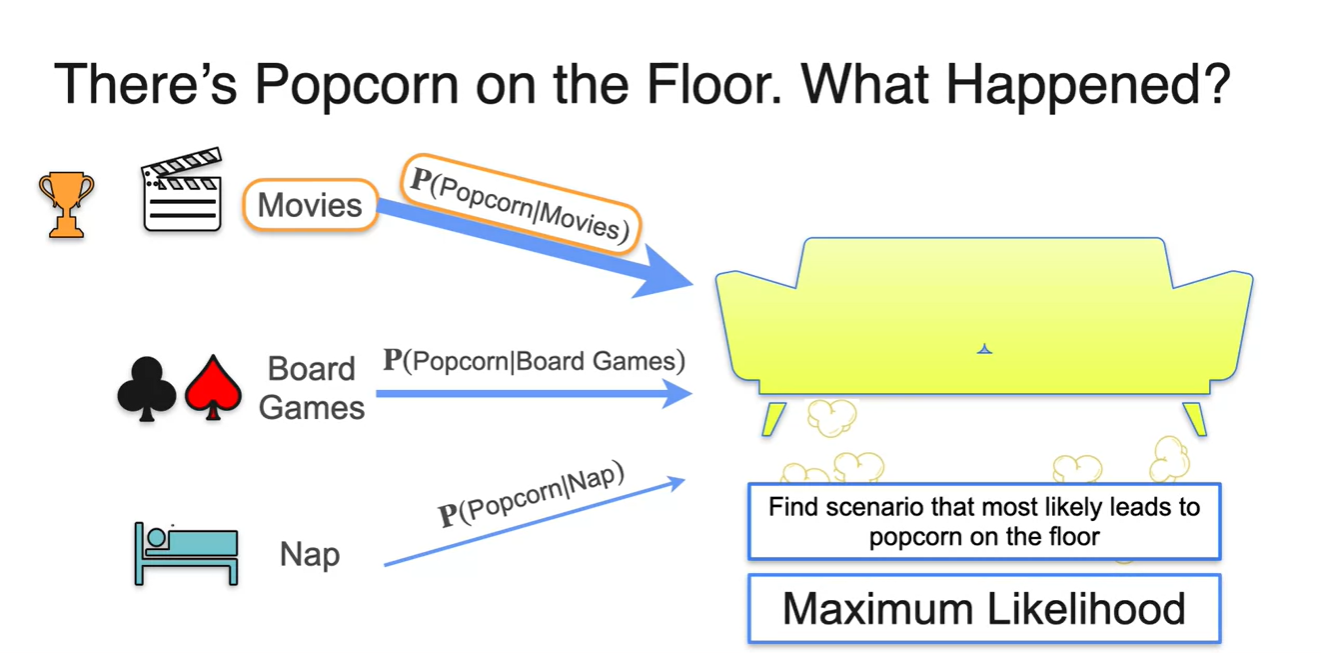
• 만일 아래와 같은 소파 아래, Popcorn이 잔뜩 떨어져 있었다고 가정하자.

  • 여기에 있었던 사람들이 했었을 행동에 대한 선택지가 Movies, Board Games, Nap 이렇게 3가지가 있다면 무엇을 했을 확률이 높은가?

• 아마도 Most likely that happened의 정답은 Movies일 것이다.

  • Movies의 확률이 제일 높고, Board Games가 중간, Nap은 거의 관련 없는 선택지일 거라는 것이다.

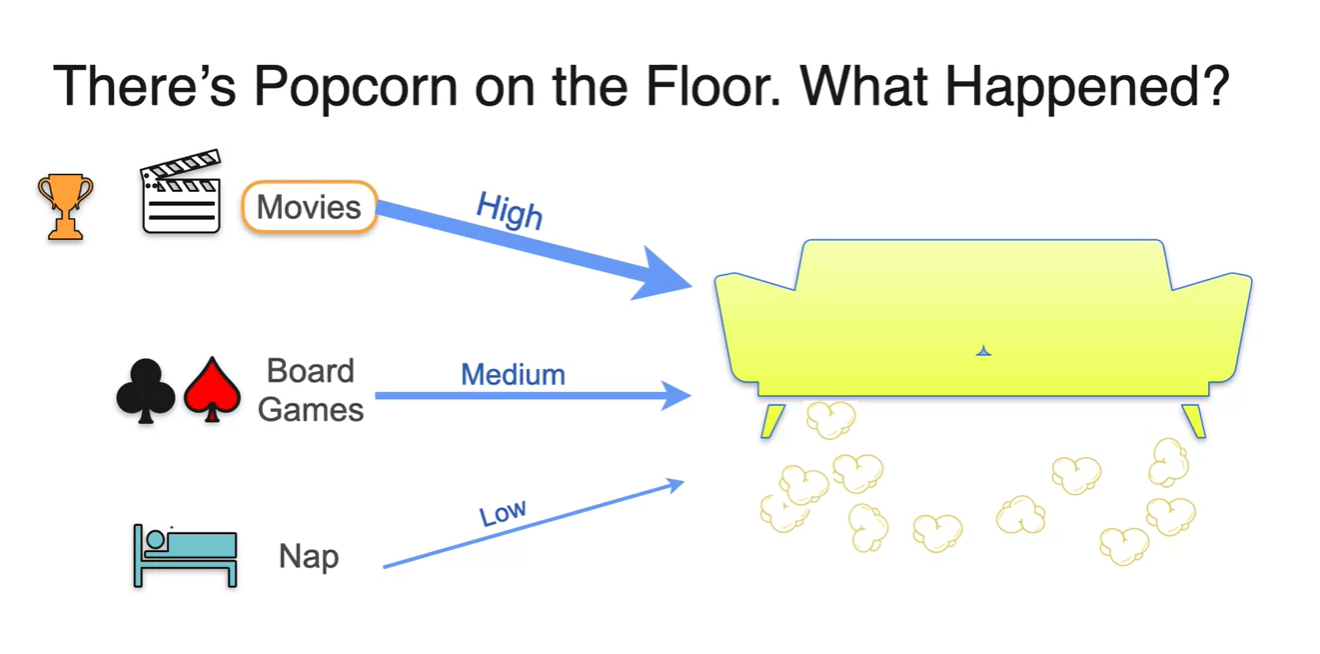
• 이를 Conditional probability로 표현하면 $P(Popcorn|Movies)$라고 표현할 수 있다.

  • 즉, 주어진 시나리오가 존재할 때 해당 시나리오 대로 흘러갈 수 있도록 하는 요인을 "Maximum Likelihood"라고 이야기 하는 것이다!

• 머신러닝에서는 Model이 likelihood의 역할을 한다.

  • 어떠한 Data의 시나리오대로 흘러갈 수 있도록 하는 만들기 때문이다.

    • 따라서 우리는 결과인 Data가 주어졌을 때, Model이 이를 내뱉을 확률 $P(Data|Model)$을 Maximize하면 된다.

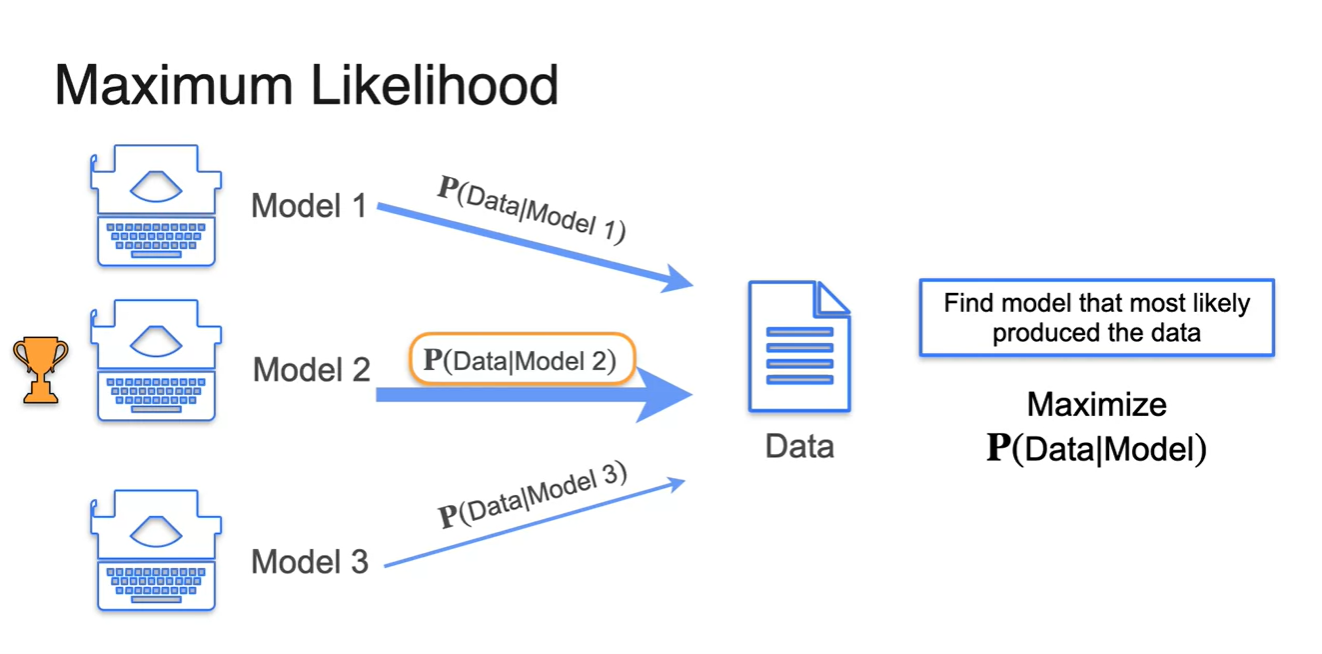
• Data를 활용하여 $P(Data|Model)$의 확률이 가장 높은 Model을 선택하는 것이 바로 머신러닝의 핵심 원리다.

MLE: Bernoulli Example

• 동전 던지기와 같은 Bernoulli distribution에서의 예시를 살펴보자.

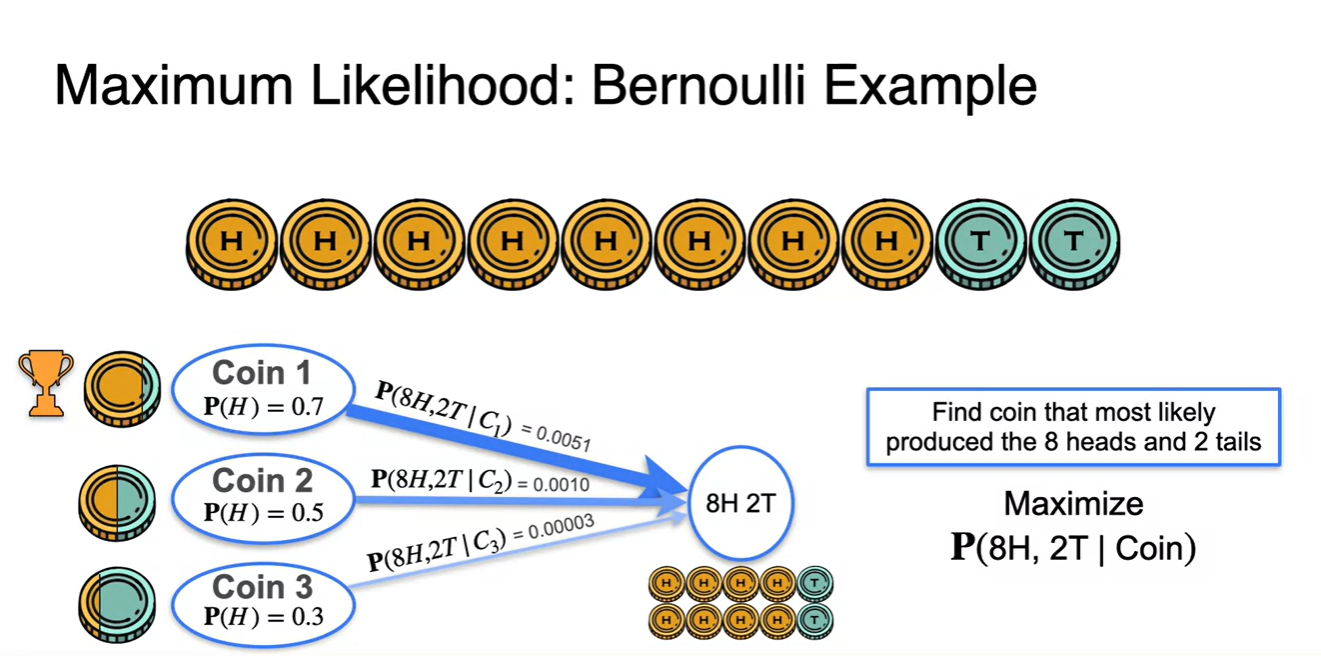
  • 아래와 같이 Head가 8번, Tail이 2번 나온 sequence 결과가 나왔다.

    • 다음 3가지 선택지 중 해당 결과를 가장 잘 만족하는 distribution은 무엇일까?

• Head의 관측이 Tail의 관측보다 높게 나왔다는 건 Head가 나올 확률이 더 높을 것이라는 것으로 추측할 수 있다.

  • 실제 계산을 통해 probability를 계산해보면 Coin 1의 distribution이 확률이 제일 높다는 것을 알 수 있다.

• 따라서 $P(8H, 2T|Coin)$ 확률을 Maximize하는 경우의 수는 $C_1$이다.

  • $P(8H, 2T|C_2)$와 $P(8H, 2T|C_3)$의 확률은 $P(8H, 2T|C_1)$에 비해 값이 그리 크지 않다.

• 그렇다면 "8H가 나오는 결과"를 얻기 위한 확률 $p$는 얼마라고 예상할 수 있을까?

  • $P(H)$가 parameter $p$가 되어, 전체 확률인 $p^8(1-p)^2$를 maximize하는 $p$를 찾아보도록 하자.

• 10개의 동전을 던져 8H가 나오는 시행 결과의 Likelihood는 $p$에 대한 function으로 전개되어 $L(p;8H) = p^8(1-p)^2$로 표기한다.

  • 이 때 확률 parameter인 $p$는 $0 \le p \le 1$의 범위를 갖기 때문에 scale 조정을 위해 log을 취하여 Log-Likelihood로 계산한다.

  • 이러한 Log-Likelihood $l(p;8H)$의 미분을 구해 최댓값을 찾으면 $\hat{p} = \displaystyle \frac{8}{10}$로 얻어짐을 알 수 있다.

• Bernoulli 예시에서의 Maximum Likelihood를 정리해보자.

  $X = (X_1, ... , X_n)$을 포함하고 i.i.d한 $X_i$가 $Bernoulli(p)$를 따른다면

  • Likelihood는 $L(p;\bold{x}) = P_p(X=\bold{x})=\displaystyle \Pi^{n}_{i=1} p_{X_i}(x_i) = \Pi^{n}_{i=1} p^{x_i}(1-p)^{1-x_i}$

    • if $x_i=1$, $p$
    • if $x_i=0$, $(1-p)$

  • 즉, 동전 하나를 던졌을 때 Head가 나올 단일 확률이 $p$, Tail이 나올 단일 확률이 $(1-p)$라는 얘기다.

• 전체 동전의 개수가 $n$이라면 head는 $\displaystyle \sum_{i=1}^{n}x_i$, tail은 $n- \displaystyle \sum_{i=1}^{n}x_i$로 나타낼 수 있다.

  • 따라서 시행 횟수가 여러 번일 때 Likelihood는 $p^{(\sum_{i=1}^{n}x_i)} (1-p)^{(n-\sum_{i=1}^{n}x_i)}$로 표현할 수 있따.

    • 이를 log 취해 Log-likelihood로 만들어 최종 최댓값을 계산한다.

• 미분해서 0이 되는 지점은 최댓값인 지점이라고 볼 수있다. (현 function 기준)

  • 계산 결과 최대화 확률 추정값 $\hat{p}$는 $\displaystyle \frac{\sum_{i=1}^{n}x_i}{n}$ 즉, sample 평균인 $\bar{x}$로 계산되었다.

MLE: Gaussian Example

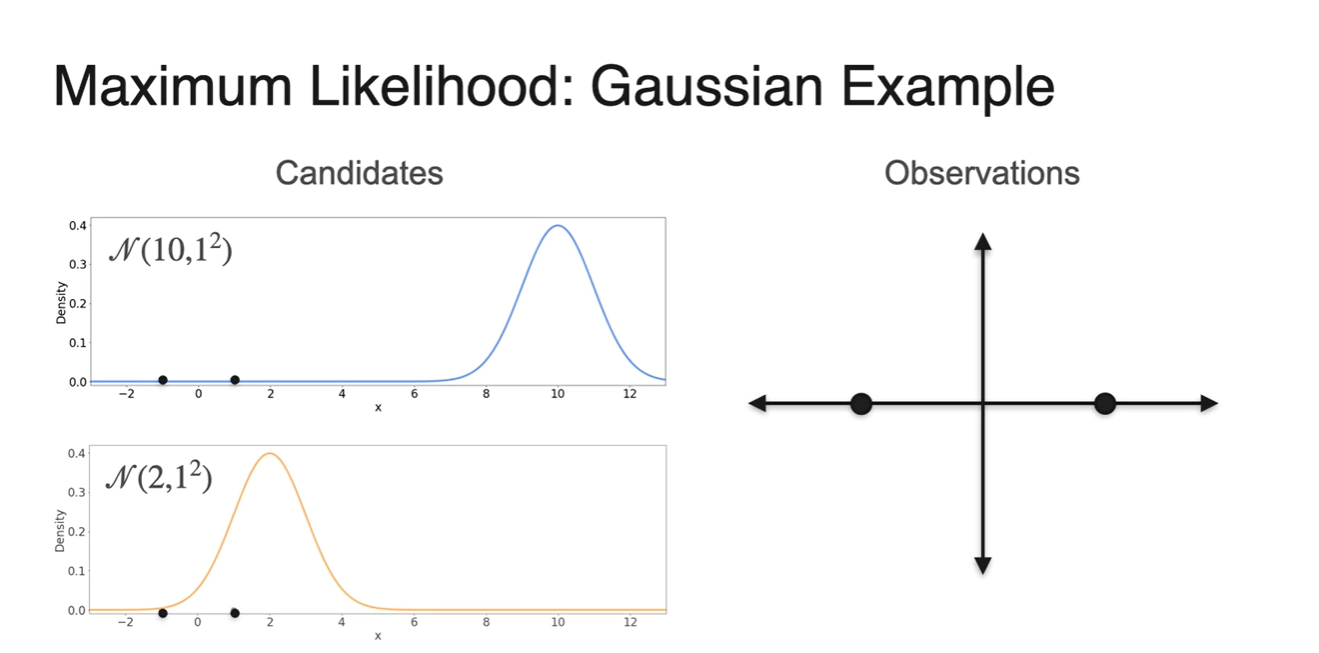
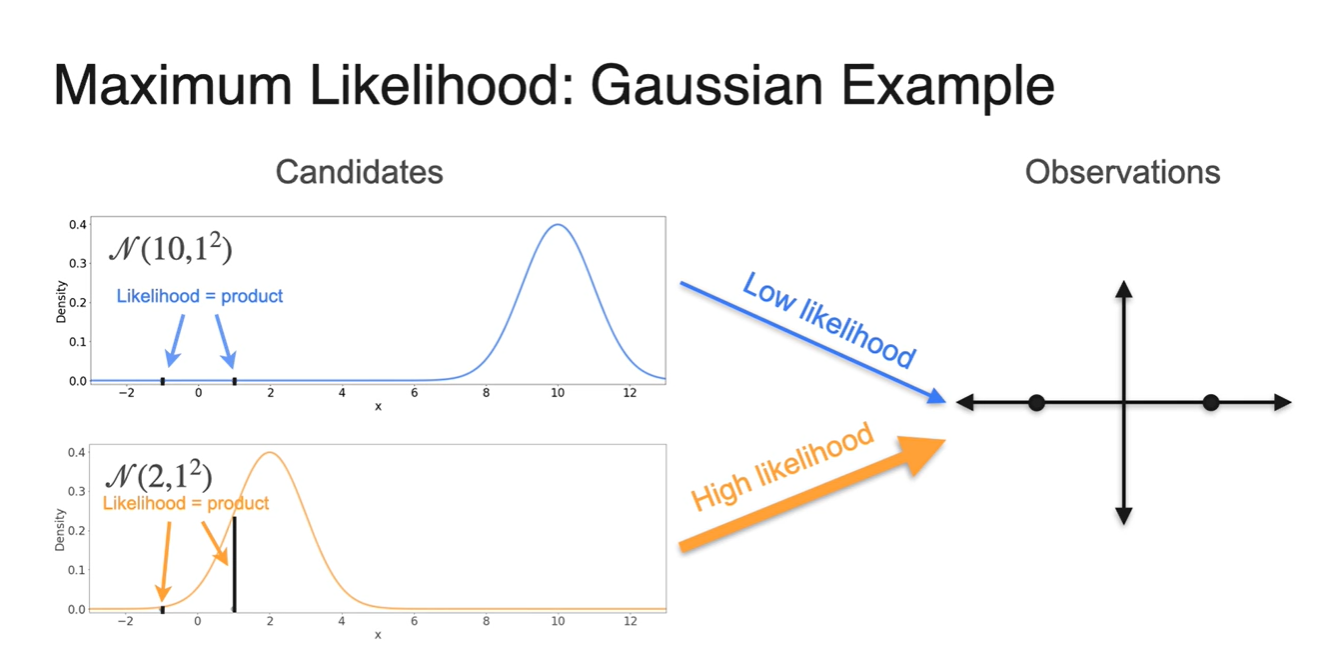
• 오른쪽 아래와 그림과 같이 Observations이 {-1, 1}로 관측되었다고 하자.

  • 왼쪽에 놓인 Normal distribution 후보 $N(10, 1^2)$, $N(2, 1^2)$ 중에서 해당 observations을 가장 잘 설명할 수 있는 분포는 무엇이겠는가?

• {-1, 1} 지점의 probability density(높이)를 구해보면 $N(10, 1^2)$는 heights가 거의 0에 가까운 값을 갖는다.

  • 그에 비해 $N(2, 1^2)$의 heights는 다소 높은 값을 가지므로 more likely하다고 말할 수 있다.

    • 즉, -1이나 1의 i.i.d random variables가 발생할 수 있는 확률이 크게 존재하는 그래프를 선택하는 것이 마땅하다.

• Likelihood는 각 i.i.d random variables의 density를 곱하여(product) 구한다.

  • 이를 통해 $N(10, 1^2)$보다 $N(2, 1^2)$ 분포가 현재의 Observations를 더 잘 설명(High likelihood)한다는 것을 증명할 수 있다.

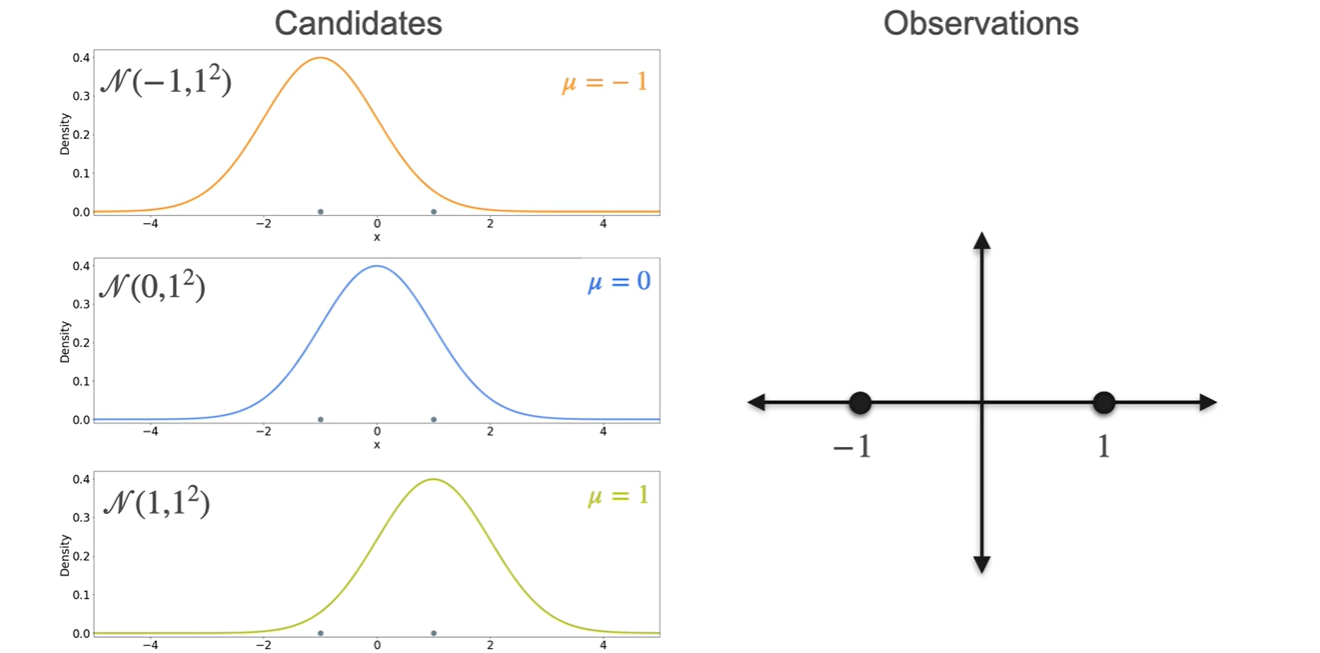
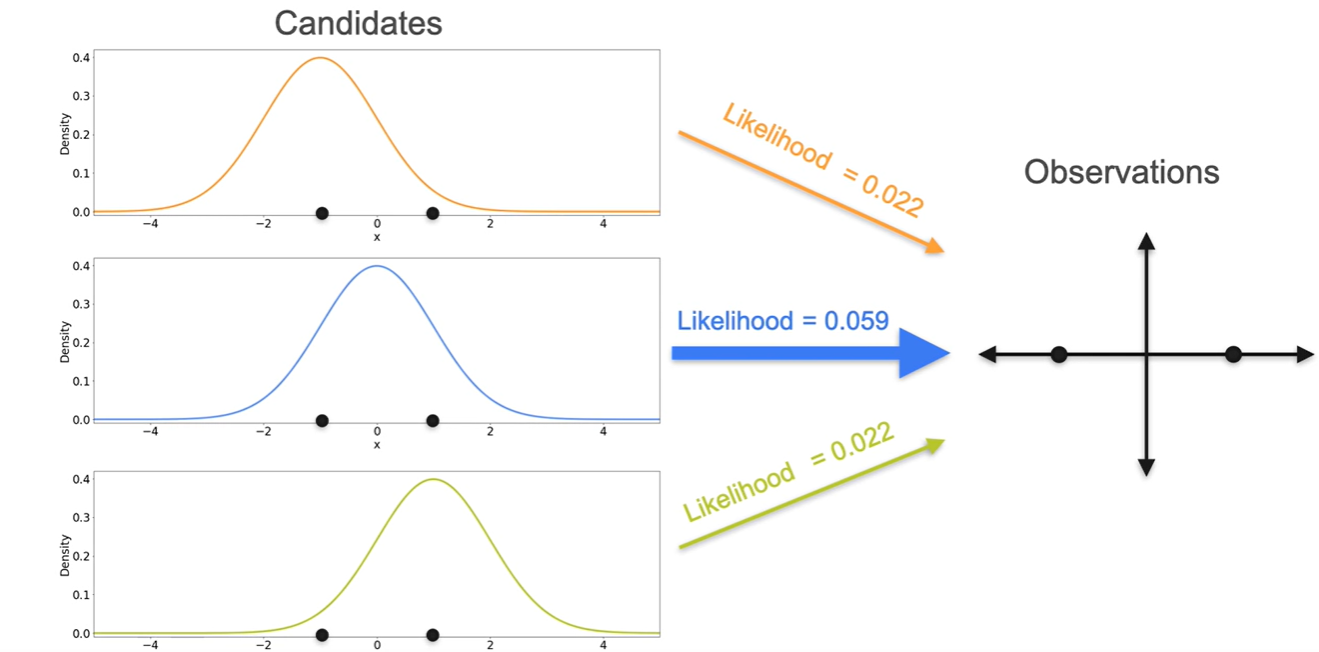
• 이번에는 아래 $N(-1, 1^2)$, $N(0, 1^2)$, $N(1, 1^2)$ 세 후보 중에서 현재 Observations를 잘 설명하는 분포가 무엇일지 Likelihood를 활용하여 찾아보도록 하자.

  • 평균은 $\mu = -1$, $\mu = 0$, $\mu = 1$인 3개의 선택지가 있다.

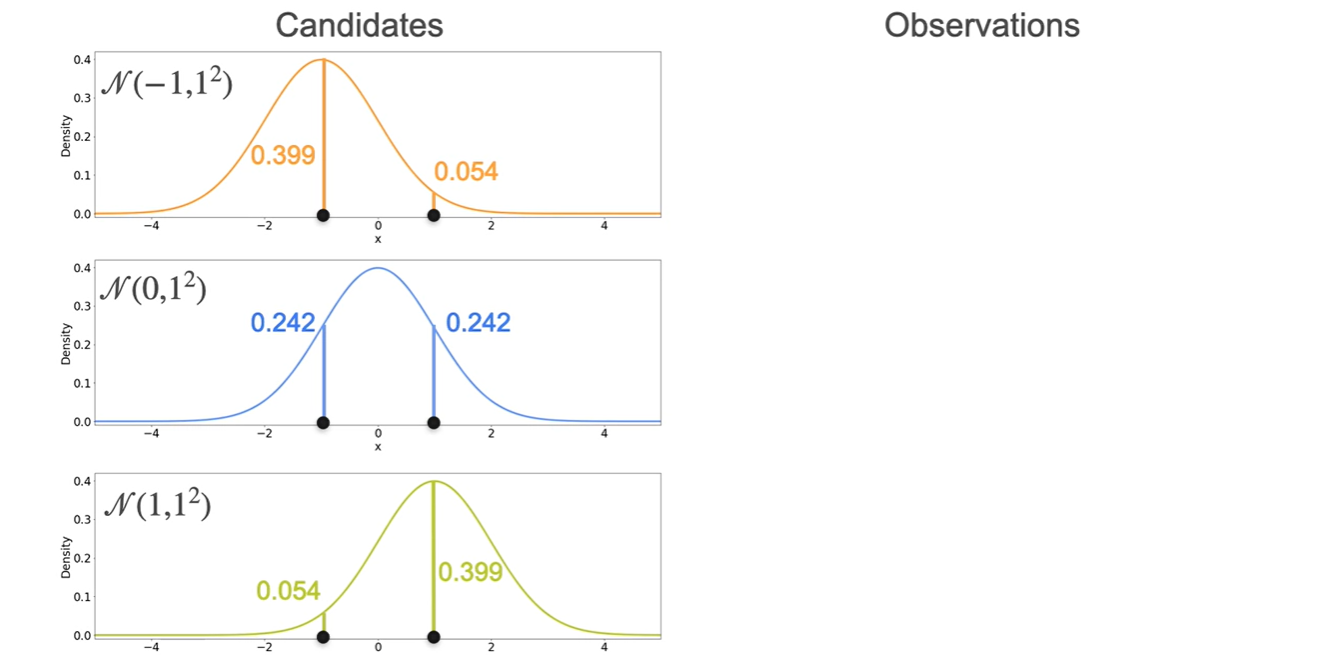
• Random variables인 $X=-1$과 $X=1$의 density를 각각 구해 그래프에 나타낸 결과가 아래와 같다.

  • 각각의 값을 곱하여 표현하는 이유는 $X=-1$과 $X=1$이 일어날 사건이 independent identically distributed(i.i.d)하다고 가정하고 있기 때문이다.

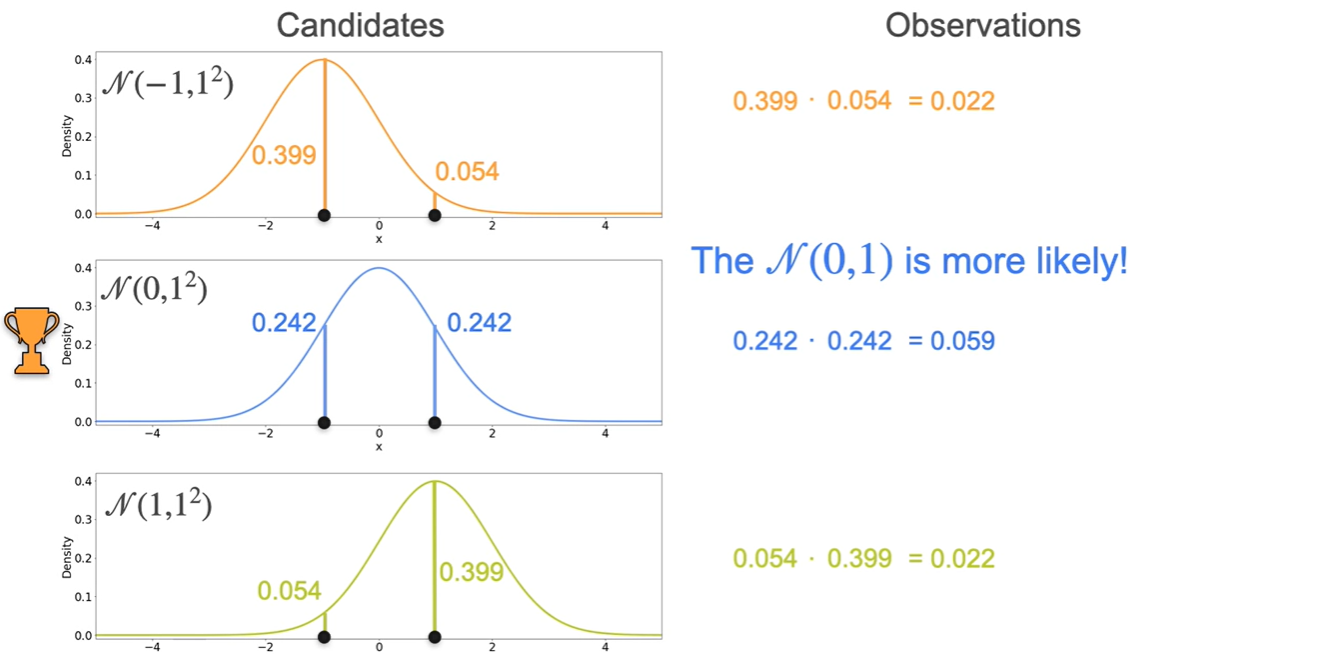
• 세 후보의 Likelihood를 계산한 결과 $N(0, 1)$이 more likely하다는 점이 밝혀졌다.

  • $N(-1, 1^2)$ : $0.399 * 0.054 = 0.022$
  • $N(0, 1^2)$ : $0.242 * 0.242 = 0.059$ ★
  • $N(1, 1^2)$ : $0.054 * 0.399 = 0.022$

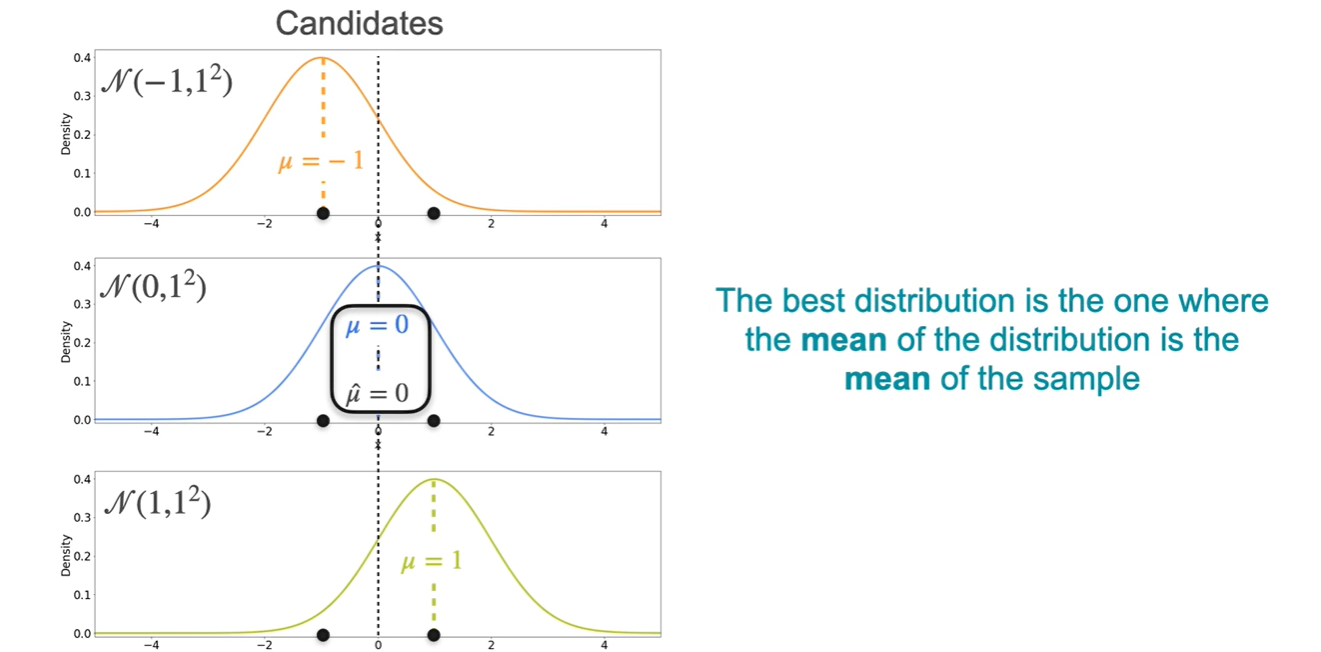
• 이를 통해 알 수 있는 사실을 일반화하면

  The best distribution은 sample mean과 동일한 mean을 갖는 distribution이다.

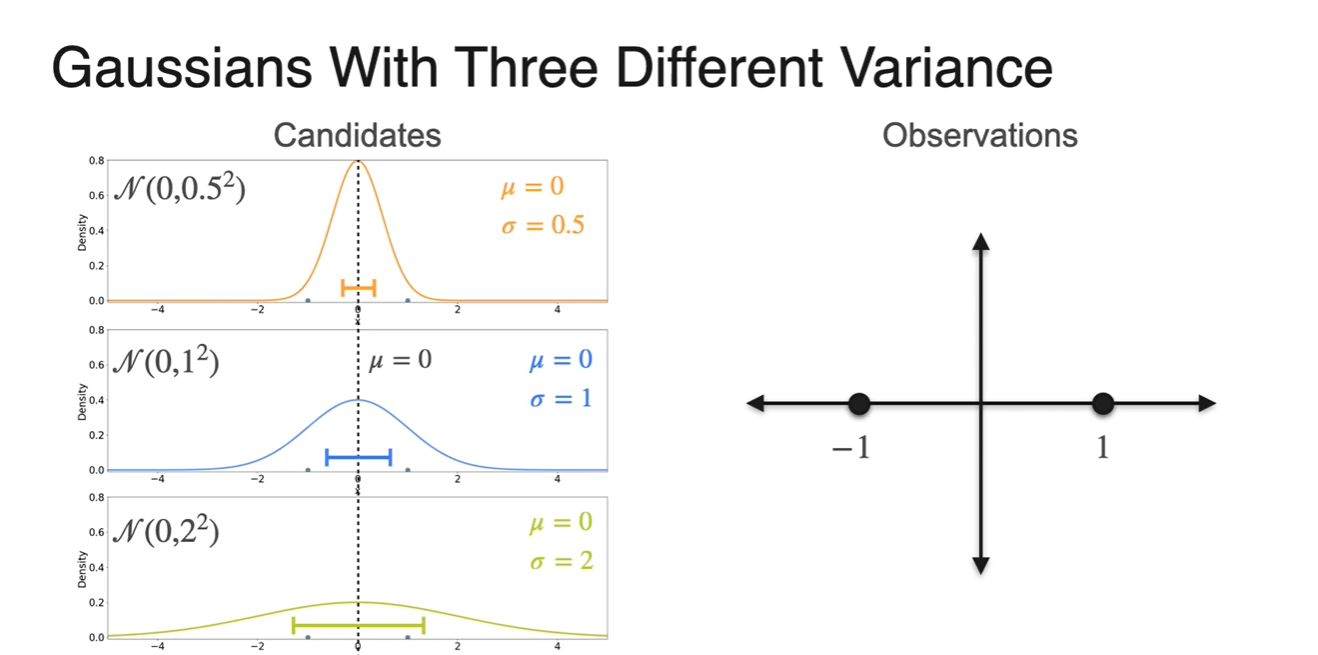
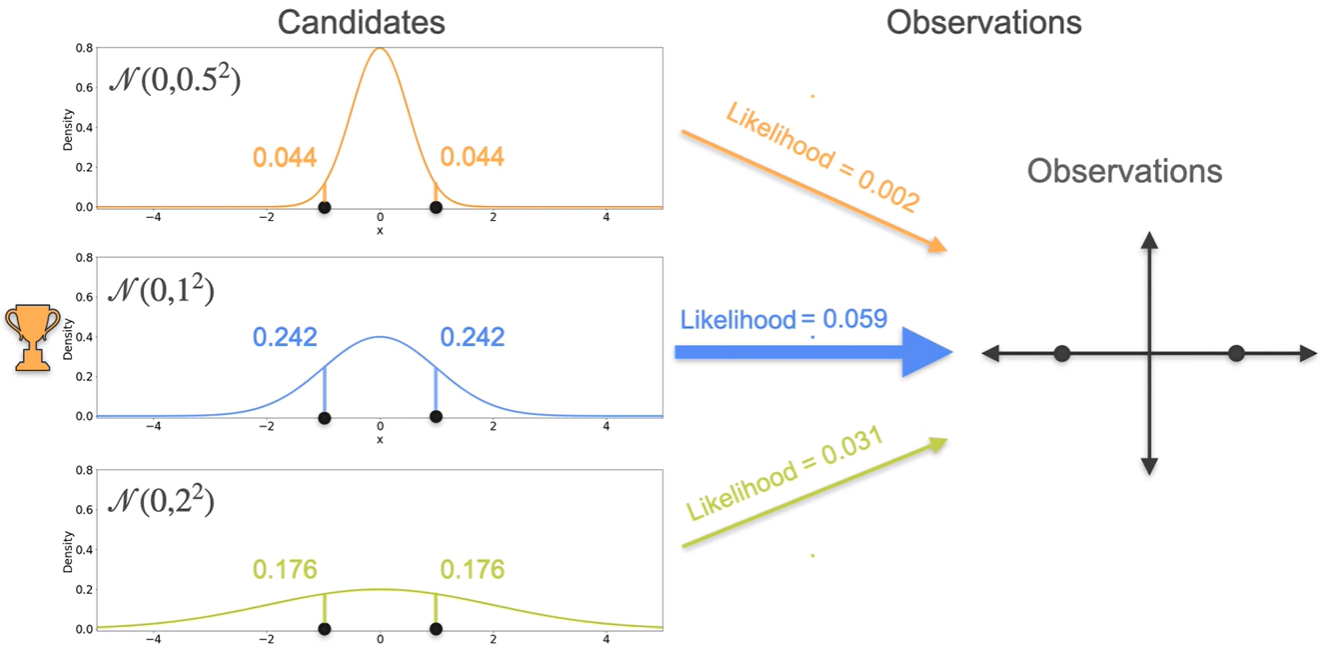
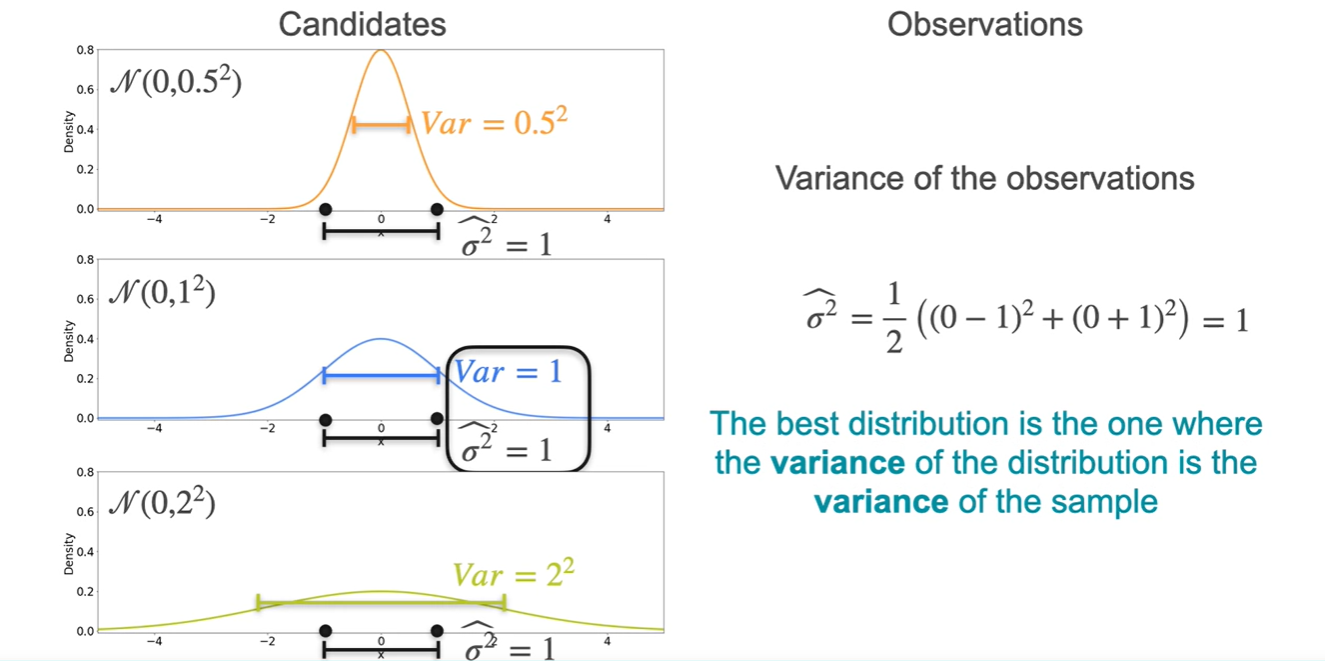
• 이제 Variance는 어떻게 설정하면 되는지 살펴보자.

  • 각 분포의 mean은 모두 0으로 동일하게 설정하였고, variance는 $0.5^2$, $1^2$, $2^2$을 3가지 후보로 설정했다.

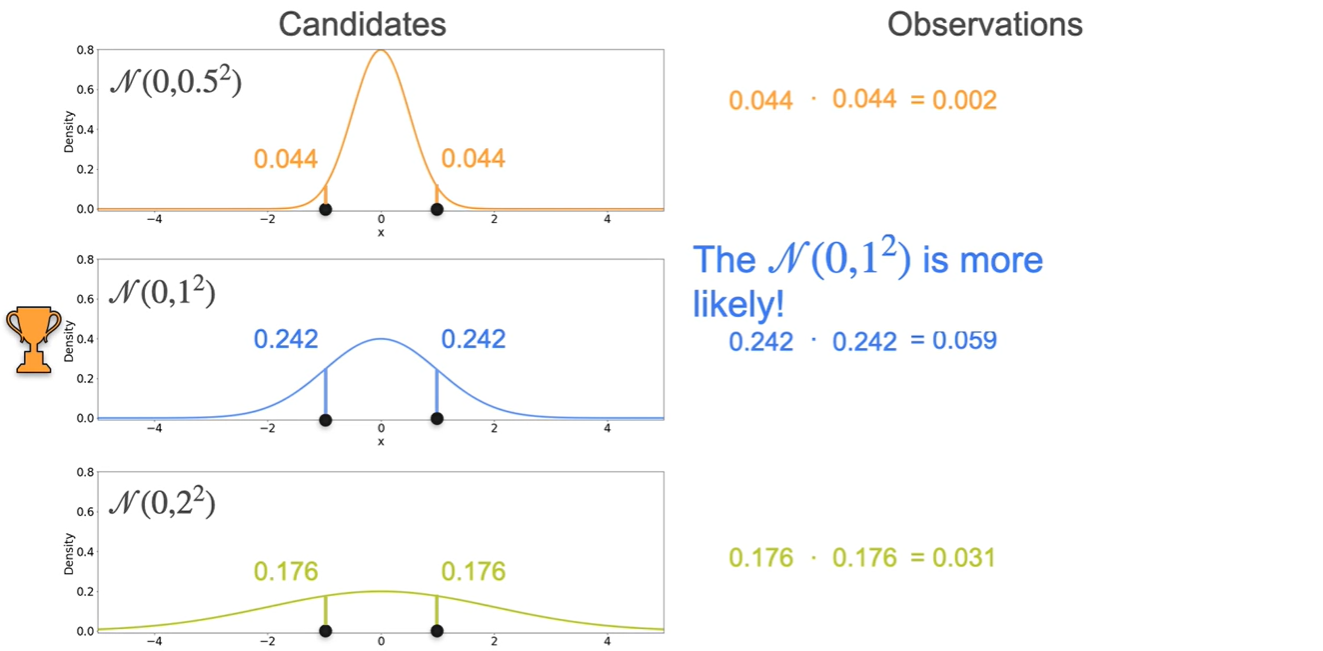
• 마찬가지로 각 분포의 density product를 통해 계산한 결과, $N(0, 1^2)$ 분포가 more likely하다는 것이 밝혀졌다.

  • $N(0, 0.5^2)$ : $0.044 * 0.044 = 0.002$
  • $N(0, 1^2)$ : $0.242 * 0.242 = 0.059$ ★
  • $N(0, 2^2)$ : $0.176 * 0.176 = 0.031$

• 이를 통해 알 수 있는 사실을 일반화하면

  The best distribution은 sample variance와 동일한 variance을 갖는 distribution이다.

  • 기존 sample variance는 population variance로 표현하기에는 다소 biased(underestimated)되어 있어 $n$이 아닌 $n-1$로 나눠주어야 한다고 했었다.

    • 그러나 MLE에서의 variance는 $n$을 사용한다는 점에서 조금 다르다.

MLE for Gaussian population (Optional)

• Mean이 $\mu$이고 Variance가 $\sigma^2$인 Gaussian distribution에서 $n$개의 samples를 뽑았다고 가정해보자.

  • $X = (X_1, X_2, ... , X_n)$

  • $X_i \overset{\underset{\mathrm{i.i.d}}{}}{\sim} N(\mu, \sigma^2)$

• MLE for $\mu$ and $\sigma$를 위해서는 먼저, likelihood를 정의해야 한다.

  • Normal distribution's PDF : $\displaystyle \frac{1}{\sqrt{2\pi} \sigma} e^{\displaystyle -\frac{1}{2} \frac{(x_i - \mu)^2}{\sigma^2}}$

  • Likelihood given $x = (x_1, x_2, ... , x_n)$

    : $L(\mu, \sigma;\bold{x}) = \Pi_{i=1}^{n} f_{X_i}(x_i) = \Pi_{i=1}^{n} \displaystyle \frac{1}{\sqrt{2\pi} \sigma} e^{\displaystyle -\frac{1}{2} \frac{(x_i - \mu)^2}{\sigma^2}} = \displaystyle \frac{1}{(\sqrt{2\pi})^n \sigma^n} e^{\displaystyle -\frac{1}{2} \frac{\sum_{i=1}^{n}(x_i-\mu)^2}{\sigma^2}}$

• Scale 조정을 위해 log를 씌워 log-likelihood를 구해보면 아래와 같다.

  • $l(\mu, \sigma) = log(L(\mu, \sigma;x)) = log(\displaystyle \frac{1}{(\sqrt{2\pi})^n \sigma^n} e^{\displaystyle -\frac{1}{2} \frac{\sum_{i=1}^{n}(x_i-\mu)^2}{\sigma^2}})$

    $= \displaystyle -\frac{n}{2} log(2\pi) - n log(\sigma) - \frac{1}{2} \frac{\sum_{i=1}^{n}(x_i-\mu)^2}{\sigma^2}$

• 이를 Maximizing하는 parameter $\mu$와 $\sigma$ 값을 찾기 위해 각 변수로 미분해보자.

  • $\displaystyle \frac{\partial}{\partial \mu} l(\mu, \sigma) = -\frac{1}{2} \frac{\sum_{i=1}^{n} 2(x_i - \mu)}{\sigma^2} (-1)$

    $= \displaystyle \frac{1}{\sigma^2}(\sum_{i=1}^{n}x_i - \sum_{i=1}^{n} \mu) = \frac{1}{\sigma^2}(\sum_{i=1}^{n}x_i - n \mu)$

  • $\displaystyle \frac{\partial}{\partial \sigma} l(\mu, \sigma) = -\frac{n}{\sigma} -\frac{1}{2} (\sum_{i=1}^{n} (x_i - \mu)^2) (-2) \frac{1}{\sigma^3}$

    $= \displaystyle -\frac{n}{\sigma} + (\sum_{i=1}^{n} (x_i - \mu)^2) \frac{1}{\sigma^3}$

• 이제 $\displaystyle \frac{\partial}{\partial \mu} l(\mu, \sigma)$와 $\displaystyle \frac{\partial}{\partial \sigma} l(\mu, \sigma)$를 0으로 만드는 parameter $\mu$와 $\sigma$를 구해보자.

  • $\displaystyle \frac{\partial}{\partial \mu} l(\mu, \sigma) = \frac{1}{\sigma^2}(\sum_{i=1}^{n}x_i - n \mu) = 0$

    • $\hat{\mu} = \displaystyle \frac{\sum_{i=1}^{n} x_i}{n} = \bar{x}$

  • $\displaystyle \frac{\partial}{\partial \sigma} l(\mu, \sigma) = \displaystyle -\frac{n}{\sigma} + (\sum_{i=1}^{n} (x_i - \mu)^2) \frac{1}{\sigma^3} = 0$ $\Rightarrow \displaystyle -n + (\sum_{i=1}^{n} (x_i - \bar{x})^2) \frac{1}{\sigma^2} = 0$

    • $\hat{\sigma} = \sqrt{\displaystyle \frac{\sum (x_i - \bar{x})^2}{n}}$

The only difference is the normalizing constant: for the MLE you have $1/n$ while for the sample standard deviation you use $1/(n-1)$

MLE: Linear Regression

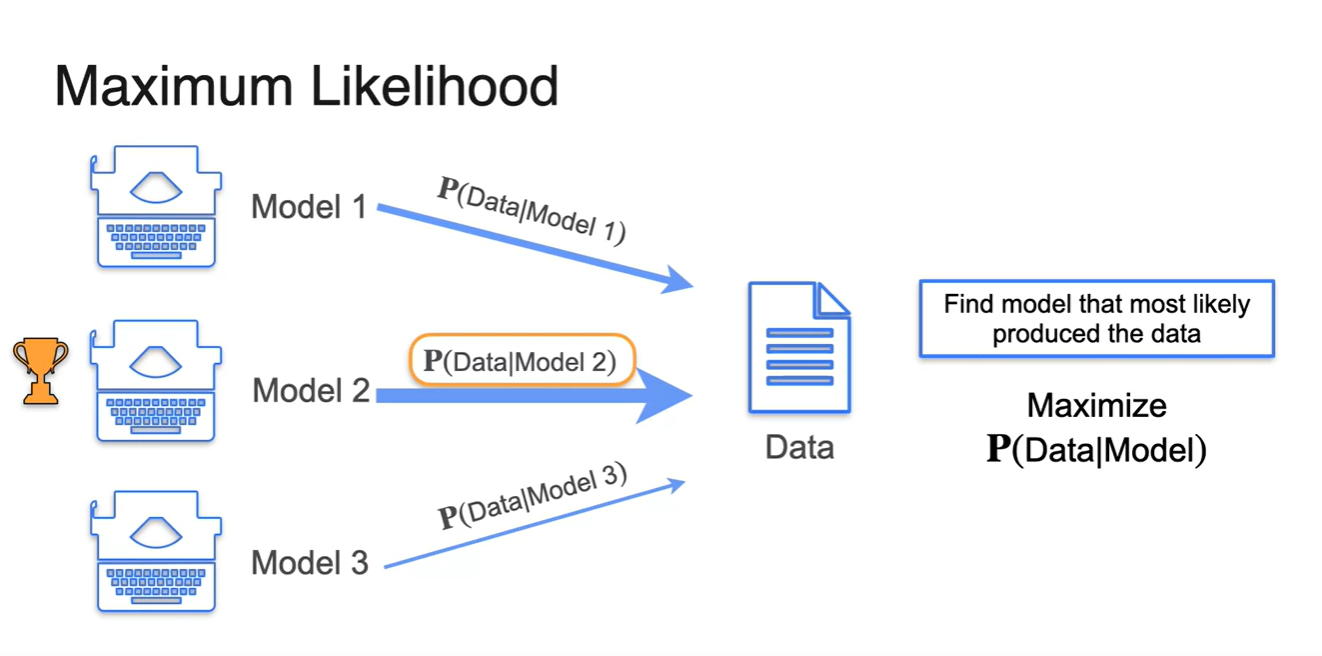
• Likelihood를 찾는 과정은 $P(Data|Model)$를 Maximize하는 model을 선정하는 것이라고 하였다.

  • 만약 Model 2의 $P(Data|Model \; 2)$가 다른 model들에 비해 값이 컸다면 해당 모델이 현재의 data를 가장 잘 설명하는 likelihood라고 할 수 있다.

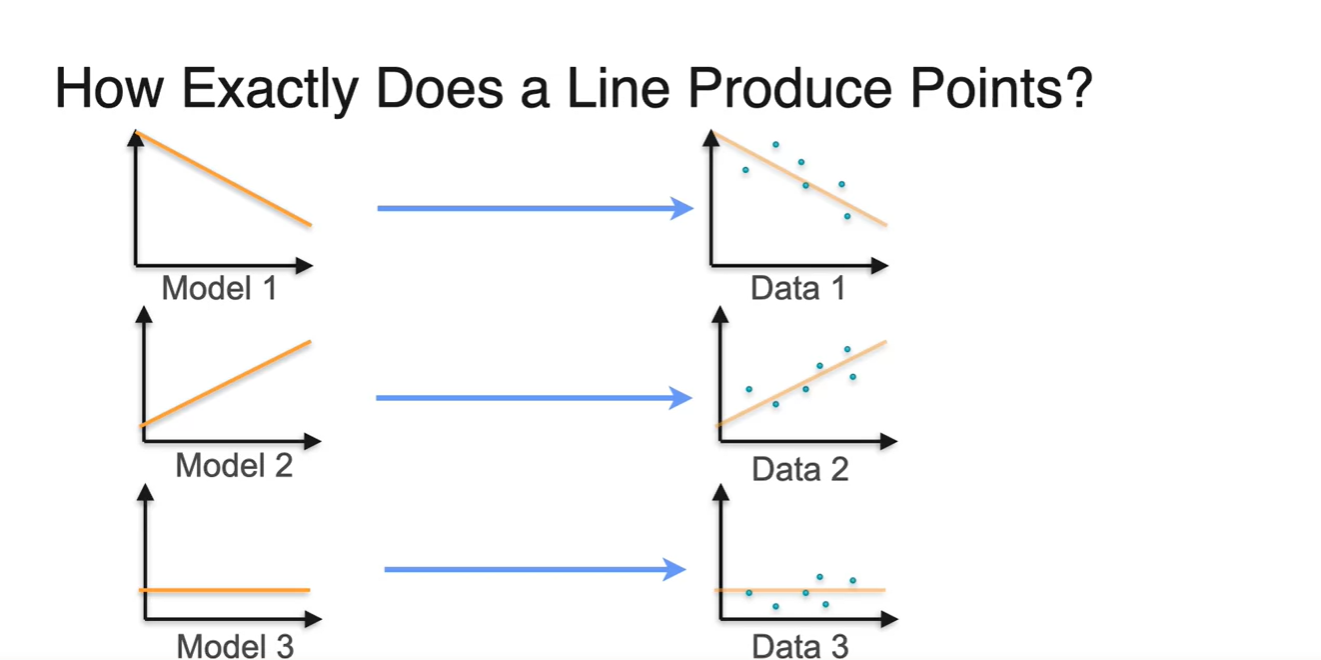
• 다음과 같은 오른쪽 Data의 likelihood는 Model 2다.

  • 육안으로 보기에도 현재 data 분포를 가장 잘 설명한다고 볼 수 있다.

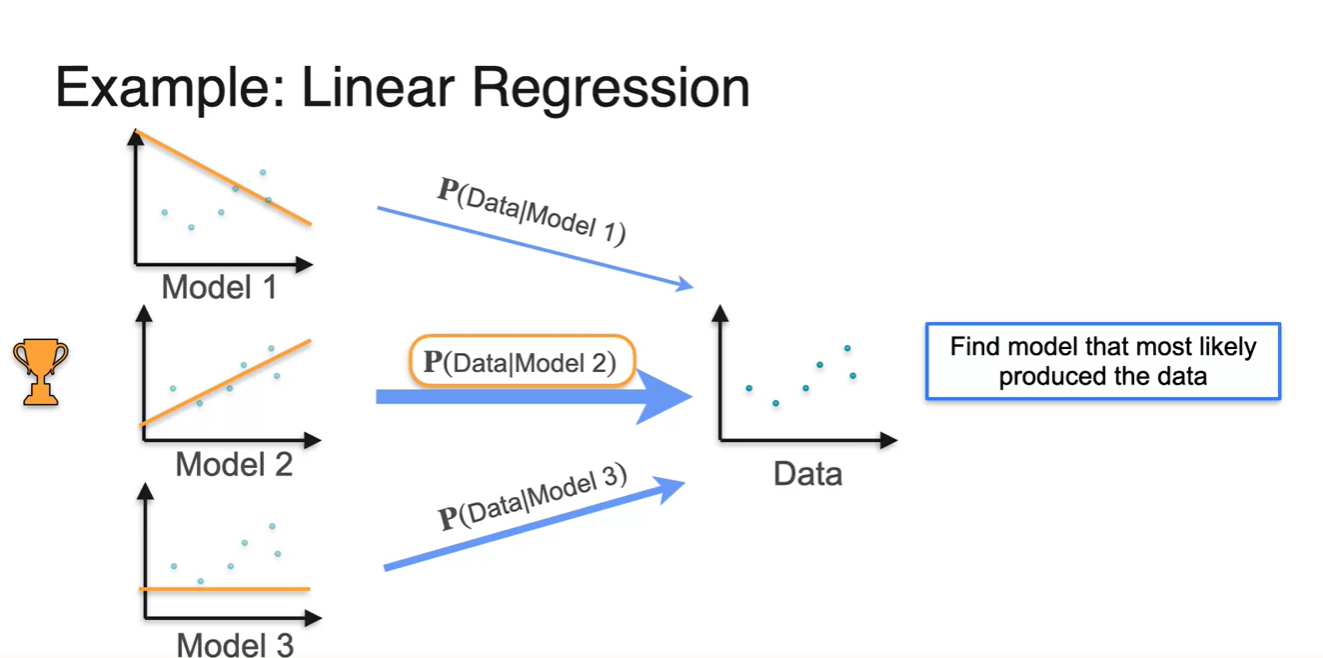
• 그렇다면 각 Model들은 어떤 점들(points)을 sampling(produce)하게 될까?

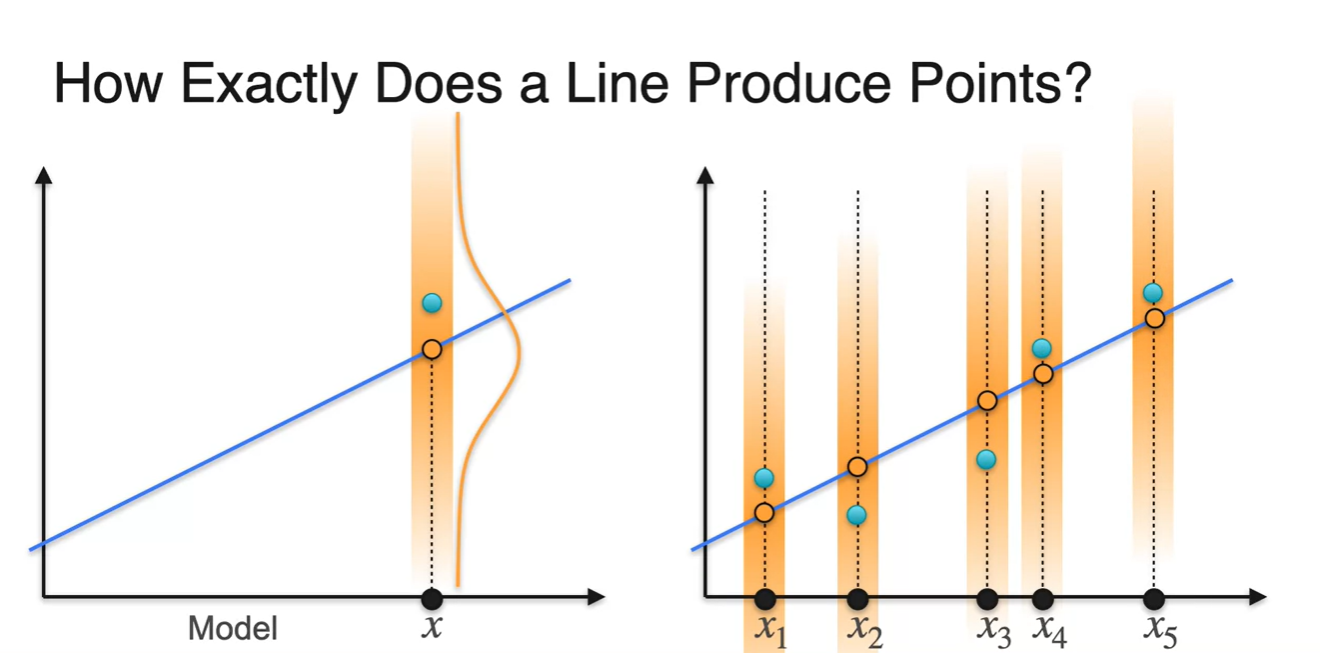
• 어떠한 모델이 나타내는 그래프의 한 점을 center(mean)로 하는 Normal distribution을 가정해보자.

  • 이 때, 실제 데이터 중 한 점이 이와 같은 분포에서 sampling된 점이라고 생각해보는 것다.

    • 그렇게 되면 실제 데이터 상에 존재하는 모든 점들은 model이 나타내는 random variables 마다의 분포에서 sampling된 것이라고 가정할 수 있게 된다.

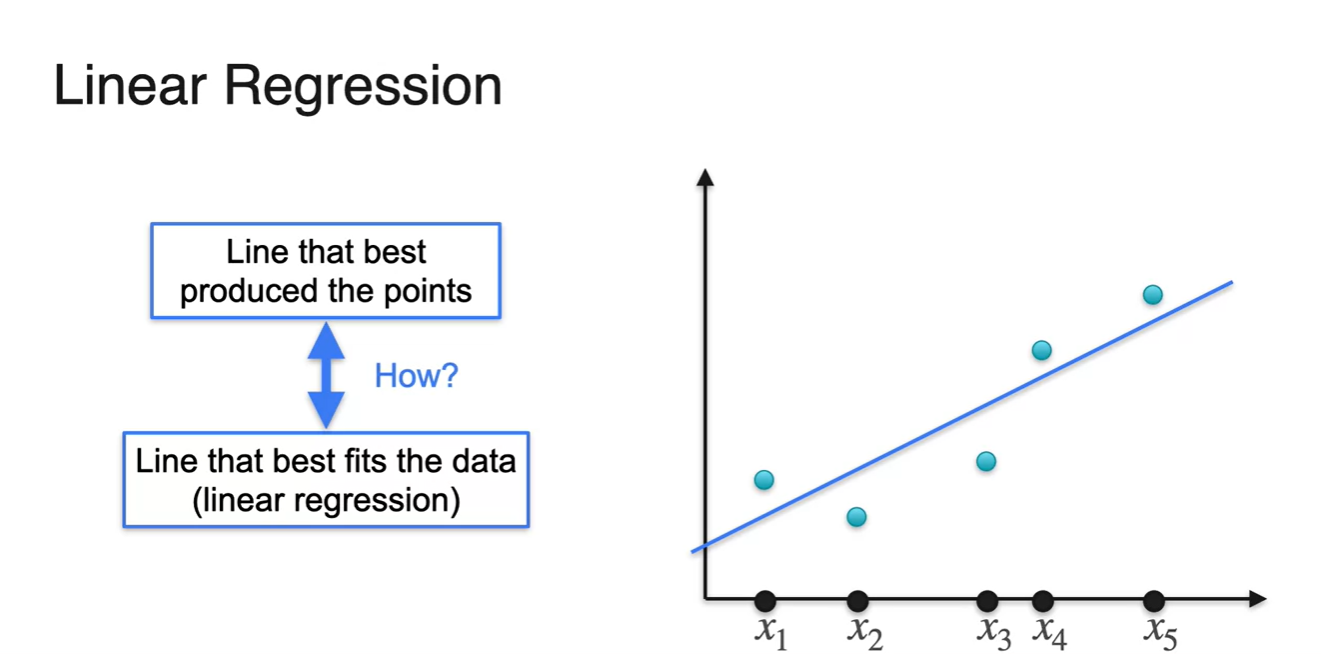
• 결국 Linear Regression은 각 point들을 가장 잘 producing하는 분포를 찾아내는 과정이라고 볼 수 있다.

  • 이는 전체 data에 가장 fit한 line을 찾아내는 과정과 일치한다. (but How?)

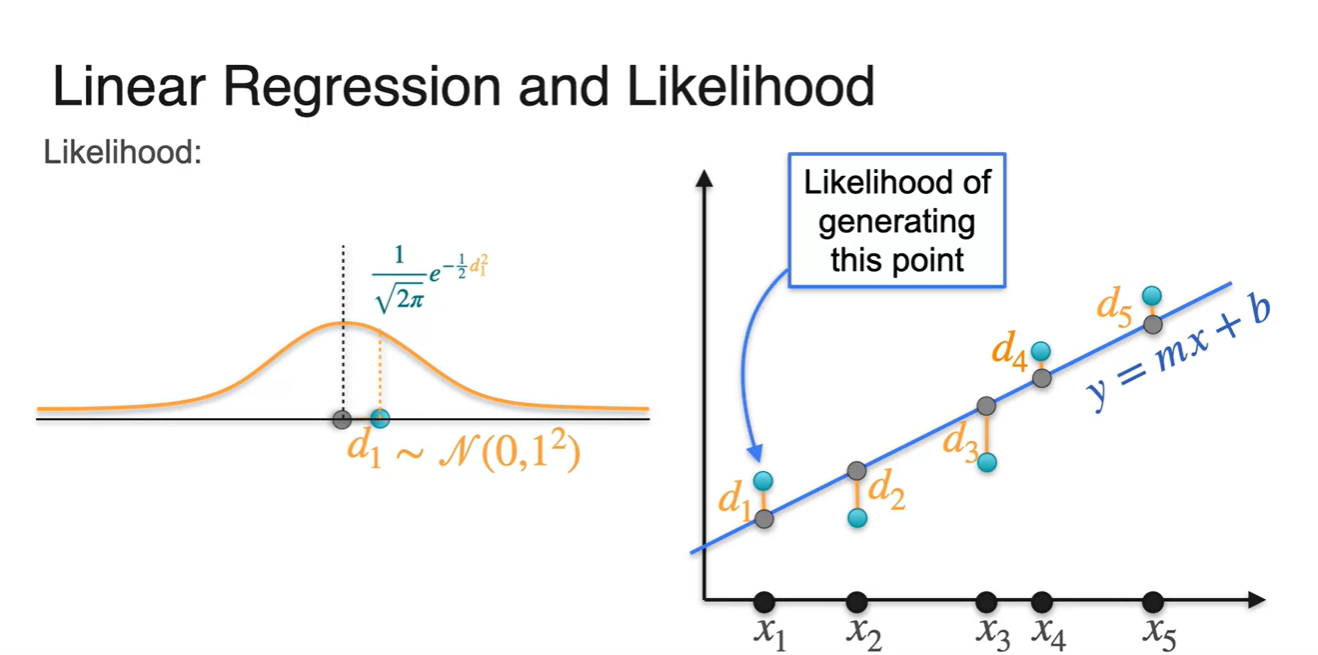
• 오른쪽 그래프에서 나타내는 line은 $m$과 $b$가 parameter인 $y= mx+b$로 표현되는 수식이다.

  • 이제 Regression line에서 표현된 point(회색)들에 의해 centered된 정규 분포로부터, 실제 data points(초록색)를 generating(or producing)하는 관점으로 바라봐보자.

    • 각 정규 분포들은 평균이 0인 $\sim N(0, 1)$를 따르므로 실제 data point와의 차이인 $d_1$은 중심으로부터 떨어진 $z$값이라 볼 수 있다.

    • 따라서 Normal distribution의 PDF에 의해 해당 probability의 density는 $\displaystyle \frac{1}{\sqrt{2 \pi}} e^{ -\frac{1}{2}d_1^2}$로 표현된다.

• 각 data points는 i.i.d하므로 likelihood의 계산식은 각 $f(d_*)$의 곱이다.

  • 이를 Maximize하기 위한 수식으로 정리하면 exponential의 지수 합으로 표현할 수 있고, $-$가 붙어있으므로 distance인 $d_{*}^2$의 합을 Minimize하는 수식으로 치환된다.

    Linear regression의 Maximize (log) likelihood = Minimize squared error다!

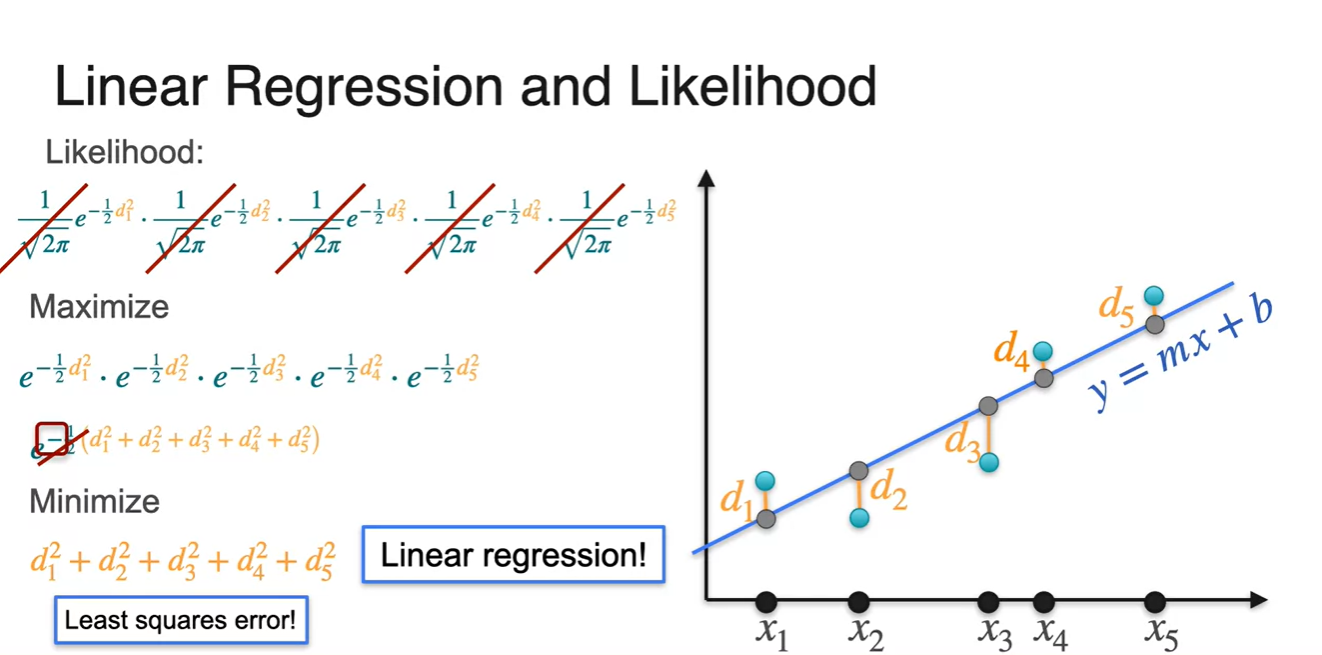
• 처음에 나왔던 model 3개의 정규 분포를 각 data point마다 나타낸 그래프가 시각화되어 있다.

  • 3가지 model의 likelihood를 계산해 본 결과, 현재 data 분포를 가장 잘 설명하는 maximized likelihood는 model 2임을 계산할 수 있게 되었다.

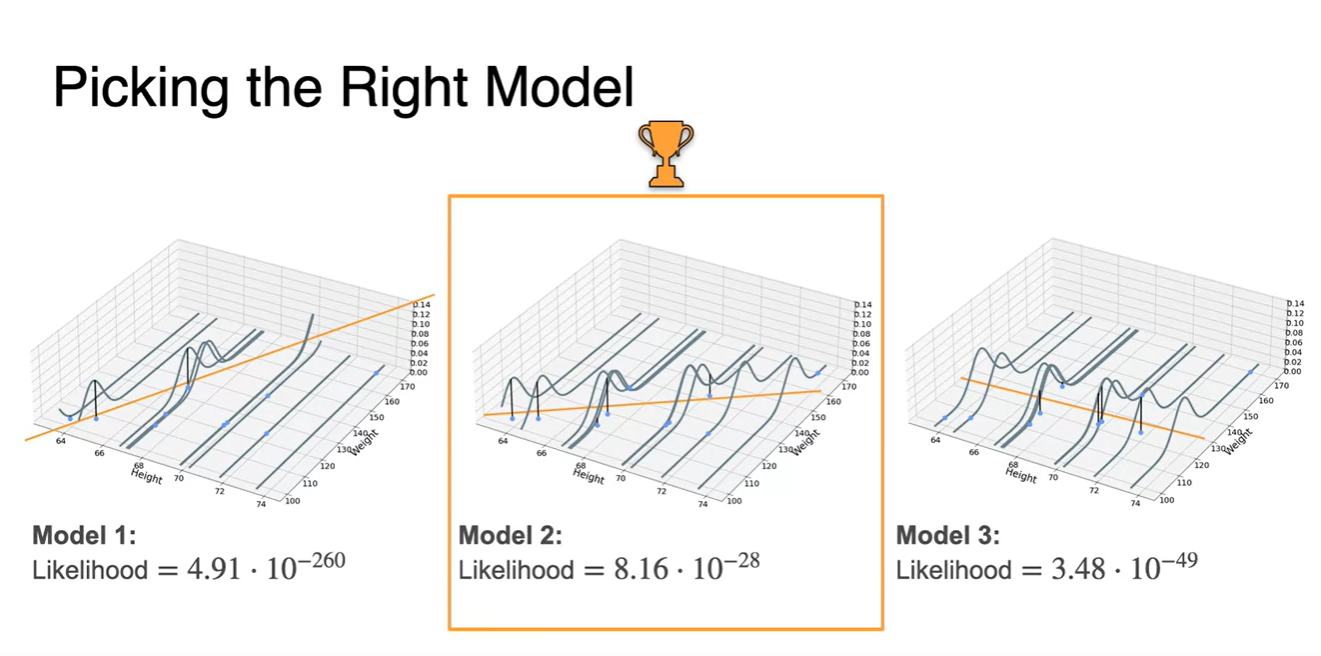
Regularization

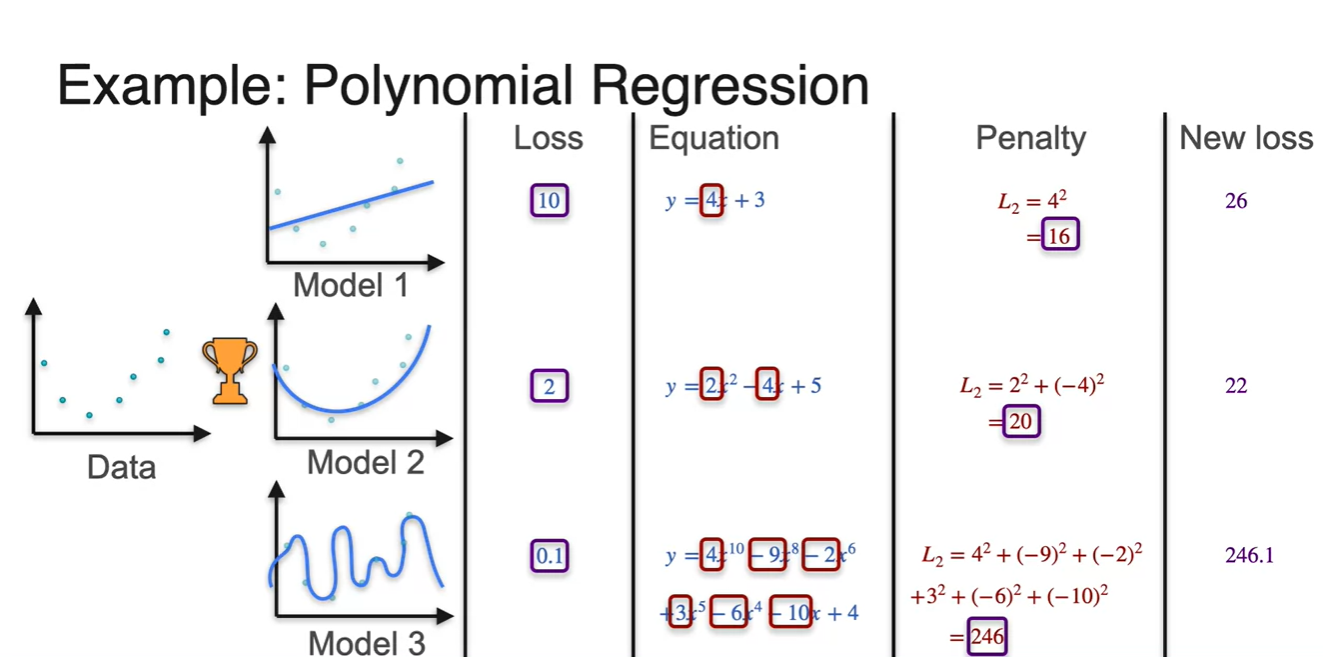
• 이번에는 Polynomial Regression 상황을 가정해보자.

  • Model을 표현할 수 있는 수식의 제한이 linear에서 polynomial로 복잡도가 늘어난 것이다.

    • 이렇게 되면 Model 3의 loss가 가장 낮기 때문에 현재로서는 가장 좋은 모델이라고 판단할 수 있다.

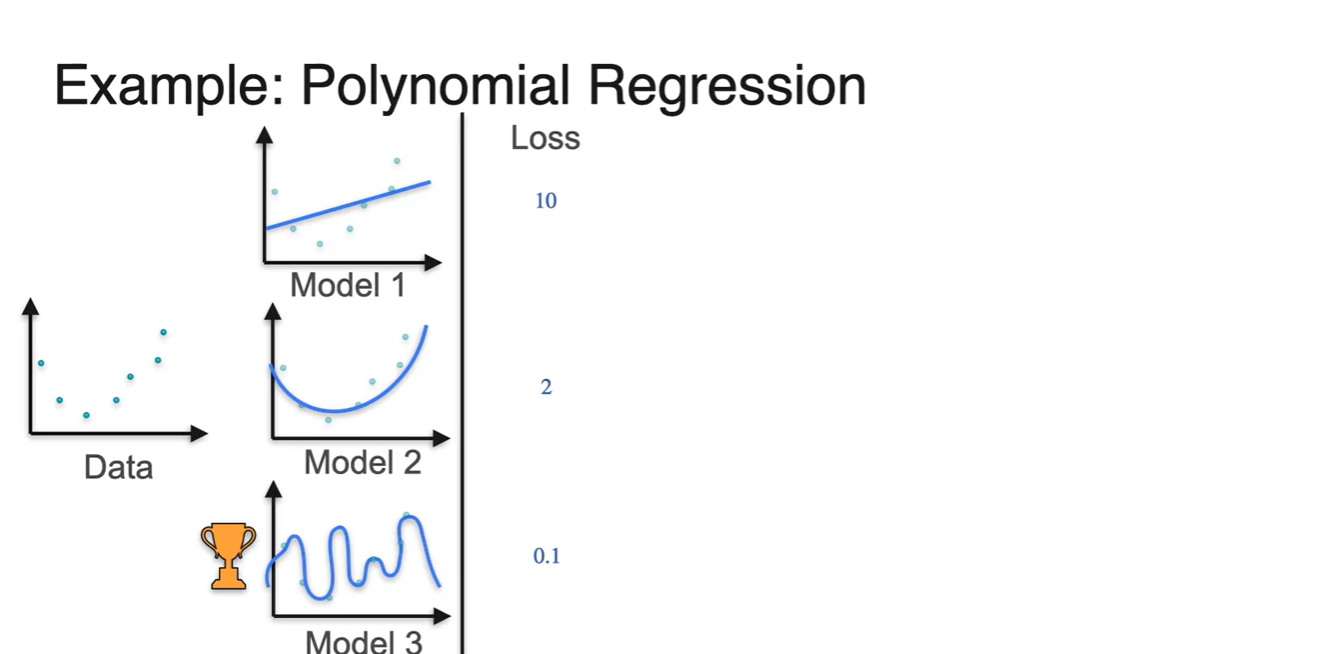
• Equation으로 표현하면 아래 수식과 같다.

  • 그러나 모델의 표현력이 너무 강할수록 caotic해지기 때문에, 이에 대한 penalty를 적절히 줄 수 있어야 한다.

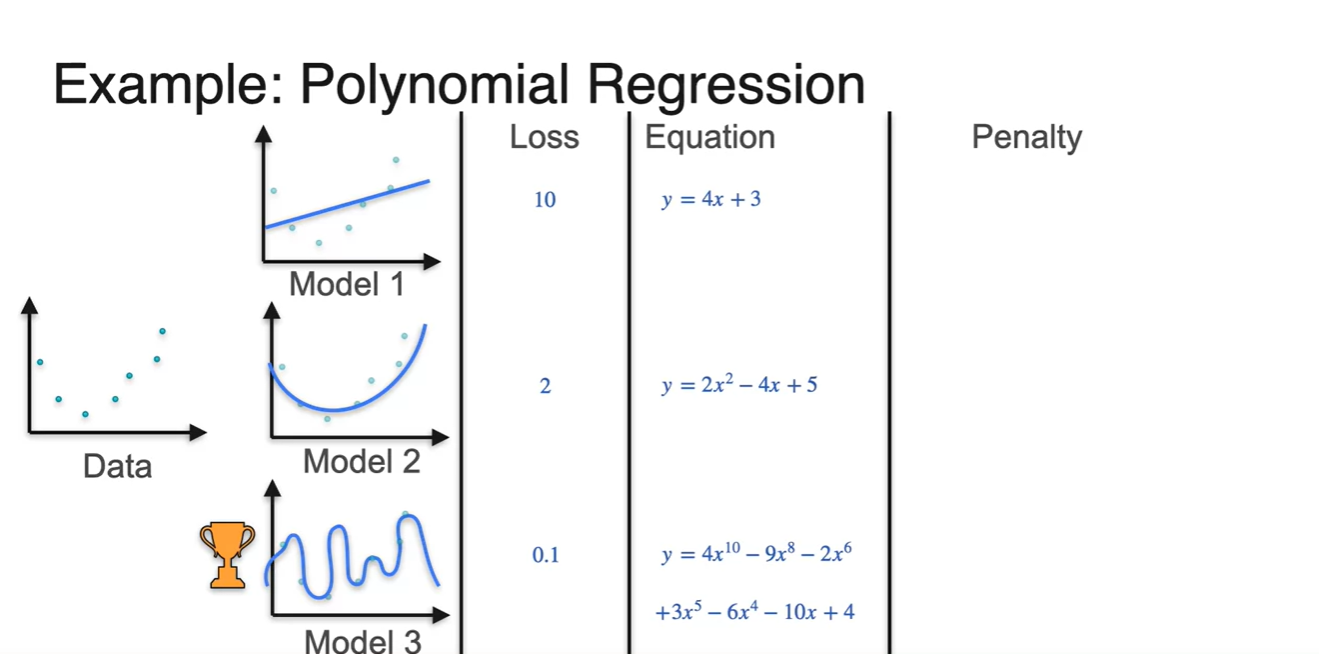
• 이제 $L_2$ penalty를 적용하여 새로운 loss를 표현해보자.

  • 각 polynomial의 계수들의 제곱을 합하여 $L_2$ penalty로 가정하고, 이를 기존 loss에 더하여 새롭게 loss를 표현한 결과가 다음과 같다.

    • 이를 통해 Model 2의 loss가 가장 작다고 계산되어 best model로 선정될 수 있게 되었다.

• Regularization Term에 대해 정리하면 아래와 같다.

  • 최종적으로 우리는 $ll + \lambda (a_n^2+a_{n-1}^2+..+a_1^2)$를 loss로 취급한다.

Back to "Bayesics"

• 우리는 바닥에 팝콘이 놓여져있을 때의 예시를 통해 likelihood에 대해 이해했었다.

  • 이곳에서 무슨 일이 일어났을지에 대한 probability가 가장 높은 값이 Movies라는 것을 알 수 있었고, 이는 evidence 역할을 하기에 충분하다.

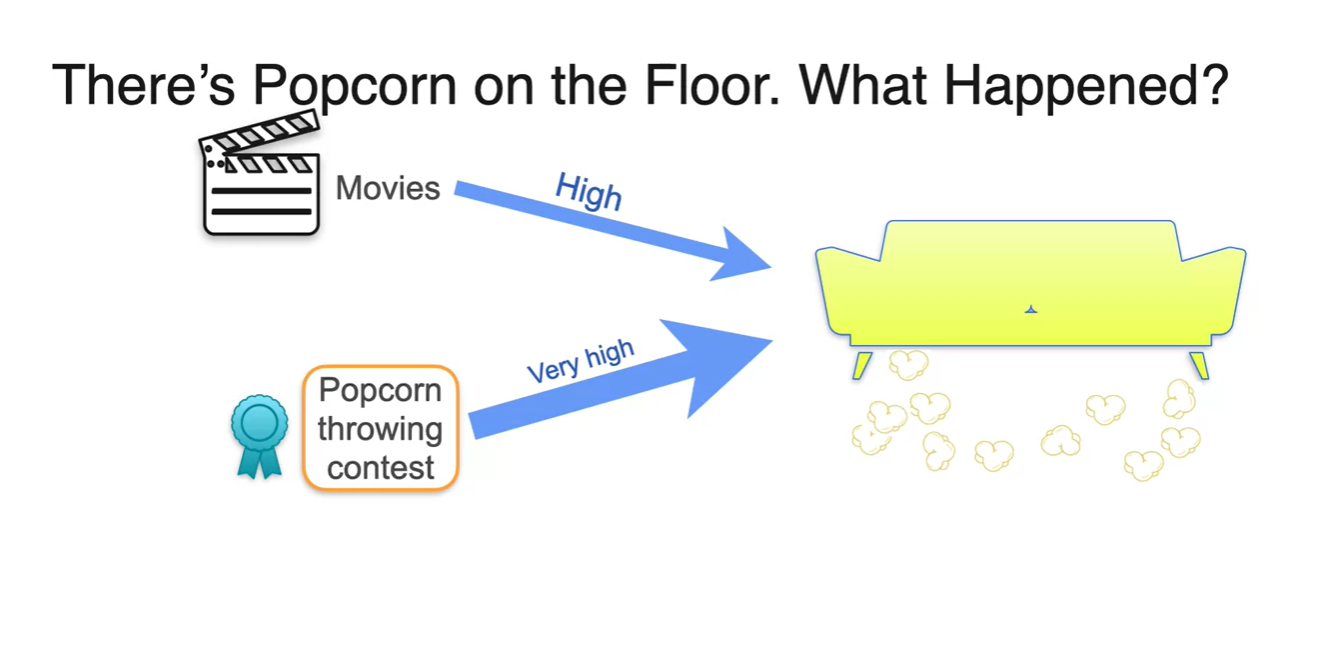
• 그런데 만약 Popcorn throwing contest가 열린 상황까지 추가된다면 어떨까?

  • 이럴 경우 팝콘이 떨어져있는 관측에 대한 evidence 확률은 throwing contest가 더 높고 more likely 하다.

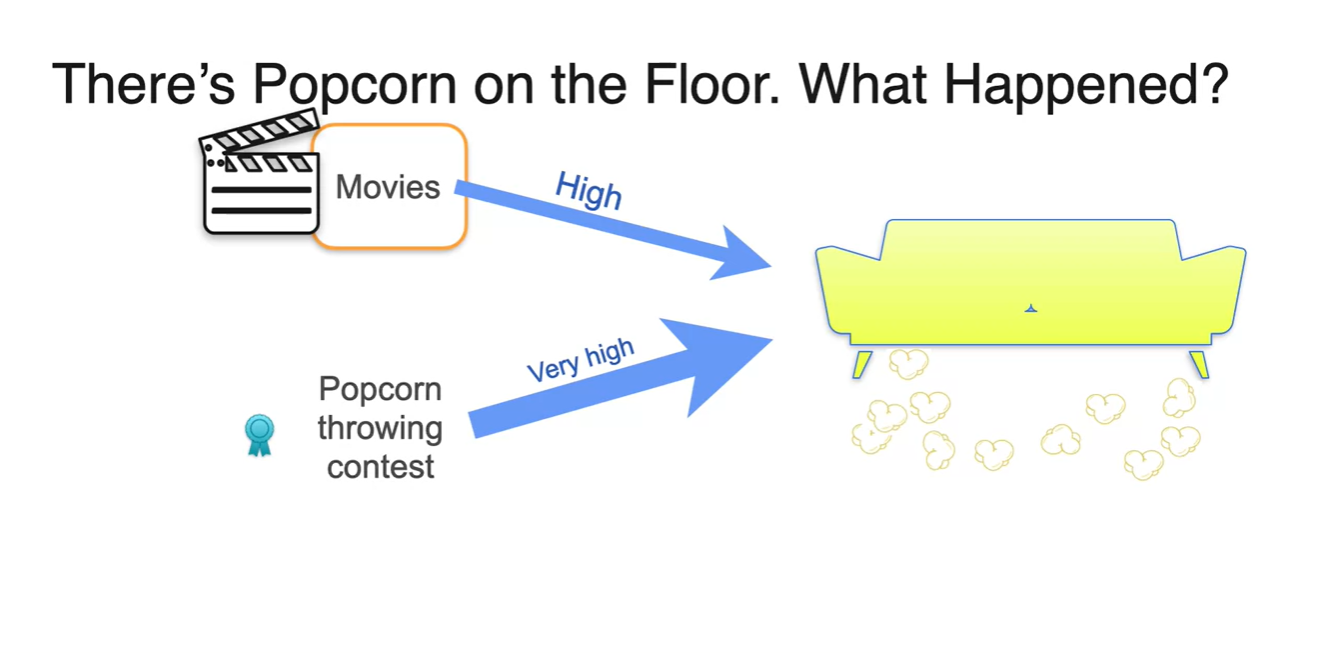
• 그러나 팝콘이 떨어져있는 상황을 제외하고 본다면 Popcorn throwing contest가 일어날 상황보다 Movies를 보는 상황이 더욱 빈번하게 일어난다.

  • 즉, Movies를 볼 독립적인 상황에 대한 확률이 더욱 크다.

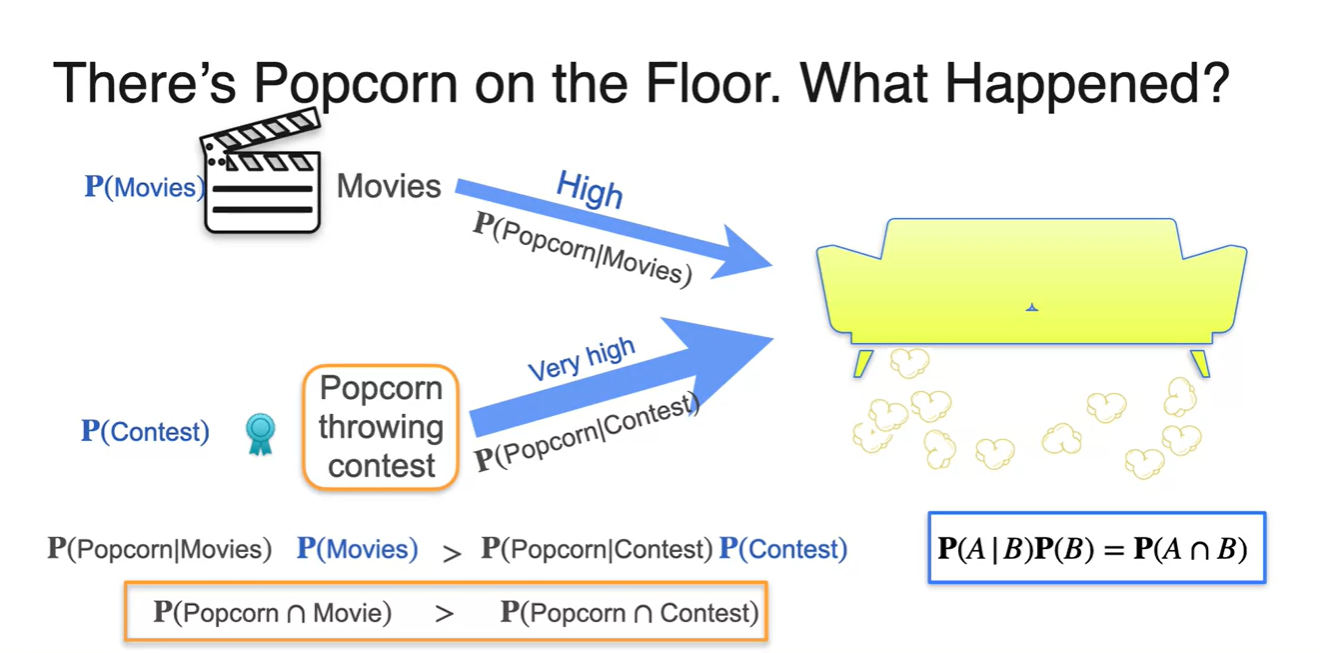
• 이럴때 우리는 각 확률의 값을 아래와 같이 비교해볼 수 있다.

  • $P(Movies) \gg P(Contest)$
  • $P(Popcorn|Movies) < P(Popcorn|Contest)$

• 위 수식을 각각에 대해 곱하여 다시 표현하면 아래와 같으며, 이 때 conditional 분포의 대소관계가 역전된다.

  • $P(Popcorn|Movies) P(Movies) > P(Popcorn|Contest) P(Contest)$
  • $P(Popcorn \cap Movies) > P(Popcorn \cap Contest)$

Bayesian Statistics - Frequentist vs. Bayesian

• Frequentist는 아래와 같이 Head가 8개, Tail이 2개가 나온 상황의 빈도수만을 보고 확률을 정의한다.

  • 그에 반해 Bayesian들은 두 확률이 같다는 가정 즉, 사전 확률(prior probability)이 존재하며 이를 Belief로 바라본다.

• Frequentist와 Bayesian statistics의 차이다.

  • Frequentists는 사건의 빈도수를 통해 likelihood를 정의하고, 관찰된 데이터를 통해 most generating 할 수 있는 model을 찾는다.

  • Bayesians는 prior 확률에 대한 belief를 갖고, 이러한 가정을 update하는 것에 목적을 둔다.

Bayesian Statistics - MAP

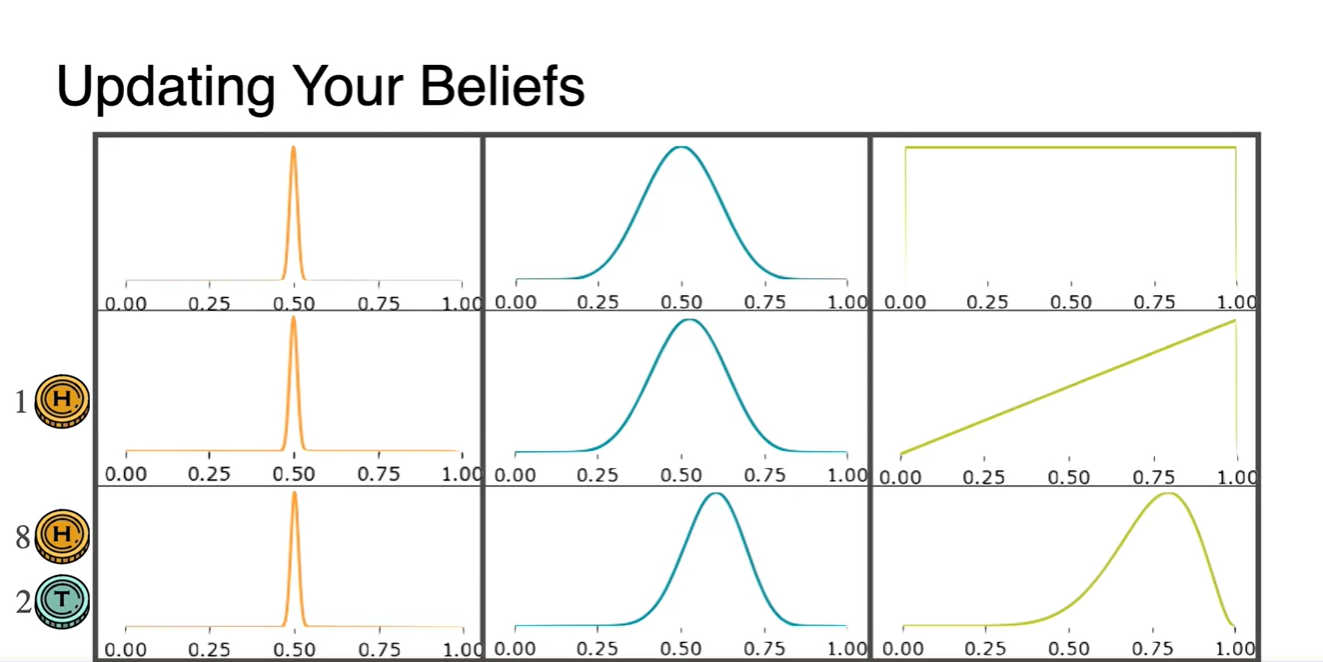
• 다음 세 가지 경우의 사전 확률 분포를 Beliefs로 가정해보자.

  1. Direc delta distribution
  2. Normal distribution
  3. Uniform distribution

  • H 1번과 {H 8, T 2}의 observaion으로 해당 분포를 update한 결과, 분포 1은 변화가 거의 없으나 분포 2와 3의 확률 밀도는 살짝 치우쳤음을 알 수 있다.

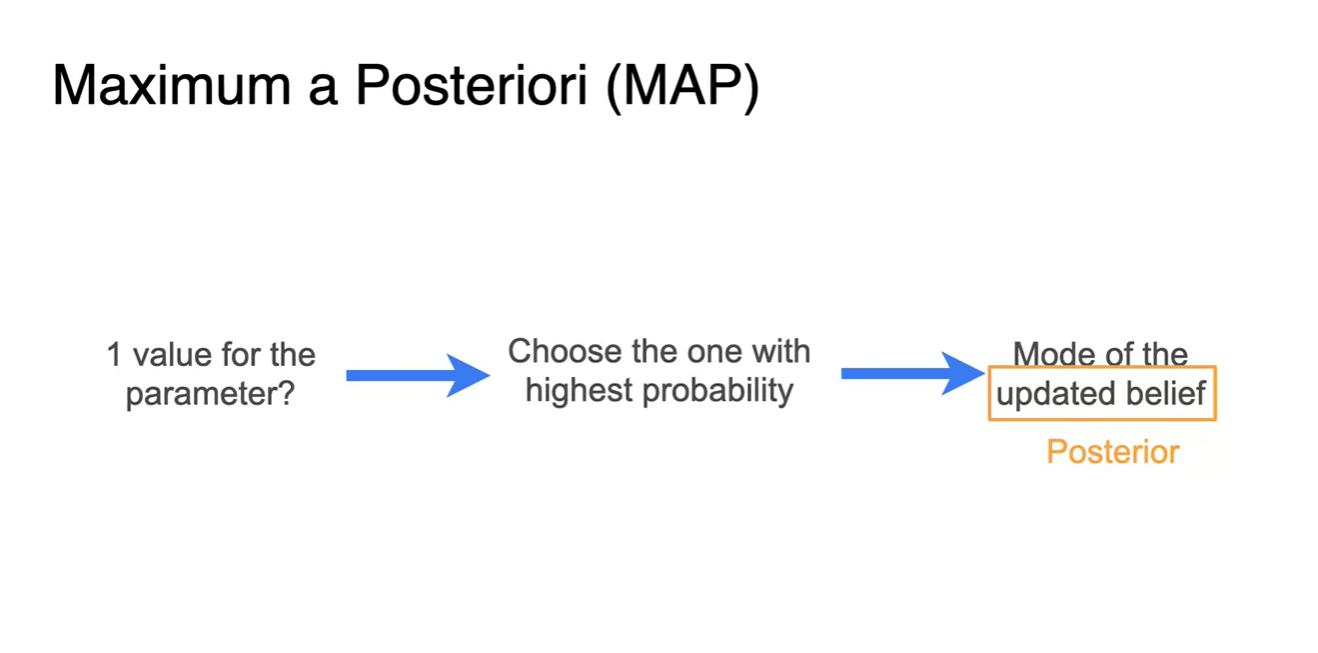
• Maximum a Posteriori(MAP)는 beliefs를 update한다는 점이 큰 특징이다.

  • 이는 확률을 최대화하는 parameter를 찾는 방법 중에 하나로, Posterior(사후 확률)를 update하는 과정이 핵심이다.

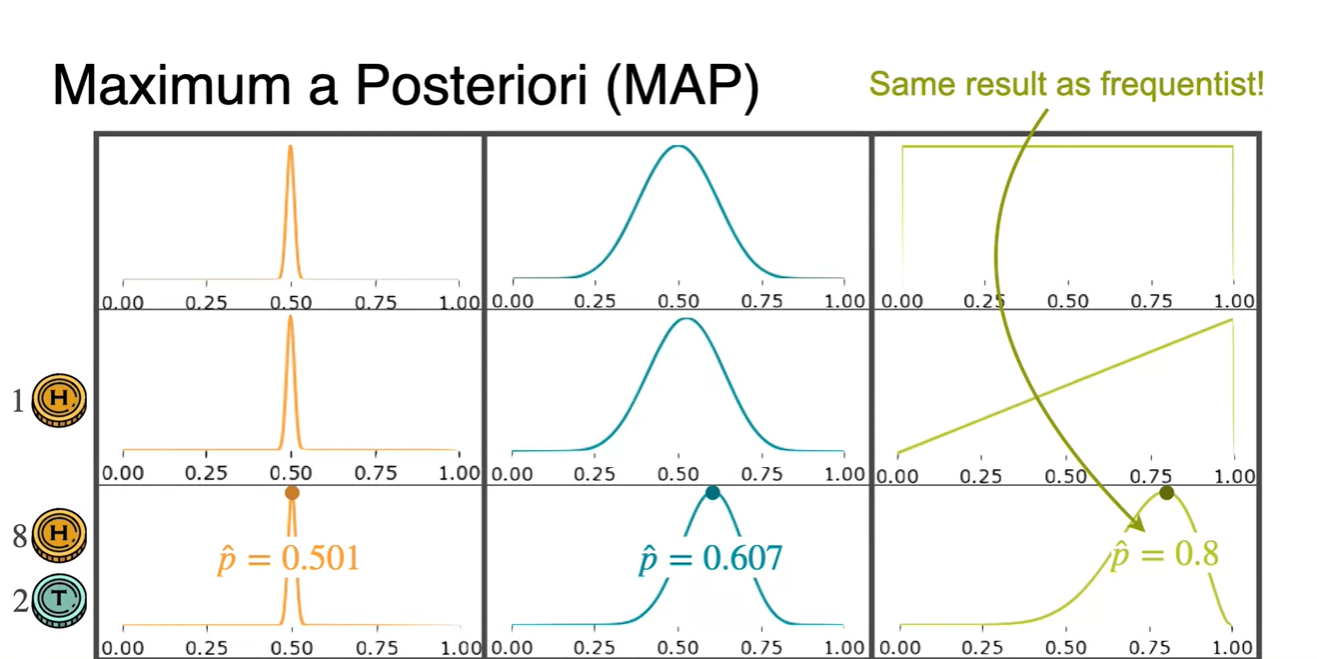
• Observation으로 $\hat{p} = P(H)$의 확률을 업데이트한 결과 0.5, 0.6, 0.8로 업데이트 되었다.

  • 처음 uniform distribution이라고 가정했던 분포는 Frequantist가 Maximum likelihood를 통해 예측한 확률값과 일치한다.

Bayesian Statistics - Updating Priors

• Bayesian 확률은 $\displaystyle P(A|B) = \frac{P(B|A) P(A)}{P(B)}$로 정리된다.

  • $P(B|A)$는 사건 A가 주어진 상황일 때 evidence B가 나타날 "likelihood"

  • $P(A)$는 predict할 사건 A의 "Prior" 확률

  • $P(A|B)$는 evidence B를 통해 추측한 A에 대한 belief를 나타내는 "Posterior"

    • $P(B)$는 $P(B|A)P(A) + P(B|A')P(A')$다.
    • 주어진 모든 상황에서 나타나는 evidence B의 확률을 말한다.

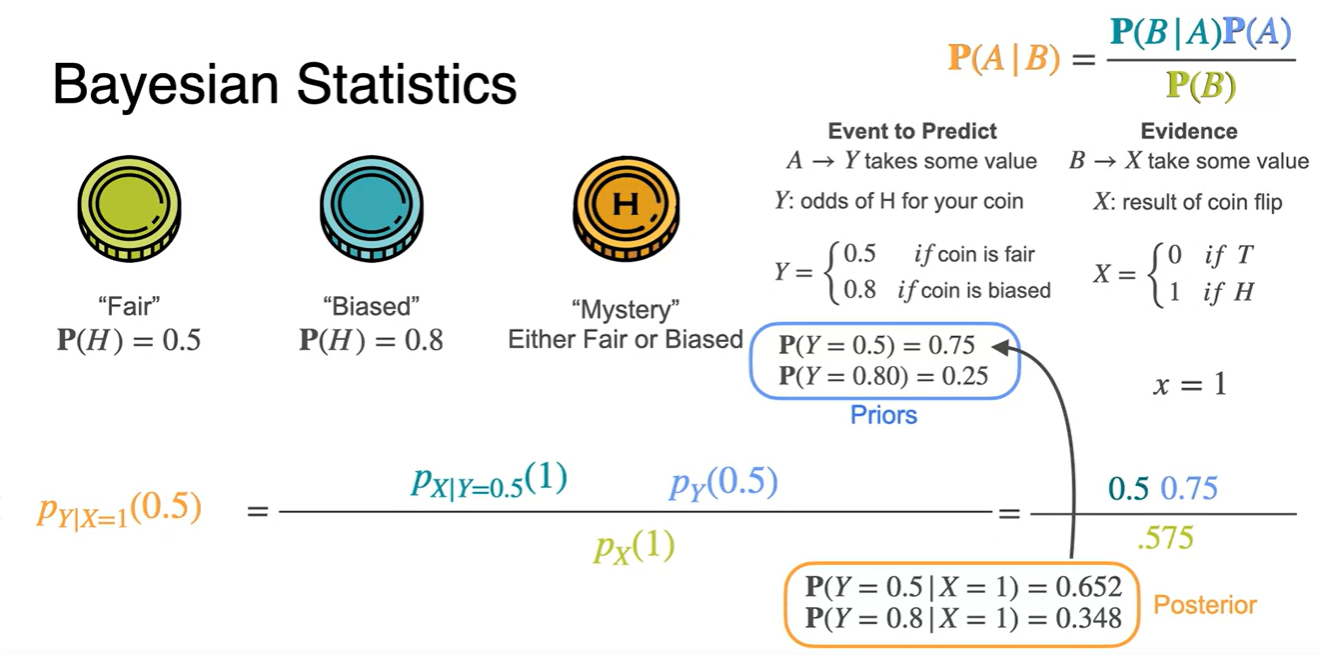
• 동전 던지기 상황을 예로 들면, Head가 나타날 확률이 Fair하다는 가정과 Biased하다는 가정을 설정할 수 있다.

  • 각각의 확률이 0.75, 0.25라는 Priors와 관측치가 $x=1$로 주어진다면, predict 해야 할 Posteriors는 아래와 같이 계산한다.

    • $P(Y=0.5|X=1) = \displaystyle \frac{P(X=1|Y=0.5) P(Y=0.5)}{P(X=1|Y=0.5)P(Y=0.5) + P(X=1|Y=0.8)P(Y=0.8)}$

      $= \displaystyle \frac{0.5 \; 0.75}{0.5 \; 0.75 + 0.8 \; 0.25}$

• $x=1$과 $x=0$의 evidence로 posterior를 계산하면 0.65, 0.35 확률값으로 계산된다.

  • Posterior 확률이 최대인 값을 찾아 parameter $\hat{p} = P(H)$가 얼마일지 추정하는 방법인 것이다.

• 수식을 최대한 단순화하면 아래와 같다.

  • $p_{Y|X=1} = \displaystyle \frac{p_{X|Y=0.5}(1) \; p_Y(0.5)}{p_X(1)}$

• 확률 변수 $x$는 evidence, $y$는 prior belief의 의미를 갖는다.

  • 즉, posterior는 $x$가 data로 주어진 상황에서 prior $y$ (domain knowledge)를 반영하여 계산한 posterior의 최대를 찾는 것이 목적이다.

• $X$와 $Y$가 discrete한 상황과 continuous한 상황의 Bayesian 확률을 정리한 내용이다.

  • 중요한 건 Prior 설정과 likelihood와의 곱으로 계산한 Posterior다.

• 이제 추정하고자 하는 parameter와 관련된 변수는 $\Theta$와 $\theta$로 설정하고자 한다.

Bayesian Statistics - Full Worked Example

• 동전을 던져 Head가 나올 확률 $P(H)$를 $\Theta$라고 하자. - continuous random variable

  • $X$는 각 시행 횟수마다 어떤 값이 나왔는지를 의미하는 discrete random variable이다. - 1 if H, 0 if T

    • Bayes' Theorem을 사용하여 정리하면 $\displaystyle f_{\Theta|\bold{X}\bold{x}}(\theta) = \frac{p_{\bold{X}|\Theta=\theta}(\bold{x}) f_{\Theta}(\theta)}{p_{\bold{X}}(\bold{x})}$와 같다.

    • 이 때, $p_{\bold{X}|\Theta=\theta}(\bold{x})$가 바로 likelihood이며 parameter $\theta$로 해당 식을 표현하면 H가 8개, T이 2개 이므로 $\theta^8(1-\theta)^2$다.

• $\Theta \sim Uniform(0, 1)$을 따른다고 가정하면 prior 확률을 나타내는 $f_{\Theta}(\theta)$는 1의 값을 가지게 된다.

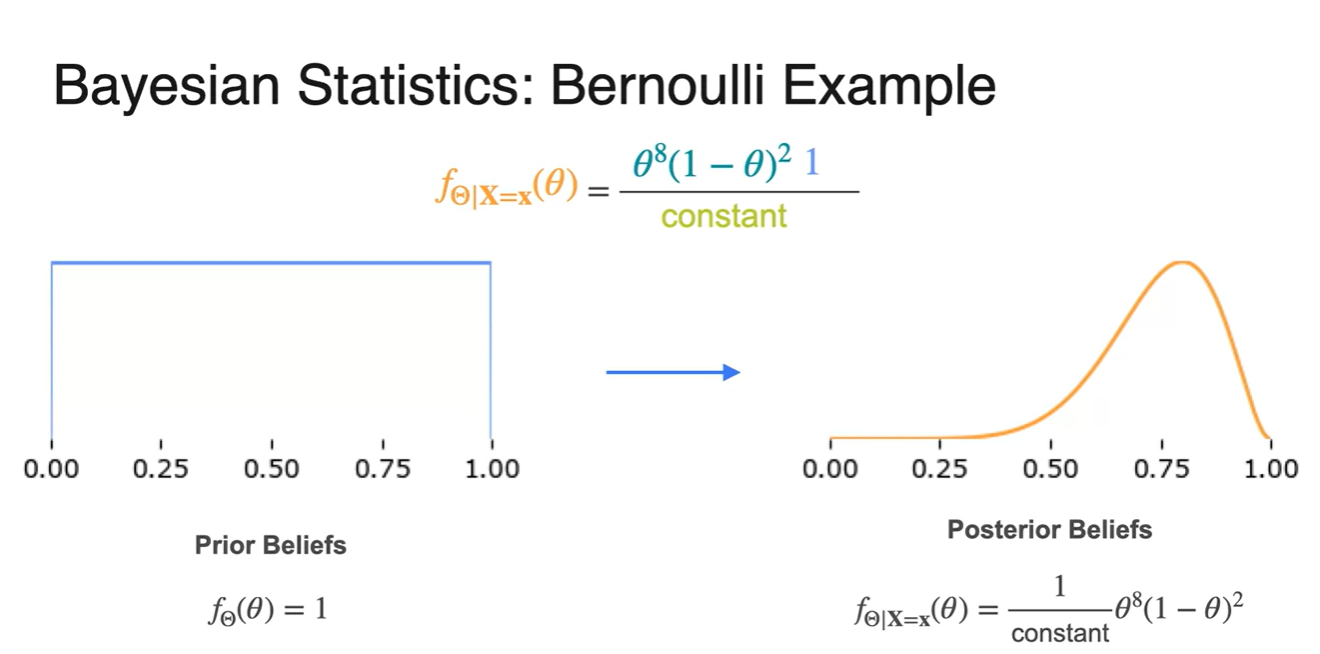
  • 이를 통해 Bayes' Theroem을 다시 정리하면 $\displaystyle f_{\Theta|\bold{X}\bold{x}}(\theta) = \frac{\theta^8(1-\theta)^2 1}{constant}$로 전개된다.

    • 이와 같은 꼴을 Beta distribution이라고 하며 constant를 계산할 수는 있지만 unnecessary하다고 설명한다.

• Prior beliefs가 Uniform하다고 가정하여 Posterior를 계산하면, 아래와 같은 분포의 변화가 생긴다.

  • $\theta^8 (1-\theta)^2$가 0.8에서 최대치를 가짐을 알 수 있다.

• MAP Estimator는 model이 동전의 Head 확률을 $\theta$라고 가정하는 것으로부터 출발하여, $P(data|model)$의 likelihood를 Maximizing하는 parameter $\theta$를 찾는 과정을 말한다.

  • Maximum a Posteriori(MAP)에 대한 수식은 $\hat{\theta} = \displaystyle \underset{\theta}{\mathrm{argmax}} f_{\Theta|\bold{X}=\bold{x}}(\theta)$로 표기한다.

    • 현재 prior를 uniform distribution으로 가정하였기 때문에 $\hat{\theta} =\displaystyle \frac{8}{10}$에서 likelihood가 최대치를 갖는 상황이다.

    • 즉, MAP = MLE라서 prior가 중요한 작용을 하고 있지 않다.

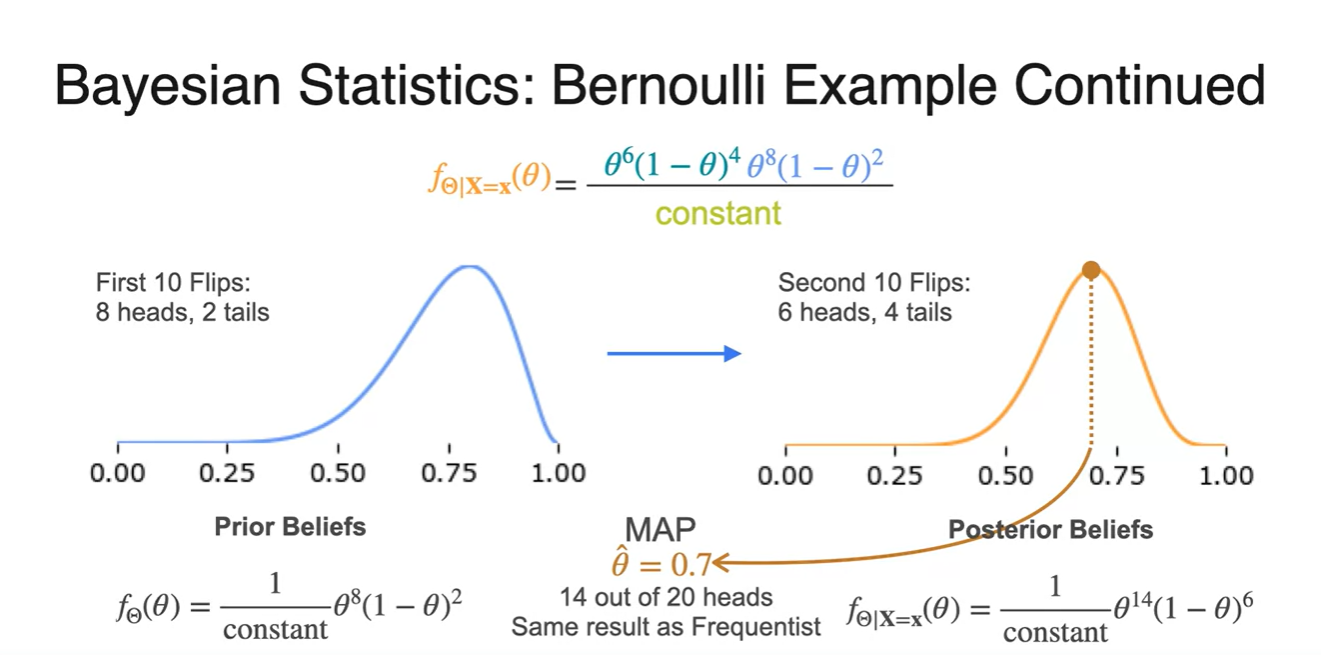
• 앞서 계산한 posterior를 new prior로 가정하면 $f_{\Theta}(\theta) = \theta^8(1-\theta)^2$로 사용할 수 있다.

  • 실제 관측 결과가 $p_{\bold{X}|\Theta=\theta} = \theta^6(1-\theta)^4$라면
    new posterior는 $f_{\Theta|\bold{X}=\bold{x}}(\theta) = \displaystyle \frac{1}{constant} \theta^{14} (1-\theta)^6$로 계산된다.

• MAP로 posterior를 업데이트 한 결과 maximum likelihood는 $\hat{\theta} = 0.7$에서 만족된다는 것을 알게 되었다.

  • 이는 20번 던져서 Head가 14번 나왔을 때 Frequentist가 예측한 maximum likelihood parameter와 같은 결과다.

    • 즉, 실제 관측 결과는 6번 Head가 나온 상황이므로 MAP는 prior가 굉장히 중요한 영향을 미치고, frequentist에게는 관측 결과에만 영향을 받는다.

• Bayesian Statistics Summary

  • Bayesian들은 prior beliefs를 업데이트 한다.
  • MAP with uninformative priors라면(ex. Uniform dist.) MLE와 같다.
  • 충분한 데이터가 있다면 MLE와 MAP는 수렴하게 될 것이다.
  • 데이터가 적거나 prior belief가 매우 중요한 상황일 때(domain specific) 유용한 방법론이다.
  • Prior가 틀린 가정이라면, 결과 또한 틀릴 수 있으므로 주의해야 한다.

Relationship between MAP, MLE and Regularization

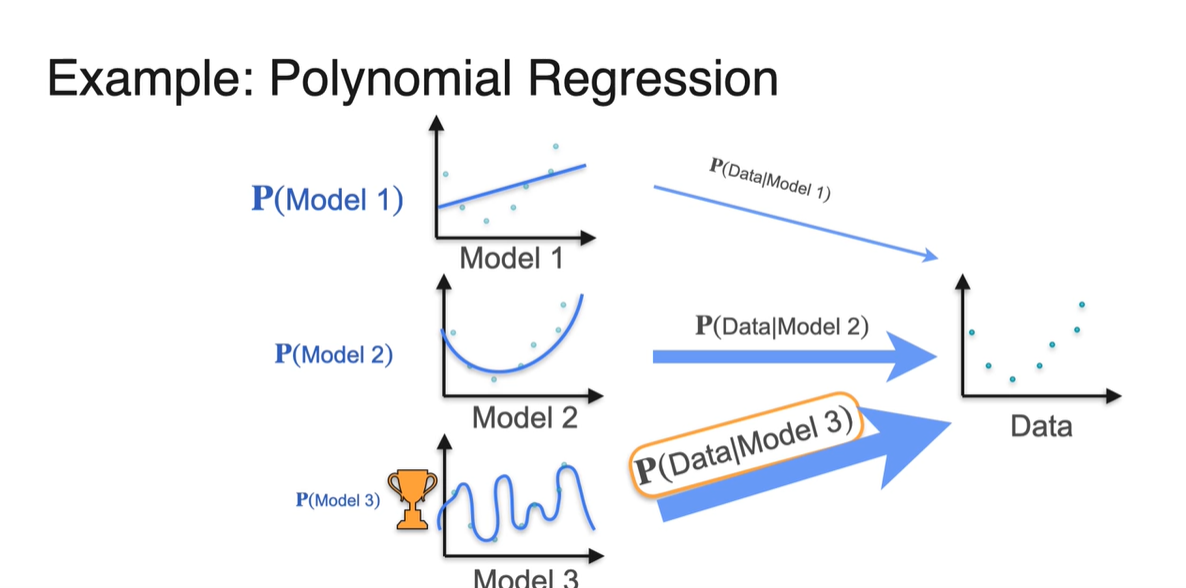
• 오른쪽과 같은 Data가 있고, 이를 설명하는 model이 왼쪽의 3개가 있다고 해보자.

  • Model이 data를 표현하는 Likelihood $P(Data|Model)$는 Model 3가 가장 크지만, 해당 모델이 사용될 일반적인 확률 $P(Model)$은 Model 3가 가장 작다.

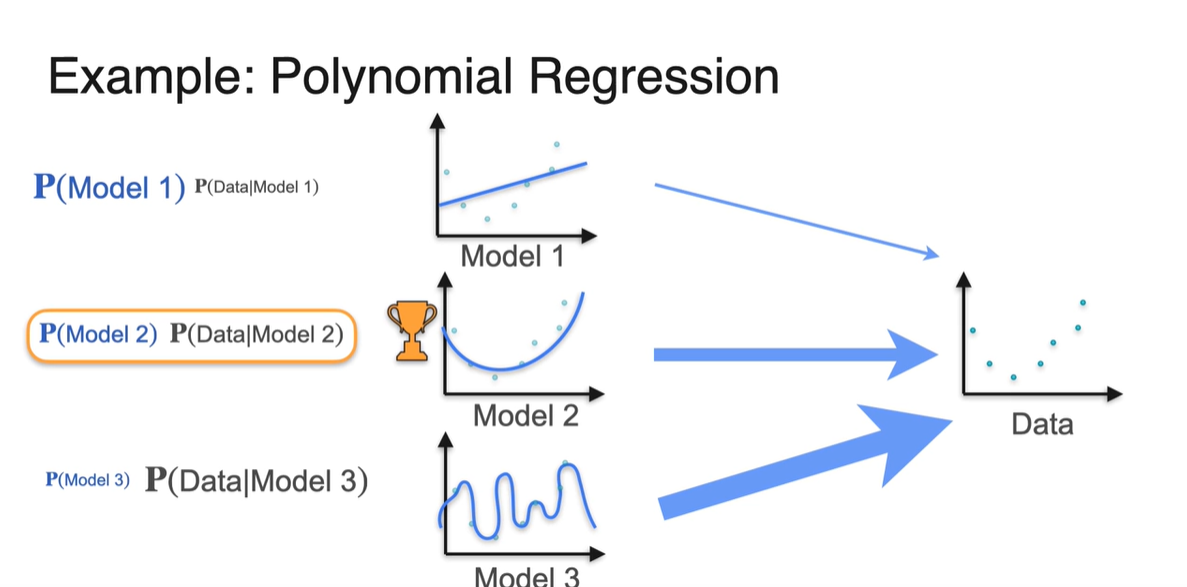
• 그리하여 우리는 두 확률 $P(Model)$과 $P(Data|Model)$를 곱하여 전체 probability를 계산하였다.

  • 결과는 $P(Model \; 2) \; P(Data|Model \; 2)$의 확률이 가장 높았음을 알 수 있다.

• 여기에 Model이 Polynomial할 수 있는 경우의 수까지 추가된다면 Regularization으로 panalty를 줄 수 있다고 하였다.

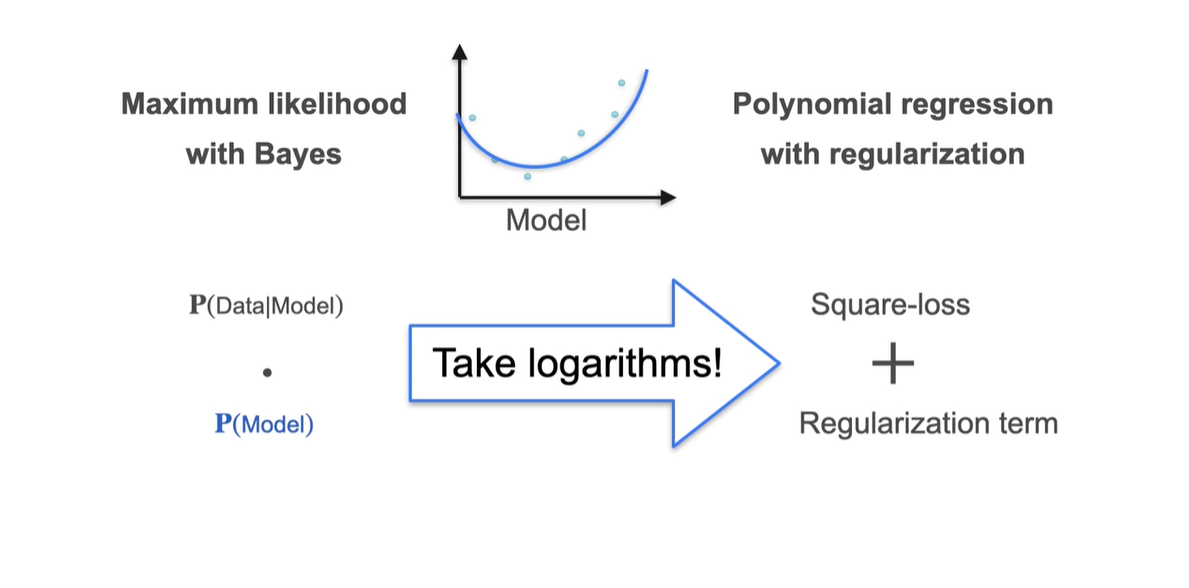
  • 따라서 Bayes 정리를 이용한 Maximum likelihood를 계산하는 방법과 polynomial term(계수)의 L2 regularization을 합치는 과정은 다음과 같이 이루어진다.

    • $P(Model) \; P(Data|Model) \overset{log}{\Rightarrow} L2 \;Regularization$

    • $P(Model)$을 어떻게 알아낼 것이냐에 관한 아주 큰(elephant에 비유) 문제를 추후 살펴보자.

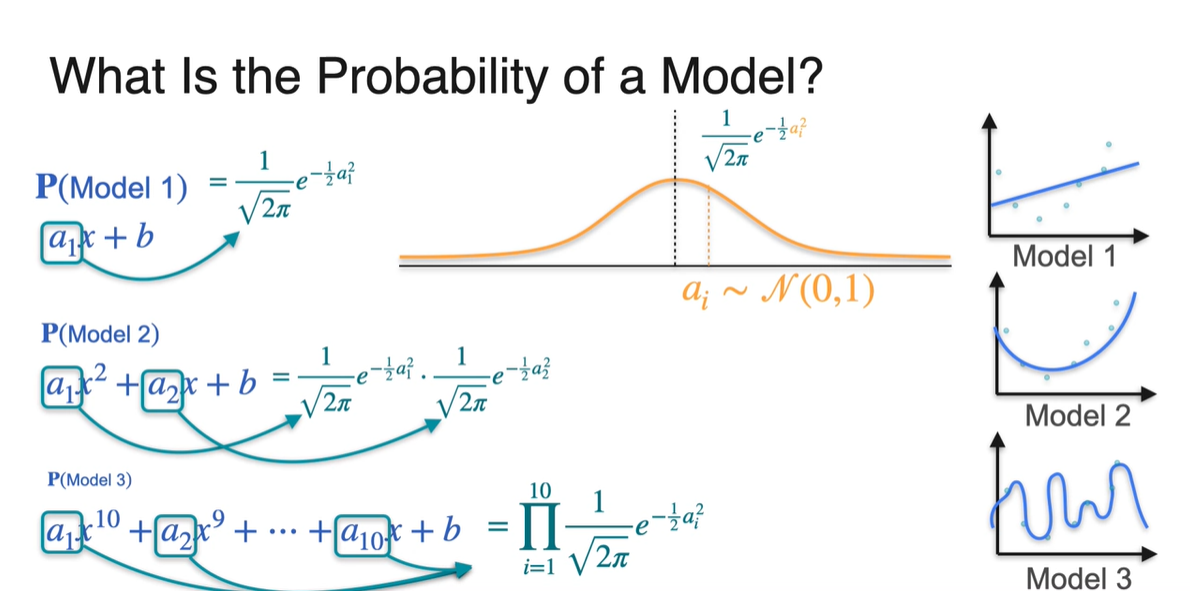
• Probability of a Model을 구할 때에는 각 항의 계수가 매우 중요한 역할을 한다.

  • 모델의 polynomial항 계수인 $a_i$가 $\sim N(0, 1)$을 따른다고 생각하면 각 항의 density를 곱한 값은 $\displaystyle \Pi_{i=1}^{n} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}a_i^2}$를 구해 알 수 있다.

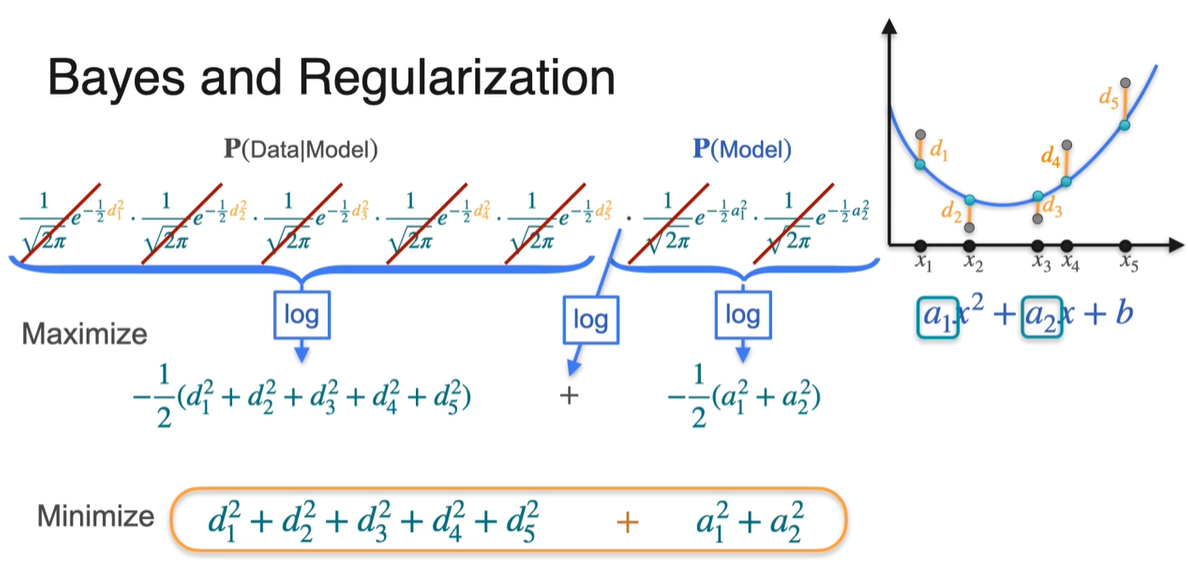
• $P(Data|Model)$와 $P(Model)$를 곱하면 아래와 같이 exponential의 지수 합으로 표현된다.

  • 앞서 보았듯이 $\displaystyle -\frac{1}{2}(d_1^2 + d_2^2 + d_3^2 + ...) + -\frac{1}{2}(a_1^2 + a_2^2 + ...)$를 Maximize하는 과정은 $(d_1^2 + d_2^2 + d_3^2 + ...) + (a_1^2 + a_2^2 + ...)$를 Minimize하는 것과 같다.

• 따라서 Bayes 정리를 사용하는 MAP는 아래와 같은 Loss term을 사용한다.

  • $(d_1^2 + d_2^2 + d_3^2 + ...) + (a_1^2 + a_2^2 + ...)$

    • 이를 Minimize함으로써 $P(Model) \; P(Data|Model)$을 최대화하는 parameter를 추정하는 과정이라 할 수 있다.

---

• 출처 : [Coursera] Mathmatics for Machine Learning and Data Science