Markov Decision Processes

Introduction to Markov Decision Processes

Markov Decision Processes

• Markov Decision Process, MDP에 대해서 알아보자.

• 이번 강의를 통해 우리는 MDP에 대해 이해하고, dynamics of MDP를 설명할 수 있게 될 것이다.

• 만약 토끼가 당근을 찾게되는 상황이라고 가정해보자.

  • 당근을 찾으면 +10을 브로콜리를 찾으면 +3의 reward를 받는다.

• Different situation은 different action을 취하도록 만든다.

  • 위의 상황에서는 오른쪽으로 가야 당근을 찾을 수 있었다면 이번에는 토끼가 왼쪽으로 가야만 최대 보상을 받을 수 있게 된다.

• 만일 당근을 찾고난 이후, 뒤에 호랑이가 기다리고 있다면?

• 당근을 찾아 +10의 reward를 받았지만 토끼는 곧바로 호랑이에게 잡아먹히고 말 것이다.

• 그러면 위 상황에서의 토끼는 당근을 찾으러 갈 것이 아니라, 브로콜리를 찾아 도망가는 편이 나을 것이다.

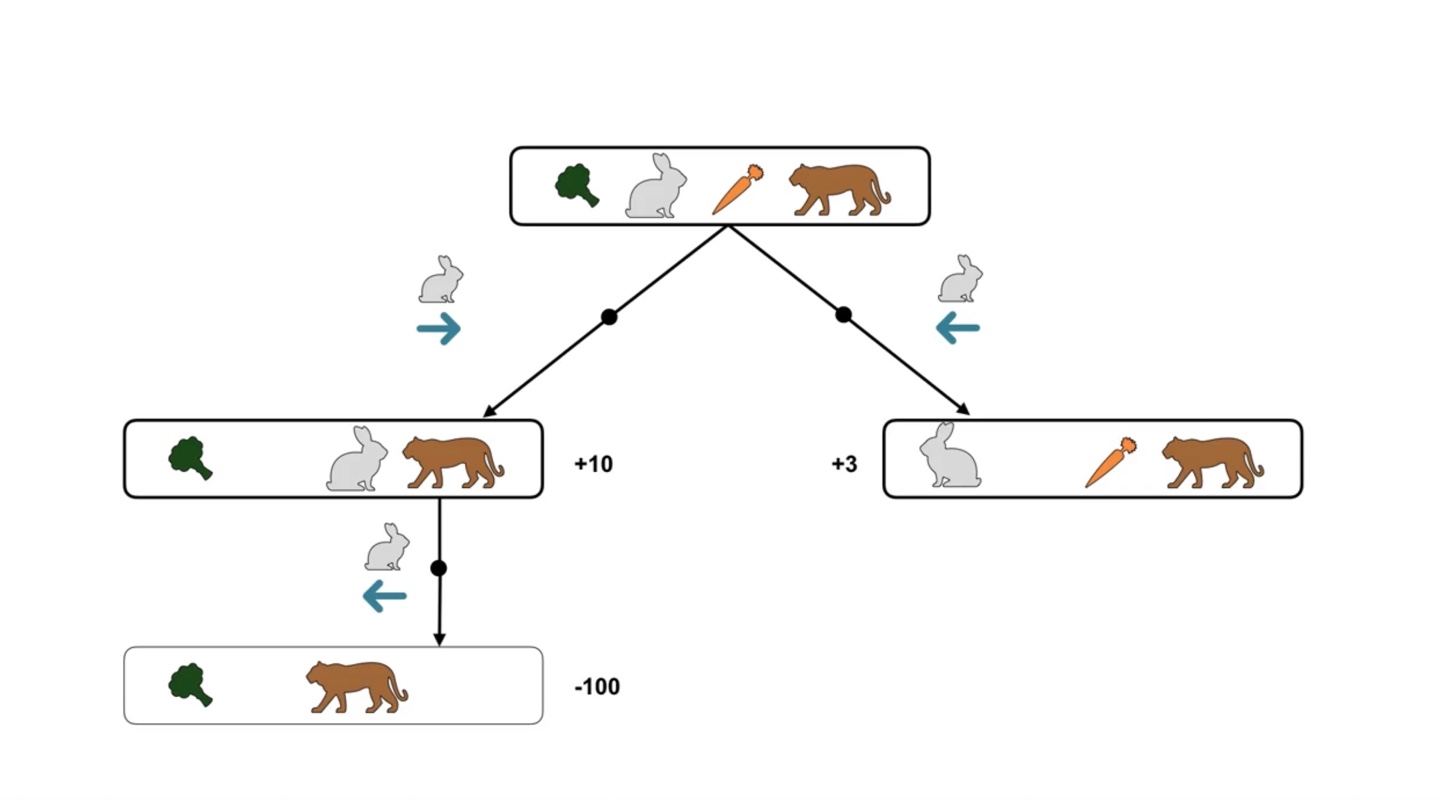
• 토끼가 취할 수 있는 action과 받는 reward를 트리 구조로 표현한 결과가 다음과 같다.

  • 호랑이를 만난 상황의 reward가 너무 negative한 나머지, 브로콜리를 찾는 선택지의 reward가 더 높다는 것을 알 수 있다.

• 토끼가 어떠한 timestep $t$에 state $S_t$에 놓여있다면 토끼가 취할 수 있는 action은 $A_t$라 표현할 수 있다.

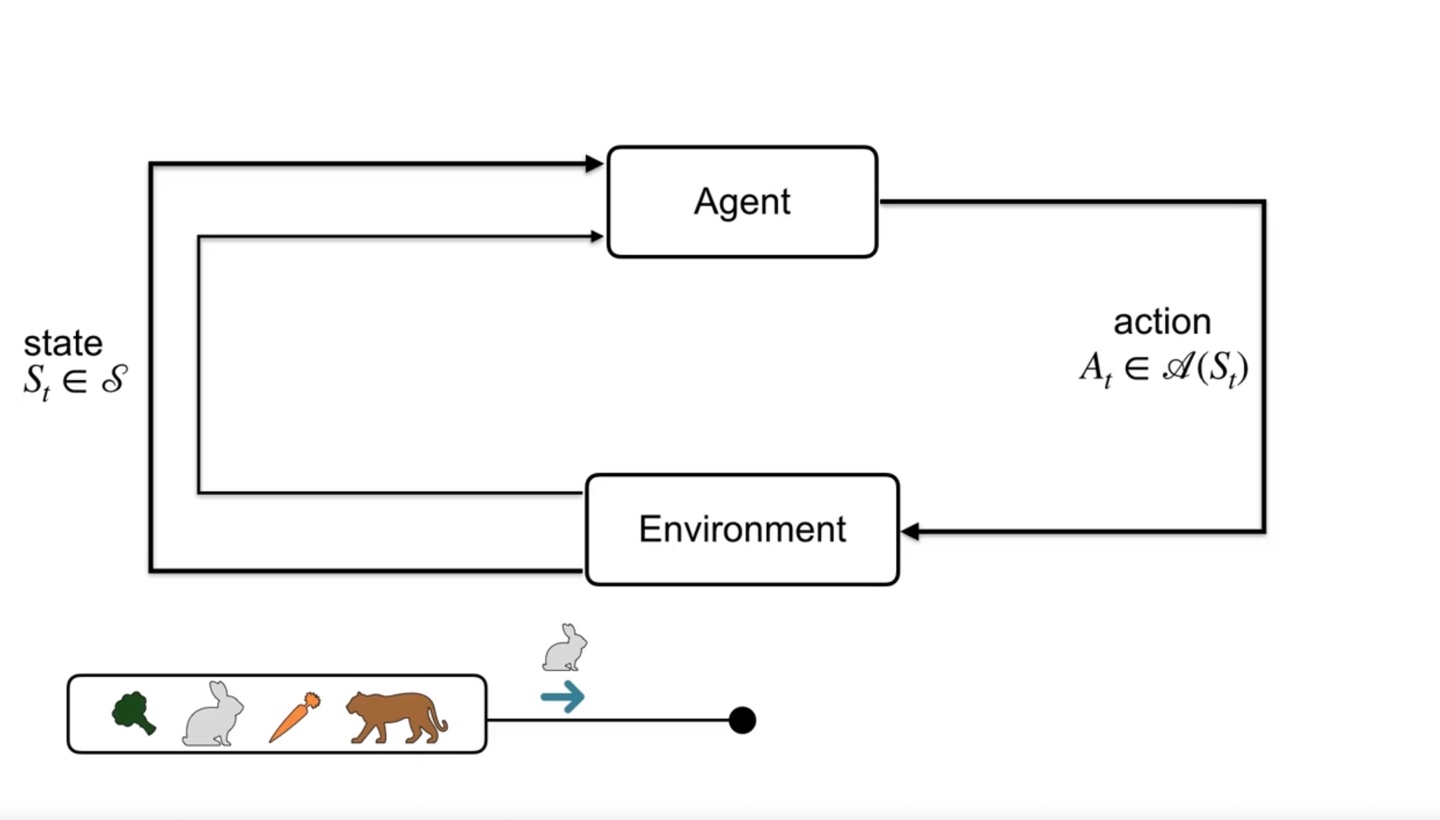
• Action을 취했을 때의 Reward는 $R_{t+1}$다.

  • $S_t$ → $A_t$ → $R_{t+1}$ → $S_{t+1}$로 이어지는 chain을 갖는다.

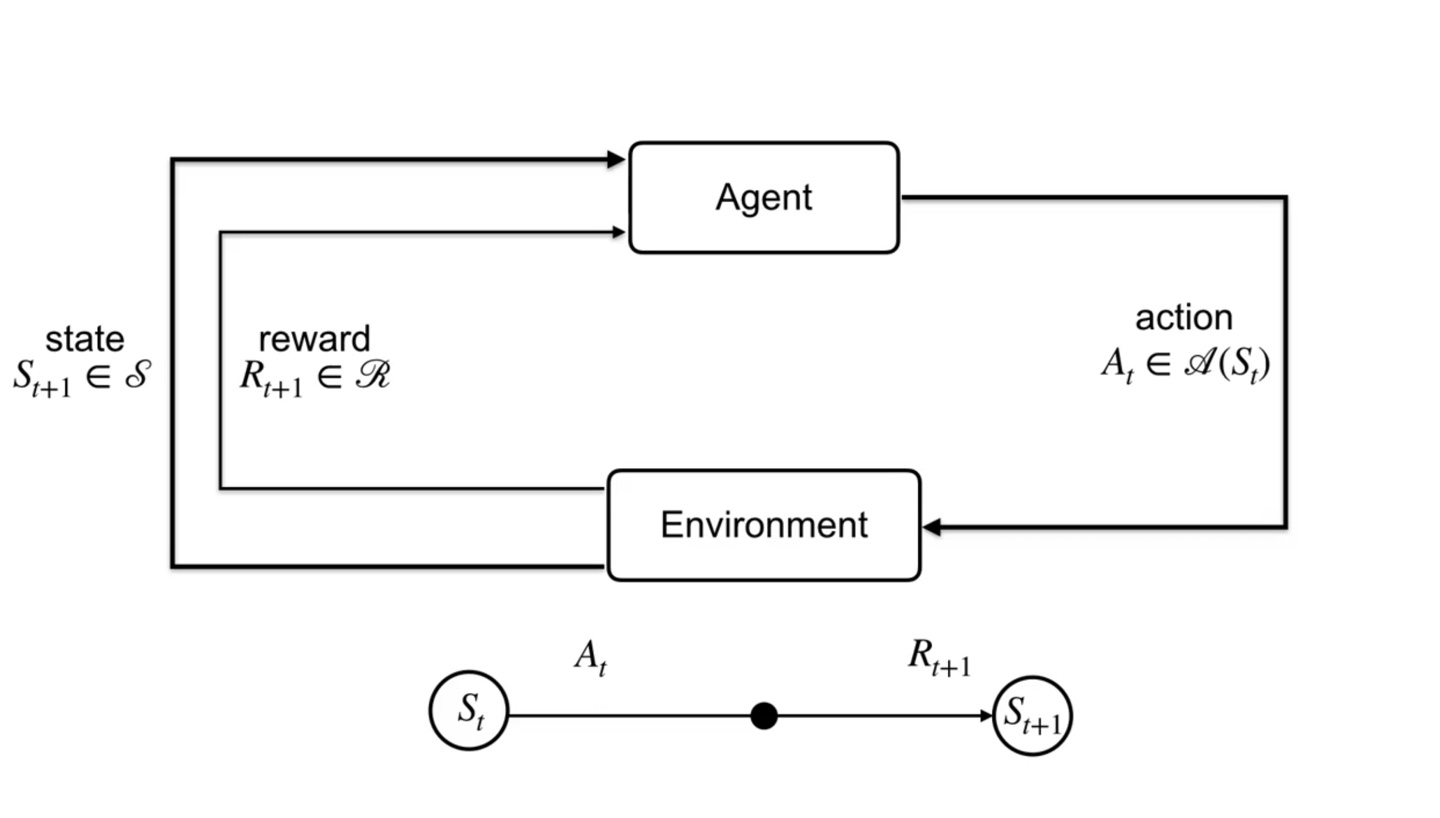
• 아까와 같은 토끼 예제에서는 +10의 positive reward를 받고 그 즉시 -100의 negative reward를 받게 될 것이다.

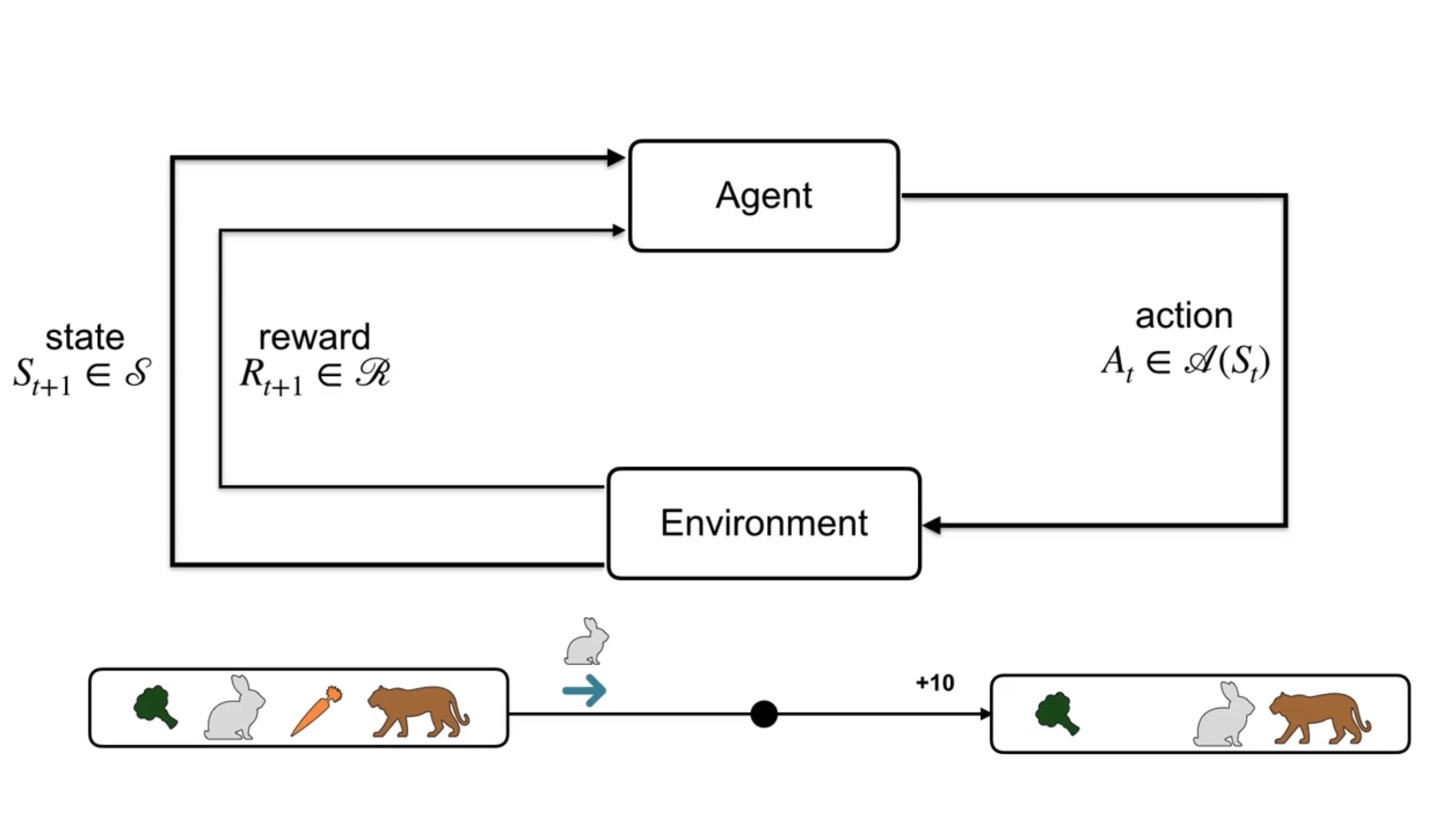
• 이렇듯 agent는 여러 timestep을 지나며 state와 action을 반복한다.

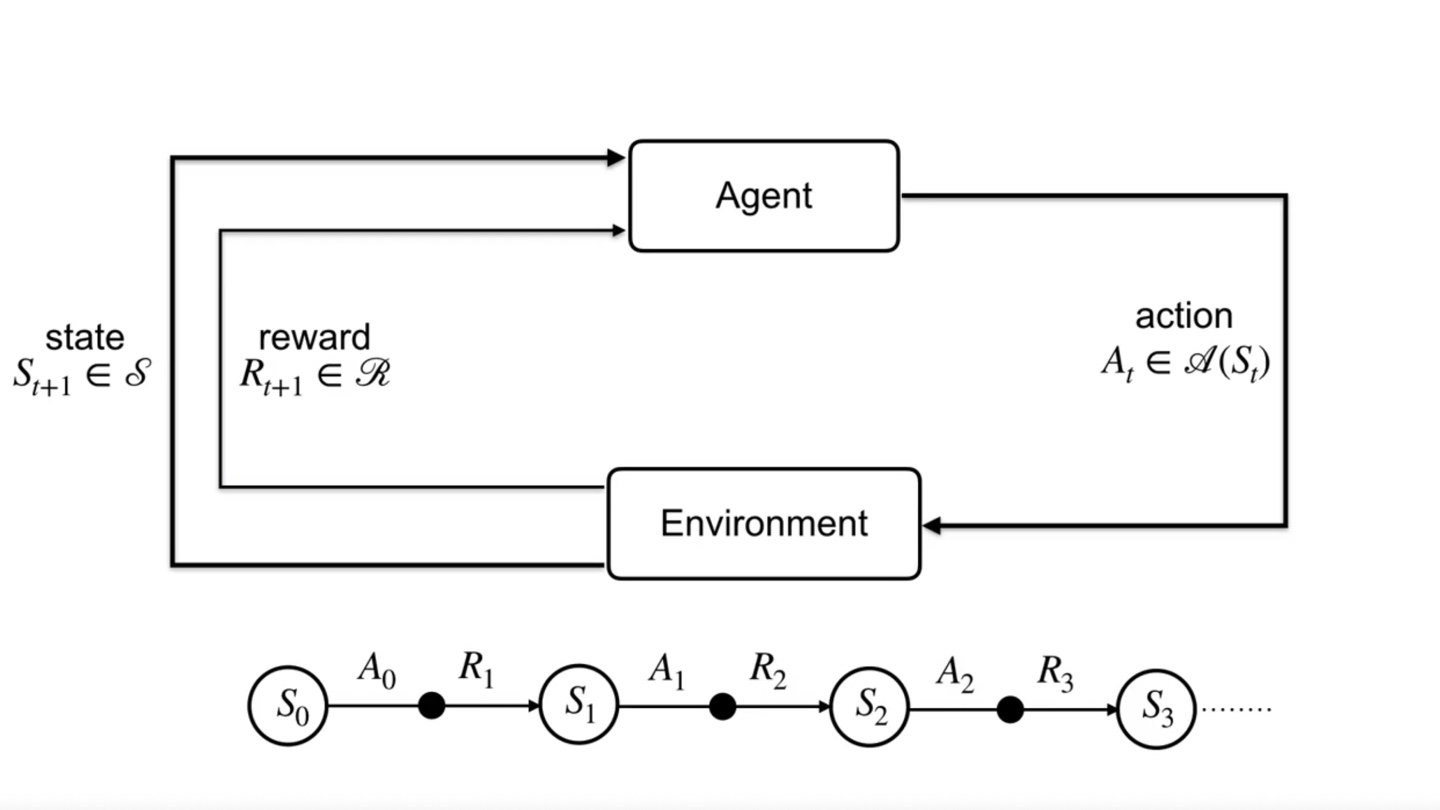
• The dynamics of an MDP는 $p(s', r | s, a)$ 기호로 표기한다.

  • State와 Action이 주어지면 다음 step의 State'와 Reward 확률을 계산하여 정보를 얻는 것이다.

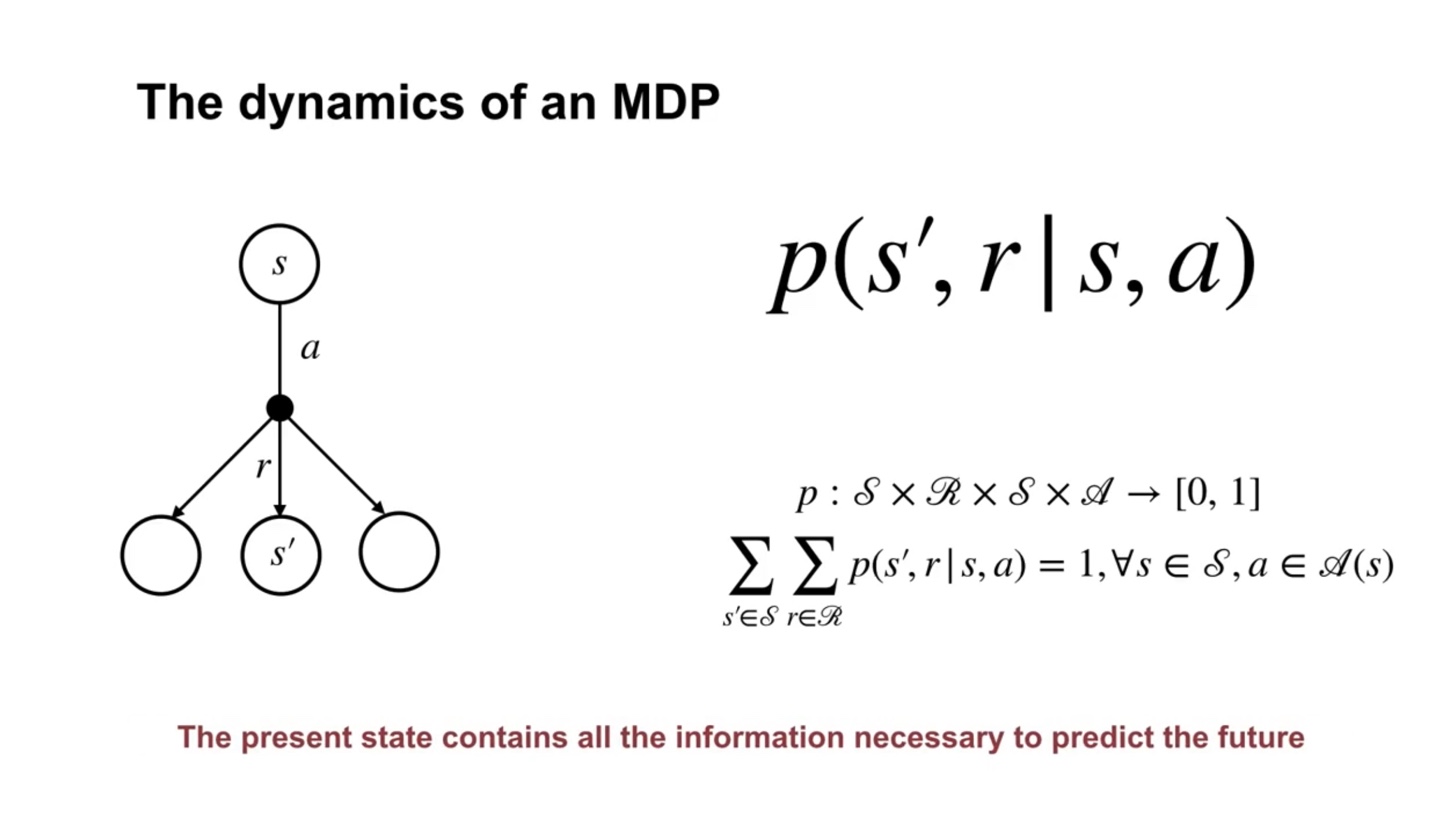
• Summary

Examples of MDPs

• MDP의 한 예시로 Recycling bot 예제를 다뤄보자.

• 이번 강의에서는 decision-making as MDP를 formalizing하는 방법을 다룬다.

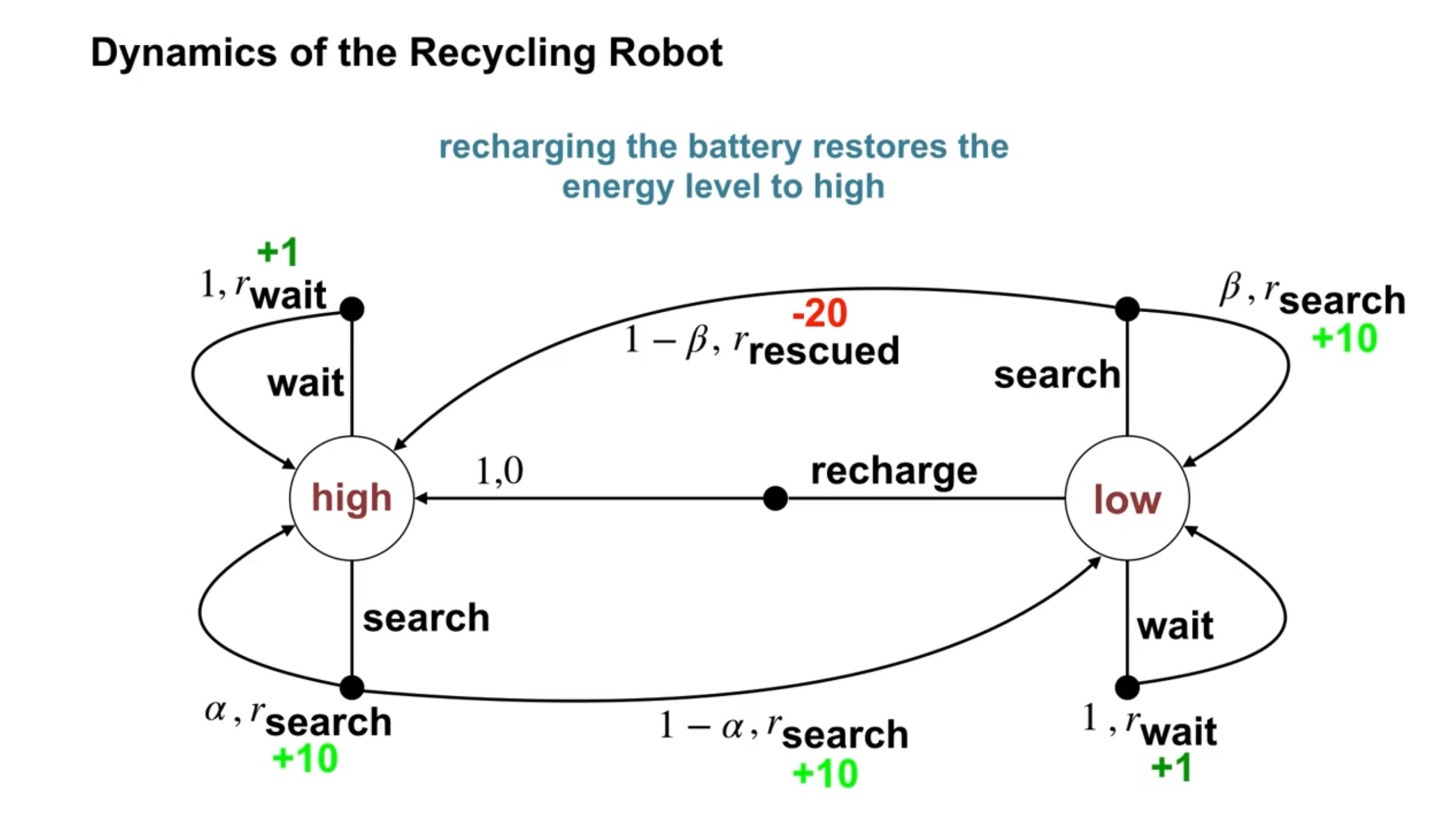
• Recycling robot은 재활용을 잘 하도록 만들어진 로봇이다.

  • 따라서 재활용을 올바르게 잘 했을 때 보상을 얻게 될 것이다.

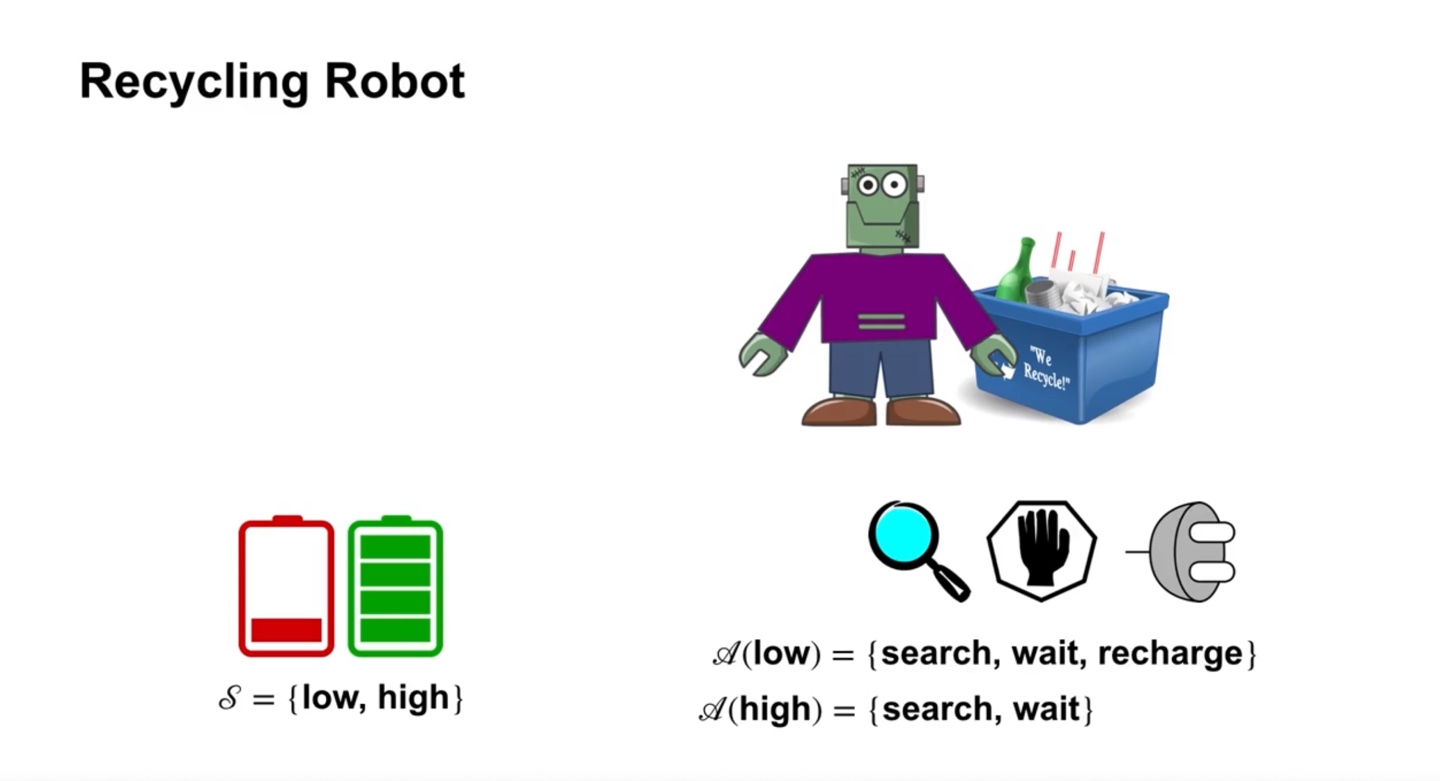
• 만일 배터리가 {low, high}의 state를 가질 수 있다고 하면, 두 상태에서의 action 선택지는 {search, wait, recharge} 세 가지다.

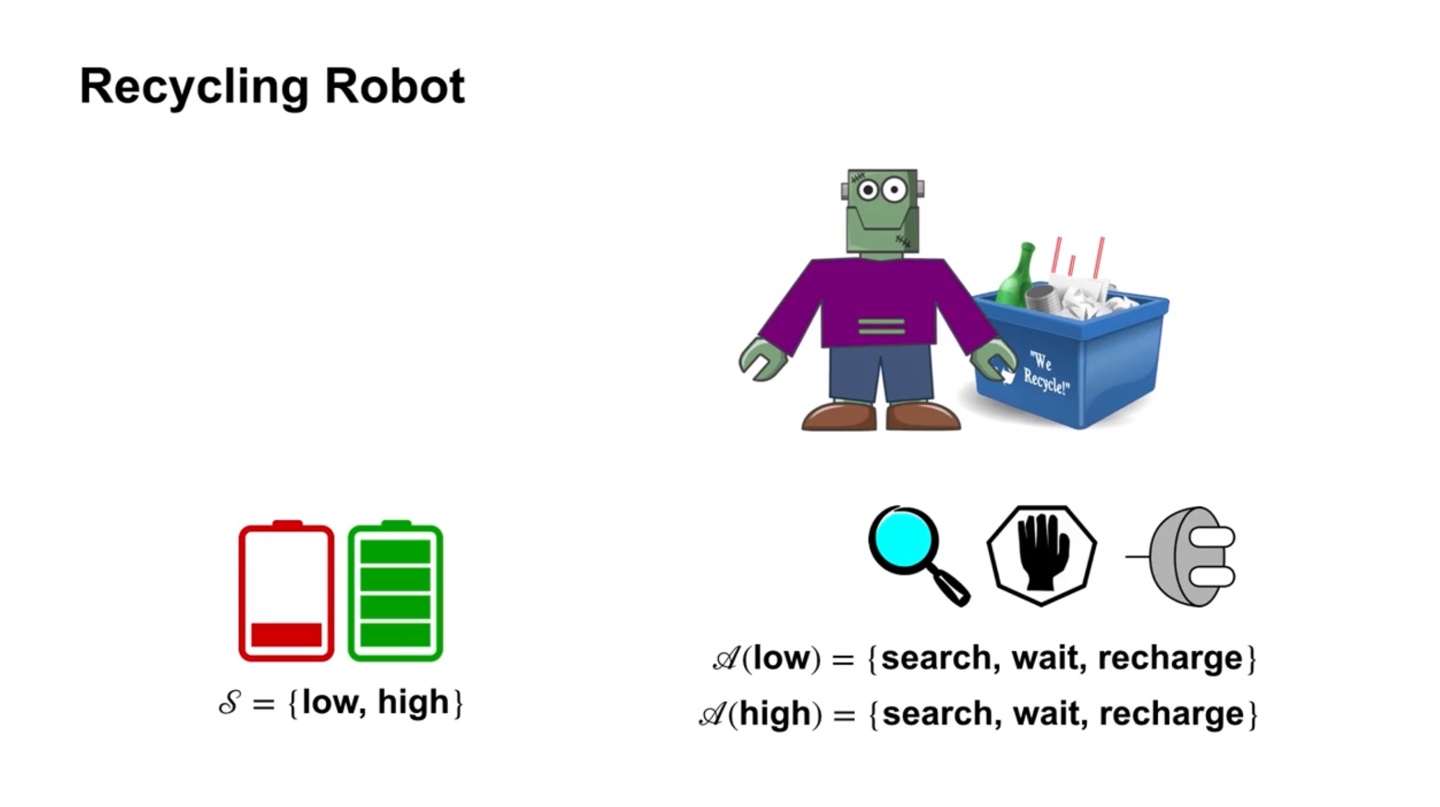
• 특히 배터리가 high인 상태에서는 recharge를 할 필요가 없으므로, {search, wait} 두 가지의 선택지로 범위가 좁혀진다.

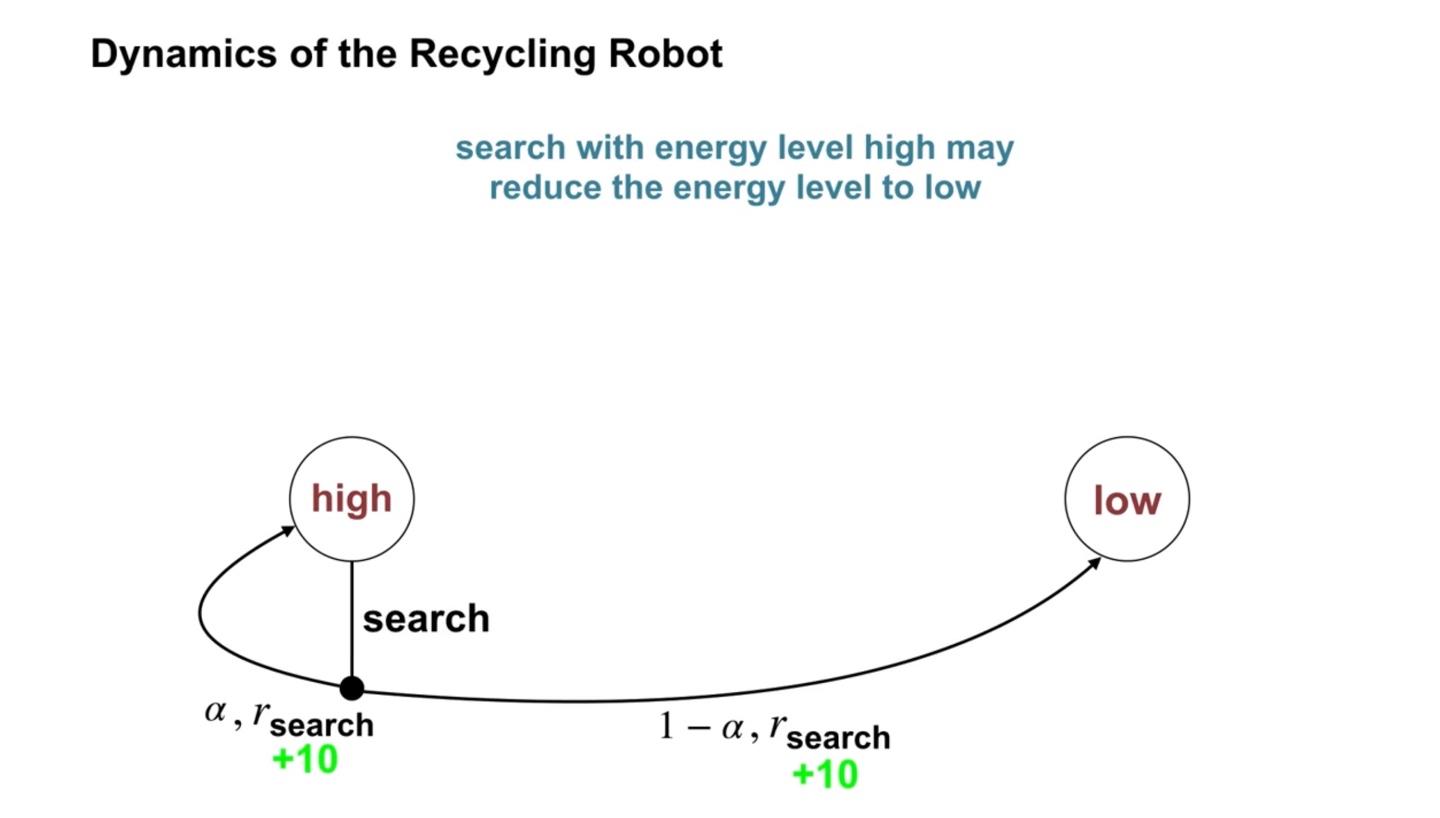
• 배터리가 high인 상태에서 출발하면 점점 배터리를 잃어 low의 상태로 흘러갈 것이다.

  • 따라서 search를 선택했을 때 $\alpha$의 확률로 계속 high, $1-\alpha$의 확률로 low의 상태로 전이(transite)하여 reward를 +10 받는다.

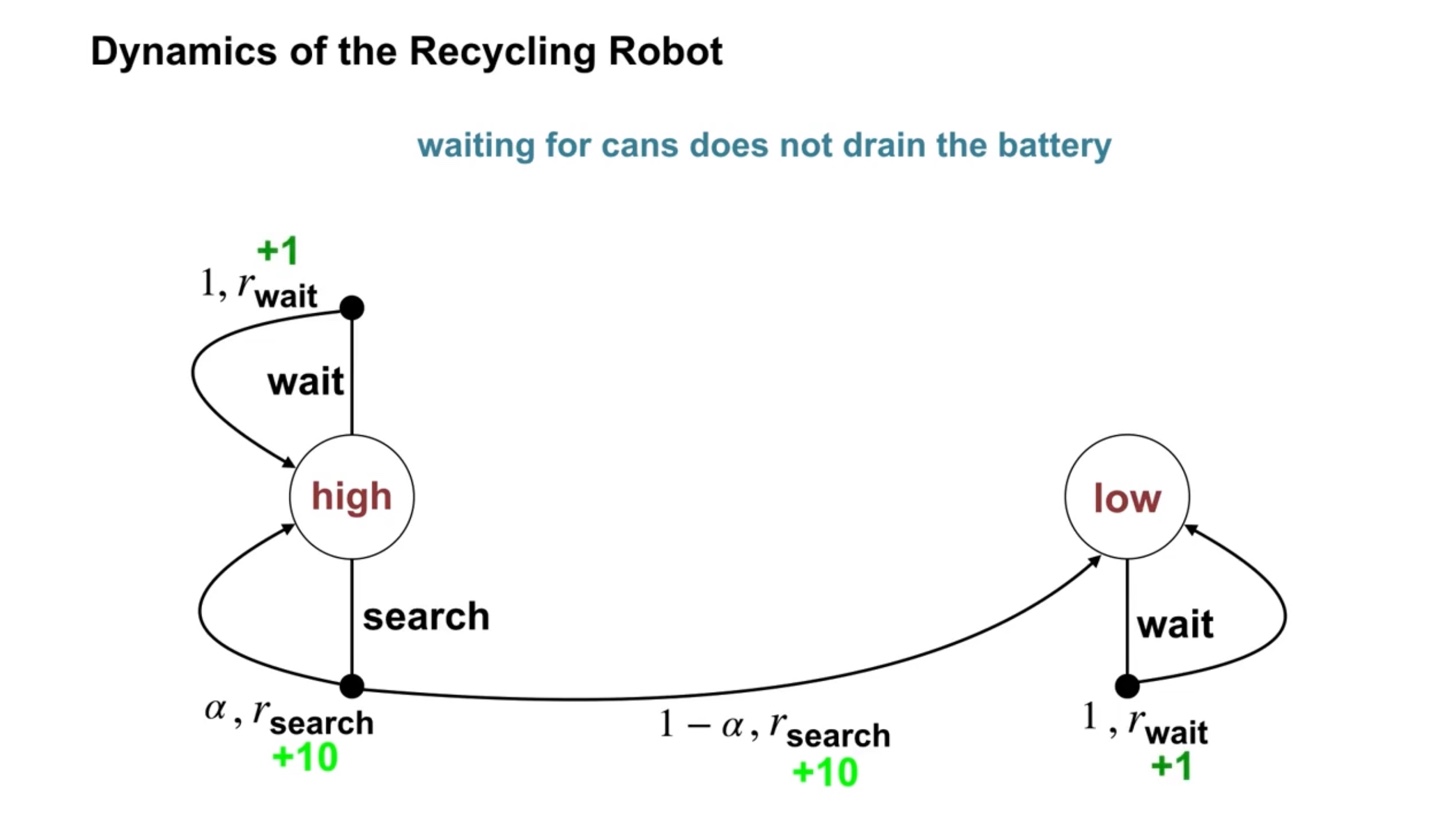
• Waiting for cans는 배터리를 많이 소모하지 않는다.

  • 따라서 $\gamma$의 확률로 wait 선택지를 고를 것이며, 이 때는 +1 reward를 받는다.

• 만일 배터리가 low인 상태에서 $1-\beta$의 확률로 배터리가 바닥나서 rescue 즉, 구조를 당한다면 -20의 reward를 받는다.

  • 이를 통해 로봇은 배터리가 low인 상태에서 무리하게 search를 향해가지 않도록 학습할 것이다.

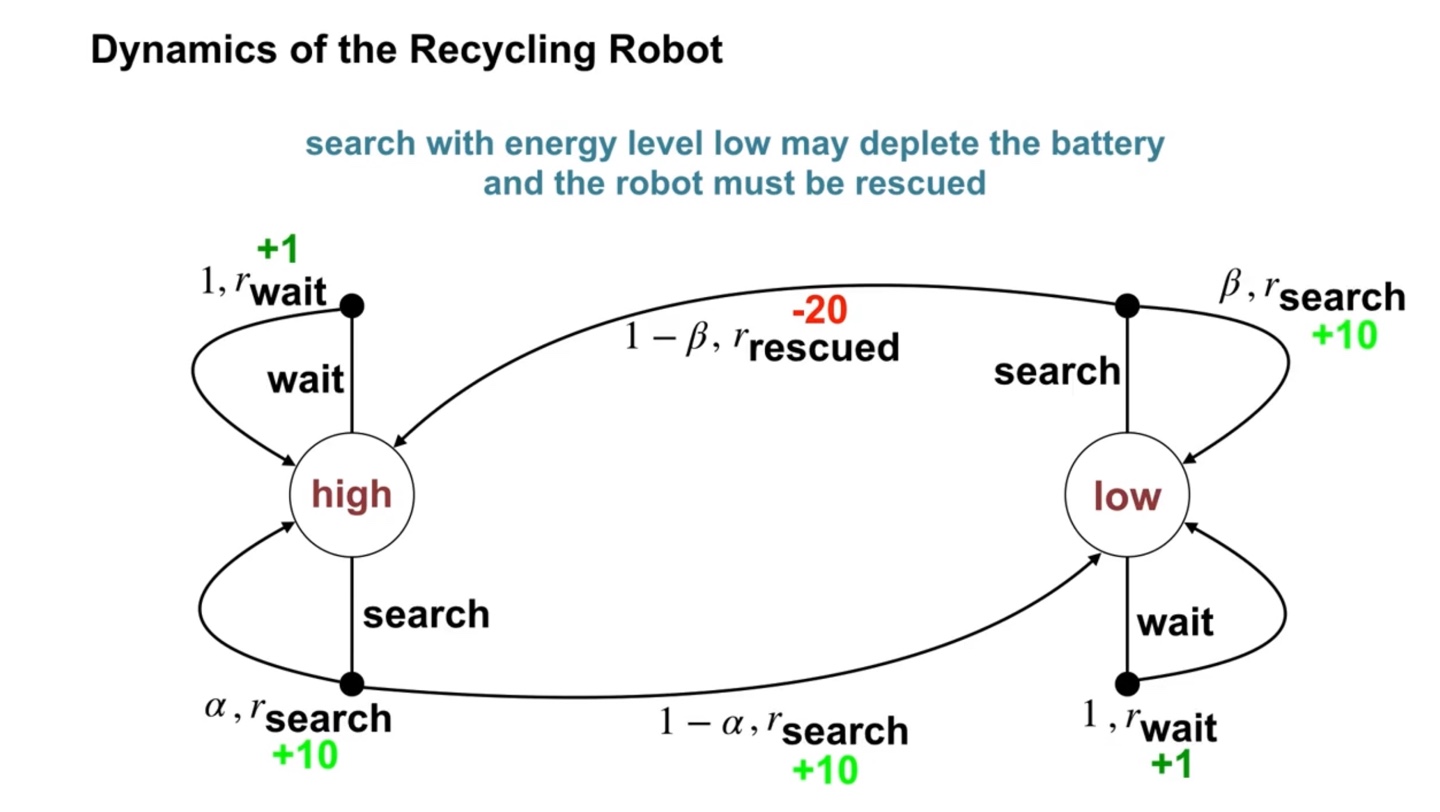
• 구조 당한다면 배터리의 상태는 다시 high를 향해간다.

• MDP formalism은 다양한 애플리케이션에 쓰일 수 있다.

• State는 영상 속 pixel의 센서 인식과 같은 낮은 수준의 상태일 수도 있고, 높은 수준의 object abstraction일 수도 있다.

• Action은 로봇의 휠 속도와 같이 낮은 수준의 동작일 수도 있고, 충전하는 것을 결정해야할 상황과 같이 높은 수준일 수도 있다.

• Time step의 interval은 1 millisecond일 수도 있고 1 month일 수도 있다.

• Pich-and-place 작업을 수행하는 robot을 만드는 상황이라 가정해보자.

  • State는 관절 각도와 속도의 측정값일 수 있다.

  • Action은 각 동작에 적용되는 전압값일 수 있다.

  • Reward는 성공적으로 옮겼을 때 +100을, 에너지 소모가 있었다면 -1을 주게 할 수도 있다.

• Summary

The Goal of Reinforcement Learning

• Reinforcement Learning의 목적(goal)은 무엇일까?

• 이번 강의를 통해서는 agent가 느끼는 goal과 reward의 의미, 그리고 episodic task에 대해서 정의 내려보자.

• Agent는 logn-term goals를 달성해야 한다.

  • Short-term에서는 최선이었던 선택지가 Long-term에서는 최선이 아닐 수 있다.

    • 토끼가 당근을 찾고 호랑이를 마주할 수 있는 상황까지 내다봐야 하는 것처럼 말이다.

• 전진하는 motion을 취하는 robot을 훈련시켜야 하는 상황이라면, 앞으로 전진할 때 reward를 건네주면 된다.

  • 그러나 당장에 놓인 reward를 maximizing 하려다 보면 robot이 넘어지는 상황이 생길 수 있다.

• Robot이 받는 reward의 합을 $G_t$로 return한다고 해보자.

  • MDP의 동작은 확률적으로 결정되기 때문에, $G_t$는 random variable이다.

• 만약 recycling robot이 적절한 곳을 search하여 재활용품을 찾아 얻었다고 하면 +3의 reward를 받을 수 있다.

  • 그런데 만약 아무것도 없는 곳을 search 해 아무런 재활용품을 찾지 못했다면 +0의 reward를 받을 것이다.

• 이처럼 상황은 다양하게 주어질 수 있고, agent가 action을 취하여 받은 모든 reward의 기댓값은 $\mathbb E[G_t]$로 표기한다.

  • 이러한 expected value를 maximize하는 것이 agent의 goal이다!

• Time step이 $R_T$로 유한하다면 전체 reward의 기댓값은 단순 합으로 표기된다.

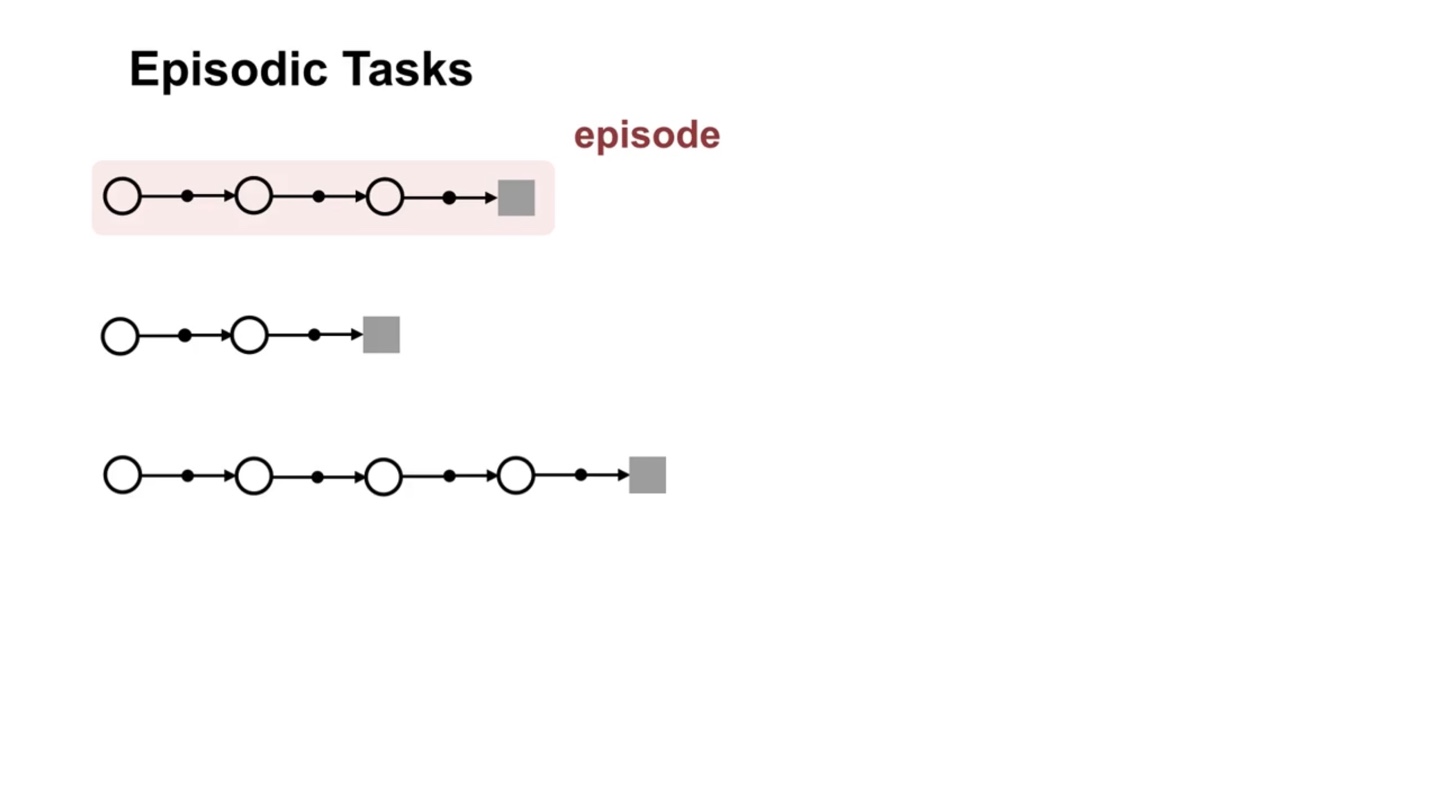
• 끝이 정해져 있는 task라면 일련의 과정이 episodic하다고 말할 수 있다.

  • 각 끝 지점에서 reward를 받아 새로운 시작으로 이어지기 때문에, 독립적인 episodic sequence의 반복일 수 있기 때문이다.

• 이를 테면 체스 게임과 같은 끝이 정해져 있는 environment라면 각 선택은 episodic task일 수 있다.

  • 한 번의 체스 게임은 하나의 episode다.

• Summary

Continuing Tasks

• Episodic tasks와 Continuing tasks와 비교해보자.

• 이번 강의에서는 continuing task를 다루는 discounting 개념에 대해 알아볼 것이다.

• Episodic task는 유한하고 끝이 존재하는(terminal) 상황에서 Reward가 단순 합으로 표현되는 상황을 말한다.

  • Continuing task는 끝이 존재하지 않는 연속적인 상황에 놓여 있을 때 reward를 어떻게 계산할지에 대한 고민으로 등장하였다.

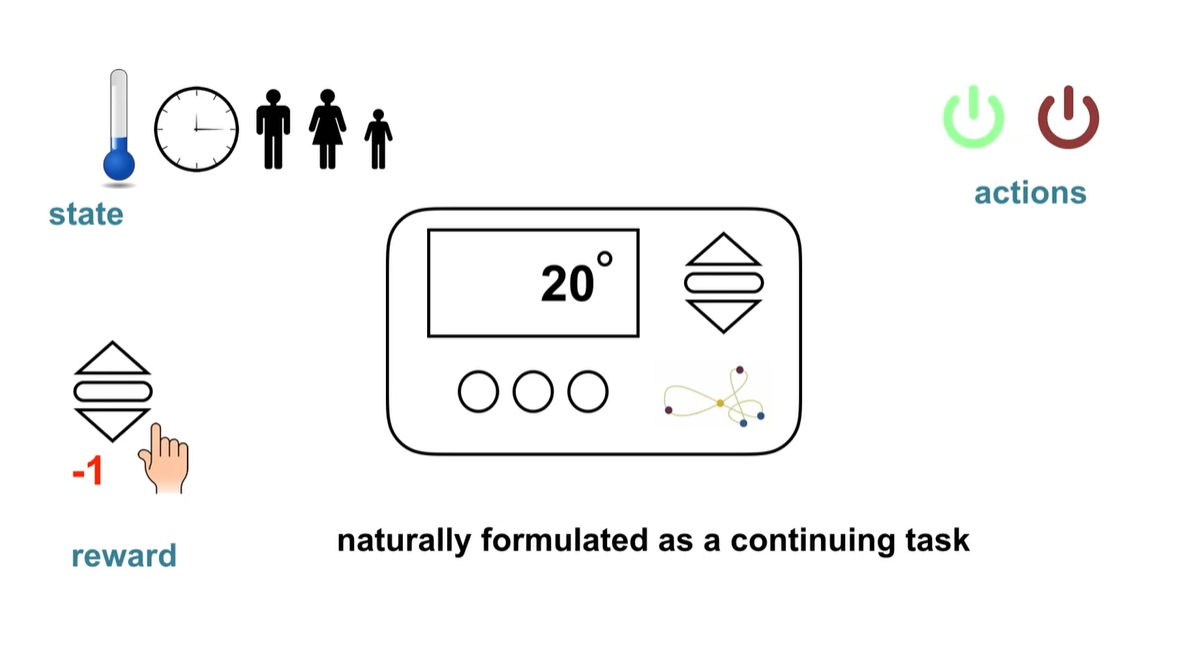
• 만약 온도를 조절해야 하는 상황이라면 State는 시간이나 사람의 수와 같은 것들을 말한다.

  • Action은 전원을 키거나 끄는 행위를 말하며, Reward는 온도를 내리면 -1을 주는 것과 같은 상황들일 것이다.

• Continuing task는 terminal이 존재하지 않는 infinite한 상황이다.

  • 무한대의 time step까지 이어지는 상황에서 reward는 어떻게 계산해야 할까?

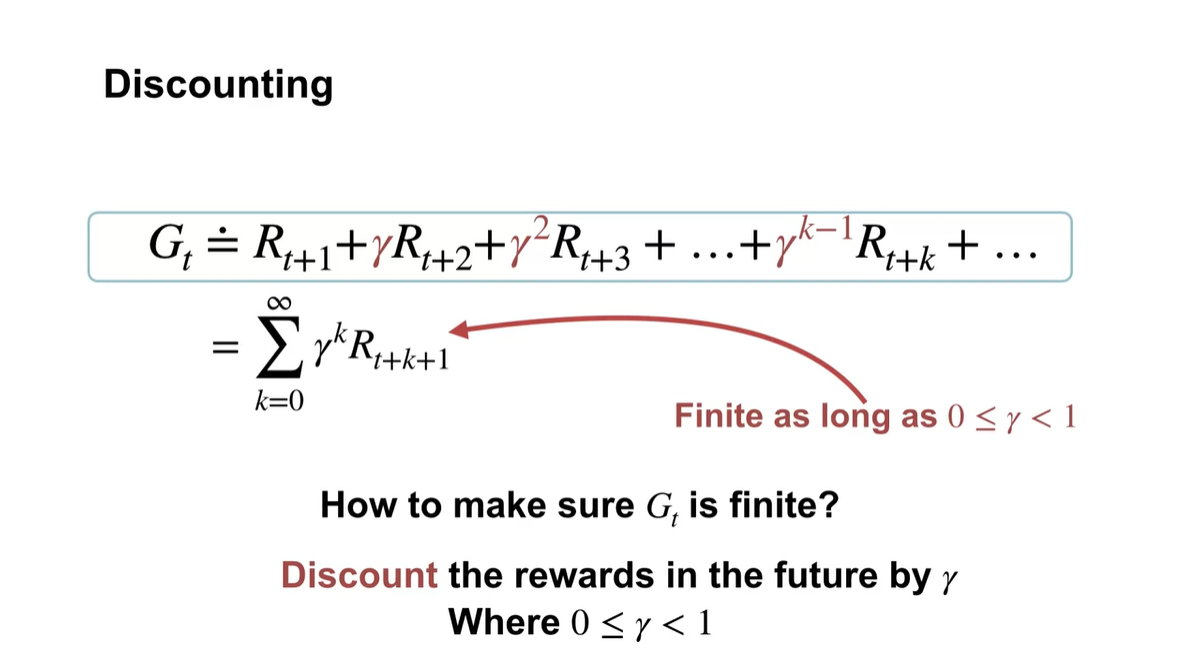
• $\gamma$라는 discounting factor를 곱함으로써 $G_t$를 finite하게 만들 수 있다.

  • $0 \le \gamma < 1$ 사이의 값을 갖는 $\gamma$를 각 time step마다 지수 곱하면 전체 reward가 급수로 표현된다.

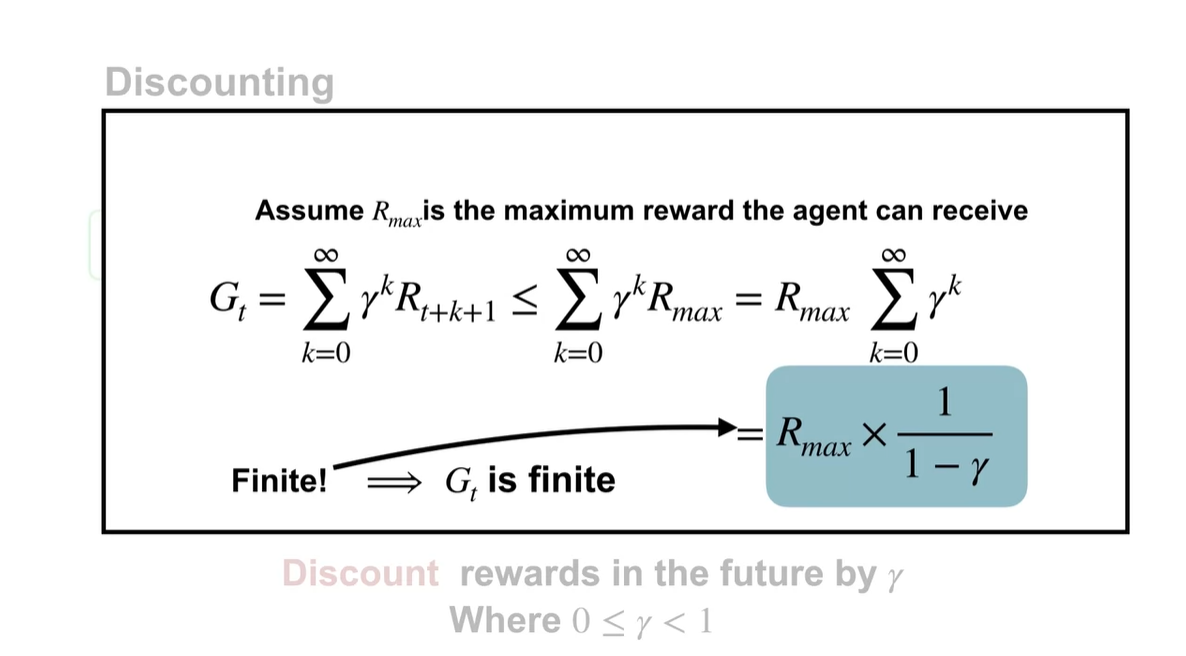
• Time step이 infinite하다면 0부터 $\infin$까지 더해지는 $\gamma$들의 합은 $\displaystyle \frac{1}{1-\gamma}$로 표기할 수 있다.

  • 즉, 무한했던 reward가 무한 급수로 인해 finite 해질 수 있다는 것이다.

• $\gamma$의 scale에 따라 agent의 행동에 영향을 미칠 수도 있다.

  • $\gamma$가 0에 가까울수록 short-term에 큰 가중치를 둔다는 얘기이며, $\gamma$가 1에 가까울수록 long-term까지 멀리 본다는 얘기가 된다.

• $\gamma$로 묶어 뒤의 reward를 다시 표기하면, 다음 step의 reward 합 $G_{t+1}$가 된다.

• 매 step의 $\gamma$ * 다음 reward($G_{t+1}$)를 reculsive하게 엮어, 전체 reward를 표현한다.

• Summary

Examples of Episodic and Continuing Tasks

• Episodic과 Continuing Tasks의 예시에 대해 알아보자.

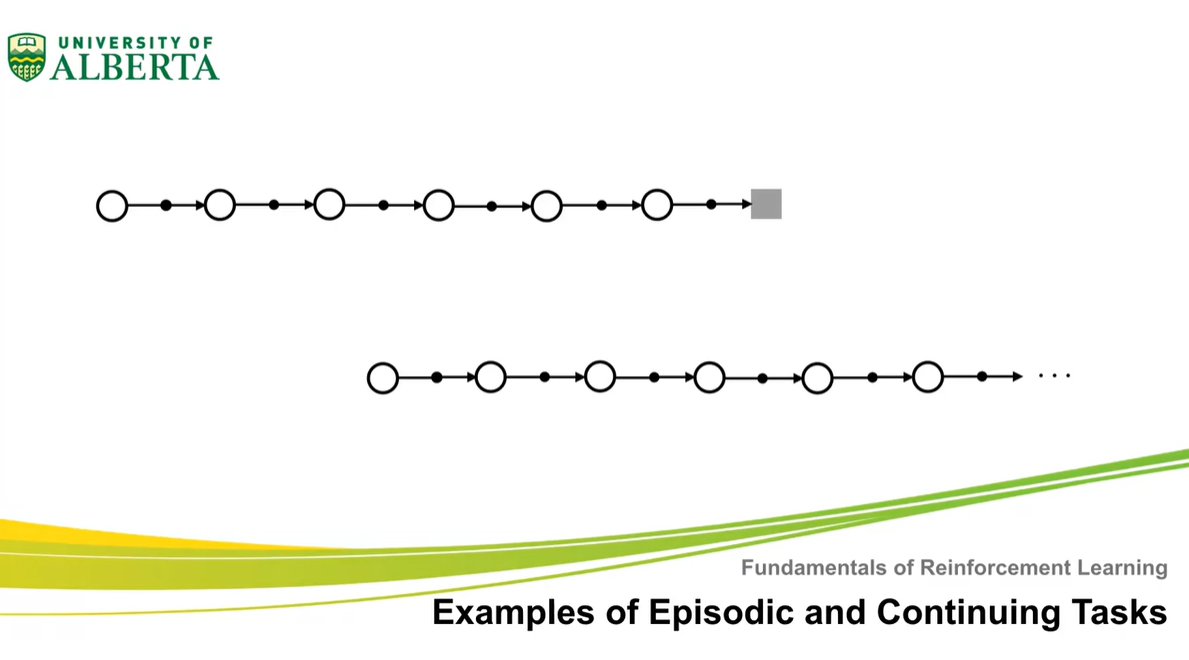
• 이번 강의에서는 episodic task의 대표적 예시와 continuing task의 대표적 예시에 대해 배운다.

• 아래와 같은 게임에서 까만 block이 하얀 block을 먹을 때 reward +1을 받는 상황은 episodic task다.

  • 까만 block의 위치는 수시로 바뀌며 매 순간 순간이 state라고 할 수 있다.

    • 이 block이 갈 수 있는 네 가지 방향은 action 선택지다.

• 컴퓨터 scheduler 예제는 continuing task다.

  • Priority를 확인하여 accept 되면 +8의 reward를, reject 되면 -4의 reward를 줌으로써 서버 process 처리를 수행하도록 하는 상황이다.

• 우선 순위에 따라 서버 process 작업을 accept/reject하는 일은 계속해서 queue 대기열에 추가하는 과정이기 때문에 중단되지 않는 task라고 할 수 있다.

• Summary

---

• 출처 : [Coursera] Reinforcement Learning Specialization